Scaling of Rain Attenuation Models: A Survey

Abstract

The scaling of rain attenuation methods is promising to quickly estimate power degradation in radio links due to rain with known findings from previous measurements. Although the frequency scaling of rain attenuation technique was introduced ages ago, it has not been addressed adequately. Furthermore, some emerging scaling techniques have recently been proposed in the literature through polarization, elevation angle, and pathlength parameters. A survey paper might play a vital role in order to comprehend all these study areas systematically. However, a survey paper on this research field is currently unavailable in the literature. This review categorizes all the research works using the inherent properties of scaling techniques. Furthermore, this study presents a comparative investigation of parameter-based scaling techniques by considering their working procedure, applicable frequency ranges, and innovative ideas incorporated with all of these models.

1. Introduction

Rain attenuation is a significant impairment in terrestrial and satellite communications wave propagation, among other environmental disturbances [1,2]. Due to the Fourth Industrial Revolution, the demand to transfer the data volume is increasing [3]. The millimeter-wave (mm-wave) frequency is a viable alternative for creating bandwidth to transfer the higher data volume [4]. However, at the same time, this mm-wave frequency is highly disturbed by rain attenuation for terrestrial or satellite communications applications [5]. As a result, accurate rain attenuation prediction requires consistent association with the link budget planning [6]. We are very familiar with rain attenuation in existing frequency bands, but there is still an opportunity to research millimeter-wave bands, although significant research has been performed. The frequency scaling technique enables precise rain attenuation prediction for another frequency band, at which the attenuation statistics is still unknown [7]. Besides, in adaptive fade mitigation measuring systems, real-time frequency attenuation scaling can be used [6]. Frequency scaling predicts attenuation values at a particular frequency using previously measured attenuation at a baseline frequency [8]. The baseline frequency attenuation is known from past investigations. The idea of frequency scaling can be expanded to other parameters of rain attenuation: polarization scaling, elevation angle scaling, and pathlength scaling, because the attenuation is a function of the pathlength, elevation angle, and frequency [9]. The polarization scaling enables us to estimate the attenuation for horizontal polarization from vertical polarization and vice versa [10]. Elevation angle scaling can help estimate the attenuation at an unknown elevation with the help of previously known attenuation at a particular elevation angle [11]. Likewise, the scaling approach of the route length may be used to assess the attenuation form of a particular microwave link with varied attenuation lengths for the link. Except for these four parameters, an additional 13 or more parameters were reported in [9]. Is it thus possible to scale rain attenuation for each of these parameters? Although the result appears intuitively reasonable, the scaling for other parameters has not yet been addressed.

Frequency attenuation scaling can be implemented with statistical scaling and instantaneous scaling techniques [12,13]. Instant frequency scaling is an attenuation of the reference frequency scaling to anticipate the attenuation in each unit period at the desired frequency [6]. Scaling of statistic frequencies allows link budgets to be determined for new systems with a fixed attenuation margin [14]. Traditional device design requires a margin to resolve the anticipated fading within a link budget. As deep fades occur several hours a year [15], cost compensation for greater transmission capacity, antenna size, or enhanced antenna capability may be acknowledged. An option to include the power margin is the use of adaptive processes such as adaptive power regulation and adaptive encoding [6]. The transmission power can be raised to compensate for the attenuation at the Earth station transmitter end. The adaptive link budget planning checks whether it is required to resolve fades, as long as the fade persisted [16]. In such a link budget plan, instantaneous scaling frequency is essential [13]. The attenuation values at the reference frequency can be employed to estimate the attenuation values at the target frequency. The significant contributions of this survey are:

• We developed a scaling rain attenuation technique taxonomy and then organized all the relevant literature according to the taxonomy;
• In this work, we developed a comparative study of the existing scaling techniques and a comparative study of these methods.

This paper’s remainder is structured as follows: Section 2 presents the taxonomy developed through different parameter-based attenuation scaling methods and different formulation basis techniques. Section 3 is associated with literature analysis and the classification of various scaling techniques of rain attenuation methods. Section 4 discusses and contrasts the state-of-the-art scaling methods, and Section 5 discusses micro- and millimeter links’ scaling research scopes and challenges. Finally, Section 6 lays forth the findings and recommendations of this survey.

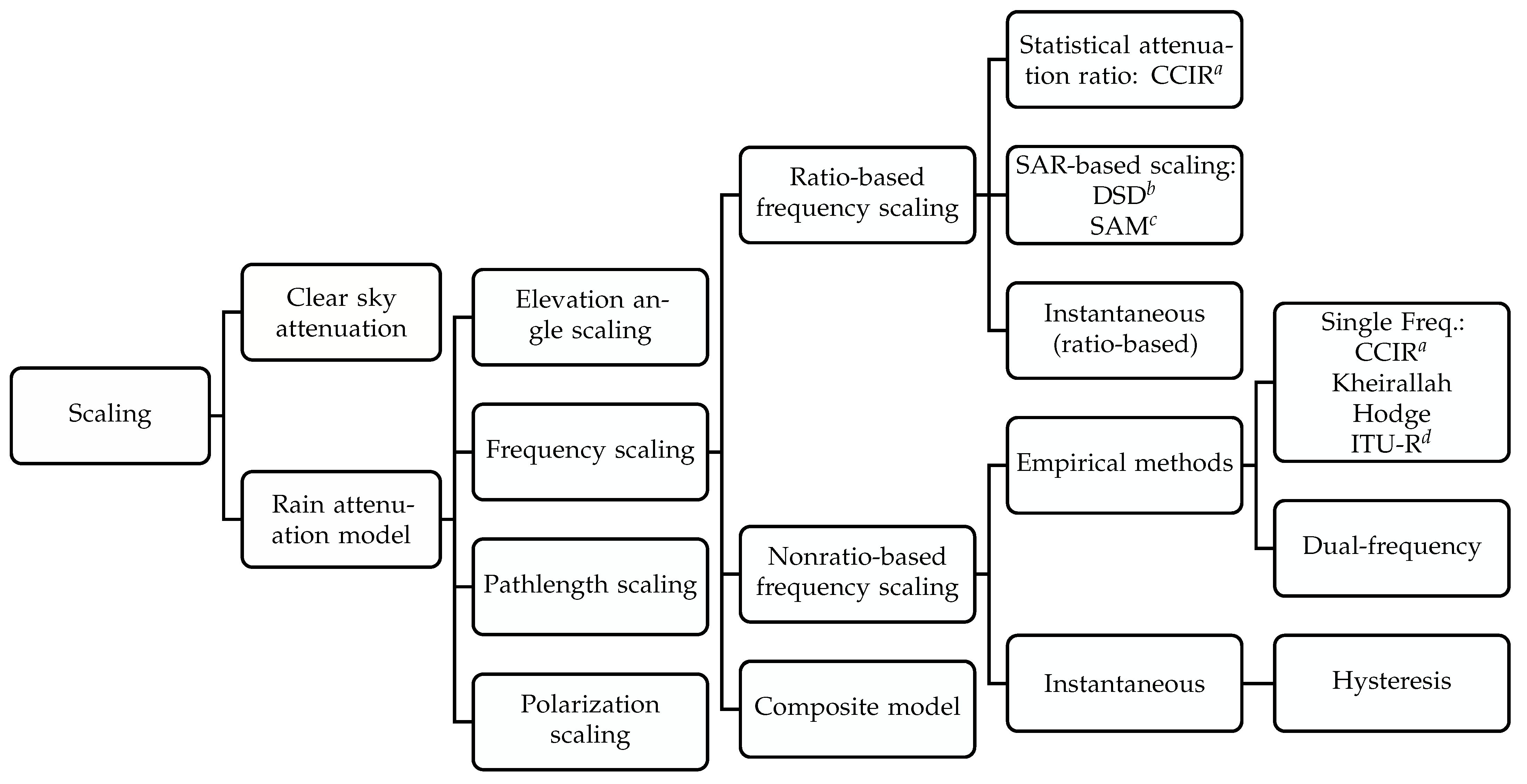
2. Taxonomy

The current approaches of rain attenuation can be categorized into scaling microwave links in clear sky conditions and the scaling of rain attenuation techniques in rainy conditions. The scaling of the rain attenuation of the radio wave link operated within several gigahertz bands can also be categorized into four types of scaling techniques currently comprehended. These are the elevation angle scaling, frequency scaling, pathlength scaling, and polarization scaling. Frequency scaling can be classified into two divisions depending on the attenuation ratio of two different frequencies and nonratio techniques. The ratio-based methods can be further divided into three kinds, and two types can be divided into nonratio-based methods, as shown in Figure 1. Frequency-based techniques may also be categorized into the statistical attenuation ratio (SAR)-based model-generated attenuation and the instantaneous approach, and the nonratio frequency-based approach can be classified into the empirical formula and instantaneous scaling schemes. In addition, the third form of frequency scaling approach known as the “composite model” is conceivable, which is based on comparing the attenuation of individual parts to the overall attenuation.

3. Existing Scaling Techniques

This section discusses the details of the rain attenuation scaling techniques as per the developed taxonomy in the earlier section.

3.1. The Clear-Sky-Based Scaling

Clear air attenuation can be calculated by subtracting the clear air reference level $S_{CA}$ from the instantaneous signal S in the dB scale. If we assume $S_{CA}$ is the signal that would be received if the propagation medium is clear air, it includes scintillation, rain, and cloud effects, but excludes gaseous absorption, and then, their relationship can be expressed as [17]:

$$A_{CA}=S-S_{CA}(dB)$$

(1)

where $A_{CA}$ follows directly from attenuation with respect to free space $A_{FS}$ by removing gaseous attenuation $(A_{GA})$; it can be written as [17]:

$$A_{CA}=A_{FS}-A_{GA}(dB)$$

(2)

This definition of $A_{CA}$ is directly applicable to most satellite system designs and can be used for the carrier-to-noise ratio ($\raisebox{1ex}{$C$}\!\left/ \!\raisebox{-1ex}{$N$}\right.$), which assumes clear air conditions; in many satellite system designs, gaseous absorption losses are included in the power budget as a loss, which is generally within $0.2\mathrm{dB}$ for $A_{CA}$ and $A_{FA}$ [17]. The nonrain frequency scaling is crucial because, most of the time (e.g., more than 95% of the time), the climate is nonrainy in temperate regions. In addition, attenuation at different frequencies occurs at different levels since it results from distinct physical processes, namely oxygen, water vapor, and clouds. This influence of oxygen, water vapor, and clouds makes it possible to estimate frequency scaling. Due to the very high air attenuation produced by oxygen absorption, the 60 GHz band is unsuitable for clear air frequency scaling (see Figure 2). Attenuation due to gases is calculated using a layer-by-layer approach of ITU-R at each atmospheric layer [18]. The liquid water level is approximated using the method of [19], through the measured data. The attenuation of the cloud is estimated with the ITU-R model [20], which is a solid physical basis for both computations of attenuation. The attenuation of the zenithal path can be computed as the total of the gas and cloud attenuation contributions, $A_g$ and $A_c$ of every atmospheric (i index) layer, as seen in (3):

$$A_L=\sum (A_g(i)+A_c(i))$$

(3)

To determine the gaseous attenuation, first, the specific attenuation of gases at each layer needs to be calculated, and later, the total number of layer thicknesses using the ITU-R technique needs to be multiplied [18]. The special attenuation, as shown in (4), comprises contributions from the oxygen and water vapor absorption layers that feature $(S_j)$ for strength and the $(F_j)$ shape factor, plus the dry continuum $N_D{}^{″}(f)$ [21].

$${\gamma }_g=0.1820f·\left[\sum _j{S}_j{F}_j+N_D^{″}(f)\right](\mathrm{dB}/\mathrm{km})$$

(4)

Cloud attenuation can be calculated by the exact attenuation and thickness of the layer as specified in (5), and the specific attenuation in the cloud layer can be computed by the ITU-R [20] technique. The complete computation procedure is shown in Algorithm 1.

$$A_c(i)={\gamma }_c(i)·\Delta h(i)$$

(5)

Algorithm 1: Clear sky frequency scaling [21].

Data: Radiosounding data Temperature $T(i)$ in $\mathrm{C}$, pressure $P(i)$ in $\mathrm{hPa}$, and

relative humidity $RH(i)$ in % at different layer heights $h(i)$ in m.

// Due to gas, fog, and cloud

1 Compute specific gas attenuation /* Equation (4) */

2 Compute liquid water content by the [19] method

3 Compute cloud attenuation by the ITU-R [20]

4 Compute gas attenuation for a layer $△h$

5 Compute cloud attenuation for a layer $△h$

6 Compute total attenuation /* Equation (3) */

// In nonrainy conditions

7 Compute $A_L$ /* Equation (3) */

8 Compute frequency-scaled attenuation $A_H$ /* Equation (6) */

The frequency scaling formula for each propagation can be appropriately calculated, depending on the physical model. A first-degree global polynomial in the form of (6) can be used to compute the frequency scaling:

$$A_H=c_0+c_1·A_L$$

(6)

where $c_1$ and $c_0$ are the coefficients determined empirically at different frequency bands.

3.2. Elevation Angle Scaling

If ${\theta }_1$ and ${\theta }_2$ are elevation angles and $A({\theta }_1)$, $A({\theta }_2)$ are the attenuations due to rain attenuation, then for a settled operating frequency, the attenuation scales with the elevation angle, which can be analytically written as:

$$A({\theta }_1)sin{\theta }_1=A({\theta }_2)sin{\theta }_2$$

(7)

The implementation of (7) can be performed through various means such as power-law-based techniques, cosecant-rule-based techniques, and synthetic time-series-based techniques. All these different implementation techniques are briefly explained below:

I.

Power-law based technique:

Elevation angle scaling is defined as the ratio of rain attenuation at the zenith and the slant paths ($\theta$ from $1^{\circ }$ to ${89}^{\circ }$) in [11]. The following simple formulation presents a competent model as the scaling factor $SF(\theta )$:

$$SF(\theta )=1.741{\theta }^{-0.6015}+0.8931$$

(8)

It was shown in [11] that this method can predict slant link attenuation at a satisfactory level of accuracy from $5^{\circ }\le \theta \le {90}^{\circ }$. According to the CCIR model [23], it is noteworthy that the elevation angle scaling is defined for $\theta >{10}^{\circ }$;

II.

Cosecant-rule-based technique [11]:

The scaling factor ($SF[P,\theta ]$) is defined as the proportion of the attenuation across $\theta$ and the one anticipated from the zenith path using the simple cosecant law:

$$SF(P,\theta )=MM{A}_{dB}(P,\theta )/csc(\theta )A_{dB}(P,{90}^{\circ })$$

(9)

The scaling factor $SF$ can be calculated as the approximated fourth-order polynomial as:

$$SF(p,\theta )={\alpha }_1(\theta )P^3+{\alpha }_2(\theta )P^2+{\alpha }_3(\theta )P+{\alpha }_4(\theta )$$

(10)

where ${\alpha }_1,{\alpha }_2,{\alpha }_3$, and ${\alpha }_4$ are the coefficients of (10);

III.

Time-series-based technique:

There is a strong impact of the elevation angle on the design of telecommunication facilities, particularly the low Earth orbit (LEO) satellites. At a low elevation angle for the LEO satellite, if a single rain cell intercepts the propagated signal from the Earth station antenna, it is possible to scale the elevation angle with the rainy time series generation technique [24] as per (11).

$$F=\left[\raisebox{1ex}{$(h_r-h_a)$}\!\left/ \!\raisebox{-1ex}{$(h_{r,1}-h_{a,1})$}\right.\right]·\left[\raisebox{1ex}{$sin({\theta }_1)$}\!\left/ \!\raisebox{-1ex}{$sin({\theta }_2)$}\right.\right]·{(\raisebox{1ex}{$f_2$}\!\left/ \!\raisebox{-1ex}{$f_1$}\right.)}^{1.72}$$

(11)

where the subscripts “1” and “2” are used for the base (reference) measured and operating (target) datasets. Here, the rain height and the antenna height are, respectively, $h_r(\mathrm{km})$ and $h_a(\mathrm{km})$, and both are with reference to the sea level, $\theta$ is the elevation angle, and f is the frequency in GHz. However, if multiple rain cells exist, it is impossible to scale the attenuation, and (11) will not be valid. It is assumed that by picking a collection of episodes from the ITALSAT database and scaling it to the factor indicated in (11), it is possible to recreate rain reduction statistics at a different frequency, height, and elevation for any other location. This technique needs several data processing steps, and among these steps, the most important things to check are: the original elevation angle needs to be mapped (e.g., from $37.7^{\circ }$ to ${107}^{\circ }$); 20 terms are then expanded to result in a database to investigate whether there exist multiple rain cells (as in the case of multiple rain cells, the assumption made by (11) will not be valid). In [25], the effect of rain attenuation on the elevation angle was assessed using the synthetic storm approach to create rain attenuation time series. The study showed that if the elevation angle decreases to ${20}^{\circ }$, the impact of rain attenuation increases significantly, and at higher elevation angles (i.e., ${40}^{\circ }$ to ${80}^{\circ }$), the influence of rain attenuation is negligible. Such results are closely related to the value of the effective pathlength. These preliminary results suggest that using a prediction model for low elevation angle application systems such as the LEO satellite should consider the significant impact of rain attenuation, particularly in the heavy rain region.

3.3. Frequency Scaling

The advantage of rain attenuation would have happened if the transmission of different frequencies had gone through the same storm. It is helpful to determine the amount of rain attenuation that will occur at a given frequency. For example, it is helpful to have experimental scale data available at one frequency to predict the device output at another frequency. The application of frequency scaling can be beneficial in determining predicted attenuation in a dual-frequency use of satellite communication or even in predicting attenuation at different frequencies [8,26].

3.3.1. Frequency-Ratio-Based Scaling

Several formulations have been proposed to scale long-term attenuation statistics, each with applications and limitations [12,27]. Most of these relations are intended for scaling attenuation statistics (that is, for calculating SAR), not for instantaneous (real-time) scaling of attenuation:

I.

SAR-based method:

Instead, in real-time applications, the frequency scaling principle has been proposed to provide static scaling attenuation. Most of the statistical scaling methods consider only frequency as the parameter. The SAR method considers the percent of time exceeded with a rain rate. The statistical attenuation due to clear air is required to be calculated similar to (1). A significant disadvantage of such a model is that these apply only to the same pair of frequencies, for which the related coefficients are determined through the investigated datasets. Electromagnetic propagation becomes disturbed by many environmental factors such as gases, raindrops, water vapor, and similar factors. Many researchers tried to establish empirical relationships of a satellite link for two channels by approximating the ratio $\raisebox{1ex}{$f_2$}\!\left/ \!\raisebox{-1ex}{$f_1$}\right.$ ($f_2$, $f_1$ is used to mean $f_2>f_1$) for different GHz frequency bands. The most straightforward approach to present the SAR through mathematical means is [28]:

$$SAR=\raisebox{1ex}{$A(f_2)$}\!\left/ \!\raisebox{-1ex}{$A(f_1)$}\right.={(\raisebox{1ex}{$f_2$}\!\left/ \!\raisebox{-1ex}{$f_1$}\right.)}^n$$

(12)

The SAR-based method implementation was proposed in [12] as:

$$SA{R}_{CCIR}=\raisebox{1ex}{$A(f_2)$}\!\left/ \!\raisebox{-1ex}{$A(f_1)$}\right.=\raisebox{1ex}{$\mathsf{\Phi }(f_2)$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\Phi }(f_1)$}\right.$$

(13)

$$\mathsf{\Phi }(f)=\raisebox{1ex}{$f^{1.72}$}\!\left/ \!\raisebox{-1ex}{$(1+3\times {10}^{-7}{f}^{3.44})$}\right.$$

(14)

where $A(f_2)$ and $A(f_1)$ are the attenuations in $\mathrm{dB}$ at frequencies $f_2$ ($\mathrm{GHz}$) and $f_1$ ($\mathrm{GHz}$), respectively;

II.

SAR from models:

These categorized models do not include an explicit dependence on frequency, but stem from attenuation models. These attenuation models yield attenuation values that can form a ratio to predict SAR for a given pair of frequencies.

$$SAR(f_1,f_2,p)=\raisebox{1ex}{$SACA(f_2,p)$}\!\left/ \!\raisebox{-1ex}{$SACA(f_1,p)$}\right.$$

(15)

where SACA is the statistical attenuation in reference to clear air; p is the percent of time exceedance of the occurring rain event for a considered pair of frequencies $f_1$ and $f_2$;

(a)

DSD-based path-averaged rain rate:

The rain attenuation is significantly influenced by the distribution of the raindrop size rather than the rain rate. The size of raindrops varies in a single rain event. Therefore, the chance of scattering, refraction, or absorption varies greatly. For this reason, the analytical raindrop-based attenuation technique has good accuracy compared to the rain-rate-based model. The specific attenuation is calculated from the rain rate, and the raindrop size impacts the specific attenuation [29]. Different types of statistical and physical raindrop size distribution models were presented in [30,31]. Based on the experimental measurements, an exponential distribution was used to represent the DSD in [32]:

$$N(D)=N_0·exp(-\mathsf{\Gamma }D)$$

(16)

where $N_0=8000$ is a constant proposed in [33] and $\mathsf{\Gamma }$ is a coefficient parameter in millimeters depending on the rainfall rate ($\mathsf{\Gamma }=4.1R$ where R is the rainfall rate measured in $mm/h$). The DSD can also be used to calculate a path-averaged rain rate; $R(z)$ is a function of distance in the horizontal direction; z is related to $N(D,z)$; $v(D)$ is the raindrop falling velocity; the diameter of the raindrop is D as in [34]. The path-averaged rain rate can be defined as:

$$\overline{R}={\int }_0^{D_m}\raisebox{1ex}{$4\pi $}\!\left/ \!\raisebox{-1ex}{$3$}\right.{(\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}^{3}v(D)\overline{N}(D)dD$$

(17)

The DSD-derived attenuation values can be used to produce a ratio, yielding a $SAR$ model, as follows:

$$SA{R}_{DSD}=\raisebox{1ex}{$A_{DSD}(f_2)$}\!\left/ \!\raisebox{-1ex}{$A_{DSD}(f_1)$}\right.$$

(18)

The problem with this approach of frequency scaling is that it needs a sophisticated device to record the drop size, and most rain attenuation-related datasets do not include the DSD-based information;

(b)

DSD-based specific attenuation ratio:

The specific attenuation ($\gamma (\mathrm{dB}/\mathrm{km})$) is given by the following integral equation [35]:

$$\gamma =4.343\times {10}^3\underset{0}{\overset{D_{max}}{\int }}{\sigma }_t(D).N(D)dD$$

(19)

where ${\sigma }_t$ is the total cross-section for a spherical raindrop, $N(D)dD$ is the number density of raindrops with an equivalent radius in the interval $dD$, $N(D)$ represents raindrop size distribution, and $D_{max}$ is the maximum mean raindrop radius. The integral equation can be changed to summation for numerical calculation as in [36,37]:

$$\gamma (f)=4.343\times \left({10}^3\raisebox{1ex}{${\lambda }^2$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.\right)\sum _{p=1}^P{\sigma }_t(p\Delta D)N(p\Delta D)\Delta D$$

(20)

where $\Delta D$ is the incremental radius, P is the integer number of $\raisebox{1ex}{$D_{max}$}\!\left/ \!\raisebox{-1ex}{$\Delta D$}\right.$, and $\lambda$ is the wavelength corresponding to the frequency f. The specific attenuation factor can be defined for the frequency $f_1$ (GHz) and $f_2$ (GHz) as ${\gamma }_{f_1}$ and ${\gamma }_{f_2}$, respectively. Now, the ratio of these two specific attenuations can be calculated as:

$${SAR}_{f_1{f}_2}=\raisebox{1ex}{${\gamma }_{f_1}$}\!\left/ \!\raisebox{-1ex}{${\gamma }_{f_2}$}\right.$$

(21)

where the notation ${SAR}_{f_1{f}_2}$ is constant. Thus, the constant $SA{R}_{f_1{f}_2}$ and the specific attenuation of a baseline link can be used to estimate a target links’ attenuation. There is a popular application of the specific attenuation to predict the attenuation of a satellites’ downlink channel using the specific attenuation of the uplink channel;

(c)

The use of the spatial rain rate profile [38]:

A real-time method for frequency scaling that was demonstrated in [13] has addressed the spatial rain distribution by adopting the exponential rain cell distribution known as the SAM, as in [38]. The fundamental concept is to provide the geographical rain rate profile for the rainfall rates, where the rain rate can be recorded. The SAM considers the rainfall rate’s spatial profile as exponential and varies as:

$$R(t,h)=\{\begin{array}{cc}\hfill \left[l\right]R_0(t),& \mathrm{for}{R}_0\le 10\mathrm{mm}/\mathrm{h}\\ \hfill R_0(t)exp[-\gamma ln(\raisebox{1ex}{$R_0$}\!\left/ \!\raisebox{-1ex}{$10$}\right.)h],& \mathrm{for}{R}_0>10\mathrm{mm}/\mathrm{h}\end{array}$$

(22)

where $R(t,h)$ is the rain rate at a range of h (the projection of the slant link up to the rainy region) from the receiver at any time and $R_0(t)$ is the point rain rate at the receiver located at the corresponding time. Frequency scaling has to do with the variation of the propagation effects as a function of frequency. The concept of frequency scaling was proposed to yield the scaling attenuation statics instead of real-time applications;

III.

Instantaneous (ratio-based):

The instantaneous scaling technique is defined as the ratio of clear air attenuation $(A_{CA})$ at a high and low frequency, respectively. In the experiment [6], additional parameter time was considered representing the sample timings in (1). Usually, the rain attenuation value given by (1) is noisy, so a moving average filter is used to smooth the samples where the window duration is 30 s [6]. However, a larger window duration of 60 s was reported in [39]. However, the downside of the proposed method is that the applicable frequency range is short in the range of 20–30 GHz, where the scaling method is given by:

$$A=(k{R}^{\alpha })\left[\raisebox{1ex}{$1-exp(-{\gamma }^{\prime }\alpha h_{r}csc\theta )$}\!\left/ \!\raisebox{-1ex}{${(\gamma }^{\prime }\alpha )$}\right.\right]$$

(23)

where ${\gamma }^{\prime }$ denotes the specific attenuation coefficient whose value can be determined with the help of the nonlinear least squares approach. The unique feature of this model is that it is a good candidate for real-time applications based on spatial variation through the specific attenuation index. The main challenge in frequency scaling is the nonuniform rain rate distribution and the nonuniformity of the DSD of the rain along its path. The distribution of the frequency scaling factors in the K and Q bands was examined with the rain rate, and the DSD measurement results in [14]. However, it was not easy to compare these two results due to the unavailability of the rain rate distribution and the DSD of the rain information along the entire path. To determine the short-term scaling, moving and block average and sampling techniques were used, and it was recommended to limit this instantaneous time within 5 min [40].

3.3.2. Nonratio-Based Frequency Scaling

In the nonratio-based scaling rule formulation, the scaling rule is not formed through a ratio-based rule; instead, the relationship is represented through an empirical formula that conveys the relation of the physical influence of scaling. The nonratio-based models can be classified into an empirical formula and instantaneous-based method, briefly discussed below:

I.

Empirical formula-based scaling method:

The link between the upper and base frequency attenuation cannot be represented in a precise ratio form in a nonratio model. Nonratio models do not predict SAR, but quantify the relationship between $A_{f_1}$ and $A_{f_2}$ through empirical relationships;

(a)

Single frequency:

The frequency scaling ratio can be implemented on the level of the attenuation of the primary frequency as explained in [41]. The primary frequency-level-based attenuation can be defined as [42]:

$$A_2=4k_2{\left[\raisebox{1ex}{$A_1$}\!\left/ \!\raisebox{-1ex}{$4k_1$}\right.\right]}^{\raisebox{1ex}{${\alpha }_2$}\!\left/ \!\raisebox{-1ex}{${\alpha }_1$}\right.}$$

(24)

where k and $\alpha$ are constants that depend on the frequency and drop size distribution and $A_1$, $A_2$ are the attenuations corresponding to the frequencies $f_1$ (GHz) and $f_2$ (GHz). In (24), the considered pathlength was developed at about 4 km, and this scaling formula can be used at the frequency of 60 GHz. The drawback of this technique is that it needs the coefficients k and $\alpha$ derived through the frequency and the DSD. This procedure was simplified in [27], and through the empirical formula, ITU-R (25) can be adopted. The polynomial-based frequency scaling technique was proposed in [43,44];

i.

ITU-R model:

ITU-R has adopted a model to predict frequency scaling as [45]:

$$A_2=A_1{({\mathsf{\Phi }}_2/{\mathsf{\Phi }}_1)}^{1-H({\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,A_1)}$$

(25)

where the values of $\mathsf{\Phi }(f)$ and $H({\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,A_1)$ are given by:

$$\begin{array}{c}\mathsf{\Phi }(f)=f^2/(1+{10}^{-4}{f}^2)\end{array}$$

(26)

$$\begin{array}{c}H({\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,A_1)=1.12{({\mathsf{\Phi }}_2/{\mathsf{\Phi }}_1)}^{0.5}{({\mathsf{\Phi }}_1{A}_1)}^{0.55}\end{array}$$

(27)

The applicable frequency of this model [45] is limited to 7–55 GHz;

ii.

Use of the specific attenuation relation:

Using the power-law-based specific attenuation relationship, we can write:

$$A(p\%)=k{R}^{\alpha }(p_{\%})l(p_{\%})$$

(28)

where $p_{\%}$ is the percentage of time exceedance, A is the attenuation, R is the point rain rate with $p_{\%}$ percentage of time exceedance and l is the corresponding effective path length.

The scaling relationship assumes that both frequencies are coincidental (that is, seen along the same path, i.e., we presume that R and l are the same).

$$A_2\approx k_2{(A_1/k_1)}^{{\alpha }_2/{\alpha }_1};$$

(29)

iii.

Rain rate depending on a Gaussian distribution:

In [46], it was assumed that the point rain rate along the propagation path could be expressed as a Gaussian function of position. Therefore, the instantaneous attenuation can be formulated as:

$$A={\int }_0^{L}kR(x)dx\mathrm{where}R(x)=R_{o}exp\left[-{(x/l_0)}^2\right]$$

(30)

$R_0$ is the peak rain rate along the path L. The distance $\mathrm{x}$ is measured from the position of maximum rain rate intensity, and $l_0>>L$ is a measure of the cellular rain structure. Under these conditions, the attenuation ratio for frequencies $f_1$ and $f_2$ was given by [46] as follows:

$$\raisebox{1ex}{$A_2$}\!\left/ \!\raisebox{-1ex}{$A_1$}\right.=\raisebox{1ex}{$k_2$}\!\left/ \!\raisebox{-1ex}{$k_1$}\right.\sqrt{\raisebox{1ex}{${\alpha }_1$}\!\left/ \!\raisebox{-1ex}{${\alpha }_2$}\right.}{\left[\raisebox{1ex}{$A_1$}\!\left/ \!\raisebox{-1ex}{$k_1$}\right.\sqrt{\raisebox{1ex}{${\alpha }_1$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.}\right]}^{(\raisebox{1ex}{${\alpha }_2$}\!\left/ \!\raisebox{-1ex}{${\alpha }_1$}\right.-1)}$$

(31)

where ${\alpha }_1,k_1,{\alpha }_2$, and $k_2$ are parameters associated with frequencies $f_1$ and $f_2$, respectively. This method does not establish a strict ratio relationship because $A_2/A_1$ is a function of $A_1$;

(b)

Dual-frequency:

Two frequency scaling models can usually be either linear or nonlinear. The ratio of attenuation at two frequencies is used in the majority of the two frequency models. Considering the same case as for linear-equation-based estimation, the estimated attenuation is formed in a different way as in [47]:

$${\widehat{A}}_3=k_3{\left[\raisebox{1ex}{$A_1$}\!\left/ \!\raisebox{-1ex}{$k_1$}\right.\right]}^{(\raisebox{1ex}{${\alpha }_3-{\alpha }_2$}\!\left/ \!\raisebox{-1ex}{${\alpha }_1-{\alpha }_2$}\right.)}{\left[\raisebox{1ex}{$A_2$}\!\left/ \!\raisebox{-1ex}{$k_2$}\right.\right]}^{(\raisebox{1ex}{${\alpha }_1-{\alpha }_3$}\!\left/ \!\raisebox{-1ex}{${\alpha }_1-{\alpha }_2$}\right.)}(dB)$$

(32)

where $k_i$ and ${\alpha }_i$ are the parameters related to the frequencies $f_i$, and it was assumed that the pathlengths in the considered links could be approximated to be the same in a condition where the Earth antennas’ station elevation angle was the same for synchronized satellite links;

II.

Instantaneous:

The instantaneous rain attenuation is performed using the spatial rain rate distribution developed through the SAM rain rate distribution. The hysteresis attenuation behavior is noticed between different frequency bands, especially the downlink and uplink operating frequency of the satellite microwave link from the Earth station facility. The rain attenuation at two frequencies shows a hysteresis behavior, which was revealed in [41,48]. Moreover, the impact of the hysteresis for less severe episodes was not seen (such as widespread stratiform rain where the peak attenuation is not exceeded). In [49], it was noticed that the isopleths of the attenuation of a pair of frequencies tend to follow medium-to-high attenuation levels, such that the attenuation process can be viewed as jointly log-normal (a log-normal model to describe the statistical behavior of rain attenuation). Consequently, the mean, standard deviation, and covariance parameters of the two frequencies were determined using the cumulative distribution function of the rain attenuation graph (Gauss integral/log). The resulted covariance parameter indicates the correlation of the frequencies. The authors recommended a modified statistical parameter “standard deviation” to control uplink power through a modification as:

$$A_2=A_1{\left[\raisebox{1ex}{$f_2$}\!\left/ \!\raisebox{-1ex}{$f_1$}\right.\right]}^{1.72}·\exp \left[\Delta a(\xi )\right]$$

(33)

where $\Delta a$ is a log-normal variable with zero mean ($\mu =0$) and standard deviation (STD) ${\sigma }_{\mathrm{depend}}$; ${\sigma }_{\mathrm{depend}}$ is the STD of a links’ attenuation depending on any other radio links. The STD for the independent case be written as ${\sigma }_{\mathrm{independ}}$. These two STD can be related to the reduction coefficient ($\xi$) as [50]:

$$\xi =\raisebox{1ex}{${\sigma }_{\mathrm{depend}}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_{\mathrm{independ}}$}\right.=0.3548{(\raisebox{1ex}{$f_2$}\!\left/ \!\raisebox{-1ex}{$f_1$}\right.-1)}^{0.1676}$$

(34)

where we can compute $f_2$ for the pair of frequencies for which we know $f_1$ and vice versa. This model supports frequency ranges up to 1–100 GHz [49]. It also relies on rain inhomogeneity and considers the significant association between the peak precipitation and attenuation values. At a lower base frequency, the attenuation levels are close to that of the CCIR relation of (13).

3.3.3. Composite Frequency Scaling Model

In the composite frequency scaling model, the effect of an element-by-element technique can be tracked to determine related coefficients at a lower frequency to yield the total attenuation of a radio link at a higher frequency. The scaling techniques of different environmental elements (oxygen, fog, cloud) can be different. These elements are oxygen, LWC, or fog, cloud, and DSD-based rain attenuation as reported in [37].

3.4. Pathlength Scaling

The pathlength is an essential parameter of rain attenuation, and an error arises if the proper estimated value is not considered developed through the rain attenuation estimation process. In [10], pathlength scaling techniques along with frequency scaling were presented. The cumulative rainfall distribution from the chosen reference path for the frequencies employed can be recalculated in the other two links through (35)–(37):

$$A_1=U·V$$

(35)

$$U=\raisebox{1ex}{$k_1{L}_1$}\!\left/ \!\raisebox{-1ex}{$(1+\raisebox{1ex}{$L_1$}\!\left/ \!\raisebox{-1ex}{$r$}\right.)$}\right.$$

(36)

$$V={\left[\frac{A_2(1+\raisebox{1ex}{$L_2$}\!\left/ \!\raisebox{-1ex}{$r$}\right.)}{k_2{L}_2}\right]}^{(\raisebox{1ex}{${\alpha }_1$}\!\left/ \!\raisebox{-1ex}{${\alpha }_2$}\right.)}$$

(37)

where $A_1$ is the attenuation on the base path, $A_2$ is the attenuation on the target path, $k_1$ and ${\alpha }_1$ are coefficients dependent on the frequency for the base path, $k_2$ and ${\alpha }_2$ are coefficients for the target path, $L_1$ is the base link’s pathlength, $L_2$ is the target link’s pathlength, and r is the path reduction factor. However, this technique is limited by the operating frequency from 38 to 58 GHz.

3.5. Polarization Scaling

In the radio wave, polarization is the orientation of electric and magnetic fields. The polarization is the variety of radio waves that include vertical, horizontal, right-hand circular, and left-hand circular. Polarization scaling is helpful to anticipate the attenuation for the type of polarization for which attenuation is unknown in a given region at a particular frequency. The ITU-R model can forecast for vertical polarization attenuation because long-term attenuation statistics are available for horizontal polarization and vice versa for a particular link. Equations (38) and (39) are the mathematical formulas for determining the conversion of polarization as specified in [45].

$$A_V=\raisebox{1ex}{$300A_H$}\!\left/ \!\raisebox{-1ex}{$(335+A_H)$}\right.(dB)$$

(38)

$$A_H=\raisebox{1ex}{$335A_V$}\!\left/ \!\raisebox{-1ex}{$(300-A_V)$}\right.(dB)$$

(39)

where $A_H$ and $A_V$ are the rain attenuations of the horizontal and vertical links, respectively. The scaling of polarization is essential for estimating the type of polarization for which attenuation is unknown at a specific frequency in climatic areas. The ITU-R model can forecast the vertical polarization attenuation since long-term attenuation data are available, with a frequency limit of 100 GHz, and it is expected to be valid in any region of the world, with an allowable link length up to 60 km. In circular polarization, the disadvantage of this model is that it cannot be used.

4. Comparison of Scaling Models

The scaling of rain attenuation models has been developed in several parts of the world. Since the climatic parameters are different in different parts of the world, the scaling parameters are also limited for the best fit in a particular geographical area. However, scaling models are always needed for better applicability, whose performance can be “fine-tuned” by the local climatic parameters. Among the climatic parameters, the rain rate is the frequently used parameter. However, in recent years, it has been validated that the DSD-based distribution gives more accurate results than the rainfall rate. However, the problem of the DSD-based model is that the rainfall distribution can change in different rain events. Furthermore, the availability of DSD-based measurement data is limited compared to rain-rate-based data. Among the developed models of scaling, the frequency-scaled models are the most common in the literature. Some scaling models consider only the ratio of frequencies, while other methods consider a more complicated one, including attenuation and frequency in the ratio-based scaling factor. Another critical feature of scaling techniques is the temporal domain perspective: “long-term” and “short-term” applicability. The “short-term” applicability is also called “instantaneous scaling [51]”. The “instantaneous scaling” techniques are sensitive to the variations of the same rain event due to the variations of the drop size distribution on the slant path [41]. In

Table 1. Comparison among the scaling of propagation links.

Ref.	Location	Link	Atten.	DSD	Camp.Time	Freq. (GHz)
[14]	Italy	Satellite		✓	06/2014–	20/40
[52]	Italy	Satellite	✓		72/36 h	11.6/17–17.8
[53]	Belgium	Satellite (Olympus)	✓		7 mo.	12.50/19.77–29.66
[54]	Italy	Satellite (ACTS, ITALSAT)	✓		–	20.2/27.5 (ACTS); 39.6/49.5(ITALSAT)
[21]	Worldwide	Satellite	✓		–	10–100
[55]	Collected	Satellite		✓	–	10-50
[51]	U.K.	Satellite	✓		8–11 mo.	12.5/20/30
[56]	Collected	Satellite/Terrestrial	✓		–	13/19/30
[57]	Czech Rep.	Terrestrial	✓		9 mo.	58/93
[58]	Malaysia	Terrestrial	✓		12 mo.	23/26/38
[6]	USA	Satellite	✓		12 mo.	12/20/30
[7]	India	Satellite	✓		5 d	20.2/30.5
[59]	India	Satellite		✓	2 y	20/30
[13]	India	Satellite	✓			20/30
[8]	Italy	Satellite (ITALSAT)	✓	✓	12 mo.	Ka/V bands (18.7/39.6/49.5)
[49]	Italy	Satellite (ITALSAT)			8 y	Ka/V (18.7/39.6/49.5)
[11]	Synthetic	Satellite	✓		–	18.7/39.6

and

Table 2. Comparison among the scaling of propagation links.

Ref.	Long-Term	Short-Term	Innovative Idea
[14]		✓	It proposed a frequency scaling technique based on the DSD distribution. The DSD-based distribution is accurate for comparing the rain rate. However, the DSD distribution is not uniform in every rain event.
[52]		✓	This study revealed that the ratio of two averaged attenuations of radio links follows a power rule of the form $\raisebox{1ex}{$A_2$}\!\left/ \!\raisebox{-1ex}{$A_1$}\right.=\alpha A_1^{\beta }$.
[53]		✓	It analyzed the effect of scintillation on frequency scaling, and according to the outcome, scintillation has a significant influence on frequency scaling.
[54]		✓	It proposed a frequency scaling scheme for real-time total atmospheric (cloud+scintillation-excluding) conditions.
[21]	✓		It proposed a method for frequency scaling in clear sky conditions.
[55]			It proposed a “statistical factor”-based method for dual-frequency scaling.
[51]	✓	✓	It revealed the “hysteresis behavior” of short-term frequency scaling.
[56]	✓		It considered the concept that the length is frequency-independent [47] and proposed a nonratio-based single-frequency frequency scaling technique.
[57]	✓		It proposed the experimental results of frequency and polarization scaling for terrestrial links.
[58]	✓		The validation of existing methods of frequency scaling in Malaysia did not show satisfactory performance close to the measured results. The reason could be that all the existing methods used were for “slant links”.
[6]	✓	✓	Proposed a general frequency scaling technique for the Ku/Ka-band, and the predicted attenuation also showed satisfactory performance with “short-term” applications.
[7]	✓		It used the ITU-R P.618-13 model [60] to calculate vertical and horizontal polarization.
[59]	✓		It proposed a very simple formula $A_{30}=C·A_{20}$ to predict rain attenuation at 30 GHz using a constant $C=1.8185092$ and the attenuation at 20 GHz. The results were not validated by the measured attenuation at 30 GHz.
[13]		✓	It used the SAM model-originated specific attenuation parameter ($\gamma$) at 20 GHz to estimate rain attenuation at 30 GHz.
[8]	✓		It proposed a method for frequency scaling, including raindrop-size-related parameters and the rain rate.
[49]		✓	It proposed a model that takes into account the attenuation variation due to the variations of the raindrop size.
[11]	–	–	Using the Multi-EXponential CELL (MultiEXCELL; a model to synthetically form rain cells) synthetic model, it proposed a method to predict attenuation within $5^{\circ }$ and ${90}^{\circ }$, as a function of the link elevation.

, all the rain attenuation models’ innovative ideas, long or short applicability, reported frequency range, and supported link are discussed.

5. Research Scopes and Challenges

The GHz-frequency band scaling mechanism remains in development and is subject to significant study. In the next section, several strategies for developing the scaling of radio links are described.

5.1. Experiment Planning

The primary challenge in scaling method studies is that long-term experiments are necessary. Besides considering the nonuniform distribution of rain, proper approximation techniques are required to be deployed that can represent the rain distribution along with the radio links. In addition, to develop a scaling method, depending on the scaling mechanism, it needs to record attenuation with varying different possible parameters. Long-term experimental data are required to enhance the scaling of rain attenuation further.

5.2. Synthetic Storm Approach-Based Elevation Angle Scaling

In [24], the SSA-based time series generation scaling techniques were proposed. An improved version of the SSA method was proposed in [61], which improved the performance over the conventional SSA technique. The characteristics can be retrieved from additional sources using this improved SSA approach, including a discriminating mechanism for distinguishing between stratiform and convective rain episodes. Consequently, there are research scopes to apply this improved version of the SSA technique for elevation scaling through rain attenuation time series.

5.3. Application of Artificial Neural Network (AI) for Radio Link Scaling

It has been recently shown that rain attenuation is more effectively determined with the help of AI-based techniques [4]. Recently, in [62] an artificial neural network was used to determine the polarization and frequency scaling for terrestrial and slant links. Typically, long-term rain attenuation, rainfall rate, and other climatic or infrastructural related parameters need to be studied for rain attenuation models. In recent years, it has been found that considering the microphysical phenomena of rainfall events can be helpful for accurate attenuation models for radio links [63,64]. Consequently, the rainfall rate and other related physical parameters can to contribute to accurate attenuation prediction models. All these parameters can be helpful to develop rain attenuation scaling models for frequency, the elevation angle of the antenna, polarization, and pathlength scaling.

5.4. Enhancement of Composite Scaling Technique

According to the study in [65], the liquid water content (LWC) can affect the attenuation over a wide frequency range up to 1000 GHz. It was shown that the attenuation due to the LWC is almost similar to the standard atmosphere condition, but within 1 GHz and 100 GHz, the attenuation due to the LWC is lower than the standard atmospheric condition. Consequently, in a particular region at a specific time, the LWC showed a more significant variation. To model the attenuation in such an area, it needs a separate procedure to calculate the attenuation due to the unusual LWC. It was mentioned in [9] that environmental visibility can affect the attenuation in terrestrial and slant links. Moreover, in [66,67], the perspective relationship was studied among the factors such as visibility, precipitation, and the presence of fog. In many regions, fog is a regular seasonal phenomenon, so the effect of the GHz-range frequency bands’ link can also be modeled according to the resulting attenuation due to fog or visibility at different frequency bands.

6. Conclusions

This survey reviewed more than 17 rain attenuation scaling models. This review included the well-known and related literature on the scaling of rain attenuation models. Existing scaling models were categorized according to the model development and framework. The comparative table included different performance parameters such as the applicable frequency range and the long-term or short-term applicability of these scaling models. In the scaling of rain attenuation models, the rain rate distribution and the radio link usually follow a uniform distribution. In such cases, in the frequency scaling method, the SAM model is used to determine the spatial rainfall distribution, but it is a simple technique. Consequently, a sophisticated spatial rainfall distribution model that can represent the rain cell structures along the radio link is necessary. Furthermore, as mentioned earlier, beyond the rainfall rate, some other factors (fog, cloud, visibility) play a significant role in deteriorating the attenuation in GHz-range radio links. However, the proper scaling mechanism of these environmental elements has not been developed yet. Massive microwave links are projected to be implemented in 5G and future wireless networks where the operating frequency is within a frequency range susceptible for rain attenuation. In this situation, the scaling approaches can assist in making fast estimation of attenuation either in rainy or nonrainy conditions to manage the link budget.