Study on the Interference Process of Liquid Radial Reflux on the Stability of a Shaped Charge Jet
Abstract
:1. Introduction
2. Theoretical Analysis
- (1)
- The radial and axial pressures of the initial reaming are equal, and the product of reaming pressure and hole wall area is constant.
- (2)
- During penetration, the jet is approximately a cylindrical rod.
- (3)
- Considering that the effect of liquid viscosity is small, it is ignored in the analysis of penetration [24].
- (4)
- The effect of shell plastic deformation in the penetration process is ignored.
3. Simulation Analysis
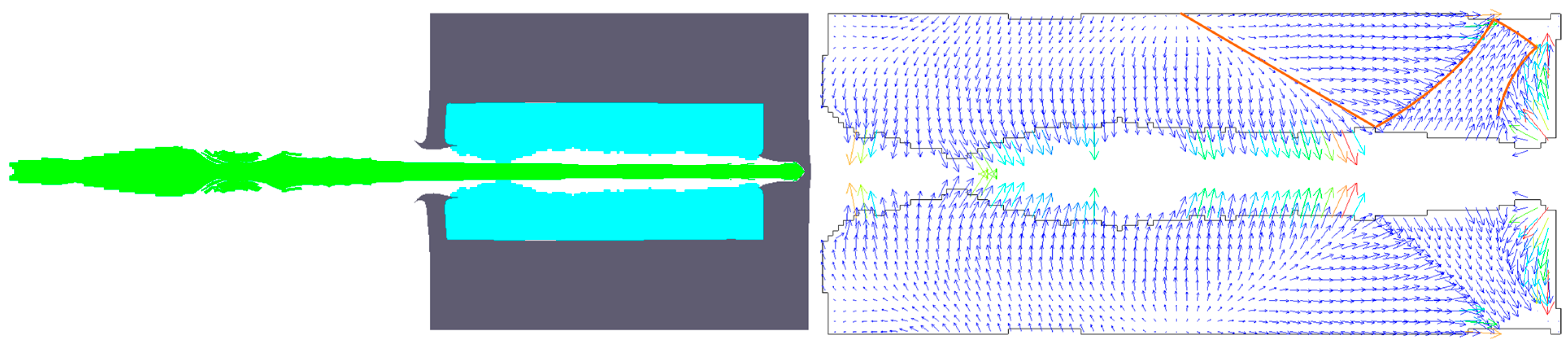
3.1. Simulation Modeling
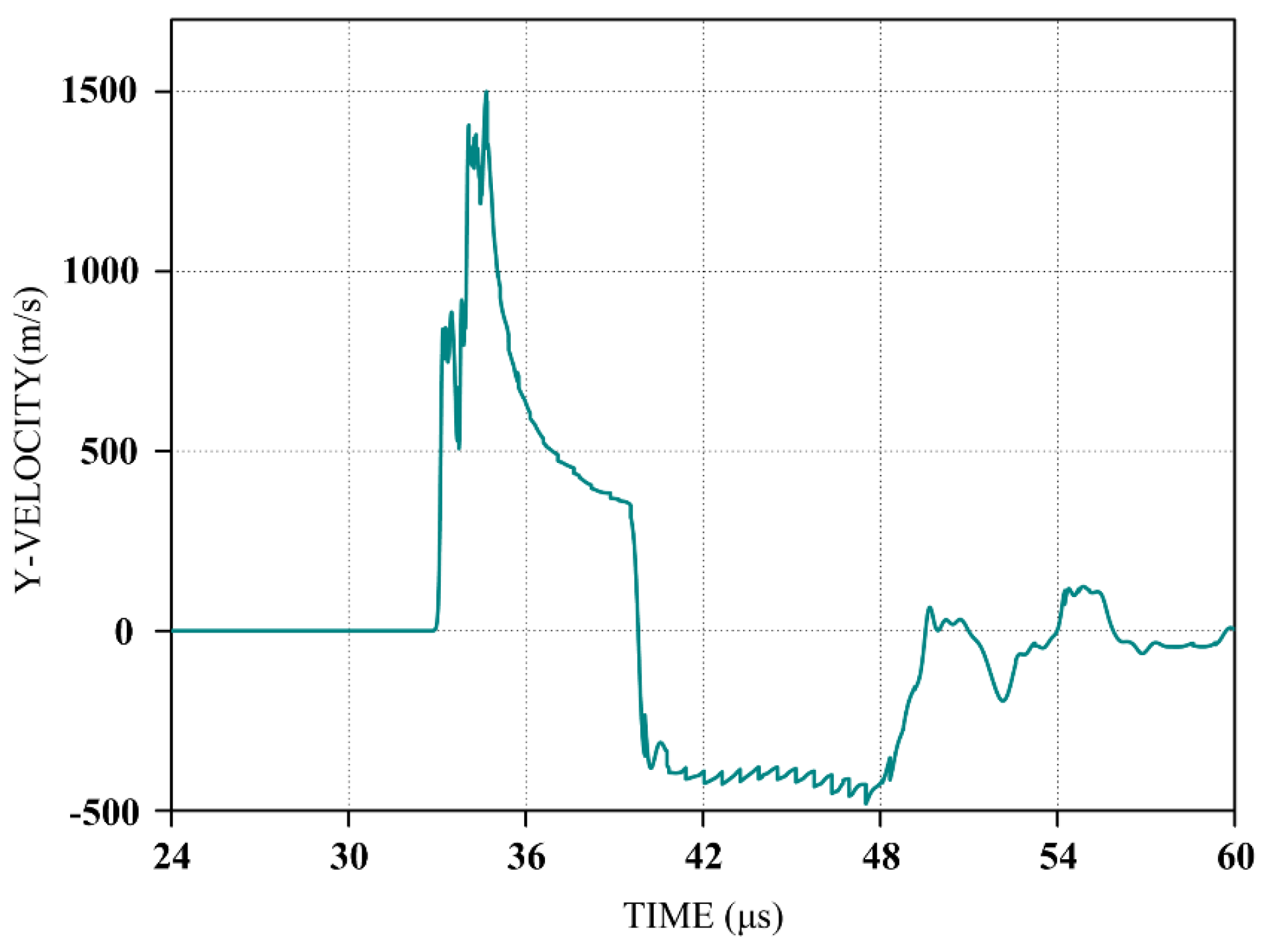
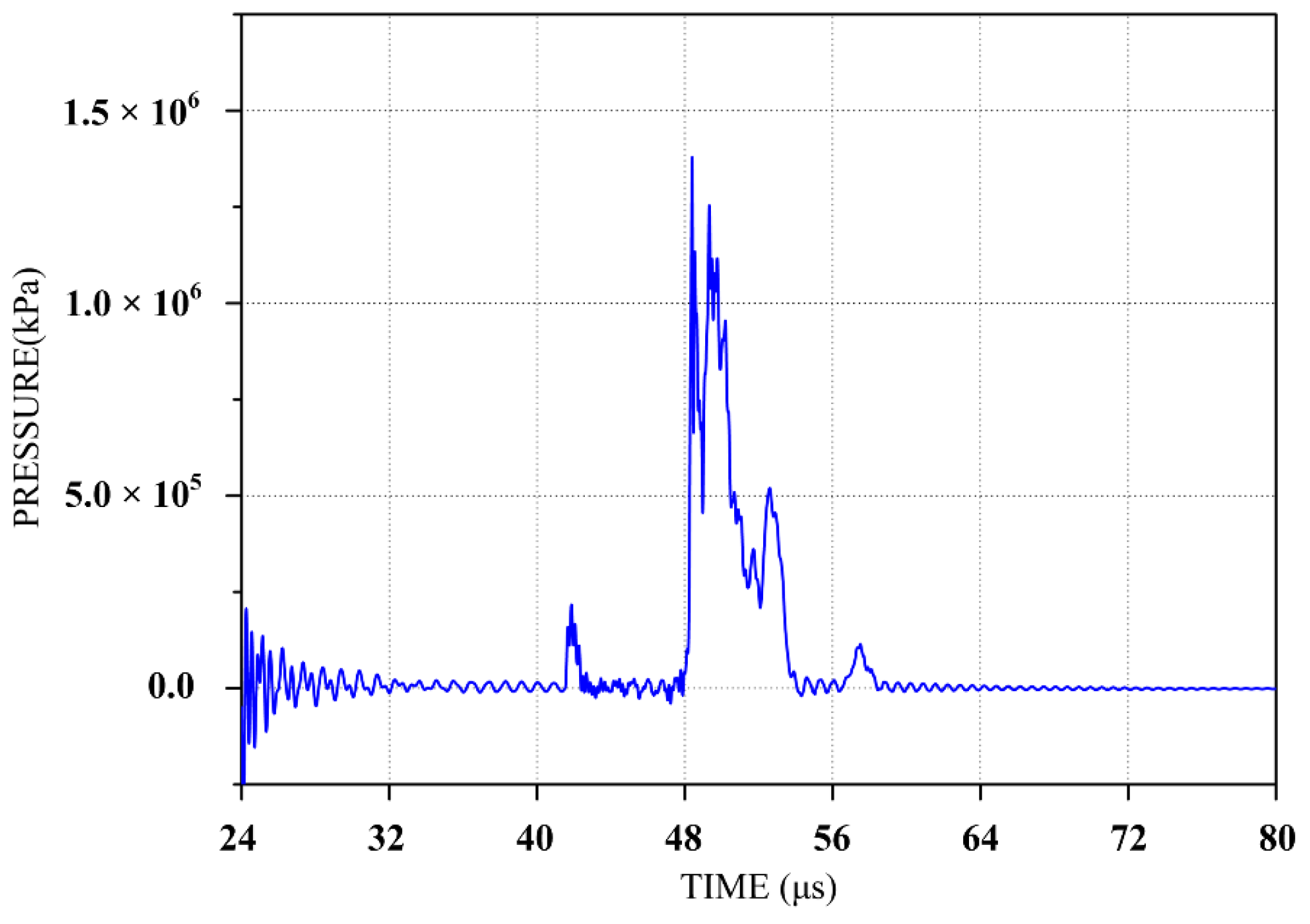
3.2. Simulation Results
4. Experiments and Calculation
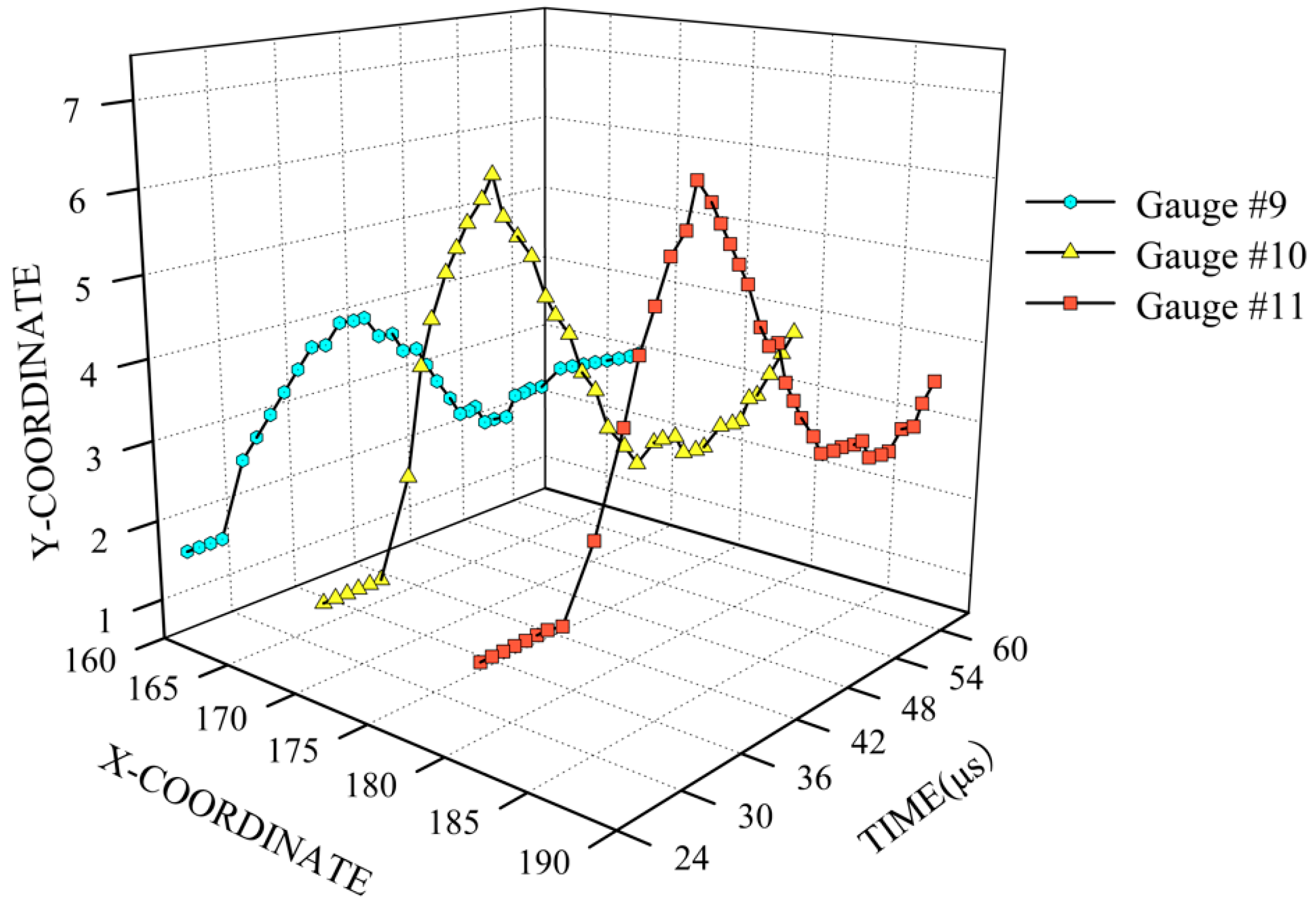
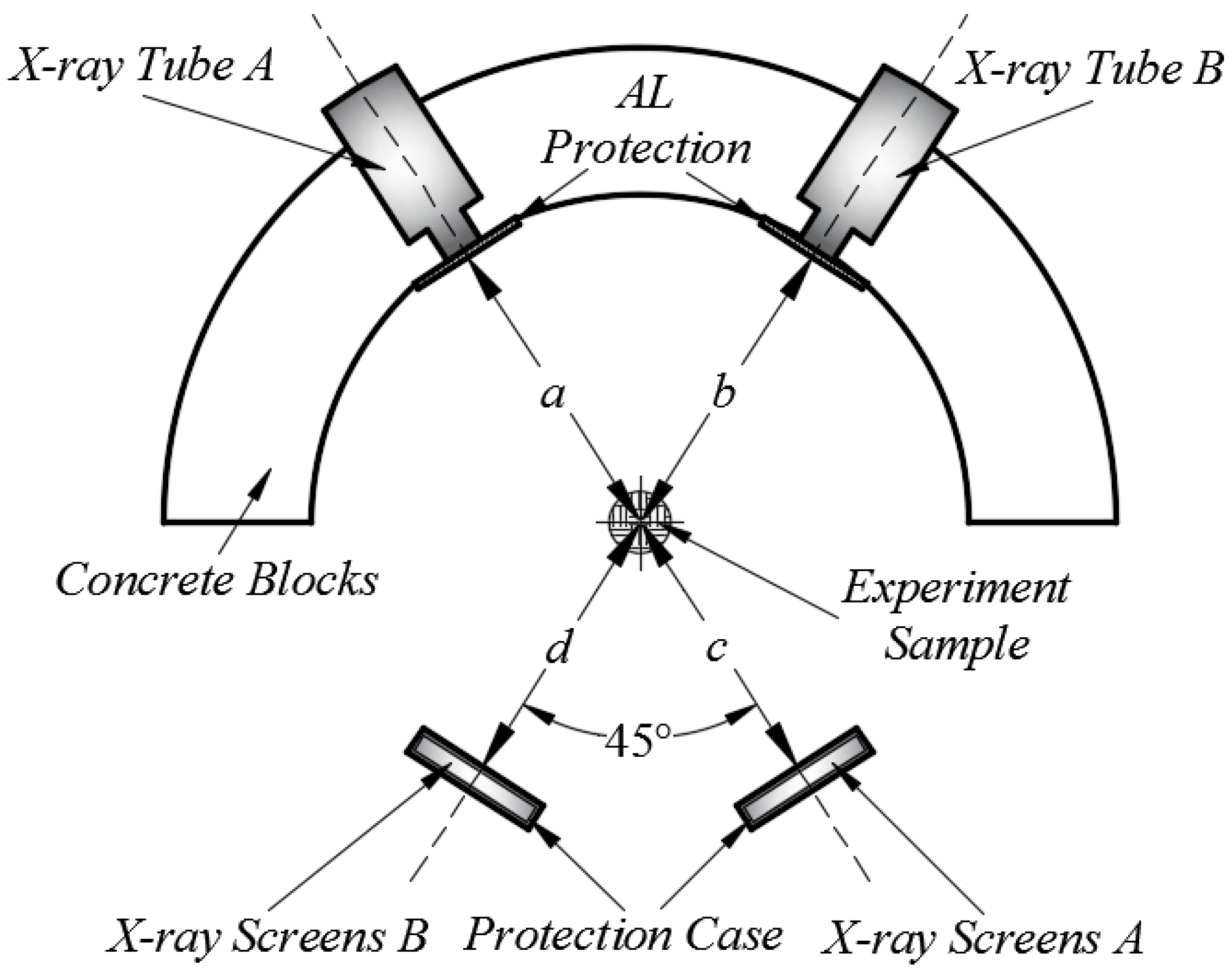
4.1. X-ray Experiment
4.2. DOP Experiment
4.3. Comparison between Experimental and Theoretical Results
5. Conclusions
- (1)
- The interference of liquid radial reflux in the SCJ mainly comprises three parts: side-wall reflection interference, bottom plate reflection interference, and side-wall secondary reflection interference. The bottom plate reflection interference has observed interference on the tip of the SCJ.
- (2)
- The interference jet velocity interval during jet penetration in the LFCS is based on the theoretical model, and the residual penetration depth can be calculated through its combination with the stand-off curve of the jet.
- (3)
- Theoretical analysis and experimental results show that the LFCS has interference on the head of the SCJ. Thus, applying the LFCS to extreme protection fields, such as ammunition safety protection, is possible.
- (4)
- The theoretical model established in this study is suitable for calculating the interference process of the LFCS with a Newtonian liquid in the SCJ to predict the anti-jet capacity of the LFCS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| penetration depth of the SCJ in liquid | |
| residual velocity after jet penetration into the cover plate | |
| coordinate value of the virtual origin | |
| stand-off | |
| thickness of the LFCS panel | |
| thickness of the bottom plate of the LFCS | |
| density of the liquid | |
| density of the SCJ | |
| residual velocity of the jet that penetrates the liquid | |
| time of jet penetration into the liquid | |
| crater radius of the liquid | |
| wall pressure of the liquid crater | |
| penetration dynamic pressure | |
| reaming pressure of the crater | |
| radius of the jet | |
| density of the liquid at atmospheric pressure | |
| crater formed by the jet | |
| penetration velocity of the jet | |
| sound velocity of the liquid | |
| velocity of the shock wave | |
| normal direction of the Mach angle | |
| initial shock wave propagation along the radial direction | |
| , | propagation times of the shock wave in two different directions |
| radius of the inner cavity of the shell | |
| closing pressure of the crater | |
| intensity of the side-wall reflection shock wave | |
| reflection coefficient of the shock wave | |
| closing velocity of the liquid particle | |
| material constant of the liquid | |
| time for the liquid particle to move from the crater wall to the jet surface | |
| , | times of liquid movements to the jet surface corresponding to the two propagation paths |
| , | jet velocities at the positions where the liquid converges to the jet surface |
| intensity of the bottom reflection shock wave at the crater wall | |
| liquid closing speed of the crater wall at the bottom of the LFCS | |
| time for the bottom plate reflection shock wave to propagate to the crater wall | |
| liquid closing time | |
| maximum velocity of the interference jet at the bottom plate reflection interference stage | |
| height of the liquid level drop caused by liquid spraying | |
| liquid-spraying velocity | |
| reaming area of the bottom plate | |
| liquid-spraying time | |
| , | propagation times of the shock wave corresponding to the two propagation paths |
| height of the inner cavity of the shell | |
| Mach angle | |
| minimum interference velocities of the liquid to the jet driven by the secondary reflection shock wave | |
| maximum interference velocities of the liquid to the jet driven by the secondary reflection shock wave | |
| distance between the bottom of the LFCS and the horizontal ground | |
| , | corresponding magnification factors of X-ray tubes A and B, respectively |
| , | exposure times of X-ray tubes A and B, respectively |
| distance of the jet movement within the time range |
References
- Fuhs, A.E.; Ball, R.E.; Power, L.H. FY73 Hydraulic Ram Studies; Naval Postgraduate School: Monterey, CA, USA, 1973. [Google Scholar]
- Fourest, T.; Laurens, J.M.; Deletombe, E.; Dupas, J.; Arrigoni, M. Analysis of bubbles dynamics created by hydrodynamic ram in confined geometries using the rayleigh–plesset equation. Int. J. Impact Eng. 2014, 73, 66–74. [Google Scholar] [CrossRef]
- Fourest, T.; Laurens, J.M.; Deletombe, E.; Arrigoni, M.; Dupas, J. Cross validation of analytical and finite element models for Hydrodynamic Ram loads prediction in thin walled liquid filled containers. J. Fluids Struct. 2015, 59, 285–296. [Google Scholar] [CrossRef]
- Varas, D.; López-Puente, J.; Zaera, R. Experimental analysis of fluid-filled aluminum tubes subjected to high-velocity impact. Int. J. Impact Eng. 2009, 36, 81–91. [Google Scholar] [CrossRef] [Green Version]
- Lecysyn, N.; Bony-Dandrieux, A.; Aprin, L.; Heymes, F.; Slangen, P.; Dusserre, G.; Munier, L.; Le Gallic, C. Experimental study of hydraulic ram effects on a liquid storage tank: Analysis of overpressure and cavitation induced by a high-speed projectile. J. Hazard. Mater. 2010, 178, 635–643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sauer, M. Simulation of high velocity impact in fluid-filled containers using finite elements with adaptive coupling to smoothed particle hydrodynamics. Int. J. Impact Eng. 2011, 38, 511–520. [Google Scholar] [CrossRef]
- Disimile, P.J.; Toy, N. Liquid spurt caused by hydrodynamic ram. Int. J. Impact Eng. 2015, 75, 65–74. [Google Scholar] [CrossRef]
- Disimile, P.J.; Davis, J.; Toy, N. Mitigation of shock waves within a liquid filled tank. Int. J. Impact Eng. 2011, 38, 61–72. [Google Scholar] [CrossRef]
- Chen, A.; Li, X.; Zhou, L.; Ji, Y. Study of liquid spurt caused by hydrodynamic ram in liquid-filled container. Int. J. Impact Eng. 2020, 144, 103658. [Google Scholar] [CrossRef]
- Ji, Y.; Li, X.; Zhou, L.; Lan, X.; Chen, A. Comparison of the hydrodynamic ram caused by one and two projectiles impacting water-filled containers. Int. J. Impact Eng. 2020, 137, 103467. [Google Scholar] [CrossRef]
- Ji, Y.; Li, X.; Zhou, L.; Lan, X. Review of study on hydrodynamic ram effect generated due to high-velocity penetrator impacting fluid-filled container. J. Vib. Shock 2019, 38, 242–252. (In Chinese) [Google Scholar]
- Held, M.; Backofen, J.E. Penetration of shaped charge into water. Presented at the 12th International Symposium on Ballistics, San Antonio, TX, USA, 30 October–1 November 1990. [Google Scholar]
- Lee, E.S.; Oh, K.H.; Song, S.Y. Penetration of particulated shaped charge jet into water. In Proceedings of the 21st International Congress on: High-Speed Photography and Photonics, Taejon, Korea, 30 May 1995; pp. 975–981. [Google Scholar]
- White, J.J.; Wahll, M.J. Shaped charge jet interactions with liquids. In Proceedings of the 6th International Symposium on Ballistics, Orlando, FL, USA, 27–29 October 1981; pp. 554–561. [Google Scholar]
- Held, M. Verification of the equation for radial crater growth by shaped charge jet penetration. Int. J. Impact Eng. 1995, 17, 387–398. [Google Scholar] [CrossRef]
- Held, M.; Huang, N.S.; Jiang, D.; Chang, C.C. Determination of the crater radius as a function of time of a shaped charge j et that penetrates water. Propellants Explos. Pyrotech. 1996, 21, 64–69. [Google Scholar] [CrossRef]
- Andersson, G.; Karlsson, S.; Watterstam, A. Shaped charge jet interaction with confined water. In Proceedings of the 17th International Symposium on Ballistics, Midrand, South Africa, 23–27 March 1998; pp. 183–190. [Google Scholar]
- Li, Y.; Gao, F.; Wang, C.; Gao, J. Engineering algorithm for a new type of protective armor disturbing jet penetration. Acta Armamentarii 2002, 23, 546–550. (In Chinese) [Google Scholar]
- Gao, Z.Y.; Huang, Z.X.; Guo, M.; Zu, X.D.; Xiao, Q.Q.; Jia, X. Theoretical Study of a Diesel-Filled Airtight Structure Unit Subjected to Shaped Charge Jet Impact. Propellants Explos. Pyrotech. 2016, 41, 62–68. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, Z.; Guo, M.; Zu, X.; Xiao, Q.; Jia, X. Anti-penetration performance analysis of diesel oil filled airtight structures against shaped charge jet. J. Vib. Shock 2016, 35. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Zu, X.; Huang, Z.; Xiao, Q.; Jia, X. Analysis of liquid-filled unit cell structure subjected to shaped charge jet impact. Explos. Shock Waves 2017, 37, 1101–1106. (In Chinese) [Google Scholar]
- Zhang, X.; Zu, X.; Huang, Z.; Xiao, Q.; Jia, X. Interference Characteristics of Liquid Composite Armor of Cell Structure against Jet. Ordnance Ind. Autom. 2017, 11, 70–75. (In Chinese) [Google Scholar]
- Zu, X.; Dai, W.; Huang, Z.; Yin, X. Effects of Liquid Parameters on Liquid-Filled Compartment Structure Defense against Metal Jet. Materials 2019, 12, 1809. [Google Scholar] [CrossRef] [Green Version]
- Tan, Y.; Jia, X.; Huang, Z.; Cai, Y.; Zu, X. Effect of Liquid Parameters on Protective Performance of a Liquid Composite Target Subjected to Jet Impact. In Proceedings of the 15th Hypervelocity Impact Symposium, Destin, FL, USA, 14–19 April 2019. [Google Scholar] [CrossRef]
- Guo, M.; Zu, X.D.; Shen, X.J.; Huang, Z.X. Study on liquid-filled structure target with shaped charge verticality penetration. Def. Technol. 2019, 15, 861–867. [Google Scholar] [CrossRef]
- Guo, M.; Zu, X.-d.; Huang, Z.-x.; Shen, X.-j. Mechanism of hermetic single-cell structure interfering with shaped charge jet. Lat. Am. J. Solids Struct. 2018, 15. [Google Scholar] [CrossRef]
- Zu, X.D.; Huang, Z.X.; Guan, Z.W.; Yin, X.C.; Zheng, Y.M. Influence of a liquid-filled compartment structure on the incoming shaped charge jet stability. Def. Technol. 2021, 17, 571–582. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication: International Series on Materials Science and Technology; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Oertel, H., Jr. Prandtl’s Essentials of Fluid Mechanics; Science Press: Beijing, China, 2008. [Google Scholar]
- Cai, Y.E.; Huang, Z.X.; Shen, X.J.; Zu, X.D.; Jia, X.; Ji, Q. Simulation Study on the influence of liquid level on anti-jet penetration ability of single-cell composite structure. J. Phys. Conf. Ser. 2020, 1507, 032050. [Google Scholar] [CrossRef]

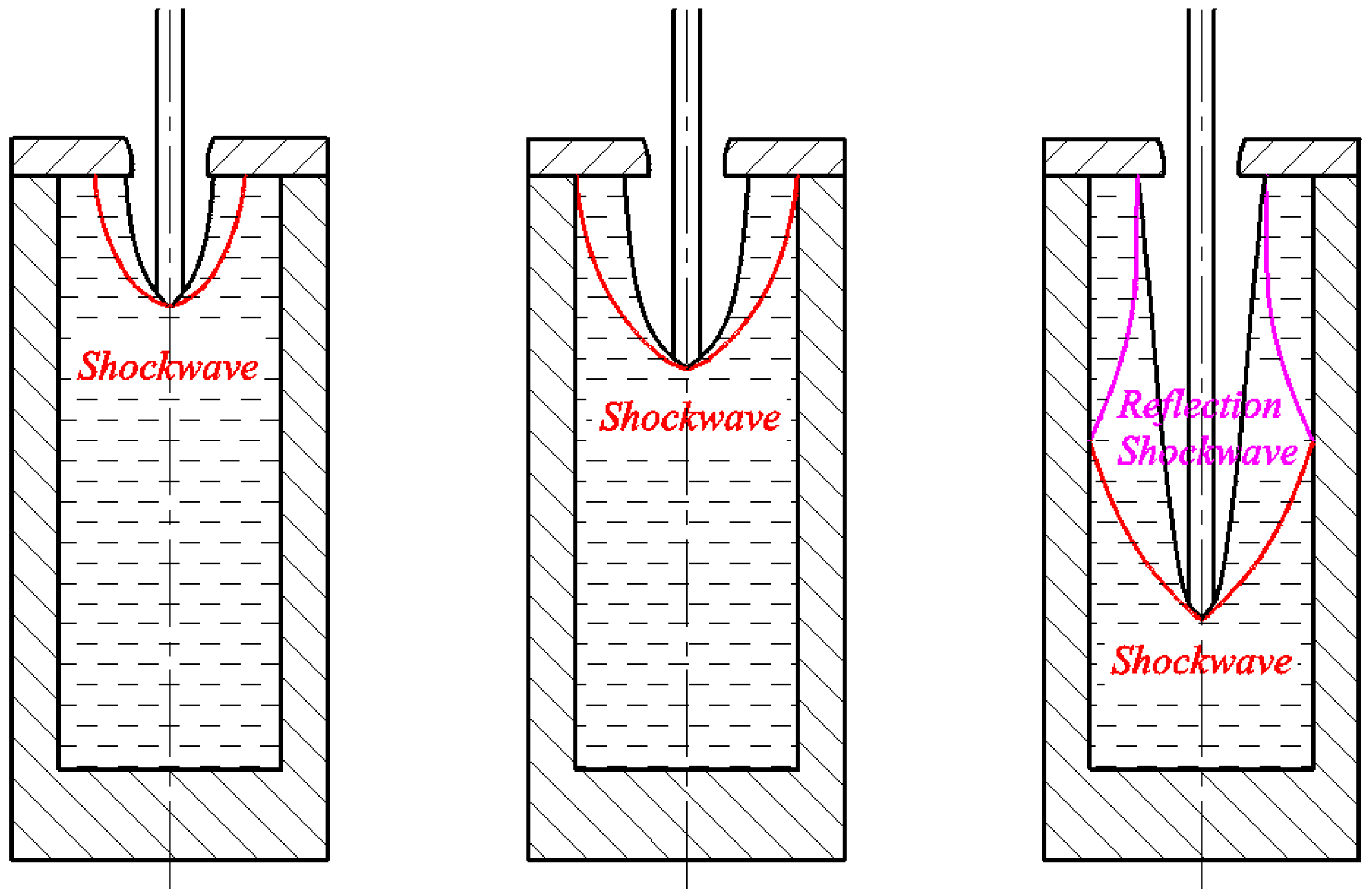
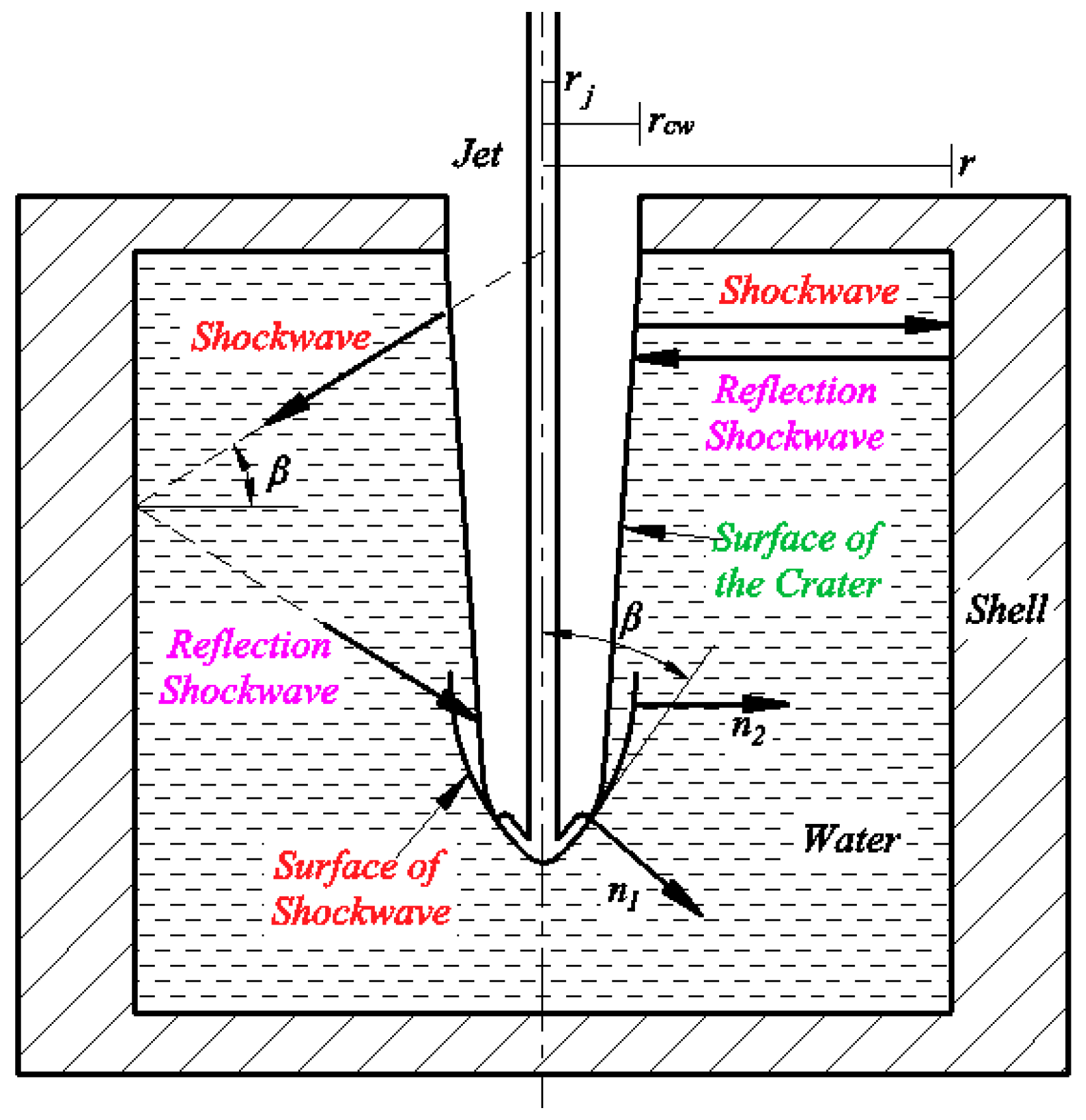
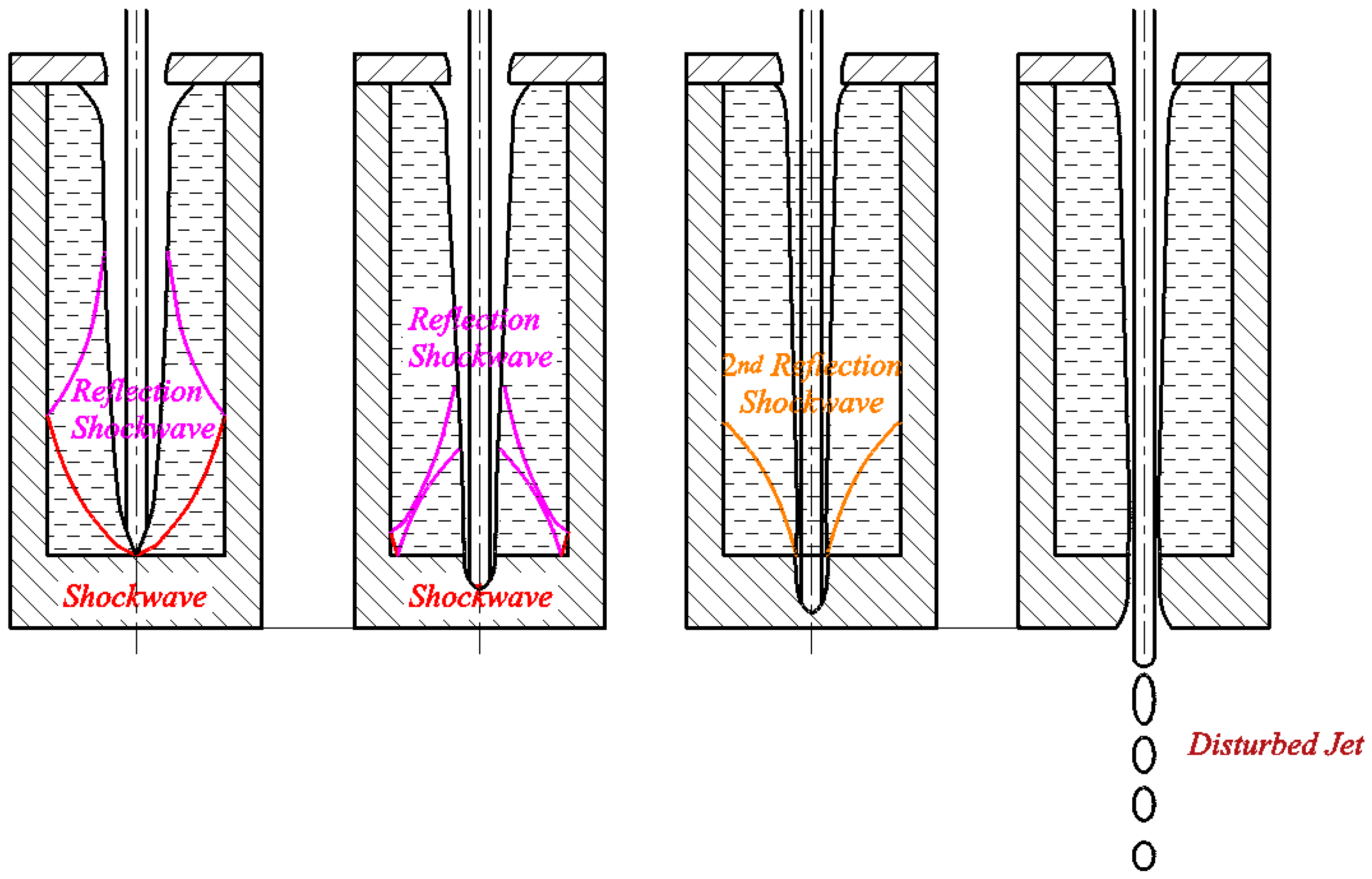


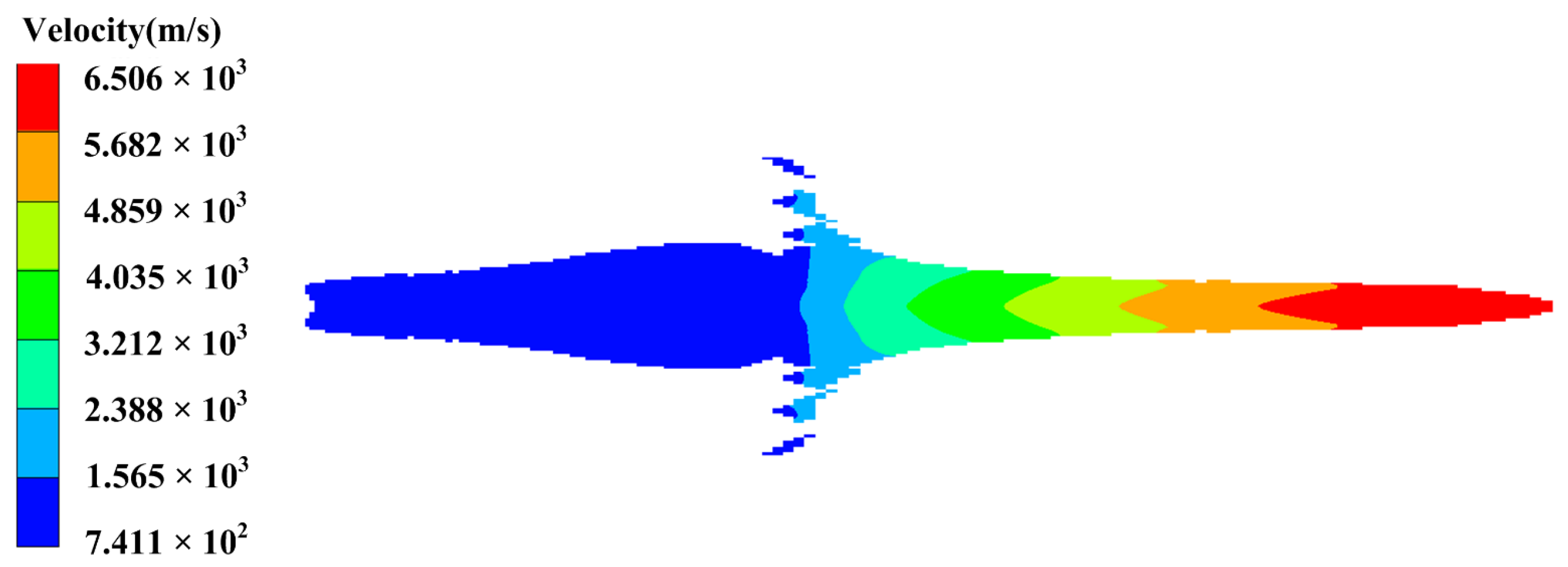



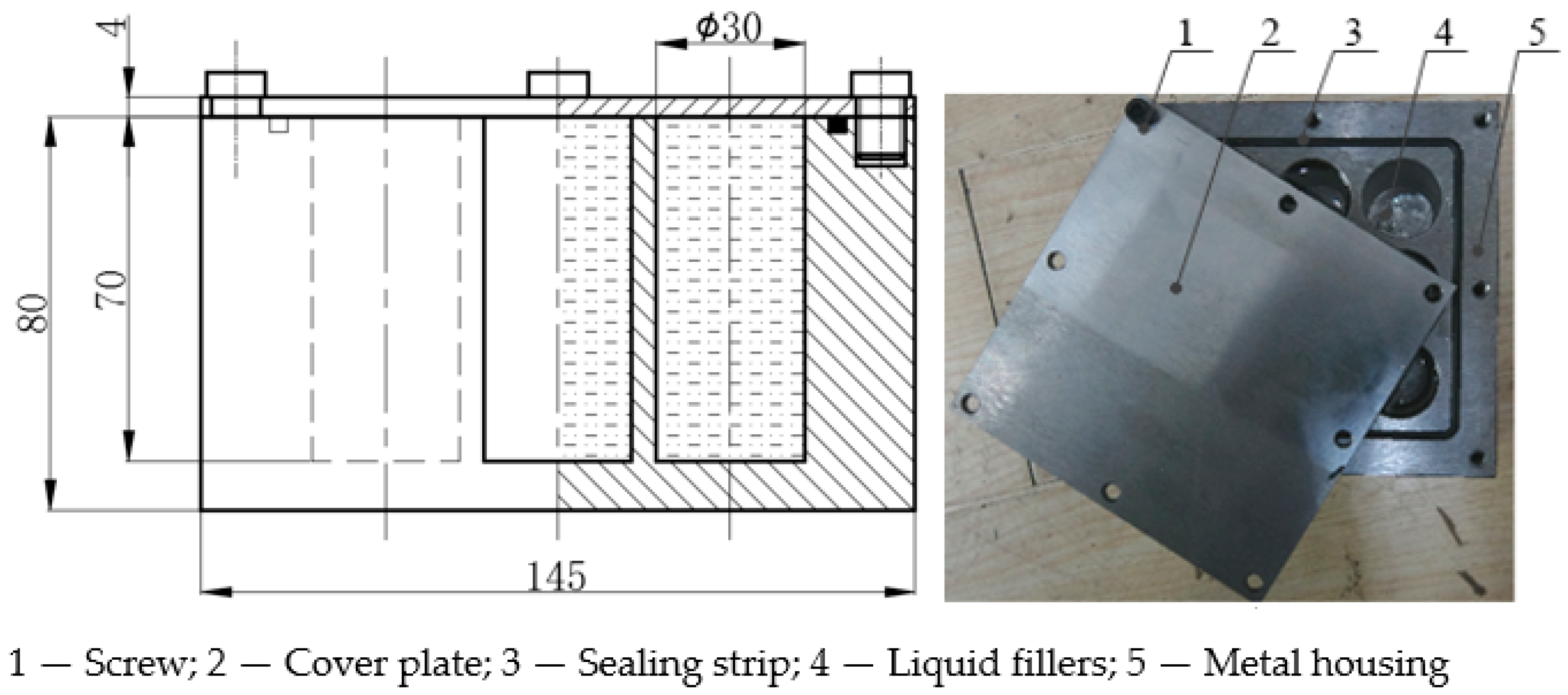
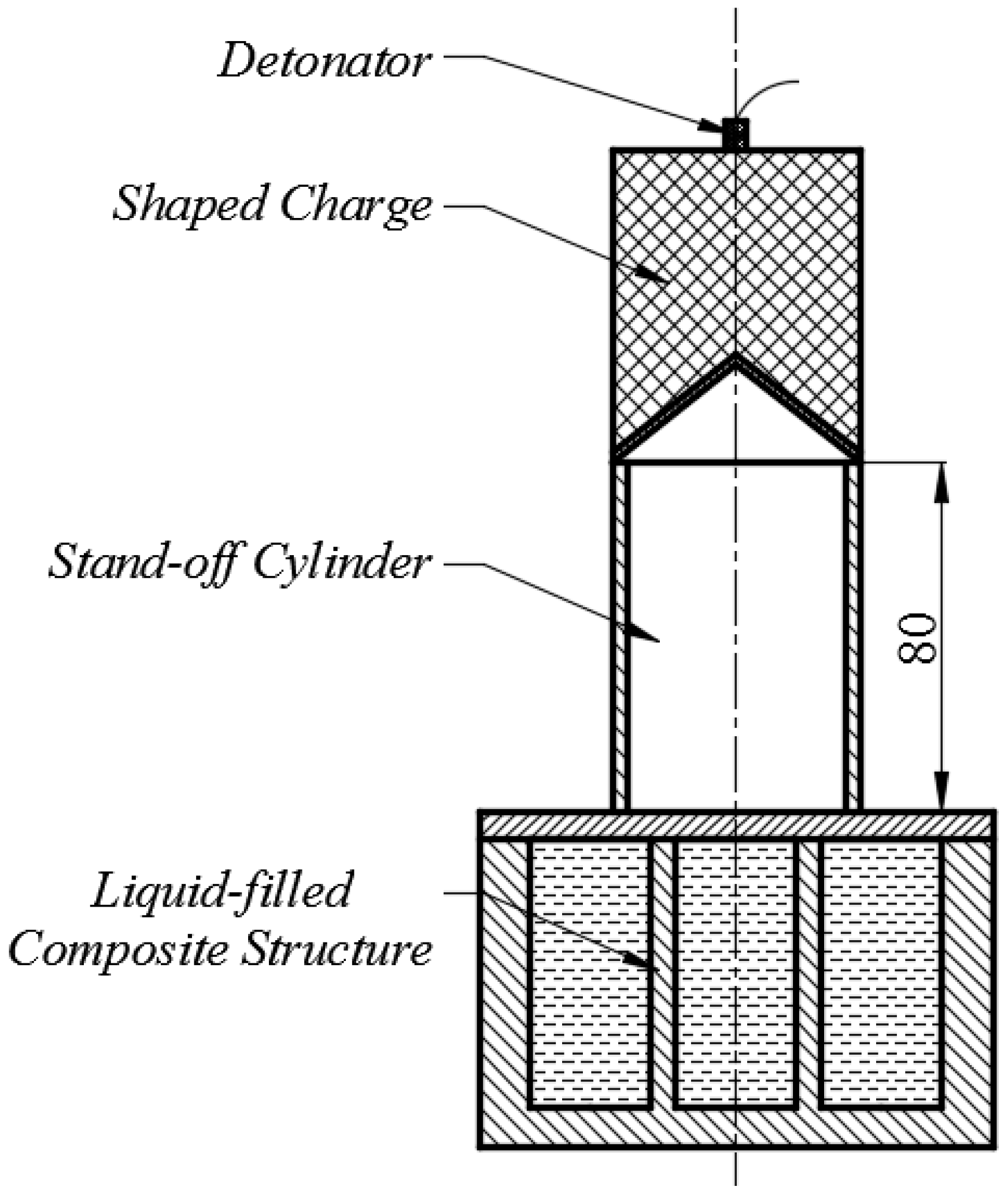




| Material | ρ/(g·cm−3) | D/(m·s−1) | PCJ/(GPa) |
|---|---|---|---|
| JH-2 | 1.717 | 8500 | 34.0 |
| Material | ρ/(g·cm−3) | Shear Modulus (GPa) | Yield Strength (MPa) |
|---|---|---|---|
| CU-OFHC | 8.93 | 47.7 | 120 |
| Material | ρ/(g·cm−3) | c/(m·s−1) |
|---|---|---|
| Water | 1.0 | 1480 |
| Material | Density (g·cm−3) | Tensile Strength (MPa) | Yield Strength (MPa) | Elongation (%) |
|---|---|---|---|---|
| Q235 | 7.85 | 235 | 375 | 26 |
(m) | (mm) | (mm) | (mm) | (mm) | (μs) | (μs) | |||
|---|---|---|---|---|---|---|---|---|---|
| Water | 1.29 | 148 | 148 | 79 | 76 | 1.53 | 1.51 | 60 | 80 |
| Data Source | Interference Velocity Interval (m/s) | Residual Penetration Depth (mm) | |
|---|---|---|---|
| Theoretical calculation results | [3131, 3813] ∪ [3916, 5321] | 76.3 | |
| Experimental result | [3389.9, 5456.7] | 78 | 79.5 (on average) |
| 81 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Zu, X.; Tan, Y.; Huang, Z. Study on the Interference Process of Liquid Radial Reflux on the Stability of a Shaped Charge Jet. Appl. Sci. 2021, 11, 8044. https://doi.org/10.3390/app11178044
Cai Y, Zu X, Tan Y, Huang Z. Study on the Interference Process of Liquid Radial Reflux on the Stability of a Shaped Charge Jet. Applied Sciences. 2021; 11(17):8044. https://doi.org/10.3390/app11178044
Chicago/Turabian StyleCai, Youer, Xudong Zu, Yaping Tan, and Zhengxiang Huang. 2021. "Study on the Interference Process of Liquid Radial Reflux on the Stability of a Shaped Charge Jet" Applied Sciences 11, no. 17: 8044. https://doi.org/10.3390/app11178044
APA StyleCai, Y., Zu, X., Tan, Y., & Huang, Z. (2021). Study on the Interference Process of Liquid Radial Reflux on the Stability of a Shaped Charge Jet. Applied Sciences, 11(17), 8044. https://doi.org/10.3390/app11178044







