Shared Mobility Problems: A Systematic Review on Types, Variants, Characteristics, and Solution Approaches
Abstract
:1. Introduction
2. Previous Review Paper
3. Research Methodology
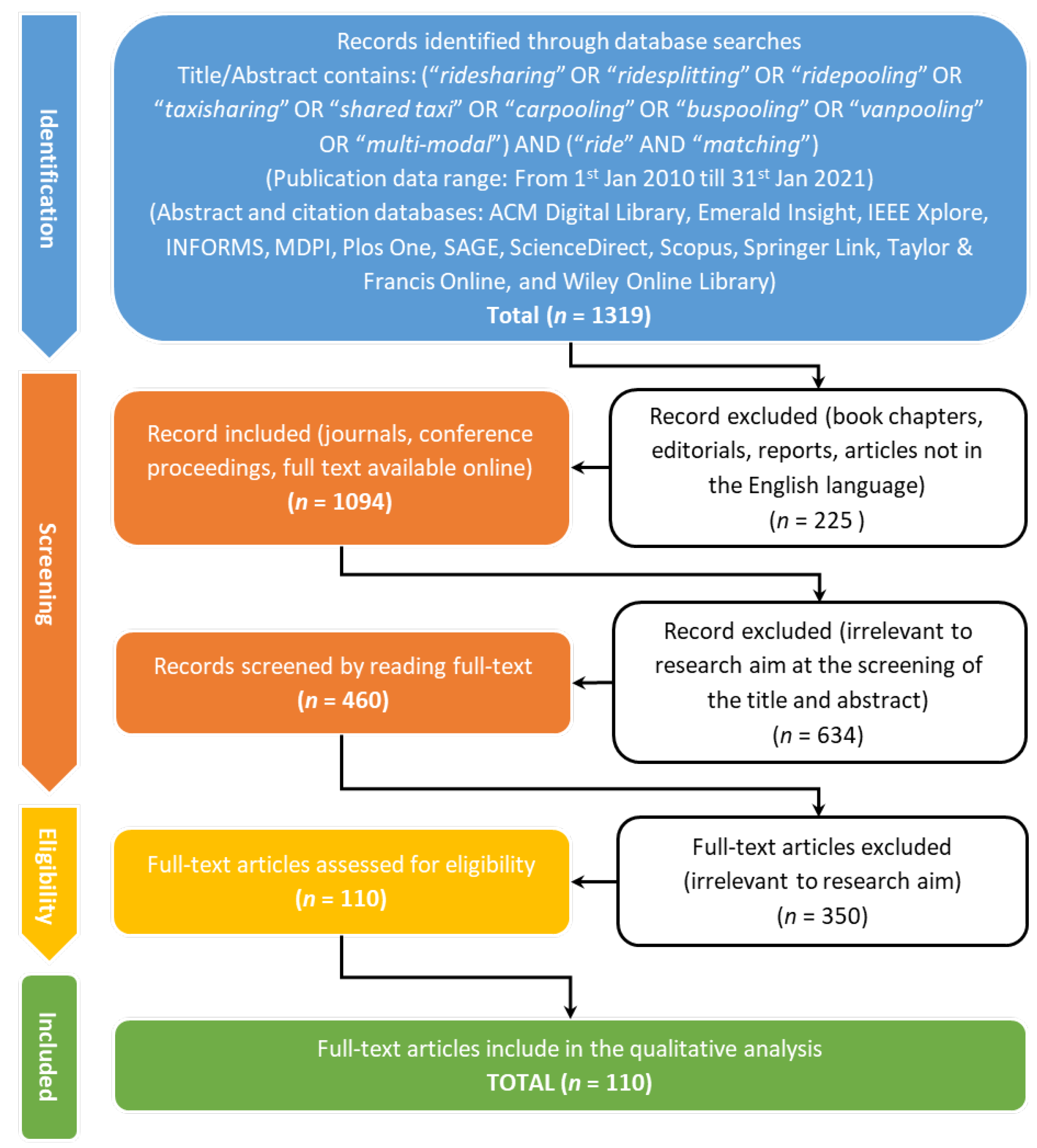
3.1. Material Collection
- What would be the classification of the SMP based on problem types, variants, and characteristics?
- What are the solution approaches that have been employed to solve the SMP?
- What are the current trends of the SMP?
- What are the challenges and future work direction in the routing and matching optimisation of SMP?
3.2. Descriptive Statistics
3.3. Category Classification
4. Review of Literature
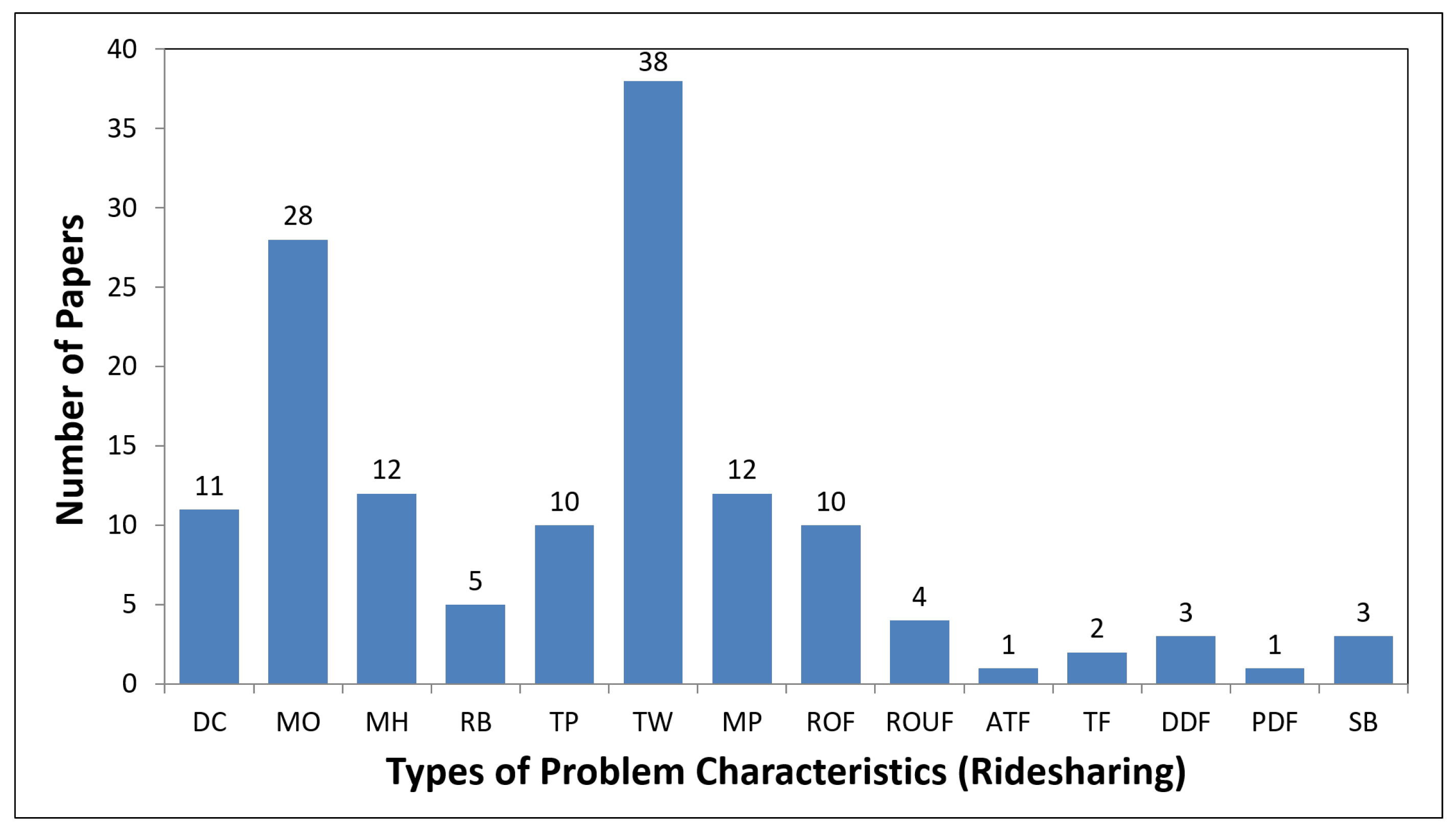
4.1. Ridesharing Problem
4.1.1. Exact Algorithms
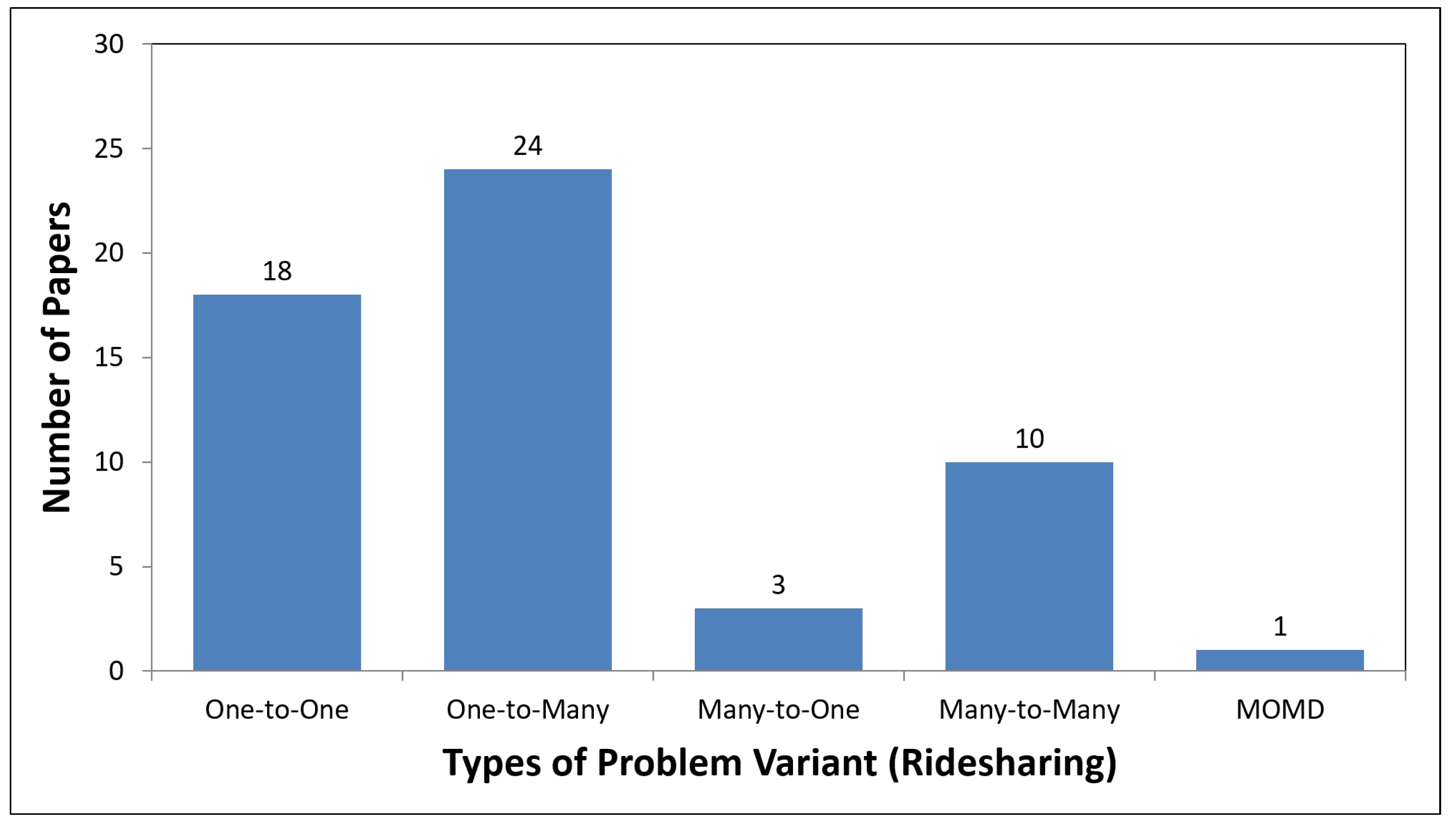
One-to-One Ridesharing Problem
One-to-Many Ridesharing Problem
Many-to-Many Ridesharing Problem
4.1.2. Heuristic and Metaheuristic Algorithms
One-to-One Ridesharing Problem
One-to-Many Ridesharing Problem
Many-to-One Ridesharing Problem
Many-to-Many Ridesharing Problem
Multiple Origins–Multiple Destinations Ridesharing Problem
4.1.3. Other Algorithms
One-to-One Ridesharing Problem
One-to-Many Ridesharing Problem
4.2. Carpooling Problem
4.2.1. Exact Algorithms
One-to-Many Carpooling Problem
Multiple Origins–Multiple Destinations Carpooling Problem
4.2.2. Heuristic and Metaheuristic Algorithms
One-to-One Carpooling Problem
One-to-Many Carpooling Problem
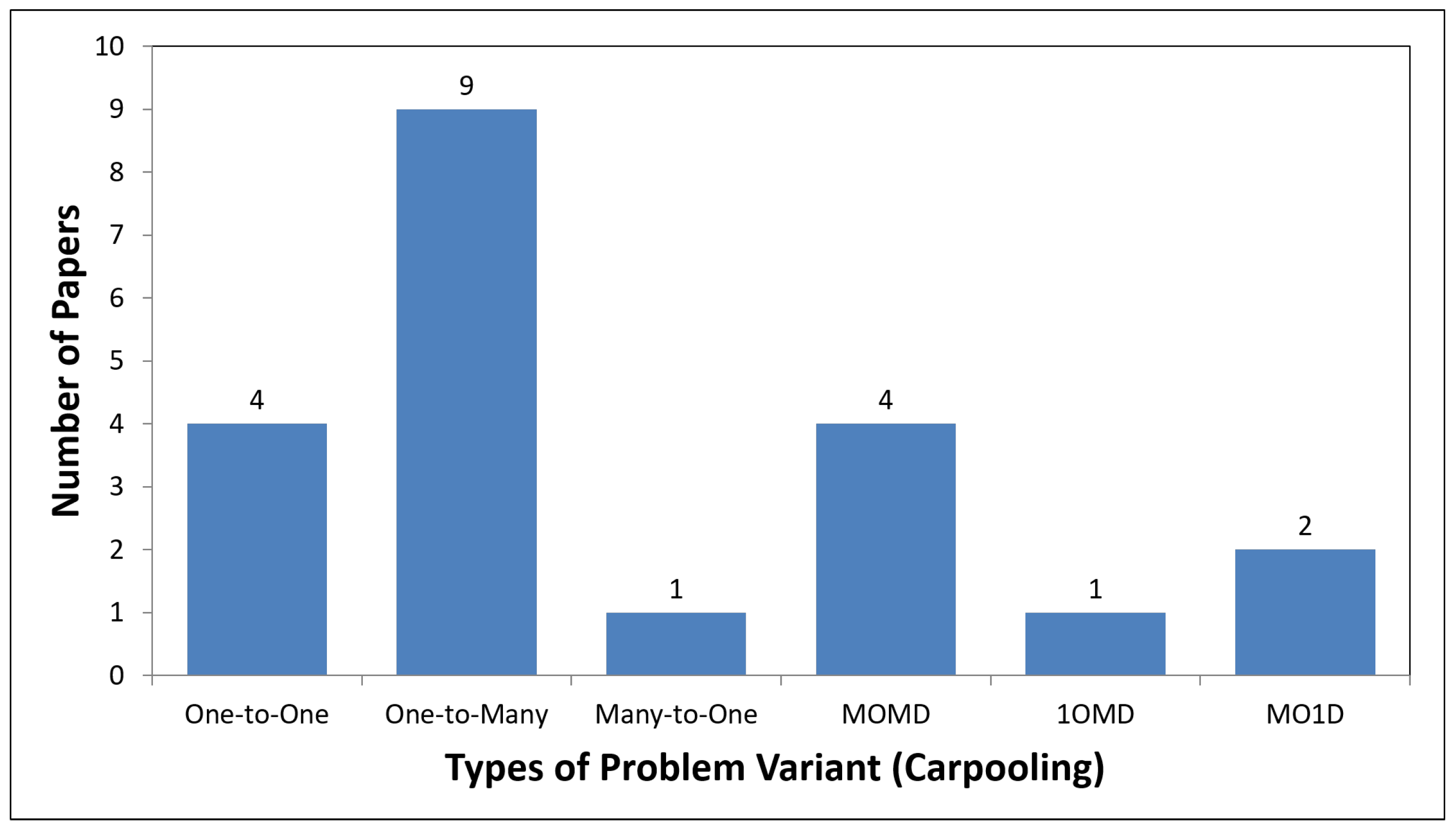
Many-to-One Carpooling Problem
Multiple Origins–One Destination Carpooling Problem
One Origin–Multiple Destinations Carpooling Problem
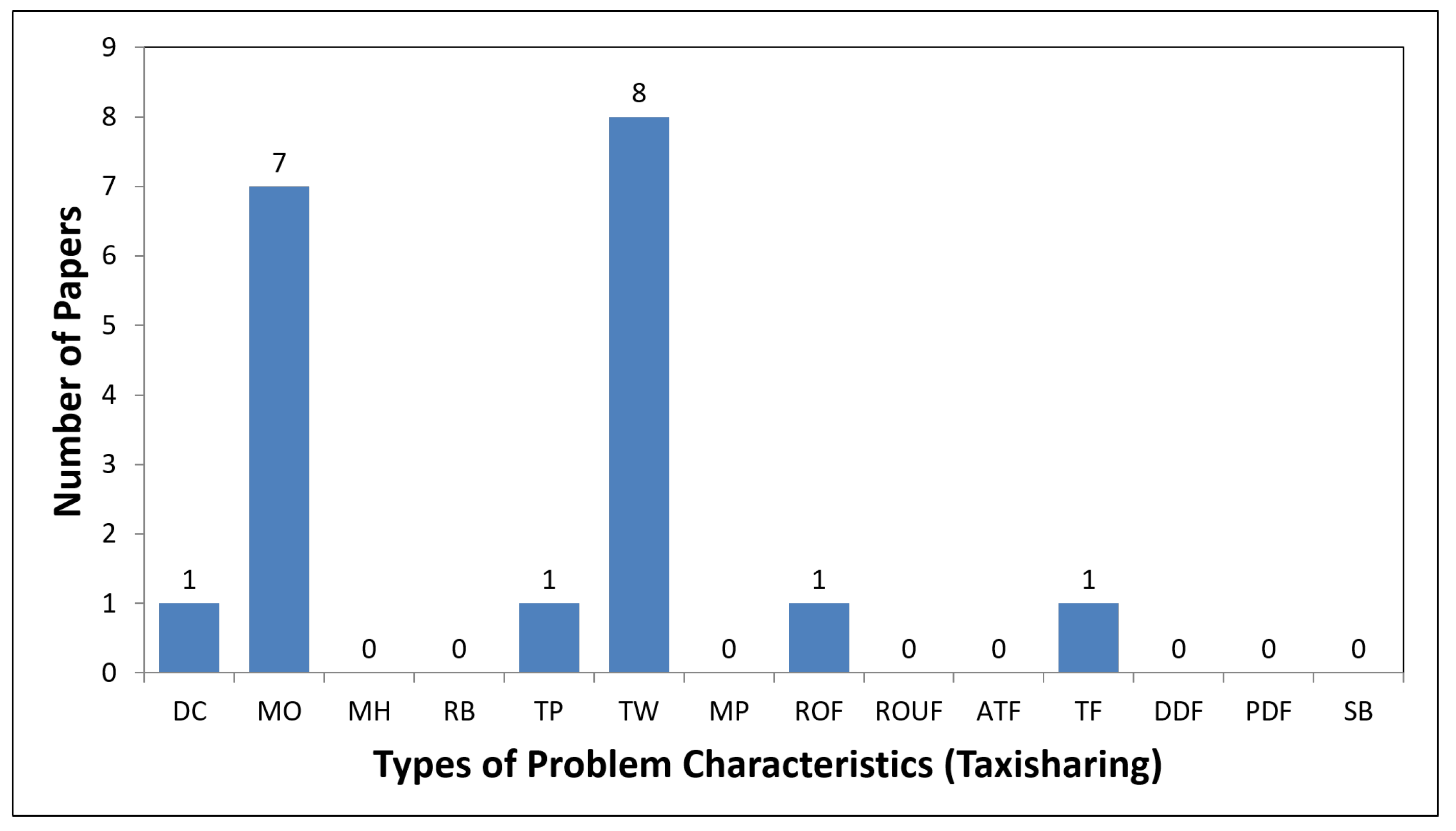
4.3. Taxisharing Problem
4.3.1. Exact Algorithms
One-to-One Taxisharing Problem
One-to-Many Taxisharing Problem
4.3.2. Heuristic and Metaheuristic Algorithms
One-to-One Taxisharing Problem
One-to-Many Taxisharing Problem
Many-to-Many Taxisharing Problem
One Origin–Multi Destinations Taxisharing Problem
Multiple Origins–Multiple Destinations Taxisharing Problem
4.4. Buspooling Problem
Heuristic and Metaheuristic Algorithms
One-to-One Buspooling Problem
One-to-Many Buspooling Problem
4.5. Vanpooling Problem
4.6. Multi-Modal Problem
4.6.1. Exact Algorithms in the Multi-Modal Problem
4.6.2. Heuristic and Metaheuristic Algorithms in Multi-Modal Problems
4.6.3. Other Algorithms in the Multi-Modal Problem
5. Current Trends
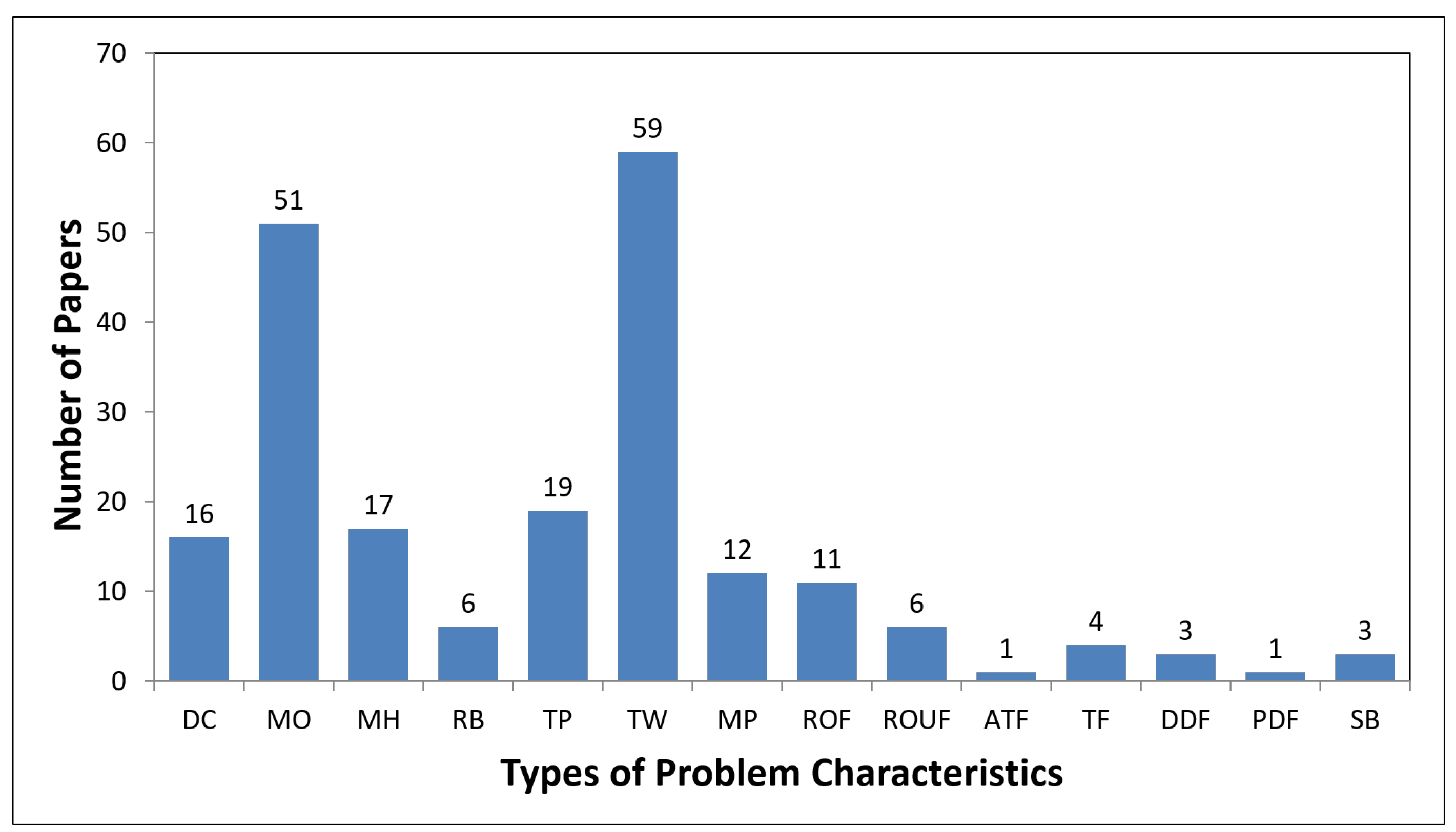
5.1. Descriptive Analysis
5.2. Overall Observations
6. Challenges and Future Works
6.1. Adoption of Hybrid Algorithms
6.2. Revitalisation of SMP during the Covid-19 Pandemic
6.3. Implementation of SMP into Mobility as a Service
6.4. Adoption of Electric Vehicles in SMP
6.5. Inclusion of Multi-Tier and Multi-Modal Characteristic into Combined People and Freight Transportation Service with the rideshare Concept
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| P2P | Peer-to-Peer |
| SMP | Shared Mobility Problem |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analysis |
| 1–1 | One-to-One |
| 1–M | One-to-Many |
| M–1 | Many-to-One |
| M–M | Many-to-Many |
| 1O1D | One Origin–One Destination |
| 1OMD | One Origin–Multiple Destinations |
| MO1D | Multiple Origins–One Destination |
| MOMD | Multiple Origins–Multiple Destinations |
References
- Furuhata, M.; Dessouky, M.; Ordóñez, F.; Brunet, M.E.; Wang, X.; Koenig, S. Ridesharing: The state-of-the-art and future directions. Transp. Res. Part B Methodol. 2013, 57, 28–46. [Google Scholar] [CrossRef]
- Chan, N.D.; Shaheen, S.A. Ridesharing in North America: Past, present, and future. Transp. Rev. 2012, 32, 93–112. [Google Scholar] [CrossRef]
- Shaheen, S.; Cohen, A.; Zohdy, I. Shared Mobility: Current Practices and Guiding Principles; U.S. Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2016.
- Amey, A.; Attanucci, J.; Mishalani, R. Real-time ridesharing: Opportunities and challenges in using mobile phone technology to improve rideshare services. Transp. Res. Rec. 2011, 2217, 103–110. [Google Scholar] [CrossRef]
- Agatz, N.; Erera, A.L.; Savelsbergh, M.W.; Wang, X. Optimization for dynamic ride-sharing: A Review. Eur. J. Oper. Res. 2012, 223, 295–303. [Google Scholar] [CrossRef]
- Siddiqi, Z.; Buliung, R. Dynamic ridesharing and information and communications technology: Past, present and future prospects. Transp. Plan. Technol. 2013, 36, 479–498. [Google Scholar] [CrossRef]
- Tafreshian, A.; Masoud, N.; Yin, Y. Frontiers in service science: Ride matching for peer-to-peer ride sharing: A review and future directions. Serv. Sci. 2020, 12, 44–60. [Google Scholar] [CrossRef]
- Martins, L.D.C.; de la Torre, R.; Corlu, C.G.; Juan, A.A.; Masmoudi, M.A. Optimizing ride-sharing operations in smart sustainable cities: Challenges and the need for agile algorithms. Comput. Ind. Eng. 2021, 153, 107080. [Google Scholar] [CrossRef]
- Shasheen, S.; Cohen, A. Shared ride services in North America: Definitions, impacts, and the future of pooling. Trans. Rev. 2019, 39, 427–442. [Google Scholar] [CrossRef]
- Stewart, L.A.; Clarke, M.; Rovers, M.; Riley, R.D.; Simmonds, M.; Stewart, G.; Tierney, J.F. Preferred reporting items for a systematic review and meta-analysis of individual participant data: The PRISMA-IPD statement. JAMA 2015, 313, 1657–1665. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med. 2009, 6, e1000097. [Google Scholar] [CrossRef] [Green Version]
- Neilson, A.; Daniel, B.; Tjandra, S. Systematic review of the literature on big data in the transportation domain: Concepts and applications. Big Data Res. 2019, 17, 35–44. [Google Scholar] [CrossRef]
- Cheng, X.; Su, L.; Yang, B. An investigation into sharing economy enabled ridesharing drivers’ trust: A qualitative study. Electron. Commer. Res. Appl. 2020, 40, 100956. [Google Scholar] [CrossRef]
- Ma, J.; Xu, M.; Meng, Q.; Cheng, L. Ridesharing user equilibrium problem under od-based surge pricing strategy. Transp. Res. Part B Methodol. 2020, 134, 1–24. [Google Scholar] [CrossRef]
- Yan, S.; Chen, C.Y.; Lin, Y.F. A model with a heuristic algorithm for solving the long-term many-to-many car pooling problem. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1362–1373. [Google Scholar] [CrossRef]
- Agatz, N.; Erera, A.L.; Savelsbergh, M.W.; Wang, X. Dynamic ride-sharing: A simulation study in metro Atlanta. Procedia Soc. Behav. Sci. 2011, 17, 532–550. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Agatz, N.; Erera, A. Stable matching for dynamic ride-sharing systems. Transp. Sci. 2018, 52, 850–867. [Google Scholar] [CrossRef]
- Pelzer, D.; Xiao, J.; Zehe, D.; Lees, M.H.; Knoll, A.C.; Aydt, H. A partition-based match making algorithm for dynamic ridesharing. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2587–2598. [Google Scholar] [CrossRef] [Green Version]
- Stiglic, M.; Agatz, N.; Savelsbergh, M.; Gradisar, M. Making dynamic ride-sharing work: The impact of driver and rider flexibility. Transp. Res. Part E Log. 2016, 91, 190–207. [Google Scholar] [CrossRef]
- Tafreshian, A.; Masoud, N. Using subsidies to stabilize peer-to-peer ridesharing markets with role assignment. Transp. Res. Part C Emerg. Technol. 2020, 120, 102770. [Google Scholar] [CrossRef]
- Armant, V.; Brown, K.N. Minimizing the driving distance in ride sharing systems. In Proceedings of the 2014 IEEE 26th International Conference on Tools with Artificial Intelligence, Limassol, Cyprus, 10–12 November 2014; pp. 568–575. [Google Scholar]
- Yu, Y.; Wu, Y.; Wang, J. Bi-objective green ride-sharing problem: Model and exact method. Int. J. Prod. Econ. 2019, 208, 472–482. [Google Scholar] [CrossRef]
- Armant, V.; Brown, K.N. Fast optimised ridesharing: Objectives, reformulations and driver flexibility. Transp. Res. Rec. 2020, 141, 112914. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Samaranayake, S.; Wallar, A.; Frazzoli, E.; Rus, D. On-demand high-capacity ride-sharing via dynamic trip-vehicle assignment. Proc. Natl. Acad. Sci. USA 2017, 114, 462–467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masoud, N.; Jayakrishnan, R. A decomposition algorithm to solve the multi-hop peer-to-peer ride-matching problems. Transp. Res. Part B Methodol. 2017, 99, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Masoud, N.; Jayakrishnan, R. A real-time algorithm to solve the peer-to-peer ride-matching problem in a flexible ridesharing system. Transp. Res. Part B Methodol. 2017, 106, 218–236. [Google Scholar] [CrossRef]
- Masoud, N.; Lloret-Batlle, R.; Jayakrishnan, R. Using bilateral trading to increase ridership and user permanence in ridesharing systems. Transp. Res. Part E Log. 2017, 102, 60–77. [Google Scholar] [CrossRef]
- Lotfi, S.; Abdelghany, K.; Hashemi, H. Modeling framework and decomposition scheme for on-demand mobility services with ridesharing and transfer. Comput.-Aided Civ. Inf. 2019, 34, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chung, S.H. Ride-sharing under travel time uncertainty: Robust optimization and clustering approaches. Comput. Ind. Eng. 2020, 149, 106601. [Google Scholar] [CrossRef]
- Aissat, K.; Oulamara, A. Dynamic ridesharing with intermediate locations. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Vehicles and Transportation Systems, Orlando, FL, USA, 9–12 December 2014; pp. 36–42. [Google Scholar]
- Aissat, K.; Oulamara, A. A priori approach of real-time ridesharing problem with intermediate meeting locations. J. Artif. Intell. Soft Comput. Res. 2014, 4. [Google Scholar] [CrossRef] [Green Version]
- Aissat, K.; Oulamara, A. A posteriori approach of real-time ridesharing problem with intermediate locations. In Proceedings of the 2015 International Conference on Operations Research and Enterprise Systems, Lisbon, Portugal, 10–12 January 2015; pp. 63–74. [Google Scholar]
- Aissat, K.; Oulamara, A. The round-trip ridesharing problem with relay stations. In Proceedings of the 2015 International Conference on Computational Logistics, Delft, The Netherlands, 23–25 September 2015; pp. 16–30. [Google Scholar]
- Aissat, K.; Oulamara, A. Meeting locations in real-time ridesharing problem: A buckets approach. In Proceedings of the 2015 International Conference on Operations Research and Enterprise Systems, Lisbon, Portugal, 10–12 January 2015; pp. 71–92. [Google Scholar]
- Lee, A.; Savelsbergh, M. Dynamic ridesharing: Is there a role for dedicated drivers? Transp. Res. Part B Methodol. 2015, 81, 483–497. [Google Scholar] [CrossRef]
- Naoum-Sawaya, J.; Cogill, R.; Ghaddar, B.; Sajja, S.; Shorten, R.; Taheri, N.; Tommasi, P.; Verago, R.; Wirth, F. Stochastic optimization approach for the car placement problem in ridesharing systems. Transp. Res. Part B Methodol. 2015, 80, 173–184. [Google Scholar] [CrossRef]
- Najmi, A.; Rey, D.; Rashidi, T.H. Novel dynamic formulations for real-time ride-sharing systems. Transp. Res. Part E Log. 2017, 108, 122–140. [Google Scholar] [CrossRef]
- Simonetto, A.; Monteil, J.; Gambella, C. Real-time city-scale ridesharing via linear assignment problems. Transp. Res. Part C Emerg. Technol. 2019, 101, 208–232. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, X. A set-based differential evolution algorithm for qos-oriented and cost-effective ridesharing. Appl. Soft Comput. 2020, 96, 106618. [Google Scholar] [CrossRef]
- Aydin, O.F.; Gokasar, I.; Kalan, O. Matching algorithm for improving ride-sharing by incorporating route splits and social factors. PLoS ONE 2020, 15, e0229674. [Google Scholar] [CrossRef]
- Tafreshian, A.; Masoud, N. Trip-based graph partitioning in dynamic ridesharing. Transp. Res. Part C Emerg. Technol. 2020, 114, 532–553. [Google Scholar] [CrossRef]
- Guan, L.; Pei, J.; Liu, X.; Zhou, Z.; Pardalos, P.M. Ridesharing in urban areas: Multi-objective optimisation approach for ride-matching and routeing with commuters’ dynamic mode choice. Int. J. Prod. Res. 2020. [Google Scholar] [CrossRef]
- Herbawi, W.; Weber, M. Ant colony vs. genetic multiobjective route planning in dynamic multi-hop ridesharing. In Proceedings of the IEEE 23rd International Conference on Tools with Artificial Intelligence, Boca Raton, FL, USA, 7–9 November 2011; pp. 282–288. [Google Scholar]
- Herbawi, W.; Weber, M. Comparison of multiobjective evolutionary algorithms for solving the multiobjective route planning in dynamic multi-hop ridesharing. In Proceedings of the 2011 IEEE Congress on Evolutionary Computation, New Orleans, LA, USA, 5–8 June 2011; pp. 2099–2106. [Google Scholar]
- Herbawi, W.; Weber, M. Evolutionary multiobjective route planning in dynamic multi-hop ridesharing. In Proceedings of the 11th 2011 European Conference on Evolutionary Computation in Combinatorial Optimization, Torino, Italy, 27–29 April 2011; pp. 84–95. [Google Scholar]
- Herbawi, W.; Weber, M. The ridematching problem with time windows in dynamic ridesharing: A model and a genetic algorithm. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Herbawi, W.; Weber, M. A genetic local search algorithm for multiobjective time-dependent route planning. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–7. [Google Scholar]
- Herbawi, W.; Weber, M. A genetic and insertion heuristic algorithm for solving the dynamic ridematching problem with time windows. In Proceedings of the 14th Annual Conference on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; pp. 385–392. [Google Scholar]
- Herbawi, W.; Weber, M. Modeling the multihop ridematching problem with time windows and solving it using genetic algorithms. In Proceedings of the 2012 IEEE 24th International Conference on Tools with Artificial Intelligence, Athens, Greece, 7–9 November 2012; pp. 89–96. [Google Scholar]
- Stiglic, M.; Agatz, N.; Savelsbergh, M.; Gradisar, M. The benefits of meeting points in ride-sharing systems. Transp. Res. Part B Methodol. 2015, 82, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Dessouky, M.; Ordonez, F. A pickup and delivery problem for ridesharing considering congestion. Transp. Lett. 2016, 8, 259–269. [Google Scholar] [CrossRef]
- Bian, Z.; Liu, X. Planning the ridesharing route for the first-mile service linking to railway passenger transportation. In Proceedings of the 2017 Joint Rail Conference, Philadelphia, PA, USA, 4–7 April 2017. [Google Scholar]
- Hou, L.; Li, D.; Zhang, D. Ride-matching and routing optimisation: Models and a large neighbourhood search heuristic. Transp. Res. Part E Log. 2018, 118, 143–162. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Hu, S.; Fan, W.; Deng, K. Modeling an enhanced ridesharing system with meet points and time windows. PLoS ONE 2018, 13, e0195927. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Yin, J.; An, S.; Wang, J.; Feng, D. Ridesharing problem with flexible pickup and delivery locations for app-based transportation service: Mathematical modeling and decomposition methods. J. Adv. Transp. 2018, 6430950. [Google Scholar] [CrossRef]
- Ma, R.; Yao, L.; Song, L.; Jin, M. A novel algorithm for peer-to-peer ridesharing match problem. Neural Comput. Appl. 2019, 31, 247–258. [Google Scholar] [CrossRef]
- Bian, Z.; Liu, X. Mechanism design for first-mile ridesharing based on personalized requirements part I: Theoretical analysis in generalized scenarios. Transp. Res. Part B Methodol. 2019, 120, 147–171. [Google Scholar] [CrossRef]
- Bian, Z.; Liu, X. Mechanism design for first-mile ridesharing based on personalized requirements part II: Solution algorithm for large-scale problems. Transp. Res. Part B Methodol. 2019, 120, 172–192. [Google Scholar] [CrossRef]
- Zhang, L.; Ye, Z.; Xiao, K.; Jin, B. A parallel simulated annealing enhancement of the optimal-matching heuristic for ridesharing. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM) Beijing, Beijing, China, 8–11 November 2019; pp. 906–915. [Google Scholar]
- Chen, S.; Wang, H.; Meng, Q. Solving the first-mile ridesharing problem using autonomous vehicles. Comput.-Aided Civ. Inf. 2020, 35, 45–60. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, S.; Li, J. The optimization model of ridesharing route for ride hailing considering both system optimization and user fairness. Sustainability 2021, 13, 902. [Google Scholar] [CrossRef]
- Cheikh, S.B.; Hammadi, S. Multi-hop ridematching optimization problem: Intelligent chromosome agent-driven approach. Expert Syst. Appl. 2012, 62, 161–176. [Google Scholar] [CrossRef]
- Ben Cheikh, S.; Tahon, C.; Hammadi, S. An evolutionary approach to solve the dynamic multihop ridematching problem. Simulation 2017, 93, 3–19. [Google Scholar] [CrossRef]
- Chen, W.; Mes, M.; Schutten, M.; Quint, J. A ride-sharing problem with meeting points and return restrictions. Transp. Sci. 2019, 53, 401–426. [Google Scholar] [CrossRef] [Green Version]
- Cheikh-Graiet, S.B.; Dotoli, M.; Hammadi, S. A tabu search based metaheuristic for dynamic carpooling optimization. Comput. Ind. Eng. 2020, 140, 106217. [Google Scholar] [CrossRef]
- Lu, W.; Liu, L.; Wang, F.; Zhou, X.; Hu, G. Two-phase optimization model for ride-sharing with transfers in short-notice evacuations. Transp. Res. Part C Emerg. Technol. 2020, 114, 272–296. [Google Scholar] [CrossRef]
- Smet, P. Ride sharing with flexible participants: A metaheuristic approach for large-scale problems. Int. Trans. Oper. Res. 2021, 28, 91–118. [Google Scholar] [CrossRef]
- Lloret-Batlle, R.; Masoud, N.; Nam, D. Peer-to-peer ridesharing with ride-back on high-occupancy-vehicle lanes: Toward a practical alternative mode for daily commuting. Transp. Res. Rec. 2017, 2668, 21–28. [Google Scholar] [CrossRef]
- Long, J.; Tan, W.; Szeto, W.; Li, Y. Ride-sharing with travel time uncertainty. Transp. Res. Part B Methodol. 2018, 118, 143–171. [Google Scholar] [CrossRef]
- Di Febbraro, A.; Gattorna, E.; Sacco, N. Optimization of dynamic ridesharing systems. Transp. Res. Rec. 2013, 2359, 44–50. [Google Scholar] [CrossRef]
- Bit-Monnot, A.; Artigues, C.; Huguet, M.J.; Killijian, M.O. Carpooling: The 2 synchronization points shortest paths problem. In Proceedings of the 13th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems, Sophia Antipolis, France, 5 September 2013. [Google Scholar]
- Tamannaei, M.; Irandoost, I. Carpooling problem: A new mathematical model, branch-and-bound, and heuristic beam search algorithm. J. Intell. Transp. Syst. 2019, 23, 203–215. [Google Scholar] [CrossRef]
- Yan, S.; Chen, C.Y. An optimization model and a solution algorithm for the many-to-many car pooling problem. Ann. Oper. Res. 2011, 191, 37–71. [Google Scholar] [CrossRef]
- Yan, S.; Chen, C.Y. A model and a solution algorithm for the car pooling problem with pre-matching information. Comput. Ind. Eng. 2011, 63, 512–524. [Google Scholar] [CrossRef]
- Yan, S.; Chen, C.Y.; Chang, S.C. A car pooling model and solution method with stochastic vehicle travel times. IEEE Trans. Intell. Transp. Syst. 2013, 15, 47–61. [Google Scholar] [CrossRef]
- Bruck, B.P.; Incerti, V.; Iori, M.; Vignoli, M. Minimizing CO2 emissions in a practical daily carpooling problem. Comput. Oper. Res. 2017, 81, 40–50. [Google Scholar] [CrossRef]
- Duan, Y.; Wu, J.; Zheng, H. A greedy approach for carpool scheduling optimisation in smart cities. Int. J. Parallel Emergent Distrib. Syst. 2020, 35, 535–549. [Google Scholar] [CrossRef]
- Hsieh, F.S.; Zhan, F.M. A discrete differential evolution algorithm for carpooling. In Proceedings of the 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), Tokyo, Japan, 23–27 July 2018; pp. 577–582. [Google Scholar]
- Wu, C.; Shankari, K.; Kamar, E.; Katz, R.; Culler, D.; Papadimitriou, C.; Horvitz, E.; Bayen, A. Optimizing the diamond lane: A more tractable carpool problem and algorithms. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1389–1396. [Google Scholar]
- Hsieh, F.S.; Zhan, F.M.; Guo, Y.H. A solution methodology for carpooling systems based on double auctions and cooperative coevolutionary particle swarms. Appl. Intell. 2019, 49, 741–763. [Google Scholar] [CrossRef]
- Huang, S.C.; Jiau, M.K.; Lin, C.H. A genetic-algorithm based approach to solve carpool service problems in cloud computing. IEEE Trans. Intell. Transp. Syst. 2014, 16, 352–364. [Google Scholar] [CrossRef]
- Huang, S.C.; Jiau, M.K.; Lin, C.H. Optimization of the carpool service problem via a fuzzy-controlled genetic algorithm. IEEE Trans. Fuzzy Syst. 2014, 23, 1698–1712. [Google Scholar] [CrossRef]
- Huang, S.C.; Jiau, M.K.; Chong, K.H. A heuristic multiobjective optimization algorithm for solving the carpool services problem featuring high-occupancy-vehicle itineraries. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2663–2674. [Google Scholar] [CrossRef]
- Huang, S.C.; Jiau, M.K.; Liu, Y.P. An ant path-oriented carpooling allocation approach to optimize the carpool service problem with time windows. IEEE Syst. J. 2018, 13, 994–1005. [Google Scholar] [CrossRef]
- Xia, J.; Curtin, K.M.; Li, W.; Zhao, Y. A new model for a carpool matching service. PLoS ONE 2015, 10, e0129257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chou, S.K.; Jiau, M.K.; Huang, S.C. Stochastic set-based particle swarm optimization based on local exploration for solving the carpool service problem. IEEE Trans. Cybern. 2016, 46, 1771–1783. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, D.; Si, Y.W.; Leung, S.C. Tabu search for the real-world carpooling problem. J. Comb. Optim. 2016, 32, 492–512. [Google Scholar] [CrossRef]
- Su, S.; Zhou, F.; Yu, H. An artificial bee colony algorithm with variable neighborhood search and tabu list for long-term carpooling problem with time window. Appl. Soft Comput. 2019, 85, 105814. [Google Scholar] [CrossRef]
- Guo, Y.; Goncalves, G.; Hsu, T. A multi-destination daily carpooling problem and an ant colony based resolution method. RAIRO Oper. Res. 2013, 47, 399–428. [Google Scholar] [CrossRef]
- Hosni, H.; Naoum-Sawaya, J.; Artail, H. The shared-taxi problem: Formulation and solution methods. Transp. Res. Part B Methodol. 2014, 70, 303–318. [Google Scholar] [CrossRef]
- Du, X.; Hu, D.; Tian, S.; Xu, T. A route choice and rate optimization model of taxisharing based on different time. In Proceedings of the 16th COTA International Conference of Transportation Professionals, Shanghai, China, 6–9 July 2016; pp. 714–723. [Google Scholar]
- Qian, X.; Zhang, W.; Ukkusuri, S.V.; Yang, C. Optimal assignment and incentive design in the taxi group ride problem. Transp. Res. Part B Methodol. 2017, 103, 208–226. [Google Scholar] [CrossRef]
- Jung, J.; Jayakrishnan, R.; Park, J.Y. Dynamic shared-taxi dispatch algorithm with hybrid-simulated annealing. Comput.-Aided Civ. Inf. 2016, 31, 275–291. [Google Scholar] [CrossRef]
- Lin, Y.; Li, W.; Qiu, F.; Xu, H. Research on optimization of vehicle routing problem for ride-sharing taxi. Procedia Soc. Behav. Sci. 2012, 43, 494–502. [Google Scholar] [CrossRef] [Green Version]
- Ye, Q.; Ma, C.; He, R.; Xiao, Q.; Zhang, W. Multi-objective optimisation for taxi ridesharing route based on non-dominated sorting genetic algorithm. Int. J. Wireless Mobile Comput. 2015, 8, 262–270. [Google Scholar] [CrossRef]
- Ma, C.; He, R.; Zhang, W. Path optimization of taxi carpooling. PLoS ONE 2018, 13, e0203221. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhang, L. Potential of taxi-pooling to reduce vehicle miles traveled in Washington, DC. Transp. Res. Rec. 2018, 2672, 775–784. [Google Scholar] [CrossRef]
- Ren, C.; Wang, J.; You, Y.; Zhang, Y. Routing optimization for shared electric vehicles with ride-sharing. Complexity 2020, 1–13. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Yuan, Z.; Wang, C.; Zhang, L. The research on planning of taxi sharing route and sharing expenses. Math. Probl. Eng. 2020, 1–9. [Google Scholar] [CrossRef]
- Santos, D.O.; Xavier, E.C. Dynamic taxi and ridesharing: A framework and heuristics for the optimization problem. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 2885–2891. [Google Scholar]
- Santos, D.O.; Xavier, E.C. Taxi and ride sharing: A dynamic dial-a-ride problem with money as an incentive. Expert Syst. Appl. 2015, 42, 6728–6737. [Google Scholar] [CrossRef]
- Massobrio, R.; Fagúndez, G.; Nesmachnow, S. Multiobjective evolutionary algorithms for the taxi sharing problem. Int. J. Metaheuristics 2016, 5, 67–90. [Google Scholar] [CrossRef]
- Yan, S.; Chen, C.Y.; Wu, C.C. Solution methods for the taxi pooling problem. Transportation 2012, 39, 723–748. [Google Scholar] [CrossRef]
- Chen, C.Y.; Yan, S.; Wu, Y.S. A model for taxi pooling with stochastic vehicle travel times. Int. J. Sustain. Transp. 2019, 13, 582–596. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, J.; Yang, Q. Bus pooling: A large-scale bus ridesharing service. IEEE Access 2019, 7, 74248–74262. [Google Scholar] [CrossRef]
- Liu, K.; Liu, J. Optimization approach to improve the ridesharing success rate in the bus ridesharing service. IEEE Access 2020, 8, 208296–208310. [Google Scholar] [CrossRef]
- Kaan, L.; Olinick, E.V. The vanpool assignment problem: Optimization models and solution algorithms. Comput. Ind. Eng. 2013, 66, 24–40. [Google Scholar] [CrossRef]
- Cangialosi, E.; Di Febbraro, A.; Sacco, N. Designing a multimodal generalised ride sharing system. IET Intell. Transp. Syst. 2016, 10, 227–236. [Google Scholar] [CrossRef]
- Regue, R.; Masoud, N.; Recker, W. Car2work: Shared mobility concept to connect commuters with workplaces. Transp. Res. Rec. 2016, 2542, 102–110. [Google Scholar] [CrossRef]
- Masoud, N.; Nam, D.; Yu, J.; Jayakrishnan, R. Promoting peer-to-peer ridesharing services as transit system feeders. Transp. Res. Rec. 2017, 2650, 74–83. [Google Scholar] [CrossRef]
- Nam, D.; Yang, D.; An, S.; Yu, J.G.; Jayakrishnan, R.; Masoud, N. Designing a transit-feeder system using multiple sustainable modes: Peer-to-peer (P2P) ridesharing, bike sharing, and walking. Transp. Res. Rec. 2018, 2672, 754–763. [Google Scholar] [CrossRef]
- Stiglic, M.; Agatz, N.; Savelsbergh, M.; Gradisar, M. Enhancing urban mobility: Integrating ride-sharing and public transit. Comput. Oper. Res. 2018, 90, 12–21. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Bucher, D.; Kissling, J.; Weibel, R.; Raubal, M. Multimodal route planning with public transport and carpooling. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3513–3525. [Google Scholar] [CrossRef]
- Enzi, M.; Parragh, S.N.; Pisinger, D.; Prandtstetter, M. Modeling and solving the multimodal car-and ride-sharing problem. Eur. J. Oper. Res. 2021, 293, 290–303. [Google Scholar] [CrossRef]
- Yu, X.; Miao, H.; Bayram, A.; Yu, M.; Chen, X. Optimal routing of multimodal mobility systems with ride-sharing. Int. Trans. Oper. Res. 2021, 28, 1164–1189. [Google Scholar] [CrossRef]
- Ma, T.Y. On-demand dynamic bi-/multi-modal ride-sharing using optimal passenger-vehicle assignments. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe, Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar]
- Auad, R.; Van Hentenryck, P. Ridesharing and fleet sizing for on-demand multimodal transit systems. arXiv 2021, arXiv:2101.10981. [Google Scholar]
- El-Sherbeny, N.A. Vehicle routing with time windows: An overview of exact, heuristic and metaheuristic methods. J. King Saud Univ. Sci. 2010, 22, 123–131. [Google Scholar] [CrossRef] [Green Version]
- Raidl, G.R.; Puchinger, J.; Blum, C. Metaheuristic hybrids. In Handbook of Metaheuristics, 3rd ed.; Gendreau, M., Potvin, J., Eds.; Springer: New York, NY, USA, 2019; pp. 385–417. [Google Scholar]
- Sorensen, K.; Sevaux, M.; Glover, F. A history of metaheuristics. In Handbook of Heuristics, 1st ed.; Martı, R., Pardalos, P.M., Resende, M.G.C., Eds.; Springer: New York, NY, USA, 2018; pp. 791–808. [Google Scholar]
- Shokouhyar, S.; Shokoohyar, S.; Sobhani, A.; Gorizi, A.J. Shared mobility in post-COVID era: New challenges and opportunities. Sustain. Cities Soc. 2021, 67, 102714. [Google Scholar] [CrossRef]
- Awad-Núñez, S.; Julio, R.; Gomez, J.; Moya-Gómez, B.; González, J.S. Post-COVID-19 travel behaviour patterns: Impact on the willingness to pay of users of public transport and shared mobility services in Spain. Eur. Transp. Res. Rev. 2021, 13, 1–18. [Google Scholar] [CrossRef]
- Kubal’ák, S.; Kalašová, A.; Hájnik, A. The bike-sharing system in Slovakia and the impact of COVID-19 on this shared mobility service in a selected city. Sustainability 2021, 13, 6544. [Google Scholar] [CrossRef]
- Hu, X.; Giang, N.K.; Shen, J.; Leung, V.C.; Li, X. Towards mobility-as-a-service to promote smart transportation. In Proceedings of the 2015 IEEE 82nd Vehicular Technology Conference: VTC2015-Fall, Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar]
- Jittrapirom, P.; Caiati, V.; Feneri, A.M.; Ebrahimigharehbaghi, S.; Alonso González, M.J.; Narayan, J. Mobility as a service: A critical review of definitions, assessments of schemes, and key challenges. Urban Plan. 2017, 2, 13–25. [Google Scholar] [CrossRef] [Green Version]
- Najmi, A.; Rashidi, T.H.; Liu, W. Ridesharing in the era of mobility as a service (MAAS): An activity-based approach with multimodality and intermodality. arXiv 2020, arXiv:2002.11712. [Google Scholar]
- Farhan, J.; Chen, T.D. Impact of ridesharing on operational efficiency of shared autonomous electric vehicle fleet. Transp. Res. Part C Emerg. Technol. 2018, 93, 310–321. [Google Scholar] [CrossRef]
- Muthukumar, M.; Rengarajan, N.; Velliyangiri, B.; Omprakas, M.; Rohit, C.; Raja, U.K. The development of fuel cell electric vehicles—A review. Mater. Today Proc. 2020, 3, 679. [Google Scholar] [CrossRef]
- Ogden, J.; Jaffe, A.M.; Scheitrum, D.; McDonald, Z.; Miller, M. Natural gas as a bridge to hydrogen transportation fuel: Insights from the literature. Energy Policy 2018, 115, 317–329. [Google Scholar] [CrossRef]
- Salimifard, K.; Raeesi, R. A green routing problem: Optimising co2 emissions and costs from a bi-fuel vehicle fleet. Int. J. Adv. Ops. Manag. 2014, 6, 27–57. [Google Scholar]
- Gnann, T.; Plötz, P. A review of combined models for market diffusion of alternative fuel vehicles and their refueling infrastructure. Renew. Sustain. Energy Rev. 2015, 47, 783–793. [Google Scholar] [CrossRef]
- Nassif, G.G.; de Almeida, S.C. Impact of powertrain hybridization on the performance and costs of a fuel cell electric vehicle. Int. J. Hydrogen Energy 2020, 45, 21722–21737. [Google Scholar] [CrossRef]
- Li, B.; Krushinsky, D.; Reijers, H.A.; Van Woensel, T. The share-a-ride problem: People and parcels sharing taxis. Eur. J. Oper. Res. 2014, 238, 31–40. [Google Scholar] [CrossRef] [Green Version]
- Ghilas, V.; Demir, E.; Van Woensel, T. The pickup and delivery problem with time windows and scheduled lines. Inf. Syst. Oper. Res. 2016, 54, 147–167. [Google Scholar] [CrossRef] [Green Version]
- Masson, R.; Trentini, A.; Lehuédé, F.; Malhéné, N.; Péton, O.; Tlahig, H. Optimization of a city logistics transportation system with mixed passengers and goods. EURO J. Transp. Logist. 2017, 6, 81–109. [Google Scholar] [CrossRef] [Green Version]

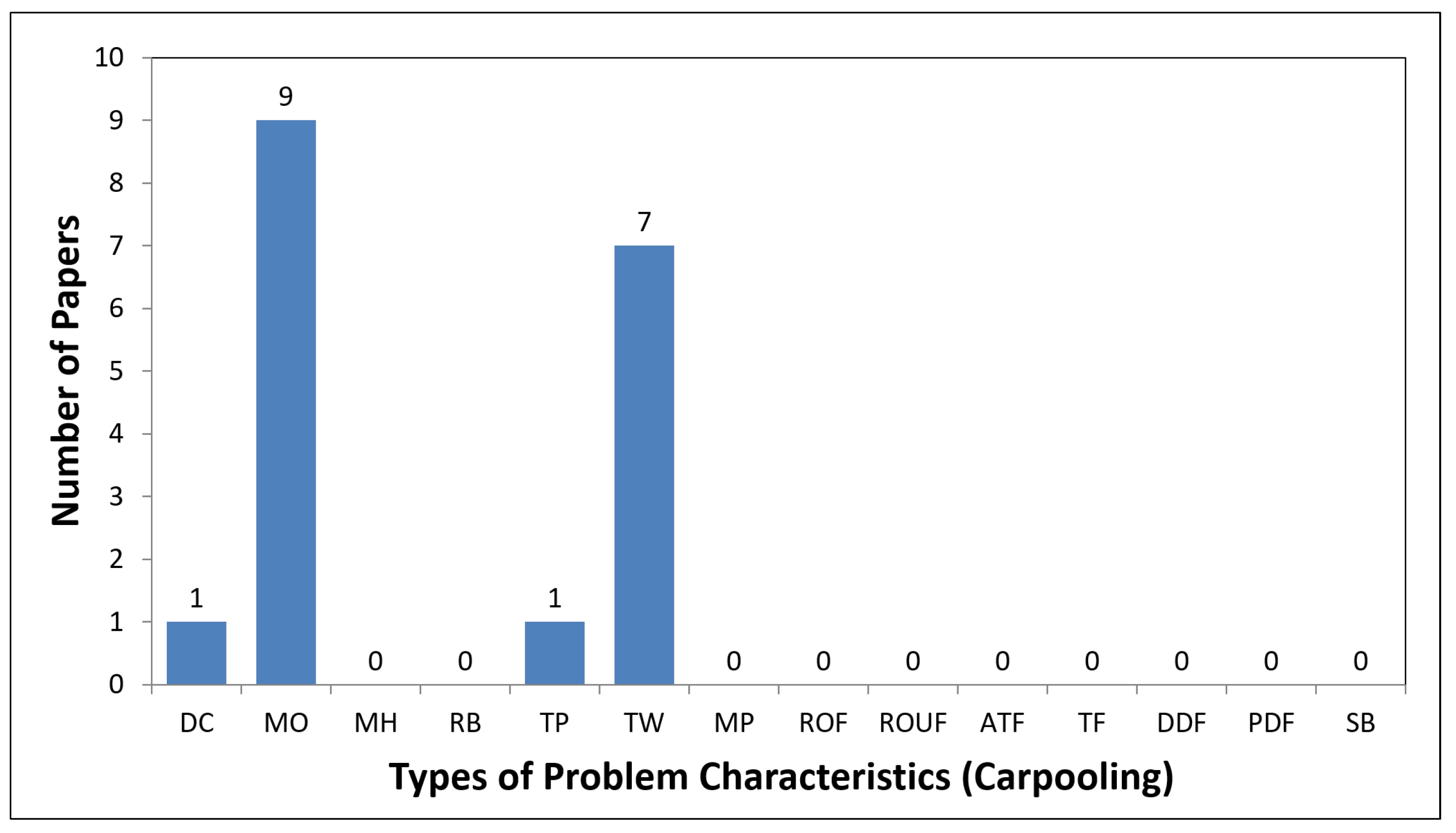

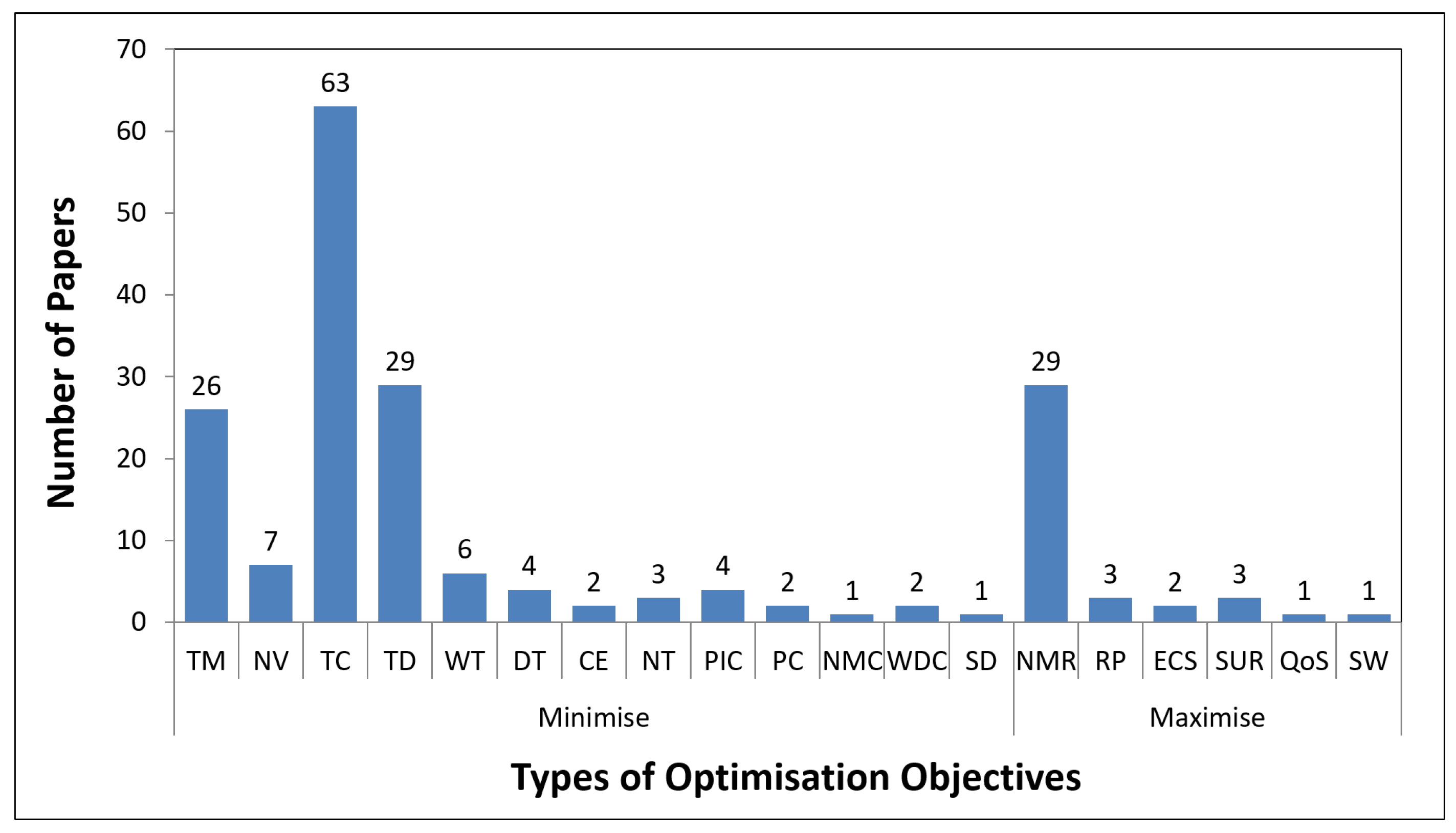
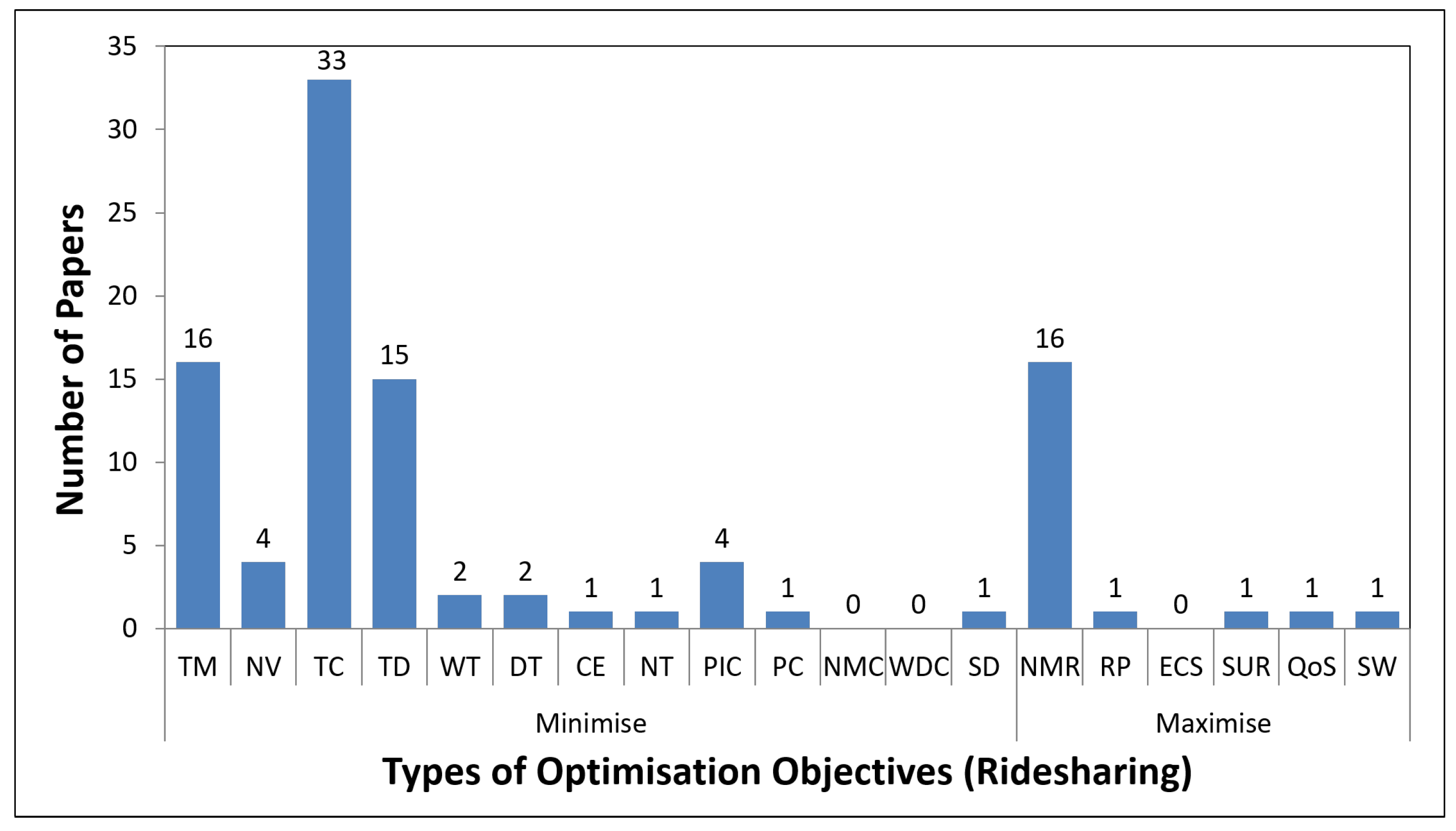

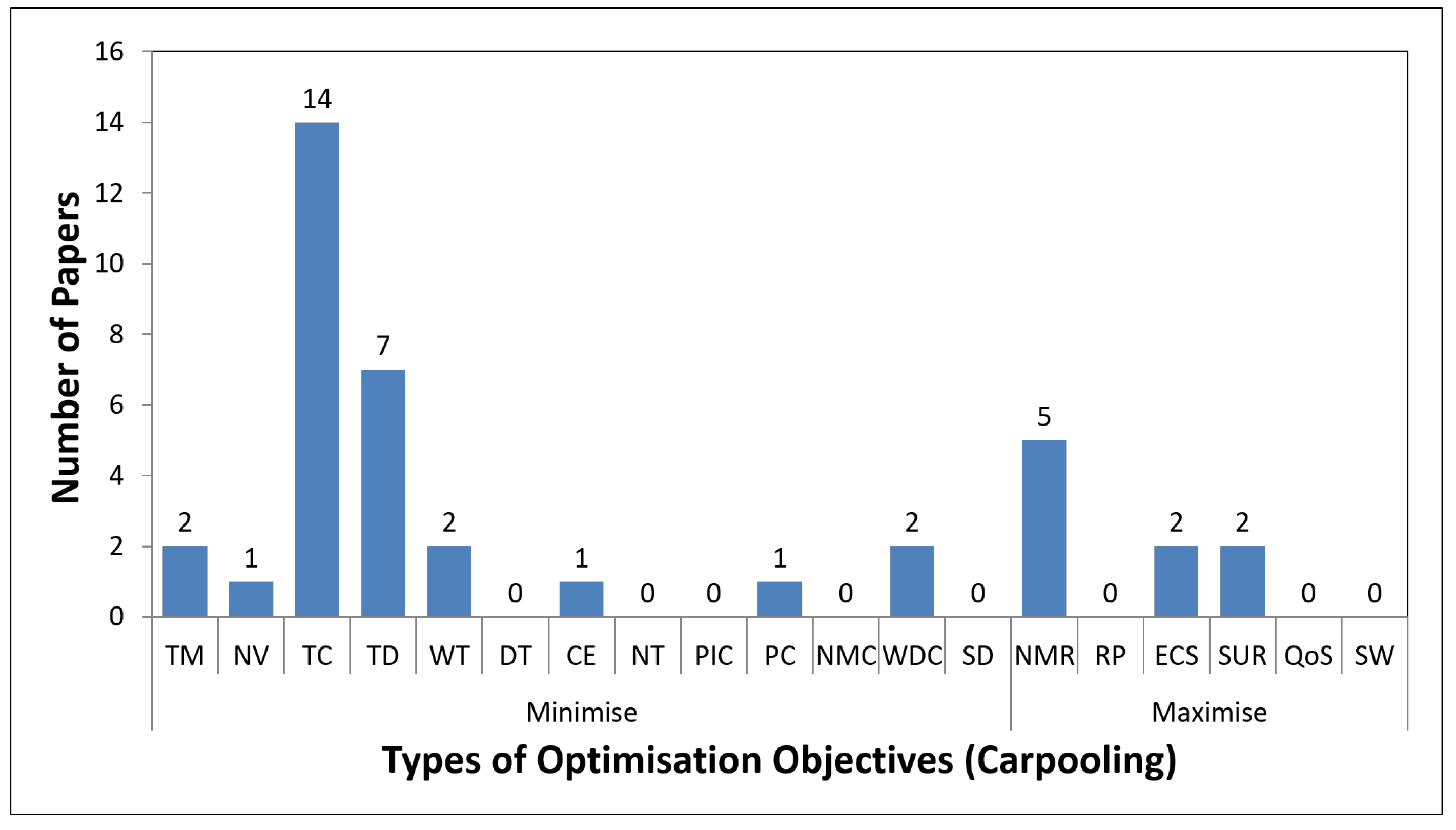

| Paper | Highlights | Year | Number of Papers |
|---|---|---|---|
| [4] | Challenges in economic, social, institutional, and technological aspects. Benefits and drawbacks of dynamic ridesharing. Future direction of dynamic ridesharing. | 1974–2010 | 12 |
| [5] | Characteristics of dynamic ridesharing, rideshare variants, and multi-modal ridesharing problem. | 1977 – 2012 | 38 |
| [2] | Explored the history of ridesharing in North America for five key phases. | 1942–2011 | 43 |
| [1] | Detailed classification of the ridesharing system and matching agencies. | 1961–2013 | 52 |
| [6] | Discussed the evolution of dynamic ridesharing from the past and present to its future with information and communication changes. | 1977–2011 | 19 |
| [7] | Reviewed P2P ridesharing variants literature with solution algorithms. Future direction is discussed. | 2004–2020 | 42 |
| [8] | Reviewed carsharing, ridesharing and carpooling with solution algorithms. Challenges and opportunities of ridesharing. | 2008–2019 | 86 |
| Type of Publication | Year | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | Total | |
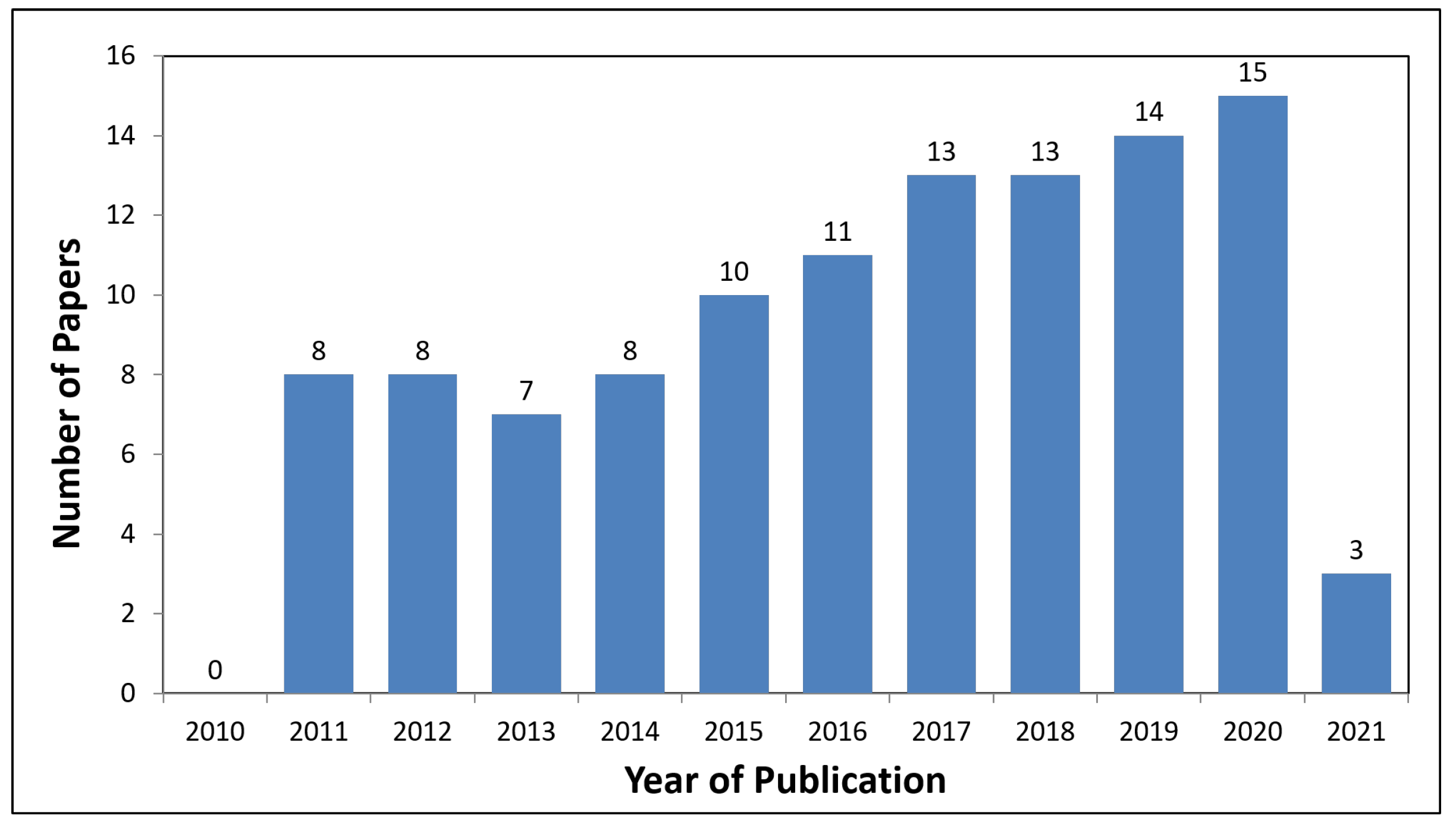
| Journal | 0 | 4 | 3 | 5 | 6 | 7 | 9 | 10 | 12 | 13 | 15 | 3 | 87 |
| Conference Proceedings | 0 | 4 | 5 | 2 | 2 | 3 | 2 | 3 | 1 | 1 | 0 | 0 | 23 |
| Total | 0 | 8 | 8 | 7 | 8 | 10 | 11 | 13 | 13 | 14 | 15 | 3 | 110 |
| Country | Year | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | Total | |
| USA | 0 | 1 | 3 | 1 | 4 | 1 | 2 | 5 | 5 | 3 | 5 | 1 | 31 |
| Ireland | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Norway | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Turkey | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| France | 0 | 0 | 0 | 2 | 0 | 3 | 1 | 1 | 0 | 0 | 1 | 0 | 8 |
| Italy | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 4 |
| Taiwan | 0 | 3 | 1 | 0 | 2 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 10 |
| Singapore | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 2 |
| Austria | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| China | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 1 | 0 | 2 | 3 | 0 | 10 |
| Switzerland | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| Korea | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| Brazil | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| Luxembourg | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| Australia | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| Iran | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Total | 0 | 4 | 4 | 5 | 7 | 9 | 8 | 10 | 7 | 8 | 13 | 1 | 76 |
| Types | Problem Variants | Data Characteristics | Solution Approaches | |
|---|---|---|---|---|
| Drivers and Riders (D–R) | Origins and Destinations (O–D) | |||
| Ridesharing | One-to-One | One Origin–One Destination | Static | Exact Algorithms |
| Carpooling | One-to-Many | One Origin–Multiple Destinations | Stochastic | Heuristic and Metaheuristic |
| Taxisharing | Many-to-One | Multiple Origins–One Destination | Dynamic | Other Algorithms |
| Vanpooling | Many-to-Many | Multiple Origins–Multiple Destinations | ||
| Buspooling | ||||
| Multi-Modal | ||||
| Data Characteristics | Year | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | Total | |
| Static | 0 | 3 | 3 | 2 | 3 | 2 | 6 | 4 | 10 | 9 | 7 | 0 | 49 |
| Stochastic | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 2 |
| Dynamic | 0 | 4 | 3 | 2 | 4 | 6 | 4 | 8 | 3 | 5 | 7 | 2 | 48 |
| Static & Dynamic | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 4 |
| Total | 0 | 7 | 6 | 5 | 8 | 10 | 11 | 13 | 13 | 14 | 14 | 2 | 103 |
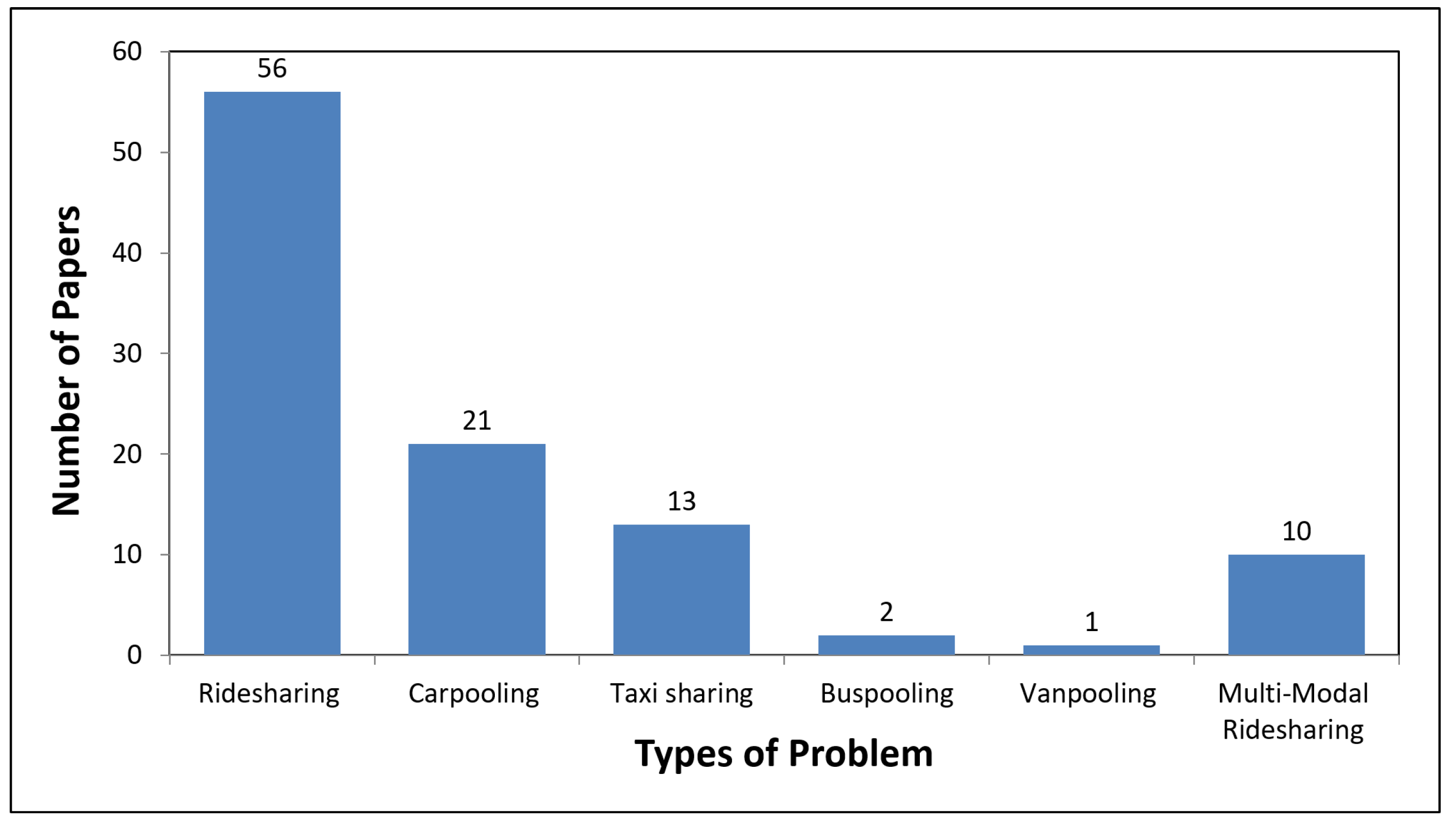
| Data Characteristics | Ridesharing | Carpooling | Taxisharing | Vanpooling | Buspooling | Multi-Modal | Total |
|---|---|---|---|---|---|---|---|
| Static | 17 | 18 | 7 | 1 | 2 | 4 | 49 |
| Stochastic | 1 | 0 | 1 | 0 | 0 | 0 | 2 |
| Dynamic | 37 | 3 | 2 | 0 | 0 | 6 | 48 |
| Static & Dynamic | 1 | 0 | 3 | 0 | 0 | 0 | 4 |
| Total | 56 | 21 | 13 | 1 | 2 | 10 | 103 |
| Solution Approaches | Year | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | Total | |
| Exact only | 0 | 1 | 0 | 0 | 2 | 3 | 4 | 4 | 3 | 2 | 3 | 0 | 22 |
| Heuristic & Metaheuristic | 0 | 6 | 6 | 3 | 3 | 5 | 7 | 4 | 9 | 10 | 10 | 1 | 64 |
| Exact, Heuristic, & Metaheuristic | 0 | 0 | 0 | 1 | 3 | 2 | 0 | 3 | 0 | 2 | 1 | 0 | 12 |
| Other Approaches | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 1 | 5 |
| Total | 0 | 7 | 6 | 5 | 8 | 10 | 11 | 13 | 13 | 14 | 14 | 2 | 103 |
| Solution Approaches | Ridesharing | Carpooling | Taxisharing | Vanpooling | Buspooling | Multi-Modal | Total |
|---|---|---|---|---|---|---|---|
| Exact only | 14 | 0 | 1 | 0 | 0 | 7 | 22 |
| Heuristic & Metaheuristic | 33 | 18 | 10 | 1 | 1 | 1 | 64 |
| Exact, Heuristic, & Metaheuristic | 6 | 3 | 2 | 0 | 1 | 0 | 12 |
| Other Approaches | 3 | 0 | 0 | 0 | 0 | 2 | 5 |
| Total | 56 | 21 | 13 | 1 | 2 | 10 | 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ting, K.H.; Lee, L.S.; Pickl, S.; Seow, H.-V. Shared Mobility Problems: A Systematic Review on Types, Variants, Characteristics, and Solution Approaches. Appl. Sci. 2021, 11, 7996. https://doi.org/10.3390/app11177996
Ting KH, Lee LS, Pickl S, Seow H-V. Shared Mobility Problems: A Systematic Review on Types, Variants, Characteristics, and Solution Approaches. Applied Sciences. 2021; 11(17):7996. https://doi.org/10.3390/app11177996
Chicago/Turabian StyleTing, Kien Hua, Lai Soon Lee, Stefan Pickl, and Hsin-Vonn Seow. 2021. "Shared Mobility Problems: A Systematic Review on Types, Variants, Characteristics, and Solution Approaches" Applied Sciences 11, no. 17: 7996. https://doi.org/10.3390/app11177996
APA StyleTing, K. H., Lee, L. S., Pickl, S., & Seow, H.-V. (2021). Shared Mobility Problems: A Systematic Review on Types, Variants, Characteristics, and Solution Approaches. Applied Sciences, 11(17), 7996. https://doi.org/10.3390/app11177996







