Abstract
While working side-by-side, humans and robots complete each other nowadays, and we may say that they work hand in hand. This study aims to evolve the grasping task by reaching the intended object based on deep reinforcement learning. Thereby, in this paper, we propose a deep deterministic policy gradient approach that can be applied to a numerous-degrees-of-freedom robotic arm towards autonomous objects grasping according to their classification and a given task. In this study, this approach is realized by a five-degrees-of-freedom robotic arm that reaches the targeted object using the inverse kinematics method. You Only Look Once v5 is employed for object detection, and backward projection is used to detect the three-dimensional position of the target. After computing the angles of the joints at the detected position by inverse kinematics, the robot’s arm is moved towards the target object’s emplacement thanks to the algorithm. Our approach provides a neural inverse kinematics solution that increases overall performance, and its simulation results reveal its advantages compared to the traditional one. The robot’s end grip joint can reach the targeted location by calculating the angle of every joint with an acceptable range of error. However, the accuracy of the angle and the posture are satisfied. Experiments reveal the performance of our proposal compared to the state-of-the-art approaches in vision-based grasp tasks. This is a new approach to grasp an object by referring to inverse kinematics. This method is not only easier than the standard one but is also more meaningful for multi-degrees of freedom robots.
1. Introduction
As Industry 4.0 technologies are in the process of development, manufacturing companies are becoming much more efficient and productive. Industry 4.0 refers to the next revolution in manufacturing and is sometimes referred to as the “Fourth Industrial Revolution”.
While these seemingly advanced Industry 4.0 solutions increase, we are only scratching the surface of what is possible with Industry 4.0. Industrial automation has been used for decades to suppress labor costs and increase productivity and efficiency. However, most people imagine automation as an automotive production line with six-axis robots used for the assembly, welding and painting of automobile bodies. Moreover, robotic technology in the manufacturing industry is now advancing rapidly. Cobots are the next-generation robots designed not to operate on their own but to work with people in their shared work space.
In addition to cobots, fully autonomous robots used in manufacturing are advancing rapidly. Furthermore, robots no longer require human intervention as they communicate with a central control system and each other. They can operate fully autonomously even when the “lights out” mode is on.
The use of autonomous equipment, robots and vehicles is one of the ways Industry 4.0 is transforming the manufacturing sector as we look to the future. Autonomous robots and cobots increase operating speeds, creating a more efficient workflow and reducing costs.
One of the difficulties of assistance robots is their inability to be able to grip objects correctly [1]. While we do it naturally, the maneuver is much more complicated for the robot, which must understand the object’s shape, weight, and function without hesitation. Today, a robot already knows how to perform complex tasks, but it still lacks the agility and ability to adapt to familiar moving objects or surroundings without being programmed. Hence, the idea of building systems to help robots develop their perceptual skills and recognize the means of catching objects is one of the major topics under study. Before interconnecting with objects in the world, a robot typically must take them up by grasping them. The robots try to overcome this difficulty using laser distance sensors, stereoscopic vision, and a 3D camera [2,3,4]. This set of sensors should recognize the size of an object, the type of the object and estimate its weight. The robot then adapts its strength to the object to lift, move and manipulate it. Here, a robot perceives an object and needs to determine where to move its gripper to pick up the object [5,6,7,8].
Solving the inverse kinematics problems (IKP) is ongoing in the field of machine learning. Therefore, despite the existence of analytical and numerical solutions to solve the grasp task, it is recommended in the field of AI to use machine learning methods (in our case, reinforcement learning) because the traditional analytical and numerical solutions depend on a model that makes them less accurate, while machine learning methods enable us to solve the IK without a known kinematic model [9]. This is the major motivation behind proposing to handle the grasping task by merging between analytic grasp metrics and learning-based approaches. To this end, we present an autonomous grasping method that firstly consists of detecting the object’s position based on vision. Further, the DDPG is trained to become an inverse kinematics solver to calculate the joints angles to reach and grasp the targeted object. Certainly, our case solves the IK with DDPG for a 5-DOF robotic arm; however, this method can be applied to a numerous-degrees-of-freedom robotic arm (more than 6-DOF), which enhances the practicality of this approach. The main contribution of our paper can be represented as follows:
- We suggest using YOLOv5 for more precise object position after its detection;
- We use backward projection for the extraction of the object’s 3D position;
- We apply IK to compute the angles of the joints at the detected position;
- We employ the DDPG algorithm to teach the arm to autonomously reach the wanted object;
- Our method outperforms the state-of-the-art approaches by reaching the goal after only 400 episodes with accuracy.
This paper is organized as follows: in Section 2, an overview of reinforcement learning is given followed by a literature review and some related works in Section 3. In Section 4, detailed explanations of our method are presented. Experiments are clearly illustrated in Section 5. Finally, conclusions and future work are discussed in Section 6.
2. Overview of Reinforcement Learning
2.1. Reinforcement Learning
Reinforcement learning (RL) is a category of machine learning. The agent in this case learns how to reach a goal through trial and error. The feedback may either be a reward or a punishment. It designates how good or bad the action was. The agent learns by adjusting its behavior in order to maximize the total reward received. RL is applied to solve a vast range of control and optimization problems involving sequential decision making. The sequential decision-making framework is illustrated as follows in Figure 1:
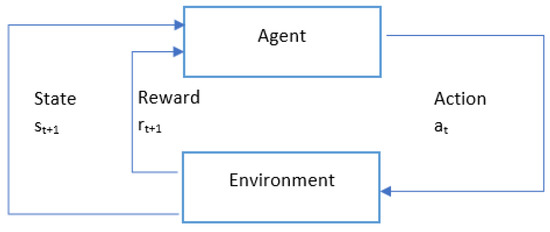
Figure 1.
Sequential decision making framework.
As a goal, the agent should maximize the total collected reward—this drives policy (value function) adjustments. Policy function produces an action to execute given a specific state .
RL algorithms can be divided into two types: value-based or policy-based. Value-based RL algorithms learn optimal action-value function . The policy may be derived from . This is what we call Q-learning. Contrarily, policy-based RL algorithms search directly for the optimal policy .
In order to observe the optimal policy for each state in the value-based RL algorithms, we have to choose the action that yields the highest Q-value . Q-values are the optimal for each (s, a) pair.
To calculate the Q-values, we rely on the Bellman update equation:
The first Q(s, a) is the next estimate. The second Q(s, a) is the current estimate. is the learning rate. is the target value- Bellman equation. is the .
Therefore,
2.1.1. Q-Learning
As RL has various classes, an off-policy RL algorithm that seeks to learn a policy that maximizes the Q-values is called Q-Learning [10]. It is a lookup table based with one entry per (s, a) pair and initialized with random Q-values. We then use the Bellman update equation to iteratively update Q(s, a) estimates. Q-values converge to optimal . This algorithm is only feasible for small state-action spaces; in large state-action spaces, many regions may never be visited, and it does not handle generalization to unvisited state-action pairs. That is why we use deep Q-learning.
2.1.2. Deep Q-Learning (DQL)
When the number of states and actions possible become more complex, we use deep learning as a function approximator [11].
When combining Q-Learning with a deep neural network (DNN) that approximates a Q-function, we obtain what we call deep Q-learning, and the deep neural network itself is called a deep Q-Network (DQN).
There are two ways to train a DQN, with or without fixed targets, as shown in Figure 2. However, deep Q-learning with one neural network can represent some problems. Figure 2 illustrates the step where these difficulties occur, which is in step 5.
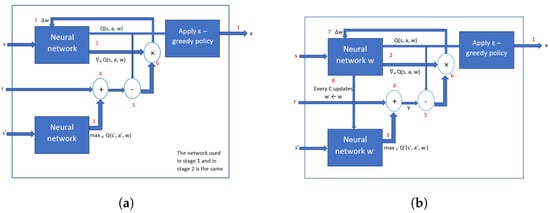
Figure 2.
Training a DQN: (a) deep Q-learning algorithm scheme, (b) deep Q-learning algorithm with 2 neural networks scheme. The two ways to train a deep Q-network.
Still, DQL has flaws as well. It can not update samples in real-time if they are not stored for some time. For this reason, we will aim to use the DDPG algorithm.
With a neural network, Q is a parameterized function with weights w. Therefore, instead of updating Q values on each iteration, we update parameter vector w that defines the function: . This can be realized through gradient descent methods.
where is the gradient.
2.1.3. Deep Deterministic Policy Gradient
In order to sustain the learning process and speed up convergence, and also referring to the Actor-Critic (AC) algorithm, the DDPG consists of adding a target network to both the actor and critic networks, respectively. The idea of the DQN algorithm is also used to replay the experiment in continuous space.
In summary, DDPG is an off-policy algorithm that can be considered as being deep Q-learning for continuous action spaces and can only be used for environments with continuous action spaces. Assuming that , represent the target networks of the critic and actor networks , , the critic and actor loss functions are, respectively, represented as follows:
where : discount factor, R: reward, ▽: gradient.
3. Literature Review
Grasping or catching is the action of gripping an object [12]. Localization, object and environment are three essential elements that must be appraised during a grasping task. The purpose of this work is to use a deep deterministic policy gradient algorithm to solve the inverse kinematics that helps accomplish the task of grasping objects by a robotic arm based on vision. In this section, we will review the recent works realized in each of the mentioned methods, which are the grasp task, object detection and reinforcement learning.
3.1. Reinforcement Learning
General learning can be difficult, since collecting data consumes a significant amount of time. Thereupon, researchers are exploring innovative solutions such as learning algorithms that could effectively reuse experience [13,14]. In [15], the authors proposed a DRL (deep reinforcement learning) approach using the deep-Q-network (DQN) algorithm to solve the problem of early classification with several classes. Simultaneous optimization classification quality and timelines are based on a user-specified compromise through agent rewards. However, the proposed method [15] encounters a certain number of problems. The agent’s memory (learning base) is out of balance. Indeed, after each acquisition of a new measurement, the agent chooses between waiting for additional data or classifying the incomplete sequence. The actions of classifying lead to the end of the acquisition process and waiting to be over represented.
In contrast, the authors in [16] highlight the fact that a deep deterministic policy gradient is the best algorithm to use to solve the case of a robotic arm grasp task based on inverse kinematics.
To this purpose, we explore how RL can be used to automatically learn robotic grasping skills for various objects. However, to avoid forgetting, the robot must repeatedly revisit previously seen objects if learning is performed primarily on policy, which makes handling extremely diverse grasping scenarios really difficult. Thus, off-policy RL methods might possess some preference for tasks such as grasping, where the variety of objects is key to generalization.
Since the 2010s, with the emergence of deep learning and better computers, the usual functions of reinforcement learning such as Q-value, advantage, value, policies and model dynamics are more and more frequently approximated by deep neural networks. Using such structures makes it possible to represent functions on a high-dimensional input space by automatically extracting a hierarchy of descriptors. In addition, the dimensions of the state spaces of reinforcement learning tasks are increasing. The first application of deep reinforcement learning learned on raw pixels and without calculating descriptors by hand used a combination of a “batch Q learning” algorithm with deep autoencoders. The “deep Q-network” (DQN) beats expert human beings in many console games. This approach uses a convolutional neuron network to approximate the Q function. Although DQN performs very well in some applications, it cannot be applied to tasks involving a continuous action space. The DDPG overcomes this difficulty by combining the “deterministic policy gradient algorithm” and the DQN. The authors in [12] present an empirical evaluation of a range of off-policy, model-free, deep reinforcement learning algorithms.
The evaluation indicates that DQL performs better on grasping tasks than other algorithms in low-data regimes for learning with both off-policy and on-policy and, furthermore, has the desirable property of being relatively robust to the hyperparameter choice [17]. The results also show that DQN, as well as the double-DQN, have comparatively higher resolution and success rates than the basic quality learning framework.
In summary, a range of challenging environments have been used successfully for model-free deep reinforcement learning (RL). Compared to on-policy learning, when data collection is complex, off-policy methods can reuse the collected data, enabling the training process. We conclude that the robot performs better at learning the objects grasp task by adapting an off-policy reinforcement learning method. Compared to all of the other algorithms cited above, the DQL and DDPG are the most successful.
3.2. Grasp Task
Many techniques have been developed to improve the grasp task, the authors in [4] give an overview of present advances with the focus on options to learn, detect, and grasp objects. A software architecture for service robots manipulating objects in human environments [2] was presented by the respected authors. Learning synergies between pushing and grasping with self-supervised deep-RL allowed us to discover and learn how pushing can help rearrange cluttered objects to make space for arms and fingers from scratch through model-free deep-RL [18]. Another technique that was developed with deep-RL is thinking while moving. The action is completed with the time evolution. However, this mechanism requires a controlled system. Such as when the robot must decide on the following activities while still performing the previous action [7]. A further scalable deep-RL for vision-based robotic manipulation was researched, in which a study of the problem of learning vision-based dynamic manipulation skills using a scalable reinforcement learning approach in the context of grasping was carried out [19]. There is also a multitasking-oriented robot arm motion planning scheme. The system is based on deep-RL, and twin synchro-control, which illustrates a technique that combines deep reinforcement learning (DRL) with digital twin technology to control humanoid robot arms [20]. Accelerating deep continuous RL through task simplification is a novel method for improving the learning process by task simplification inspired by the Goldilocks effect. The process is known for developmental psychology to solve the problem of collecting the enormous amount of required training samples in a realistic time that surpasses the possibilities of many robotic platforms [21]. Unity 3D machine learning-based research on robot arm control includes DRL strategies to train the robotic arm through machine learning, using the reward function for intelligent control of the robotic arm [22]. The authors in [13] introduced a new approach to promote the exchange of objects between robots and humans. The authors in [23] propose, via the grasping for stacking network (GSN), a system that jointly learns the grasping and the stacking policies. This (GSN) enables a robotic arm to pick boxes from a table and put them on a platform properly. The grasp task has also been developed through different kinds of methods, such as in [24], which proposes a method of detecting fruits and automatically harvesting using a robot arm. There are other developed techniques based on inverse kinematics, such as [3], which proposes a methodology to generate joint-space trajectories of stable configurations for solving inverse kinematics using deep reinforcement learning (RL).
3.3. Object Detection
Object detection is one of the most important tasks in computer vision, which involves determining the location of certain objects in the image if they are present, as well as classifying those objects [23,24].
YOLO was first introduced in a paper released by Joseph Redmon et al. [25] and immediately got tremendous attention from fellow computer vision researchers [26].
Five versions of YOLO have been published to date [27,28,29]. Each version has been upgraded and integrated with the most advanced ideas emerging from the computer vision research community. YOLOv5 is the latest version not developed by the original author of YOLO. It was released in May 2020, a month after the release of YOLOv4. However, the performance of YOLOv5 is higher than the YOLOv4 in terms of both accuracy and speed [30].
4. Methodology
This study aims to compute the robot arm kinematics to grasp a specific object. The robot is equipped with a camera that detects the object and classifies it with YOLOv5. A model of deep reinforcement learning is computed to calculate the joint angles of the robot’s arm with inverse kinematics for the desired position of the end-effector intending to grasp the set object.
In our paper, the robot is equipped with a camera and an arm. Figure 3 represents the detection and grasp algorithm.
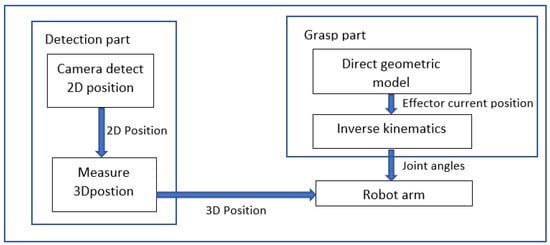
Figure 3.
Flow chart for grasp task.
4.1. Object Pose Detection Method
The first step of the detection part is detecting the 2D position of the targeted object. With YOLOv5, we detected the 2D object position in the received frame, as shown in Figure 4.
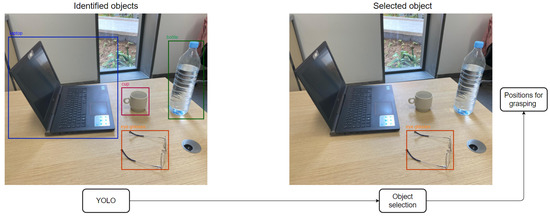
Figure 4.
Object recognition process.
However, as we need the 3D position of the object , we proceeded with the backward projection method. From the pixel coordinates, we were able to determine the world coordinates after calibrating the camera. To do so, we used the inverse of the following method illustrated in Figure 5:
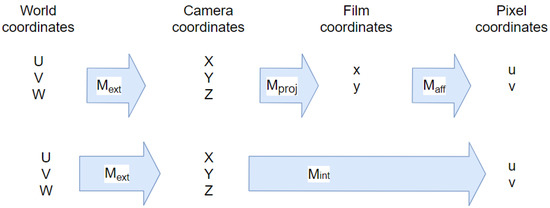
Figure 5.
Forward projection.
represents the intrinsic matrix, which provides the relationship between the camera coordinate system and its image space, and represents the extrinsic matrix, which, in turn, represents the relationship between the camera coordinate system and the object coordinate system.
=
With representing the rotations and representing the translations.
=
is the matrix that represents the affine transformation, which is a geometric transformation that conserves lines and parallelism. It occurs between film coordinates and pixel coordinates. On the other hand, is the matrix that describes the mapping from the 3D points in the world to 2D points in an image of the camera.
Since our purpose is to determine the 3D coordinates of the object in the world and not the other way around, we used the inverse of our matrices, and the computation was realized with the following equation.
4.2. Kinematic Modeling and Inverse Kinematics
The structure of our 5-DOF robotic arm is a simple open structure. This structure makes it possible to bring the end device into the desired position [31]. Our robotic arm has 5-DOF and is articulated because it has a series manipulator having all joints as revolute. It is structured as so: base rotation, shoulder, elbow, wrist and gripper, as shown in Figure 6.
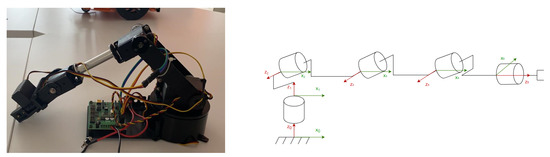
Figure 6.
The robotic arm in the real world and its coordinate frame.
- Direct Geometric Model
The direct geometric model of a robot provides the location of the end-effector in terms of the joint coordinates. To determine it, we will use the Denavit Hartenberg (DH) method shown in Table 1. Those parameters reveal the related five joints parameters of the robotic arm manipulator to find the end-effector position in comparison with the base of the arm, where,

Table 1.
D-H parameters of our 5-DOF robotic arm.
- : the distance from to measured along ;
- : the twist angle between and measured about ;
- : the offset distance from to measured along ;
- : the angle between and measured about .
To find the direct geometric model, we solve the following equation, which represents the transformation matrix from joint 0 to joint 5 ():
where .
represents the transformation matrix from joint i to joint . and represent the translation matrices along the z axis with respect to the d parameter of the joint and the x axis with respect to the parameter of the joint, respectively. and represent the rotation matrices around the z axis with respect to the parameter of the joint and the x axis with respect to the parameter of the joint, respectively.
In addition, represent the position and represent the orientation of the end-effector.
The direct geometric model is represented by the equations below:
With and
- Inverse kinematics
We consider that the inverse kinematic case of the robot arm has five links. Based on this method, the joint angles can be calculated for any desired position and orientation in Cartesian space. We obtain the angles of each joint when we are given the position and orientation of the end-effector.
With Equation (6), the angles of each joint of the robot arm can be obtained with the traditional geometric method as follows:
As we may see here, with only a 5-DOF robotic arm, the extraction of the joint angles was quite tricky. It is not possible to determine the angle joints with no margin of error, with this traditional method, so let us assume that the robot arm has numerous degrees of freedom (more than 6-DOF). That is why we handle the grasping task by merging analytic grasp metrics and learning-based approaches. It should be noted that in this use case, we are working on a 5-DOF robotic arm, but the method that we are presenting in this paper can be applied to an n-DOF robotic arm. To this end, we present an autonomous grasping method that firstly consists of detecting the object’s position based on vision as explained above. Further, the DDPG is trained to become an inverse kinematics solver to calculate the angles of the joints in order to reach and grasp the targeted object. This DDPG inverse kinematics solver takes as input, in the actor network, the 3D position of each joint and the distance between the joints and the object and outputs the joint angles. These joint angles are implemented in the critic network as inputs as well as the end effector 3D position and outputs the distance between the object and the end effector.
5. Experiments
In robotics, reinforcement learning plays a significant role in solving goal-oriented problems in a completely simple and reasonable manner. The bodywork of the algorithm of DDPG is described in the last section. This section follows by applying the entire algorithm to the genuine problem, which is to obtain our 5-DOF robot’s arm inverse kinematics. This involves evaluating the efficiency of our 5-DOF arm robot to grasp a determined object.
5.1. Setup and Environment
For the equipment, we used a camera with a resolution of 8 MP, which was calibrated using 13 images of a checkerboard. The robot arm can tolerate lifting 2 kg, and YOLO v5 allows us to see inference times up to 0.007 s per image, meaning 140 frames per second.
For the hardware setup, we worked with an Intel Core i7 8th generation processor CPU, a RAM with 16 GB. As GPU, we used NVIDIA GeForce GTX 960, and our operating system was Ubuntu. As a software environment, we worked on the Anaconda Python package. As a notebook, we implemented our models on Jupyter, Tenserflow, Keras and Matplotlib, which were the most used libraries.
5.2. Implementation and Results
Knowing that in order to obtain the reward it is imperative for the agent to interact with the environment, a significant part of the network is the reward function R. Keeping that in mind, it is requisite to put up a flawless reward function. This function should be able to respond correctly to the robot’s arm to make sure that the parameters are suitable to resolve the robotic’s arm inverse kinematics.
In order to reach the targeted object, the actor-network takes the 3D position of each joint and the distance between the joints and the object as input and outputs the joint angles. The critic network then evaluates the last actor by taking as inputs the end effector 3D position calculated with the joint angles found and the object 3D position, which was found with the backward projection to determine the distance between the object position and the end-effector. The smaller the distance, the more significant the reward. Therefore, the reward function is represented as follows:
represent the positions needed to calculate the distance between the end effector and the object along the axis x, y and z.
In DDPG, the critic network and the actor network help the learning of the Q-value function and the policy, respectively. Both of these networks utilize target networks, which are updated using the trajectory . The Algorithm 1 below states the pseudo-code for training. For the exploration noise, a usual distributed decreasing random noise N is employed. It is noted to deliver fine results in training. As given in Equations (4) and (5), the critic and actor networks are, respectively, updated.
| Algorithm 1: DDPG algorithm for inverse kinematics learning |
 |
From the Table 2, it can be noticed that the accuracy is increasing with the training. The highest mean accuracy obtained is at 400 episodes.

Table 2.
IK solver performance.
5.3. Visualization and Discussion
Bearing all of the criteria explained in the preceding sections in mind, the model of the arm was trained. The training was completed for 400 episodes. Each episode contains 160 steps.
After 400 episodes of training, the normalized reward is shown in Figure 7, while the distance error between the end-effector and the object is shown in Figure 8. The error goes down slightly after 100 episodes to an error interval of (0.2, 0.4). It goes down even further after 200 episodes to an interval error of (0, 0.2), which means that the end-effector reaches the goal position.
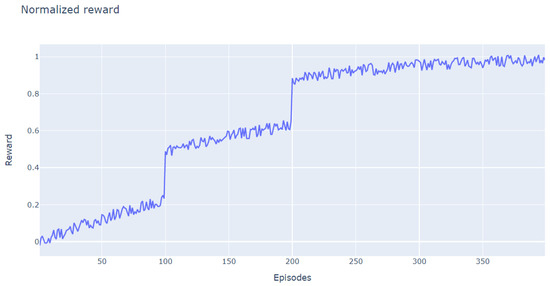
Figure 7.
DDPG learning: visualization of the normalized reward with Matplotlib.
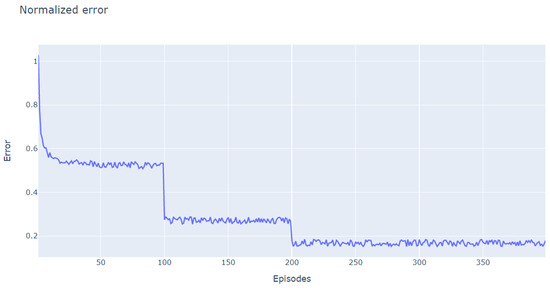
Figure 8.
DDPG learning: visualization of the normalized error with Matplotlib.
Compared to the state-of-the-art methods [8], our method outperforms it with accuracy. As shown in the Table 3 below, their method reached accuracy after 9900 episodes, while we reached accuracy after only 400 episodes. This accuracy was reached in a minor amount of episodes, which makes it a valid method to use in the grasp task.

Table 3.
Accuracy of the IK solver.
6. Conclusions
In the present study, the inverse kinematic solution of our 5-DOF arm robot to reach an object is attained by using the DDPG algorithm. Within 400 episodes, a robust IK solver was able to be learned by the approach. Various tasks were given to evaluate the robustness of the model. The results show that, despite some error, every joint angle can be calculated and the end-effector can reach the determined location. The error range is decreasing throughout episodes, so this study proves that the reinforcement learning algorithm DDPG can reach a targeted object with an inverse kinematic of the robot’s arm. Our method allowed us an accuracy of .
Since we reached an important rate of accuracy in the grasp task with our method, as a future work, we aim to expand our model by integrating the pick and place task.
Author Contributions
Conceptualization, S.T. and H.S.; methodology, H.S. and S.T.; software, H.S.; validation, S.T., H.S., R.S., A.C.; formal analysis, S.T., H.S.; investigation, H.S.; resources, H.S.; data curation, H.S., R.S., A.C.; writing—original draft preparation, H.S., A.C.; writing—review and editing, S.T., R.S., H.S., A.C.; visualization, H.S., S.T.; supervision, S.T.; project administration, S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Euro-Med University of Fez.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study did not report any data.
Acknowledgments
We would like to thank the anonymous referees for their valuable comments and helpful suggestions. Special thanks goes to anyone that improved the language quality and made this paper more readable.
Conflicts of Interest
We declare that we have no conflict of interest and no financial or other interest with any entity to disclose.
References
- Danielczuk, M.; Mahler, J.; Correa, C.; Goldberg, K. Linear Push Policies to Increase Grasp Access for Robot Bin Picking. In Proceedings of the IEEE 14th International Conference on Automation Science and Engineering (CASE), Munich, Germany, 20–24 August 2018; pp. 1249–1256. [Google Scholar] [CrossRef]
- Nam, C.; Lee, S.; Lee, J.; Cheong, S.H.; Kim, D.H.; Kim, C.; Kim, I.; Park, S.K. A Software Architecture for Service Robots Manipulating Objects in Human Environments. IEEE Access 2020, 8, 117900–117920. [Google Scholar] [CrossRef]
- Phaniteja, S.; Dewangan, P.; Guhan, P.; Sarkar, A.; Krishna, K.M. A deep reinforcement learning approach for dynamically stable inverse kinematics of humanoid robots. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, Macao, 5–8 December 2017; pp. 1818–1823. [Google Scholar] [CrossRef] [Green Version]
- Vincze, M. Learn, Detect, and Grasp Objects in Real-World Settings; Springer: Berlin/Heidelberg, Germany, 2020; p. 7. [Google Scholar]
- Morrison, D.; Corke, P.; Leitner, J. Learning robust, real-time, reactive robotic grasping. Int. J. Robot. Res. 2019, 19. [Google Scholar] [CrossRef]
- Du, G.; Wang, K.; Lian, S.; Zhao, K. Vision-based Robotic Grasping From Object Localization, Object Pose Estimation to Grasp Estimation for Parallel Grippers: A Review. arXiv 2020, arXiv:1905.06658. [Google Scholar] [CrossRef]
- Xiao, T.; Jang, E.; Kalashnikov, D.; Levine, S.; Ibarz, J.; Hausman, K.; Herzog, A. Thinking While Moving: Deep Reinforcement Learning with Concurrent Control. arXiv 2020, arXiv:2004.06089. [Google Scholar]
- Ficuciello, F. Hand-arm autonomous grasping: Synergistic motions to enhance the learning process. Intell. Serv. Robot. 2019, 12, 17–25. [Google Scholar] [CrossRef]
- Von Oehsen, T.; Fabisch, A.; Kumar, S.; Kirchner, E.F. Comparison of Distal Teacher Learning with Numerical and Analytical Methods to Solve Inverse Kinematics for Rigid-Body Mechanisms. arXiv 2020, arXiv:2003.00225. [Google Scholar]
- Nian, R.; Liu, J.; Huang, E.B. A review On reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886. [Google Scholar] [CrossRef]
- Nguyen, H. Review of Deep Reinforcement Learning for Robot Manipulation. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 590–595. [Google Scholar] [CrossRef]
- Quillen, D.; Jang, E.; Nachum, O.; Finn, C.; Ibarz, J.; Levine, S. Deep Reinforcement Learning for Vision-Based Robotic Grasping: A Simulated Comparative Evaluation of Off-Policy Methods. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; p. 8. [Google Scholar]
- Mohammed, M.Q.; Chung, K.L.; Chyi, C.S. Review of Deep Reinforcement Learning-Based Object Grasping: Techniques, Open Challenges and Recommendations. IEEE Access 2020, 8, 178450–178481. [Google Scholar] [CrossRef]
- Aitygulov, E.E. The Use of Reinforcement Learning in the Task of Moving Objects with the Robotic Arm. In Proceedings of the Artificial Intelligence 5th RAAI Summer School, Dolgoprudny, Russia, 4–7 July 2019. [Google Scholar]
- Franceschetti, A.; Tosello, E.; Castaman, N.; Ghidoni, S. Robotic Arm Control and Task Training through Deep Reinforcement Learning. arXiv 2020, arXiv:2005.02632. [Google Scholar]
- Guo, Z.; Huang, J. A Reinforcement Learning Approach for Inverse Kinematics of Arm Robot. In Proceedings of the 2019 The 4th International Conference on Robotics, Control and Automation, Guangzhou, China, 26–28 July 2019; p. 5. [Google Scholar]
- Joshi, S.; Kumra, S.; Sahin, F. Robotic Grasping using Deep Reinforcement Learning. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1461–1466. [Google Scholar] [CrossRef]
- Zeng, A.; Song, S.; Welker, S.; Lee, J.; Rodriguez, A.; Funkhouser, T.A. Learning Synergies between Pushing and Grasping with Self-supervised Deep Reinforcement Learning. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; p. 8. [Google Scholar]
- Kalashnikov, D. Scalable Deep Reinforcement Learning for Vision-Based Robotic Manipulation. Available online: http://proceedings.mlr.press/v87/kalashnikov18a.html (accessed on 17 August 2021).
- Liu, C.; Gao, J.; Bi, Y.; Shi, X.; Tian, D. A Multitasking-Oriented Robot Arm Motion Planning Scheme Based on Deep Reinforcement Learning and Twin Synchro-Control. Sensors 2020, 20, 3515. [Google Scholar] [CrossRef] [PubMed]
- Kerzel, M.; Mohammadi, H.B.; Zamani, M.A.; Wermter, S. Accelerating Deep Continuous Reinforcement Learning through Task Simplification. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Lin, M.; Shan, L.; Zhang, Y. Research on robot arm control based on Unity3D machine learning. J. Phys. 2020, 1633, 012007. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Yang, H.; Bian, G.B.; Wu, W. Multi-Target Detection and Grasping Control for Humanoid Robot NAO. Int. J. Adapt. Control. Signal Process. 2019, 33, 1225–1237. [Google Scholar] [CrossRef]
- Onishi, Y. An Automated Fruit Harvesting Robot by Using Deep Learning. Robomech J. 2019, 6, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, T.; Ma, Y.; Yahya, M.; Ahmad, B.; Nazir, S.; Haq, A.U. Object Detection through Modified YOLO Neural Network. Sci. Program. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Sang, J.; Wu, Z.; Guo, P.; Hu, H.; Xiang, H.; Zhang, Q.; Cai, B. An Improved YOLOv2 for Vehicle Detection. Sensors 2018, 18, 4272. [Google Scholar] [CrossRef] [Green Version]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Kasper-Eulaers, M.; Hahn, N.; Berger, S.; Sebulonsen, T.; Myrland, Ø.; Kummervold, P.E. Short Communication: Detecting Heavy Goods Vehicles in Rest Areas in Winter Conditions Using YOLOv5. Algorithms 2021, 14, 114. [Google Scholar] [CrossRef]
- Akkar, H.A.R.; A-Amir, A.N. Kinematics Analysis and Modeling of 6 Degree of Freedom Robotic Arm from DFROBOT on Labview. Res. J. Appl. Sci. Eng. Technol. 2016, 13, 69–575. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).