Finite Element Simulation of the Flat Crush Behavior of Corrugated Packages
Abstract
:1. Introduction
2. Experiment Design
2.1. Flat Crush Test
2.2. FE Modeling and Analysis Procedures
2.3. Material Properties
3. Results and Discussion
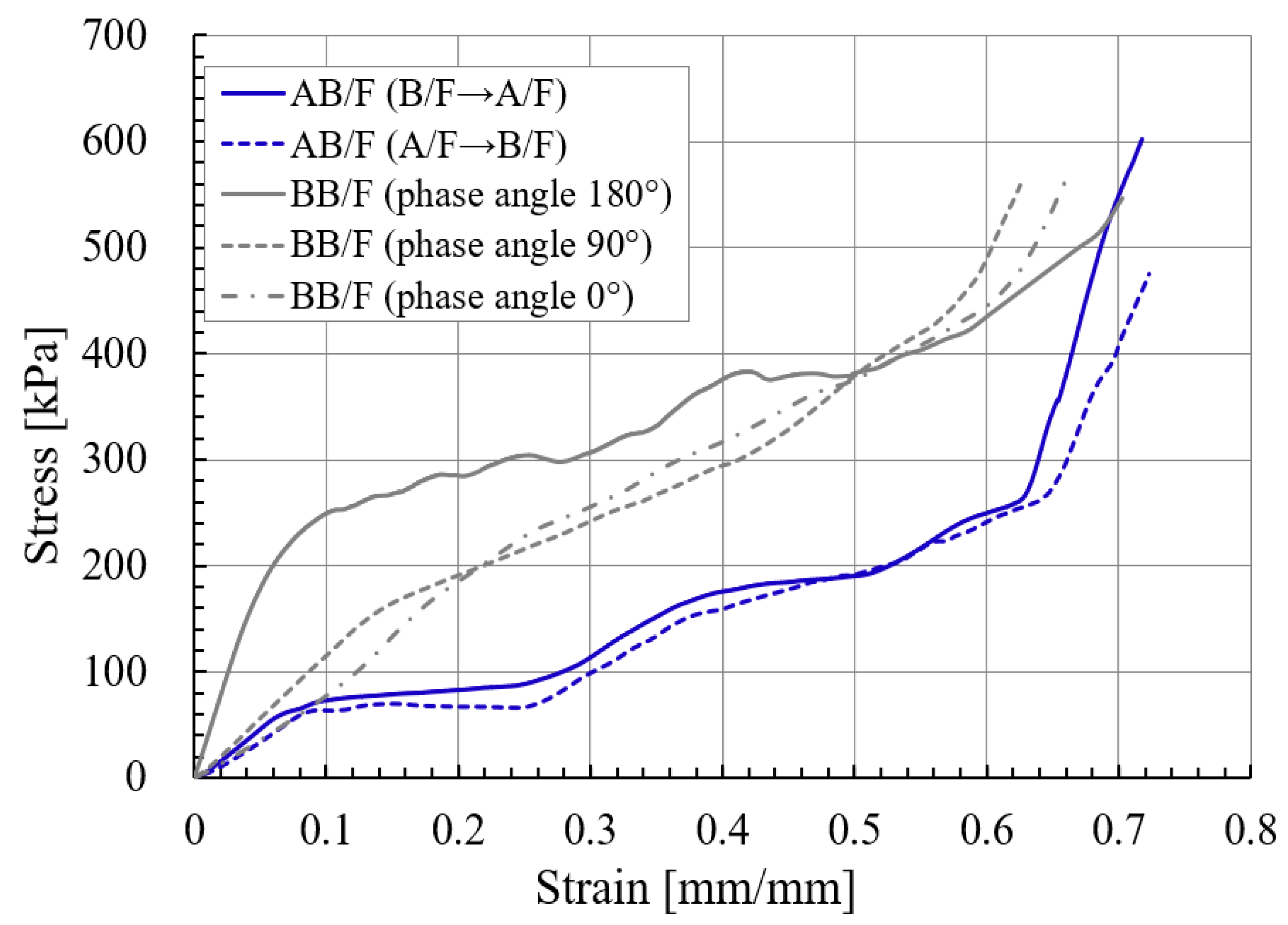
3.1. FE Simulation for Flat Crush Behavior
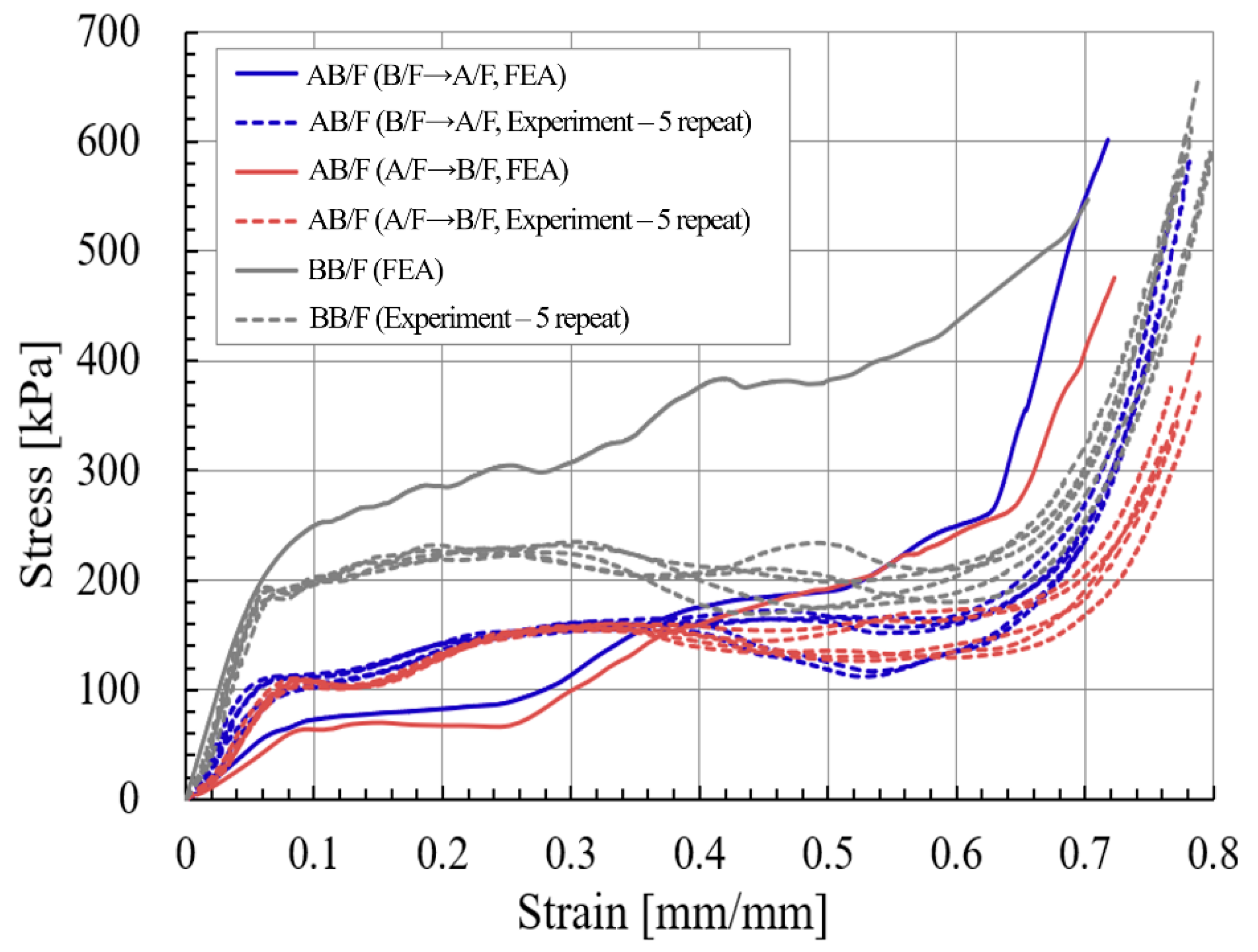
3.2. Comparison with the Experimental Study
4. Conclusions
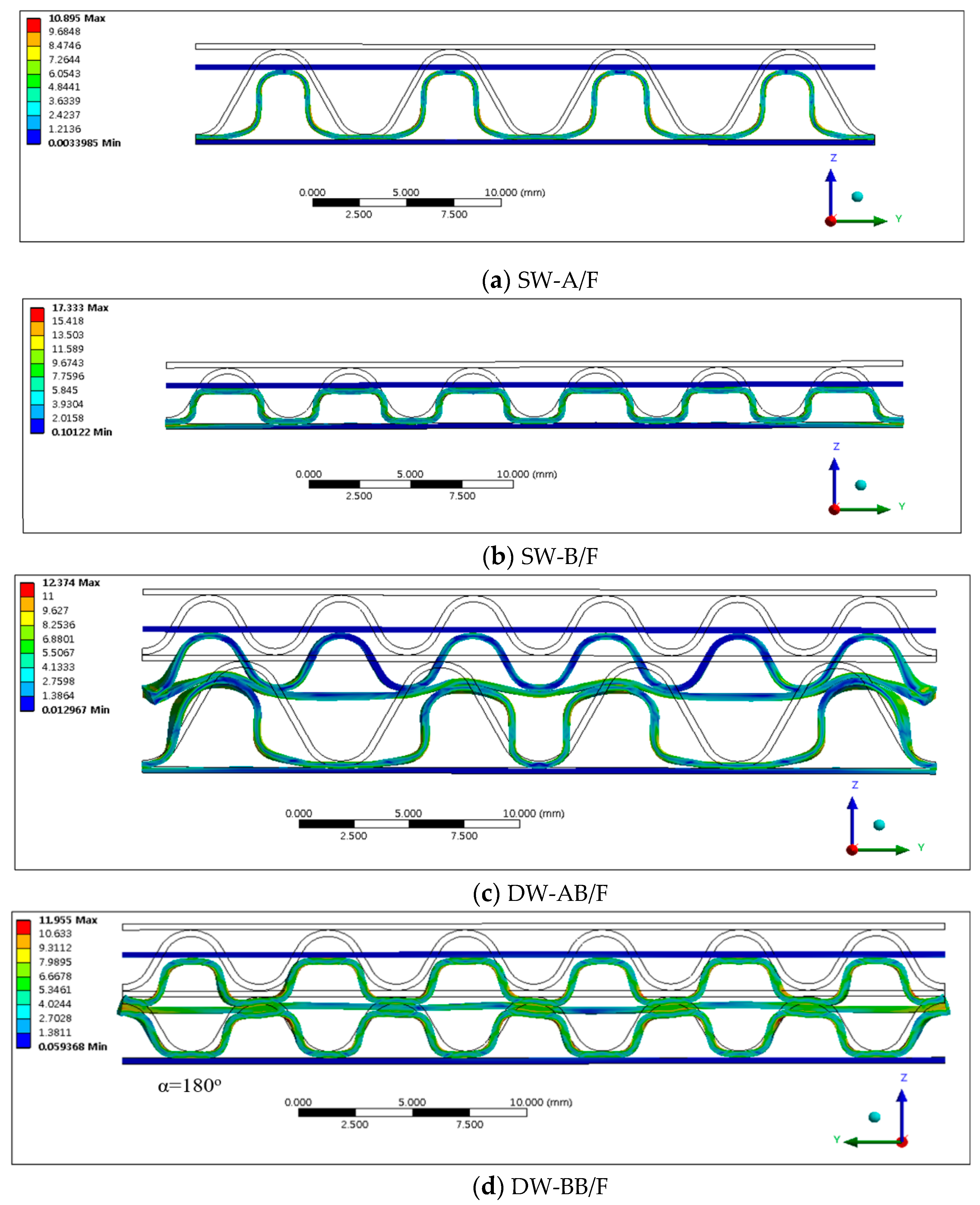
- The experimental results confirmed that when the SW corrugated paperboard was flat-compressed, the shape of the flute changed in the order of half-sine wave, trapezoid, square, and character ‘ohm’ shape.
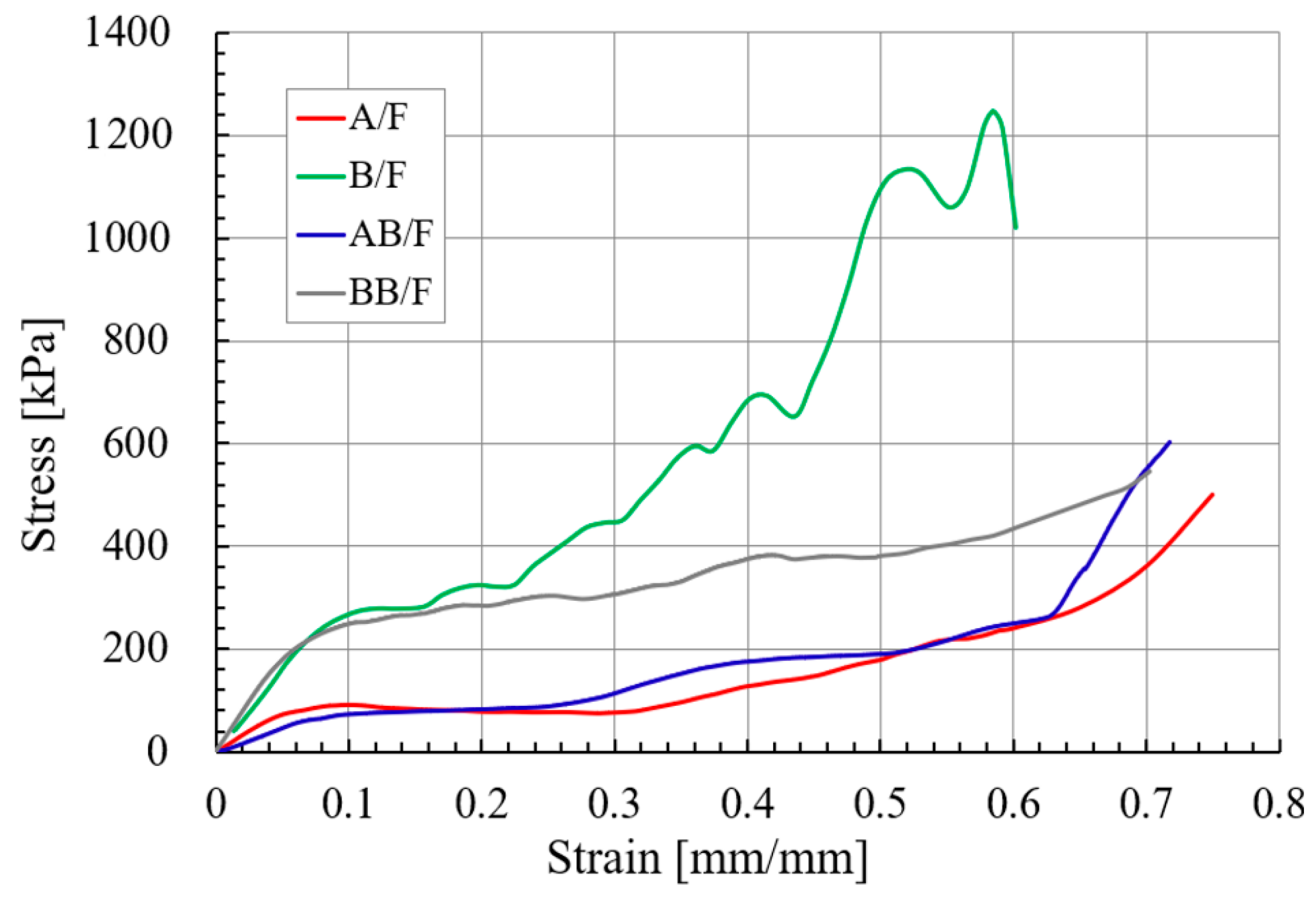
- In both the experimental and FEA results of the flat crush behavior of the DW-AB/F corrugated paperboard, we found that A/F deformed more and faster than B/F to reach a state of collapse, regardless of the compression direction. Therefore, the effect of A/F on the resistance to flat crushing and deformation of the DW-AB/F corrugated paperboard was significant.
- In the case of DW-BB/F, the phase difference between the upper and lower flutes had a significant effect on the variation in the flute shape. In the case of a phase difference of 180°, wherein the top and bottom of the upper and lower flutes coincide, the effect of the middle liner on the change of the flute shape was smaller than that in the case of other phase differences. This is because the two flutes changed symmetrically, and the resistance to flat crush was significant. In addition, differences in the SS curve according to the phase difference between the upper and lower flutes were observed. For a phase difference of 180°, the slope of the curve was larger within 50% of the compressive strain, compared to other phase differences.
- The slope of the SS curve for flat crushing of the corrugated paperboard by flute type through FEA was significantly larger in B/F, followed by BB/F, A/F, and AB/F; moreover, the difference between A/F and AB/F was minimal. This tendency was also confirmed in the experimental results. However, there was an absolute difference in the SS curves obtained by FEA and experiment. The difference could be significantly reduced by applying the viscoelastic properties of the paperboard in the FEA.
- If the material properties of the corrugated paperboard components and its modeling methods are further studied, the FE-based simulation technique will be a useful alternative tool that can replace the flat crush test.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lorentzen & Wettre. Lorentzen & Wettre Handbook; Pulp and Paper Testing; Lorentzen & Wettre: Kista, Sweden, 2013. [Google Scholar]
- Armentani, E.; Caputo, F.; Esposito, R. FE analyses of stability of single and double corrugated boards. In Proceedings of the 4th International Conference on Axiomatic Design, Firenze, Italy, 13–16 June 2006; pp. 13–16. [Google Scholar]
- Park, J.M.; Park, M.J.; Choi, D.S.; Jung, H.M.; Hwang, S.W. Finite Element-Based Simulation for Edgewise Compression Behavior of Corrugated Paperboard for Packaging of Agricultural Products. Appl. Sci. 2020, 10, 6716. [Google Scholar] [CrossRef]
- Gilchrist, A.C.; Suhling, J.C.; Urbanik, T.J. Nonlinear finite element modeling of corrugated board. Mech. Cellul. Mater. 1999, 85, 101–106. [Google Scholar]
- Haj-Ali, R.J.; Choi, B.S.; Wei, R. Refined nonlinear finite element models for corrugated fiberboards. Compos. Struct. 2009, 87, 321–333. [Google Scholar] [CrossRef]
- Rahman, A.A.; Abubakr, S. A finite element investigation of the role of adhesive in the buckling failure of corrugated fiberboard. Wood Fiber Sci. 2004, 36, 260–268. [Google Scholar]
- Park, J.M.; Kim, G.S.; Kwon, S.H. Finite element analysis of corrugated board under bending stress. J. Fac. Agric. Kyushu Univ. 2012, 57, 181–188. [Google Scholar] [CrossRef]
- Jiménez, M.A.; Liarte, E. Simulation of the edge crush test of corrugated paperboard using ABAQUS. In Proceedings of the ABAQUS World Users Conference 2003, Munich, Germany, 4–6 June 2003. [Google Scholar]
- Biancolini, M.E. Evaluation of equivalent stiffness properties of corrugated board. Compos. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Aboura, Z.; Talbi, N.; Allaoui, S.; Benzeggagh, M.L. Elastic behavior of corrugated cardboard—Experiments and modelling. Compos. Struct. 2004, 63, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Hallbäck, N.; Korin, C.; Barbier, C. Finite element analysis of hot melt adhesive joints in carton board. Packag. Technol. Sci. 2014, 27, 701–712. [Google Scholar] [CrossRef]
- Han, J.G.; Park, J.M. Finite element analysis of vent/hand hole designs for corrugated fiberboard boxes. Packag. Technol. Sci. 2007, 20, 39–47. [Google Scholar] [CrossRef]
- Urbanik, T.J.; Saliklis, E.P. Finite element corroboration of buckling phenomena observed in corrugated boxes. Wood Fiber Sci. 2003, 35, 322–333. [Google Scholar]
- FEFCO NO. 8. Edgewise Crush Resistance of Corrugated Fiberboard; FEFCO: Brussel, Belgium, 1997. [Google Scholar]
- Korea Corrugated Packaging Case Industry Association (KCCA). 2013 production status of corrugated package. Corrugat. Packag. Logist. 2014, 114, 50–54. [Google Scholar]
- Korean Standard Association (KSA). Corrugated Fiberboard-Determination of Edgewise Crush Resistance; KS M 7063; KSA: Seoul, Korea, 2015. [Google Scholar]
- TAPPI T 838 cm-12. Edge Crush Test Using Neckdown; TAPPI: Peachtree Corners, GA, USA, 2009. [Google Scholar]
- Korean Standard Association (KSA). Corrugated Fiberboards for Shipping Containers; KS T 1034; KSA: Seoul, Korea, 2014. [Google Scholar]
- Korean Standard Association (KSA). Corrugated Fiberboard—Determination of Flat Crush Resistance; KS M ISO 3035; KSA: Seoul, Korea, 2011. [Google Scholar]
- Korean Standard Association (KSA). Paper, Board and Pulps—Standard Atmosphere for Conditioning and Testing and Procedure for Monitoring the Atmosphere and Conditioning of Samples; KS M ISO 187; KSA: Seoul, Korea, 1990. [Google Scholar]
- ANSYS Inc. ANSYS Design Xplorer 14.5, Workbench User Guide; ANSYS Inc.: Canonsburg, PA, USA, 2014. [Google Scholar]
- Baum, G.A.; Brennan, D.C.; Habeger, C.C. Orthotropic elastic constants of paper. Tappi 1981, 64, 97–101. [Google Scholar]
- Pilkey, W.D. Formulas for Stress, Strain and Structure Matrices; John Wiley & Sons, Inc.: New York, NY, USA, 1994; p. 1536. [Google Scholar]
- Sim, J.M. Corrugated Packaging Simulation by Finite Element Structural Analysis-Bending and Flat Crush Behavior; Pusan National University: Pusan, Korea, 2015. [Google Scholar]

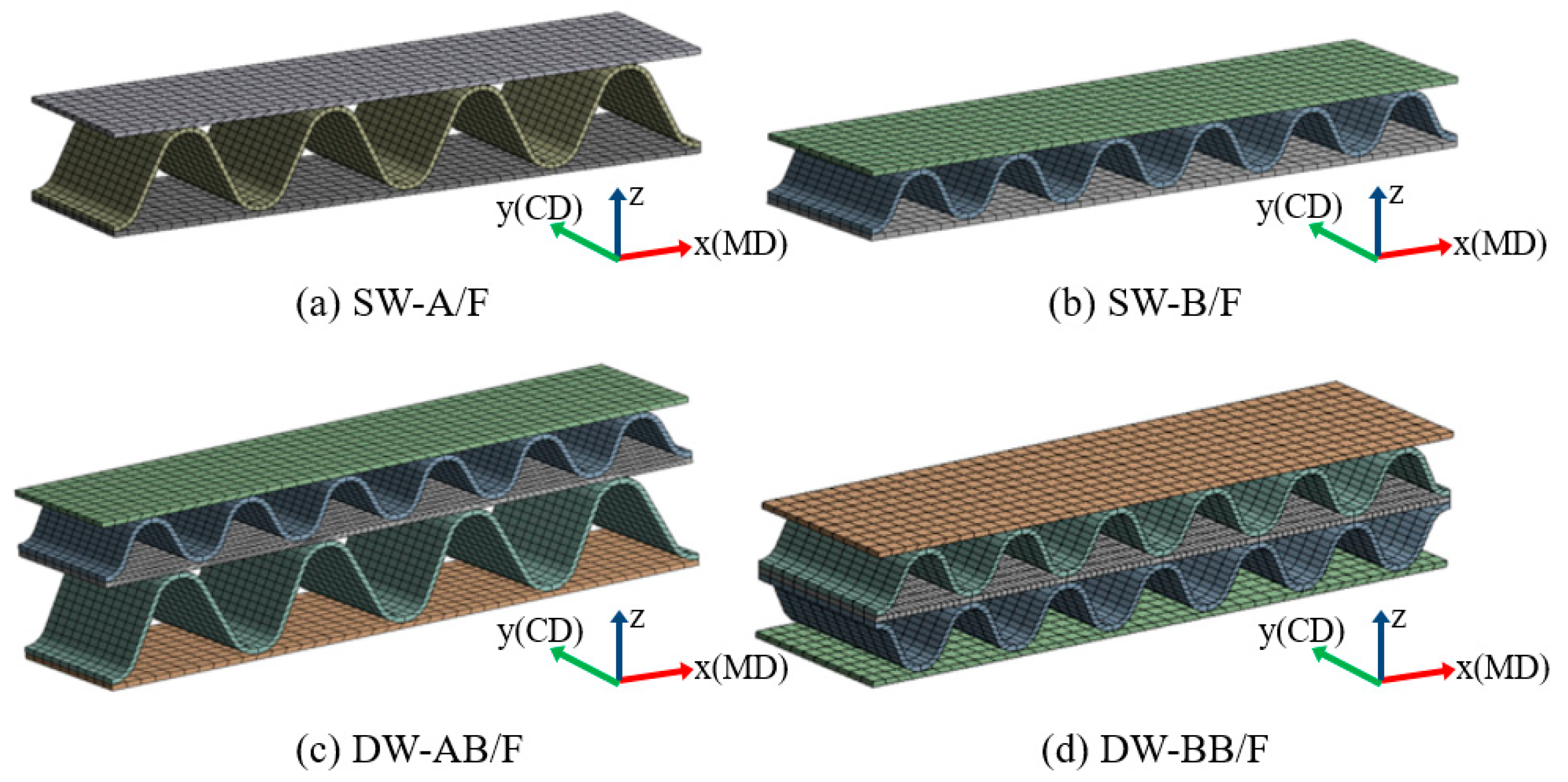
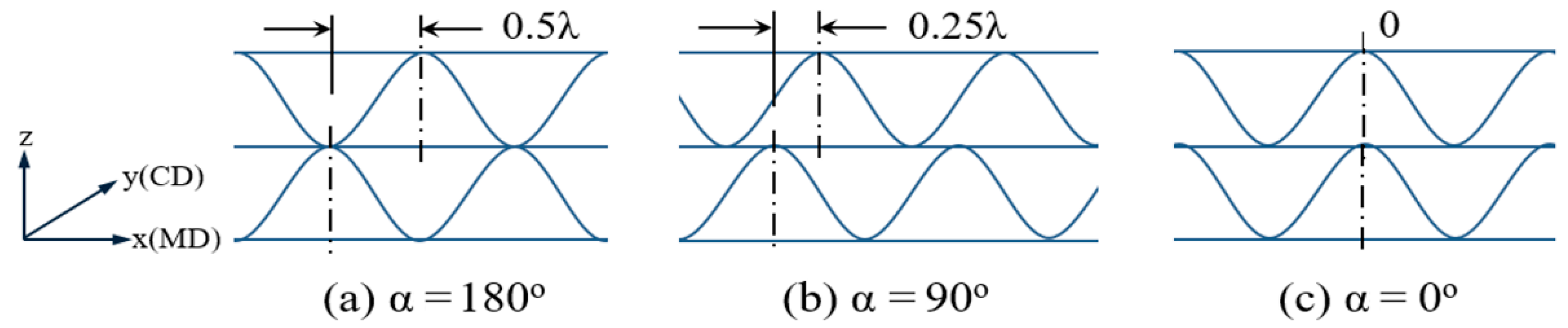

| Kinds | Board Combination | Flute | Paperboards | |||
|---|---|---|---|---|---|---|
| Wave Length (λ) (mm) | Height (h) (mm) | Take-Up Factor | ||||
| SW | A/F | SK180/K180/SK180 | 9.00 (8.33–9.38) | 4.90 (4.5–4.8) | 1.560 (1.6) |
|
| B/F | SK180/K180/SK180 | 6.00 (5.27–6.25) | 2.65 (2.5–2.8) | 1.424 (1.4) | ||
| DW | AB/F | SK180/K180/K180/K180/SK180 | - | - | - | |
| BB/F | SK180/K180/K180/K180/SK180 | - | - | - | ||
| Paperboards | Young’s Modulus (GPa) | Poisson’s Ratio | Shear Modulus (GPa) | Yield Strength (MPa) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ex (MD) | Ey (CD) | Ez | μxy | μxz | μyz | Gxy | Gxz | Gyz | σx ( MD) | σy (CD) | |
| K180 | 2.20 (±0.02) | 0.37 (±0.01) | 0.011 | 0.34 | 0.01 | 0.01 | 0.349 | 0.040 | 0.010 | 29.09 (±0.8) | 12.12 (±0.1) |
| SK180 | 3.16 (±0.07) | 0.40 (±0.01) | 0.016 | 0.34 | 0.01 | 0.01 | 0.435 | 0.057 | 0.011 | 42.50 (±0.8) | 19.50 (±0.5) |
| Classify | Static-Frictional Coefficient | ||
|---|---|---|---|
| MD-MD | CD-CD | MD-CD | |
| K180-K180 | 0.23 (±0.02) | 0.29 (±0.01) | 0.26 (±0.02) |
| SK180-SK180 | 0.37 (±0.06) | 0.41 (±0.03) | 0.39 (±0.03) |
| K180-SK180 | 0.23 (±0.04) | 0.35 (±0.02) | 0.32 (±0.04) |
| Average | 0.28 | 0.35 | 0.32 |
| Flute Type | Compression Degree for Total Thickness of the Modeled Test Specimen | |||||
|---|---|---|---|---|---|---|
| 0% | 10% | 20% | 30% | 40% | 50% | |
| A/F | 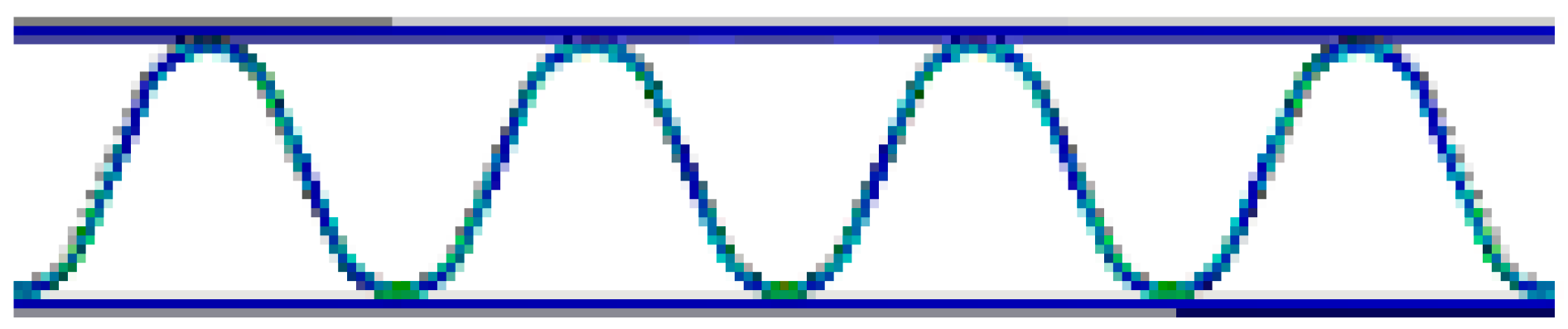 |  | 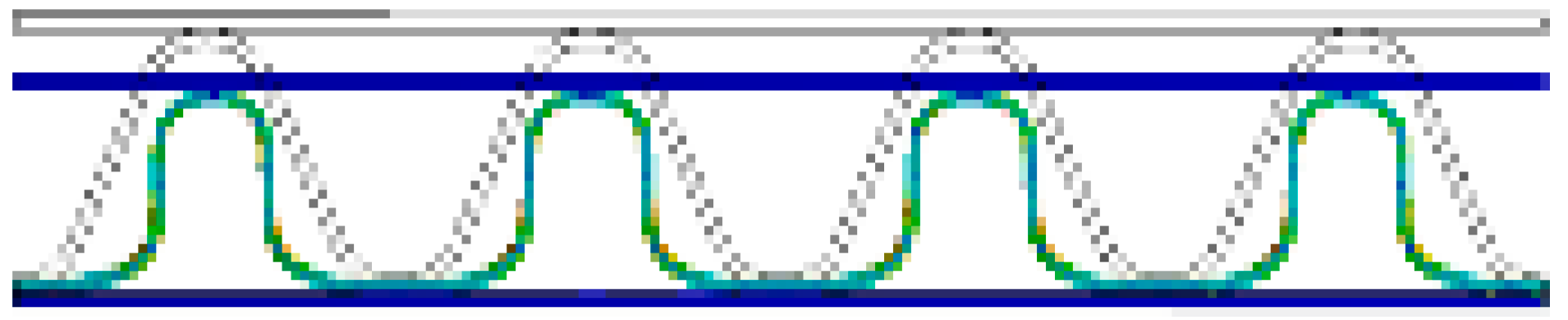 | 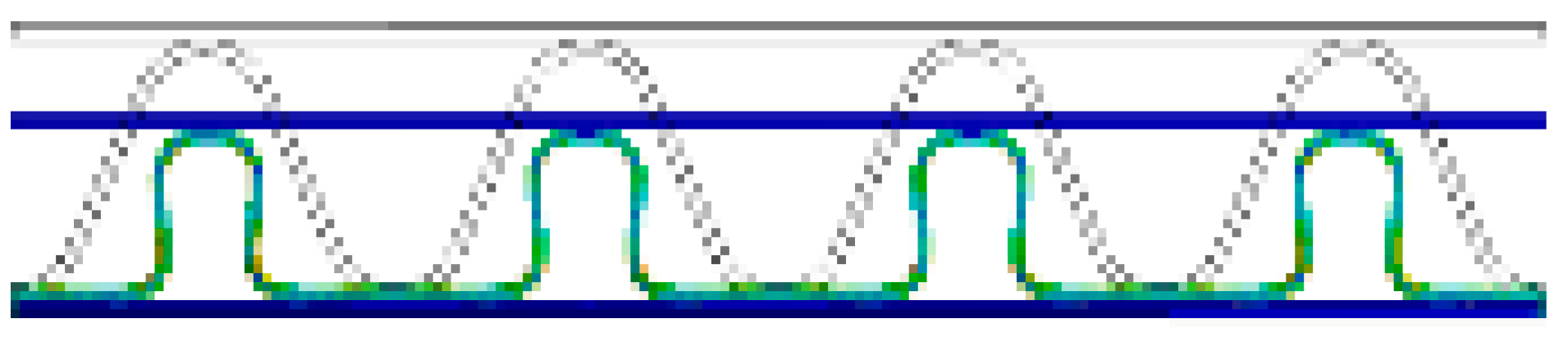 |  |  |
| B/F |  |  |  |  |  |  |
| AB/F (B/F→A/F) |  |  | 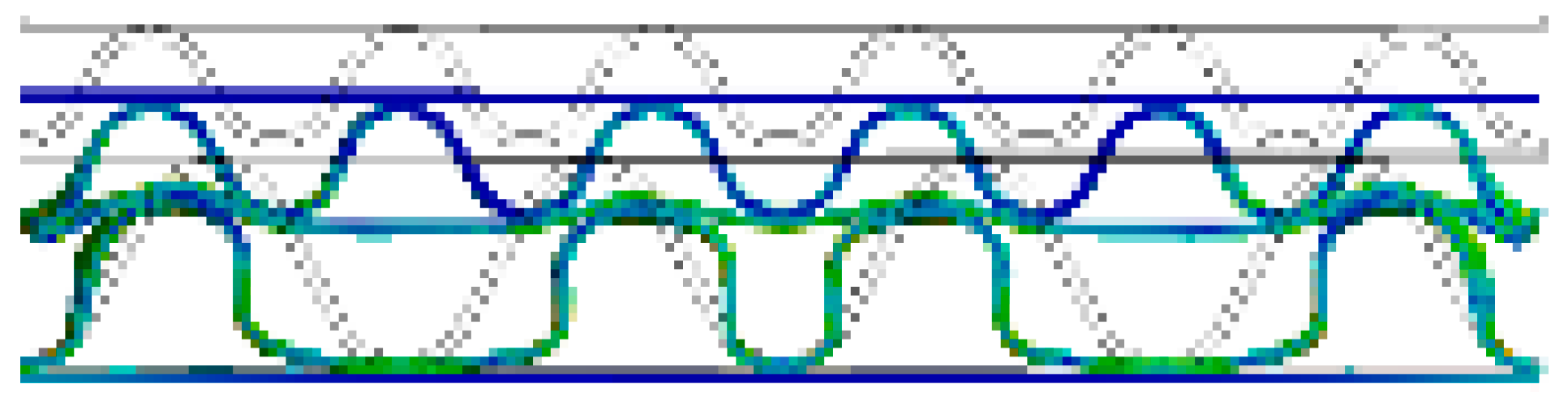 |  | 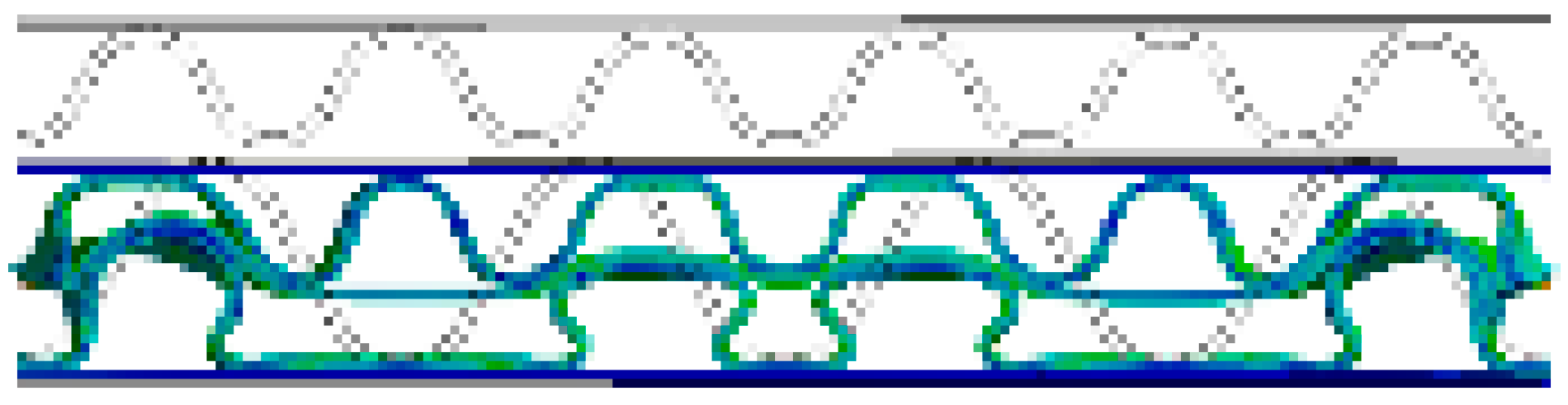 | 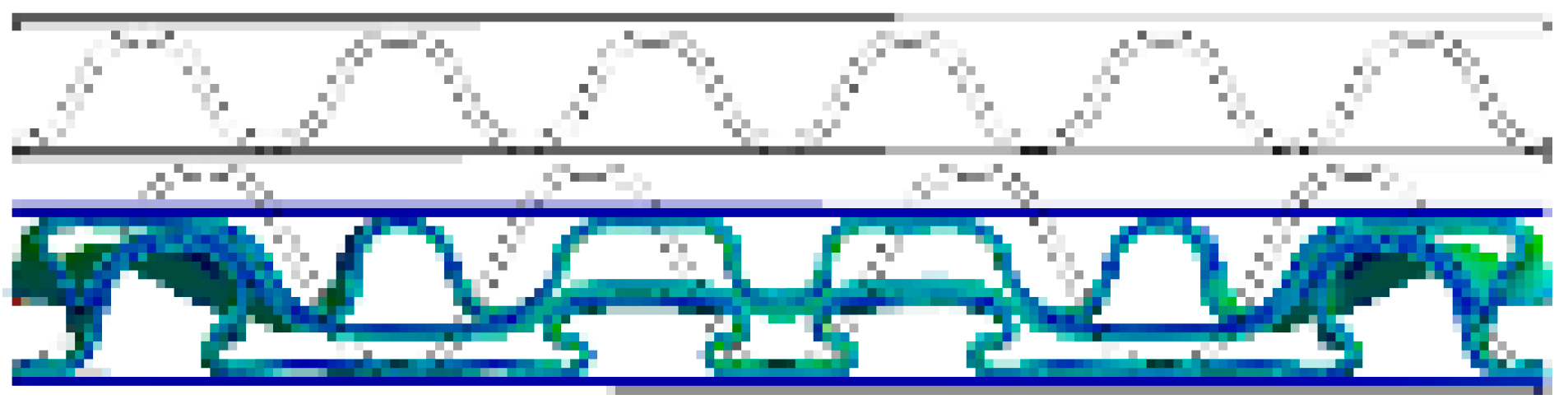 |
| AB/F (A/F→B/F) |  | 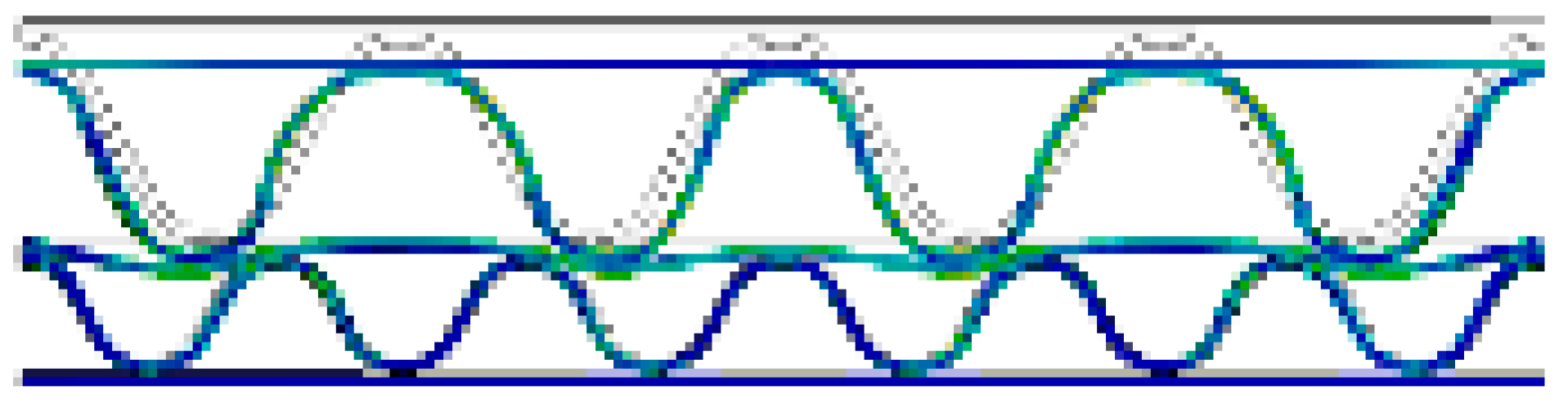 | 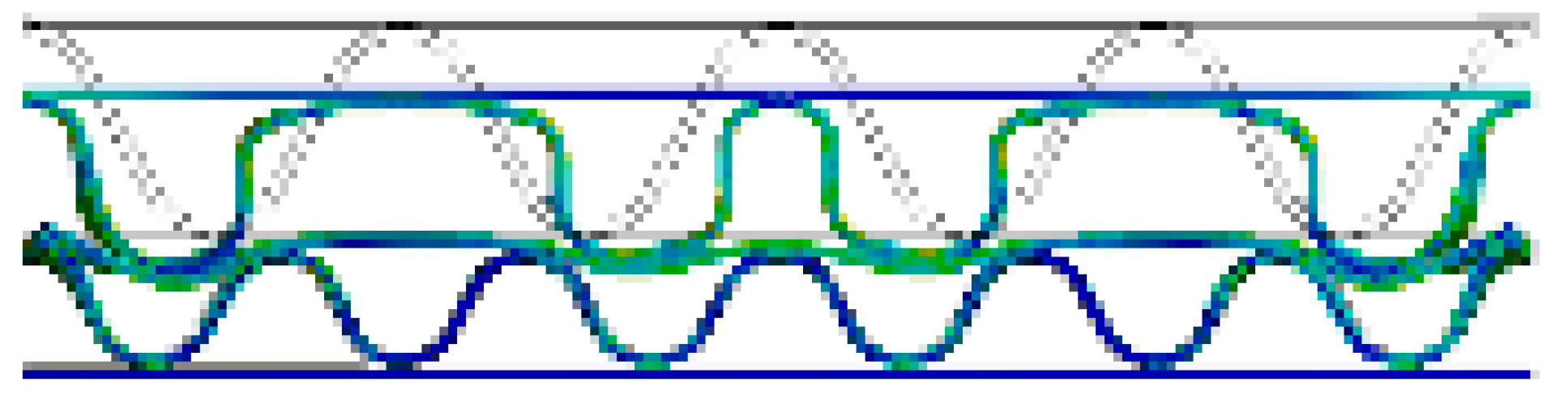 | 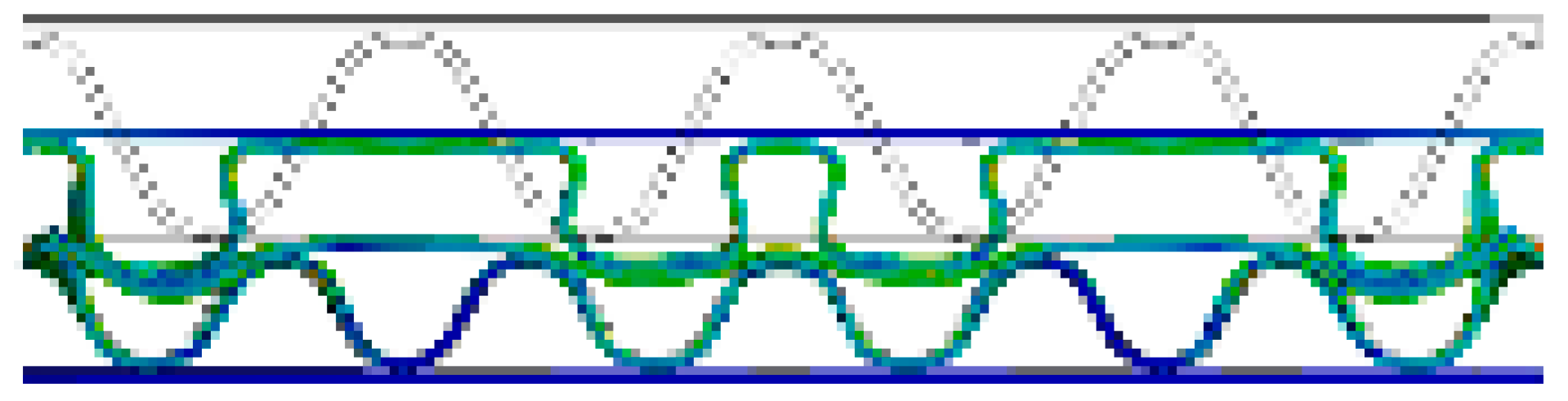 | 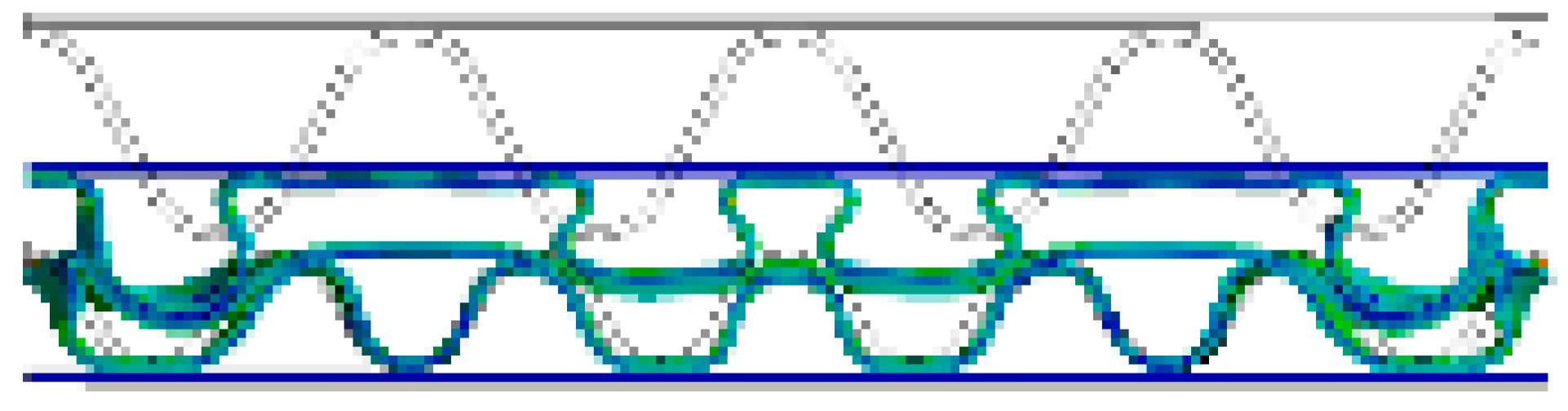 | 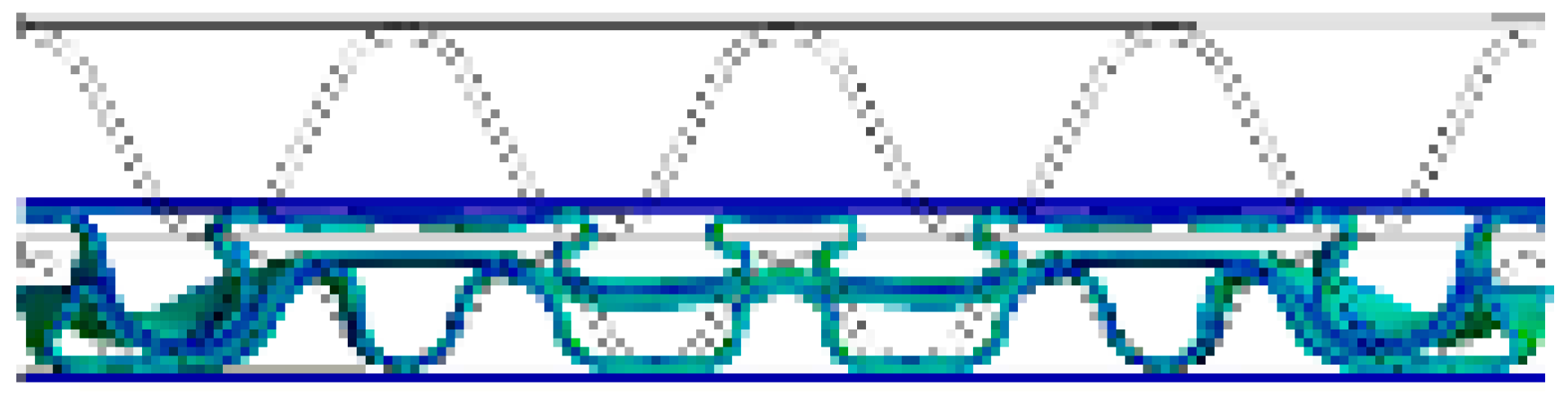 |
| BB/F (α = 180°) | 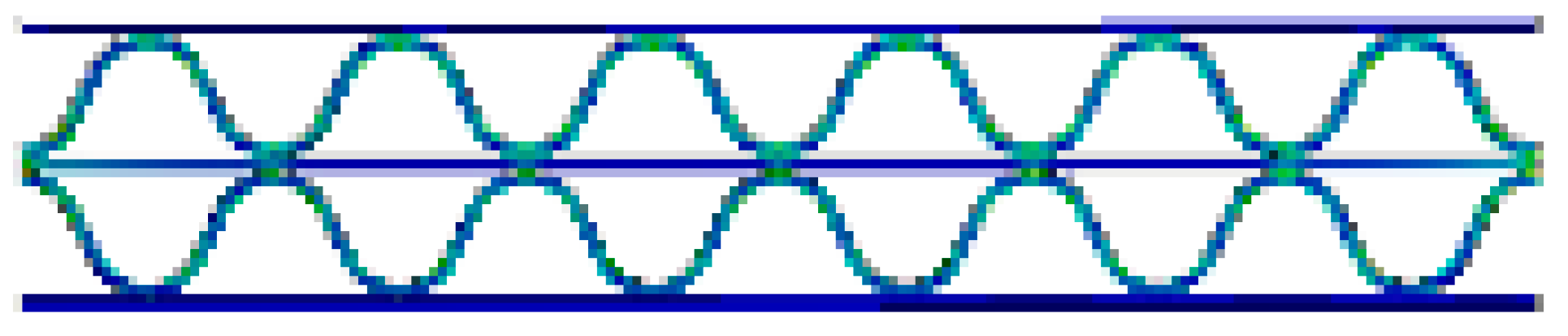 | 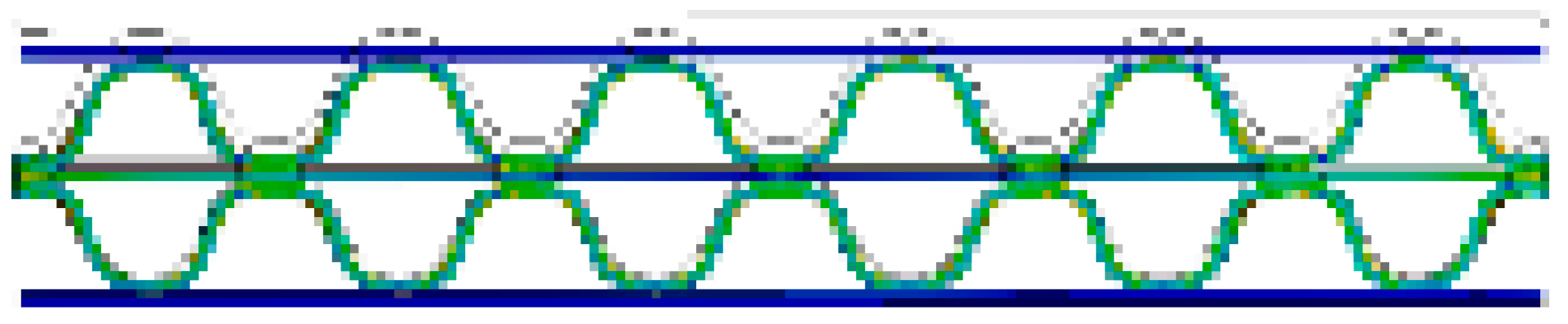 | 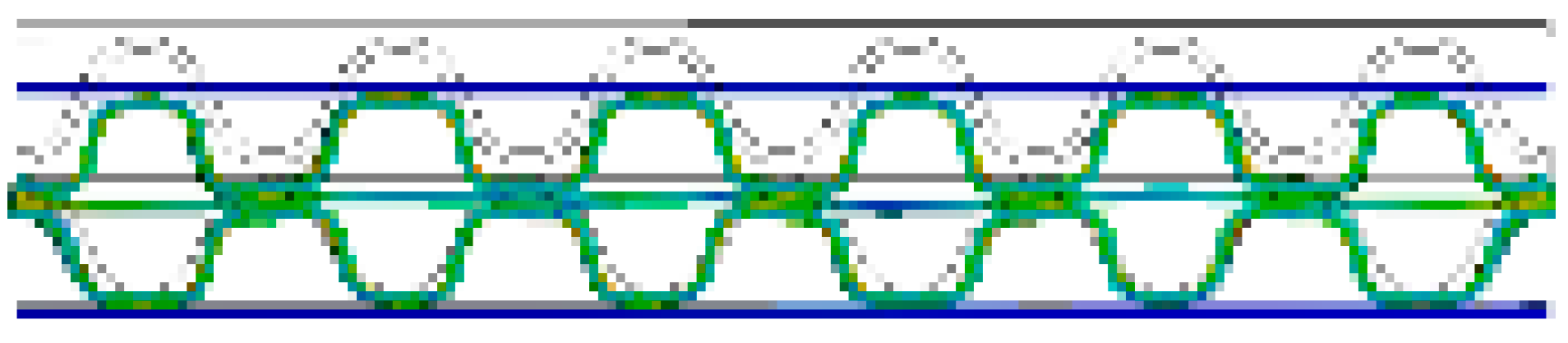 | 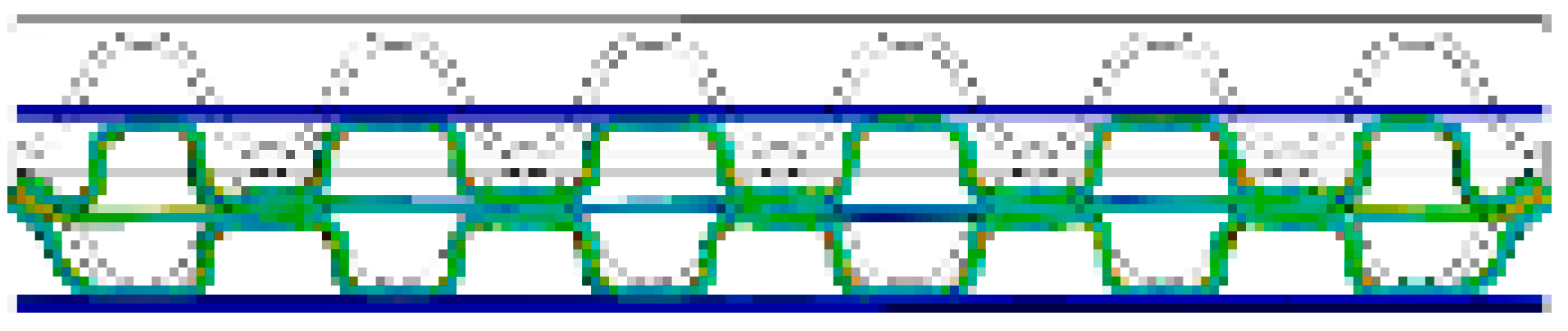 |  |  |
| BB/F (α = 90°) | 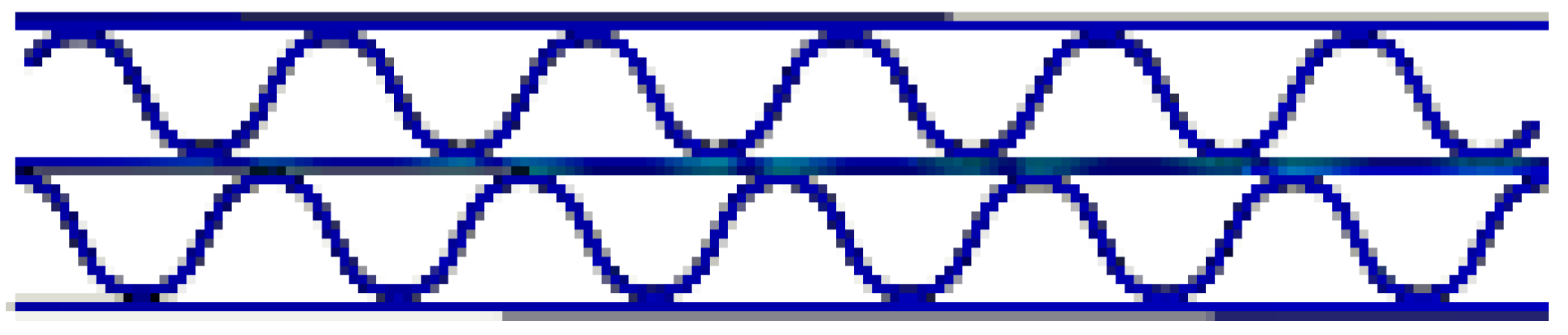 | 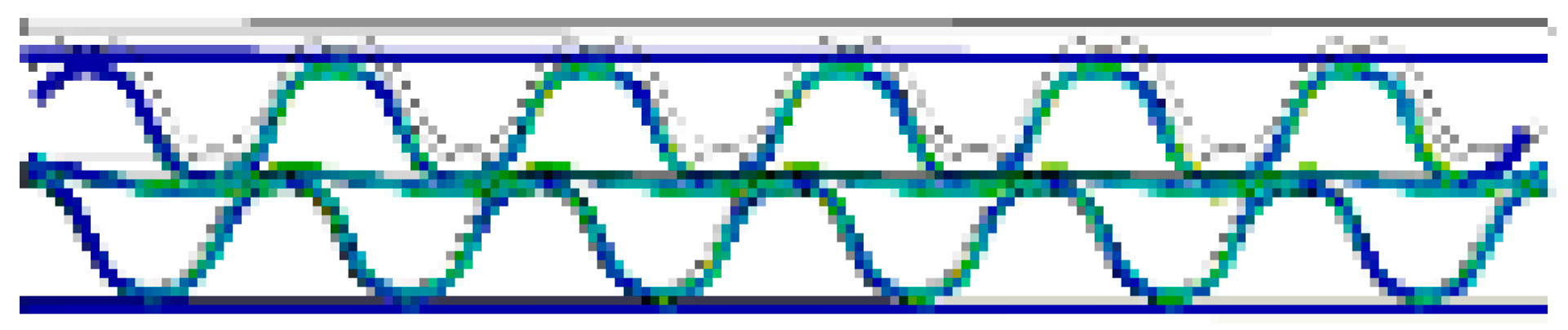 | 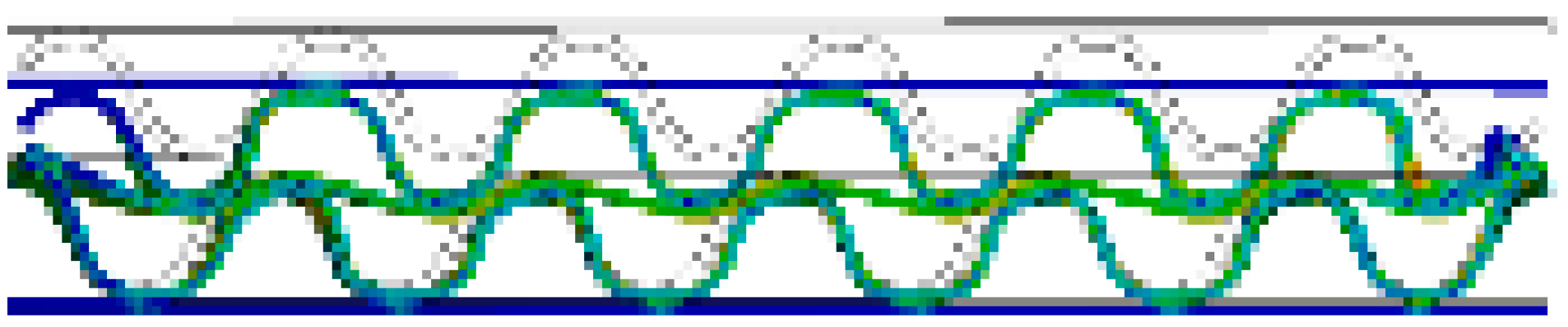 | 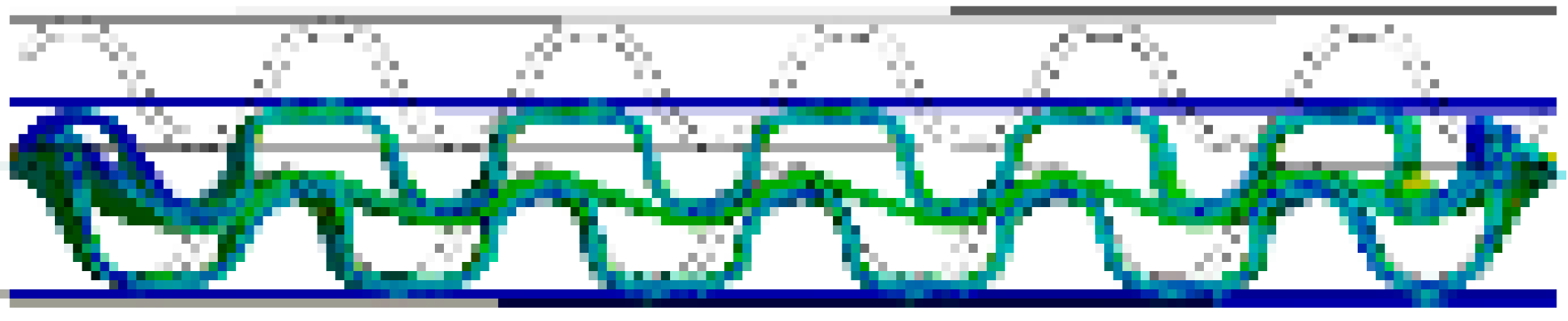 |  |  |
| BB/F (α = 0°) | 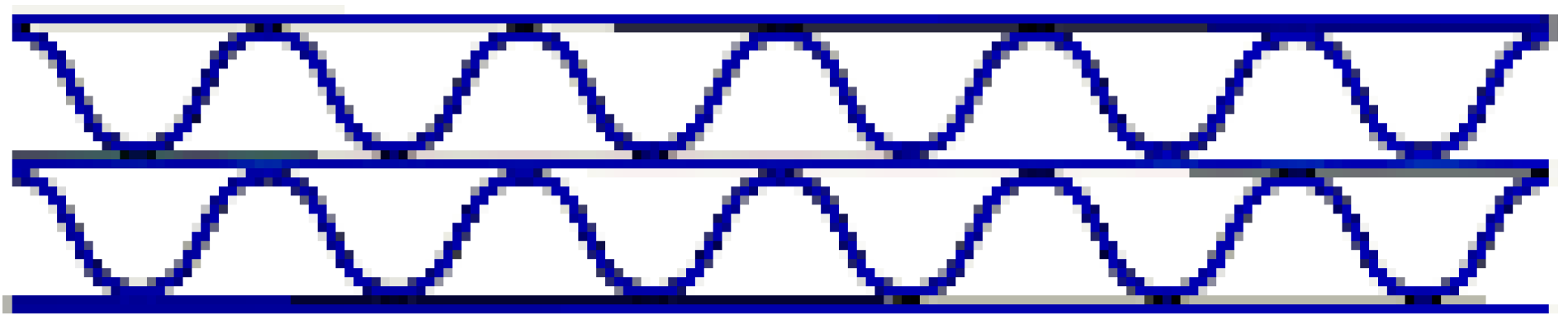 | 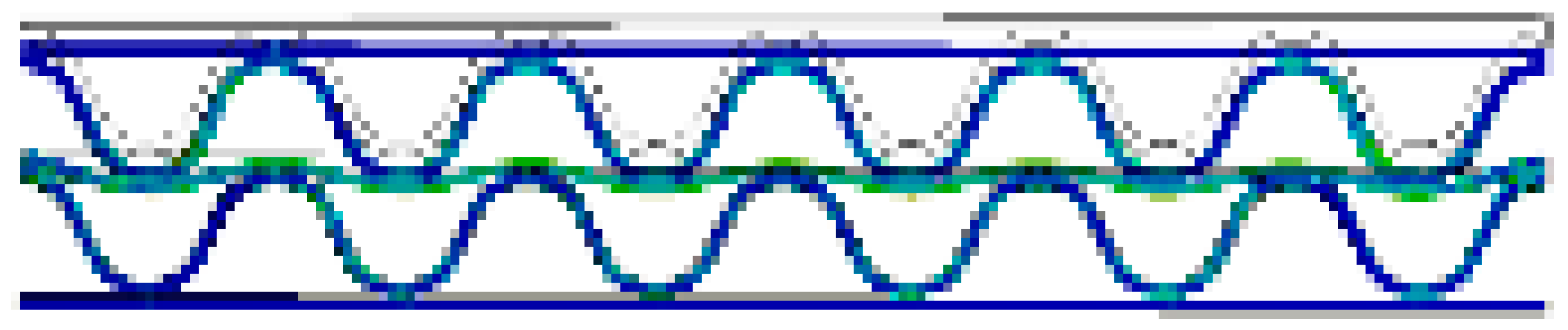 | 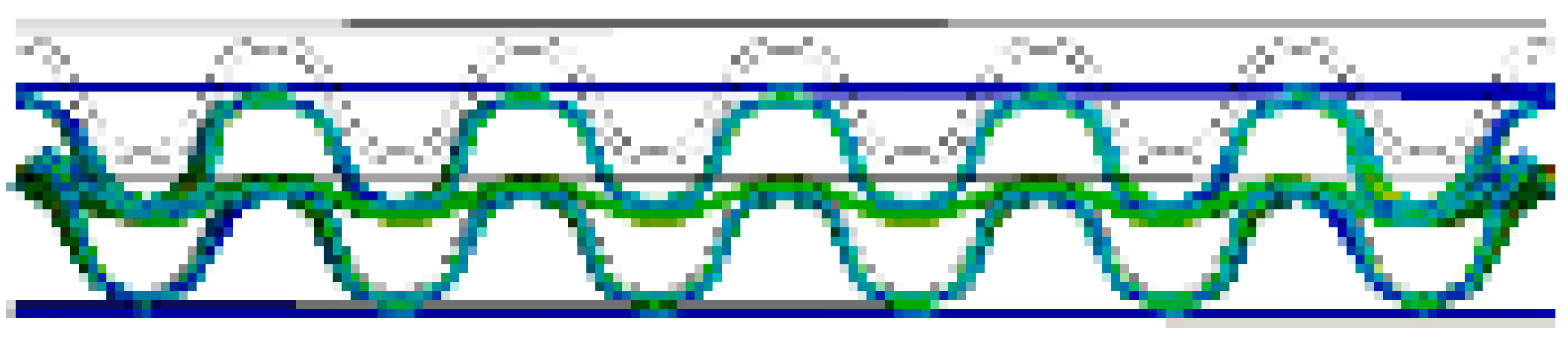 |  |  | 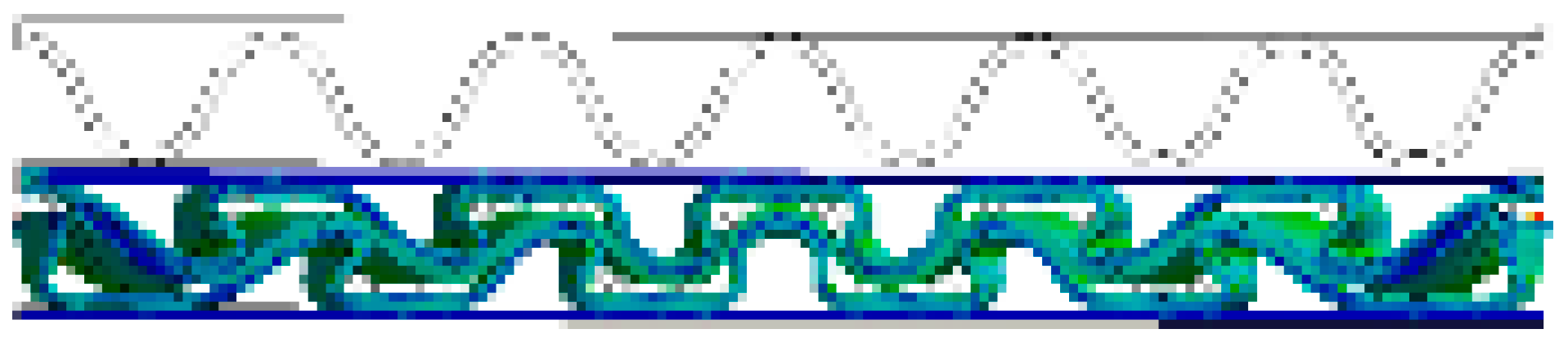 |
| Flute Type | Compressive Degree of the Modeled Test Specimen | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| A/F B/F |  |  |  |  |  | |
| AB/F (B/F→A/F) |  |  |  |  |  |  |
| AB/F (A/F→B/F) |  |  |  |  |  |  |
| BB/F (α = 180°) |  |  |  |  | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.-M.; Sim, J.-M.; Jung, H.-M. Finite Element Simulation of the Flat Crush Behavior of Corrugated Packages. Appl. Sci. 2021, 11, 7867. https://doi.org/10.3390/app11177867
Park J-M, Sim J-M, Jung H-M. Finite Element Simulation of the Flat Crush Behavior of Corrugated Packages. Applied Sciences. 2021; 11(17):7867. https://doi.org/10.3390/app11177867
Chicago/Turabian StylePark, Jong-Min, Jae-Min Sim, and Hyun-Mo Jung. 2021. "Finite Element Simulation of the Flat Crush Behavior of Corrugated Packages" Applied Sciences 11, no. 17: 7867. https://doi.org/10.3390/app11177867
APA StylePark, J.-M., Sim, J.-M., & Jung, H.-M. (2021). Finite Element Simulation of the Flat Crush Behavior of Corrugated Packages. Applied Sciences, 11(17), 7867. https://doi.org/10.3390/app11177867







