Failure Mechanism of Rock Specimens with a Notched Hole under Compression—A Numerical Study
Abstract
1. Introduction
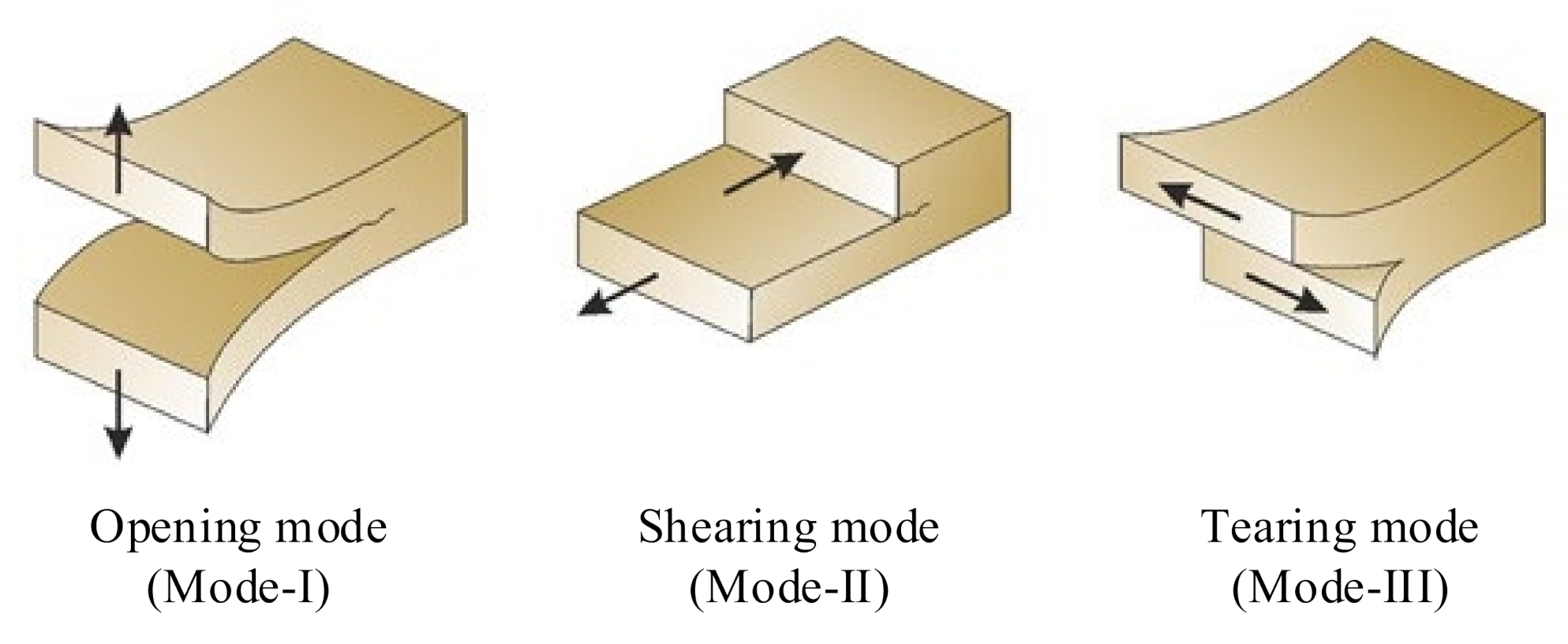
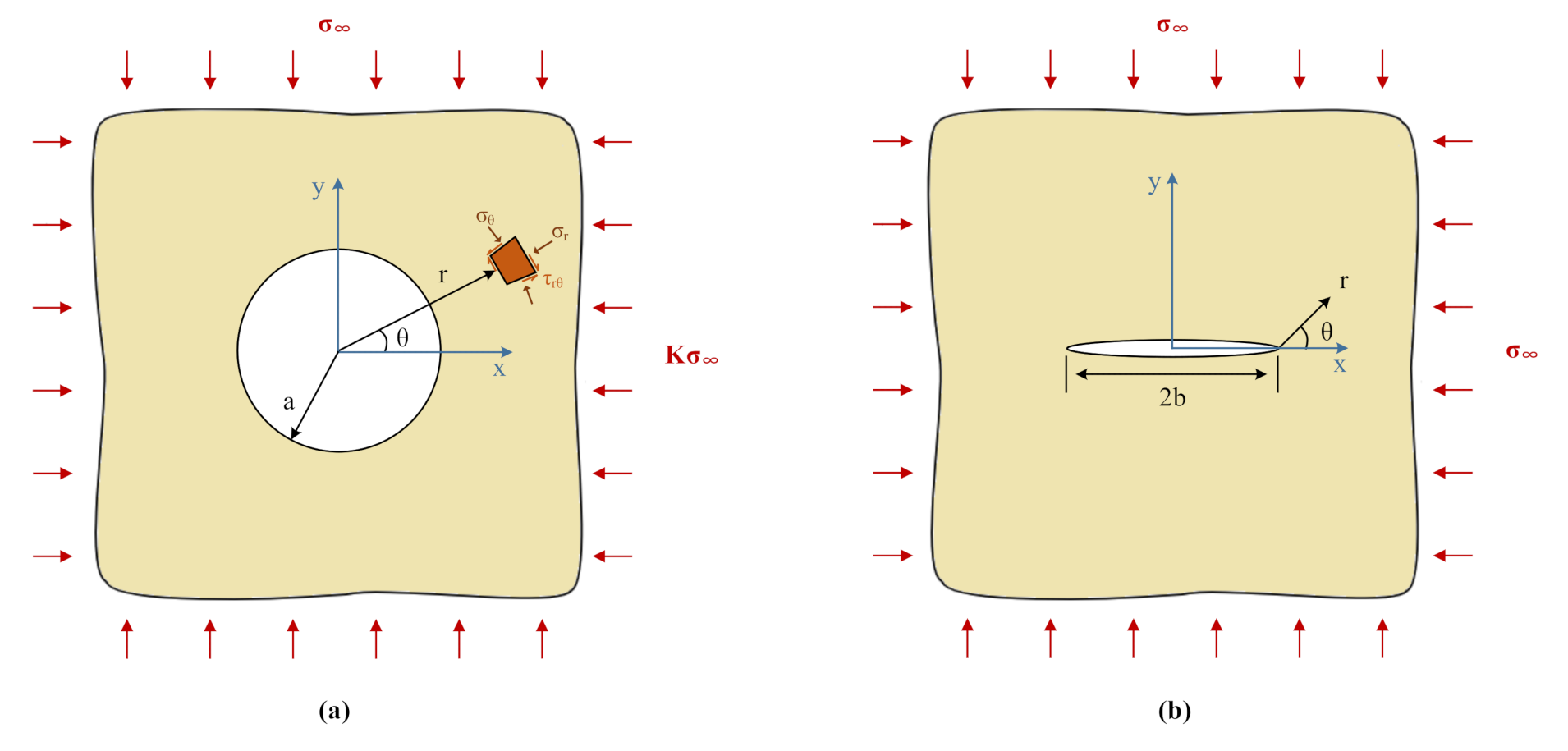
2. Stress State around Circular Holes and Cracks under Mode-I Loading Condition
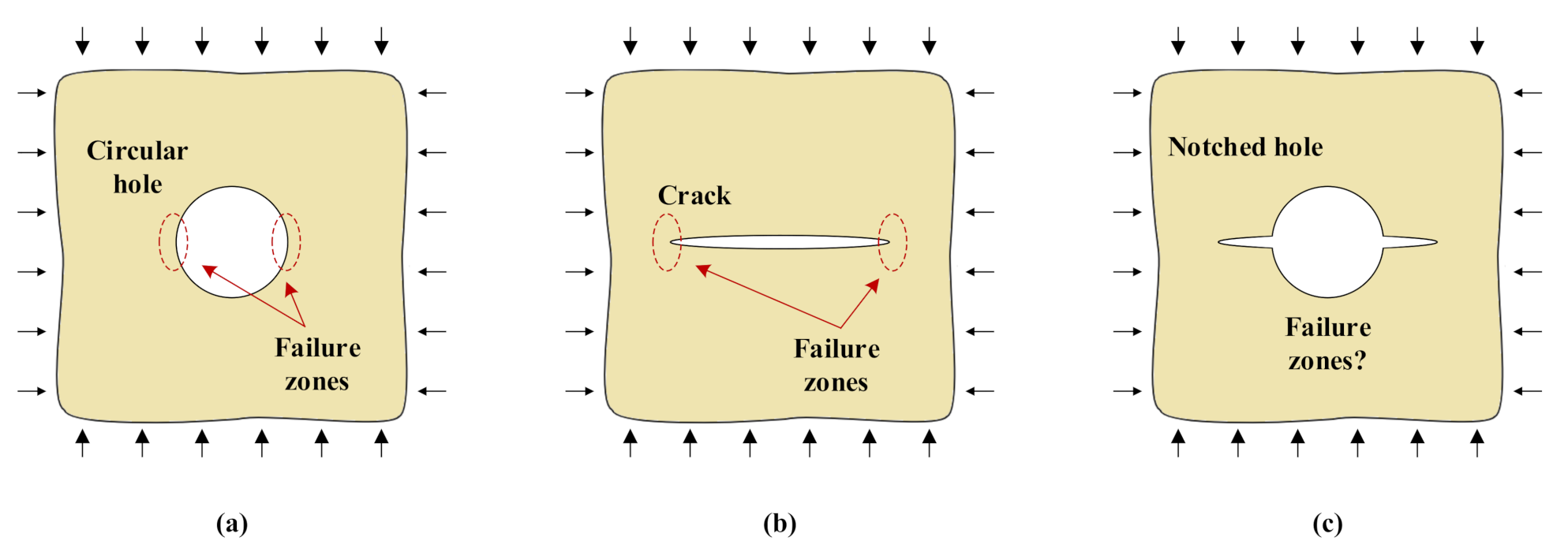
3. Simulation of Failure in a Rock Specimen with a Notched Hole
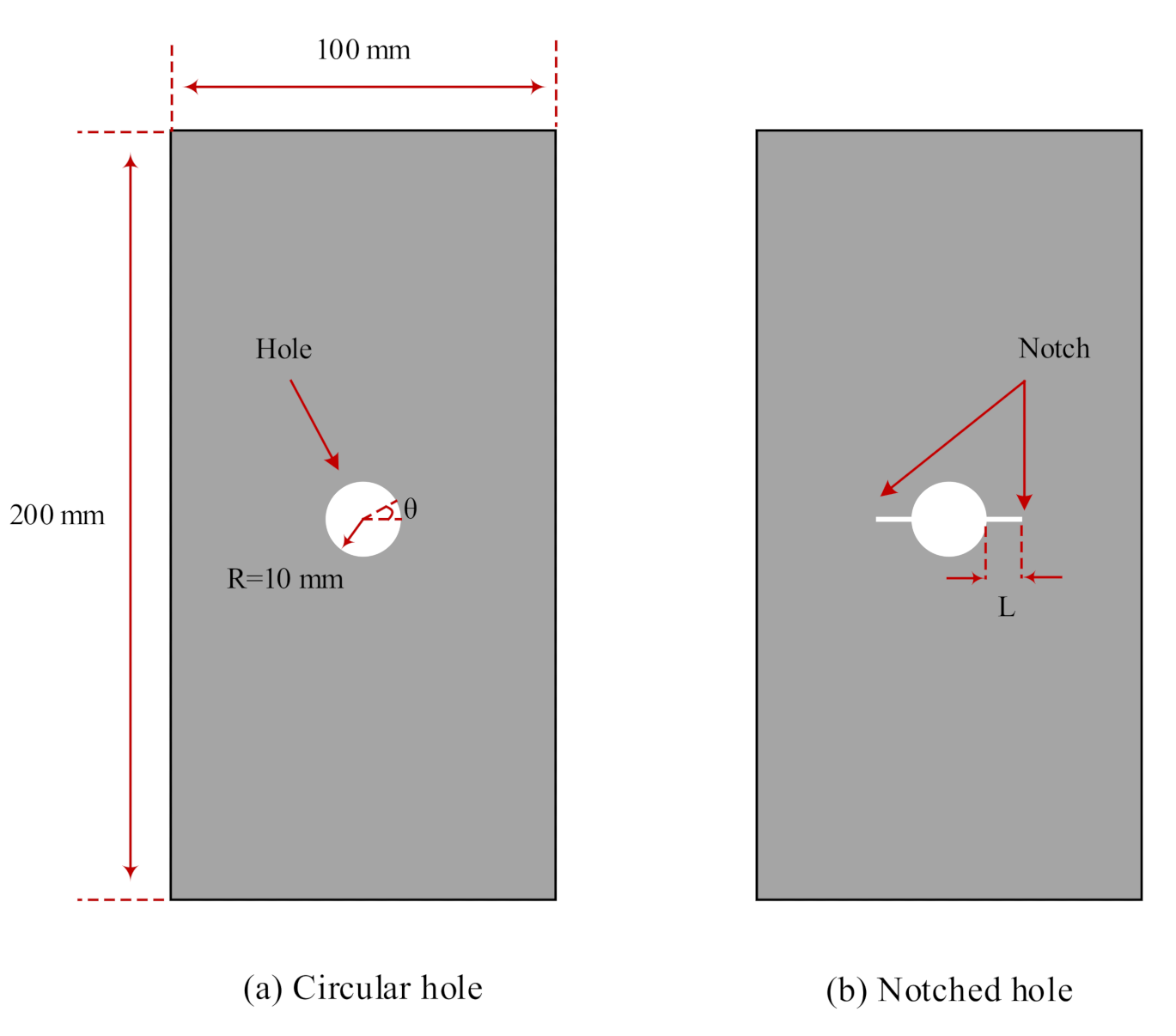
3.1. Model Setup
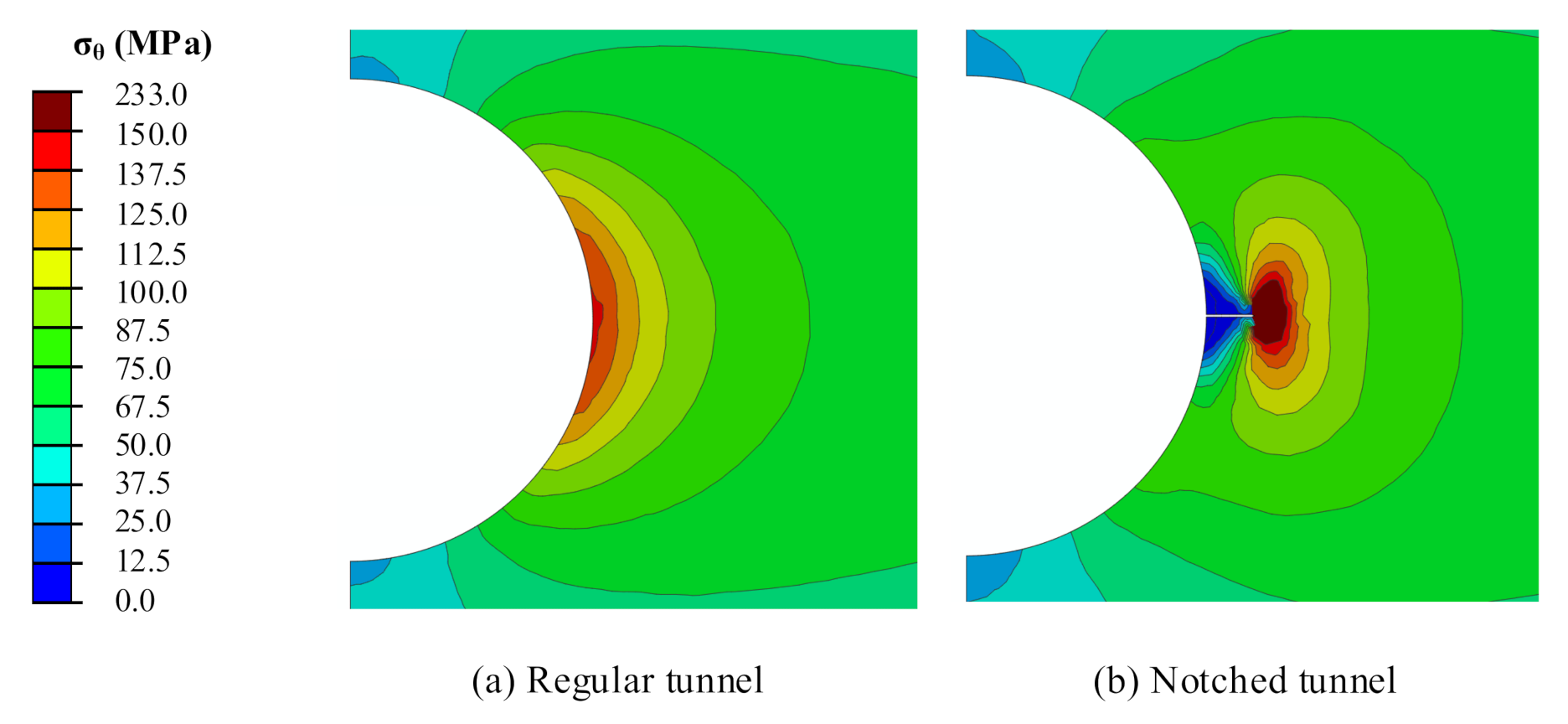
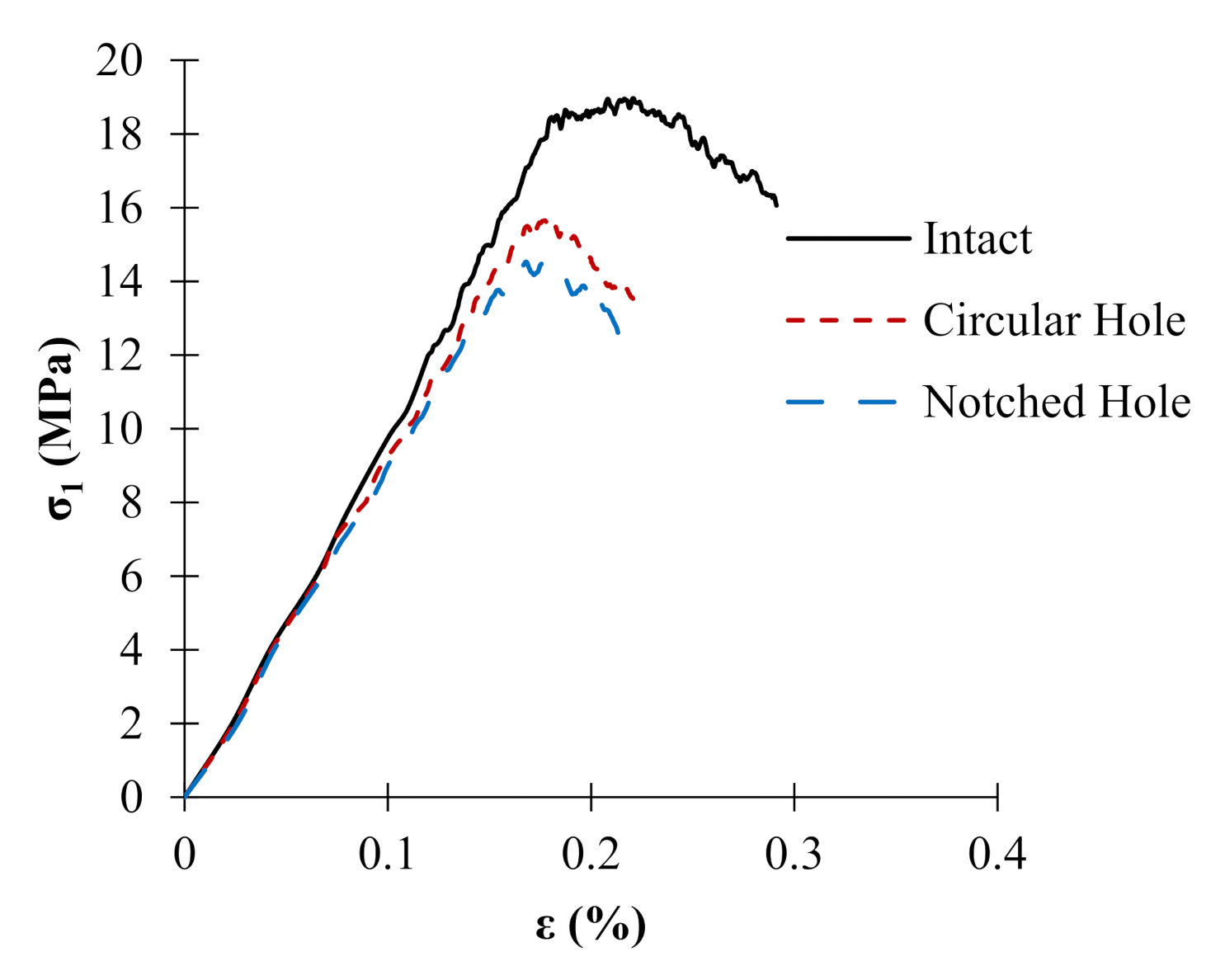
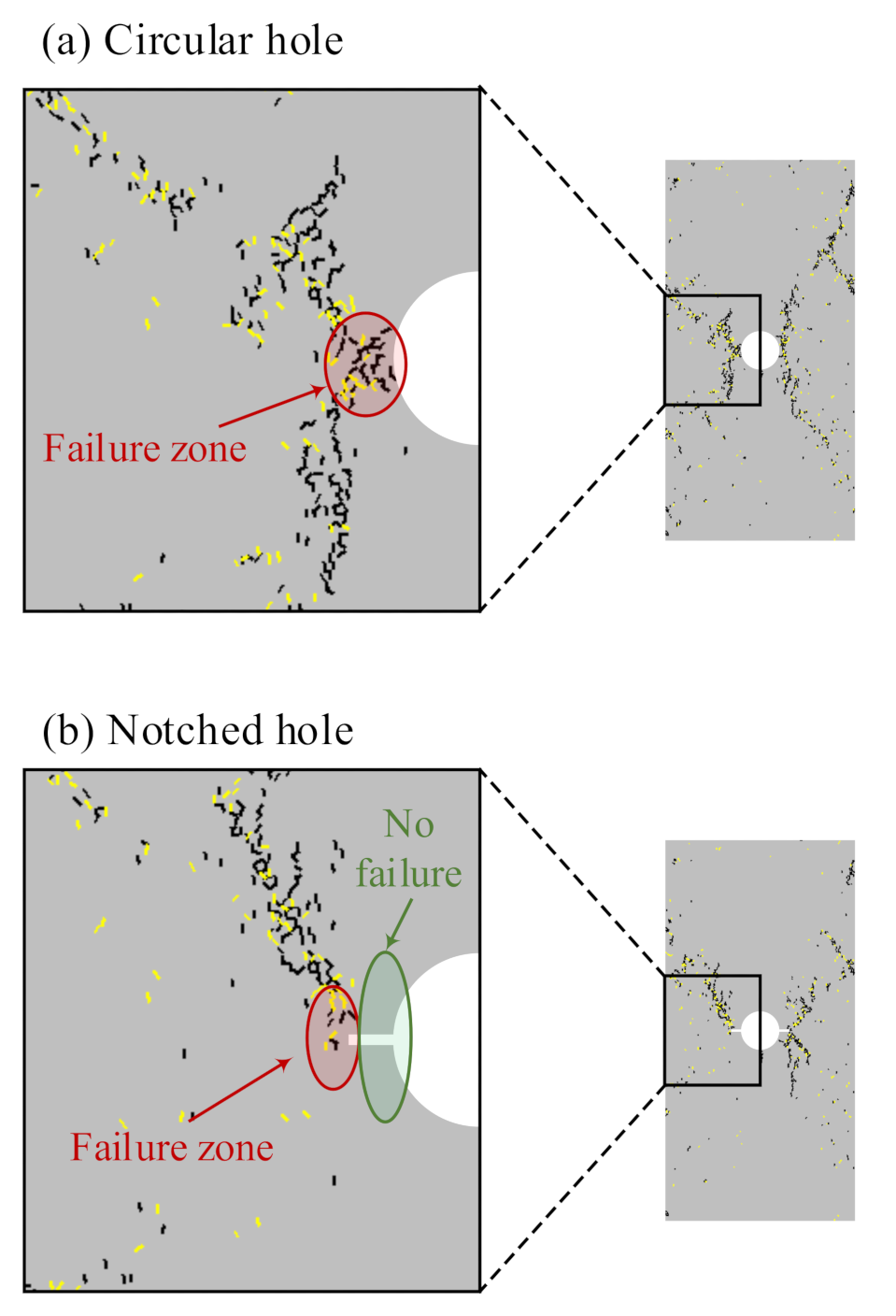
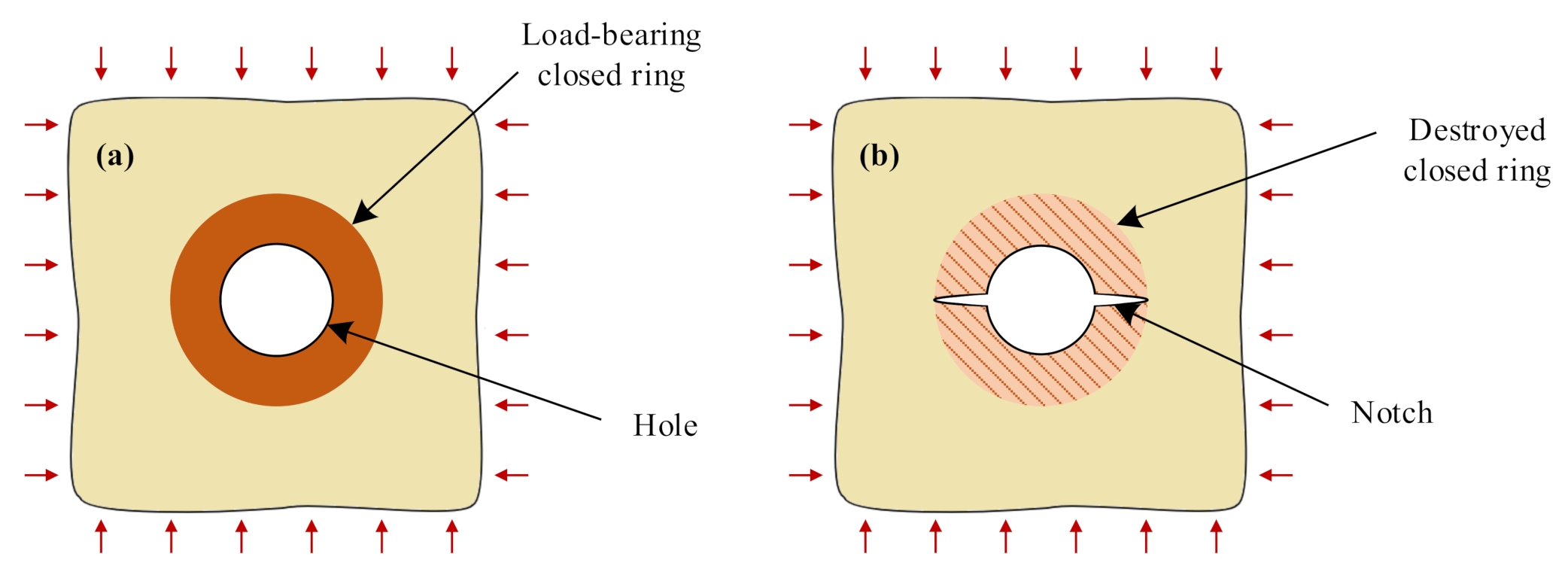
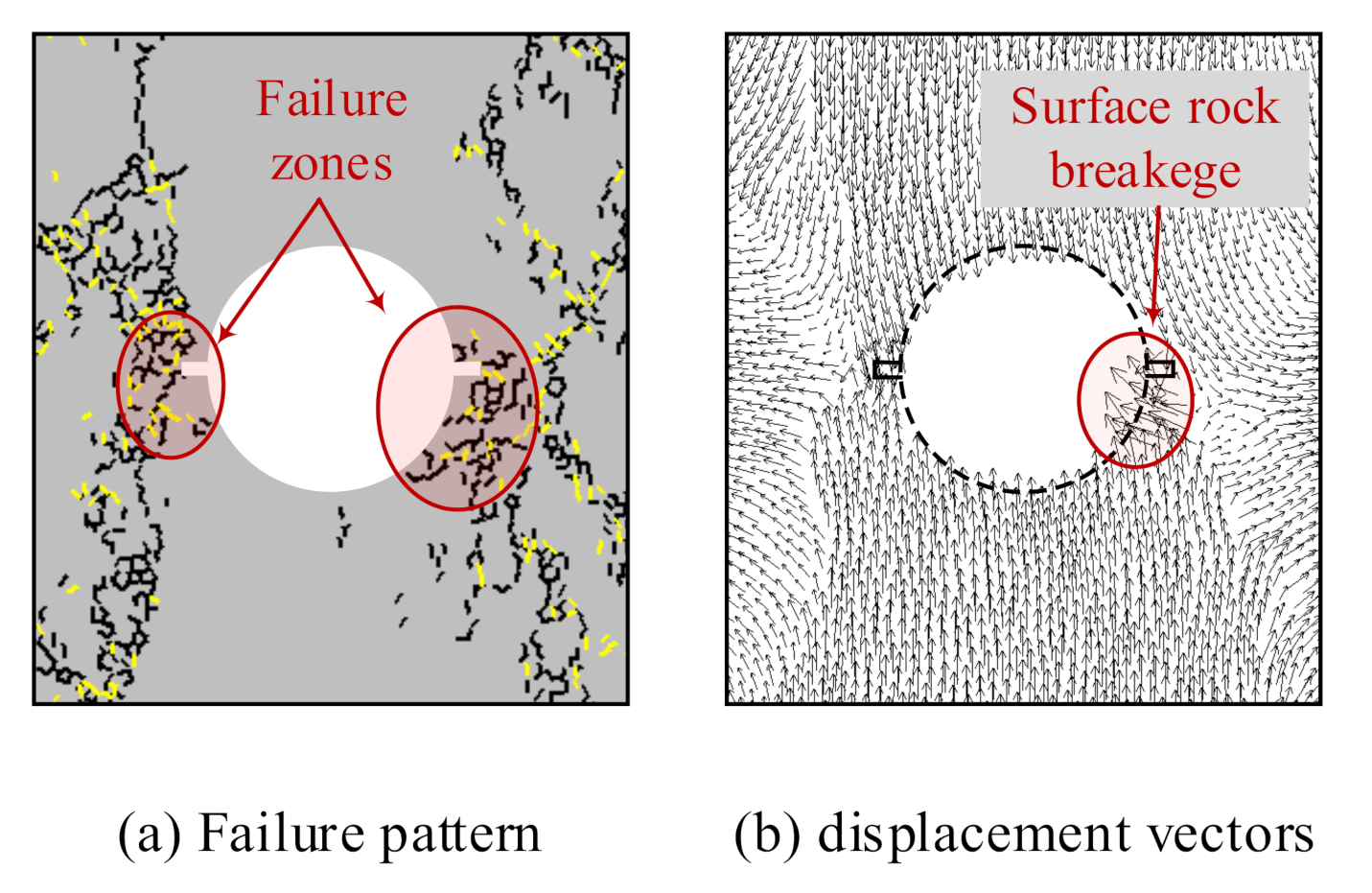
3.2. Failure Evolution in the Circular Hole and the Notched Hole
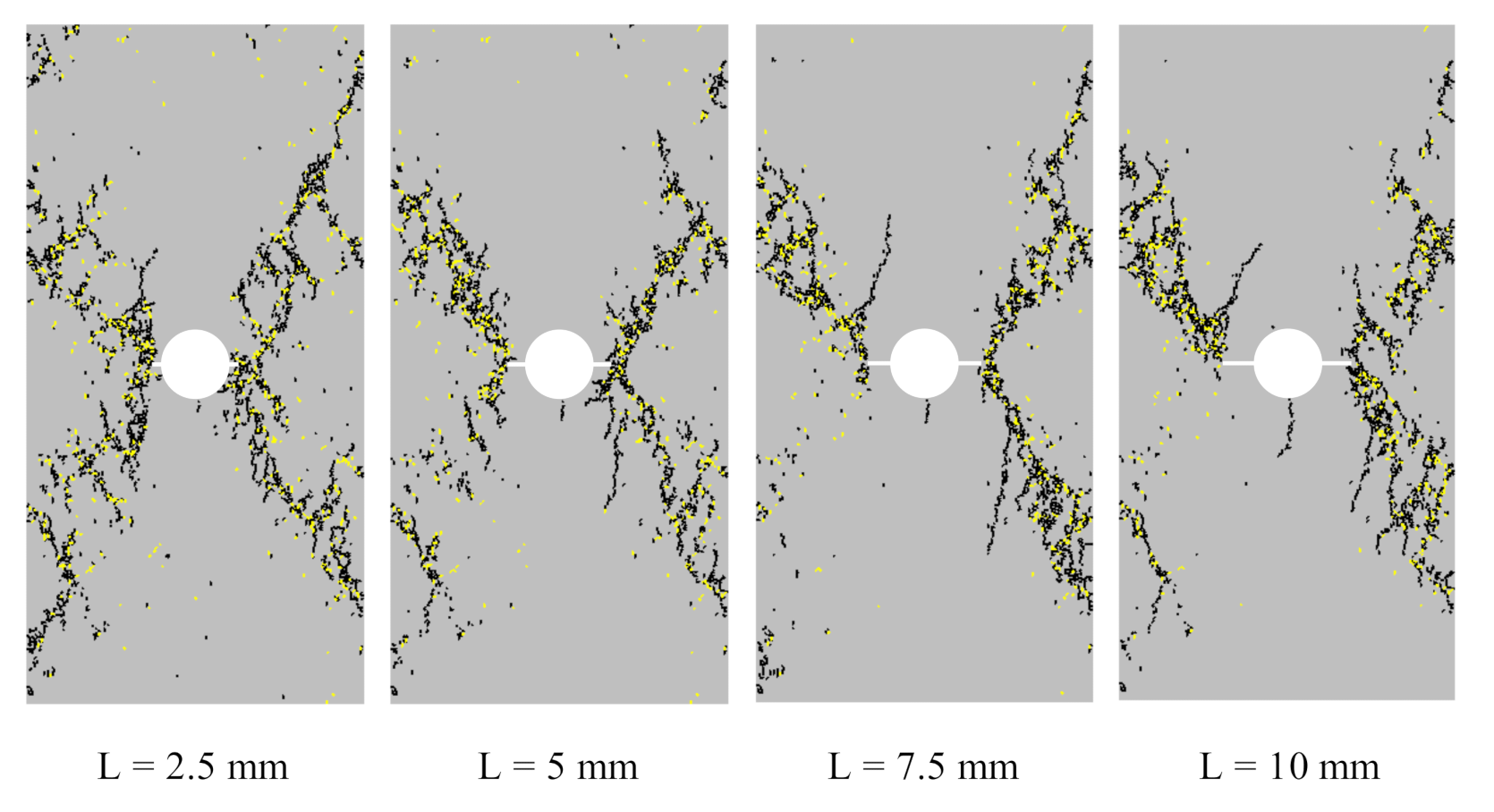
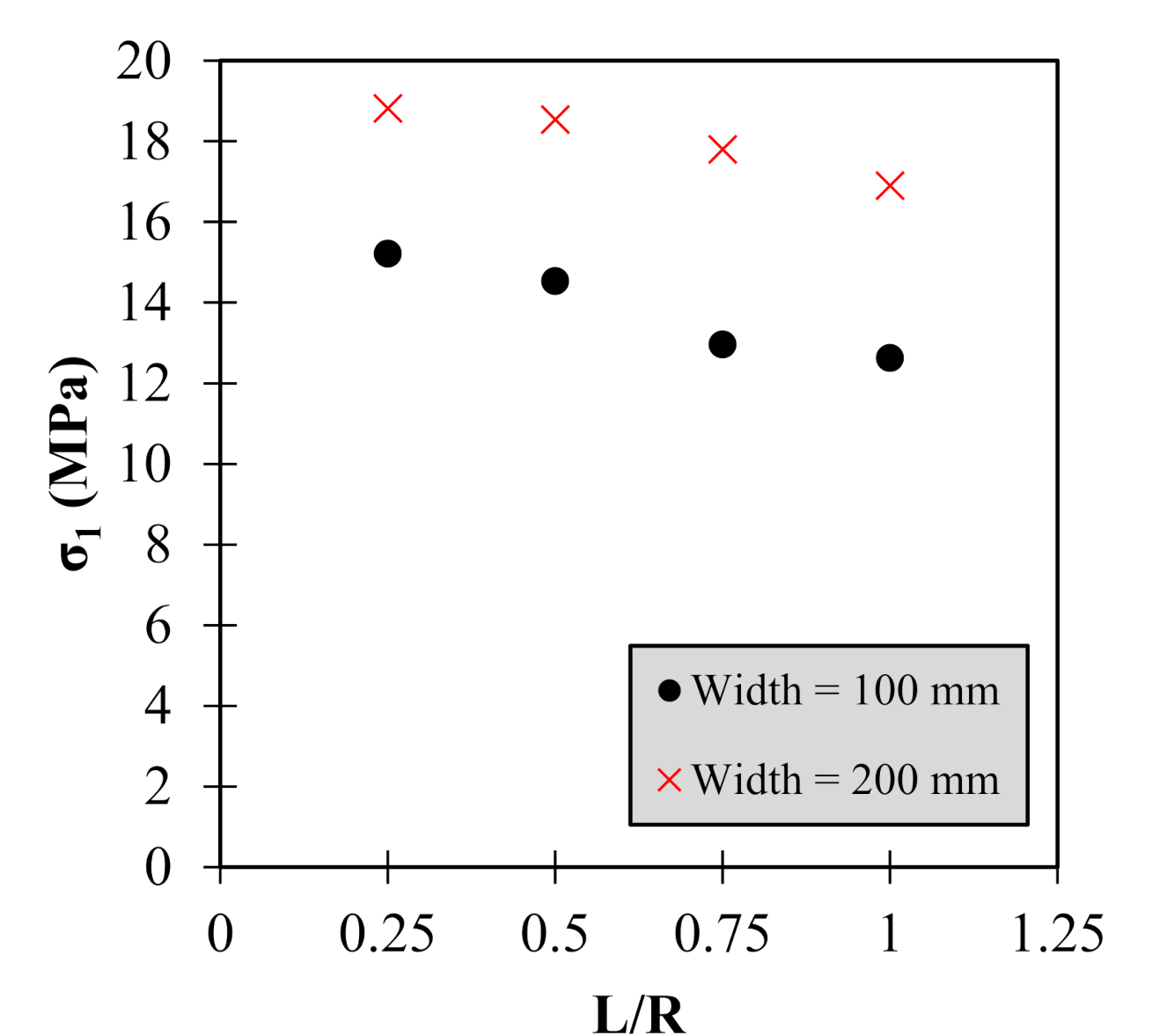
3.3. Influence of the Notch Length on the Failure Mechanism
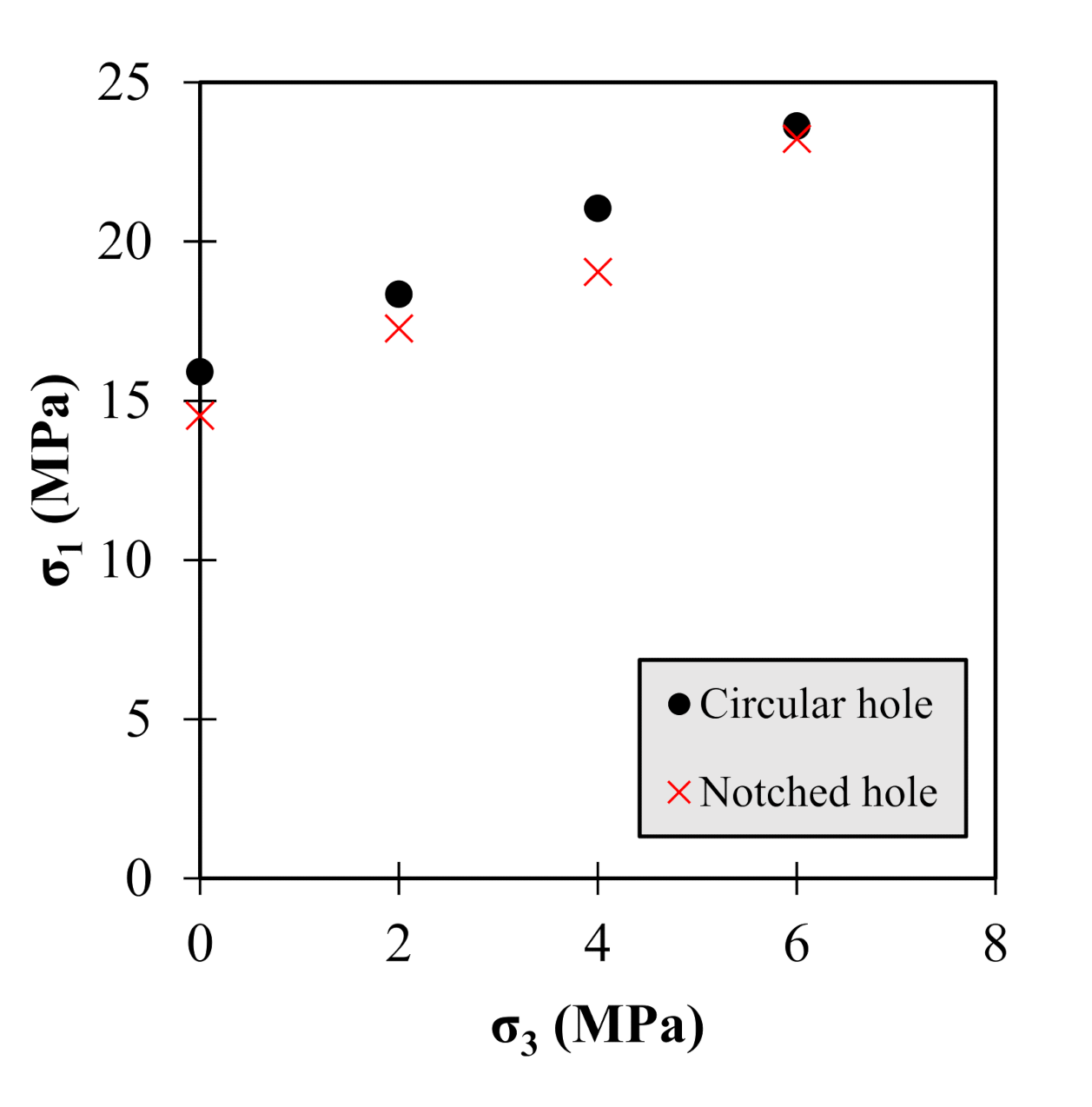
3.4. Influence of Confinement on the Failure Mechanism
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brace, W.F. Dependence of Fracture Strength of Rocks on Grain Size. In Proceedings of the 4th U.S. Symposium on Rock Mechanics (USRMS), University Park, PA, USA, 30 March–1 April 1961. Paper Number: ARMA-61-099. [Google Scholar]
- Howarth, D.F.; Rowlands, J.C. Quantitative assessment of rock texture and correlation with drillability and strength properties. Rock Mech. Rock Engng. 1987, 20, 57–85. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Uno, H.; Tasaka, Y.; Minami, M. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2004, 41, 3–19. [Google Scholar] [CrossRef]
- Kemeny, J. Time-dependent drift degradation due to the progressive failure of rock bridges along discontinuities. Int. J. Rock Mech. Min. Sci. 2005, 42, 35–46. [Google Scholar] [CrossRef]
- Lee, H.; Jeon, S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression. Int. J. Solids Struct. 2011, 48, 979–999. [Google Scholar] [CrossRef]
- Gehle, C.; Kutter, H.K. Breakage and shear behaviour of intermittent rock joints. Int. J. Rock Mech. Min. Sci. 2003, 40, 687–700. [Google Scholar] [CrossRef]
- Zhang, P.; Li, N.; Li, X.-B.; Nordlund, E. Compressive failure model for brittle rocks by shear faulting and its evolution of strength components. Int. J. Rock Mech. Min. 2009, 46, 830–841. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chau, K.T. Crack coalescence in a rock-like material containing two cracks. Int. J. Rock Mech. Min. Sci. 1998, 35, 147–164. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Einstein, H.H. Systematic evaluation of cracking behavior in specimens containing single flaws under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2009, 46, 239–249. [Google Scholar] [CrossRef]
- Lee, S.; Ravichandran, G. Crack initiation in brittle solids under multiaxial compression. Eng. Fract. Mech. 2003, 70, 1645–1658. [Google Scholar] [CrossRef]
- Wang, Q.Z.; Feng, F.; Ni, M.; Gou, X.P. Measurement of mode I and mode II rock dynamic fracture toughness with cracked straight through flattened Brazilian disc impacted by split Hopkinson pressure bar. Eng. Fract. Mech. 2011, 78, 2455–2469. [Google Scholar] [CrossRef]
- Park, C.H.; Bobet, A. Crack initiation, propagation and coalescence from frictional flaws in uniaxial compression. Eng. Fract. Mech. 2010, 77, 2727–2748. [Google Scholar] [CrossRef]
- Zhuang, X.; Chun, J.; Zhu, H. A comparative study on unfilled and filled crack propagation for rock-like brittle material. Theor. Appl. Fract. Mech. 2014, 72, 110–120. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Liu, X.-R.; Jing, H.-W. Experimental investigation on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2013, 63, 82–92. [Google Scholar] [CrossRef]
- Manouchehrian, A.; Sharifzadeh, M.; Marji, M.F.; Gholamnejad, J. A bonded particle model for analysis of the flaw orientation effect on crack propagation mechanism in brittle materials under compression. Arch. Civ. Mech. Eng. 2014, 14, 40–52. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Malama, B.; Wang, J. Physical and particle flow modeling of jointed rock block behavior under uniaxial loading. Int. J. Rock Mech. Min. Sci. 2001, 38, 641–657. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.; Kulatilake, P.H.S.W.; Liang, W.; Wang, E. Fracturing behaviour of sandstone specimens with a cavity formed by intersecting excavations under compression: Experimental study and numerical modelling. Strain 2019, 55, e12316. [Google Scholar] [CrossRef]
- Le, H.; Sun, S.; Kulatilake Pinnaduwa, H.S.W.; Wei, J. Effect of Grout on Mechanical Properties and Cracking Behavior of Rock-Like Specimens Containing a Single Flaw under Uniaxial Compression. Int. J. Geomech. 2018, 18, 04018129. [Google Scholar] [CrossRef]
- Wu, H.; Kulatilake, P.H.S.W.; Zhao, G.; Liang, W. Stress distribution and fracture evolution around a trapezoidal cavity in sandstone loaded in compression. Theor. Appl. Fract. Mech. 2019, 104, 102348. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.; Liang, W. Investigation of cracking behavior and mechanism of sandstone specimens with a hole under compression. Int. J. Mech. Sci. 2019, 163, 105084. [Google Scholar] [CrossRef]
- Lin, Q.; Cao, P.; Liu, Y.; Cao, R.; Li, J. Mechanical behaviour of a jointed rock mass with a circular hole under compression-shear loading: Experimental and numerical studies. Theor. Appl. Fract. Mech. 2021, 114, 102998. [Google Scholar] [CrossRef]
- Han, W.; Jiang, Y.; Luan, H.; Du, Y.; Zhu, Y.; Liu, J. Numerical investigation on the shear behavior of rock-like materials containing fissure-holes with FEM-CZM method. Comput. Geotech. 2020, 125, 103670. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P.; Ayatollahi, M.R. Brittle fracture of sharp and blunt V-notches in isostatic graphite under pure compression loading. Carbon 2013, 63, 101–116. [Google Scholar] [CrossRef]
- Torabi, A.R.; Firoozabadi, M.; Ayatollahi, M.R. Brittle fracture analysis of blunt V-notches under compression. Int. J. Solids Struct. 2015, 67, 219–230. [Google Scholar] [CrossRef]
- Bura, E.; Derpeński, Ł.; Seweryn, A. Fracture in PMMA notched specimens under compression–Experimental study. Polym. Test. 2019, 77, 105923. [Google Scholar] [CrossRef]
- Sharma, D.S. Stress concentration around circular/elliptical/triangular cutouts in infinite composite plate. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011; p. 6. [Google Scholar]
- Hubbert, M.K.; Willis, D.G. Mechanics of Hydraulic Fracturing. Trans. AIME 1957, 210, 153–168. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Manouchehrian, A.; Kulatilake, H.S.W.; Wu, R. Strainburst control in deep tunnels using a notched excavation method. Int. J. Geomech. 2021. revision submitted. [Google Scholar]
- Javanmardi, M.R.; Maheri, M.R. Extended finite element method and anisotropic damage plasticity for modelling crack propagation in concrete. Finite Elem. Anal. Des. 2019, 165, 1–20. [Google Scholar] [CrossRef]
- Peng, X.; Atroshchenko, E.; Kerfriden, P.; Bordas, S.P.A. Isogeometric boundary element methods for three dimensional static fracture and fatigue crack growth. Comput. Methods Appl. Mech. Eng. 2017, 316, 151–185. [Google Scholar] [CrossRef]
- Schöpfer, M.P.J.; Abe, S.; Childs, C.; Walsh, J.J. The impact of porosity and crack density on the elasticity, strength and friction of cohesive granular materials: Insights from DEM modelling. Int. J. Rock Mech. Min. Sci. 2009, 46, 250–261. [Google Scholar] [CrossRef]
- Tan, X.C.; Kou, S.Q.; Lindqvist, P.A. Application of the DDM and fracture mechanics model on the simulation of rock breakage by mechanical tools. Eng. Geol. 1998, 49, 277–284. [Google Scholar] [CrossRef]
- Manouchehrian, A.; Marji, M.F. Numerical analysis of confinement effect on crack propagation mechanism from a flaw in a pre-cracked rock under compression. Acta Mech. Sin. 2012, 28, 1389–1397. [Google Scholar] [CrossRef]
- Sukumar, N.; Moës, N.; Moran, B.; Belytschko, T. Extended finite element method for three-dimensional crack modelling. Int. J. Numer. Methods Eng. 2000, 48, 1549–1570. [Google Scholar] [CrossRef]
- Fatehi Marji, M.; Dehghani, I. Kinked crack analysis by a hybridized boundary element/boundary collocation method. Int. J. Solids Struct. 2010, 47, 922–933. [Google Scholar] [CrossRef][Green Version]
- Wu, H.; Kulatilake, P.H.S.W.; Zhao, G.; Liang, W.; Wang, E. A comprehensive study of fracture evolution of brittle rock containing an inverted U-shaped cavity under uniaxial compression. Comput. Geotech. 2019, 116, 103219. [Google Scholar] [CrossRef]
- Itasca. PFC 3D Manual, version 3.1; Itasca Consulting Group: Minneapolis, MN, USA, 2004. [Google Scholar]
- Yang, X.; Kulatilake, P.H.S.W.; Jing, H.; Yang, S. Numerical simulation of a jointed rock block mechanical behavior adjacent to an underground excavation and comparison with physical model test results. Tunn. Undergr. Space Technol. 2015, 50, 129–142. [Google Scholar] [CrossRef]
- Mehranpour, M.H.; Kulatilake, P.H.S.W. Improvements for the smooth joint contact model of the particle flow code and its applications. Comput. Geotech. 2017, 87, 163–177. [Google Scholar] [CrossRef]
- Hudson, J.A.; Crouch, S.L.; Fairhurst, C. Soft, stiff and servo-controlled testing machines: A review with reference to rock failure. Eng. Geol. 1972, 6, 155–189. [Google Scholar] [CrossRef]
- Banks, J.; Carson II, J.; Nelson, B.; Nicol, D. Discrete Event System Simulation, 5th ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]




| Micro-Parameters | Value |
|---|---|
| Particle minimum radius, R (mm) | 0.4 |
| Particle radius ratio, Rmax/Rmin | 1.66 |
| Particle density (kg/m3) | 2000 |
| Particle contact modulus, Ec (GPa) | 6.1 |
| Particle stiffness ratio, kn/ks | 1.0 |
| Particle friction coefficient, μ | 0.5 |
| Parallel-bond modulus, c (GPa) | 6.1 |
| Parallel-bond stiffness ratio, | 1.0 |
| Parallel-bond radius multiplier, | 1.0 |
| Parallel-bond normal strength, mean (MPa) | 12 |
| Parallel-bond normal strength, std. dev. (MPa) | 2.0 |
| Parallel-bond shear strength, mean (MPa) | 12 |
| Parallel-bond shear strength, std. dev. (MPa) | 2.0 |
| Macro-Parameters | Value |
|---|---|
| Uniaxial compressive strength, (MPa) | 18.95 |
| Brazilian tensile strength, (MPa) | 2.92 |
| Young’s modulus, E (GPa) | 10.02 |
| Poisson ratio, | 0.11 |
| Cohesion, c (MPa) | 7.03 |
| Internal friction angle, (°) | 18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manouchehrian, A.; Kulatilake, P.H.S.W.; Wu, R. Failure Mechanism of Rock Specimens with a Notched Hole under Compression—A Numerical Study. Appl. Sci. 2021, 11, 7797. https://doi.org/10.3390/app11177797
Manouchehrian A, Kulatilake PHSW, Wu R. Failure Mechanism of Rock Specimens with a Notched Hole under Compression—A Numerical Study. Applied Sciences. 2021; 11(17):7797. https://doi.org/10.3390/app11177797
Chicago/Turabian StyleManouchehrian, Amin, Pinnaduwa H. S. W. Kulatilake, and Rui Wu. 2021. "Failure Mechanism of Rock Specimens with a Notched Hole under Compression—A Numerical Study" Applied Sciences 11, no. 17: 7797. https://doi.org/10.3390/app11177797
APA StyleManouchehrian, A., Kulatilake, P. H. S. W., & Wu, R. (2021). Failure Mechanism of Rock Specimens with a Notched Hole under Compression—A Numerical Study. Applied Sciences, 11(17), 7797. https://doi.org/10.3390/app11177797






