Sensorless Control for DC–DC Boost Converter via Generalized Parameter Estimation-Based Observer
Abstract
1. Introduction
- A PI-PBC is proposed to stabilize a DC–DC boost converter with exponential stability.
- A GPEBO is constructed to estimate the inductor current. It is noted that the FTC of this observer is ensured and a very weak persistence of excitation (PE) condition is needed. Moreover, this result can be easily extended to a large class of converters.
- The experimental results are given to assess the performance of the proposed sensorless control law.
2. System Model and Problem Formation
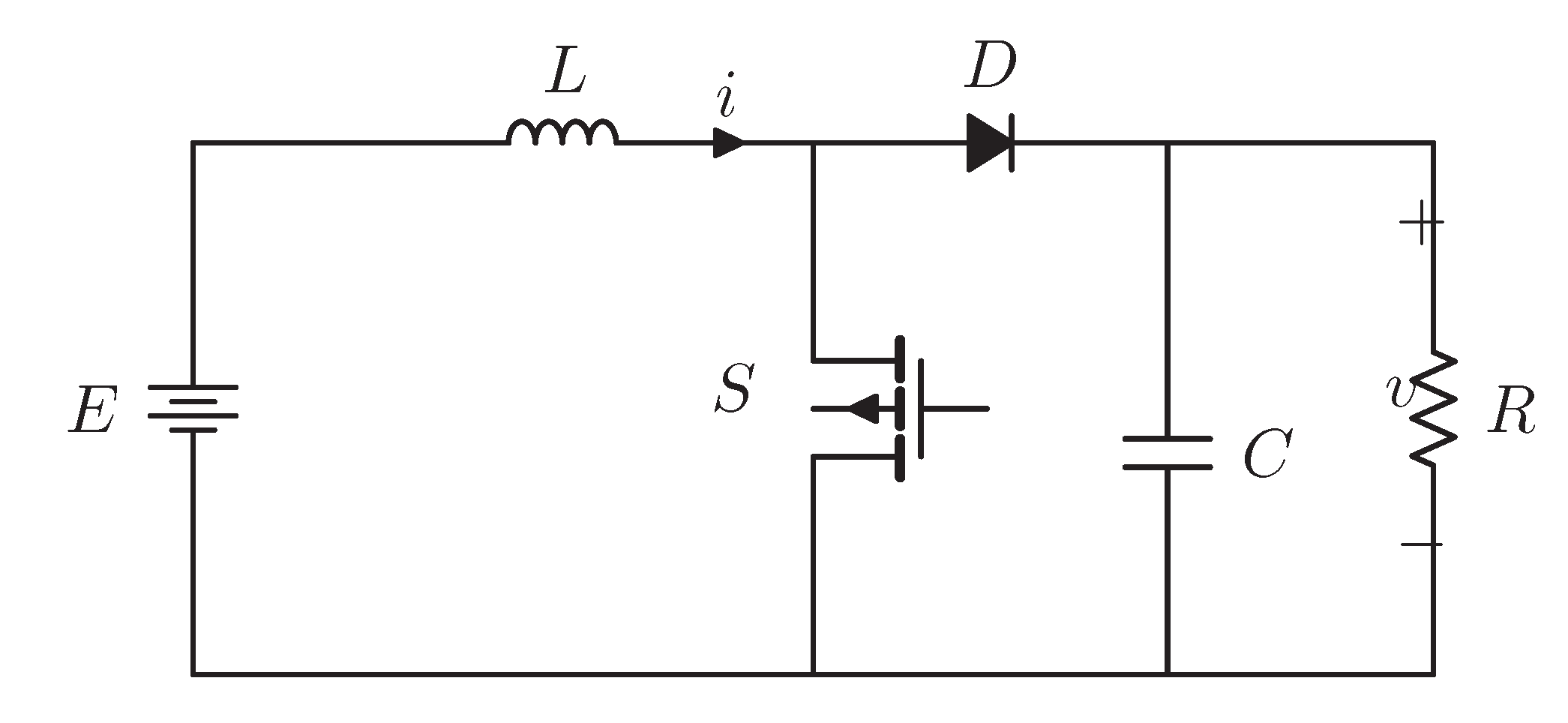
2.1. Model of DC–DC Boost Converter with CPL
2.2. Problem Formulation
- F1.
- The estimate of the state i can converge to its real value with the FTC. That is,
- F2.
- is an exponentially stable equilibrium of the closed-loop system. Namely, for all initial conditions, the following claim is achieved with the estimate .with all signals bounded.
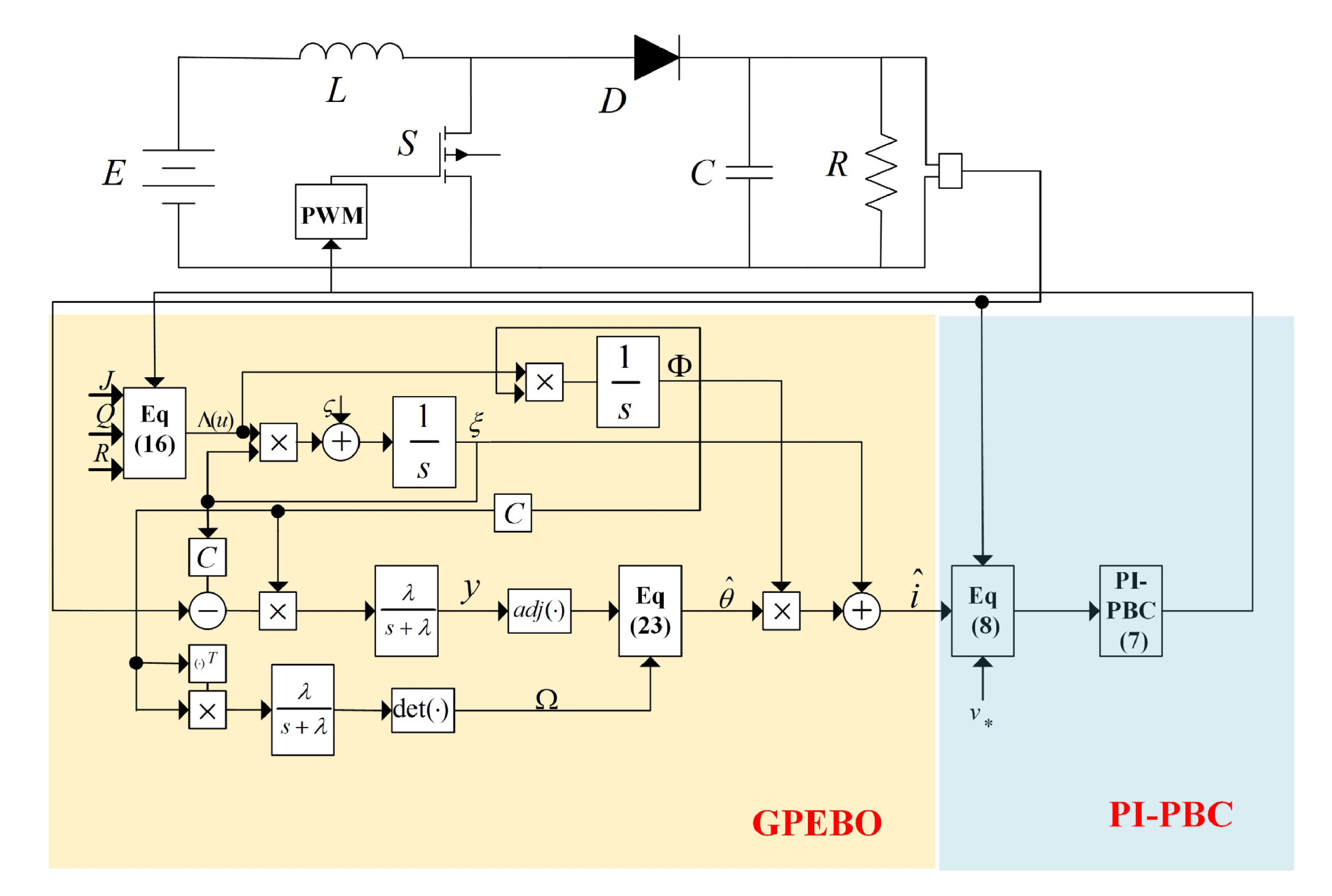
3. Sensorless Controller Design
- It is supposed that the state i is measured. The full-information PI-PBC is designed.
- A GPEBO is devised to estimate the current with FTC.
- By combining the PI-PBC and GPEBO, a sensorless control scheme is achieved.
3.1. PI-PBC Design
3.2. GPEBO Design
3.3. Observer-Based PI-PBC
4. Simulation Results
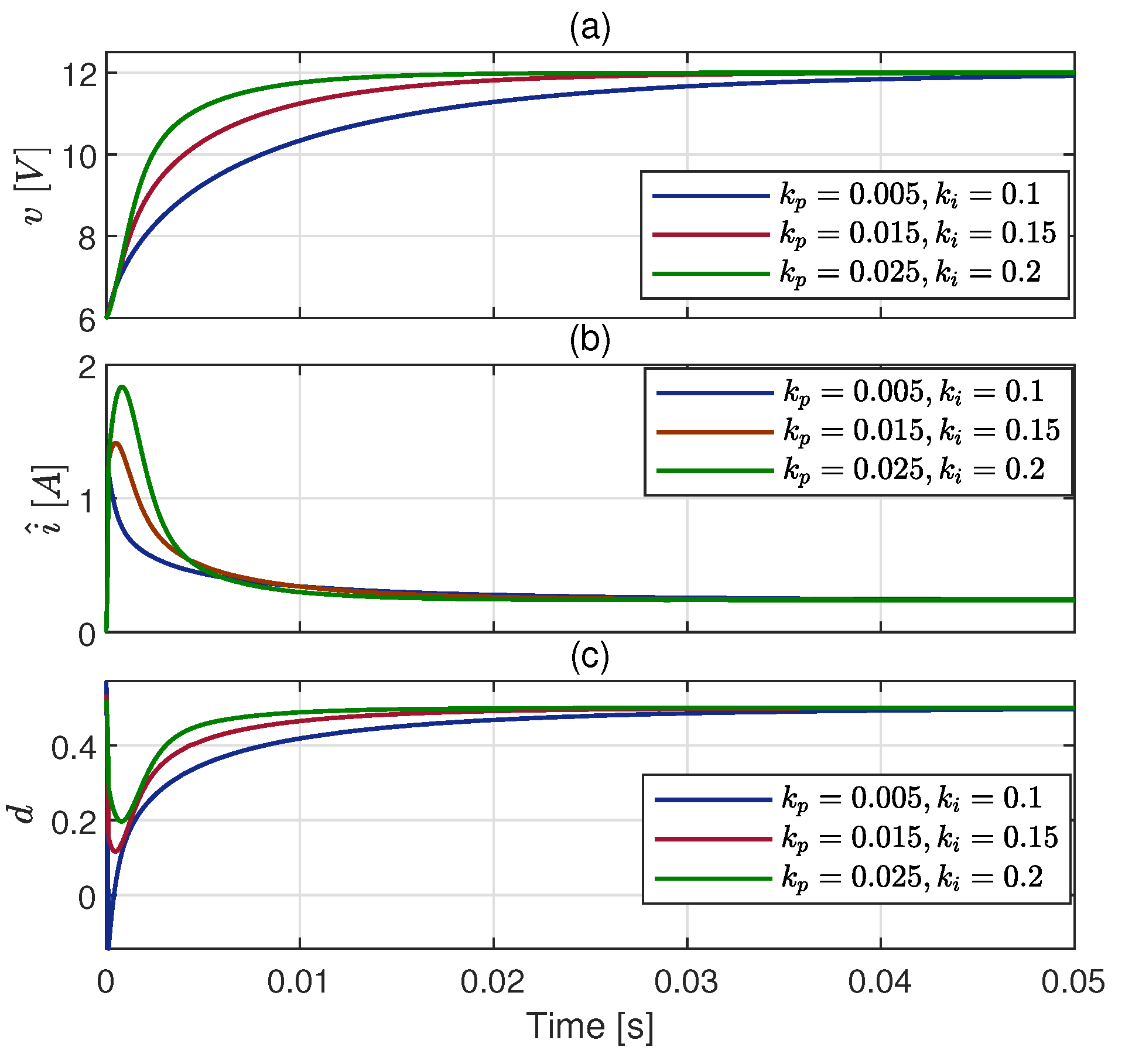
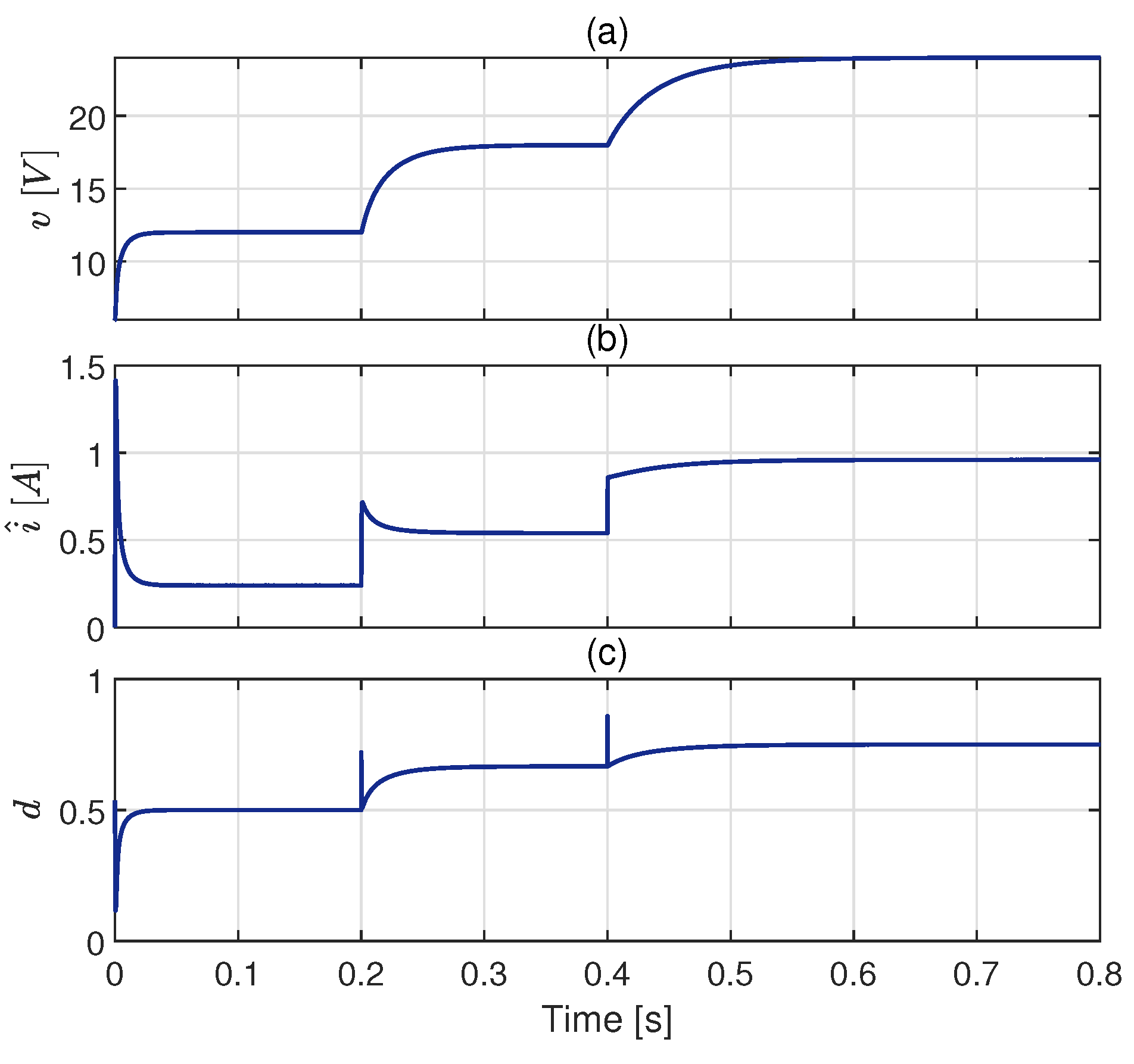
4.1. Scenario 1: Tracking Performance Test
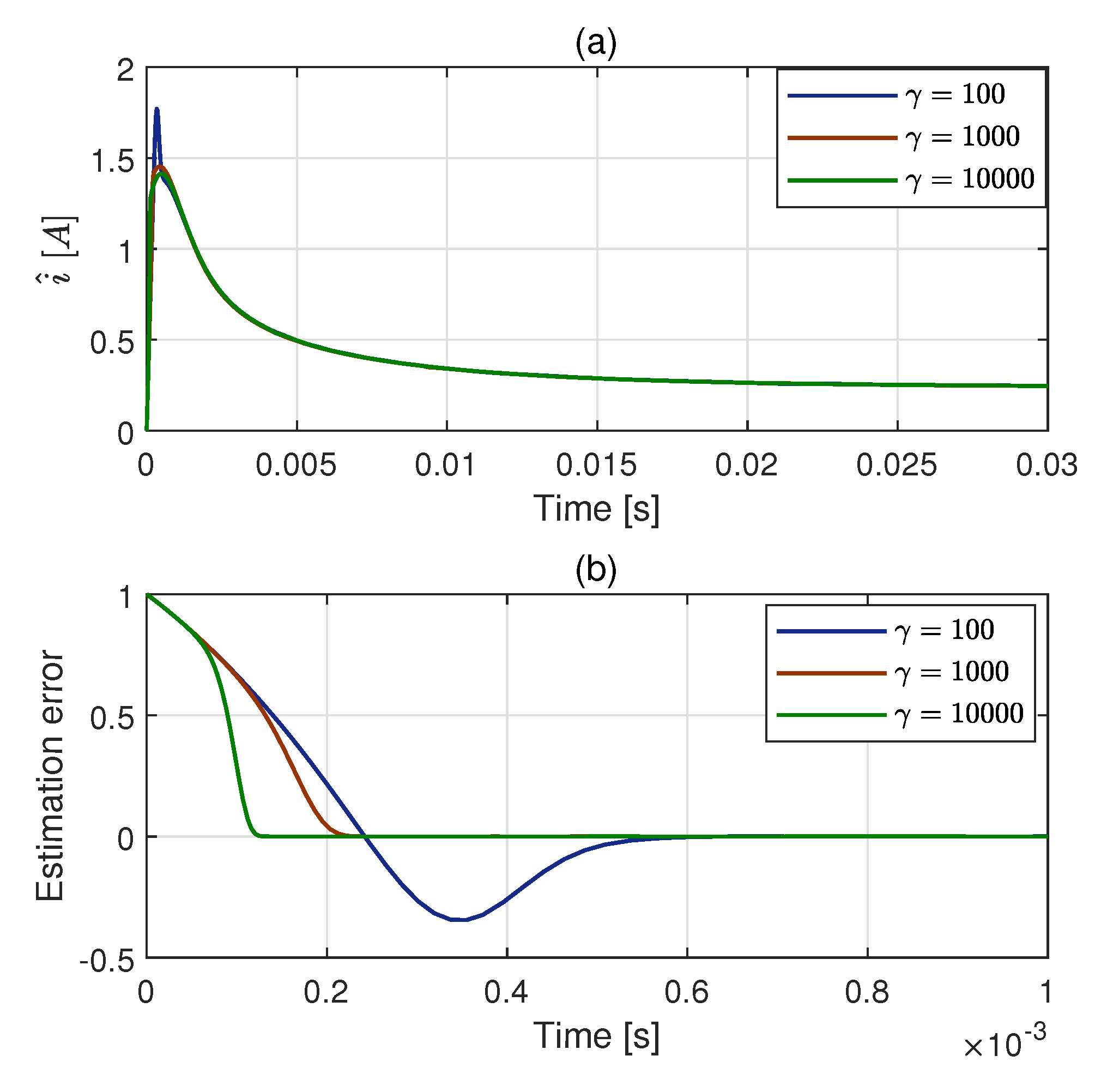
4.2. Scenario 2: GPEBO Performance Test
4.3. Scenario 3: Robustness Performance Test
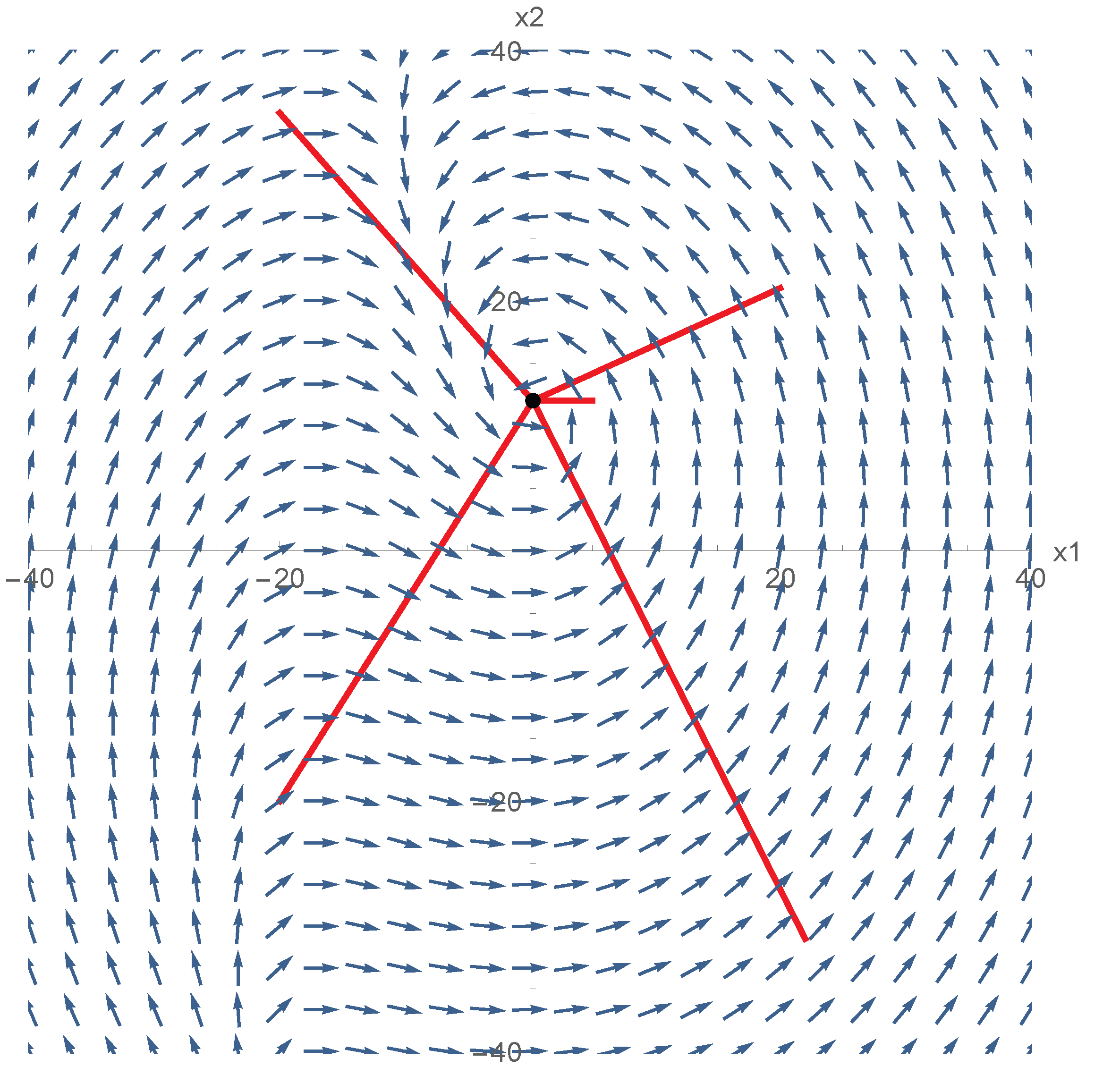
4.4. Scenario 4: Phase Portrait
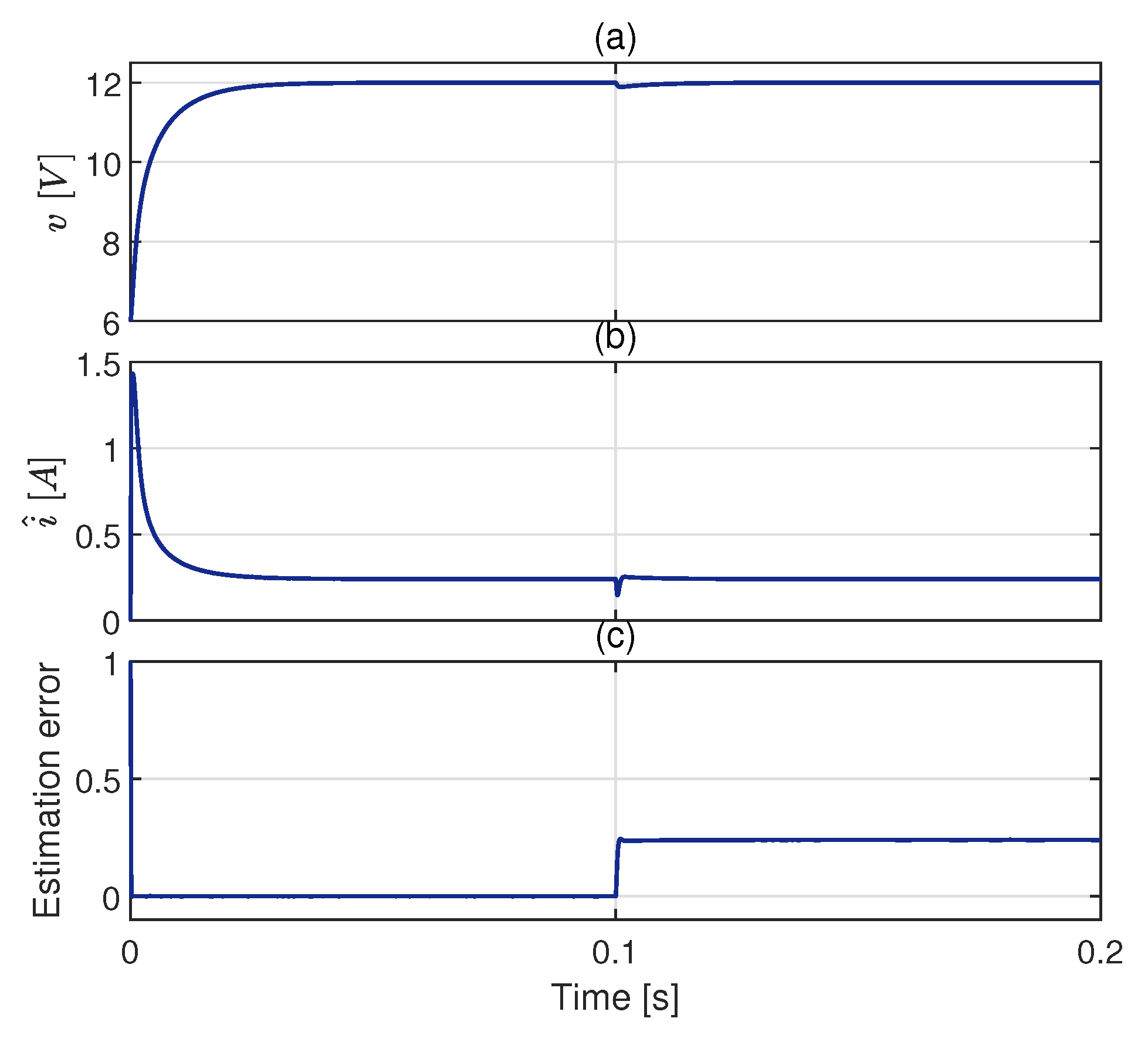
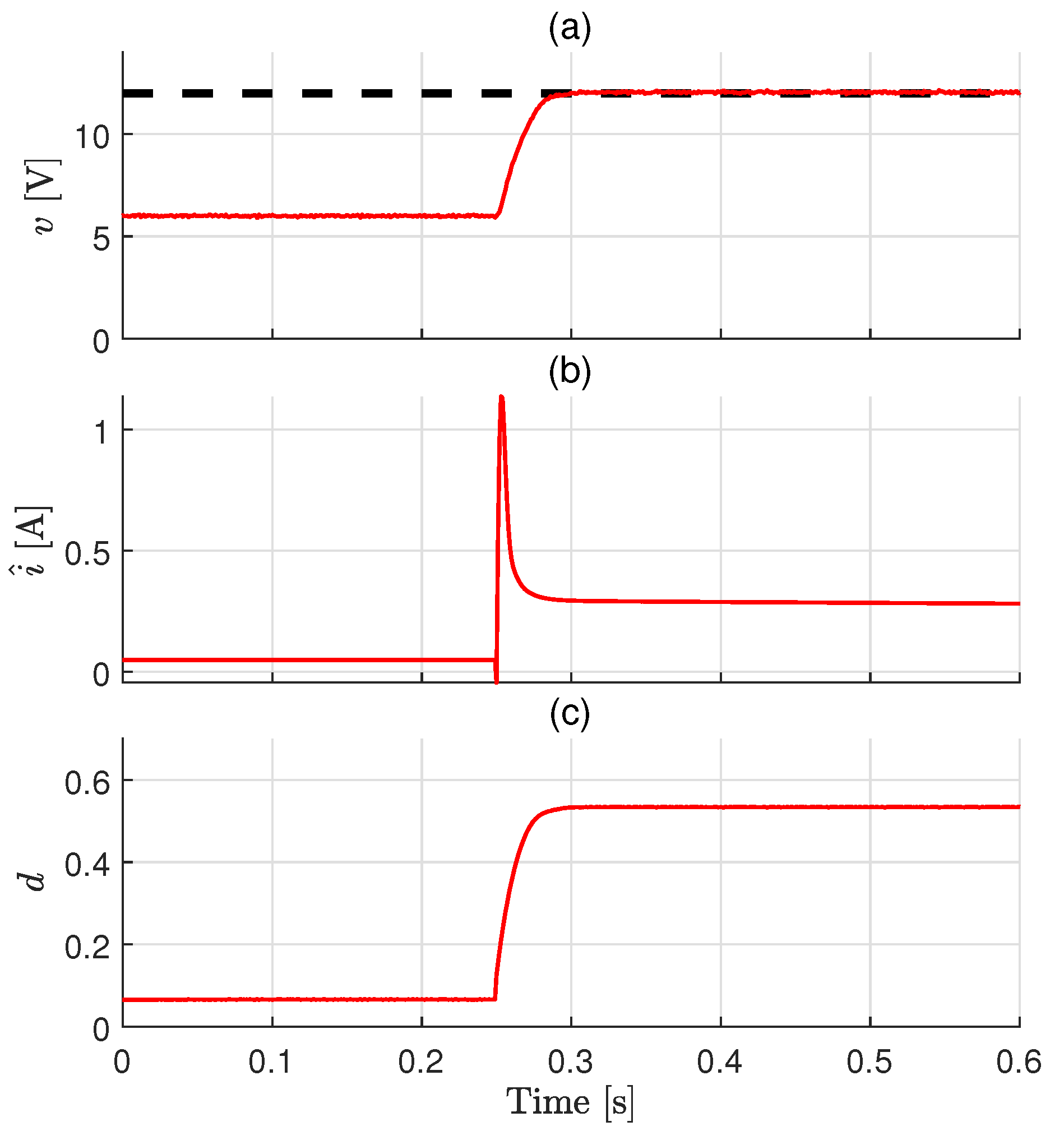
5. Experimental Result
6. Conclusions and Future Work
- Although the proposed controller is insensitive to the perturbations of the circuit parameters including , the implementation of the designed GPEBO depends on the exact knowledge of these parameters.
- In this paper, a full-order GPEBO is proposed to estimate two states. In fact, the state can be measured. Hence, to avoid the heavy computation task in digital signal processors, a reduced-order observer is desired to only reconstruct the state . This does not mean that the full-order GPEBO is useless. Indeed, the estimate can be used to view the performance of the power system. An alternative method is still needed to suit different application scenarios.
- The proposed method can deal with the sensorless control problem of boost converters with resistance load. However, the constant power load (CPL) exists in many practical applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hwu, K.; Yau, Y. Performance enhancement of boost converter based on PID controller plus linear-to-nonlinear translator. IEEE Trans. Power Electron. 2009, 25, 1351–1361. [Google Scholar] [CrossRef]
- Xu, Q.; Jiang, W.; Blaabjerg, F.; Zhang, C.; Zhang, X.; Fernando, T. Backstepping control for large signal stability of high boost ratio interleaved converter interfaced DC microgrids with constant power loads. IEEE Trans. Power Electron. 2019, 35, 5397–5407. [Google Scholar] [CrossRef]
- He, W.; Ortega, R. Design and implementation of adaptive energy shaping control for DC–DC converters with constant power loads. IEEE Trans. Ind. Inform. 2019, 16, 5053–5064. [Google Scholar] [CrossRef]
- He, W.; Li, S.; Yang, J.; Wang, Z. Incremental passivity based control for DC-DC boost converters under time-varying disturbances via a generalized proportional integral observer. J. Power Electron. 2018, 18, 147–159. [Google Scholar]
- Chang, H.C.; Liaw, C.M. On the front-end converter and its control for a battery powered switched-reluctance motor drive. IEEE Trans. Power Electron. 2008, 23, 2143–2156. [Google Scholar] [CrossRef]
- Li, C.; Wang, G.; Li, H.; Li, F.; Xia, Z.; Liu, Z. Fault-tolerant analysis of two boost inverters for open-end winding induction motor drives. J. Power Electron. 2021, 21, 647–659. [Google Scholar] [CrossRef]
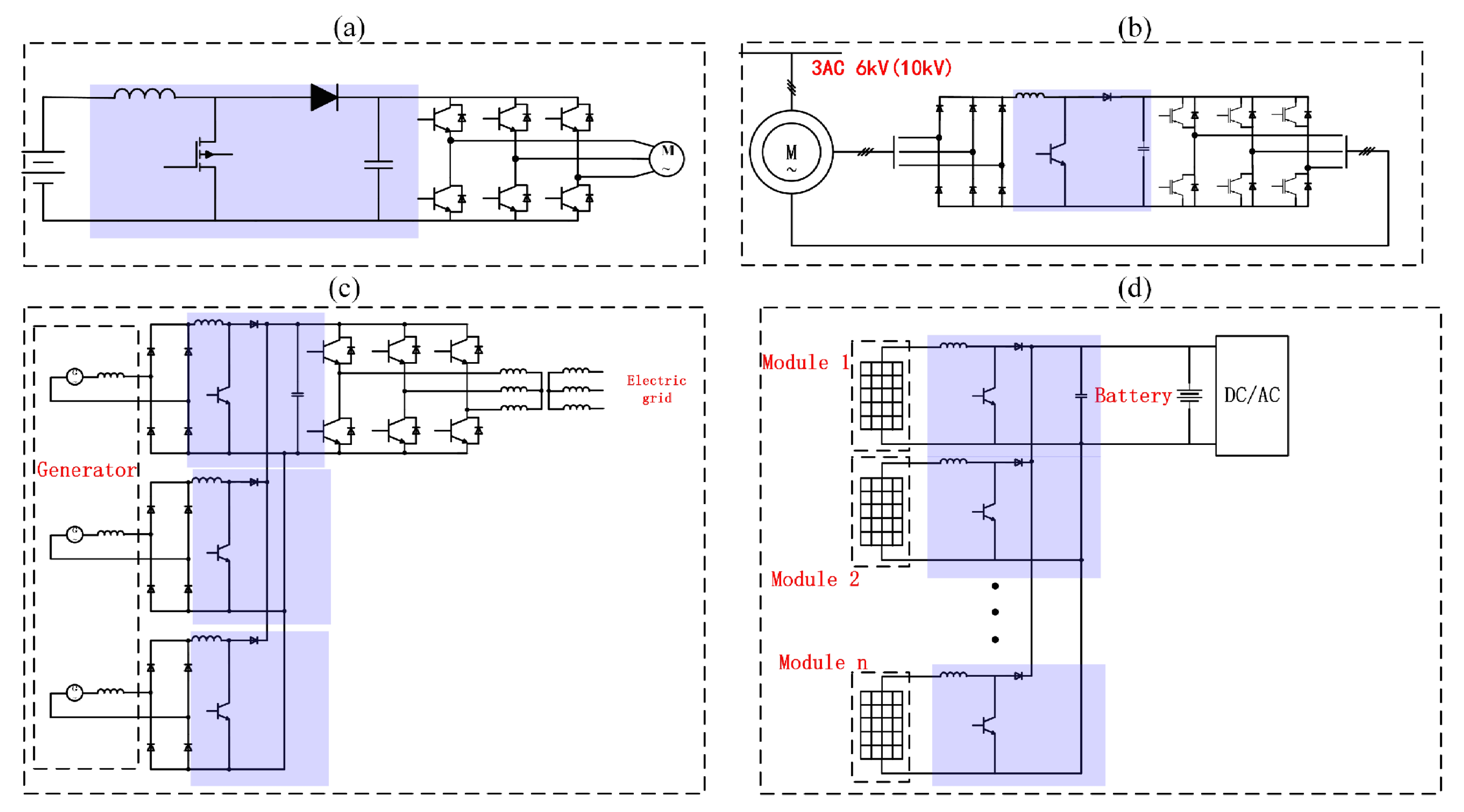
- Kavousi, A.; Fathi, S.H.; Milimonfared, J.; Soltani, M.N. Application of boost converter to increase the speed range of dual-stator winding induction generator in wind power systems. IEEE Trans. Power Electron. 2018, 33, 9599–9610. [Google Scholar] [CrossRef]
- Xia, C.; Geng, Q.; Gu, X.; Shi, T.; Song, Z. Input–output feedback linearization and speed control of a surface permanent-magnet synchronous wind generator with the boost-chopper converter. IEEE Trans. Ind. Electron. 2012, 59, 3489–3500. [Google Scholar]
- Matsuo, H.; Kurokawa, F. New solar cell power supply system using a boost type bidirectinal dc-dc converter. IEEE Trans. Ind. Electron. 1984, IE-31, 51–55. [Google Scholar] [CrossRef]
- Chini, A.; Soci, F. Boost-converter-based solar harvester for low power applications. Electron. Lett. 2010, 46, 296–298. [Google Scholar] [CrossRef]
- Ganapati, V.; Steiner, M.A.; Yablonovitch, E. The voltage boost enabled by luminescence extraction in solar cells. IEEE J. Photovoltaics 2016, 6, 801–809. [Google Scholar] [CrossRef]
- Oucheriah, S.; Guo, L. PWM-based adaptive sliding-mode control for boost DC–DC converters. IEEE Trans. Ind. Electron. 2012, 60, 3291–3294. [Google Scholar] [CrossRef]
- Song, T.T.; Chung, H.S.h. Boundary control of boost converters using state-energy plane. IEEE Trans. Power Electron. 2008, 23, 551–563. [Google Scholar] [CrossRef]
- Chu, G.; Chi, K.T.; Wong, S.C.; Tan, S.C. A unified approach for the derivation of robust control for boost PFC converters. IEEE Trans. Power Electron. 2009, 24, 2531–2544. [Google Scholar] [CrossRef]
- Son, Y.I.; Kim, I.H. Complementary PID controller to passivity-based nonlinear control of boost converters with inductor resistance. IEEE Trans. Control Syst. Technol. 2011, 20, 826–834. [Google Scholar] [CrossRef]
- Naim, R.; Weiss, G.; Ben-Yaakov, S. H/sup/spl infin//control applied to boost power converters. IEEE Trans. Power Electron. 1997, 12, 677–683. [Google Scholar] [CrossRef]
- El Fadil, H.; Giri, F. Backstepping based control of PWM DC-DC boost power converters. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 395–400. [Google Scholar]
- Malekzadeh, M.; Khosravi, A.; Tavan, M. A novel sensorless control scheme for DC-DC boost converter with global exponential stability. Eur. Phys. J. Plus 2019, 134, 338. [Google Scholar] [CrossRef]
- Malekzadeh, M.; Khosravi, A.; Tavan, M. A novel adaptive output feedback control for DC–DC boost converter using immersion and invariance observer. Evol. Syst. 2020, 11, 707–715. [Google Scholar] [CrossRef]
- Cho, H.; Yoo, S.J.; Kwak, S. State observer based sensor less control using Lyapunov’s method for boost converters. IET Power Electron. 2015, 8, 11–19. [Google Scholar] [CrossRef]
- Cimini, G.; Ippoliti, G.; Orlando, G.; Pirro, M. Current sensorless solution for PFC boost converter operating both in DCM and CCM. In Proceedings of the 21st Mediterranean Conference on Control and Automation, Platanias, Greece, 25–28 June 2013; pp. 137–142. [Google Scholar]
- Li, X.; Chen, M.; Shinohara, H.; Yoshihara, T. Design of a low-order sensorless controller by robust H control for boost converters. J. Power Electron. 2016, 16, 1025–1035. [Google Scholar] [CrossRef]
- Cimini, G.; Ippoliti, G.; Orlando, G.; Pirro, M. Sensorless power factor control for mixed conduction mode boost converter using passivity-based control. IET Power Electron. 2014, 7, 2988–2995. [Google Scholar] [CrossRef]
- Das, D.; Madichetty, S.; Singh, B.; Mishra, S. Luenberger observer based current estimated boost converter for PV maximum power extraction—A current sensorless approach. IEEE J. Photovoltaics 2018, 9, 278–286. [Google Scholar] [CrossRef]
- Tong, Q.; Zhang, Q.; Min, R.; Zou, X.; Liu, Z.; Chen, Z. Sensorless predictive peak current control for boost converter using comprehensive compensation strategy. IEEE Trans. Ind. Electron. 2013, 61, 2754–2766. [Google Scholar] [CrossRef]
- Cimini, G.; Ippoliti, G.; Orlando, G.; Longhi, S.; Miceli, R. A unified observer for robust sensorless control of DC–DC converters. Control Eng. Pract. 2017, 61, 21–27. [Google Scholar] [CrossRef]
- Chen, C.; Li, L.; Zhang, Q.; Tong, Q.; Liu, K.; Lyu, D.; Min, R. Online inductor parameters identification by small-signal injection for sensorless predictive current controlled boost converter. IEEE Trans. Ind. Inform. 2016, 13, 1554–1564. [Google Scholar] [CrossRef]
- Tong, Q.; Chen, C.; Zhang, Q.; Zou, X. A sensorless predictive current controlled boost converter by using an EKF with load variation effect elimination function. Sensors 2015, 15, 9986–10003. [Google Scholar] [CrossRef]
- Beccuti, A.G.; Mariéthoz, S.; Cliquennois, S.; Wang, S.; Morari, M. Explicit model predictive control of DC–DC switched-mode power supplies with extended Kalman filtering. IEEE Trans. Ind. Electron. 2009, 56, 1864–1874. [Google Scholar] [CrossRef]
- Stitou, M.; El Fadili, A.; Chaoui, F.Z.; Giri, F. Output feedback control of sensorless photovoltaic systems, with maximum power point tracking. Control Eng. Pract. 2019, 84, 1–12. [Google Scholar] [CrossRef]
- Su, M.; Feng, W.; Jiang, T.; Guo, B.; Wang, H.; Zheng, C. Disturbance observer-based sliding mode control for dynamic performance enhancement and current-sensorless of buck/boost converter. IET Power Electron. 2021, 14, 1421–1432. [Google Scholar] [CrossRef]
- Pati, A.K.; Sahoo, N.C. A super-twisting sliding mode observer for boost inverter-based hybrid photovoltaic-battery system control. Trans. Inst. Meas. Control 2020, 42, 2139–2154. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Wack, M. Observer-based higher order sliding mode control of power factor in three-phase AC/DC converter for hybrid electric vehicle applications. Int. J. Control 2014, 87, 1117–1130. [Google Scholar] [CrossRef]
- Liu, G.; Wang, M.; Zhou, W.; Wu, Q.; Fu, Y. A sensorless current balance control method for interleaved boost converters based on output voltage ripple. IEEE Trans. Power Electron. 2020, 36, 7138–7149. [Google Scholar] [CrossRef]
- Kim, S.K.; Ahn, C.K. Proportional-derivative voltage control with active damping for dc/dc boost converters via current sensorless approach. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 737–741. [Google Scholar] [CrossRef]
- Min, R.; Tong, Q.; Zhang, Q.; Chen, C.; Zou, X.; Lv, D. Corrective frequency compensation for parasitics in boost power converter with sensorless current mode control. Int. J. Electr. Power Energy Syst. 2018, 96, 274–281. [Google Scholar] [CrossRef]
- Pahlevani, M.; Pan, S.; Eren, S.; Bakhshai, A.; Jain, P. An adaptive nonlinear current observer for boost PFC AC/DC converters. IEEE Trans. Ind. Electron. 2014, 61, 6720–6729. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Yang, J.; Li, Q. Current sensorless finite-time control for buck converters with time-varying disturbances. Control Eng. Pract. 2018, 77, 127–137. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Li, S.; Yang, J.; Li, Q. Finite-time output feedback control for PWM-based DC–DC buck power converters of current sensorless mode. IEEE Trans. Control Syst. Technol. 2016, 25, 1359–1371. [Google Scholar] [CrossRef]
- Nizami, T.K.; Chakravarty, A.; Mahanta, C. Analysis and experimental investigation into a finite time current observer based adaptive backstepping control of buck converters. J. Frankl. Inst. 2018, 355, 4996–5017. [Google Scholar] [CrossRef]
- Ortega, R.; Bobtsov, A.; Nikolaev, N.; Schiffer, J.; Dochain, D. Generalized parameter estimation-based observers: Application to power systems and chemical–biological reactors. Automatica 2021, 129, 109635. [Google Scholar] [CrossRef]
- Middlebrook, R.D.; Ćuk, S. A general unified approach to modelling switching-converter power stages. Int. J. Electron. Theor. Exp. 1977, 42, 521–550. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sun, J.; Mitchell, D.M.; Greuel, M.F.; Krein, P.T.; Bass, R.M. Averaged modeling of PWM converters operating in discontinuous conduction mode. IEEE Trans. Power Electron. 2001, 16, 482–492. [Google Scholar]
- Hernandez-Gomez, M.; Ortega, R.; Lamnabhi-Lagarrigue, F.; Escobar, G. Adaptive PI stabilization of switched power converters. IEEE Trans. Control Syst. Technol. 2009, 18, 688–698. [Google Scholar] [CrossRef]
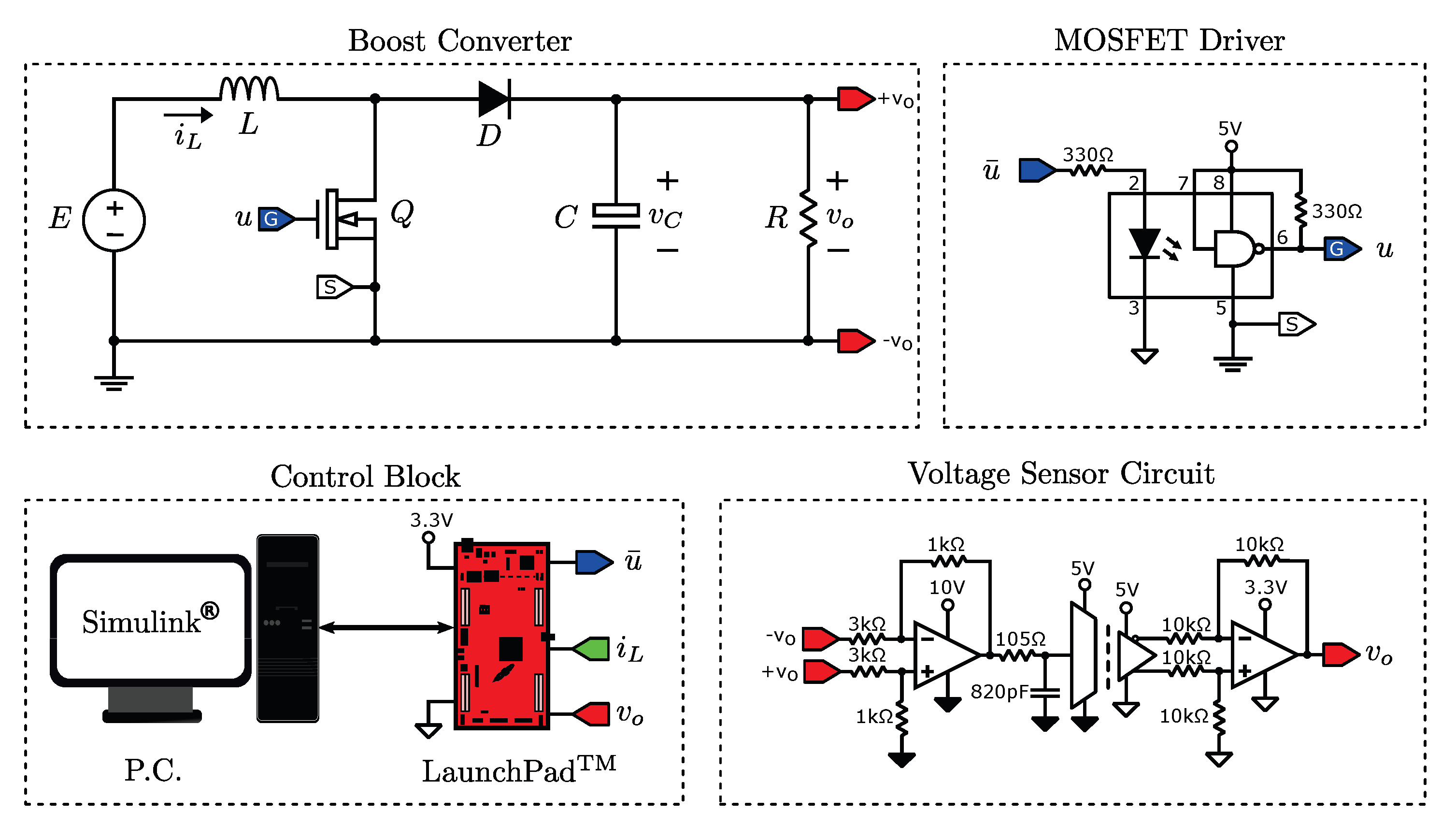
| Parameter | Symbol (Unit) | Value |
|---|---|---|
| Input voltage | 6 | |
| Reference output voltage | 12 | |
| Gain | 2 | |
| Resistance | 100 | |
| Inductance | 5 | |
| Capacitance | 680 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Martinez-Lopez, M.; He, W.; Shang, Y.; Jiang, C.; Moreno-Valenzuela, J. Sensorless Control for DC–DC Boost Converter via Generalized Parameter Estimation-Based Observer. Appl. Sci. 2021, 11, 7761. https://doi.org/10.3390/app11167761
Zhang X, Martinez-Lopez M, He W, Shang Y, Jiang C, Moreno-Valenzuela J. Sensorless Control for DC–DC Boost Converter via Generalized Parameter Estimation-Based Observer. Applied Sciences. 2021; 11(16):7761. https://doi.org/10.3390/app11167761
Chicago/Turabian StyleZhang, Xiaoyu, Mizraim Martinez-Lopez, Wei He, Yukai Shang, Chen Jiang, and Javier Moreno-Valenzuela. 2021. "Sensorless Control for DC–DC Boost Converter via Generalized Parameter Estimation-Based Observer" Applied Sciences 11, no. 16: 7761. https://doi.org/10.3390/app11167761
APA StyleZhang, X., Martinez-Lopez, M., He, W., Shang, Y., Jiang, C., & Moreno-Valenzuela, J. (2021). Sensorless Control for DC–DC Boost Converter via Generalized Parameter Estimation-Based Observer. Applied Sciences, 11(16), 7761. https://doi.org/10.3390/app11167761







