Petri Net Modeling for Ising Model Formulation in Quantum Annealing
Abstract
:1. Introduction
2. Preliminaries
2.1. Combinatorial Optimization Problems
2.2. Quantum Annealing and Ising Models
2.3. Petri Net Fundamentals
3. Binary Quadratic Nets
3.1. Formal Definition
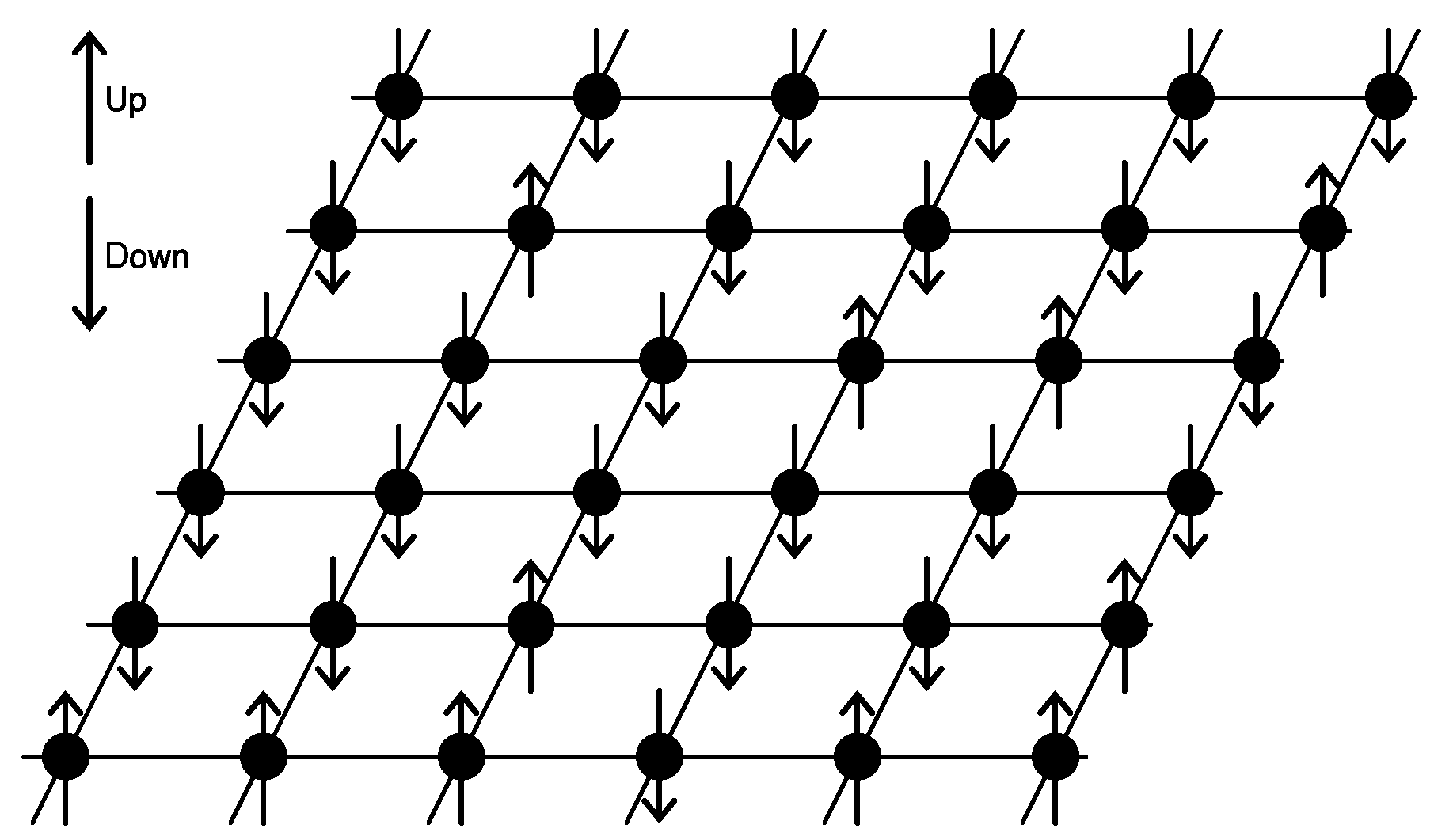
3.2. Binary Quadratic Net Examples
4. Binary Quadratic Net Construction from Problem Domain Petri Nets
4.1. Incremental Construction Based on Superposition Principle
4.2. Marking-Based Construction
4.2.1. Boundedness
4.2.2. Invariant
4.3. Firing-Based Construction
4.3.1. Resource Conflict
4.3.2. Firing Count
4.3.3. Precedence Relation
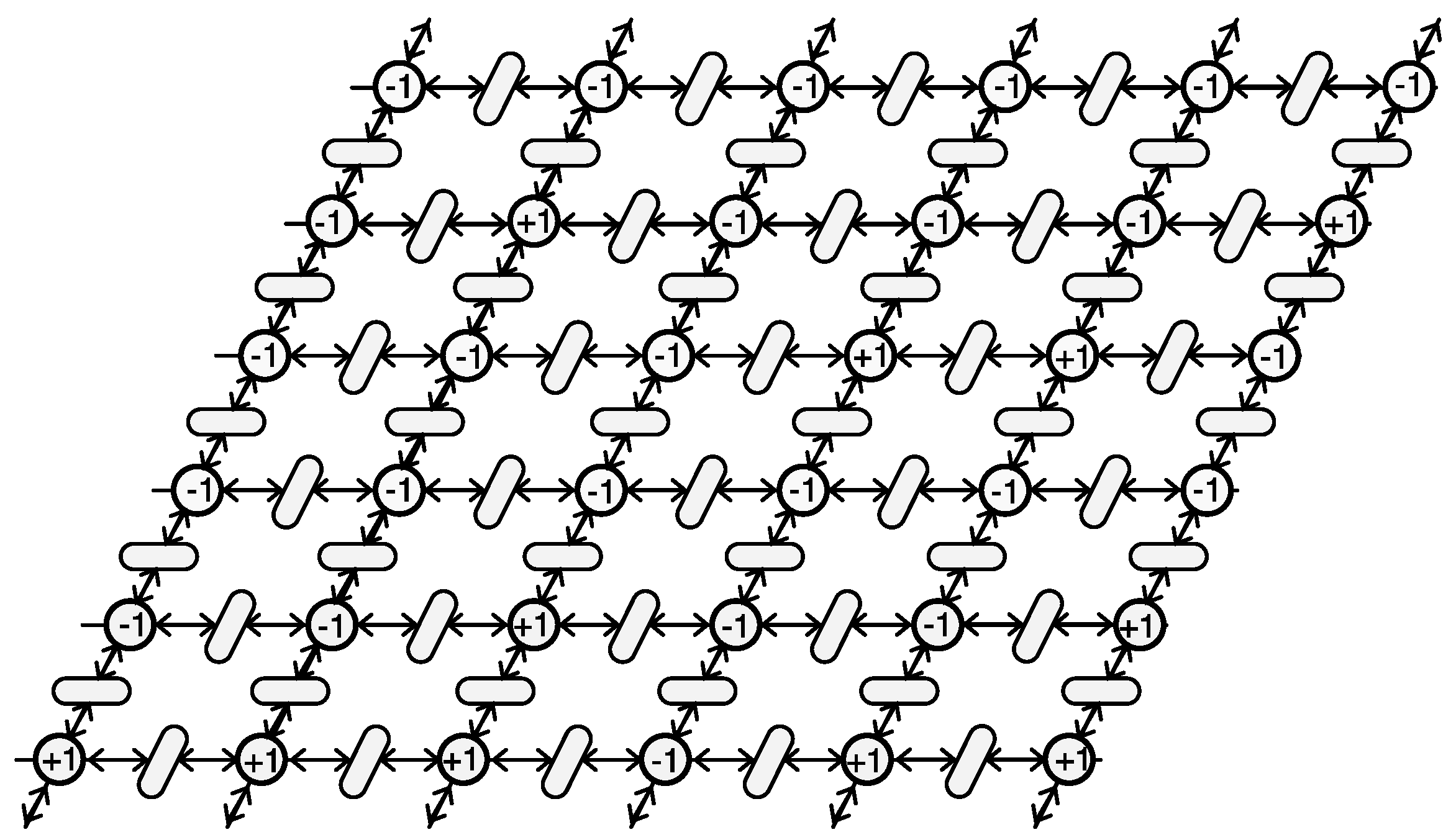
4.4. Application Example 1 (Marking-Based Construction): Traveling Salesman Problems
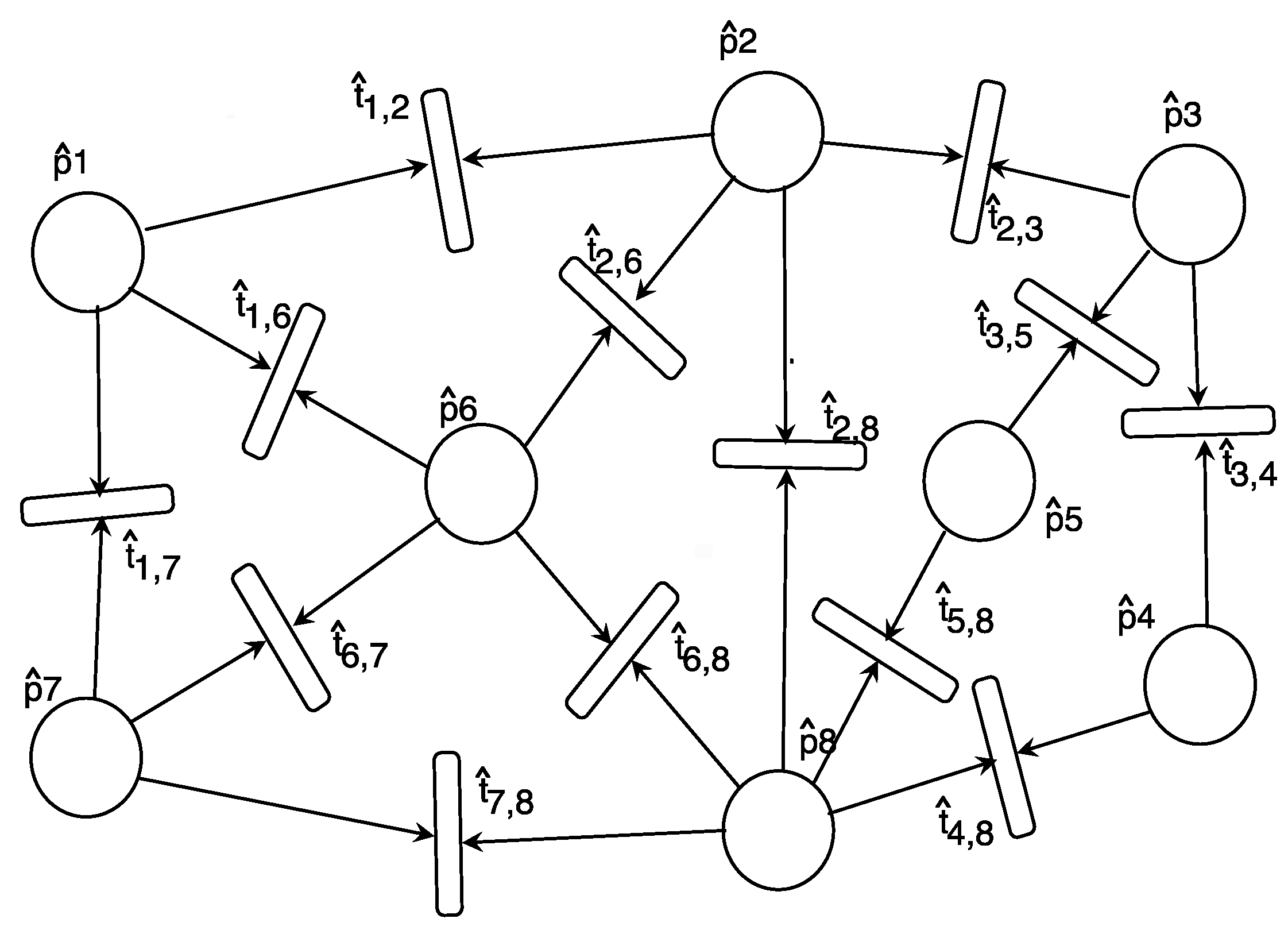
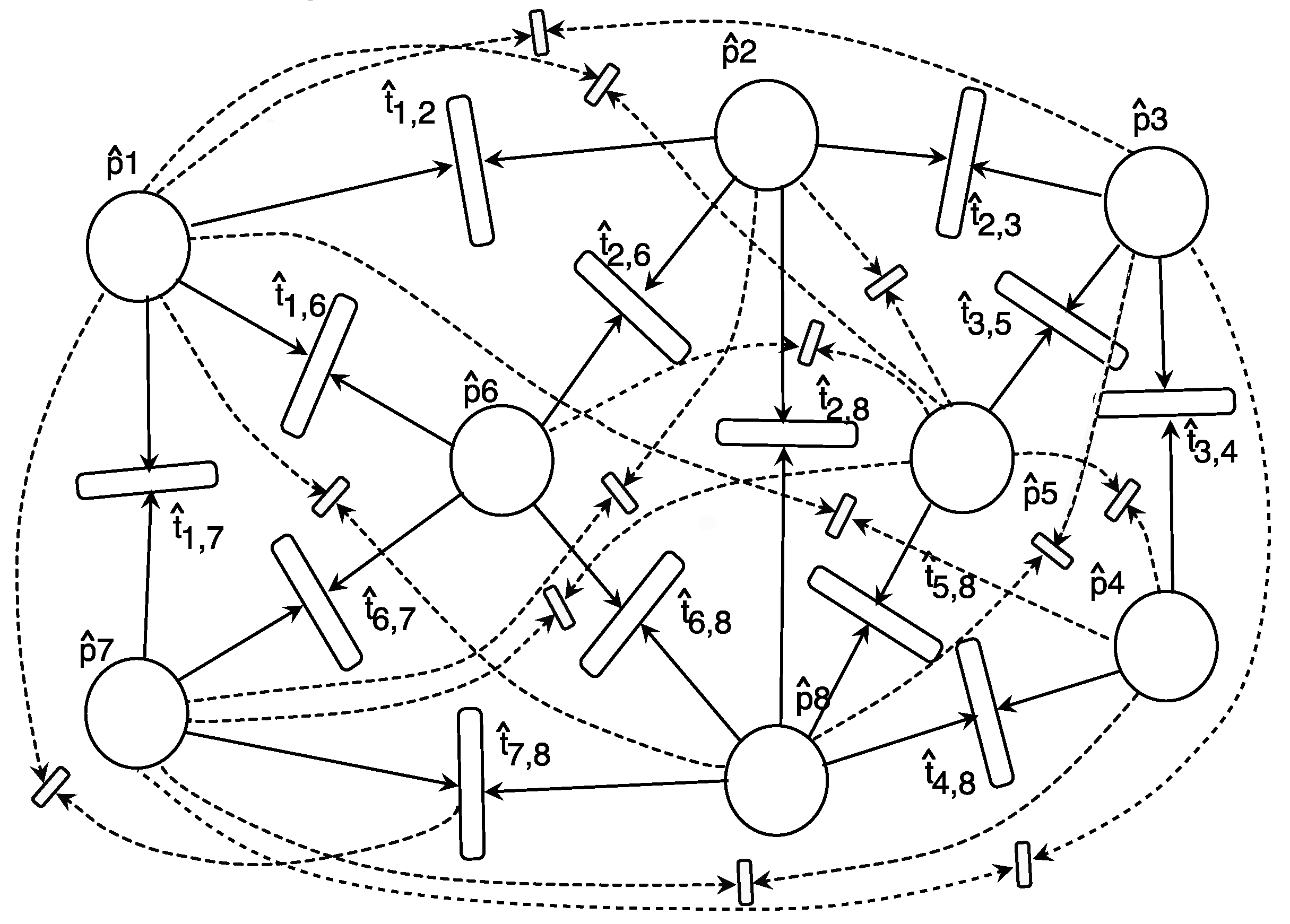
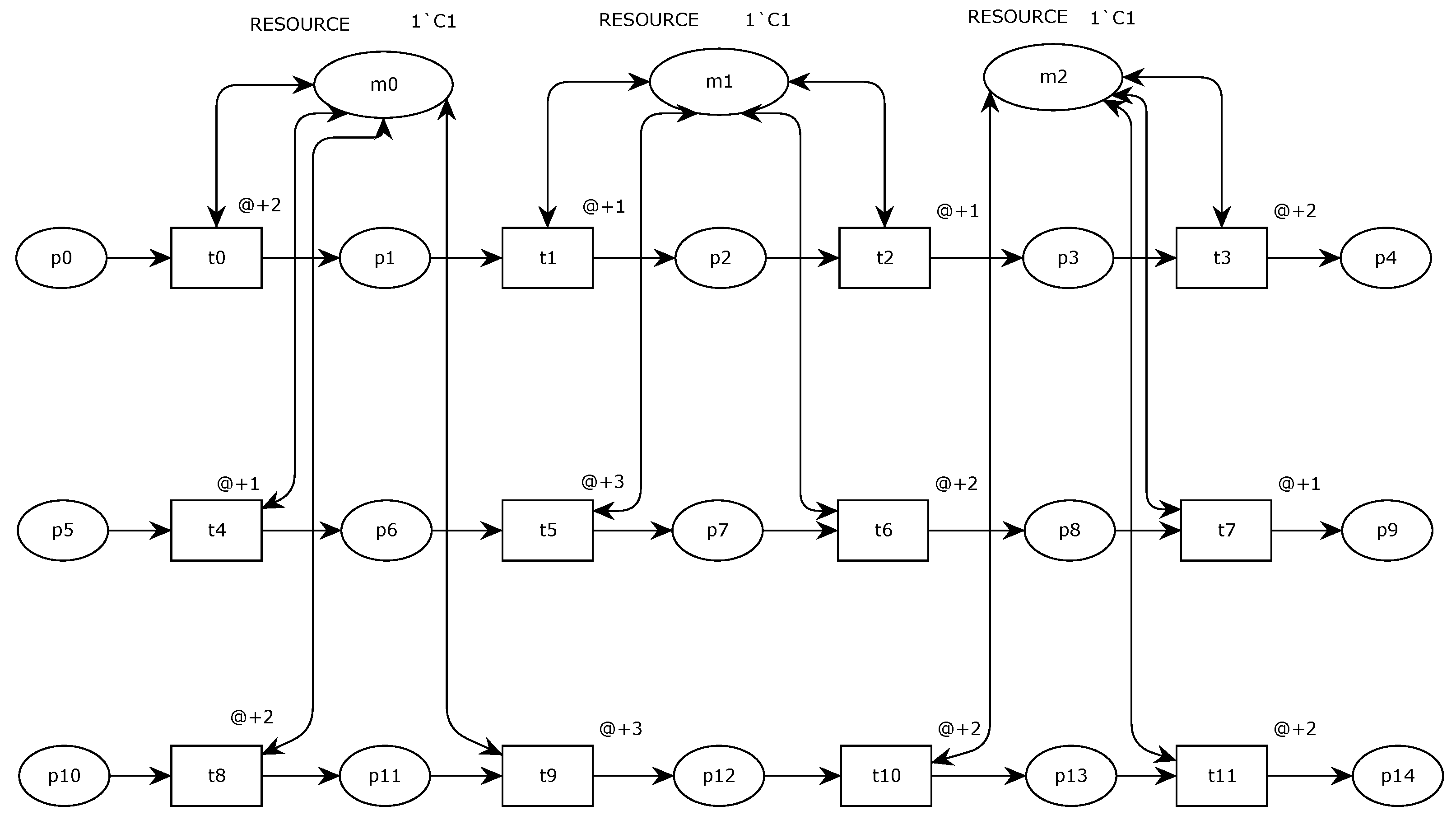
4.5. Application Example 2 (Firing-Based Construction): Job-Shop Scheduling Problems
5. Conclusions
- Step 1:
- Model the target combinatorial optimization problem with a problem-domain Petri net such as a timed and colored Petri net;
- Step 2:
- Extract constraints and objective functions as properties from problem-domain Petri net models and construct a binary quadratic net incrementally;
- Step 3:
- Convert the binary quadratic net to the specified format of the corresponding quantum annealing machine;
- Step 4:
- Invoke the annealing process with the converted Hamiltonian.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
Interaction Primitives
| (0, 0) | (0, 1) | (1, 0) | (1, 1) | Energy Function | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 1 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | ||
| 1 | 1 | 1 | 0 | ||
| 1 | 1 | 1 | 1 | 1 |
| Energy Function | |||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 1 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | ||
| 1 | 1 | 1 | 0 | ||
| 1 | 1 | 1 | 1 | 1 |
References
- Kadowaki, T.; Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 1998, 58, 5355–5363. [Google Scholar] [CrossRef] [Green Version]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Lapan, J.; Lundgren, A.; Preda, D. A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem. Science 2001, 292, 472–475. [Google Scholar] [CrossRef] [Green Version]
- Morita, S.; Nishimori, H. Mathematical foundation of quantum annealing. J. Math. Phys. 2008, 49, 125210. [Google Scholar] [CrossRef]
- Johnson, M.W.; Amin, M.H.S.; Gildert, S.; Lanting, T.; Hamze, F.; Dickson, N.; Harris, R.; Berkley, A.J.; Johansson, J.; Bunyk, P.; et al. Quantum annealing with manufactured spins. Nature 2011, 473, 194–198. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1990. [Google Scholar]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef] [Green Version]
- Grant, E.; Humble, T.S.; Stump, B. Benchmarking Quantum Annealing Controls with Portfolio Optimization. Phys. Rev. Appl. 2021, 15, 014012. [Google Scholar] [CrossRef]
- Stollenwerk, T.; O’Gorman, B.; Venturelli, D.; Mandrà, S.; Rodionova, O.; Ng, H.; Sridhar, B.; Rieffel, E.G.; Biswas, R. Quantum Annealing Applied to De-Conflicting Optimal Trajectories for Air Traffic Management. IEEE Trans. Intell. Transp. Syst. 2020, 21, 285–297. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, K.; Nakamura, Y.; Humble, T.S. Application of Quantum Annealing to Nurse Scheduling Problem. Sci. Rep. 2019, 9, 12837. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Lidar, D.A. Why and When Pausing is Beneficial in Quantum Annealing. Phys. Rev. Appl. 2020, 14, 014100. [Google Scholar] [CrossRef]
- Graß, T. Quantum Annealing with Longitudinal Bias Fields. Phys. Rev. Lett. 2019, 123, 120501. [Google Scholar] [CrossRef] [Green Version]
- Brady, L.T.; Baldwin, C.L.; Bapat, A.; Kharkov, Y.; Gorshkov, A.V. Optimal Protocols in Quantum Annealing and Quantum Approximate Optimization Algorithm Problems. Phys. Rev. Lett. 2021, 126, 070505. [Google Scholar] [CrossRef]
- Hauke, P.; Katzgraber, H.G.; Lechner, W.; Nishimori, H.; Oliver, W.D. Perspectives of quantum annealing: Methods and implementations. Rep. Prog. Phys. 2020, 83, 054401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanahashi, K.; Takayanagi, S.; Motohashi, T.; Tanaka, S. Application of Ising Machines and a Software Development for Ising Machines. J. Phys. Soc. Jpn. 2019, 88, 061010. [Google Scholar] [CrossRef]
- Waidyasooriya, H.M.; Hariyama, M. A GPU-Based Quantum Annealing Simulator for Fully-Connected Ising Models Utilizing Spatial and Temporal Parallelism. IEEE Access 2020, 8, 67929–67939. [Google Scholar] [CrossRef]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- David, R.; Alla, H. Discrete, Continuous, and Hybrid Petri Nets, 2nd ed.; Springer Publishing Company, Incorporated: Heidelberg, Germany, 2010. [Google Scholar]
- Richard, P. Modelling integer linear programs with petri nets*. RAIRO-Oper. Res. 2000, 34, 305–312. [Google Scholar] [CrossRef]
- Nakamura, M.; Tengan, T.; Yoshida, T. A Petri Net Approach to Generate Integer Linear Programming Problems. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2019, E102.A, 389–398. [Google Scholar] [CrossRef]
- Porco, A.V.; Ushijima, R.; Nakamura, M. Automatic Generation of Mixed Integer Programming for Scheduling Problems Based on Colored Timed Petri Nets. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2018, E101.A, 367–372. [Google Scholar] [CrossRef]
- Hoos, H.H.; Stützle, T. 1-Introduction. In Stochastic Local Search; Hoos, H.H., Stützle, T., Eds.; The Morgan Kaufmann Series in Artificial Intelligence; Morgan Kaufmann: San Francisco, CA, USA, 2005; pp. 13–59. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.Y. Metaheuristics in Combinatorial Optimization. Ann. Oper. Res. 2005, 140, 189–213. [Google Scholar] [CrossRef]
- van der Aalst, W.M.P. Petri net based scheduling. Oper. Res. Spektrum 1996, 18, 219–229. [Google Scholar] [CrossRef] [Green Version]
- Jensen, K.; Kristensen, L.M.; Wells, L. Coloured Petri Nets and CPN Tools for modeling and validation of concurrent systems. Int. J. Softw. Tools Technol. Transf. 2007, 9, 213–254. [Google Scholar] [CrossRef]
- Oku, D.; Terada, K.; Hayashi, M.; Yamaoka, M.; Tanaka, S.; Togawa, N. A Fully-Connected Ising Model Embedding Method and Its Evaluation for CMOS Annealing Machines. IEICE Trans. Inf. Syst. 2019, E102.D, 1696–1706. [Google Scholar] [CrossRef] [Green Version]
- Pommereau, F. SNAKES: A Flexible High-Level Petri Nets Library (Tool Paper). In Application and Theory of Petri Nets and Concurrency; Devillers, R., Valmari, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 254–265. [Google Scholar]
- Venturelli, D.; Marchand, D.J.J.; Rojo, G. Quantum Annealing Implementation of Job-Shop Scheduling. arXiv 2016, arXiv:1506.08479. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, M.; Kaneshima, K.; Yoshida, T. Petri Net Modeling for Ising Model Formulation in Quantum Annealing. Appl. Sci. 2021, 11, 7574. https://doi.org/10.3390/app11167574
Nakamura M, Kaneshima K, Yoshida T. Petri Net Modeling for Ising Model Formulation in Quantum Annealing. Applied Sciences. 2021; 11(16):7574. https://doi.org/10.3390/app11167574
Chicago/Turabian StyleNakamura, Morikazu, Kohei Kaneshima, and Takeo Yoshida. 2021. "Petri Net Modeling for Ising Model Formulation in Quantum Annealing" Applied Sciences 11, no. 16: 7574. https://doi.org/10.3390/app11167574
APA StyleNakamura, M., Kaneshima, K., & Yoshida, T. (2021). Petri Net Modeling for Ising Model Formulation in Quantum Annealing. Applied Sciences, 11(16), 7574. https://doi.org/10.3390/app11167574






