Evaluation of the Microsoft Excel Solver Spreadsheet-Based Program for Nonlinear Expressions of Adsorption Isotherm Models onto Magnetic Nanosorbent

Abstract

The sorption of basic dyes onto magnetic nanosorbent is commonly used as a novel material to combat powdered activated carbon, which is difficult to handle and separate during water and wastewater treatment. This adsorption method is commonly implemented in water and wastewater treatment due to its low cost and high performance. To explore the feasibility of adsorption, six different nonlinear isotherm models were applied and introduced to evaluate the performance and adsorption mechanisms via Microsoft Excel, and they were then compared to those of MATLAB and OriginPro. The Langmuir best provided the sorption of methylene blue adsorbed for a two-parameter isotherm model. The three-parameter model Toth gave a goodness of fit indicating a heterogeneous sorbent surface. Error function analysis found that the Residual Sum of Squares Error, Chi-square, Coefficient of determination, Average Relative Error, Hybrid Fractional Error Function, Marquardt’s Percent Standard Deviation and Root Mean Square Error provided the best overall results. In comparison, it could be concluded that six isotherm models showed the confidence interval that is simply the best fit at all experimental data points provided by the three software tools. All error function results indicated that the Microsoft Excel Solver function spreadsheet method satisfied all the statistic measures to predict the real variance of the probability of experimental data for all six isotherm models of adsorption of basic dye removal. One added benefit of this Microsoft Excel software tool is the built-in function associated with the desired type of application, which designates the desired type of error/statistical functions not mentioned in this research to the adsorbent materials used.

1. Introduction

In a water treatment plant, it is a necessity to remove contaminants, such as organic and inorganic materials, which can act as precursors for the production of disinfection by-products. Various types of activated carbon are widely used for the treatment of contaminants in many environmental applications by an adsorption process because of the high specific surface area; the high degree of surface reactivity [1,2]; and the existence of specific surface chemistry, such as the presence of heteroatoms, including oxygen, nitrogen, hydrogen, sulfur and phosphorous- [3] and nitrogen-containing groups [4]. However, it is widely known that powdered activated carbon is extremely difficult to handle and separate from water and wastewater treatment plants. Recently, magnetic particles and magnetic nanosorbents were used to adsorb pollutants from water and air [5], but their applications are limited due to their small surface area and morphology structures. A magnetic field has previously been used to separate the adsorbent from aqueous solutions after the adsorption process [6]. Many researchers have used magnetite (Fe₃O₄) for adsorption from air and wastewater because magnetite has good performance and biocompatibility [7]. However, magnetite or magnetic particles can remove about 60% of natural organic matter from the water [8]. Magnetite can be combined with amorphous carbon (activated carbon) by an impregnation process to enhance the adsorption of various pollutants in an aqueous solution. For instance, Bastami and Entezari [9] studied and characterized a composite of activated carbon and iron oxide applied for the removal of p-nitrophenol from aqueous solutions. Moreover, Cheng and Gao [10] developed a magnetic nanosorbent when removing strontium ions from aqueous solutions. Wongcharee et al. modified magnetic nanosorbent prepared from macadamia nut shell for the removal of basic dye [11]. The results indicated that the magnetic nanosorbent was suitable for specific water and wastewater treatment application using the advanced software tools of OriginPro and MATLAB in the interpretation of the adsorption isotherm models.

Artificial dyes are being utilized in various applications such as food, paper, printing industries, cosmetics, textiles and dye houses in order to color products [12]. In general, dyes are synthetic organic pollutants composed of complex aromatic structures [13]. The discharge of colored wastewater causes significant harmful effects downstream, increasing the toxicity and chemical oxygen demand (COD) [12]. Methylene blue (MB) is considered to be one of the basic dyes that is commonly soluble in water and used by textile industries, which can cause eye and skin irritation; vomiting; nausea; and sympathetic effects, including blood changes [14]. The literature shows that patterns of the evacuation of contaminant dyes in water bodies and the development of outcome measure limitations have resulted in the utilization of adsorption processes amongst other suitable techniques [15,16].

Adsorption methods are applied in various water treatments depending on the condition of the water sources when eliminating colors, inorganic and organic pollutants, odor and oil [17] due to low capital and operation cost. For basic dye adsorption, the process is combined in two mechanism steps of adsorption and/or ion exchange, including being controlled by various parameters, such as pH, temperature, adsorbent and contact time [18]. A proper understanding of the mechanism of adsorption may involve chemisorption and physisorption or both in the sorption process [19], which indicate the adsorption equilibrium information. Several literature reports necessitate the interpretation of adsorption isotherms due to them being extremely important for the general improvement of adsorption mechanism pathways and process design for removing basic dyes in wastewater sources. Linear regression analysis has long been applied and developed to evaluate the adsorption isotherm parameters and statistical results, along with indicating the best fitting and theoretical assumptions of adsorption models [20]. However, linearization is still poorly defined for the distribution of error change for experimental data and the predicted adsorption isotherm. Therefore, nonlinear regression needs to address shortfalls based on the convergence criteria of the experimental data and the predicted adsorption isotherm as has become inevitable [21]. Residual Sum of Squares Error (ERRSQ/SSE) [22], Chi-square (χ²) [23], Average Relative Error (ARE) [24], Hybrid Fractional Error Function (HYBRID) [25], Marquardt’s Percent Standard Deviation (MPSD) [26] and Root Mean Square Error (RMSE, polynomial p: the number of terms) [27,28,29] can usually be utilized to predict the best fitting of isotherms to minimize the residual between the experimental data measurement and the mathematical isotherm model. These error functions are normally used for water and wastewater treatment applications to predict the adsorption capacity and adsorption mechanism via advanced software tools, such as MATLAB, OriginPro, Minitab and Sigma Plot. Even though advanced program software tools are not available for built-in error functions as mentioned above, Microsoft Excel is a readily available operation that is not difficult, as isotherm functions can be built owing to the availability of computer algorithms.

This research recognizes the importance of magnetic nanosorbent to deal with basic dyes in an aqueous solution. The objective of this study is to present a magnetic nanosorbent composite that increases the affinities for specific contaminants and allows the use of efficient batch reactors and resolves the challenge of separating the spent adsorbent from water using magnetic fields for the removal of basic dyes from water. Treatment performance and efficiencies were evaluated using adsorption isotherm models to clarify the involved mechanisms through the Microsoft Excel Solver spreadsheet-based program by nonlinear regression analyses to explore the theoretical assumptions. A comparison of parameter values for the isotherm models obtained by nonlinear fitting was also evaluated with advanced software tools, such as MATLAB and OriginPro (free trial).

2. Materials and Methods

Experimental data of isotherms (Table 1) were taken from a previous study using a magnetic nanosorbent for methylene blue adsorption [11]. The magnetic nanosorbent was derived from waste macadamia nut shell and magnetite nanoparticles. They were used for removing the basic dye with simple handling and separation during water and wastewater treatment in various applications and conditions. Batch sorption of isotherm studies was performed following the equations as shown below.

$${\mathrm{q}}_{\mathrm{e}}=\frac{{\mathrm{C}}_0{-\mathrm{C}}_{\mathrm{e}}}{m}V$$

(1)

where q_e (mg g⁻¹) is the methylene adsorbed at equilibrium, C₀ is an initial concentration, C_e is an equilibrium concentration of methylene blue (mg L⁻¹), V (L) is the volume of the raw water used in a previous study (the synthetic solution was prepared from methylene blue) and m (g) is the mass of the prepared magnetic nanosorbent.

Table 1. Experimental data of methylene blue adsorbed onto magnetic nanosorbent.

Ce, Equilibrium Concentration (mg L−1)	qe,exp at Equilibrium (mg g−1)
0	0
0.5693	4.7154
1.3183	6.8409
2.0673	8.9664
4.3142	17.8429
9.2576	25.3712
19.5937	30.2031
38.0190	30.9905
57.9422	31.0289
74.7197	32.6401
96.1409	31.9295

2.1. Isotherm Models

Numerous nonlinear regression approaches to isotherm parameter estimation have appeared in the literature. Two- and/or three-parameter isotherm models are normally applied to classify and characterize an adsorption mechanism process in various applications in water and wastewater treatment, even for specific pollution, such as gas phase or particles. Sorption isotherm models have described the information on the affinity between magnetic nanosorbent and methylene blue [18,23,30] for this case study. The experimental data as shown in Table 1 were computed using Langmuir [31], Freundlich [32], Temkin [33], Khan [34], Toth [35] and Liu [36] isotherm models as follows in Equations (2)–(7), respectively, via Microsoft Excel, MATLAB and OriginPro programs. Nonlinearized empirical models are expressed as follows:

$${\mathrm{Langmuir}=\mathrm{q}}_{\mathrm{e}}{=\mathrm{q}}_{\mathrm{m}}·{\mathrm{k}}_{\mathrm{l}}\frac{{\mathrm{C}}_{\mathrm{e}}}{{1+\mathrm{k}}_{\mathrm{l}}·{\mathrm{C}}_{\mathrm{e}}}$$

(2)

$${\mathrm{Freundlich}=\mathrm{q}}_{\mathrm{e}}{=\mathrm{k}}_{\mathrm{f}}·{\mathrm{C}}_{\mathrm{e}}^{{1/\mathrm{n}}_{\mathrm{f}}}$$

(3)

$$\mathrm{Temkin}={\mathrm{q}}_{\mathrm{e}}{=\mathrm{b}}_{\mathrm{t}}·{\ln (\mathrm{k}}_{\mathrm{t}}·{\mathrm{C}}_{\mathrm{e}})$$

(4)

$$\mathrm{Khan}={\mathrm{q}}_{\mathrm{e}}=\frac{{\mathrm{q}}_{\mathrm{m}}·{\mathrm{k}}_{\mathrm{k}}·{\mathrm{C}}_{\mathrm{e}}}{{{(1+\mathrm{k}}_{\mathrm{k}}·{\mathrm{C}}_{\mathrm{e}})}^{{\mathrm{a}}_{\mathrm{k}}}}$$

(5)

$$\mathrm{Liu}={\mathrm{q}}_{\mathrm{e}}=\frac{{\mathrm{q}}_{\mathrm{m}}{{(\mathrm{k}}_{\mathrm{g}}·{\mathrm{C}}_{\mathrm{e}})}^{{1/\mathrm{n}}_{\mathrm{g}}}}{{1+(\mathrm{k}}_{\mathrm{g}}·{\mathrm{C}}_{\mathrm{e}}{)}^{{1/\mathrm{n}}_{\mathrm{g}}}}$$

(6)

$$\mathrm{Toth}={\mathrm{q}}_{\mathrm{e}}{=\mathrm{q}}_{\mathrm{m}}\frac{{\mathrm{k}}_{\mathrm{th}}·{\mathrm{C}}_{\mathrm{e}}}{{{(1+(\mathrm{k}}_{\mathrm{th}}·{\mathrm{C}}_{\mathrm{e}}{)}^{{\mathrm{n}}_{\mathrm{th}}})}^{{1/\mathrm{n}}_{\mathrm{th}}}}$$

(7)

2.2. Error Function Analysis

The error functions are an important statistical parameter used to measure the deviation of theoretically predicted isotherm parameters for evaluating the suitability of the nonlinearized empirical model onto experimental results. Various error functions have been established either empirically or based on theoretical considerations. To validate the best fitting of the adsorption isotherm of two- and three-parameter models as mentioned above, seven different statistical error functions, namely Residual Sum of Squares Error (ERRSQ/SSE) [22], Chi-square (χ²) [23], Coefficient of determination (R²), Average Relative Error (ARE) [24], Hybrid Fractional Error Function (HYBRID) [25], Marquardt’s Percent Standard Deviation (MPSD) [26] and Root Mean Square Error (RMSE, polynomial p: the number of terms) [27,28,29], were assessed to describe the adsorption characteristics of methylene blue adsorbed onto the magnetic nanosorbent. The error analysis equations are conveyed as follows:

$$\mathrm{ERRSQ}/\mathrm{SSE}={{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{{(\mathrm{q}}_{\mathrm{e}, \exp }-{ \mathrm{q}}_{\mathrm{e}, \mathrm{cal}})}^2$$

(8)

$${\mathrm{Chi}\text{-}\mathrm{square}/}^2={{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}\frac{{{(\mathrm{q}}_{\mathrm{e}, \mathrm{cal}}-{ \mathrm{q}}_{\mathrm{e}, \exp })}^2}{{\mathrm{q}}_{\mathrm{e}, \exp }}$$

(9)

$${\mathrm{R}}^2=1 – \frac{{{\displaystyle \sum }}_{\mathrm{n}=1}^{\mathrm{n}}{{(\mathrm{q}}_{\mathrm{e}, \exp }-{ \mathrm{q}}_{\mathrm{e}, \mathrm{cal}})}^2}{{{\displaystyle \sum }}_{\mathrm{n}=1}^{\mathrm{n}}{{(\mathrm{q}}_{\mathrm{e}, \exp }-\overline{{ \mathrm{q}}_{\mathrm{e}, \exp }})}^2}$$

(10)

$$\mathrm{ARE}=\frac{100}{\mathrm{n}}.{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{{(\mathrm{q}}_{\mathrm{e}, \exp }-{ \mathrm{q}}_{\mathrm{e}, \mathrm{cal}})}{{\mathrm{q}}_{\mathrm{e}, \exp }}\right)$$

(11)

$$\mathrm{RMSE}=\sqrt{\frac{{{\displaystyle \sum }}_{\mathrm{n}=1}^{\mathrm{n}}{{(\mathrm{q}}_{\mathrm{e}, \exp }-{ \mathrm{q}}_{\mathrm{e}, \mathrm{cal}})}^2}{\mathrm{n} - \mathrm{p}}}$$

(12)

$$\mathrm{HYBRID}=\frac{100}{\mathrm{n} - \mathrm{p}}.{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{{(\mathrm{q}}_{\mathrm{e}, \exp }-{ \mathrm{q}}_{\mathrm{e}, \mathrm{cal}})}{{\mathrm{q}}_{\mathrm{e}, \exp }}\right)$$

(13)

$$\mathrm{MPSD}=100·\sqrt{\frac{1}{\mathrm{n} - \mathrm{p}}.{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left(\frac{{(\mathrm{q}}_{\mathrm{e}, \exp }-{ \mathrm{q}}_{\mathrm{e}, \mathrm{cal}})}{{\mathrm{q}}_{\mathrm{e}, \exp }}\right)}^2}$$

(14)

where n is the number of experimental data points, p (polynomial model) is the number of parameters in each isotherm model, q_e,cal (mg g⁻¹) is the theoretically calculated adsorption capacity of methylene blue adsorbed at equilibrium and q_e,exp (mg g⁻¹) is the experimental capacity of methylene blue adsorbed at equilibrium.

2.3. Operational Software Tools

Microsoft Excel was used as a tool for the determination of nonlinear isotherm models and error functions via Windows 10 and Microsoft 365 2020 on PC. The experimental data were entered manually into an Excel sheet operating the graphical data of the isotherm models. Statistical analysis was also performed and compared to that of MATLAB and OriginPro via the formulated algorithm that follows [37,38,39]. The steps of the operation are shown in Figure 1.

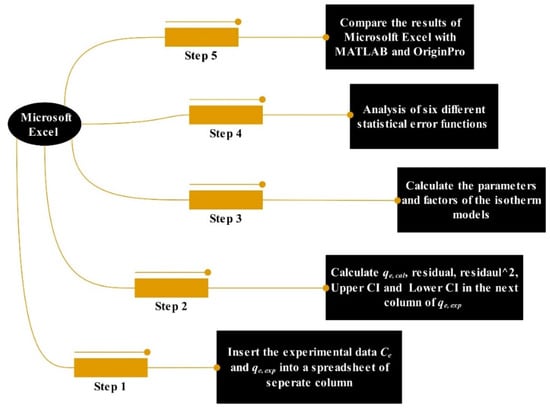
Figure 1. Operation steps of software tools for predicting the experimental data.

The following step demonstrates how to solve the experimental data of basic dye (methylene blue as a model substrate) loaded onto magnetic nanosorbent in the Microsoft Excel spreadsheet using six isotherm models and seven statistical error functions as mentioned in Section 2.1 and Section 2.2, respectively. Table 2 shows the formulas of factors for the model, the statistical analysis results and the calculated excel codes/formulas. In Table 2, the Freundlich isotherm model was used as an example model to elucidate how to solve the isotherm model via the Microsoft Excel solver spreadsheet-based program. The other isotherm models as mentioned above in Section 2.1 can be applied using the procedures as described below.

Table 2. Microsoft Excel Solver spreadsheet-based program for Freundlich isotherm model.

	Ce	qe, exp	qe, cal	Residual	Residaul^2	Upper, CI	Lower, CI	Factors for the Model		Statistical Results
Row/Column	A	B	C	D	E	F	G	H	I	J	K
1	0	0	0	0	0	9.7822	−9.7822	SSR	168.2962	ERRSQ/SSE	168.2962
2	0.5693	4.7154	9.2629	−4.5475	20.6802	19.0452	−0.5193	kf	10.7618	Chi-square	13.3924
3	1.3183	6.8409	11.5833	−4.7424	22.4905	21.3655	1.8010	n	3.7564	ARE	−108.8583
4	2.0673	8.9664	13.0571	−4.0908	16.7343	22.8394	3.2749	Mean of qe,exp	20.0481	RMSE	4.3243
5	4.3142	17.8429	15.8820	1.9609	3.8450	25.6643	6.0998	df	9.0000	HYBRID	−20.8825
6	9.2576	25.3712	19.4617	5.9095	34.9221	29.2440	9.6795	SE of qe,exp	4.3243	MPSD	118.1294
7	19.5937	30.2031	23.7610	6.4421	41.5008	33.5433	13.9788	R-square	0.8956
8	38.0190	30.9905	28.3468	2.6437	6.9892	38.1290	18.5645	Critical t	2.2622
9	57.9422	31.0289	31.7117	−0.6828	0.4663	41.4940	21.9295	CI	9.7822
10	74.7197	32.6401	33.9329	−1.2927	1.6711	43.7151	24.1506	Adjust R-square	0.8839
11	96.1409	31.9295	36.2881	−4.3585	18.9968	46.0703	26.5058
Formula or Excel code
qe, cal = $I$2 * A^(1/$I$3) Array Note: Values in column C (qe, cal) were depended on the values in column A (Ce), * = Multiplication sign (×). SSR = SUM(E1:E11) Array Mean of qe,exp = AVERAGE(B1:B11) Array df = COUNT(B1:B11)–COUNT(I2:I3) Array SE of qe,exp = SQRT(SUM((B1:B11–C1:C11)^2)/I6) Array R-square = 1-(SUM((B1:B11–C1:C11)^2)/(SUM((B1:B11-I5)^2))) Array Critical t = TINV(0.05,I6) Array CI = I7 * I9 Array Adjust R-square = (1–((COUNT(B1:B11)–1)/(COUNT(B1:B11)–2)) * (1–I8)) Array ERRSQ/SSE = SUM((C1:C11–B1:B11)^2) Array Chi-square = SUM(((C2:C11–B2:B11)^2)/(B2:B11)) Array ARE = (100 / (COUNT(B2:B11))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array RMSE = SQRT(SUM((B1:B11–C1:C11)^2)/(COUNT(C1:C11)–2)) Array HYBRID = (100/((COUNT(B2:B11))–(COUNT(I2:I3)))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array MPSD = 100 * SQRT((1/COUNT(B2:B11–I2:I3)*(SUM((B2:B11–C2:C11)/(B2:B11))^2))) Array

The Application of the Microsoft Excel Solver Spreadsheet Are as Follows

(a) Experimental data from Table 1 were entered into rows A1–A11 (C_e, mg L⁻¹) and B1–B11 (q_{e, exp}, mg g⁻¹, Equation (1)) or were more than those values depending on the experimental data sets. Column C is the equilibrium capacity (q_e,cal, mg g⁻¹) of the cationic dye adsorbed onto the magnetic nanosorbent for the equilibrium adsorption capacity (Equation (3)) as shown in the Excel form of Figure 2 and Figure 3. Before calculating q_e,cal values, the factors for the model in columns H2 (kf) and H3 (n) are very critical for nonlinear regression analysis of the isotherm models selected. Therefore, n and kf must be computed using residual^2 values in column E to calculate the sum of squared residuals (SSR, column I1, = SUM(E1:E11), 3860.74). In the next stage, the initial estimate parameter values of 0.5 and 1.5 (any values can be inserted instead of 0.5 and 1.5) were inserted into lows I2 and I3 before operating the algorithm, respectively. It can be seen that the q_{e, cal} values (poorly defined, as shown in the right inset) did not parallel with the q_{e, exp} values together with the residual values that may be shown in a different type of line as shown in Figure 2.

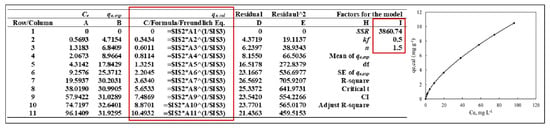
Figure 2. The first stage to find the n and kf factors of the nonlinear isotherm model selected to solve the q_{e, cal} parameter results.

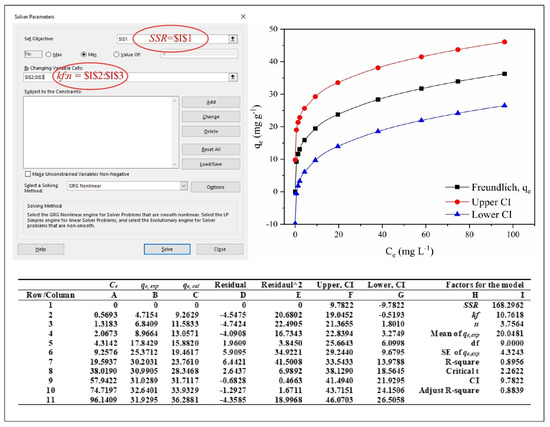
Figure 3. Running nonlinear of Microsoft Excel Solver function for isotherm models to obtain recognized equilibrium adsorption values (q_{e, cal}), order reaction (n) and Freundlich isotherm rate constant (kf) in Excel.

Hence, the Solver function from the Tools menu of Microsoft Excel was needed to fit the experimental data of the nonlinear isotherm model regression analysis as displayed in Figure 3.

(b) To manipulate the nonlinear isotherm model using the Microsoft Excel Solver function, open the Microsoft Excel Tools menu followed by Data, Solver and Solver parameters, respectively, as shown in Figure 3. The dialogue box shown in Figure 3 appears as the Solver parameters. To fit the nonlinear function of the Freundlich isotherm model, the Solver parameters of set objectives (SSR) and changing variable cells (kf and n) were required. SSR (column I1, 3860.74) was set up with the objective as $I$1, along with changing the variable cells of kf (column I2) and n (column I3) to $I$2:$I$3. Then, click the Solve button to formulate the algorithm for the Freundlich isotherm model that achieved the q_e,cal data results, the fitted data curve and the lower CI and upper CI (up-right inset) in the Excel sheet as indicated in the bottom inset and up-right inset of Figure 3, respectively.

(c) To identify and describe the statistical results and isotherm model parameters for the controlling mechanism, MATLAB and OriginPro were used as tools for comparison with the Microsoft Excel Solver function spreadsheet-based program for nonlinear expressions of adsorption isotherm models onto magnetic nanosorbent. This research work only proposed and described the method of how to minimize the statical error functions and isotherm parameters via the Microsoft Excel Solver function. MATLAB and OriginPro procedure details are not shown here.

3. Results and Discussion

3.1. Authentication of Isotherm Model Data Using Microsoft Excel Solver Spreadsheet-Based Program

The experimental data of methylene blue adsorbed onto magnetic nanosorbent were evaluated and analyzed via the Microsoft Excel Solver spreadsheet-based program for the six different nonlinearized forms of Freundlich, Langmuir, Temkin, Liu, Toth and Khan models described above. The error functions (the goodness of fit) were also examined with the same time period to achieve the statistical values from the isotherm models, such as ERRSQ/SSE, χ², R², HYBRID, ARE, MPSD and RMSE. The values of the isotherm parameters and the regression statistics with formulas (factors for the model and statistical results) are shown in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7.

Table 3. Microsoft Excel Solver spreadsheet-based program for Langmuir isotherm model.

	Ce	qe, exp	qe, cal	Residual	Residaul^2	Upper, CI	Lower, CI	Factors for the Model		Statistical Results
Row/Column	A	B	C	D	E	F	G	H	I	J	K
1	0	0	0	0	0	3.0777	−3.0777	SSR	16.6590	ERRSQ/SSE	16.6590
2	0.5693	4.7154	4.0612	0.6541	0.4279	7.1389	0.9835	kl	0.2346	Chi-square	1.2540
3	1.3183	6.8409	8.1426	−1.3018	1.6946	11.2203	5.0649	qm	34.4765	ARE	−2.1538
4	2.0673	8.9664	11.2583	−2.2919	5.2529	14.3360	8.1806	Mean of qe,exp	20.0481	RMSE	1.3605
5	4.3142	17.8429	17.3405	0.5024	0.2524	20.4182	14.2628	df	9.0000	HYBRID	−2.3931
6	9.2576	25.3712	23.6056	1.7656	3.1174	26.6833	20.5279	SE of qe,exp	1.3605	MPSD	15.2297
7	19.5937	30.2031	28.3154	1.8877	3.5634	31.3931	25.2377	R-square	0.9897
8	38.0190	30.9905	31.0002	−0.0097	0.0001	34.0779	27.9226	Critical t	2.2622
9	57.9422	31.0289	32.1136	−1.0848	1.1767	35.1913	29.0359	CI	3.0777
10	74.7197	32.6401	32.6156	0.0246	0.0006	35.6933	29.5379	Adjust R-square	0.9885
11	96.1409	31.9295	33.0126	−1.0831	1.1730	36.0903	29.9349
Formula or Excel code
qe, cal = ($I$3 * ($I$2 * (A/(1 + ($I$2 * A)))) Array Note: Values in column C (qe, cal) were depended on the values in column A (Ce), * = Multiplication sign (×). SSR = SUM(E1:E11) Array Mean of qe,exp = AVERAGE(B1:B11) Array df = COUNT(B1:B11)–COUNT(I2:I3) Array SE of qe,exp = SQRT(SUM((B1:B11–C1:C11)^2)/I6) Array R-square = 1-(SUM((B1:B11–C1:C11)^2)/(SUM((B1:B11-I5)^2))) Array Critical t = TINV(0.05,I6) Array CI = I7 * I9 Array Adjust R-square = (1–((COUNT(B1:B11)–1)/(COUNT(B1:B11)–2)) * (1–I8)) Array ERRSQ/SSE = SUM((C1:C11–B1:B11)^2) Array Chi-square = SUM(((C2:C11–B2:B11)^2)/(B2:B11)) Array ARE = (100/(COUNT(B2:B11))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array RMSE = SQRT(SUM((B1:B11–C1:C11)^2)/(COUNT(C1:C11)–2)) Array HYBRID = (100/((COUNT(B2:B11))–(COUNT(I2:I3)))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array MPSD = 100 * SQRT((1/COUNT(B2:B11–I2:I3) * (SUM((B2:B11–C2:C11) / (B2:B11))^2))) Array

Table 4. Microsoft Excel Solver spreadsheet-based program for Temkin isotherm model.

	Ce	qe, exp	qe, cal	Residual	Residaul^2	Upper, CI	Lower, CI	Factors for the Model		Statistical Results
Row/Column	A	B	C	D	E	F	G	H	I	J	K
1	0	0	0	0	0	6.9196	−6.9196	SSR	72.0332	ERRSQ/SSE	72.0332
2	0.5693	4.7154	4.3210	0.3943	0.1555	11.2406	−2.5986	bt	6.0492	Chi-square	4.0547
3	1.3183	6.8409	9.4006	−2.5598	6.5524	16.3202	2.4810	kt	3.5884	ARE	−4.0175
4	2.0673	8.9664	12.1222	−3.1558	9.9593	19.0418	5.2026	Mean of qe,exp	20.0481	RMSE	2.8291
5	4.3142	17.8429	16.5726	1.2703	1.6137	23.4922	9.6530	df	8.0000	HYBRID	−4.4639
6	9.2576	25.3712	21.1913	4.1799	17.4718	28.1109	14.2717	SE of qe,exp	3.0007	MPSD	28.4083
7	19.5937	30.2031	25.7267	4.4764	20.0382	32.6463	18.8071	R-square	0.9553
8	38.0190	30.9905	29.7366	1.2539	1.5723	36.6562	22.8170	Critical t	2.3060
9	57.9422	31.0289	32.2855	−1.2566	1.5790	39.2051	25.3659	CI	6.9196
10	74.7197	32.6401	33.8238	−1.1836	1.4010	40.7434	26.9042	Adjust R-square	0.9503
11	96.1409	31.9295	35.3486	−3.4191	11.6900	42.2682	28.4290
Formula or Excel code
qe, cal = $I$2 * LN($I$3 * A) Array, Note: Values in column C (qe, cal) were depended on the values in column A (Ce), * = Multiplication sign (×). SSR = SUM(E1:E11) Array Mean of qe,exp = AVERAGE(B1:B11) Array df = COUNT(B1:B11)–COUNT(I2:I3) Array SE of qe,exp = SQRT(SUM((B1:B11–C1:C11)^2)/I6) Array R-square = 1-(SUM((B1:B11–C1:C11)^2)/(SUM((B1:B11-I5)^2))) Array Critical t = TINV(0.05,I6) Array CI = I7 * I9 Array Adjust R-square = (1–((COUNT(B1:B11)–1)/(COUNT(B1:B11)–2)) * (1–I8)) Array ERRSQ/SSE = SUM((C1:C11–B1:B11)^2) Array Chi-square = SUM(((C2:C11–B2:B11)^2)/(B2:B11)) Array ARE = (100/(COUNT(B2:B11))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array RMSE = SQRT(SUM((B1:B11–C1:C11)^2)/(COUNT(C1:C11)–2)) Array HYBRID = (100/((COUNT(B2:B11))–(COUNT(I2:I3)))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array MPSD = 100 * SQRT((1/COUNT(B2:B11–I2:I3) * (SUM((B2:B11–C2:C11)/(B2:B11))^2))) Array

Table 5. Microsoft Excel Solver spreadsheet-based program for Liu isotherm model.

	Ce	qe, exp	qe, cal	Residual	Residaul^2	Upper, CI	Lower, CI	Factors for the Model		Statistical Results
Row/Column	A	B	C	D	E	F	G	H	I	J	K
1	0	0	0	0	0	2.3600	−2.3600	SSR	8.3791	ERRSQ/SSE	8.3791
2	0.5693	4.7154	2.6272	2.0882	4.3606	4.9872	0.2672	qm	32.7792	Chi-squar	1.2093
3	1.3183	6.8409	6.7230	0.1179	0.0139	9.0830	4.3629	kg	0.2660	ARE	3.2148
4	2.0673	8.9664	10.3521	−1.3858	1.9204	12.7122	7.9921	ng	0.7735	RMSE	1.0234
5	4.3142	17.8429	17.8449	−0.0021	0.0000	20.2050	15.4849	Mean of qe,exp	20.0481	HYBRID	4.5926
6	9.2576	25.3712	24.9867	0.3845	0.1479	27.3467	22.6267	df	8.0000	MPSD	18.5609
7	19.5937	30.2031	29.3115	0.8916	0.7950	31.6715	26.9515	SE of qe,exp	1.0234
8	38.0190	30.9905	31.2120	−0.2215	0.0490	33.5720	28.8520	R-square	0.9948
9	57.9422	31.0289	31.8516	−0.8227	0.6769	34.2116	29.4916	Critical t	2.3060
10	74.7197	32.6401	32.1062	0.5340	0.2851	34.4662	29.7462	CI	2.3600
11	96.1409	31.9295	32.2906	−0.3610	0.1304	34.6506	29.9306	Adjust R-square	0.9935
Formula or Excel code
qe, cal = ($I$2 * ($I$3 * A)^(1/$I$4))/(1 + ($I$3 * A)^(1/$I$4)) Array, Note: Values in column C (qe, cal) were depended on the values in column A (Ce), * = Multiplication sign (×). SSR = SUM(E1:E11) Array Mean of qe,exp = AVERAGE(B1:B11) Array df = COUNT(B1:B11)–COUNT(I2:I3) Array SE of qe,exp = SQRT(SUM((B1:B11–C1:C11)^2)/I6) Array R-square = 1-(SUM((B1:B11–C1:C11)^2)/(SUM((B1:B11-I5)^2))) Array Critical t = TINV(0.05,I6) Array CI = I7 * I9 Array Adjust R-square = (1–((COUNT(B1:B11)–1)/(COUNT(B1:B11)–3)) * (1–I8)) Array ERRSQ/SSE = SUM((C1:C11–B1:B11)^2) Array Chi-square = SUM(((C2:C11–B2:B11)^2)/(B2:B11)) Array ARE = (100/(COUNT(B2:B11))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array RMSE = SQRT(SUM((B1:B11–C1:C11)^2)/(COUNT(C1:C11)–3)) Array HYBRID = (100/((COUNT(B2:B11))–(COUNT(I2:I4)))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array MPSD = 100 * SQRT((1/COUNT(B2:B11–I2:I4) * (SUM((B2:B11–C2:C11)/(B2:B11))^2))) Array

Table 6. Microsoft Excel Solver spreadsheet-based program for Toth isotherm model.

	Ce	qe, exp	qe, cal	Residual	Residaul^2	Upper, CI	Lower, CI	Factors for the Model		Statistical Results
Row/Column	A	B	C	D	E	F	G	H	I	J	K
1	0	0	0	0	0	1.9260	−1.9260	SSR	5.5806	ERRSQ/SSE	5.5806
2	0.5693	4.7154	2.9784	1.7369	3.0169	4.9044	1.0525	qm	32.1326	Chi-squar	0.8143
3	1.3183	6.8409	6.6830	0.1579	0.0249	8.6090	4.7570	kth	0.1645	ARE	2.8665
4	2.0673	8.9664	10.0211	−1.0547	1.1124	11.9471	8.0951	nth	1.7045	RMSE	0.8325
5	4.3142	17.8429	17.5856	0.2573	0.0662	19.5116	15.6596	Mean of qe,exp	20.0481	HYBRID	4.0951
6	9.2576	25.3712	25.4476	−0.0764	0.0058	27.3736	23.5216	df	8.0000	MPSD	16.5500
7	19.5937	30.2031	29.8163	0.3869	0.1497	31.7422	27.8903	SE of qe,exp	0.8352
8	38.0190	30.9905	31.3320	−0.3415	0.1166	33.2580	29.4060	R-square	0.9965
9	57.9422	31.0289	31.7354	−0.7065	0.4991	33.6614	29.8094	Critical t	2.3060
10	74.7197	32.6401	31.8736	0.7666	0.5877	33.7996	29.9476	CI	1.9260
11	96.1409	31.9295	31.9634	−0.0338	0.0011	33.8894	30.0374	Adjust R-square	0.9957
Formula or Excel code
qe, cal = $I$2 * (($I$3 * A)/((1 + ($I$3 * A)^($I$4))^(1/$I$4))) Array, Note: Values in column C (qe, cal) were depended on the values in column A (Ce), * = Multiplication sign (×). SSR = SUM(E1:E11) Array Mean of qe,exp = AVERAGE(B1:B11) Array df = COUNT(B1:B11)–COUNT(I2:I3) Array SE of qe,exp = SQRT(SUM((B1:B11–C1:C11)^2)/I6) Array R-square = 1-(SUM((B1:B11–C1:C11)^2)/(SUM((B1:B11-I5)^2))) Array Critical t = TINV(0.05,I6) Array CI = I7 * I9 Array Adjust R-square = (1–((COUNT(B1:B11)–1)/(COUNT(B1:B11)–3)) * (1–I8)) Array ERRSQ/SSE = SUM((C1:C11–B1:B11)^2) Array Chi-square = SUM(((C2:C11–B2:B11)^2)/(B2:B11)) Array ARE = (100/(COUNT(B2:B11))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array RMSE = SQRT(SUM((B1:B11–C1:C11)^2)/(COUNT(C1:C11)–3)) Array HYBRID = (100/((COUNT(B2:B11))–(COUNT(I2:I4)))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array MPSD = 100 * SQRT((1/COUNT(B2:B11–I2:I4) * (SUM((B2:B11–C2:C11)/(B2:B11))^2))) Array

Table 7. Microsoft Excel Solver spreadsheet-based program for Khan isotherm model.

	Ce	qe, exp	qe, cal	Residual	Residaul^2	Upper, CI	Lower, CI	Factors for the Model		Statistical Results
Row/Column	A	B	C	D	E	F	G	H	I	J	K
1	0	0	0	0	0	2.3249	−2.3249	SSR	8.1318	ERRSQ/SSE	8.1318
2	0.5693	4.7154	3.5660	1.1494	1.3211	5.8909	1.2410	qm	48.6815	Chi-squar	0.7585
3	1.3183	6.8409	7.4303	−0.5894	0.3474	9.7552	5.1054	kk	0.1404	ARE	0.3101
4	2.0673	8.9664	10.5790	−1.6126	2.6006	12.9039	8.2541	ak	1.1361	RMSE	1.0082
5	4.3142	17.8429	17.2192	0.6237	0.3890	19.5441	14.8943	Mean of qe,exp	20.0481	HYBRID	0.4430
6	9.2576	25.3712	24.5664	0.8048	0.6477	26.8913	22.2415	df	8.0000	MPSD	1.7904
7	19.5937	30.2031	29.8242	0.3789	0.1436	32.1492	27.4993	SE of qe,exp	1.0082
8	38.0190	30.9905	31.8887	−0.8982	0.8067	34.2136	29.5638	R-square	0.9950
9	57.9422	31.0289	32.0809	−1.0520	1.1068	34.4058	29.7560	Critical t	2.3060
10	74.7197	32.6401	31.8781	0.7621	0.5808	34.2030	29.5531	CI	2.3249
11	96.1409	31.9295	31.4957	0.4338	0.1882	33.8206	29.1708	Adjust R-square	0.9937
Formula or Excel code
qe, cal = ($I$2 * $I$3 * A)/((1 + ($I$3 * A))^$I$4) Array, Note: Values in column C (qe, cal) were depended on the values in column A (Ce), * = Multiplication sign (×). SSR = SUM(E1:E11) Array Mean of qe,exp = AVERAGE(B1:B11) Array df = COUNT(B1:B11)–COUNT(I2:I3) Array SE of qe,exp = SQRT(SUM((B1:B11–C1:C11)^2)/I6) Array R-square = 1-(SUM((B1:B11–C1:C11)^2)/(SUM((B1:B11-I5)^2))) Array Critical t = TINV(0.05,I6) Array CI = I7 * I9 Array Adjust R-square = (1–((COUNT(B1:B11)–1)/(COUNT(B1:B11)–3)) * (1–I8)) Array ERRSQ/SSE = SUM((C1:C11–B1:B11)^2) Array Chi-square = SUM(((C2:C11–B2:B11)^2)/(B2:B11)) Array ARE = (100/(COUNT(B2:B11))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array RMSE = SQRT(SUM((B1:B11–C1:C11)^2)/(COUNT(C1:C11)–3)) Array HYBRID = (100/((COUNT(B2:B11))–(COUNT(I2:I4)))) * (SUM((B2:B11–C2:C11)/(B2:B11))) Array MPSD = 100 * SQRT((1/COUNT(B2:B11–I2:I4) * (SUM((B2:B11–C2:C11)/(B2:B11))^2))) Array

The nonlinear regression of isotherm models and the goodness of fit were built-in functions using the Microsoft Excel Solver spreadsheet-based program available in Microsoft Office. They were appropriate to describe the experimental data with accuracy to predict the best fit for the methylene blue adsorbed onto the magnetic nanosorbent material. These parameter values were evaluated with MATLAB and OriginPro and described under Section 3.2.

Within this framework, Table 2, Table 3 and Table 4 concern the prediction of two-parameter isotherm models, such as the Freundlich, Langmuir and Temkin models. The parameters for these isotherm models are k_f (10.7618 (mg g⁻¹) (mg L⁻¹)^1/n), n (3.7564), q_m (34.4765 mg g⁻¹), k_l (0.2346 L mg⁻¹), b_t (6.0492 J mol⁻¹) and k_t (3.5884 L mol⁻¹). q_m is the maximum adsorption capacity of methylene blue adsorbed onto magnetic nanosorbent (mg g⁻¹), and k_l is the affinity constant or Langmuir isotherm rate constant (L mg⁻¹) to the apparent energy of sorption. k_f is the Freundlich isotherm rate constant (mg g⁻¹) (mg L⁻¹)^1/n, and n_f is the order of reaction or the heterogeneous factor surfaces (dimensionless) for the Freundlich model. b_t is the Temkin isotherm constant (J mol⁻¹), and k_t is the Temkin isotherm rate constant (L mol⁻¹). q_{e, cal} in column C was computed as appropriate for the values of C_e data and the empirical equation of each model shown in Equations (2)–(4) and/or the formula array shown in Table 2, Table 3 and Table 4 (Langmuir = $I$3 * ($I$2 * (A/(1 + ($I$2*A)))), Freundlich = $I$2 * A^(1/$I$3) and Temkin = $I$2*LN($I$3*A)), respectively. It can be observed that the q_{e, cal} values of each model and row were different and were affected by the statistical results, R-square and Adjust R-square together with residual values, upper CI, lower CI and SSR and parameter models also. From the perspective of ERRSQ/SSE, Chi-square, ARE, RMSE, HYBRID and MPSD, the built-in formula is shown in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7. It was found that the statistical results were different depending on the isotherm model function. Likewise, a comparison for the best fitting of two nonlinear parameters of the isotherm models demonstrated that the Langmuir model presented an R-square (0.9897) and Adjust R-square (0.9885) close to 1. ERRSQ/SSE (16.6590), Chi-square (1.2540), ARE (−2.1538), RMSE (1.2907), HYBRID (−2.3931) and MPSD (15.2297) values also indicated that all small values of significance were evidence for the acceptance of the nonlinear regression modeling. It could be confirmed that the adsorption of methylene blue or cationic dye onto the magnetic nanosorbent surface involves homogenous sites, with all active sites having equivalent energy, which had no more adsorption onto the magnetic nanosorbent and/or with no interaction among the adsorbed molecules [30,40]. However, the Langmuir model is not applicable for the explanation of the adsorption mechanism for the adsorption process; it just provides the information of the ability of adsorption and equilibrium processes as mentioned (q_e, q_m and k_l) [41]. Therefore, three-parameter isotherm models (Table 5, Table 6 and Table 7) were required to explain the adsorption mechanism as described below.

Table 5, Table 6 and Table 7 provide a summary of the three-parameter isotherm model types for this task, including Liu, Toth and Khan models. The model parameters of q_m, k_g, n_g, k_th, n_th, k_k and a_k are summarized followed by the statistical analysis results via the Microsoft Excel Solver spreadsheet-based program. The nonlinear regression values of three-parameter isotherm models were compared and presented in Table 5, Table 6 and Table 7 in columns I and K. Table 5, Table 6 and Table 7 summarize that for the magnetic nanosorbent, mathematically the Toth model provides a significant goodness of fit that was better than that of the Liu and Khan models. The Toth model was modified from the Langmuir isotherm model equation (homogeneous surface, n = 1, the Toth equation reduces to Langmuir model) that is useful to describe the heterogeneous systems with both a low- and high-end boundary of methylene blue concentration [42,43]. This model correlates and/or assumes an asymmetrical quasi-Gaussian site energy distribution [44]. The Liu and Khan models had a slightly reduced mathematical complexity; however, each of them showed an excellent fit. In this case, the Khan model also gave a goodness of fit but was unable to forecast the q_m (48.6815 mg g⁻¹, error 34%) as shown in Table 7. In terms of the overall statistical results, it was clear that the Toth model was the best fitting and close to the Liu model.

3.2. Comparison of Parameter Values for the Isotherm Models Obtained by Nonlinear Fitting

Usually, various advanced nonlinear regression programs are used to assess the standard error of the isotherm parameters. Those parameter values sometimes distort the forecasts for nonlinear isotherm functions, additive or symmetrical errors, and exact confidence intervals cannot be calculated. The nonlinear regression equations of isotherm models are formulated from the linear assumptions that constantly provide underestimates of the true uncertainty of asymptotic standard errors. Therefore, Microsoft Excel was used for calculating the isotherm parameters and statical results; however, it was complex and took a long time to operate for the built-in function to conduct the necessary evaluation and comparison. Consequently, an approach was implemented for this research in order to evaluate the standard error of the results obtained derived from the experimental and predicted data that were computed by the software tools as mentioned above.

Table 8 presents the comparison results for parameter values for the isotherm models obtained by nonlinear fitting via the Microsoft Excel Solver function with MATLAB and OriginPro. Virtually the same results can be noted for the magnetic nanosorbent material and that the Langmuir and Toth provided the best (and very good) statistics among the two-parameter and three-parameter isotherm models, respectively. It can be seen that the model parameters were close/similar for the three software tools of the Microsoft Excel Solver function with MATLAB and OriginPro. However, there are some statistical results and model parameters that are discussed below.

Table 8. Comparison of isotherm parameters and error functions from Microsoft Excel Solver function with MATLAB and OriginPro.

Model Parameter	Equation	Parameter Values for the Isotherm Models
		Microsoft Excel Solver Functions	MATLAB	OriginPro
Freundlich
kf	$q_e=k_f·C_e{}^{1/n_f}$	10.76	10.76	10.76
nf		3.7564	3.757	3.756
1/nf		0.2662	0.2662	2.2662
R-square		0.8955	0.8955	0.8955
Adj R-square		0.8839	0.8839	0.8839
ERRSQ/SSE		168.2962	168.2962	168.2963
Chi-square		13.39	-	13.39
ARE		−16.71	-	-
RMSE		4.3243	4.3243	-
HYBRID		−20.88	-	-
MPSD		118.1294	-	-
Langmuir
qm	$q_e=q_m·k_l\frac{C_e}{1+k_l·C_e}$	34.48	34.48	34.48
kl		0.2346	0.2343	0.2346
R-square		0.9897	0.9897	0.9897
Adj R-square		0.9885	0.9885	0.9885
ERRSQ/SSE		16.6590	16.6590	16.6590
Chi-square		1.254	-	1.254
ARE		−2.154	-	-
RMSE		1.3605	1.3605	-
HYBRID		−2.393	-	-
MPSD		15.2297	-	-
Temkin
bt	$q_e=b_t·\ln \left(k_t·C_e\right)$	6.049	6.049	6.049
kt		3.588	3.588	3.588
R-square		0.9553	0.9384	0.9553
Adj R-square		0.9503	0.9306	0.9503
ERRSQ/SSE		72.0332	72.0332	72.0332
Chi-square		4.055	-	4.055
ARE		−4.018	-	-
RMSE		2.8291	3.0001	-
HYBRID		−4.464	-	-
MPSD		28.4083	-	-
Liu [45]
qm	$q_e=\frac{q_m{(k_g·C_e)}^{n_g}}{1+{(k_g·C_e)}^{n_g}}$	32.78	32.78	32.78
kg		0.2660	0.2660	0.2660
ng		0.7735	0.7735	1.2928
R-square		0.9948	0.9948	0.9948
Adj R-square		0.9935	0.9935	0.9935
ERRSQ/SSE		8.3791	8.3791	8.3791
Chi-square		1.209	-	1.209
ARE		3.215	-	-
RMSE		1.0234	1.0234	-
HYBRID		4.593	-	-
MPSD		18.5609	-	-
Toth [35]
qm	$q_e=q_m\frac{k_{th}·C_e}{{\left(1+{(k_{th}·C_e)}^{n_{th}}\right)}^{1/n_{th}}}$	32.13	32.13	32.13
kth		0.1645	0.1645	0.1645
nth		1.705	1.705	1.705
R-square		0.9965	0.9965	0.9965
Adj R-square		0.9957	0.9957	0.9957
ERRSQ/SSE		5.5806	5.5806	5.5086
Chi-square		0.814	-	0.814
ARE		2.867	-	-
RMSE		0.8352	0.8352	-
HYBRID		4.095	-	-
MPSD		16.5500	-	-
Khan
qm	$q_e=\frac{q_m·k_k·C_e}{{\left(1+k_k·C_e\right)}^{a_k}}$	48.68	43.84	48.71
kk		0.1404	0.1462	0.1403
ak		1.136	1.105	1.136
R-square		0.9950	0.9954	0.9950
Adj R-square		0.9937	0.9943	0.9937
ERRSQ/SSE		8.1318	7.3538	8.1318
Chi-squar		0.7585	-	0.7585
ARE		0.310	-	-
RMSE		1.0082	0.9588	-
HYBRID		0.4430	-	-
MPSD		1.7904	-	-

Note: the symbol (-) = It is not available in the program software tool.

It can be seen that the result of R-square (0.9384) of the Temkin isotherm model for MATLAB was different with Microsoft Excel (0.9553) and OriginPro (0.9553) due to the real natural logarithm function ln (experimental data, C_e) being defined only for C_e as more than zero; the natural logarithm of zero was undefined (log 0, it is not a real number) in MATLAB. For that reason, it might be that the number of degrees of freedom (df, maximum number of logically independent values) were reduced to 8 from the data sample set of q_e and C_e (11, Table 1) as compared to Microsoft Excel (9) and OriginPro (9). Therefore, the relation to various forms of hypothesis testing in some statistical results was effected by the Adj R-square (0.9306) and RMSE (3.0001) as presented in Table 8.

In terms of the Khan isotherm model, the parameter and statistical results were similar for Microsoft Excel and OriginPro, while MATLAB showed differences in all results. It might be that the zero is undefined (It has no meaning) that cannot be proven without math for zero divided by any nonzero number [46]. On the other hand, zero does not have a multiplicative inverse under any circumstances [47] for the MATLAB software tool.

It can be concluded that the six isotherm models showed the confidence interval that was simply the best fit at all experimental data points using the three software tools. The results indicated that the Microsoft Excel Solver function spreadsheet method fulfilled all the statistic measures to predict the real variance of the probability of experimental data for all six isotherm models of adsorption of cationic dye removal. Nevertheless, whether it is a suitable program method for water and wastewater application depends on the user.

Figure 4 and Figure 5 illustrate the discussed isotherms for a visual confirmation of the results. Observation of the graphs confirms that magnetic nanosorbents fit the Langmuir and Toth isotherm models well. Moreover, the results confirm the arguments of the regression results of isotherm parameters and error functions from the Microsoft Excel Solver function with MATLAB and OriginPro programs as shown in Table 8. Considering these good fits to all isotherm models as shown in Figure 4 and Figure 5, it can be concluded that the Microsoft Excel Solver spreadsheet-based program has achieved its place among the tools in the product to express the parameter and statistical results of the isotherm models when providing the mechanism of the adsorption process in water and wastewater treatment or any specific pollutants needed in the treatment plant.

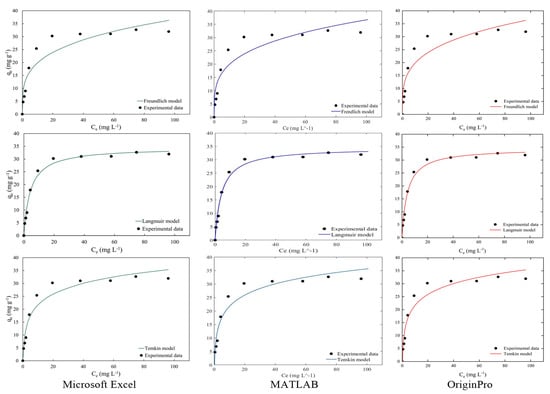
Figure 4. The comparison of two-parameter isotherm plots from a Microsoft Excel-based program, MATLAB and OriginPro.

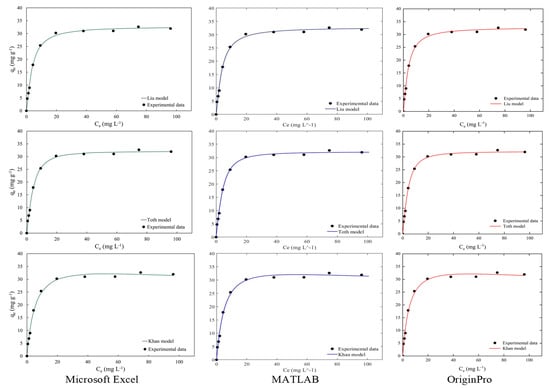
Figure 5. The comparison of three-parameter isotherm plots from a Microsoft Excel-based program, MATLAB and OriginPro.

A comparison using the Microsoft Excel Solver spreadsheet-based program was also achieved for analyzing nonlinear isotherm models and error functions when designing an adsorption process system, such as adsorption of lead ions on powdered corn cobs [38], adsorption metals using biosorption in water and wastewater [37], adsorption of methylene blue onto rice husk [48] and biocomposite for phosphate ion removal [49].

4. Conclusions

Isotherm adsorption studies were conducted on magnetic nanosorbent, and methylene blue was chosen as a model substrate to evaluate the capacity of the adsorbent obtained, the controlling mechanism of the adsorption process and the relationship between the amounts of methylene blue adsorbed per unit mass. The complexity of nonlinear regression was applied for standardizing the experimental data through the Microsoft Excel program. It can be concluded that the characteristics of the methylene blue adsorbed onto the magnetic nanosorbent forms monolayer and multilayer physical types, which illustrated monolayer coverage (Langmuir model, q_m = 34.48 mg g⁻¹, R² = 0.9897 close to 1) for a two-parameter model, followed by multilayer adsorption (Freundlich and Temkin model). The three-parameter model Toth (q_m = 32.13 mg g⁻¹ was close to experimental data and R² = 0.9965 close to 1) provided a significant goodness of fit and was better than the Liu and Khan models, which indicated the heterogeneous systems had both a low- and high-end boundary of methylene blue concentration adsorbed onto the magnetic nanosorbent. When comparing the software tools, the results indicated that the Microsoft Excel Solver function spreadsheet method satisfied all the statistic and isotherm parameter measures to predict the adsorption of basic dye removal for all six isotherm models. However, it possesses a few negative points that need to be considered before devising the adsorption isotherm model, such as its time consuming nature, the precision of the isotherm model function and the sensible initial parameter of the experimental data set. It could be concluded that the predicted values of the parameter and the statistical analysis for the adsorption isotherm models are reasonable when predicting them for the user who is not an expert in advanced software tools.