Thermal Performance Enhancement Using Absorber Tube with Inner Helical Axial Fins in a Parabolic Trough Solar Collector
Abstract
:1. Introduction
2. Materials, Methods and Boundary Conditions
- The inlet fluid at all velocities is 30 °C.
- The flow is turbulent and in a steady mood.
- The heat flux applied to the surface of the outer tube is 60,000 W·m−2.
3. Governing Equations and Dimensionless Parameters
4. Results
4.1. Grid Independency Study
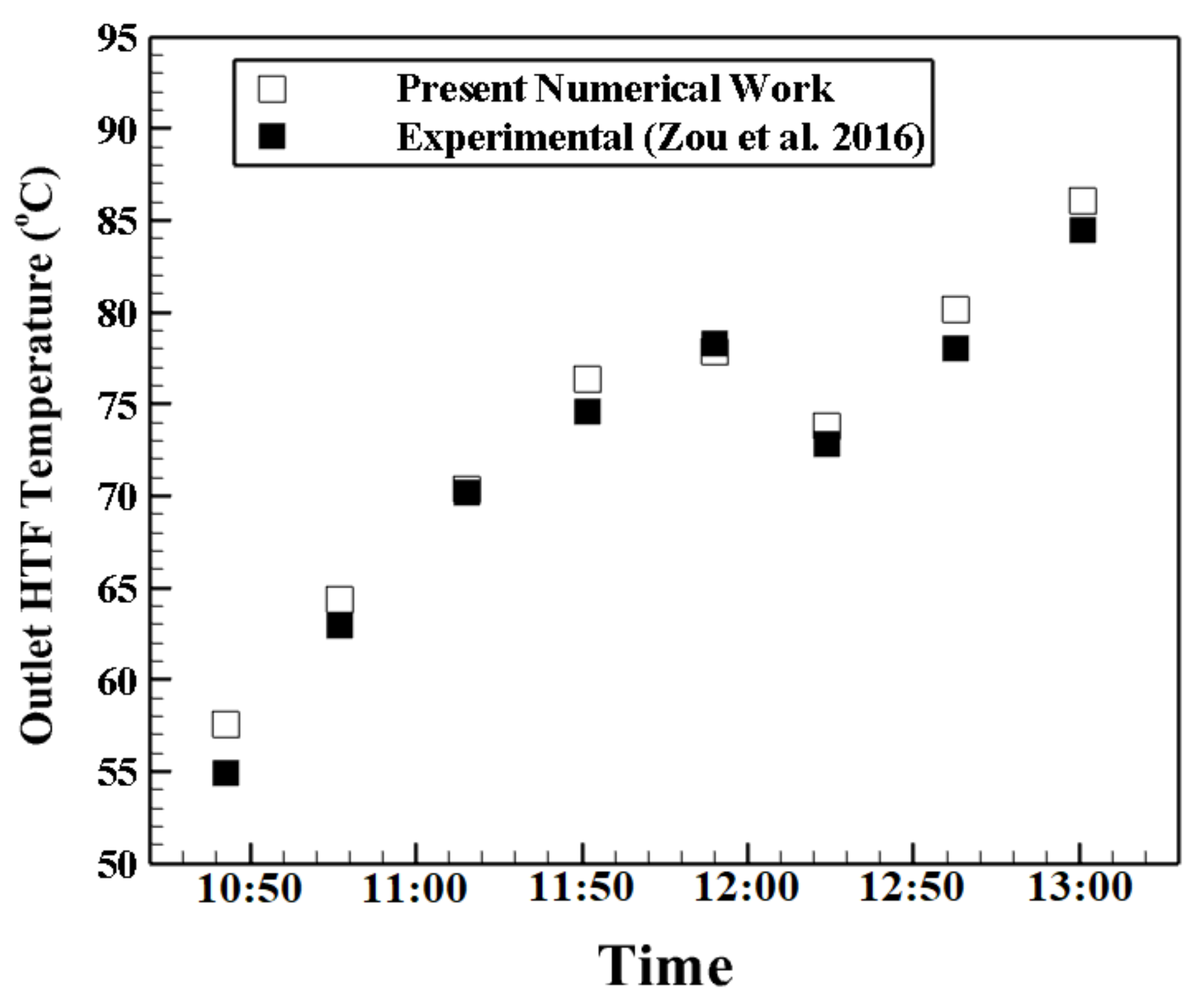
4.2. Validation Study
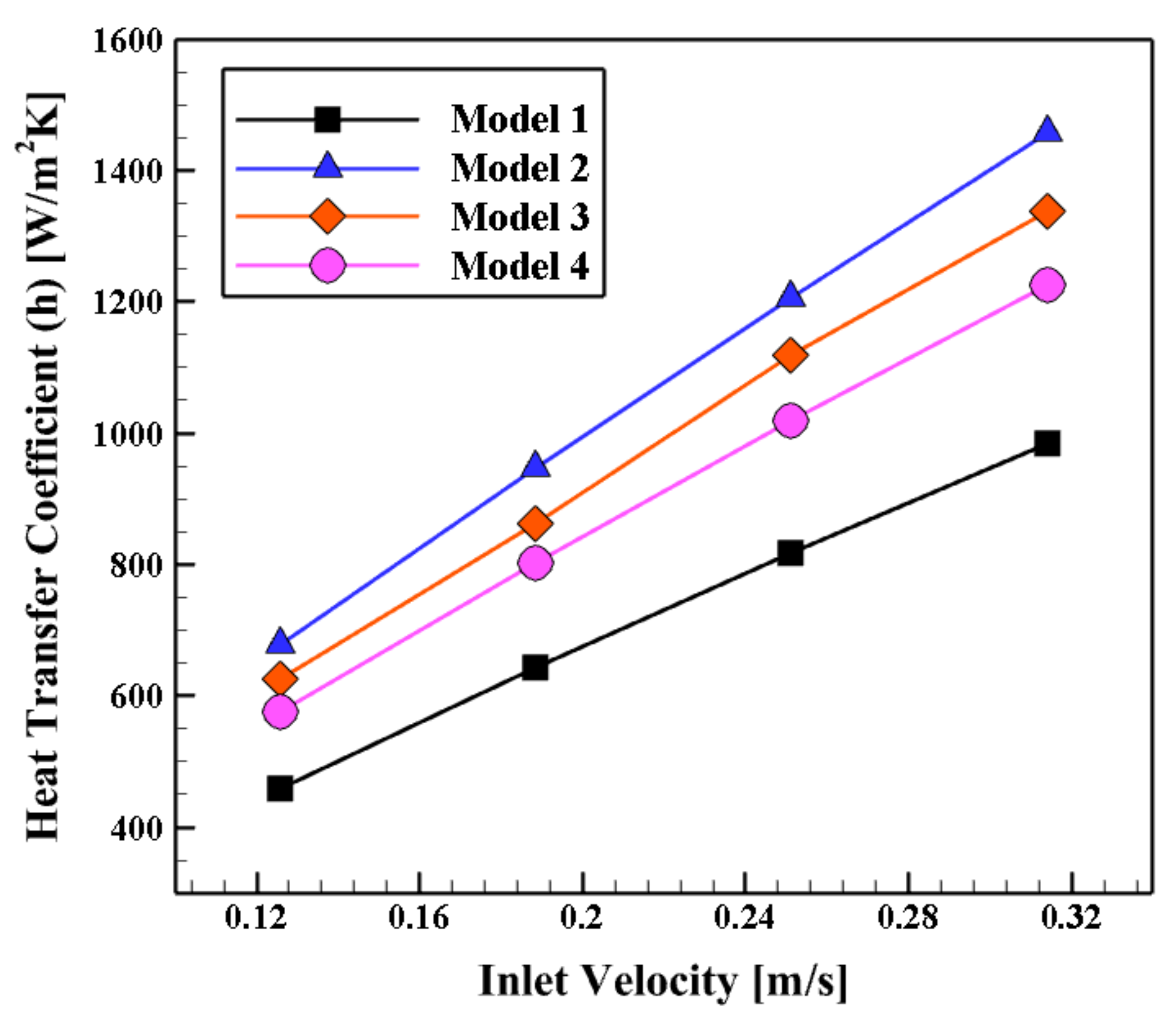
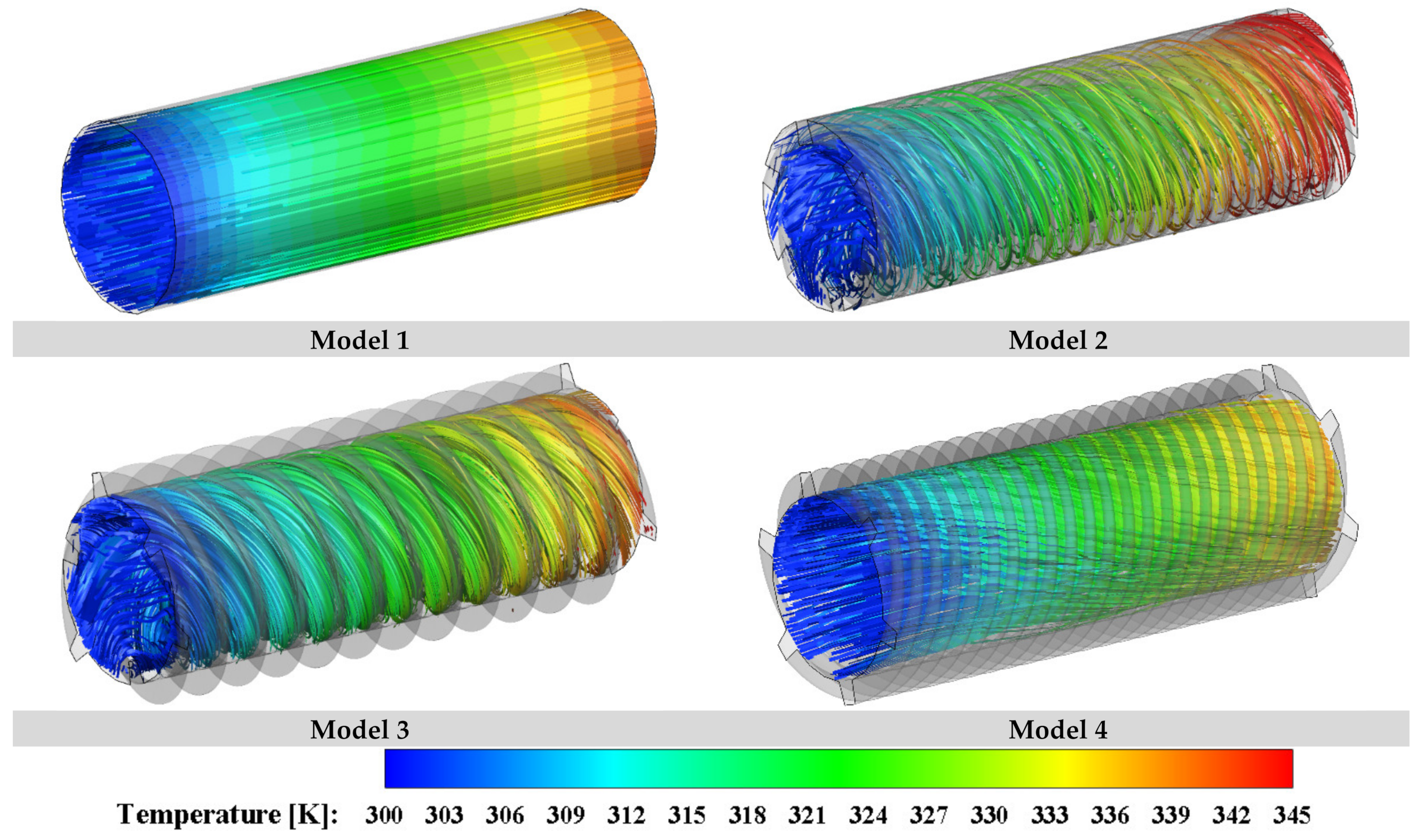
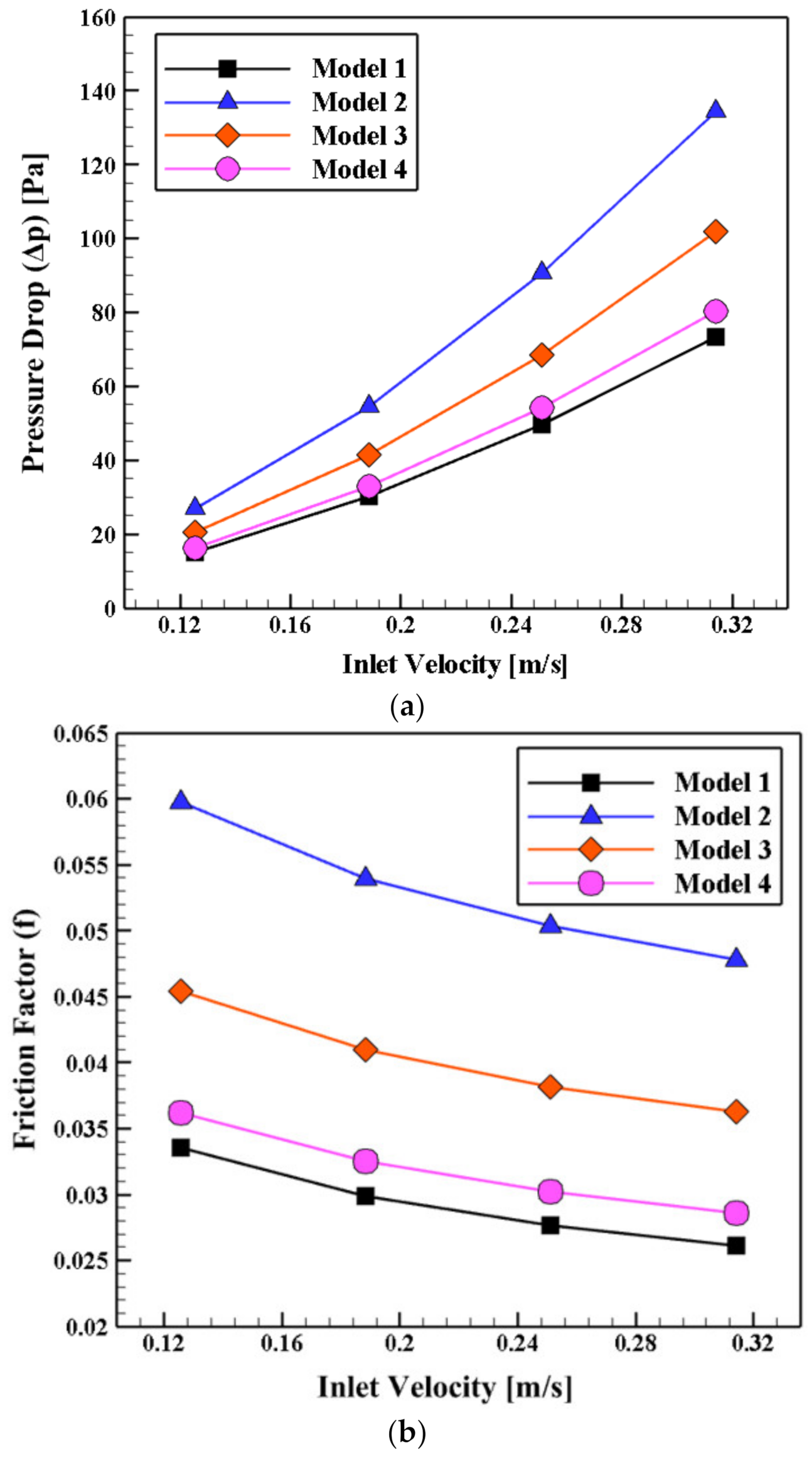
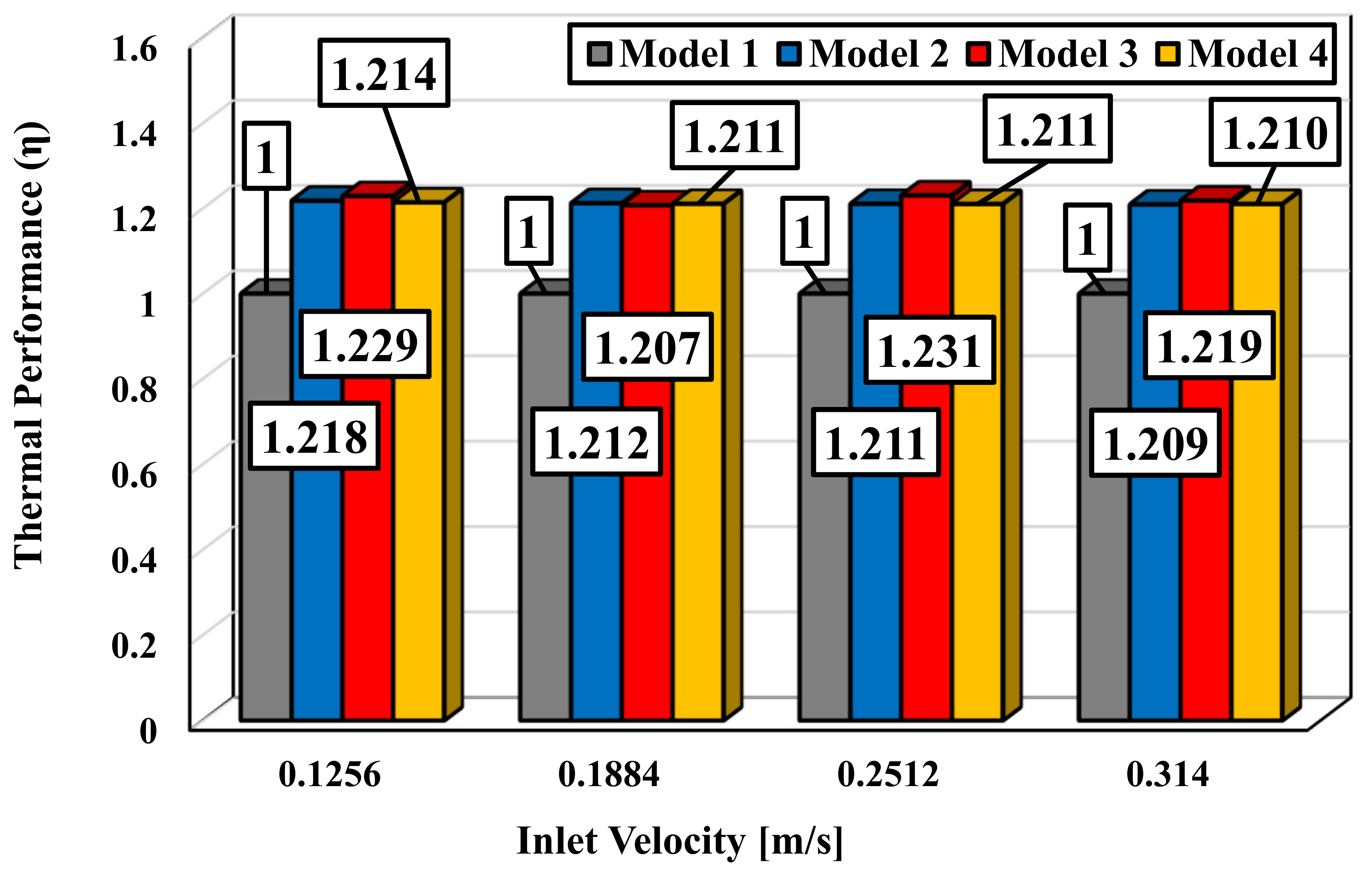
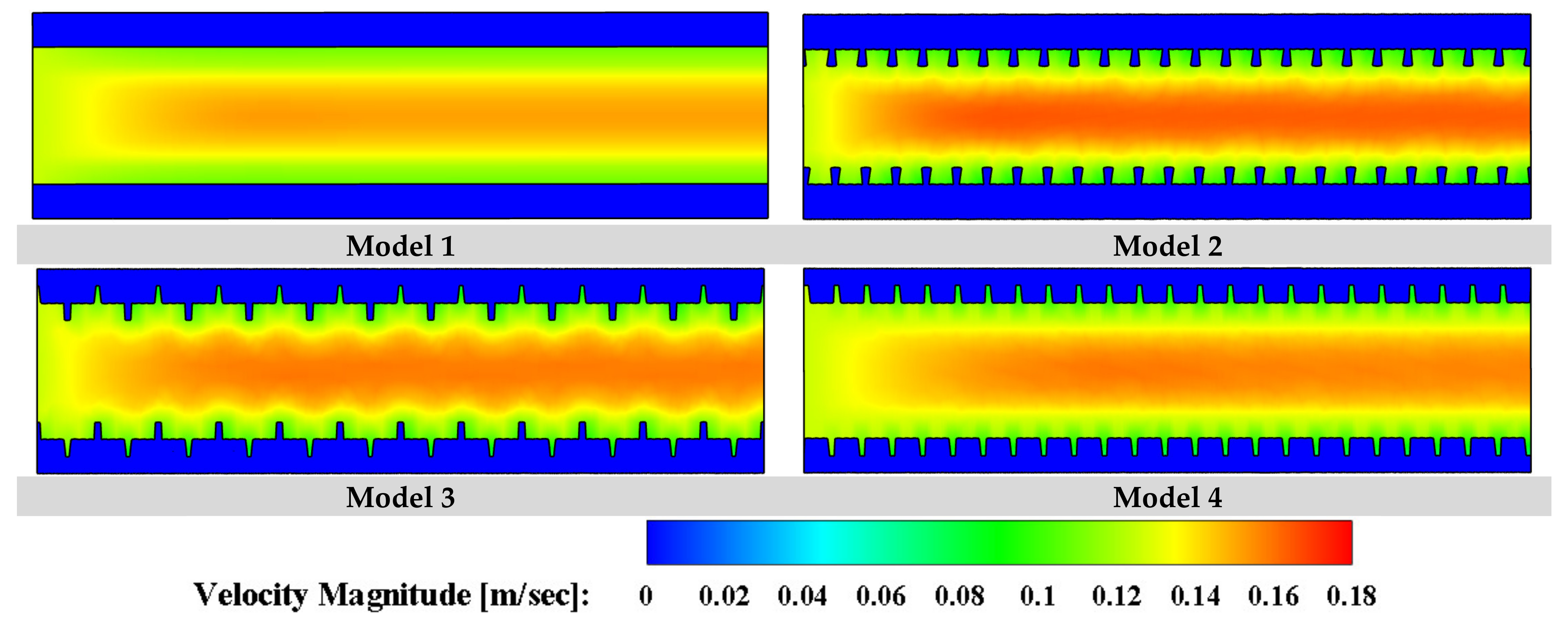
4.3. The Impact of the Schematic of the Proposed Collector’s Fins
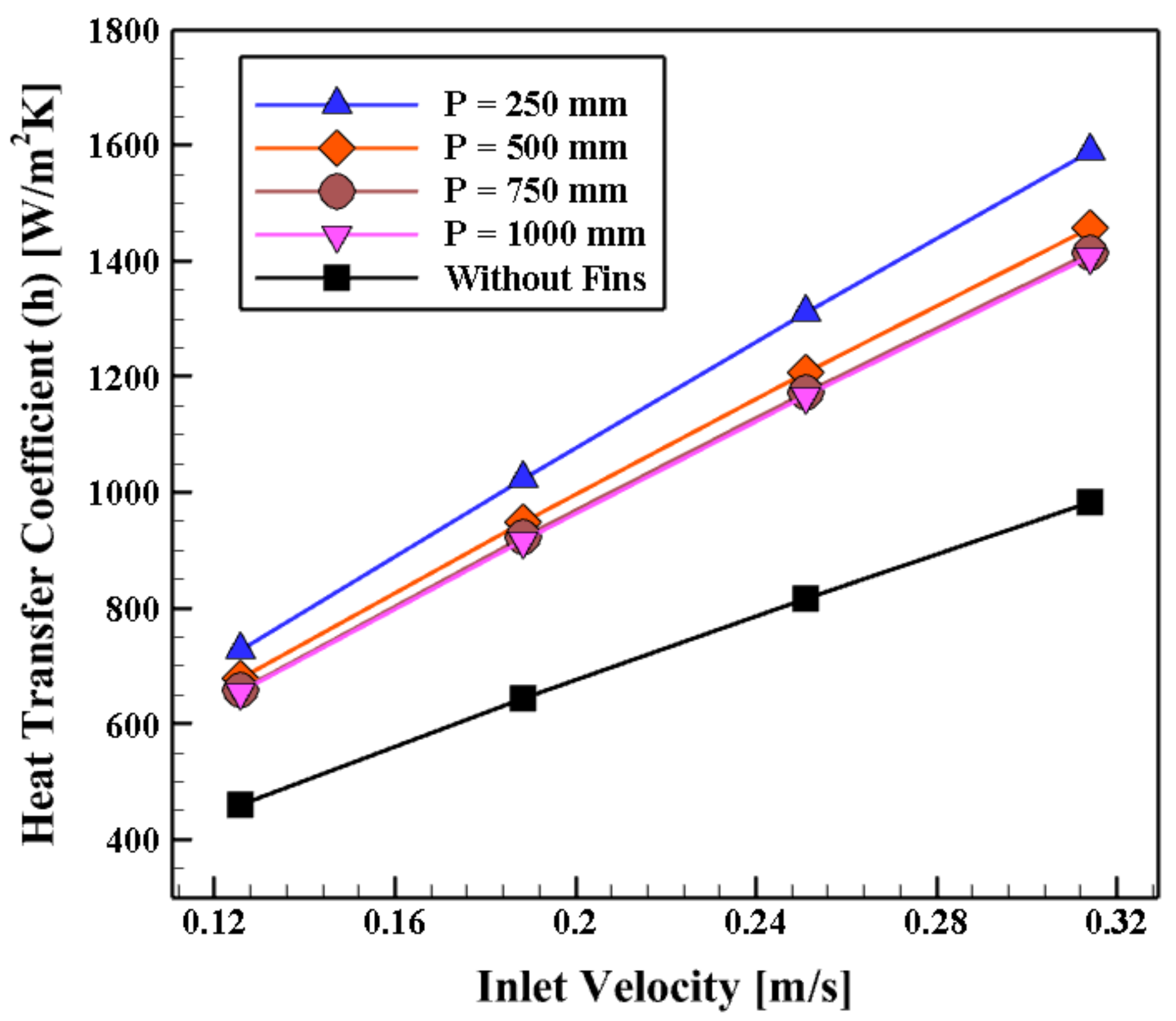
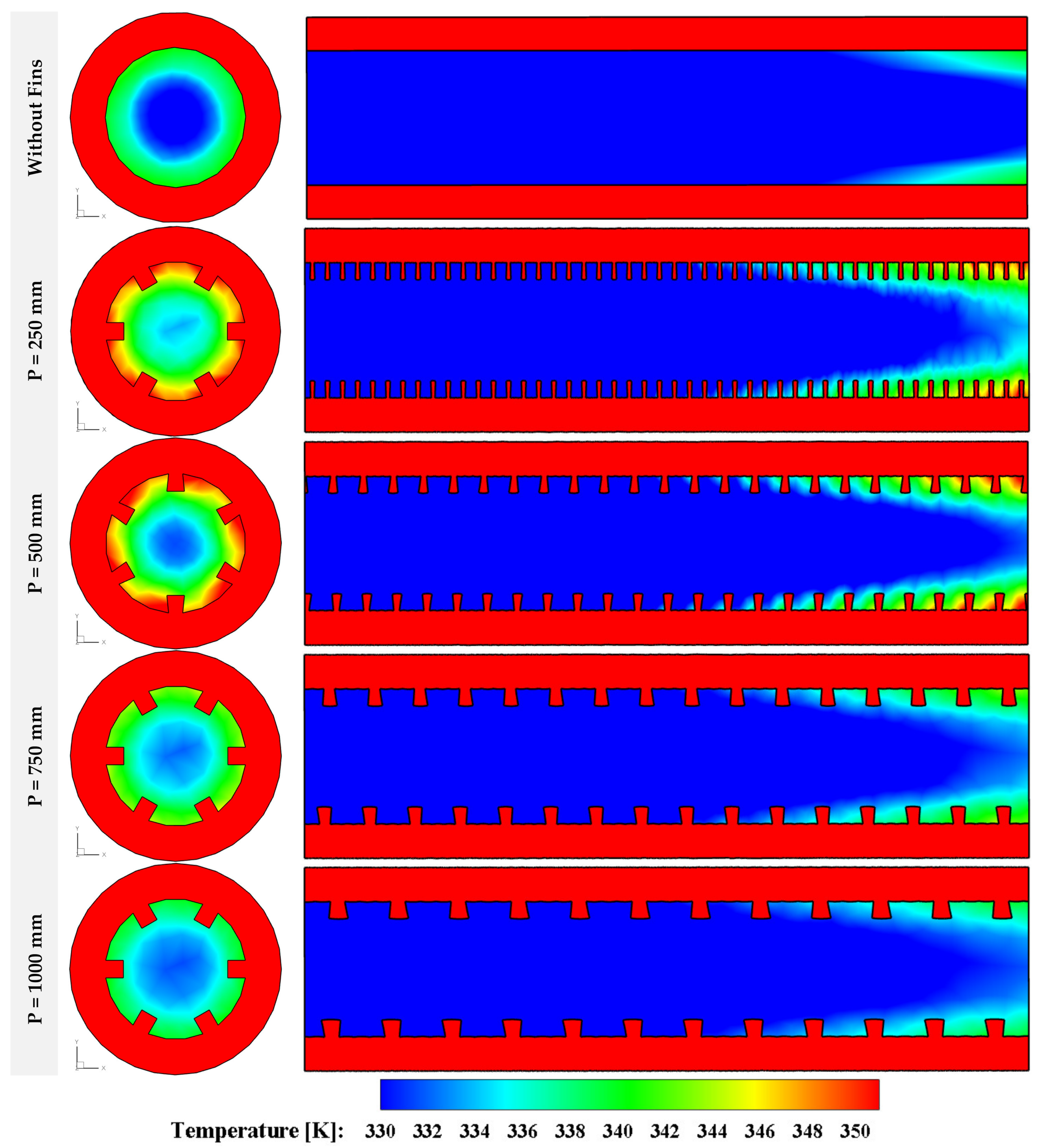
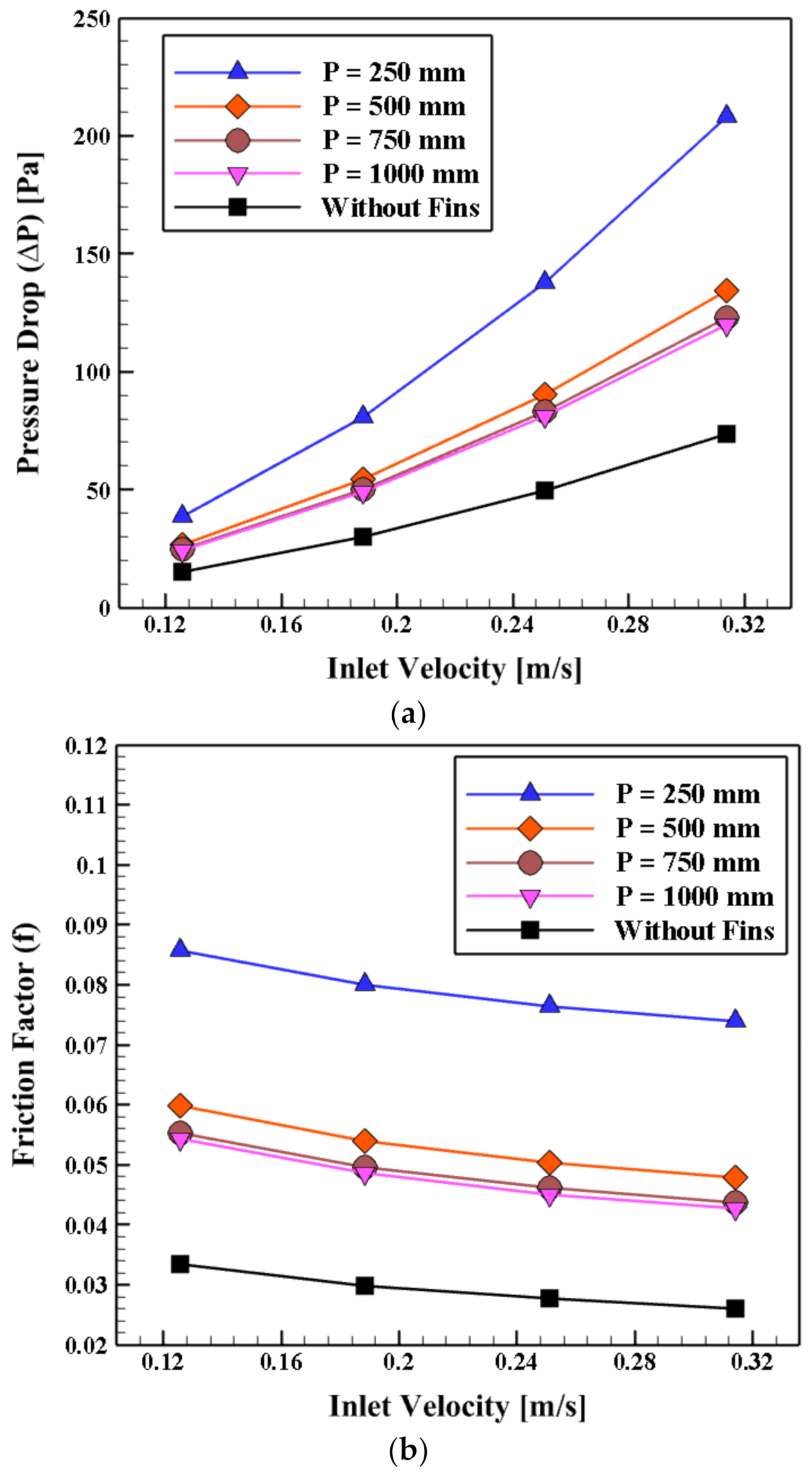
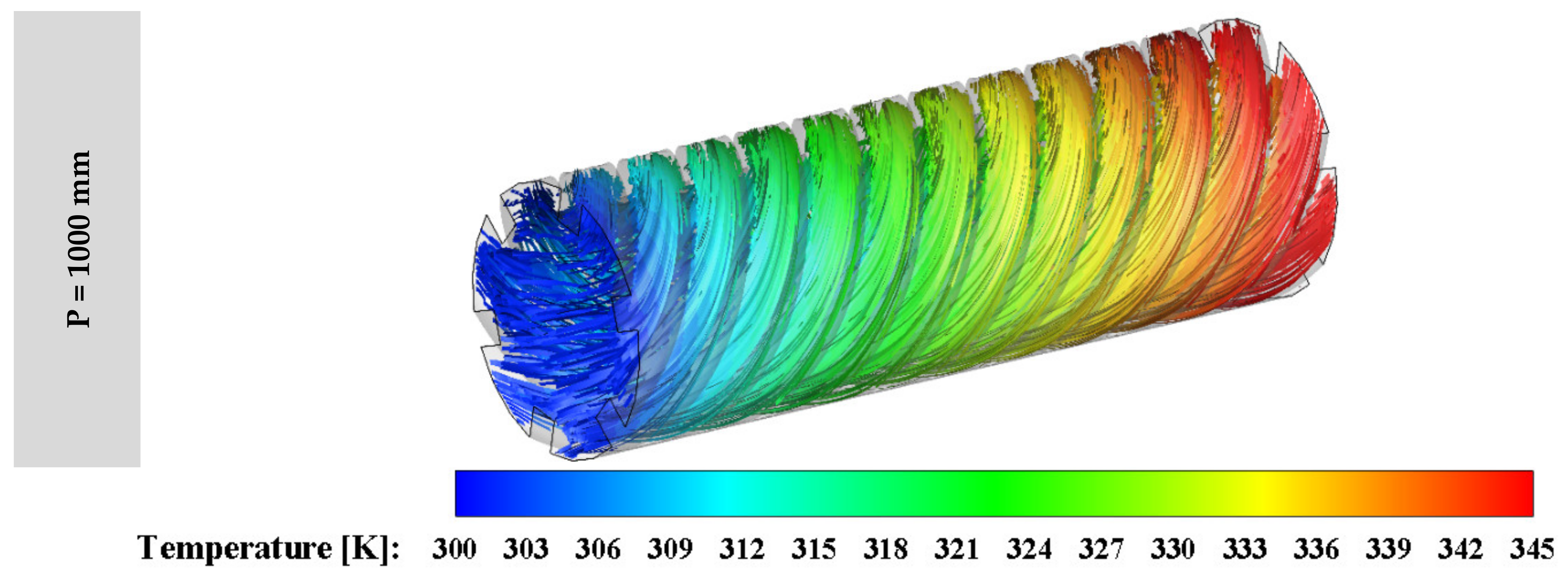
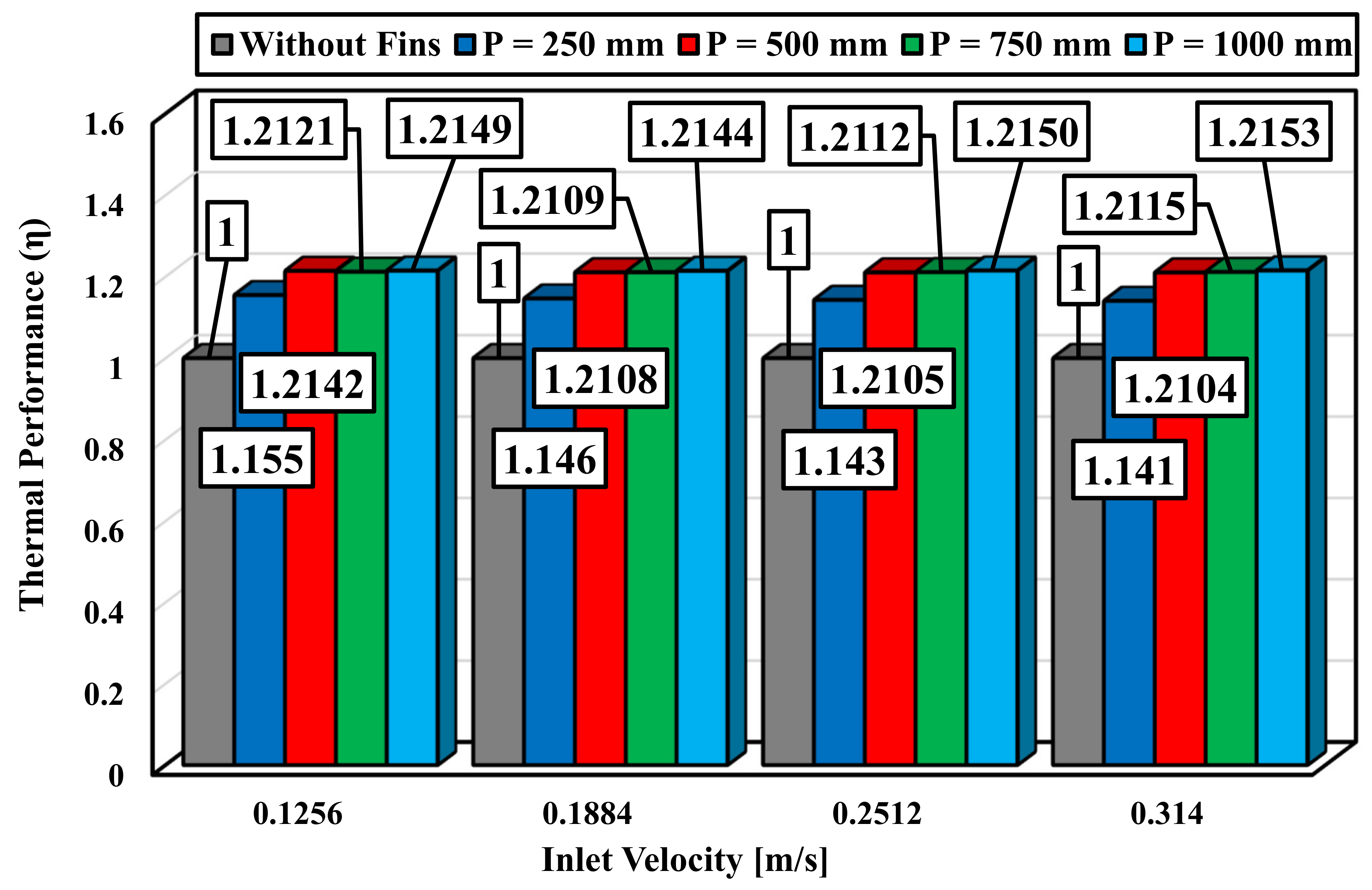
4.4. The Impact of the Inner Helical Fins Pitch (P)
5. Conclusions and Future Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Expects Data
Nomenclature
| A | Area, m2 | Greek and Symbols | |
| CP | Specific heat capacity, [kJ/(kg. K)] | ρ | Density, kg/m3 |
| D1 | Diameter of inner the tube, [m] | μ | Viscosity, kg/m·s |
| D2 | Diameter of outer the tube, [m] | Stress tensor | |
| d | Diameter, [m] | σ | Turbulent Prandtl number |
| f | Darcy friction factor, [nd] | Thermal performance, [nd] | |
| Gb | Generation of turbulence kinetic energy due to buoyancy, [J/kg] | α | Helical angle of the Fins, [degree] |
| Gk | Generation of turbulence kinetic energy due to the mean velocity gradients, [J/kg] | k | turbulent kinetic energy per unit mass, [J/kg] |
| g | Gravity, [m/s2] | ε | energy dissipation rate per unit mass, [W/kg] |
| H | Height of the Fins, [m] | Dimensionless Parameter | |
| h | Heat transfer coefficient, [W/(m2·K)] | Pe | Péclet number, , [nd] |
| k | Thermal conductivity, [W/(m·K)] | Pr | Prandtl number, , [nd] |
| L | Length of the tube, [m] | Nu | Nusselt number, , [nd] |
| Mt | Turbulent Mach number, [nd] | Re | Reynolds number, , [nd] |
| P | Helix pitch of the Fins, [m] | Index | |
| p | Pressure, [Pa] | 0 | Reference |
| Sh | Heat generation, [J/m3] | eff | Effective |
| Sm | Mass generation, [kg/m3] | h | Hydraulic |
| T | Temperature, [°C] | m | Average |
| t | Time, [s] | PR | Performance Ratio |
| th | Thickness of the Fins, [m] | ref | reference |
| v | Velocity, [m·s−1] | t | turbulence |
| Abbreviation | |||
| PTCs | Parabolic Trough Collectors | ||
| Exp | Experimental | ||
| Num | Numerical | ||
References
- Berger, S.A.; Talbot, L.; Yao, L.S. Flow in curved pipes. Annu. Rev. Fluid Mech. 1983, 15, 461–512. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D. Review of heat transfer enhancement methods: Focus on passive methods using swirl flow devices. Renew. Sustain. Energy Rev. 2015, 49, 444–469. [Google Scholar] [CrossRef]
- Esfe, M.H.; Saedodin, S.; Wongwises, S.; Toghraie, D. An experimental study on the effect of diameter on thermal conductivity and dynamic viscosity of Fe/water nanofluids. J. Therm. Anal. Calorim. 2015, 119, 1817–1824. [Google Scholar] [CrossRef]
- Zaboli, M.; Ajarostaghi, S.S.; Noorbakhsh, M.; Delavar, M.A. Effects of geometrical and operational parameters on heat transfer and fluid flow of three various water based nanofluids in a shell and coil tube heat exchanger. SN Appl. Sci. 2019, 1, 1387. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Lee, K.S. Frosting and defrosting characteristics of surface-treated louvered-fin heat exchangers: Effects of fin pitch and experimental conditions. Int. J. Heat Mass Transf. 2013, 60, 505–511. [Google Scholar] [CrossRef]
- Gao, D.; Wang, Y. Generating high-purity orbital angular momentum vortex waves from Cassegrain meta-mirrors. Eur. Phys. J. Plus 2020, 135. [Google Scholar] [CrossRef]
- Hobbi, A.; Siddiqui, K. Experimental study on the effect of heat transfer enhancement devices in flat-plate solar collectors. Int. J. Heat Mass Transf. 2009, 52, 4650–4658. [Google Scholar] [CrossRef]
- Nuntaphan, A.; Vithayasai, S.; Vorayos, N.; Vorayos, N.; Kiatsiriroat, T. Use of oscillating heat pipe technique as extended surface in wire-on-tube heat exchanger for heat transfer enhancement. Int. Commun. Heat Mass Transf. 2010, 37, 287–292. [Google Scholar] [CrossRef]
- Dizaji, H.S.; Jafarmadar, S.; Asaadi, S. Experimental exergy analysis for shell and tube heat exchanger made of corrugated shell and corrugated tube. Exp. Therm. Fluid Sci. 2017, 81, 475–481. [Google Scholar] [CrossRef]
- Tang, L.H.; Zeng, M.; Wang, Q.W. Experimental and numerical investigation on air-side performance of fin-and-tube heat exchangers with various fin patterns. Exp. Therm. Fluid Sci. 2009, 33, 818–827. [Google Scholar] [CrossRef]
- Azari, M.; Sadeghi, A.; Chakraborty, S. Electroosmotic flow and heat transfer in a heterogeneous circular microchannel. Appl. Math. Model. 2020, 87, 640–654. [Google Scholar] [CrossRef]
- Darzi, A.A.R.; Farhadi, M.; Sedighi, K. Experimental investigation of convective heat transfer and friction factor of Al2O3/water nanofluid in helically corrugated tube. Exp. Therm. Fluid Sci. 2014, 57, 188–199. [Google Scholar] [CrossRef]
- Du, T.; Chen, Q.; Du, W.; Cheng, L. Performance of continuous helical baffled heat exchanger with varying elliptical tube layouts. Int. J. Heat Mass Transf. 2019, 133, 1165–1175. [Google Scholar] [CrossRef]
- Bahiraei, M.; Mazaheri, N.; Rizehvandi, A. Application of a hybrid nanofluid containing graphene nanoplatelet-platinum composite powder in a triple-tube heat exchanger equipped with inserted ribs. Appl. Therm. Eng. 2019, 149, 588–601. [Google Scholar] [CrossRef]
- Abolarin, S.M.; Everts, M.; Meyer, J.P. Heat transfer and pressure drop characteristics of alternating clockwise and counter clockwise twisted tape inserts in the transitional flow regime. Int. J. Heat Mass Transf. 2019, 133, 203–217. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhou, F.; Kang, J. Flow and heat transfer in drag-reducing polymer solution flow through the corrugated tube and circular tube. Appl. Therm. Eng. 2020, 115185. [Google Scholar] [CrossRef]
- Rashidi, S.; Hormozi, F.; Sundén, B.; Mahian, O. Energy saving in thermal energy systems using dimpled surface technology—A review on mechanisms and applications. Appl. Energy 2019, 250, 1491–1547. [Google Scholar] [CrossRef]
- Kareem, Z.S.; Abdullah, S.; Lazim, T.M.; Jaafar, M.M.; Wahid, A.F. Heat transfer enhancement in three-start spirally corrugated tube: Experimental and numerical study. Chem. Eng. Sci. 2015, 134, 746–757. [Google Scholar] [CrossRef]
- Lu, G.; Zhou, G. Numerical simulation on performances of plane and curved winglet type vortex generator pairs with punched holes. Int. J. Heat Mass Transf. 2016, 102, 679–690. [Google Scholar] [CrossRef]
- Mashoofi, N.; Pesteei, S.M.; Moosavi, A.; Dizaji, H.S. Fabrication method and thermal-frictional behavior of a tube-in-tube helically coiled heat exchanger which contains turbulator. Appl. Therm. Eng. 2017, 111, 1008–1015. [Google Scholar] [CrossRef]
- Aghaei, A.; Sheikhzadeh, G.A.; Goodarzi, M.; Hasani, H.; Damirchi, H.; Afrand, M. Effect of horizontal and vertical elliptic baffles inside an enclosure on the mixed convection of a MWCNTs-water nanofluid and its entropy generation. Eur. Phys. J. Plus 2018, 133, 486. [Google Scholar] [CrossRef]
- Noorbakhsh, M.; Zaboli, M.; Ajarostaghi, S.S. Numerical evaluation of the effect of using twisted tapes as turbulator with various geometries in both sides of a double-pipe heat exchanger. J. Therm. Anal. Calorim. 2020, 140, 1341–1353. [Google Scholar] [CrossRef]
- Kwon, B.; Liebenberg, L.; Jacobi, A.M.; King, W.P. Heat transfer enhancement of internal laminar flows using additively manufactured static mixers. Int. J. Heat Mass Transf. 2019, 137, 292–300. [Google Scholar] [CrossRef]
- Ho, C.J.; Hsieh, Y.J.; Rashidi, S.; Orooji, Y.; Yan, W.M. Thermal-hydraulic analysis for alumina/water nanofluid inside a mini-channel heat sink with latent heat cooling ceiling—An experimental study. Int. Commun. Heat Mass Transf. 2020, 112, 104477. [Google Scholar] [CrossRef]
- Liu, H.L.; Qi, D.H.; Shao, X.D.; Wang, W.D. An experimental and numerical investigation of heat transfer enhancement in annular microchannel heat sinks. Int. J. Therm. Sci. 2019, 142, 106–120. [Google Scholar] [CrossRef]
- Ramalingam, S.; Dhairiyasamy, R.; Govindasamy, M. Assessment of heat transfer characteristics and system physiognomies using HYBRID nanofluids in an automotive radiator. Chem. Eng. Process. Process. Intensif. 2020, 107886. [Google Scholar] [CrossRef]
- Qi, C.; Fan, F.; Pan, Y.; Liu, M.; Yan, Y. Effects of turbulator with round hole on the thermo-hydraulic performance of nanofluids in a triangle tube. Int. J. Heat Mass Transf. 2020, 146, 118897. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Esfahani, J.A. Numerical investigation of heat transfer enhancement inside heat exchanger tubes fitted with perforated hollow cylinders. Int. J. Therm. Sci. 2020, 147, 106153. [Google Scholar] [CrossRef]
- Rahbarshahlan, S.; Esmaeilzadeh, E.; Khosroshahi, A.R.; Bakhshayesh, A.G. Numerical simulation of fluid flow and heat transfer in microchannels with patterns of hydrophobic/hydrophilic walls. Eur. Phys. J. Plus 2020, 135, 157. [Google Scholar] [CrossRef]
- Jamesahar, E.; Sabour, M.; Shahabadi, M.; Mehryan, S.A.; Ghalambaz, M. Mixed convection heat transfer by nanofluids in a cavity with two oscillating flexible fins: A fluid-structure interaction approach. Appl. Math. Model. 2020, 82, 72–90. [Google Scholar] [CrossRef]
- Benabderrahmane, A.; Benazza, A.; Hussein, A.K. Heat transfer enhancement analysis of tube receiver for parabolic trough solar collector with central corrugated insert. J. Heat Transf. 2020, 142. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Valipour, M.S. Experimental study on the heat transfer enhancement in helically corrugated tubes under the non-uniform heat flux. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Chakraborty, O.; Das, B.; Gupta, R.; Debbarma, S. Heat transfer enhancement analysis of parabolic trough collector with straight and helical absorber tube. Therm. Sci. Eng. Prog. 2020, 20, 100718. [Google Scholar] [CrossRef]
- Amani, K.; Ebrahimpour, M.; Akbarzadeh, S.; Valipour, M.S. The utilization of conical strip inserts in a parabolic trough collector. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Khan, M.S.; Yan, M.; Ali, H.M.; Amber, K.P.; Bashir, M.A.; Akbar, B.; Javed, S. Comparative performance assessment of different absorber tube geometries for parabolic trough solar collector using nanofluid. J. Therm. Anal. Calorim. 2020, 142, 2227–2241. [Google Scholar] [CrossRef]
- Saedodin, S.; Zaboli, M.; Ajarostaghi, S.S.M. Hydrothermal analysis of heat transfer and thermal performance characteristics in a parabolic trough solar collector with Turbulence-Inducing elements. Sustain. Energy Technol. Assess. 2021, 46, 101266. [Google Scholar] [CrossRef]
- Vasanthi, P.; Reddy, G.J.C. Experimental Investigations on Heat Transfer and Friction Factor of Hybrid Nanofliud Equiped with Angular Twisted Strip Inserts in a Parabolic Trough Solar Collector under Turbulent Flow. Int. J. Innov. Sci. Eng. Technol. 2021, 8, 315–336. [Google Scholar]
- Chakraborty, O.; Roy, S.; Das, B.; Gupta, R. Effects of helical absorber tube on the energy and exergy analysis of parabolic solar trough collector—A computational analysis. Sustain. Energy Technol. Assess. 2021, 44, 101083. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Valipour, M.S. The thermo-hydraulic performance of a parabolic trough collector with helically corrugated tube. Sustain. Energy Technol. Assess. 2021, 44, 101013. [Google Scholar] [CrossRef]
- Peng, H.; Li, M.; Hu, F.; Feng, S. Performance analysis of absorber tube in parabolic trough solar collector inserted with semi-annular and fin shape metal foam hybrid structure. Case Stud. Therm. Eng. 2021, 101112. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Farshad, S.A. Nanofluid flow inside a solar collector utilizing twisted tape considering exergy and entropy analysis. Renew. Energy 2019, 141, 246–258. [Google Scholar] [CrossRef]
- Moghaddaszadeh, N.; Esfahani, J.A.; Mahian, O. Performance enhancement of heat exchangers using eccentric tape inserts and nanofluids. J. Therm. Anal. Calorim. 2019, 137, 865–877. [Google Scholar] [CrossRef]
- Ghasemi, S.E.; Ranjbar, A.A. Thermal performance analysis of solar parabolic trough collector using nanofluid as working fluid: A CFD modelling study. J. Mol. Liq. 2016, 222, 159–166. [Google Scholar] [CrossRef]
- Reddy, K.S.; Ravi, K.K.; Satyanarayana, G.V. Numerical Investigation of Energy-Efficient Receiver for Solar Parabolic Trough Concentrator. Heat Transf. Eng. 2008, 29, 961–972. [Google Scholar] [CrossRef]
- He, W.; Toghraie, D.; Lotfipour, A.; Pourfattah, F.; Karimipour, A.; Afrand, M. Effect of twisted-tape inserts and nanofluid on flow field and heat transfer characteristics in a tube. Int. Commun. Heat Mass Transf. 2020. [Google Scholar] [CrossRef]
- Eiamsa-Ard, S.; Thianpong, C.; Promvonge, P. Experimental investigation of heat transfer and flow friction in a circular tube fitted with regularly spaced twisted tape elements. Int. Commun. Heat Mass Transf. 2006, 33, 1225–1233. [Google Scholar] [CrossRef]
- Fluent, A.N. 18.2, Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zaboli, M.; Nourbakhsh, M.; Ajarostaghi, S.S. Numerical evaluation of the heat transfer and fluid flow in a corrugated coil tube with lobe-shaped cross-section and two types of spiral twisted tape as swirl generator. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Saedodin, S.; Zaboli, M.; Rostamian, S.H. Effect of twisted turbulator and various metal oxide nanofluids on the thermal performance of a straight tube: Numerical study based on experimental data. Chem. Eng. Process. Process. Intensif. 2020, 158, 108106. [Google Scholar] [CrossRef]
- Baragh, S.; Shokouhmand, H.; Ajarostaghi, S.S.M.; Nikian, M. An experimental investigation on forced convection heat transfer of single-phase flow in a channel with different arrangements of porous media. Int. J. Therm. Sci. 2018, 134, 370–379. [Google Scholar] [CrossRef]
- Baragh, S.; Shokouhmand, H.; Ajarostaghi, S.S.M. Experiments on mist flow and heat transfer in a tube fitted with porous media. Int. J. Therm. Sci. 2019, 137, 388–398. [Google Scholar] [CrossRef]
- Karouei, S.H.H.; Ajarostaghi, S.S.M.; Gorji-Bandpy, M.; Fard, S.R.H. Laminar heat transfer and fluid flow of two various hybrid nanofluids in a helical double-pipe heat exchanger equipped with an innovative curved conical turbulator. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Hamedani, F.A.; Ajarostaghi, S.S.M.; Hosseini, S.A. Numerical evaluation of the effect of geometrical and operational parameters on thermal performance of nanofluid flow in convergent-divergent tube. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Moghadam, H.K.; Ajarostaghi, S.S.M.; Poncet, S. Extensive numerical analysis of the thermal performance of a corrugated tube with coiled wire. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Outokesh, M.; Ajarostaghi, S.S.M.; Bozorgzadeh, A.; Sedighi, K. Numerical evaluation of the effect of utilizing twisted tape with curved profile as a turbulator on heat transfer enhancement in a pipe. J. Therm. Anal. Calorim. 2020, 140, 1537–1553. [Google Scholar] [CrossRef]
- Olfian, H.; Sheshpoli, A.Z.; Ajarostaghi, S.S.M. Numerical evaluation of the thermal performance of a solar air heater equipped with two different types of baffles. Heat Transf. 2020, 49, 1149–1169. [Google Scholar] [CrossRef]
- Ajarostaghi, S.S.M.; Delavar, M.A.; Poncet, S. Thermal mixing, cooling and entropy generation in a micromixer with a porous zone by the lattice Boltzmann method. J. Therm. Anal. Calorim. 2020, 140, 1321–1339. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Zou, B.; Dong, J.; Yao, Y.; Jiang, Y. An experimental investigation on a small-sized parabolic trough solar collector for water heating in cold areas. Appl. Energy 2016, 163, 396–407. [Google Scholar] [CrossRef]







| Author | Year | Method (Exp/Num) | Inserts | Result |
|---|---|---|---|---|
| Kareem et al. [18] | 2015 | Experimental and Numerical | Spirally corrugated tube | The tube of higher severity index has the best thermal performance. |
| Lu et al. [19] | 2016 | Numerical | Vortex generator | Their results pointed out that holes close to the leading-edge give better efficiency. |
| Mashoofi et al. [20] | 2017 | Experimental | Helically coiled | Findings showed that the use of a turbulator increases Nusselt number around 8–32%. |
| Aghaei et al. [21] | 2018 | Experimental and Numerical | Horizontal and vertical elliptic baffles | The heat exchange attains the utmost at the arrangement angle of 15°. |
| Noorbakhsh et al. [22] | 2019 | Numerical | Twisted-tapes | The enhancement of fin number goes up the heat exchange. |
| Kwon et al. [23] | 2019 | Numerical | static mixers | Static mixers registered heat transfer coefficient an increase of about 100%. |
| Ho et al. [24] | 2019 | Experimental | Mini-channel | Conforming outcomes, the friction factor reduced as the temperature of the inlet rises. |
| Liu et al. [25] | 2019 | Experimental | Heat sinks | Heat exchange had a peak at θ = 20° and β = 0.8. |
| Ramalingam et al. [26] | 2020 | Experimental | Automotive radiator | Enhancement heat dissipation was got for nanofluid at 0.8. |
| Qi et al. [27] | 2020 | Experimental | Triangle tube | Triangular tubes have the most positive impact on the rate of increase of heat exchange. |
| Nakhchi et al. [28] | 2020 | Numerical | Perforated hollow cylinders | Outcomes saw that the resistance of flow can be decreased up to 86.2% with go upping the perforated index. |
| Rahbarshahln et al. [29] | 2020 | Numerical | Microchannels | The use of hydrophobic models could decline the required power fluid pump up to 69% and go up heat flux up to 15%. |
| Jamesahar et al. [30] | 2020 | Numerical | Flexible fins | Due to the oscillation of the fins, the heat exchange rate goes up. |
| Benabderrahmane et al. [31] | 2020 | Numerical | Central corrugated insert | The overall heat transfer performance was achieved in the range of 1.3–2.6. |
| Akbarzadeh and Valipour [32] | 2020 | Experimental | Helically corrugated tube | The maximum obtained thermal performance (2.29) belongs to the case with pitch length and roughness height of 3 mm and 1.5 mm, respectively. |
| Chakraborty et al. [33] | 2020 | Numerical | Helical absorber tube | Thermal efficiency and exergy rise by 1–10% and 0.2–3.2%, correspondingly. |
| Amani et al. [34] | 2020 | Numerical | Conical strip inserts | The overall thermal–hydraulic performance was obtained in the range of 0.679–1.107. |
| Khan et al. [35] | 2020 | Numerical | Absorber tube with twisted tape insert and tube with longitudinal fins | Thermal efficiency of the cases with twisted tape insert, tube with internal fins, and plain tube are by 72.26%, 72.10% and 71.09%, respectively. |
| Saedodin et al. [36] | 2021 | Numerical | Turbulence-Inducing elements | The maximum achieved thermal efficiency was by 29%. |
| Vasanthi and Jaya Chandra reddy [37] | 2021 | Experimental | Angular twisted strip inserts | The obtained enhancement efficiency was in the range of 145–215%. |
| Chakraborty et al. [38] | 2021 | Numerical | Helical absorber tube | Thermal efficiency and exergy rises by 4–10%, and 4–5%, correspondingly. |
| Akbarzadeh and Valipour [39] | 2021 | Numerical | Helically corrugated tube | The thermal performance shows a growth of 26–176%. |
| Peng et al. [40] | 2021 | Experimental and Numerical | Semi-annular and fin shape metal foam hybrid structure | Performance evaluation criteria augmentation, total entropy generation decrease in addition to exergetic efficiency growth maximally reach 360, 93.3 and 10.2%, correspondingly. |
| Parameters | Value | |
|---|---|---|
| Diameter of inner the tube | D1 | 30 mm |
| Diameter of outer the tube | D2 | 60 mm |
| Length of the tube | L | 2000 mm |
| Height of the fins | H | 10 mm |
| Thickness of the fins | th | 5 mm |
| Helix pitch of the fins | P | 500 mm |
| Helical angle of the fins | α | 180 ° |
| Fluid (Water) | Pipe (Steel) | Property |
|---|---|---|
| 4182 | 502 | Specific Heat [J/(kg·K)] |
| 0.6 | 16 | Thermal Conductivity [W/(m·K)] |
| 998.2 | 7881.8 | Density [kg/m3] |
| 0.001003 | − | Viscosity [kg/m·s] |
| Nusselt Number Error | Grid Number |
|---|---|
| 17.2% | 65421 |
| 9.04% | 121470 |
| 2.13% | 164957 |
| 1.98% | 235712 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaboli, M.; Mousavi Ajarostaghi, S.S.; Saedodin, S.; Saffari Pour, M. Thermal Performance Enhancement Using Absorber Tube with Inner Helical Axial Fins in a Parabolic Trough Solar Collector. Appl. Sci. 2021, 11, 7423. https://doi.org/10.3390/app11167423
Zaboli M, Mousavi Ajarostaghi SS, Saedodin S, Saffari Pour M. Thermal Performance Enhancement Using Absorber Tube with Inner Helical Axial Fins in a Parabolic Trough Solar Collector. Applied Sciences. 2021; 11(16):7423. https://doi.org/10.3390/app11167423
Chicago/Turabian StyleZaboli, Mohammad, Seyed Soheil Mousavi Ajarostaghi, Seyfolah Saedodin, and Mohsen Saffari Pour. 2021. "Thermal Performance Enhancement Using Absorber Tube with Inner Helical Axial Fins in a Parabolic Trough Solar Collector" Applied Sciences 11, no. 16: 7423. https://doi.org/10.3390/app11167423
APA StyleZaboli, M., Mousavi Ajarostaghi, S. S., Saedodin, S., & Saffari Pour, M. (2021). Thermal Performance Enhancement Using Absorber Tube with Inner Helical Axial Fins in a Parabolic Trough Solar Collector. Applied Sciences, 11(16), 7423. https://doi.org/10.3390/app11167423








