CAD/CAM System for Additive Manufacturing with a Robust and Efficient Topology Optimization Algorithm Based on the Function Representation
Abstract
:1. Introduction
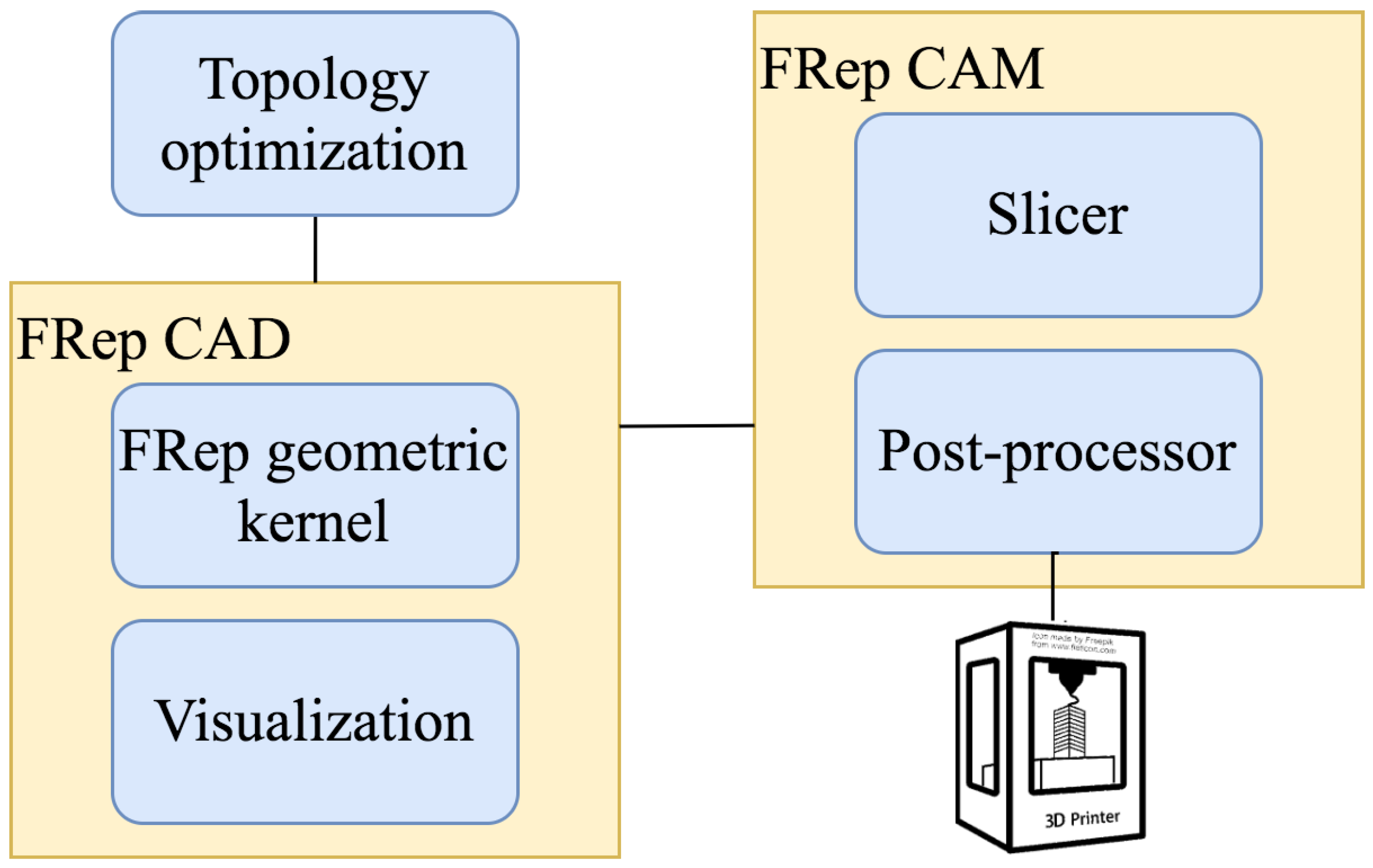
2. Software Structure and Methods
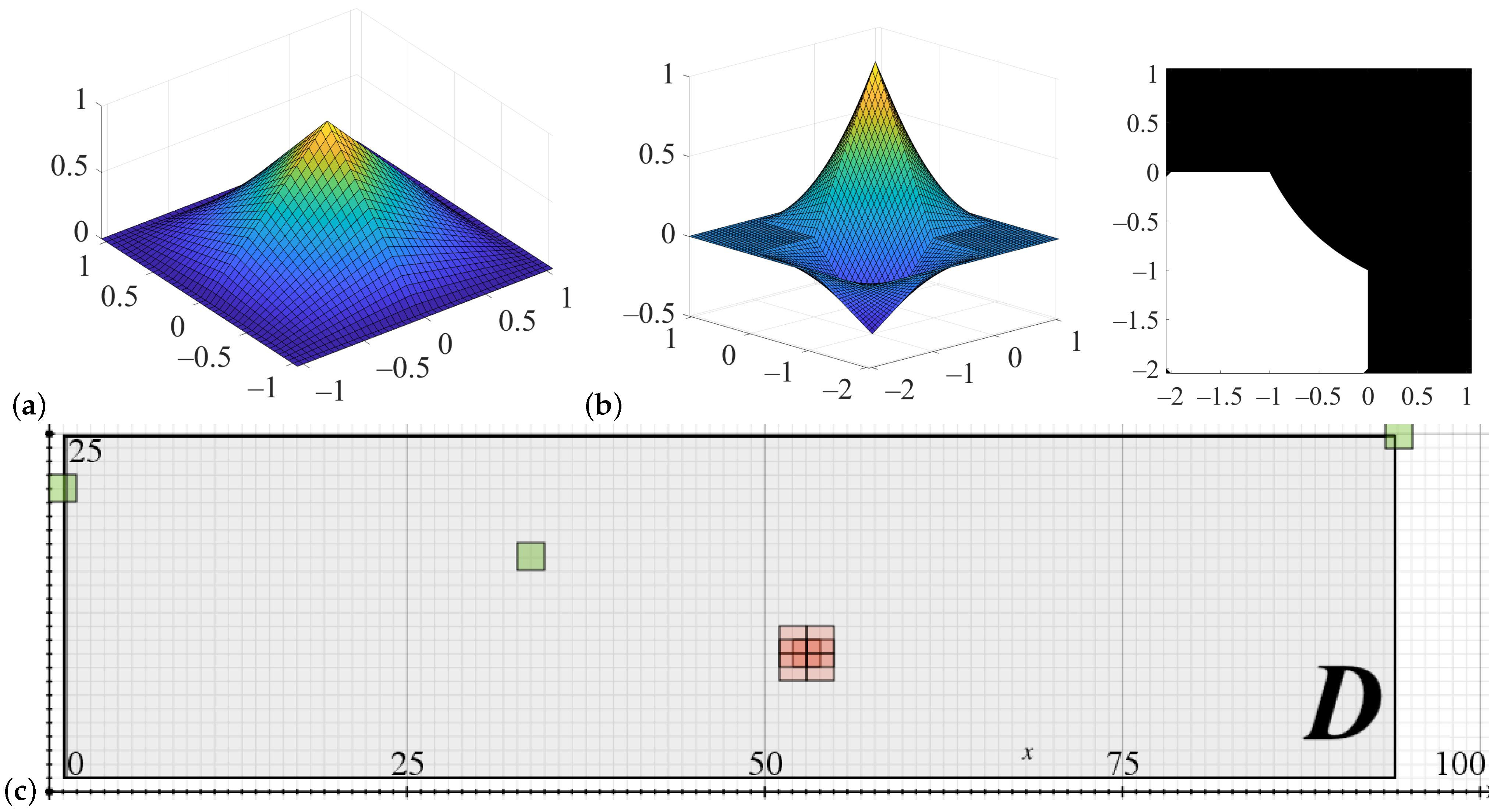
2.1. Topology Optimization
| Algorithm 1: The proposed topology optimization algorithm. |
| Step 1. Define the number of grid elements in the rectangular domain ; Step 2. Initialize coefficients of the bilinear spline; Step 3. Define boundary conditions for FEM analysis; Step 4. Initialize parameters of the optimization loop; Step 5. Perform FEM analysis of the domain; Step 6. If the algorithm converges, then quit, else update and go to Step 5. |
2.2. FRep Geometric Kernel
2.3. Visualization
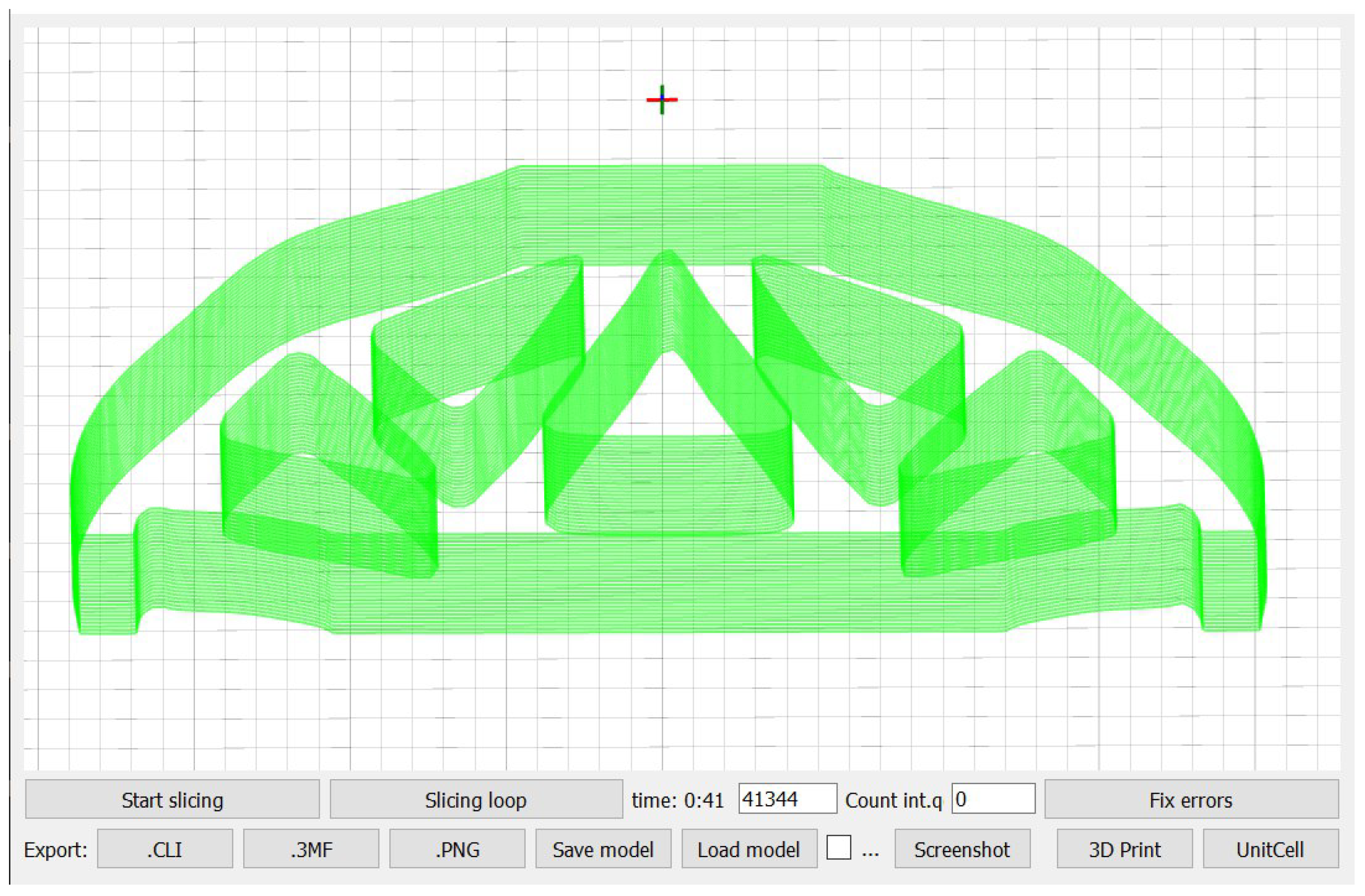
2.4. Direct Slicing
- Slicing of the model.
- Contour extraction (contouring).
- Generation of the supports and infilling.
- Generation of the management protocol for the additive manufacturing equipment.
2.5. 3D Printing
2.6. Experimental Validation
3. Results and Discussion
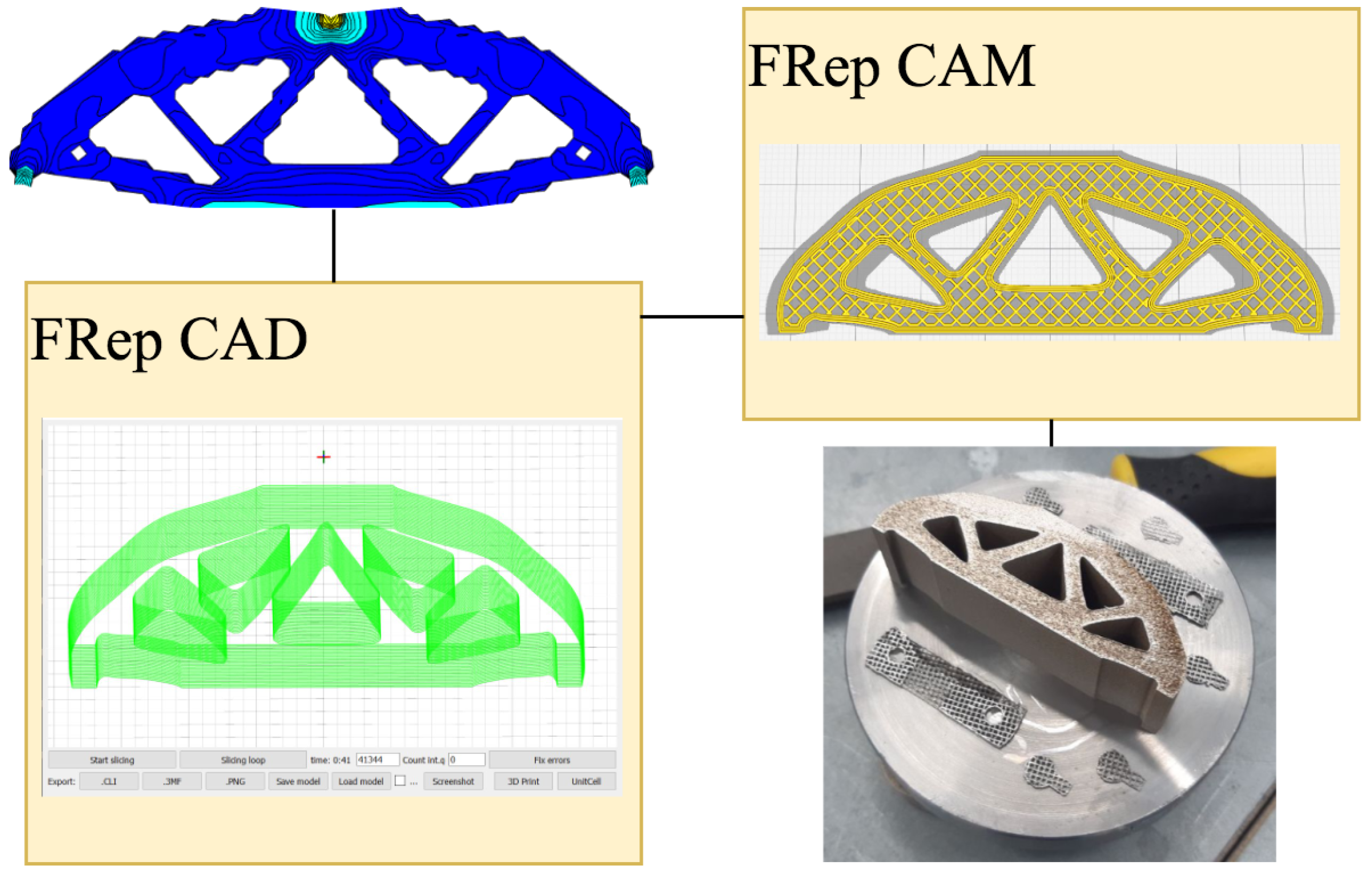
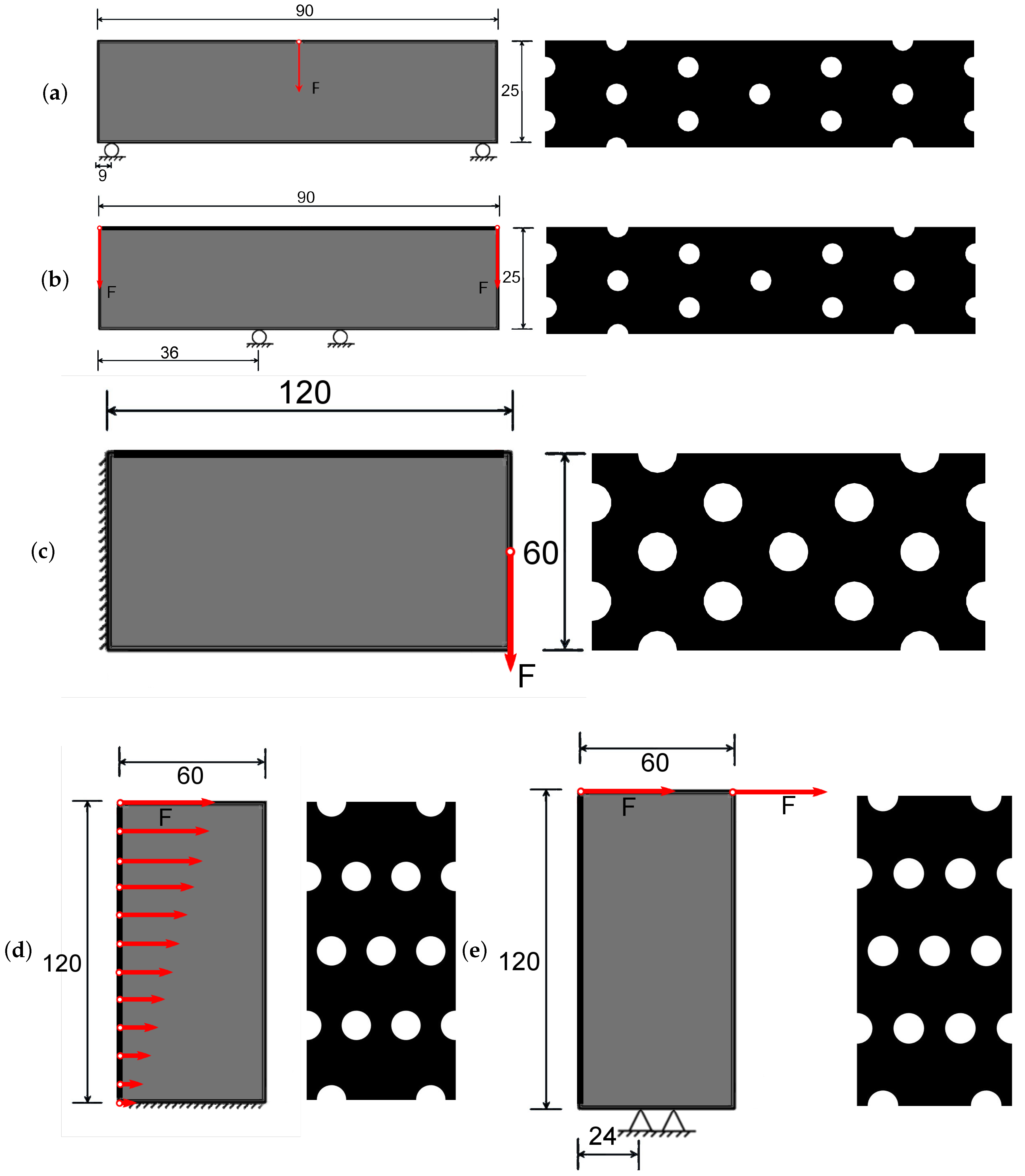
3.1. Modifications of the Topology Optimization Algorithm
3.2. The Developed FRep CAD/CAM System
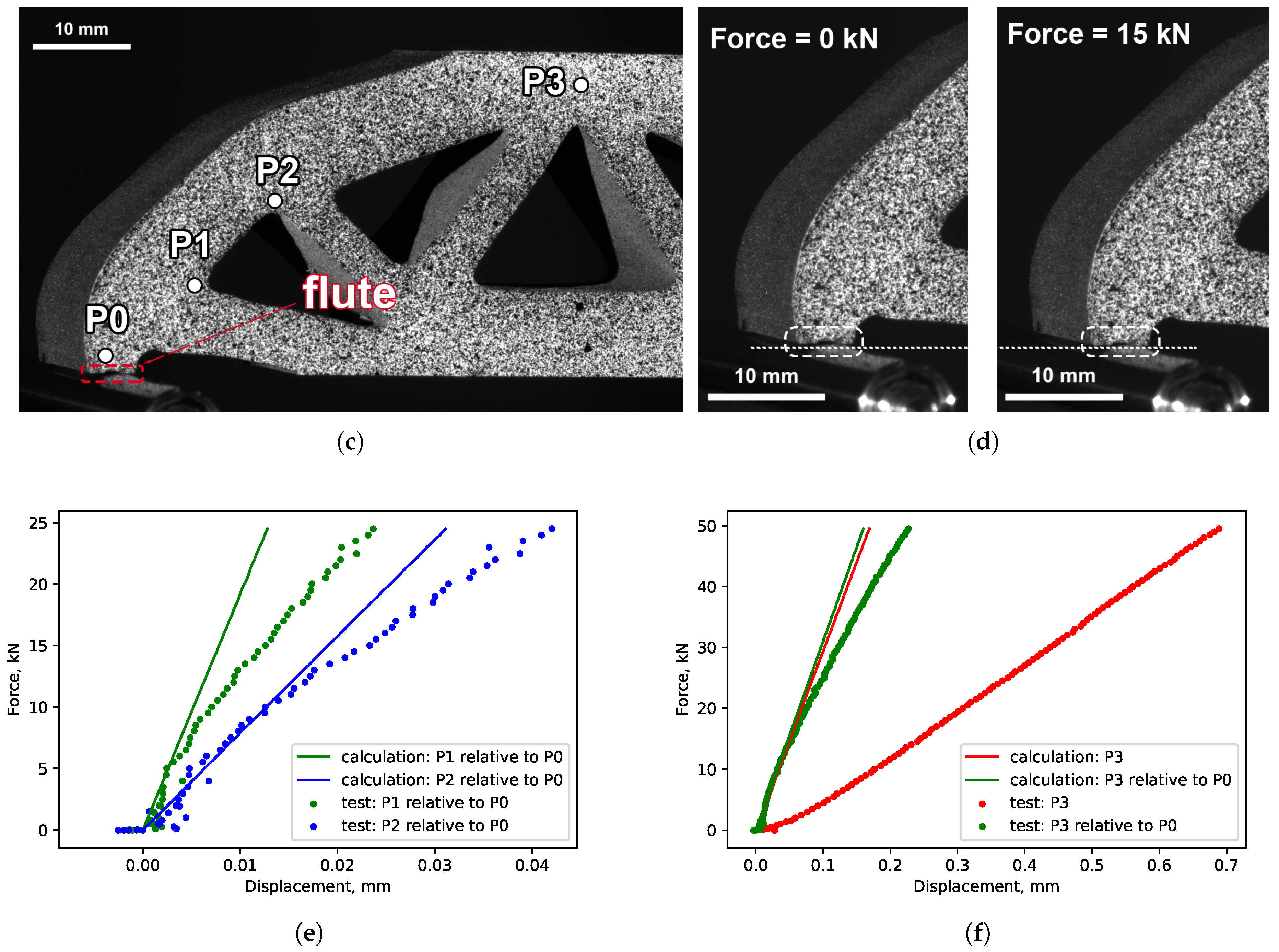
3.3. Results of the Experimental Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| BRep | Boundary representation |
| CAD | Computer-aided design |
| CAM | Computer-aided manufacturing |
| CNC | computer numerical control |
| DLP | Digital light processing |
| DMD | Direct metal deposition |
| FFF | Fused filament fabrication |
| FRep | Function representation |
| MS | Marching squares |
| PDE | Partial differential equations |
| SIMP | Solid isotropic material with penalization |
Appendix A. MATLAB Implementation of the Optimization Algorithm


Appendix B. Modifications of the Optimization Algorithm











References
- Zhang, B.; Goel, A.; Ghalsasi, O.; Anand, S. CAD-based design and pre-processing tools for additive manufacturing. J. Manuf. Syst. 2019, 52, 227–241. [Google Scholar] [CrossRef]
- Gisario, A.; Kazarian, M.; Martina, F.; Mehrpouya, M. Metal additive manufacturing in the commercial aviation industry: A review. J. Manuf. Syst. 2019, 53, 124–149. [Google Scholar] [CrossRef]
- Kumar, V.; Dutta, D. An assessment of data formats for layered manufacturing. Adv. Eng. Softw. 1997, 28, 151–164. [Google Scholar] [CrossRef]
- Schumacher, C.; Bickel, B.; Rys, J.; Marschner, S.; Daraio, C.; Gross, M. Microstructures to Control Elasticity in 3D Printing. ACM Trans. Graph. 2015, 34. [Google Scholar] [CrossRef] [Green Version]
- Vilbrandt, C.; Pasko, G.; Pasko, A.; Fayolle, P.A.; Vilbrandt, T.; Goodwin, J.R.; Goodwin, J.M.; Kunii, T.L. Cultural Heritage Preservation Using Constructive Shape Modeling. Comput. Graph. Forum 2004, 23, 25–41. [Google Scholar] [CrossRef]
- Pasko, A.; Adzhiev, V.; Sourin, A.; Savchenko, V. Function representation in geometric modeling: Concepts, implementation and applications. Vis. Comput. 1995, 11, 429–446. [Google Scholar] [CrossRef]
- Rvachev, V. Method of R-functions in boundary-value problems. Sov. Appl. Mech. 1975, 11, 345–354. [Google Scholar] [CrossRef]
- Sourin, A.I.; Pasko, A.A. Function representation for sweeping by a moving solid. IEEE Trans. Vis. Comput. Graph. 1996, 2, 11–18. [Google Scholar] [CrossRef]
- Pasko, G.; Pasko, A. Trimming implicit surfaces. Vis. Comput. 2004, 20, 437–447. [Google Scholar] [CrossRef]
- Pasko, G.; Pasko, A.; Kunii, T. Space–time blending. Comput. Animat. Virtual Worlds 2004, 15, 109–121. [Google Scholar] [CrossRef]
- Rvachev, V.L.; Sheiko, T.I.; Shapiro, V. Application of the method of R-functions to integration of differential equations with partial derivatives. Cybern. Syst. Anal. 1999, 35, 1–18. [Google Scholar] [CrossRef]
- Chen, J.; Shapiro, V.; Suresh, K.; Tsukanov, I. Shape optimization with topological changes and parametric control. Int. J. Numer. Methods Eng. 2007, 71, 313–346. [Google Scholar] [CrossRef]
- Gibou, F.; Fedkiw, R.; Osher, S. A review of level-set methods and some recent applications. J. Comput. Phys. 2018, 353, 82–109. [Google Scholar] [CrossRef]
- Van Dijk, N.P.; Maute, K.; Langelaar, M.; Van Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Kang, Z.; Zhang, N. A multi-material level set-based topology and shape optimization method. Comput. Methods Appl. Mech. Eng. 2015, 283, 1570–1586. [Google Scholar] [CrossRef]
- Safonov, A.A. 3D topology optimization of continuous fiber-reinforced structures via natural evolution method. Compos. Struct. 2019, 215, 289–297. [Google Scholar] [CrossRef]
- Goh, G.; Toh, W.; Yap, Y.; Ng, T.; Yeong, W. Additively manufactured continuous carbon fiber-reinforced thermoplastic for topology optimized unmanned aerial vehicle structures. Compos. Part B Eng. 2021, 216, 108840. [Google Scholar] [CrossRef]
- Popov, D.; Maltsev, E.; Fryazinov, O.; Pasko, A.; Akhatov, I. Efficient contouring of functionally represented objects for additive manufacturing. Comput. Aided Des. 2020, 129, 102917. [Google Scholar] [CrossRef]
- Song, Y.; Yang, Z.; Liu, Y.; Deng, J. Function representation based slicer for 3D printing. Comput. Aided Geom. Des. 2018, 62, 276–293. [Google Scholar] [CrossRef]
- Wei, P.; Li, Z.; Li, X.; Wang, M.Y. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Struct. Multidiscip. Optim. 2018, 58, 831–849. [Google Scholar] [CrossRef]
- Lopes, H.; Oliveira, J.B.; de Figueiredo, L.H. Robust adaptive polygonal approximation of implicit curves. Comput. Graph. 2002, 26, 841–852. [Google Scholar] [CrossRef]
- Olszta, P.W.; Umbach, A.; Baker, S.; Fay, J.F.; Tsiombikas, J.; Niehorster, D.C. The Free OpenGL Utility Toolkit. 2019. Available online: http://freeglut.sourceforge.net (accessed on 10 August 2021).
- Jamieson, R.; Hacker, H. Direct slicing of CAD models for rapid prototyping. Rapid Prototyp. J. 1995, 1, 4–12. [Google Scholar] [CrossRef]
- Ultimaker. CuraEngine. 2013. Available online: https://github.com/Ultimaker/CuraEngine (accessed on 10 August 2021).
- Kuzminova, Y.; Firsov, D.; Konev, S.; Dudin, A.; Dagesyan, S.; Akhatov, I.; Evlashin, S. Structure control of 316L stainless steel through an additive manufacturing. Lett. Mater. 2019, 9, 551–555. [Google Scholar] [CrossRef] [Green Version]
- Standard Test Methods for Tension Testing of Metallic Materials; ASTM International Standard: West Conshohocken, PA, USA, 2021.
- Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials; ASTM International Standard: West Conshohocken, PA, USA, 2017.
- Skoltech. FRepCADCAM. 2020. Available online: https://github.com/Torrero/FRepCAM (accessed on 10 August 2021).
- Moore, R. Interval Analysis; Prentice-Hall: Englewood Cliff, NJ, USA, 1966. [Google Scholar]
- Stolfi, J.; Figueiredo, L. An Introduction to Affine Arithmetic. Trends Appl. Comput. Math. 2003, 4, 297–312. [Google Scholar] [CrossRef]
- Digital Materialization Group. HyperFun Project Description. 2014. Available online: http://hyperfun.org/ (accessed on 10 August 2021).
- Maltsev, E.; Popov, D.; Chugunov, S.; Pasko, A.; Akhatov, I. An Accelerated Slicing Algorithm for Frep Models. Appl. Sci. 2021, 11, 6767. [Google Scholar] [CrossRef]
- Safonov, A.; Maltsev, E.; Chugunov, S.; Tikhonov, A.; Konev, S.; Evlashin, S.; Popov, D.; Pasko, A.; Akhatov, I. Design and Fabrication of Complex-Shaped Ceramic Bone Implants via 3D Printing Based on Laser Stereolithography. Appl. Sci. 2020, 10, 7138. [Google Scholar] [CrossRef]
- Safonov, A.; Chugunov, S.; Tikhonov, A.; Gusev, M.; Akhatov, I. Numerical simulation of sintering for 3D-printed ceramics via SOVS model. Ceram. Int. 2019, 45, 19027–19035. [Google Scholar] [CrossRef]


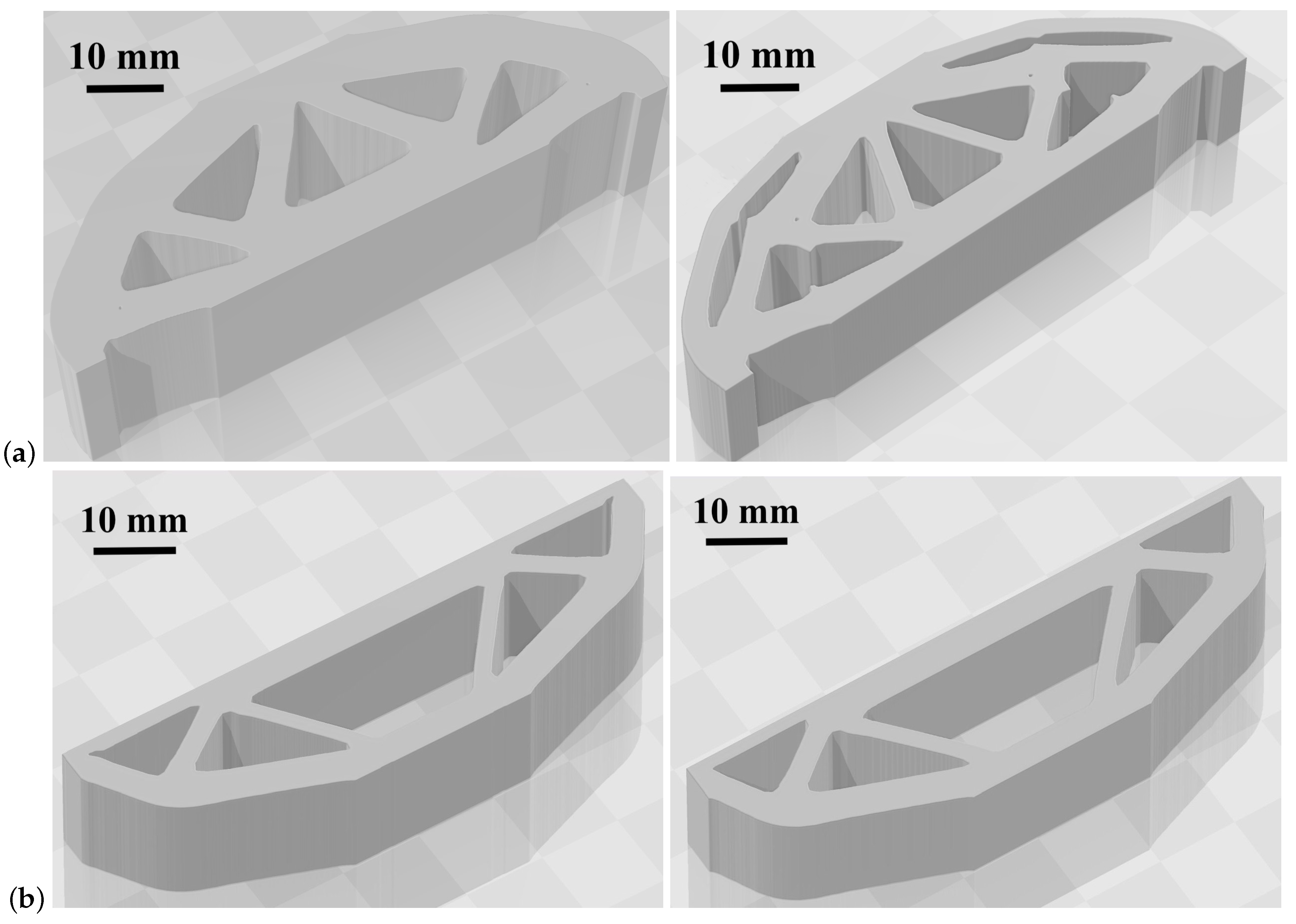
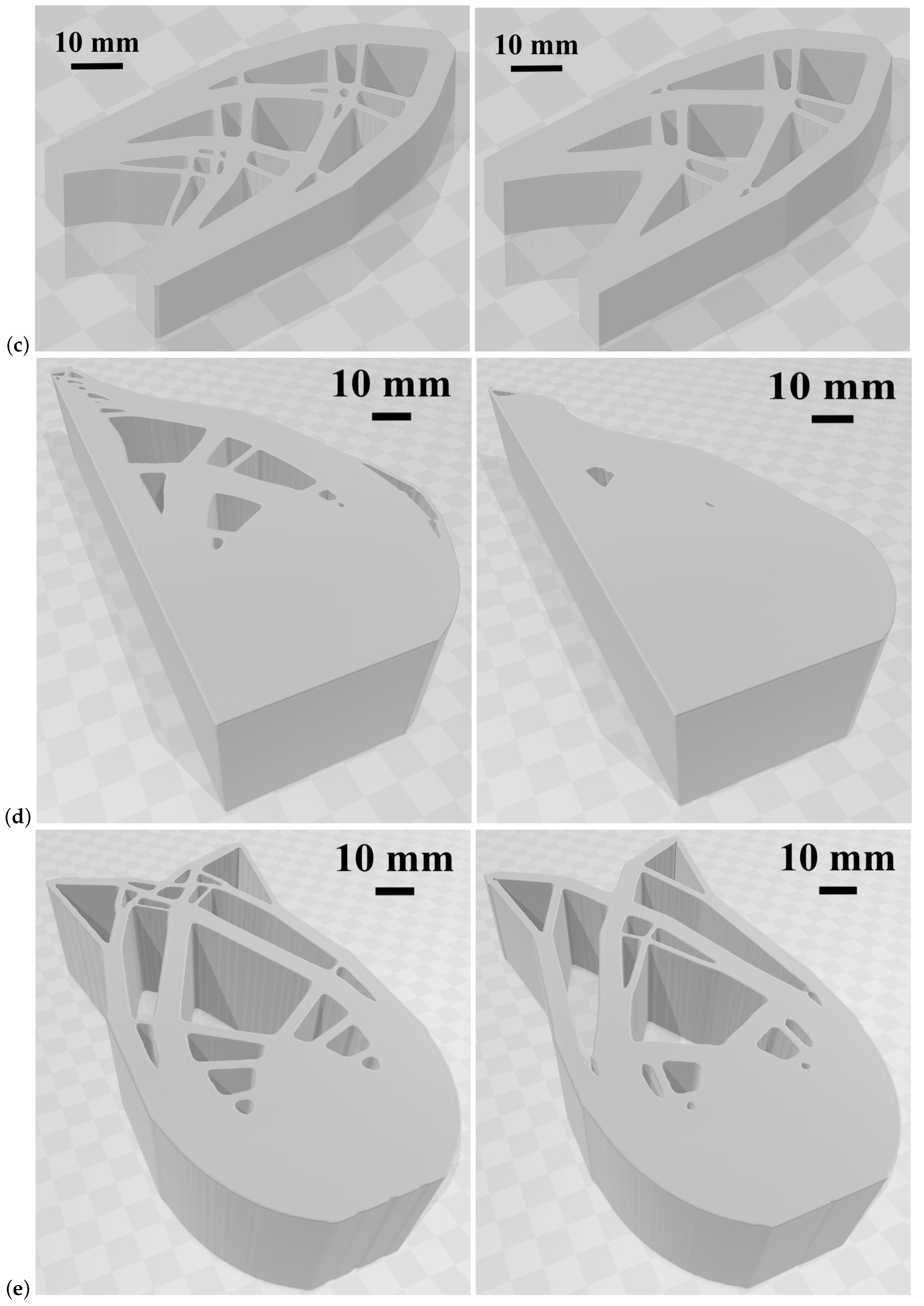


| Test Number | Modified Algorithm, s | Wei’s Algorithm, s |
|---|---|---|
| 1 | 36.8 | 80.8 |
| 2 | 35.2 | 77.3 |
| 3 | 36.1 | 81.7 |
| 4 | 35.9 | 75.8 |
| 5 | 35.2 | 76.6 |
| 6 | 35.9 | 77.3 |
| 7 | 35.4 | 76.2 |
| 8 | 35.5 | 76.4 |
| 9 | 35.9 | 76.1 |
| 10 | 36.3 | 76.8 |
| Average time, s | 35.8 | 77.5 |
| Number of iterations | 213 | 179 |
| Objective function | 1.71 × 10 | 1.71 × 10 |
| Volume | 0.45 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, D.; Kuzminova, Y.; Maltsev, E.; Evlashin, S.; Safonov, A.; Akhatov, I.; Pasko, A. CAD/CAM System for Additive Manufacturing with a Robust and Efficient Topology Optimization Algorithm Based on the Function Representation. Appl. Sci. 2021, 11, 7409. https://doi.org/10.3390/app11167409
Popov D, Kuzminova Y, Maltsev E, Evlashin S, Safonov A, Akhatov I, Pasko A. CAD/CAM System for Additive Manufacturing with a Robust and Efficient Topology Optimization Algorithm Based on the Function Representation. Applied Sciences. 2021; 11(16):7409. https://doi.org/10.3390/app11167409
Chicago/Turabian StylePopov, Dmitry, Yulia Kuzminova, Evgenii Maltsev, Stanislav Evlashin, Alexander Safonov, Iskander Akhatov, and Alexander Pasko. 2021. "CAD/CAM System for Additive Manufacturing with a Robust and Efficient Topology Optimization Algorithm Based on the Function Representation" Applied Sciences 11, no. 16: 7409. https://doi.org/10.3390/app11167409
APA StylePopov, D., Kuzminova, Y., Maltsev, E., Evlashin, S., Safonov, A., Akhatov, I., & Pasko, A. (2021). CAD/CAM System for Additive Manufacturing with a Robust and Efficient Topology Optimization Algorithm Based on the Function Representation. Applied Sciences, 11(16), 7409. https://doi.org/10.3390/app11167409









