Theories and Analysis of Functionally Graded Beams
Abstract
:1. Introduction
1.1. Preliminary Comments
1.2. Functionally Graded Structures
1.2.1. Background
1.2.2. FGM Material Models
1.3. Modified Couple Stress Effects
1.3.1. Background
1.3.2. The Strain Energy Functional
2. Classical Theory of Beams (CBT)
2.1. Kinematics
2.2. Equations of Equilibrium
2.3. Governing Equations in Terms of Displacements
2.4. Exact Solutions
2.4.1. General Solution
2.4.2. Pinned-Hinged Beams
2.4.3. Pinned-Pinned Beams
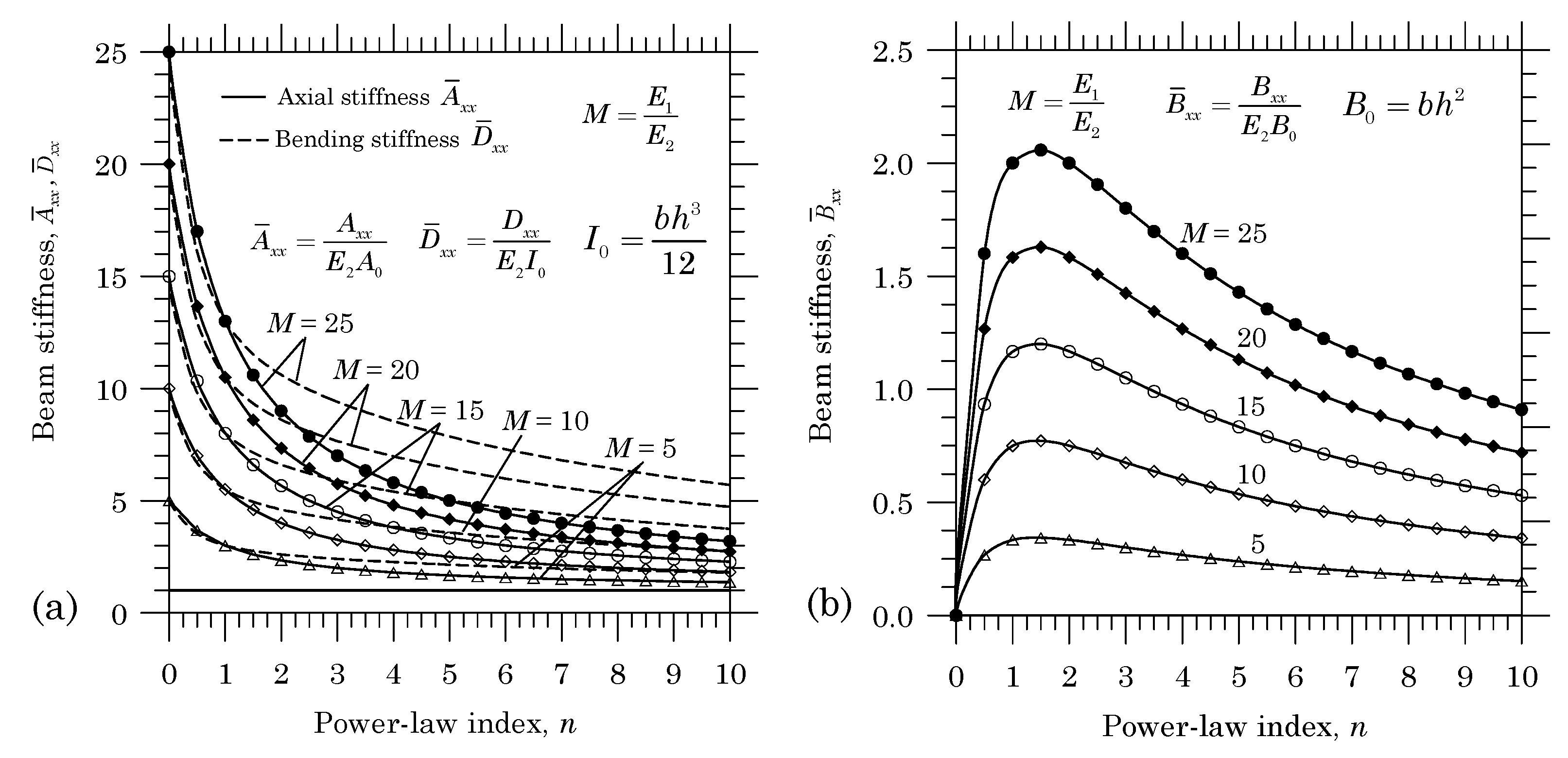
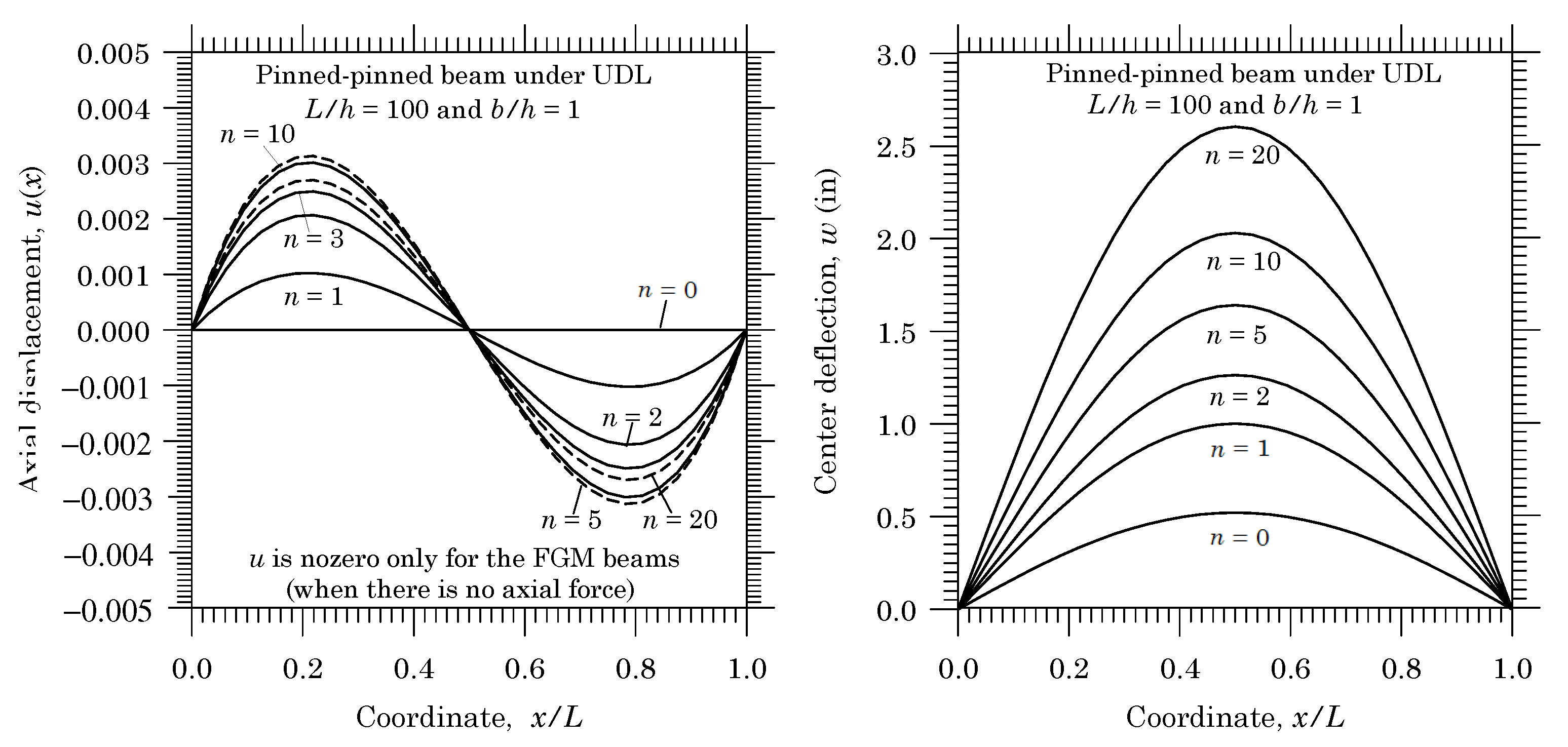
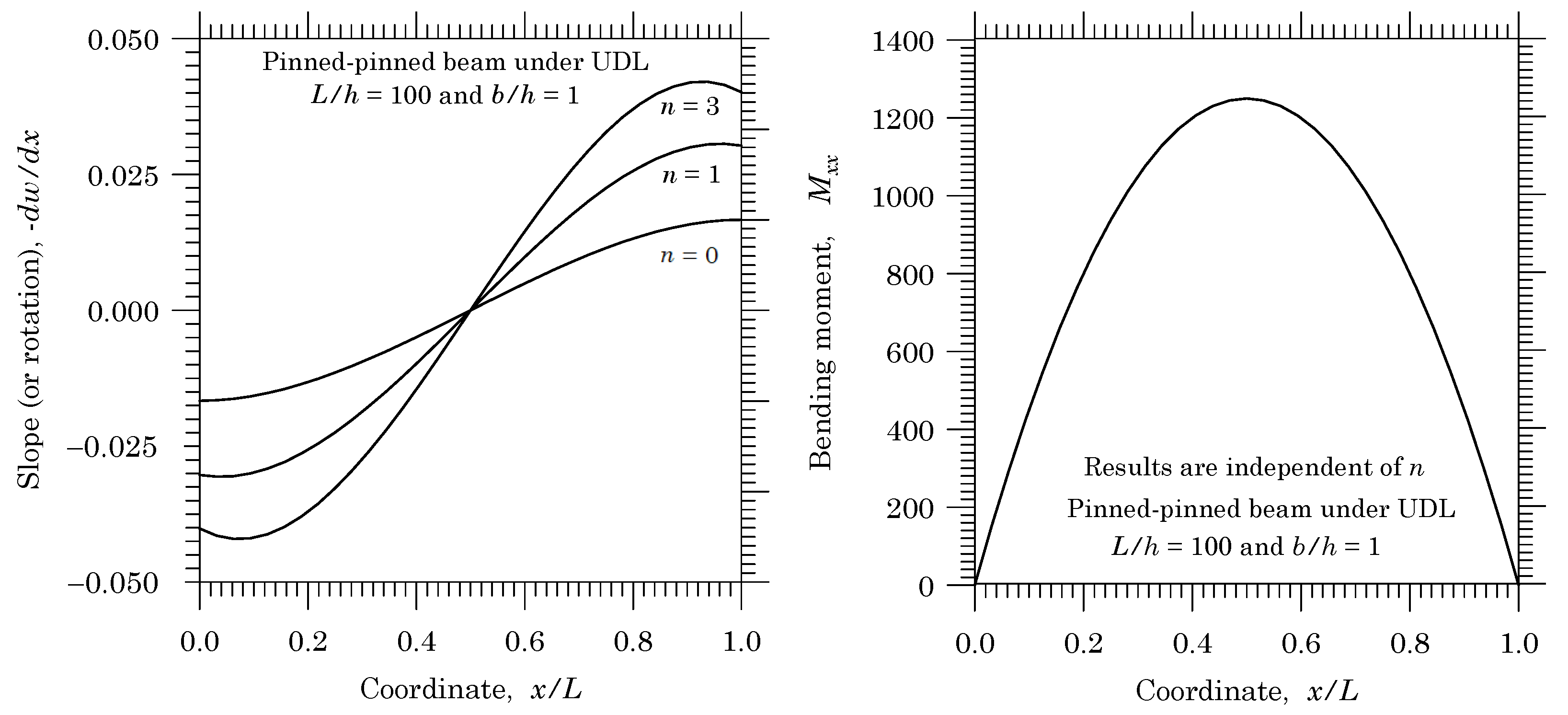
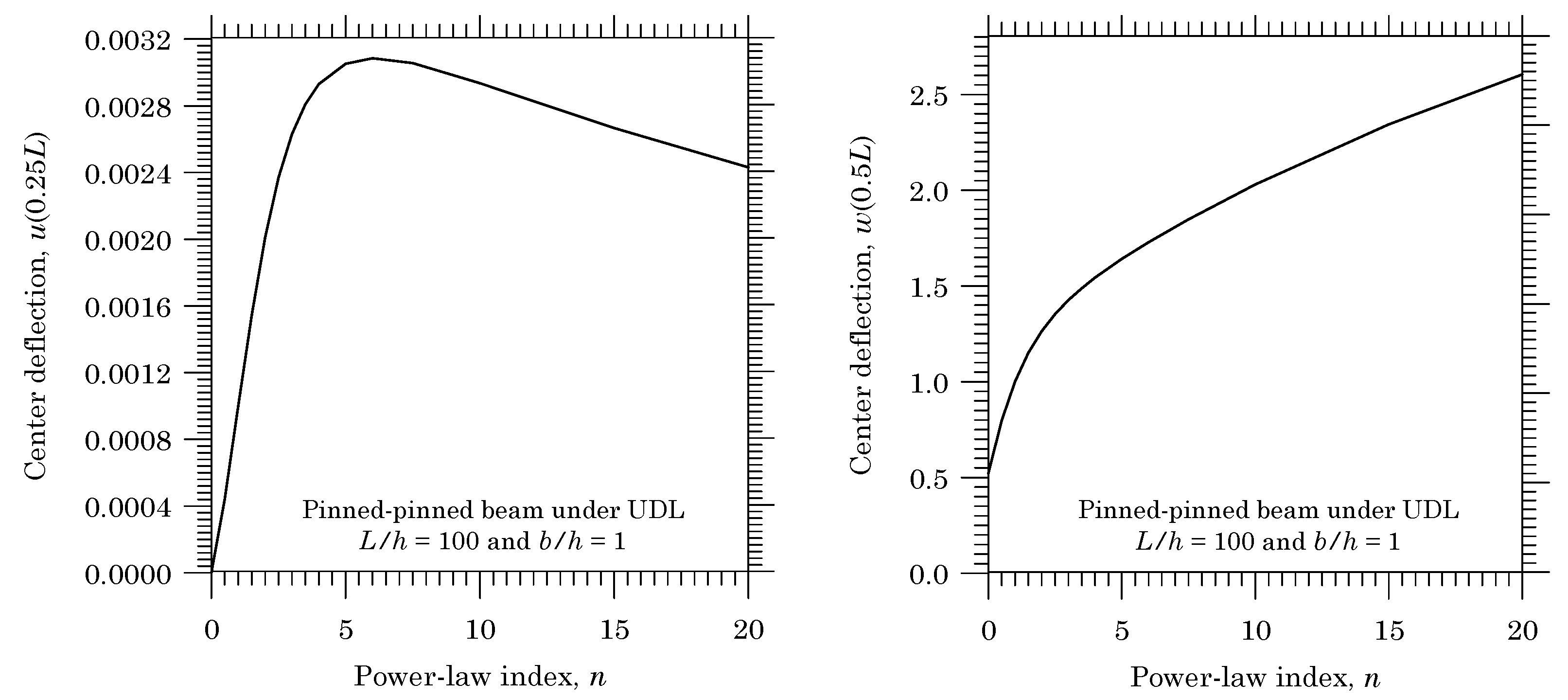
2.4.4. Numerical Results
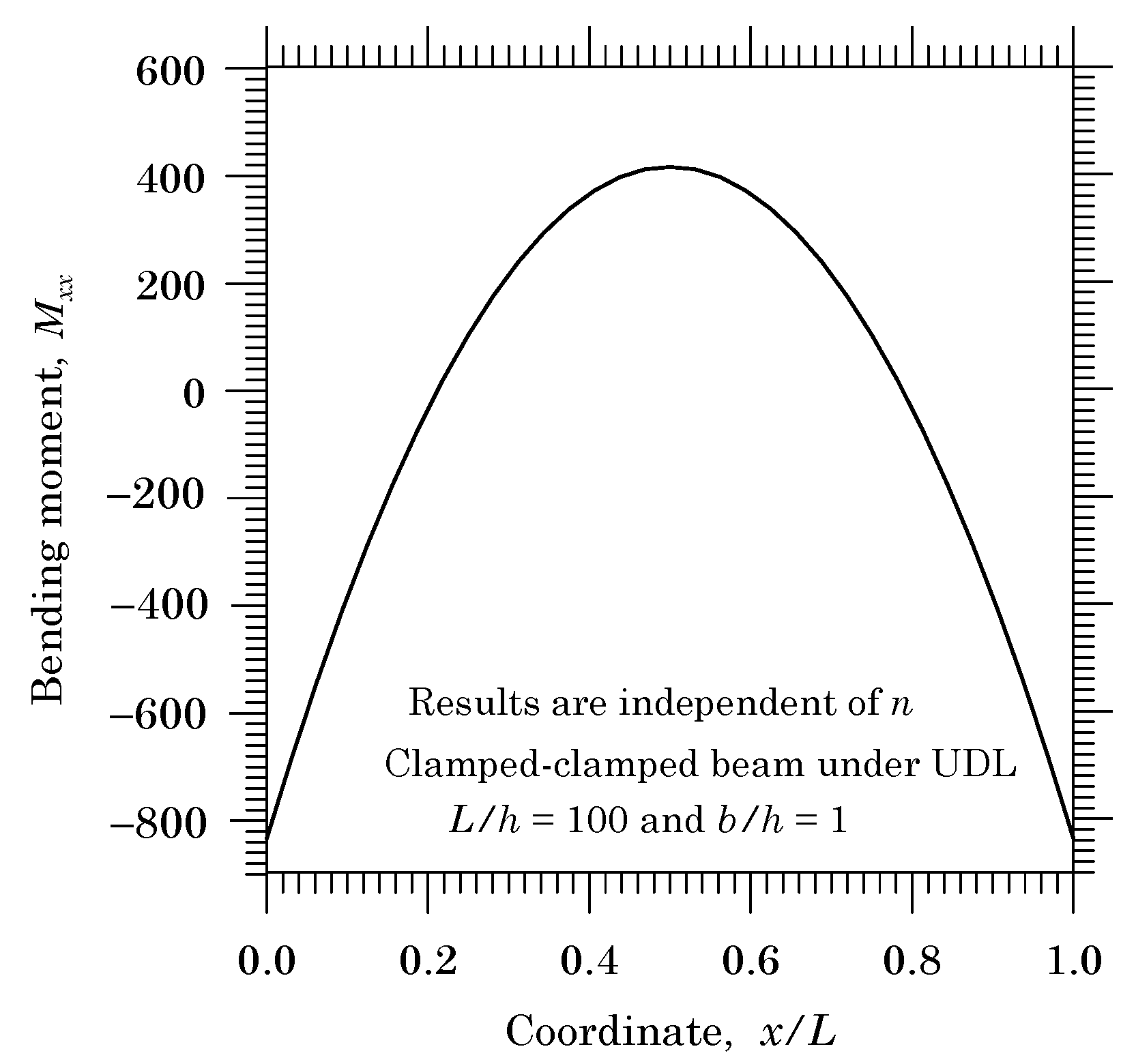
2.4.5. Clamped Beams
3. First-Order Theory of Beams (TBT)
3.1. Preliminary Comments
3.2. Displacements and Strains
3.3. Equations of Equilibrium
3.4. Governing Equations in Terms of Displacements
Beam Constitutive Equations
3.5. Exact Solutions
3.5.1. General Solution
3.5.2. Pinned-Pinned Beams
4. The Third-Order Beam Theory
4.1. Preliminary Comments
4.2. Kinematics
4.3. Equations of Equilibrium
4.4. Beam Constitutive Relations
4.5. Beam Stiffness Coefficients for FGM Beams
4.6. Equilibrium Equations in Terms of the Displacements
4.7. Exact Solutions for Bending
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Timoshenko, S.P. A Course of Easticity Theory. Part 2: Rods and Plates, 2nd ed.; Naukova Dumka: Kiev, Ukraine, 1972. (In Russian) [Google Scholar]
- Timoshenko, S.P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Philos. Mag. 1921, 41, 744–746. [Google Scholar] [CrossRef] [Green Version]
- Ruocco, E.; Reddy, J.N.; Sacco, E. Analytical solution for a 5-parameter displacement model. Int. J. Mech. Sci. 2021, 201, 106496. [Google Scholar] [CrossRef]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Reddy, J.N. A refined nonlinear theory of plates with transverse shear deformation. Int. J. Solids Struct. 1984, 20, 881–896. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Plates and Shells, Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2017. [Google Scholar]
- Heyliger, P.R.; Reddy, J.N. A higher order beam finite element for bending and vibration problems. J. Sound Vib. 1988, 126, 309–326. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modelling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Klusemann, B.; Svendsen, B. Homogenization methods for multi-phase elastic composites: Comparison and benchmarks. Tech. Mech. 2010, 30, 374–386. [Google Scholar]
- Praveen, G.N.; Reddy, J.N. Nonlinear Transient Thermoelastic Analysis of Functionally Graded Ceramic-Metal Plates. J. Solids Struct. 1998, 35, 4457–4476. [Google Scholar] [CrossRef]
- Shen, H.-H.; Wang, Z.X. Assessment of Voigt and Mori–Tanaka models for vibration analysis of functionally graded plates. Compos. Struct. 2012, 94, 2197–2208. [Google Scholar] [CrossRef]
- Reddy, J.N.; Chin, C.D. Thermomechanical Analysis of Functionally Graded Cylinders and Plates. J.Thermal Stress. 1998, 26, 593–626. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of couple-stresses on stress concentrations. Exp. Mech. 1963, 3, 1–7. [Google Scholar] [CrossRef]
- Koiter, W.T. Couple-stresses in the theory of elasticity: I and II. K. Ned. Akad. Van Wet. (R. Neth. Acad. Arts Sci.) 1964, B67, 17–44. [Google Scholar]
- Toupin, R.A. Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 1964, 17, 85–112. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 217–238. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Srinivasa, A.R.; Reddy, J.N. A model for a constrained, finitely deforming, elastic solid with rotation gradient dependent strain energy, and its specialization to von Karman plates and beams. J. Mech. Phys. Solids 2013, 61, 873–885. [Google Scholar] [CrossRef]
- Reddy, J.N.; Srinivasa, A.R. Nonlinear theories of beams and plates accounting for moderate rotations and material length scales. Int. J. Non-Linear Mech. 2014, 66, 43–53. [Google Scholar] [CrossRef]
- Park, S.K.; Gao, X.L. Bernoulli-Euler beam model based on a modified couple stress theory. J. Micromech. Microeng. 2006, 16, 2355–2359. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.L.; Reddy, J.N. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Solids 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.L.; Reddy, J.N. A nonclassical Reddy-Levinson beam model based on a modified couple stress theory. Int. J. Multiscale Comput. 2010, 8, 167–180. [Google Scholar] [CrossRef]
- Araujo dos Santos, J.V.; Reddy, J.N. A model for free vibration analysis of Timoshenko beams with couple stress. Acta Mech. Solida Sin. 2010, 23, 24–248. [Google Scholar]
- Araujo dos Santos, J.V.; Reddy, J.N. Vibration of Timoshenko beams using non-classical elasticity theories. Shock Vib. 2012, 19, 251–256. [Google Scholar] [CrossRef]
- Araujo dos Santos, J.V.; Reddy, J.N. Free vibration and buckling analysis of beams with a modified couple-stress theory. Int. J. Appl. Mech. 2012, 4, 1250056. [Google Scholar] [CrossRef]
- Reddy, J.N. Microstructure-dependent couple stress theories of functionally graded beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Arbind, A.; Reddy, J.N. Nonlinear analysis of functionally graded microstructure-dependent beams. Compos. Struct. 2013, 98, 272–281. [Google Scholar] [CrossRef]
- Arbind, A.; Reddy, J.N.; Srinivasa, A. Modified couple stress-based third-order theory for nonlinear analysis of functionally graded beams. Lat. Am. J. Solids Struct. 2014, 11, 459–487. [Google Scholar] [CrossRef]
- Li, X.; Bhushan, B.; Takashima, K.; Baek, C.W.; Kim, Y.K. Mechanical characterization of micro/nanoscale structures for MEMS/NEMS applications using nanoindentation techniques. Ultramicroscopy 2003, 97, 481–494. [Google Scholar] [CrossRef]
- Pei, J.; Tian, F.; Thundat, T. Glucose biosensor based on the microcantilever. Anal. Chem. 2004, 76, 292–297. [Google Scholar] [CrossRef] [PubMed]
- Khorshidi, M.A. The material length scale parameter used in couple stress theories is not a material constant. Int. J. Eng. Sci. 2018, 133, 15–25. [Google Scholar] [CrossRef]
- Reddy, J.N. Theories and Analyses of Beams and Circular Plates; CRC Press: Boca Raton, FL, USA, 2022; in press. [Google Scholar]
- Reddy, J.N. An Introduction to Nonlinear Finite Element Analysis, 2nd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Timoshenko’s Shear Coefficient for Flexural Vibrations of Beams; Technical Report No. 10, ONR Project NR064-388; Columbia University: New York, NY, USA, 1953. [Google Scholar]
- Cowper, G.R. The shear coefficient in Timoshenko’s beam theory. J. Appl. Mech. 1966, 33, 335–340. [Google Scholar] [CrossRef]
- Levinson, M. A new rectangular beam theory. J. Sound Vib. 1981, 74, 81–87. [Google Scholar] [CrossRef]
- Bickford, W.B. A consistent higher order beam theory. Dev. Theor. Appl. Mech. 1982, 11, 137–150. [Google Scholar]
- Reddy, J.N.; Ruocco, E.; Loya, J.A.; Neves, A.M.A. Theories and Analyses of Functionally Graded Circular Plates. Compos. Part C Open Access 2021, 5, 100166. [Google Scholar] [CrossRef]
- Ruocco, E.; Reddy, J.N. Buckling analysis of elastic–plastic nanoplates resting on a Winkler–Pasternak foundation based on nonlocal third-order plate theory. Int. J. Non-Linear Mech. 2020, 121, 103453. [Google Scholar] [CrossRef]
- Paola, M.D.; Reddy, J.N.; Ruocco, E. On the application of fractional calculus for the formulation of viscoelastic Reddy beam. Meccanica 2020, 55, 1365–1378. [Google Scholar] [CrossRef]
- Ruocco, E.; Reddy, J.N.; Wang, C.M. An enhanced Hencky bar-chain model for bending, buckling and vibration analyses of Reddy beams. Eng. Struct. 2020, 221, 111056. [Google Scholar] [CrossRef]
- Fernandez-Saez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler-Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef] [Green Version]

| n | -CBT | -TBT | w-CBT | w-TBT | ||
|---|---|---|---|---|---|---|
| 0.0 | 0.00000 | 0.00000 | 0.5208 | 0.5210 | 0.01657 | 0.01657 |
| 1.0 | 0.09973 | 0.09973 | 1.0014 | 1.0016 | 0.03062 | 0.03062 |
| 2.0 | 0.20118 | 0.20118 | 1.2635 | 1.2638 | 0.03722 | 0.03722 |
| 3.0 | 0.26301 | 0.26301 | 1.4261 | 1.4265 | 0.04148 | 0.04148 |
| 4.0 | 0.29297 | 0.29297 | 1.5440 | 1.5445 | 0.04495 | 0.04495 |
| 5.0 | 0.30523 | 0.30523 | 1.6415 | 1.6420 | 0.04806 | 0.04806 |
| 6.0 | 0.30850 | 0.30850 | 1.7286 | 1.7292 | 0.05097 | 0.05097 |
| 10.0 | 0.29367 | 0.29367 | 2.0305 | 2.0312 | 0.06131 | 0.06131 |
| 20.0 | 0.24302 | 0.24302 | 2.6047 | 2.6056 | 0.08080 | 0.08080 |
| n | w-CBT | w-TBT | -CBT | -TBT | -CBT | -TBT |
| 0.0 | 0.06510 | 0.06517 | 0.04167 | 0.04193 | 0.05208 | 0.05338 |
| 1.0 | 0.12517 | 0.12529 | 0.08011 | 0.08058 | 0.10014 | 0.10250 |
| 2.0 | 0.15793 | 0.15809 | 0.10108 | 0.10173 | 0.12635 | 0.12960 |
| 3.0 | 0.17827 | 0.17847 | 0.11409 | 0.11409 | 0.14261 | 0.14661 |
| 4.0 | 0.19300 | 0.19324 | 0.12352 | 0.12445 | 0.15440 | 0.15905 |
| 5.0 | 0.20518 | 0.20544 | 0.13132 | 0.13236 | 0.16415 | 0.16935 |
| 6.0 | 0.21608 | 0.21636 | 0.13829 | 0.13943 | 0.17286 | 0.17855 |
| 10.0 | 0.25382 | 0.25417 | 0.16244 | 0.16387 | 0.20305 | 0.21020 |
| 20.0 | 0.32559 | 0.32605 | 0.20838 | 0.21020 | 0.26047 | 0.26957 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reddy, J.N.; Ruocco, E.; Loya, J.A.; Neves, A.M.A. Theories and Analysis of Functionally Graded Beams. Appl. Sci. 2021, 11, 7159. https://doi.org/10.3390/app11157159
Reddy JN, Ruocco E, Loya JA, Neves AMA. Theories and Analysis of Functionally Graded Beams. Applied Sciences. 2021; 11(15):7159. https://doi.org/10.3390/app11157159
Chicago/Turabian StyleReddy, J. N., Eugenio Ruocco, Jose A. Loya, and Ana M. A. Neves. 2021. "Theories and Analysis of Functionally Graded Beams" Applied Sciences 11, no. 15: 7159. https://doi.org/10.3390/app11157159
APA StyleReddy, J. N., Ruocco, E., Loya, J. A., & Neves, A. M. A. (2021). Theories and Analysis of Functionally Graded Beams. Applied Sciences, 11(15), 7159. https://doi.org/10.3390/app11157159









