A Feature-Based Analysis for Time-Series Classification of COVID-19 Incidence in Chile: A Case Study
Abstract
:1. Introduction
- The development of a three-level or three-category prediction model of COVID-19 incidence tested in a Chilean case study. In order to achieve this model of incidence levels, the time series problem was transformed into a classification problem. Four classifiers were then compared to predict these levels to select the one with the best performance;
- Support of the prediction of COVID-19 risk levels, considering an automatic analysis of epidemiological indicators (classifier features or variables) linked to the behavior of the disease in the community. This model is the initial attempt to create a national model that can guide the response and intensity of the active search effort to control COVID-19 according to the trends in communal, regional, and national features in Chile expressed in incidence risk levels.
2. Related Work
3. Materials and Methods
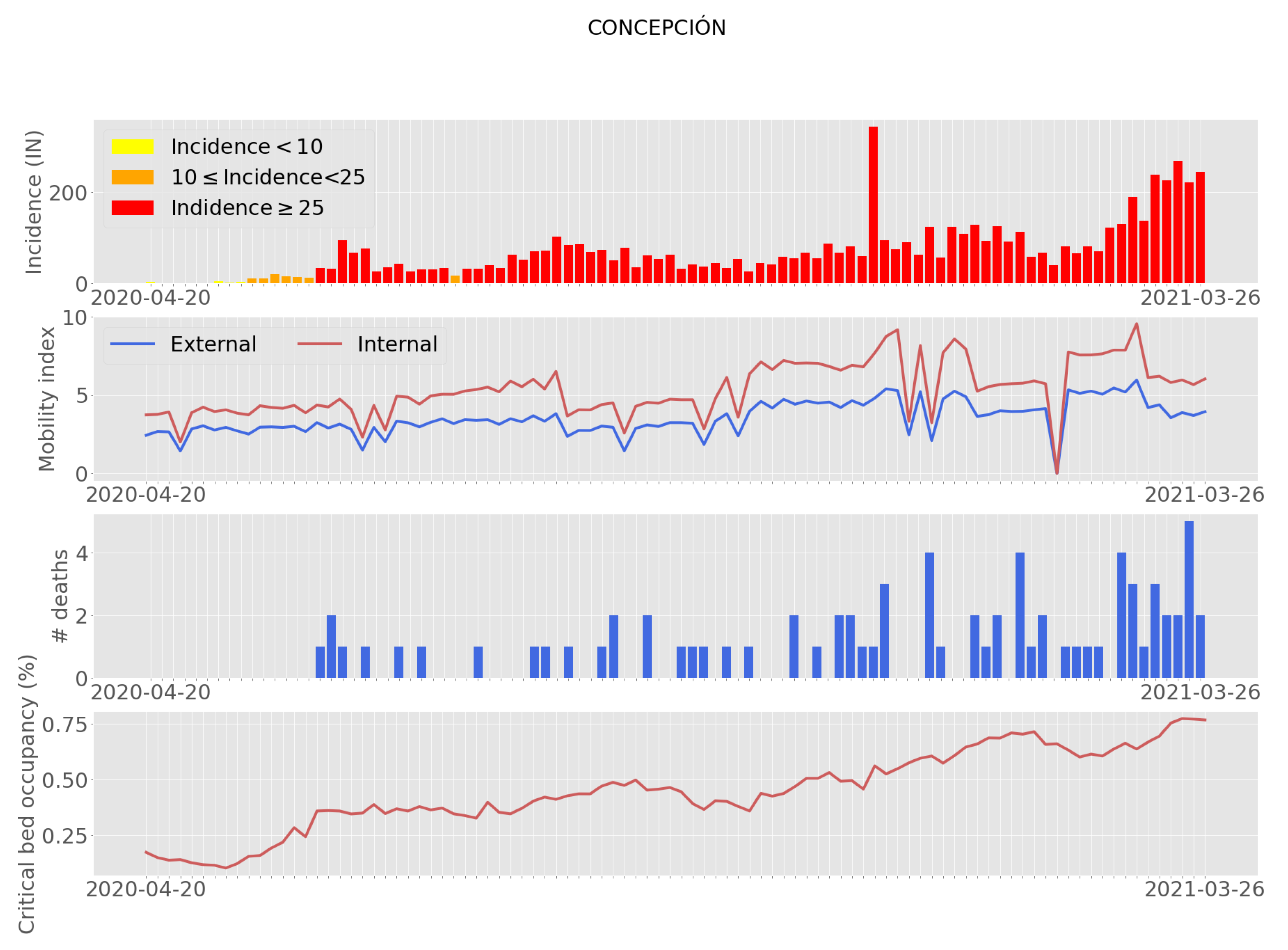
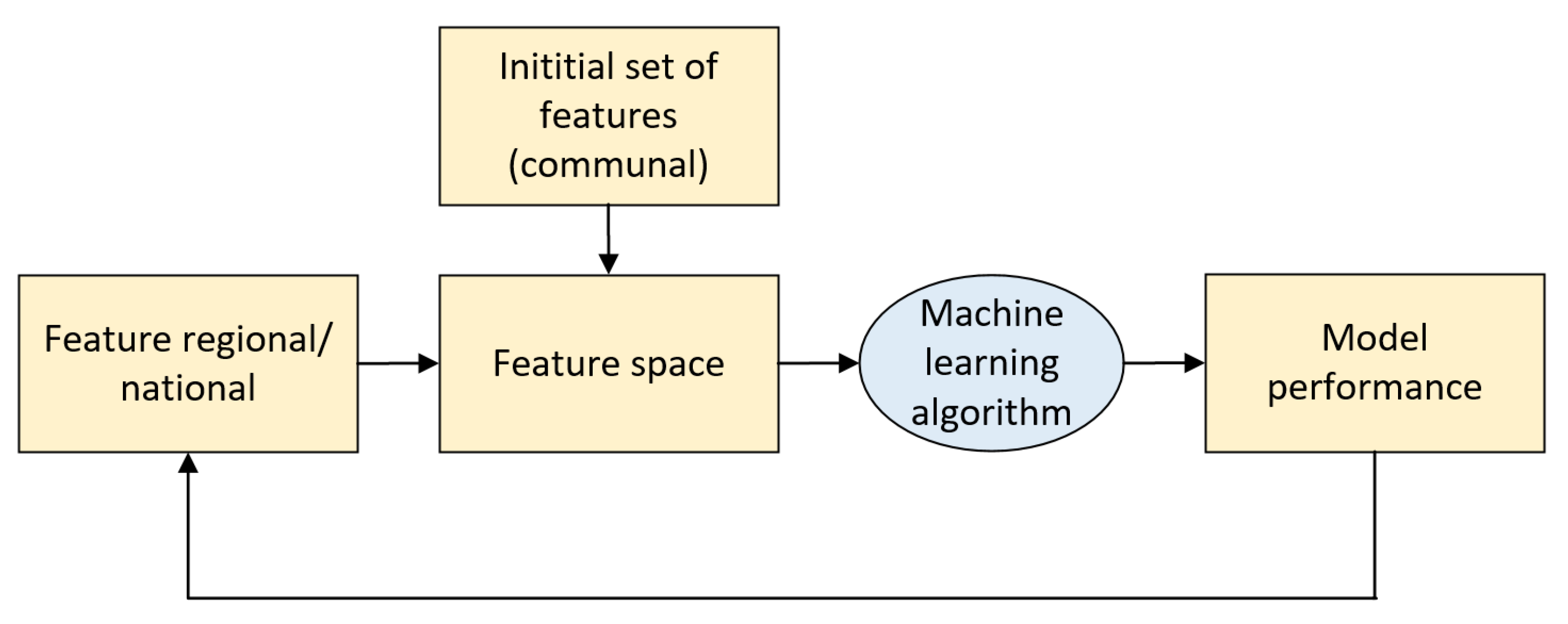
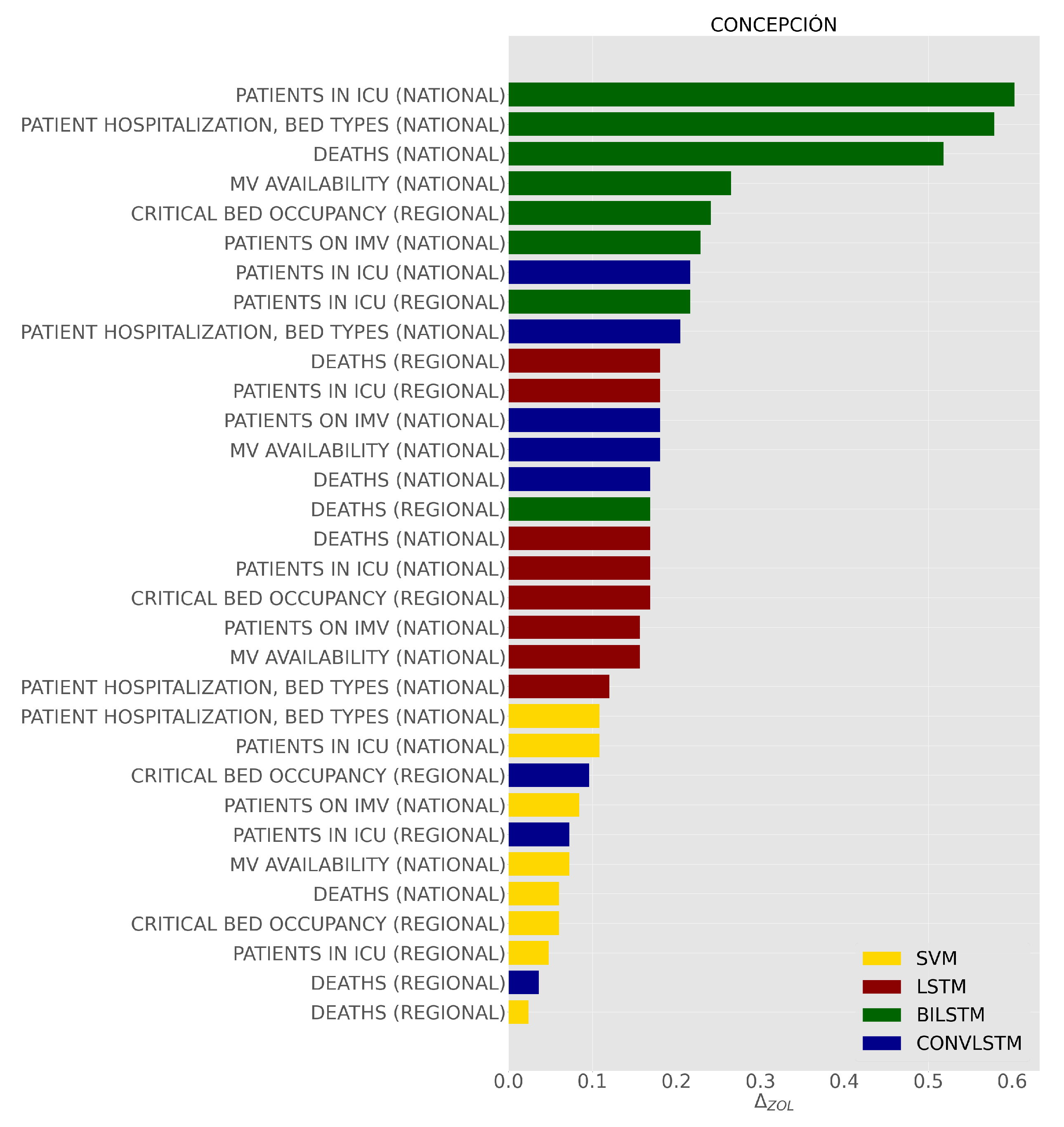
3.1. Datasets and Pre-Processing
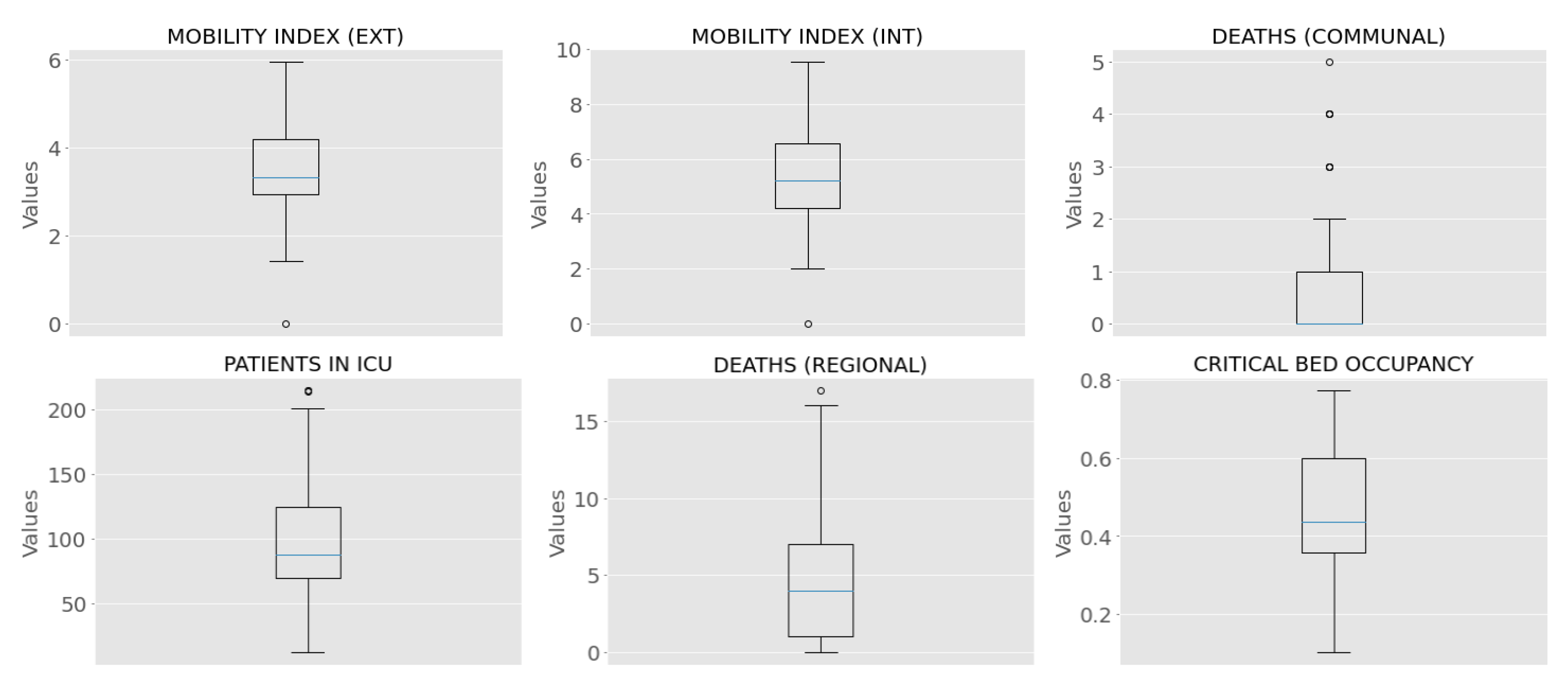
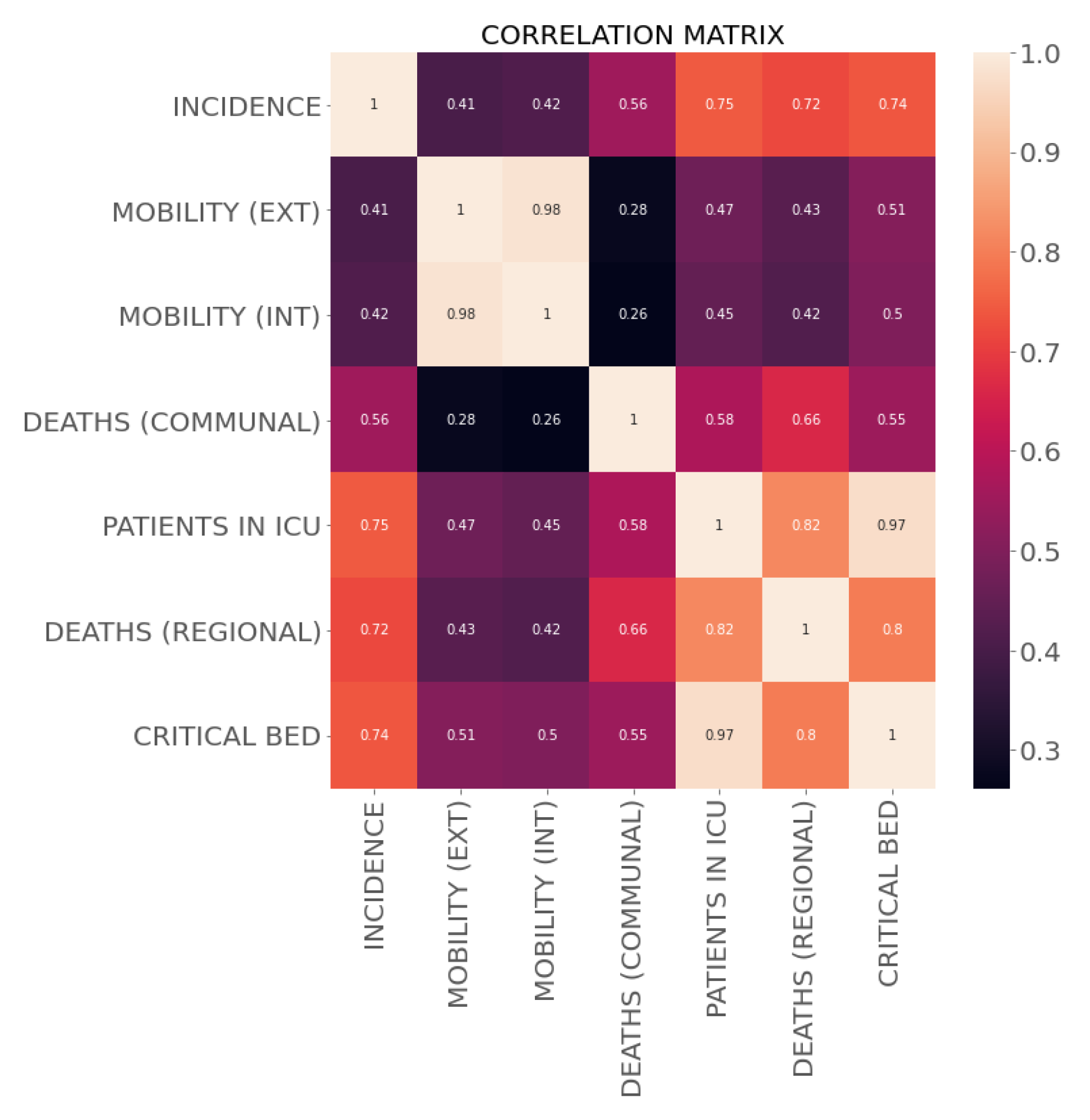
- Mobility: This feature was reported as the movements of mobile phones (antenna transitions) connected to Telefonica’s national network, in a grouped and anonymous way. The internal mobility is measured as the evolution of travel occurring within the commune, and the external mobility is calculated as the movement from outside the commune into the commune. The mobility index corresponds to the number of trips within a specific commune normalized by the number of commune residents.
- Deaths: Number of deaths by residence and date in the commune of Concepcion.
- Patients in ICU: Number of patients in an ICU who are COVID-19 confirmed cases by region, reported daily.
- Deaths: Number of COVID-19 diagnosed deaths per day, according to the region of residence, reported daily.
- Critical bed occupancy: Number of beds in an adult ICU by region, total occupation, and occupation by COVID-19.
- Patients in ICU (age group): Number of patients in an ICU by age groups (<=39; 40–49; 50–59; 60–69; and >=70) who are COVID-19 confirmed cases, reported daily.
- Deaths (age group): Number of people who died of COVID-19, grouped by age ranges (<=39; 40–49; 50–59; 60–69; 70–79; 80–89; and >=90) reported daily.
- Mechanical ventilator availability: Number of mechanical ventilators available and the number of ventilators occupied for each date reported.
- Patient hospitalization (bed type): Number of hospitalized patients with a COVID-19 diagnosis according to the type of bed they occupy: basic, medium, ITU and ICU.
- Patients on mechanical ventilation: Number of hospitalized patients in the ICU. The number of patients who require invasive mechanical ventilation, patients without mechanical ventilation and those connected to noninvasive mechanical ventilation who are COVID-19 confirmed cases.
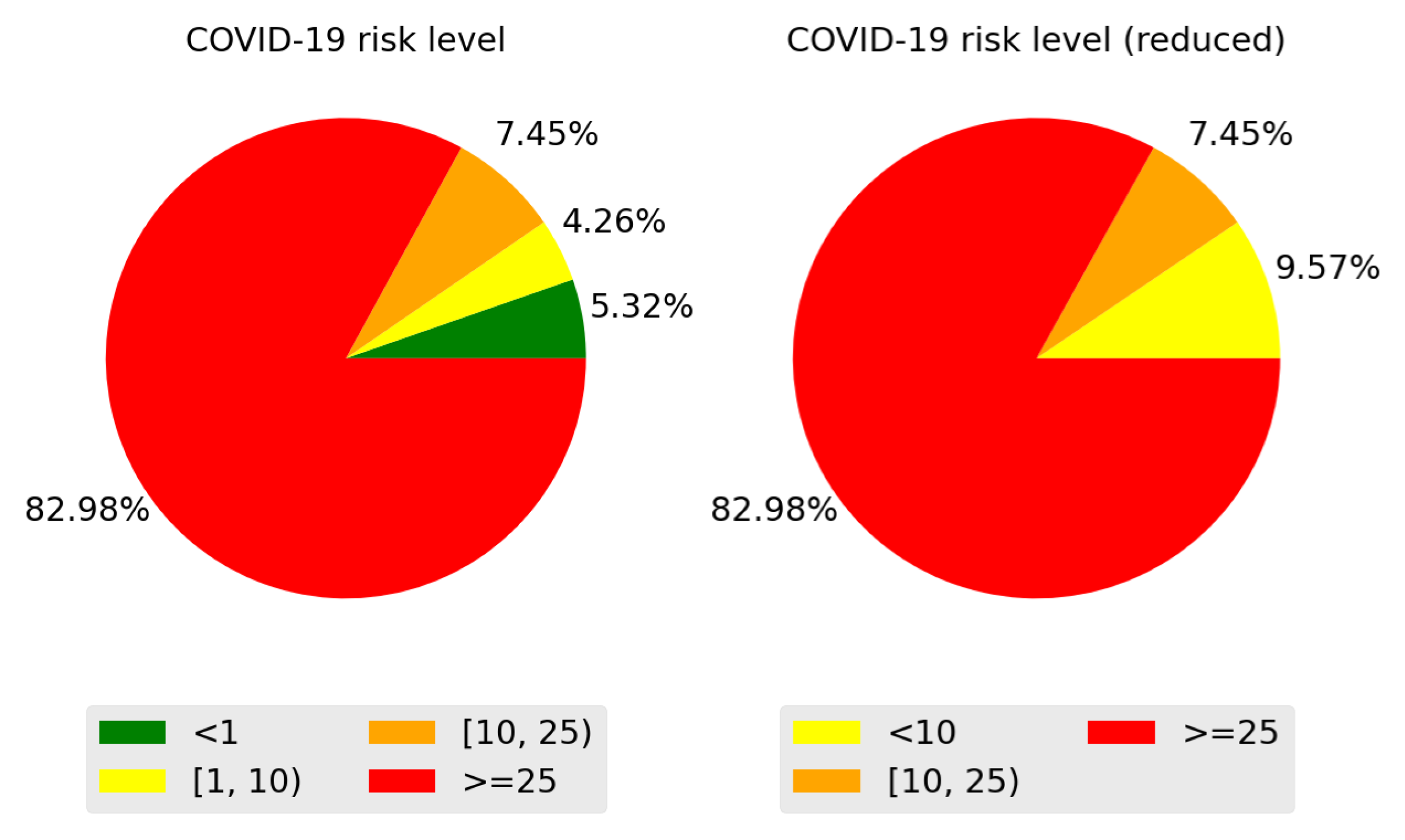
3.2. Problem Definition
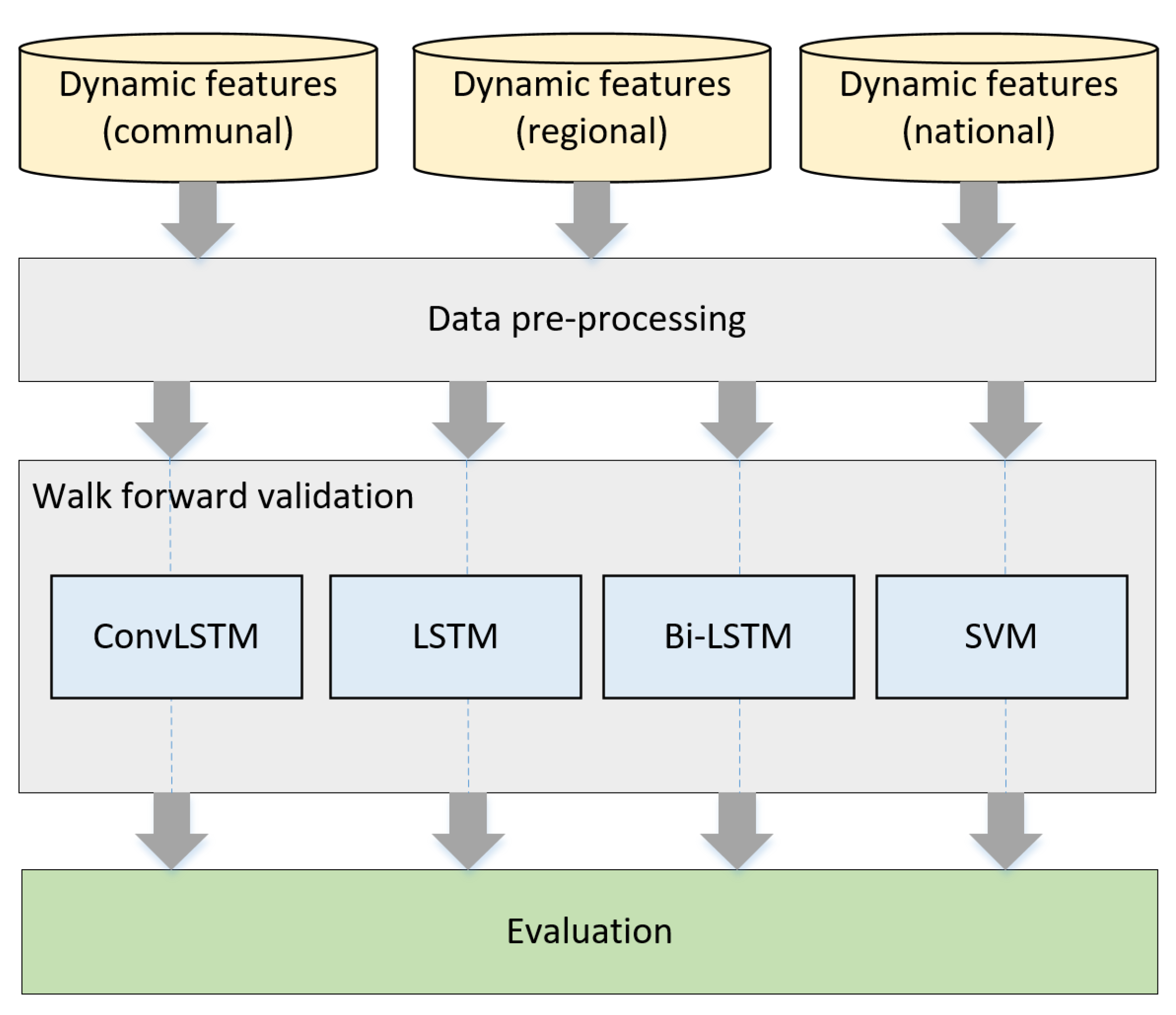
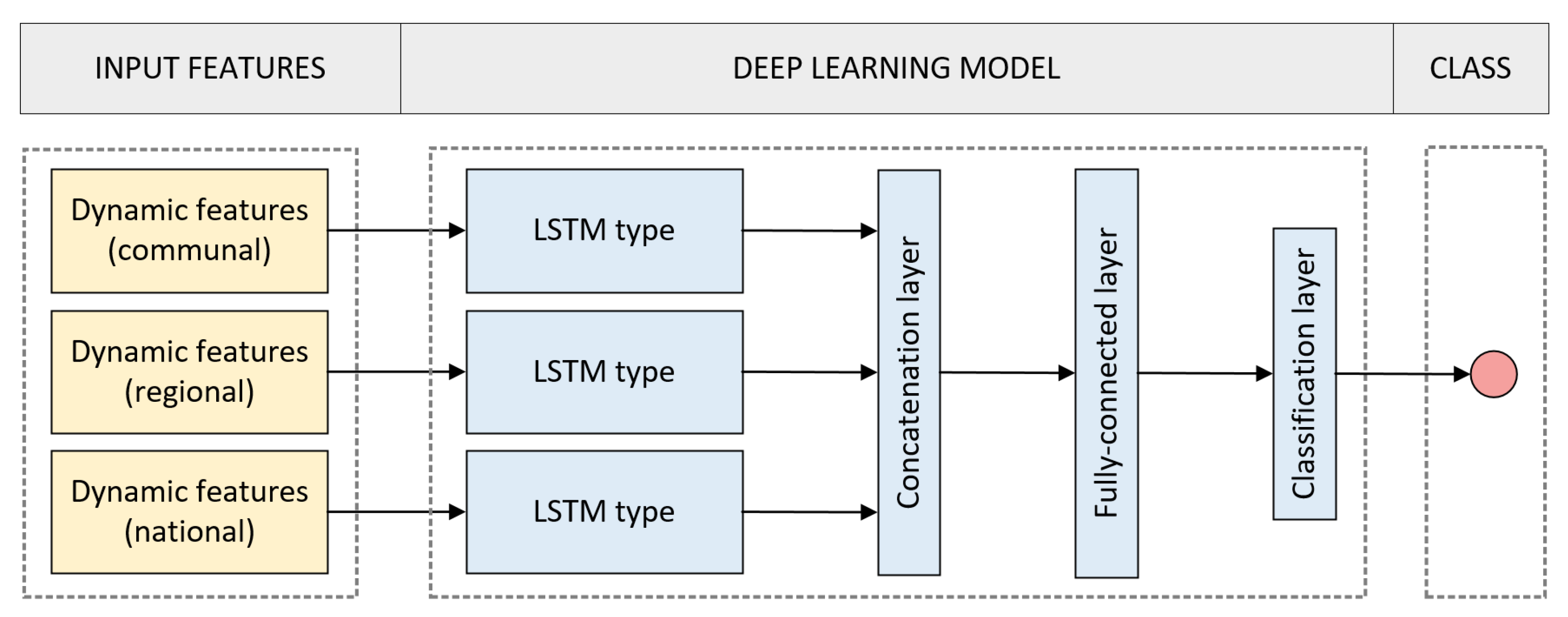
3.3. Classification Algorithms
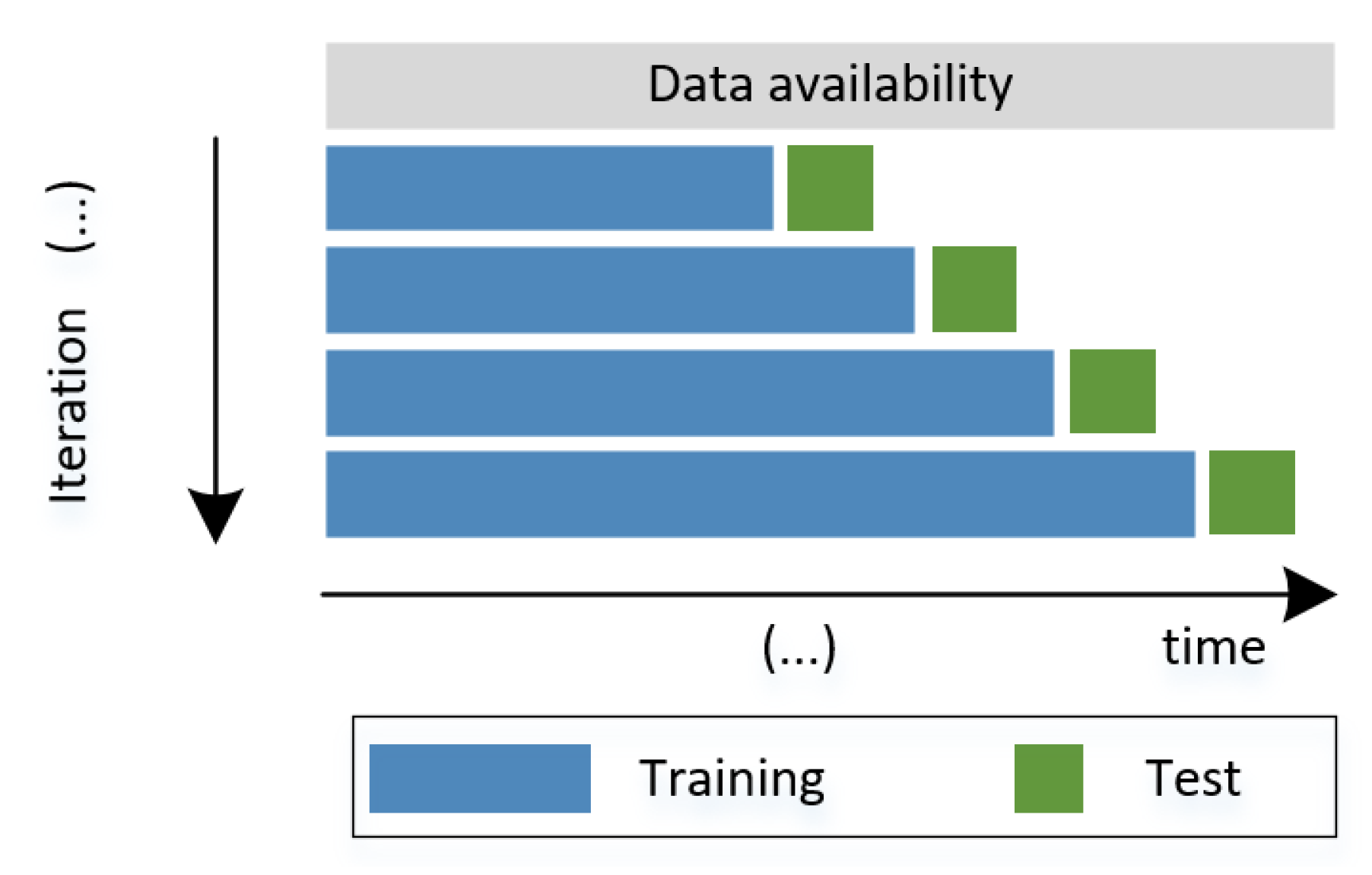
3.4. Evaluation of Algorithms
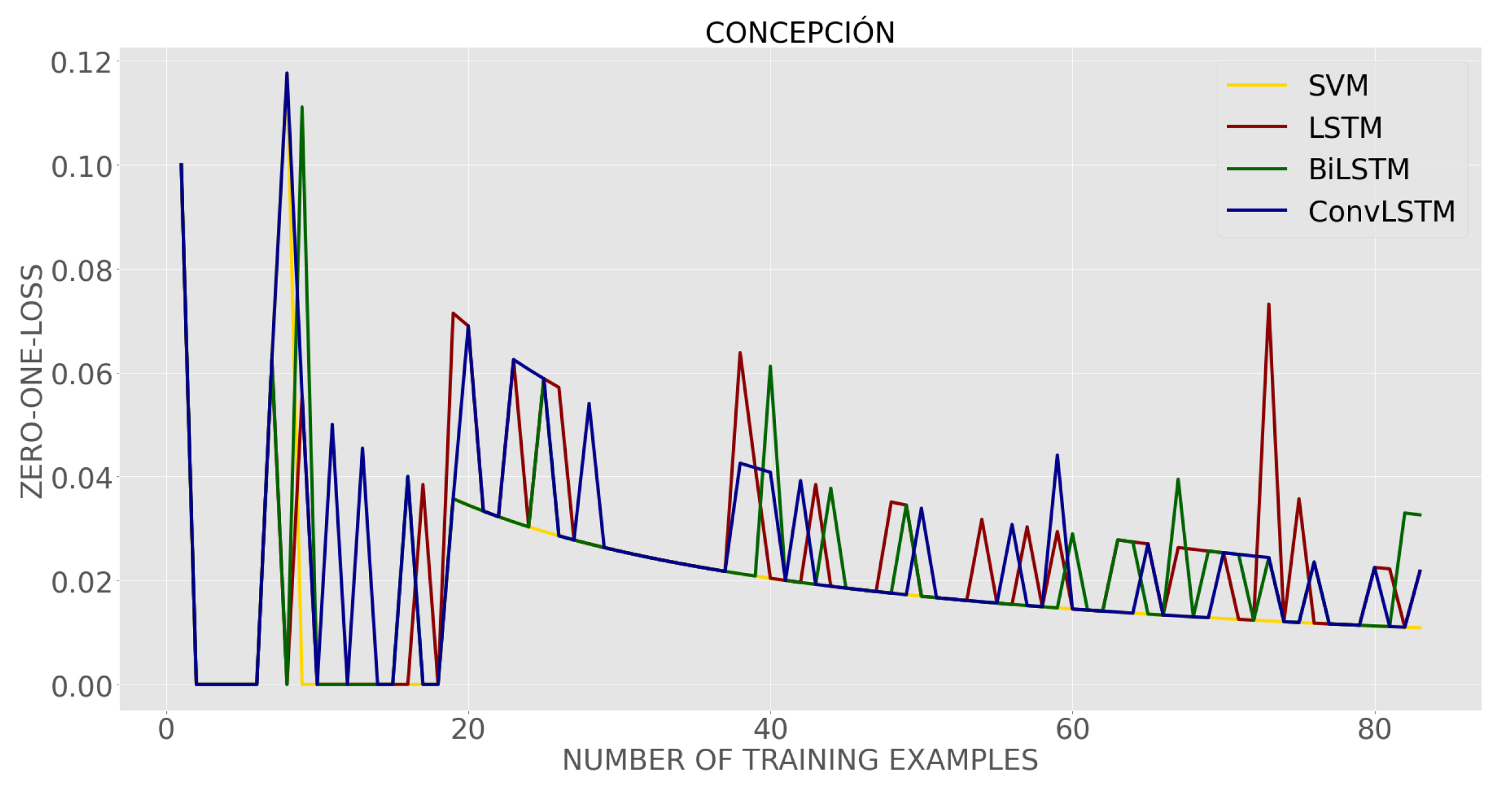
4. Results
5. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Honein, M.A.; Christie, A.; Rose, D.A.; Brooks, J.T.; Meaney-Delman, D.; Cohn, A.; Sauber-Schatz, E.K.; Walker, A.; McDonald, L.C.; Liburd, L.C.; et al. Summary of Guidance for Public Health Strategies to Address High Levels of Community Transmission of SARS-CoV-2 and Related Deaths, December 2020. Morb. Mortal. Wkly. Rep. 2020, 69, 1860. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef] [Green Version]
- Toniati, P.; Piva, S.; Cattalini, M.; Garrafa, E.; Regola, F.; Castelli, F.; Franceschini, F.; Focà, E.; Andreoli, L.; Latronico, N.; et al. Tocilizumab for the treatment of severe COVID-19 pneumonia with hyperinflammatory syndrome and acute respiratory failure: A single center study of 100 patients in Brescia, Italy. Autoimmun. Rev. 2020, 19, 102568. [Google Scholar] [CrossRef]
- Shah, K.; Kamrai, D.; Mekala, H.; Mann, B.; Desai, K.; Patel, R.S. Focus on mental health during the coronavirus (COVID-19) pandemic: Applying learnings from the past outbreaks. Cureus 2020, 12, e7405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benavides, G.A.; Larach, F.; Marchant, V.; Fernández, J.; Montoya, F.; Domínguez, S.; Mejías, C. The evolution of the COVID-19 pandemic in Chile during 2020: A data perspective. arXiv 2021, arXiv:2102.11841. [Google Scholar]
- Canals, M.; Cuadrado, C.; Canals, A.; Yohannessen, K.; Lefio, L.A.; Bertoglia, M.P.; Eguiguren, P.; Siches, I.; Iglesias, V.; Arteaga, O. Epidemic trends, public health response and health system capacity: The Chilean experience in four months of the COVID-19 pandemic. Rev. Panam. Salud Públic. 2020, 44, e99. [Google Scholar] [CrossRef] [PubMed]
- Jayaweera, M.; Perera, H.; Gunawardana, B.; Manatunge, J. Transmission of COVID-19 virus by droplets and aerosols: A critical review on the unresolved dichotomy. Environ. Res. 2020, 188, 109819. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Q.; Feng, L.; Rodewald, L.; Xia, Y.; Yu, H.; Zhang, R.; An, Z.; Yin, W.; Chen, W.; et al. Active case finding with case management: The key to tackling the COVID-19 pandemic. Lancet 2020, 396, 63–70. [Google Scholar] [CrossRef]
- Ministerio de Salud. Manual Operativo para la Búsqueda Activa de Casos en la Comunidad y Diagnóstico Precoz Covid-19. 2021. Available online: https://www.minsal.cl/wp-content/uploads/2020/10/201005-MANUAL-BAC.pdf (accessed on 30 June 2021).
- Corman, V.M.; Landt, O.; Kaiser, M.; Molenkamp, R.; Meijer, A.; Chu, D.K.; Bleicker, T.; Brünink, S.; Schneider, J.; Schmidt, M.L.; et al. Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR. Eurosurveillance 2020, 25, 2000045. [Google Scholar] [CrossRef] [Green Version]
- Fontanet, A.; Autran, B.; Lina, B.; Kieny, M.P.; Karim, S.S.A.; Sridhar, D. SARS-CoV-2 variants and ending the COVID-19 pandemic. Lancet 2021, 397, 952–954. [Google Scholar] [CrossRef]
- Roser, M.; Ritchie, H.; Ortiz-Ospina, E.; Hasell, J. Coronavirus Pandemic (COVID-19). Our World Data 2020. Available online: https://ourworldindata.org/coronavirus (accessed on 30 June 2021).
- Dalsgaard, S.; Thorsteinsson, E.; Trabjerg, B.B.; Schullehner, J.; Plana-Ripoll, O.; Brikell, I.; Wimberley, T.; Thygesen, M.; Madsen, K.B.; Timmerman, A.; et al. Incidence rates and cumulative incidences of the full spectrum of diagnosed mental disorders in childhood and adolescence. JAMA Psychiatry 2020, 77, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Safra, E.J. Key Metrics for COVID Suppression: A Framework for Policy Makers and the Public; 2020; Available online: https://ethics.harvard.edu/files/center-for-ethics/files/key_metrics_and_indicators_v4.pdf (accessed on 30 June 2021).
- Qi, H.; Xiao, S.; Shi, R.; Ward, M.P.; Chen, Y.; Tu, W.; Su, Q.; Wang, W.; Wang, X.; Zhang, Z. COVID-19 transmission in Mainland China is associated with temperature and humidity: A time-series analysis. Sci. Total. Environ. 2020, 728, 138778. [Google Scholar] [CrossRef]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef]
- Hu, Z.; Ge, Q.; Li, S.; Jin, L.; Xiong, M. Artificial intelligence forecasting of covid-19 in china. arXiv 2020, arXiv:2002.07112. [Google Scholar]
- Bertozzi, A.L.; Franco, E.; Mohler, G.; Short, M.B.; Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 16732–16738. [Google Scholar] [CrossRef] [PubMed]
- Malavika, B.; Marimuthu, S.; Joy, M.; Nadaraj, A.; Asirvatham, E.S.; Jeyaseelan, L. Forecasting COVID-19 epidemic in India and high incidence states using SIR and logistic growth models. Clin. Epidemiol. Glob. Health 2021, 9, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Calafiore, G.C.; Novara, C.; Possieri, C. A modified SIR model for the COVID-19 contagion in Italy. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju Island, Korea, 14–18 December 2020; pp. 3889–3894. [Google Scholar]
- Giuliani, D.; Dickson, M.M.; Espa, G.; Santi, F. Modelling and predicting the spatio-temporal spread of COVID-19 in Italy. BMC Infect. Dis. 2020, 20, 1–10. [Google Scholar] [CrossRef]
- Deb, S.; Majumdar, M. A time series method to analyze incidence pattern and estimate reproduction number of COVID-19. arXiv 2020, arXiv:2003.10655. [Google Scholar]
- Hamidouche, M. COVID-19 outbreak in Algeria: A mathematical model to predict the incidence. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Panuganti, B.A.; Jafari, A.; MacDonald, B.; DeConde, A.S. Predicting COVID-19 Incidence Using Anosmia and Other COVID-19 Symptomatology: Preliminary Analysis Using Google and Twitter. Otolaryngol. Head Neck Surg. 2020, 163, 491–497. [Google Scholar] [CrossRef]
- Yuan, X.; Xu, J.; Hussain, S.; Wang, H.; Gao, N.; Zhang, L. Trends and prediction in daily new cases and deaths of COVID-19 in the United States: An internet search-interest based model. Explor. Res. Hypothesis Med. 2020, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Stübinger, J.; Schneider, L. Epidemiology of coronavirus covid-19: Forecasting the future incidence in different countries. In Healthcare; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2020; Volume 8, p. 99. [Google Scholar] [CrossRef] [Green Version]
- Paul, M.; Held, L. Predictive assessment of a non-linear random effects model for multivariate time series of infectious disease counts. Stat. Med. 2011, 30, 1118–1136. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Bhunia, G.S.; Shit, P.K. Spatial prediction of COVID-19 epidemic using ARIMA techniques in India. Model. Earth Syst. Environ. 2020, 7, 1385–1391. [Google Scholar] [CrossRef] [PubMed]
- Mollalo, A.; Rivera, K.M.; Vahedi, B. Artificial neural network modeling of novel coronavirus (COVID-19) incidence rates across the continental United States. Int. J. Environ. Res. Public Health 2020, 17, 4204. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Parmar, K.S.; Makkhan, S.J.S.; Kaur, J.; Peshoria, S.; Kumar, J. Study of ARIMA and least square support vector machine (LS-SVM) models for the prediction of SARS-CoV-2 confirmed cases in the most affected countries. Chaos Solitons Fractals 2020, 139, 110086. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. Predictions for COVID-19 with deep learning models of LSTM, GRU and Bi-LSTM. Chaos Solitons Fractals 2020, 140, 110212. [Google Scholar] [CrossRef]
- Harb, A.M.; Harb, S.M. Corona COVID-19 spread-a nonlinear modeling and simulation. Comput. Electr. Eng. 2020, 88, 106884. [Google Scholar] [CrossRef]
- Rohith, G.; Devika, K. Dynamics and control of COVID-19 pandemic with nonlinear incidence rates. Nonlinear Dyn. 2020, 101, 2013–2026. [Google Scholar] [CrossRef]
- Ramchandani, A.; Fan, C.; Mostafavi, A. Deepcovidnet: An interpretable deep learning model for predictive surveillance of covid-19 using heterogeneous features and their interactions. IEEE Access 2020, 8, 159915–159930. [Google Scholar] [CrossRef]
- Haarhaus, M.; Santos, C.; Haase, M.; Mota Veiga, P.; Lucas, C.; Macario, F. Risk prediction of COVID-19 incidence and mortality in a large multi-national hemodialysis cohort: Implications for management of the pandemic in outpatient hemodialysis settings. Clin. Kidney J. 2021, 14, 805–813. [Google Scholar] [CrossRef] [PubMed]
- Ayyoubzadeh, S.M.; Ayyoubzadeh, S.M.; Zahedi, H.; Ahmadi, M.; Kalhori, S.R.N. Predicting COVID-19 incidence through analysis of google trends data in iran: Data mining and deep learning pilot study. JMIR Public Health Surveill. 2020, 6, e18828. [Google Scholar] [CrossRef] [PubMed]
- Shastri, S.; Singh, K.; Kumar, S.; Kour, P.; Mansotra, V. Time series forecasting of Covid-19 using deep learning models: India-USA comparative case study. Chaos Solitons Fractals 2020, 140, 110227. [Google Scholar] [CrossRef]
- Singh, V.; Poonia, R.C.; Kumar, S.; Dass, P.; Agarwal, P.; Bhatnagar, V.; Raja, L. Prediction of COVID-19 corona virus pandemic based on time series data using Support Vector Machine. J. Discret. Math. Sci. Cryptogr. 2020, 23, 1583–1597. [Google Scholar] [CrossRef]
- Rustam, F.; Reshi, A.A.; Mehmood, A.; Ullah, S.; On, B.W.; Aslam, W.; Choi, G.S. COVID-19 future forecasting using supervised machine learning models. IEEE Access 2020, 8, 101489–101499. [Google Scholar] [CrossRef]
- Wilde, H.; Mellan, T.; Hawryluk, I.; Dennis, J.M.; Denaxas, S.; Pagel, C.; Duncan, A.; Bhatt, S.; Flaxman, S.; Mateen, B.A.; et al. The association between mechanical ventilator availability and mortality risk in intensive care patients with COVID-19: A national retrospective cohort study. medRxiv 2021. [Google Scholar] [CrossRef]
- Nouvellet, P.; Bhatia, S.; Cori, A.; Ainslie, K.E.; Baguelin, M.; Bhatt, S.; Boonyasiri, A.; Brazeau, N.F.; Cattarino, L.; Cooper, L.V.; et al. Reduction in mobility and COVID-19 transmission. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xu, R.; Hu, D.; Yue, Y.; Li, Q.; Xia, J. Effects of human mobility restrictions on the spread of COVID-19 in Shenzhen, China: A modelling study using mobile phone data. Lancet Digit. Health 2020, 2, e417–e424. [Google Scholar] [CrossRef]
- Shi, Z.; Fang, Y. Temporal relationship between outbound traffic from Wuhan and the 2019 coronavirus disease (COVID-19) incidence in China. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Mazzoli, M.; Mateo, D.; Hernando, A.; Meloni, S.; Ramasco, J.J. Effects of mobility and multi-seeding on the propagation of the COVID-19 in Spain. MedRxiv 2020. [Google Scholar] [CrossRef]
- Andersen, M.S.; Bento, A.I.; Basu, A.; Marsicano, C.; Simon, K. College openings, mobility, and the incidence of covid-19 cases. medRxiv 2020. [Google Scholar] [CrossRef]
- Prada, J. Understanding studentification dynamics in low-income neighbourhoods: Students as gentrifiers in Concepcion (Chile). Urban Studies 2019, 14, 2863–2879. [Google Scholar] [CrossRef]
- Stajkowski, S.; Zeynoddin, M.; Farghaly, H.; Gharabaghi, B.; Bonakdari, H. A Methodology for Forecasting Dissolved Oxygen in Urban Streams. Water 2020, 12, 2568. [Google Scholar] [CrossRef]
- Dick, G.; Owen, C.A.; Whigham, P.A. Feature standardisation and coefficient optimisation for effective symbolic regression. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 306–314. [Google Scholar] [CrossRef]
- Parbat, D.; Chakraborty, M. A python based support vector regression model for prediction of COVID19 cases in India. Chaos Solitons Fractals 2020, 138, 109942. [Google Scholar] [CrossRef] [PubMed]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.-k.; Woo, W.-c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 2015, 802–810. [Google Scholar]
- Song, H.; Wang, W.; Zhao, S.; Shen, J.; Lam, K.M. Pyramid dilated deeper convlstm for video salient object detection. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 October 2018; pp. 715–731. [Google Scholar] [CrossRef]
- Kim, S.; Hong, S.; Joh, M.; Song, S.k. Deeprain: Convlstm network for precipitation prediction using multichannel radar data. arXiv 2017, arXiv:1711.02316. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H. Insights into LSTM fully convolutional networks for time series classification. IEEE Access 2019, 7, 67718–67725. [Google Scholar] [CrossRef]
- Yildirim, O.; Baloglu, U.B.; Tan, R.S.; Ciaccio, E.J.; Acharya, U.R. A new approach for arrhythmia classification using deep coded features and LSTM networks. Comput. Methods Programs Biomed. 2019, 176, 121–133. [Google Scholar] [CrossRef]
- Sharif, O.; Hossain, E.; Hoque, M.M. TechTexC: Classification of Technical Texts using Convolution and Bidirectional Long Short Term Memory Network. arXiv 2020, arXiv:2012.11420. [Google Scholar]
- Yuan, J.; Wu, Y.; Jing, W.; Liu, J.; Du, M.; Wang, Y.; Liu, M. Non-linear correlation between daily new cases of COVID-19 and meteorological factors in 127 countries. Environ. Res. 2021, 193, 110521. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM networks. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 4, pp. 2047–2052. [Google Scholar] [CrossRef]
- Nabavi, S.S.; Rochan, M.; Wang, Y. Future semantic segmentation with convolutional lstm. arXiv 2018, arXiv:1807.07946. [Google Scholar]
- Hu, M.Y.; Zhang, G.; Jiang, C.X.; Patuwo, B.E. A cross-validation analysis of neural network out-of-sample performance in exchange rate forecasting. Decis. Sci. 1999, 30, 197–216. [Google Scholar] [CrossRef]
- Charuvaka, A.; Rangwala, H. HierCost: Improving Large Scale Hierarchical Classification with Cost Sensitive Learning; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Yu, X.; Zhang, X. Levenberg-Marquardt algorithm for Mackey-Glass chaotic time series prediction. Discret. Dyn. Nat. Soc. 2014, 2014. [Google Scholar] [CrossRef]
- Cao, L.J.; Tay, F.E.H. Support vector machine with adaptive parameters in financial time series forecasting. IEEE Trans. Neural Netw. 2003, 14, 1506–1518. [Google Scholar] [CrossRef] [Green Version]
- Mena, G.E.; Martinez, P.P.; Mahmud, A.; Marquet, P.; Buckee, C.; Santillana, M. Socioeconomic status determines COVID-19 incidence and related mortality in Santiago, Chile. medRxiv 2021. [Google Scholar] [CrossRef]
| Classifier | Parameter | Value |
|---|---|---|
| LSTM models | filters | 64 |
| kernel size | (1,2) | |
| epochs | 40 | |
| activation function (units) | ReLU | |
| dropout | 0.2 | |
| optimizer | Adam | |
| learning rate | ||
| batch size | 8 | |
| hidden units | 128 | |
| activation function (class) | Softmax | |
| loss function | Categorical crossentropy | |
| SVM | kernel | rbf |
| C | 1.0 | |
| escale * |
| Classifier | ACC (%) | P (%) | R (%) | F1 (%) |
|---|---|---|---|---|
| SVM | 93.98 | 95.66 | 93.98 | 94.81 |
| LSTM | 95.18 | 96.05 | 95.18 | 95.61 |
| BiLSTM | 93.98 | 95.66 | 93.98 | 94.81 |
| ConvLSTM | 96.39 | 96.71 | 96.39 | 96.55 |
| Classifier | Classification Error (Zero-One Loss) |
|---|---|
| SVM | 0.0180 ± 0.0178 |
| LSTM | 0.0241 ± 0.0197 |
| BiLSTM | 0.0218 ± 0.0188 |
| ConvLSTM | 0.0250 ± 0.0210 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores, C.; Taramasco, C.; Lagos, M.E.; Rimassa, C.; Figueroa, R. A Feature-Based Analysis for Time-Series Classification of COVID-19 Incidence in Chile: A Case Study. Appl. Sci. 2021, 11, 7080. https://doi.org/10.3390/app11157080
Flores C, Taramasco C, Lagos ME, Rimassa C, Figueroa R. A Feature-Based Analysis for Time-Series Classification of COVID-19 Incidence in Chile: A Case Study. Applied Sciences. 2021; 11(15):7080. https://doi.org/10.3390/app11157080
Chicago/Turabian StyleFlores, Christopher, Carla Taramasco, Maria Elena Lagos, Carla Rimassa, and Rosa Figueroa. 2021. "A Feature-Based Analysis for Time-Series Classification of COVID-19 Incidence in Chile: A Case Study" Applied Sciences 11, no. 15: 7080. https://doi.org/10.3390/app11157080
APA StyleFlores, C., Taramasco, C., Lagos, M. E., Rimassa, C., & Figueroa, R. (2021). A Feature-Based Analysis for Time-Series Classification of COVID-19 Incidence in Chile: A Case Study. Applied Sciences, 11(15), 7080. https://doi.org/10.3390/app11157080







