A Decoupling Strategy for Reliability Analysis of Multidisciplinary System with Aleatory and Epistemic Uncertainties
Abstract
1. Introduction
2. Related Works
2.1. Mixed Uncertainties Quantification Based on Probability Theory and Convex Set Theory
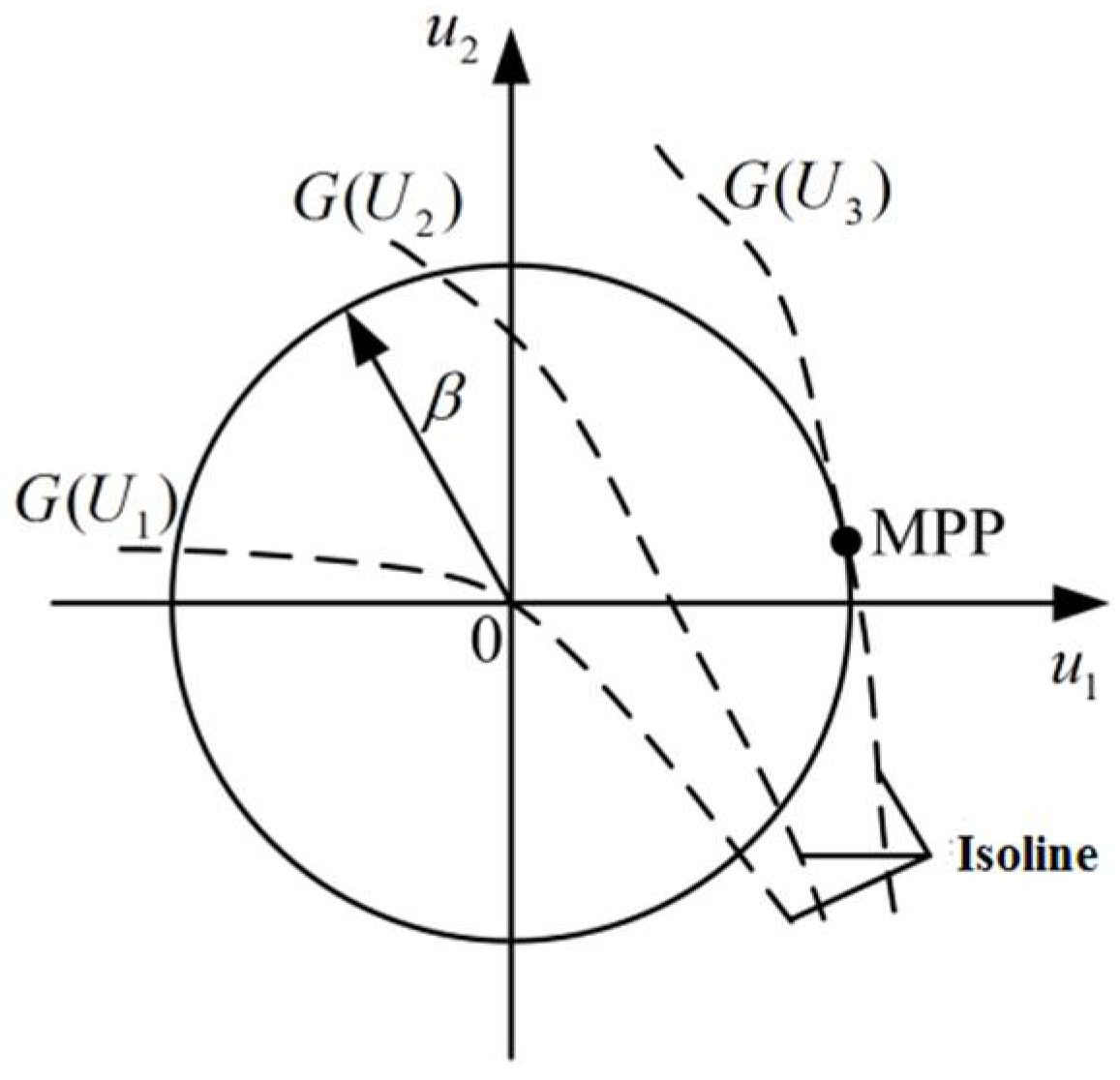
2.2. Performance Measure Approach (PMA) for Reliability Analysis
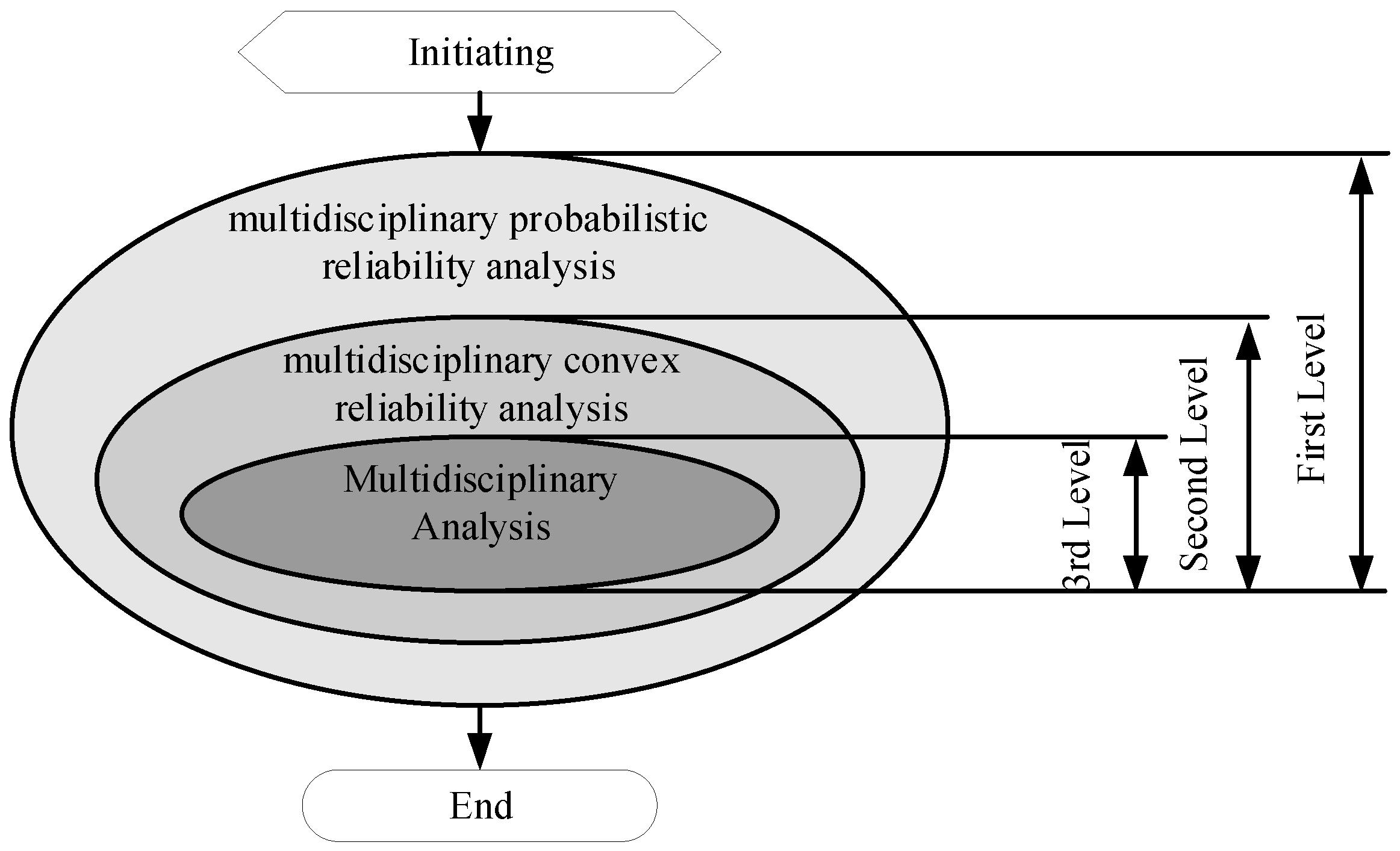
3. Materials and Methods
3.1. Reliability Comprehensive Evaluation Index Considering Multisource Uncertainties
3.2. Mathematical Model of Reliability with Aleatory and Epistemic Uncertainties
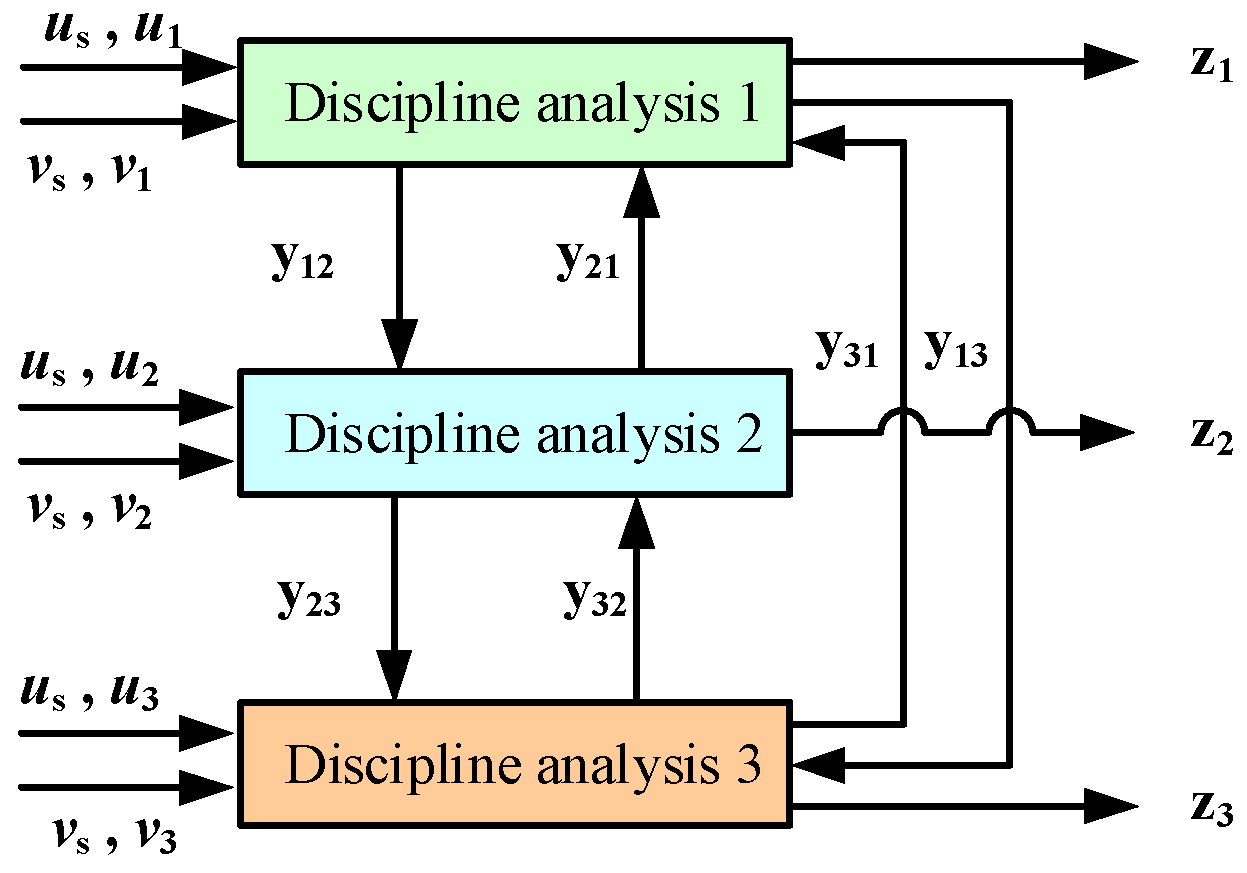
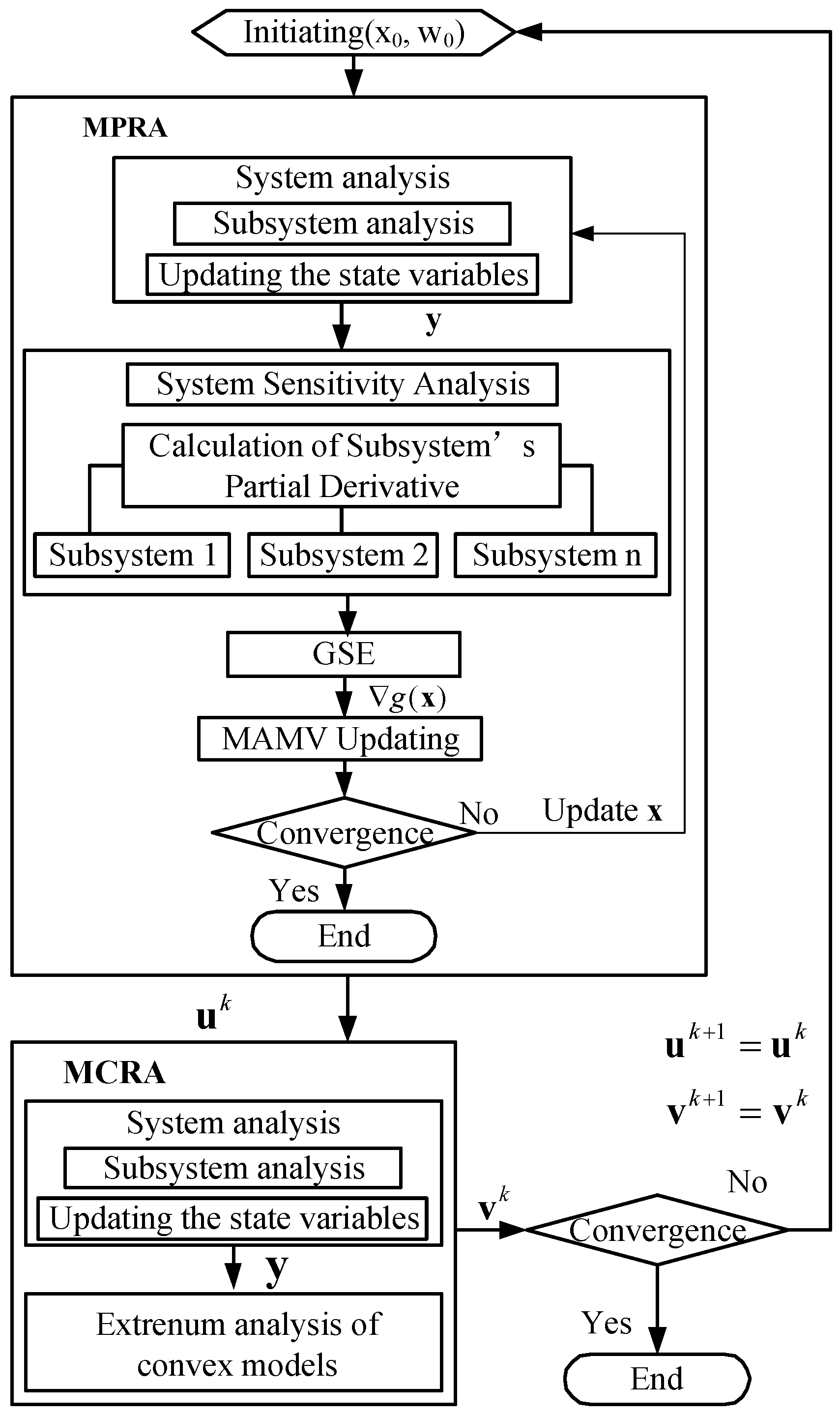
3.3. Decoupling Strategy for Multidisciplinary Reliability Approach
4. Evaluation and Discussion
4.1. Numerical Example
4.2. Speed Reducer
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, R.; Sun, T.; Liu, D.; Pan, Z.; Wang, D. Multi-objective reliability-based optimization of control arm using MCS and NSGA-II coupled with entropy weighted GRA. Appl. Sci. 2021, 11, 5825. [Google Scholar] [CrossRef]
- Chun, J. Reliability based design optimization of structures using the second-order reliability method and complex-step derivative approximation. Appl. Sci. 2021, 11, 5312. [Google Scholar] [CrossRef]
- Faes, M.G.R.; Daub, M.; Marelli, S.; Patelli, E.; Beer, M. Engineering analysis with probability boxes: A review on computational methods. Struct. Saf. 2021, 93, 102092. [Google Scholar] [CrossRef]
- Xiang, Z.; Bao, Y.; Tang, Z.; Li, H. Deep reinforcement learning-based sampling method for structural reliability assessment. Reliab. Eng. Syst. Saf. 2020, 199, 106901. [Google Scholar] [CrossRef]
- Ghoreishi, S.F.; Imani, M. Bayesian Surrogate Learning for Uncertainty Analysis of Coupled Multidisciplinary Systems. J. Comput. Inf. Sci. Eng. 2021, 21, 041009. [Google Scholar] [CrossRef]
- Park, I.; Amarchinta, H.; Grandhi, R. A Bayesian approach for quantification of model uncertainty. Reliab. Eng. Syst. Saf. 2010, 95, 777–785. [Google Scholar] [CrossRef]
- Wang, C.; Matthies, H.G. Epistemic uncertainty-based reliability analysis for engineering system with hybrid evidence and fuzzy variables. Comput. Methods Appl. Mech. Eng. 2019, 355, 438–455. [Google Scholar] [CrossRef]
- Huang, H.-Z.; He, L.; Liu, Y.; Xiao, N.-C.; Li, Y.-F.; Wang, Z. Possibility and evidence-based reliability analysis and design optimization. Am. J. Eng. Appl. Sci. 2013, 6, 95–136. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, C.; Wang, G.G.; Han, X. First and second order approximate reliability analysis methods using evidence theory. Reliab. Eng. Syst. Saf. 2015, 137, 40–49. [Google Scholar] [CrossRef]
- Li, F.; Liu, J.; Wen, G.; Rong, J. Extending SORA method for reliability-based design optimization using probability and convex set mixed models. Struct. Multidiplinary Optim. 2019, 59, 1163–1179. [Google Scholar] [CrossRef]
- Du, L.; Choi, K.K.; Youn, B.D. Inverse possibility analysis method for possibility-based design optimization. AIAA J. 2006, 44, 2682–2690. [Google Scholar] [CrossRef][Green Version]
- Shah, H.; Hosder, S.; Winter, T. Quantification of margins and mixed uncertainties using evidence theory and stochastic expansions. Reliab. Eng. Syst. Saf. 2015, 138, 59–72. [Google Scholar] [CrossRef]
- Huang, H.Z.; Zhang, X.D. Design optimization with discrete and continuous variables of aleatory and epistemic uncertainties. J. Mech. Des. 2009, 131, 031006. [Google Scholar] [CrossRef]
- Du, X.; Guo, J.; Beeram, H. Sequential optimization and reliability assessment for multidisciplinary systems design. Struct. Multidiplinary Optim. 2008, 35, 117–130. [Google Scholar] [CrossRef]
- Meng, D.; Xie, T.; Wu, P.; He, C.; Hu, Z.; Lv, Z. An uncertainty-based design optimization strategy with random and interval variables for multidisciplinary engineering systems. Structures 2021, 32, 997–1004. [Google Scholar] [CrossRef]
- Kang, Z.; Luo, Y. Reliability-based Structural Optimization with Probability and Convex Set Hybrid Models. Struct. Multidiplinary Optim. 2010, 42, 165–175. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on a multivariate transformation. Ann. Math. Stat. 1952, 3, 470–472. [Google Scholar] [CrossRef]
- Youn, B.; Choi, K.; Du, L. Enriched Performance Measure Approach for Reliability-based Design Optimization. AIAA J. 2012, 43, 874–884. [Google Scholar] [CrossRef]
- Li, M. Generalized Lagrange multiplier Method and KKT conditions with an application to distributed optimization. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 252–256. [Google Scholar] [CrossRef]
- Hajela, P.; Bloebaum, C.L.; Sobieszczanski-Sobieski, J. Application of global sensitivity Equations in multidisciplinary aircraft synthesis. J. Aircr. 2012, 27, 12. [Google Scholar] [CrossRef]
- Du, X.; Chen, W. An integrated framework for optimization under uncertainty using inverse reliability strategy. J. Des. Manuf. Autom. 2004, 126, 562–570. [Google Scholar] [CrossRef]
- Du, X.; Chen, W. Collaborative Reliability Analysis under the Framework of Multidisciplinary Systems Design. Optim. Eng. 2005, 6, 63–84. [Google Scholar] [CrossRef]
- Golinski, J. An adaptive optimization system applied to machine synthesis. Mech. Mach. Theory 1973, 8, 419–436. [Google Scholar] [CrossRef]
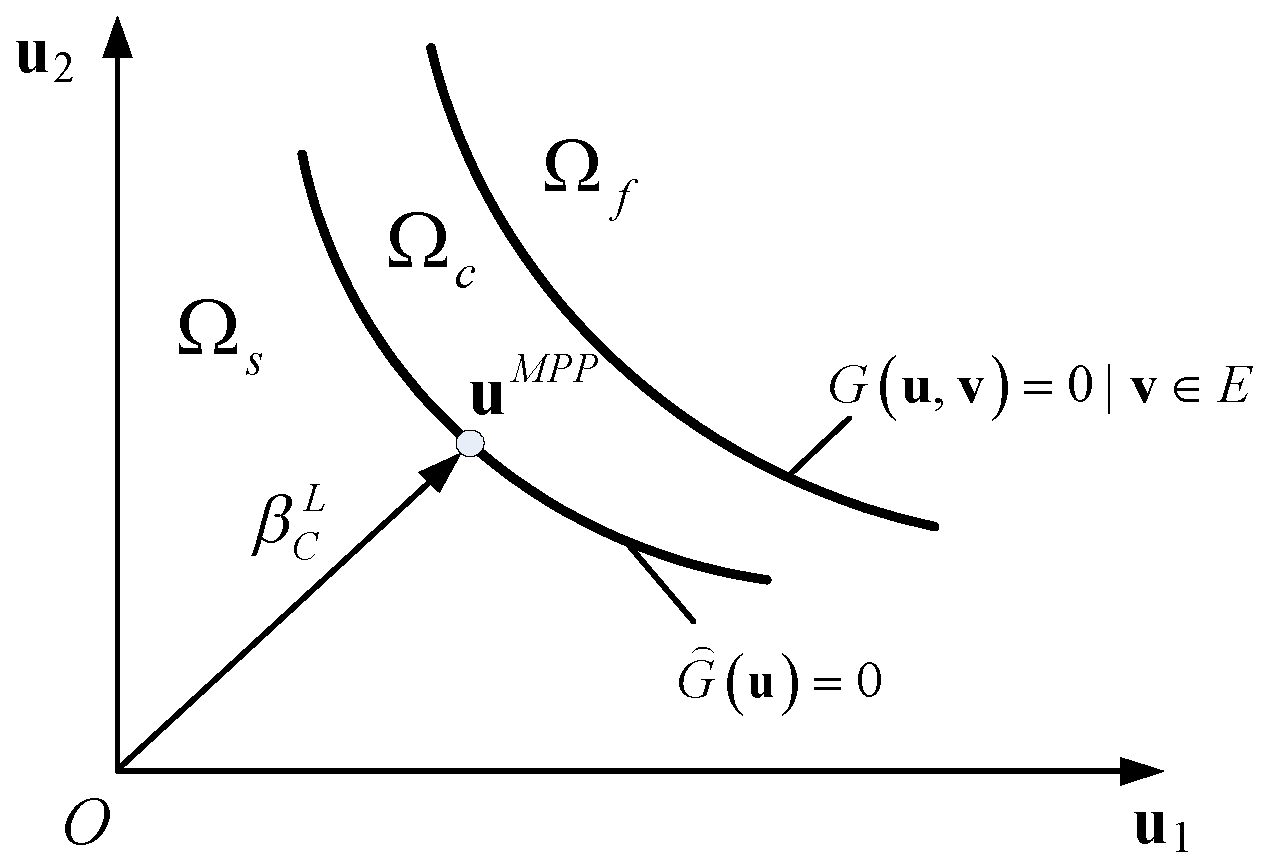
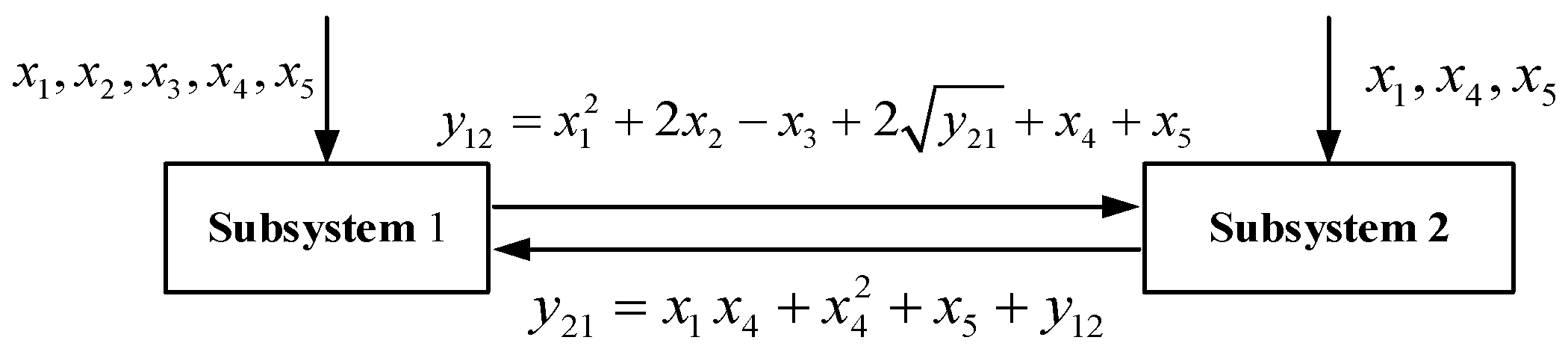
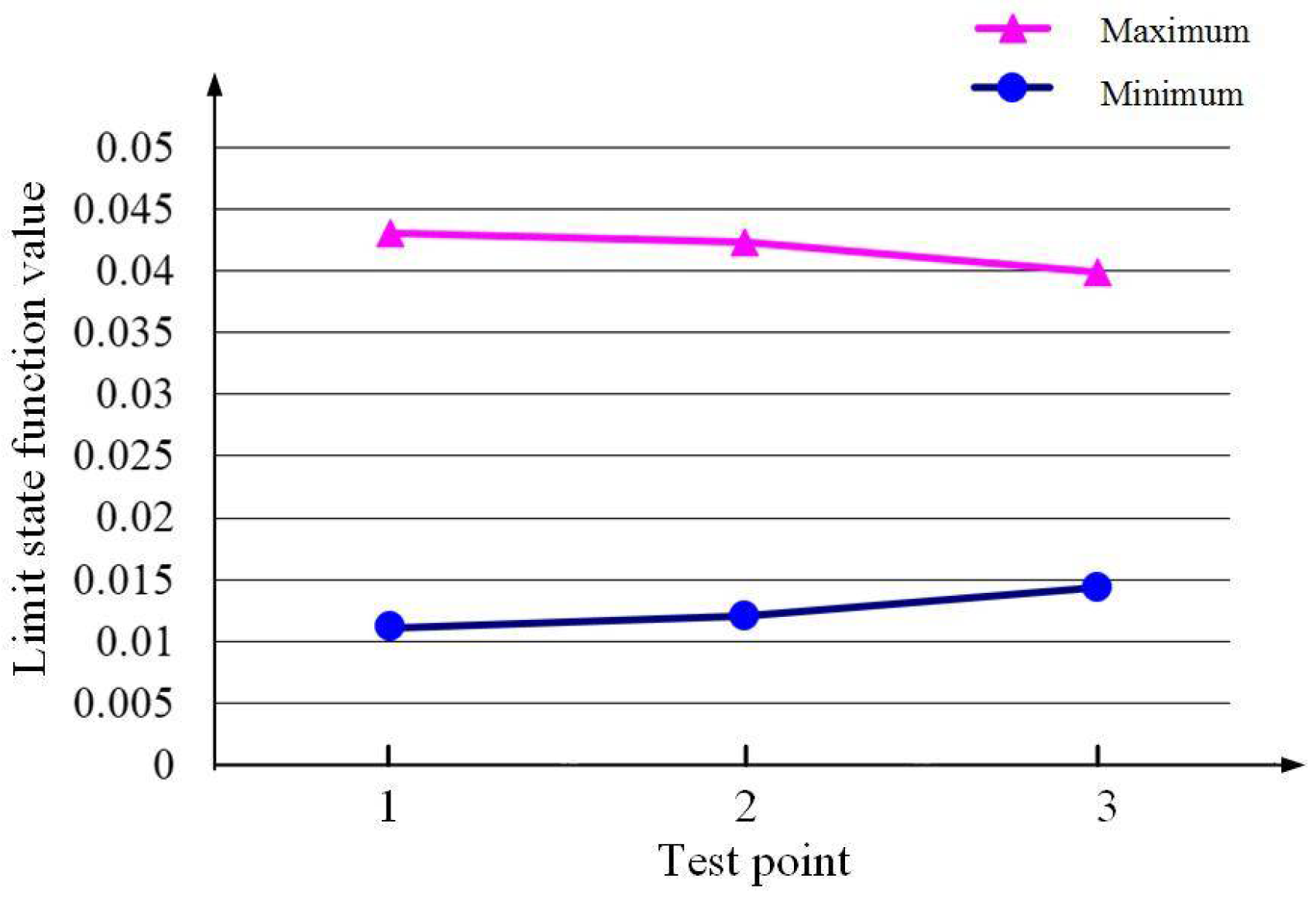
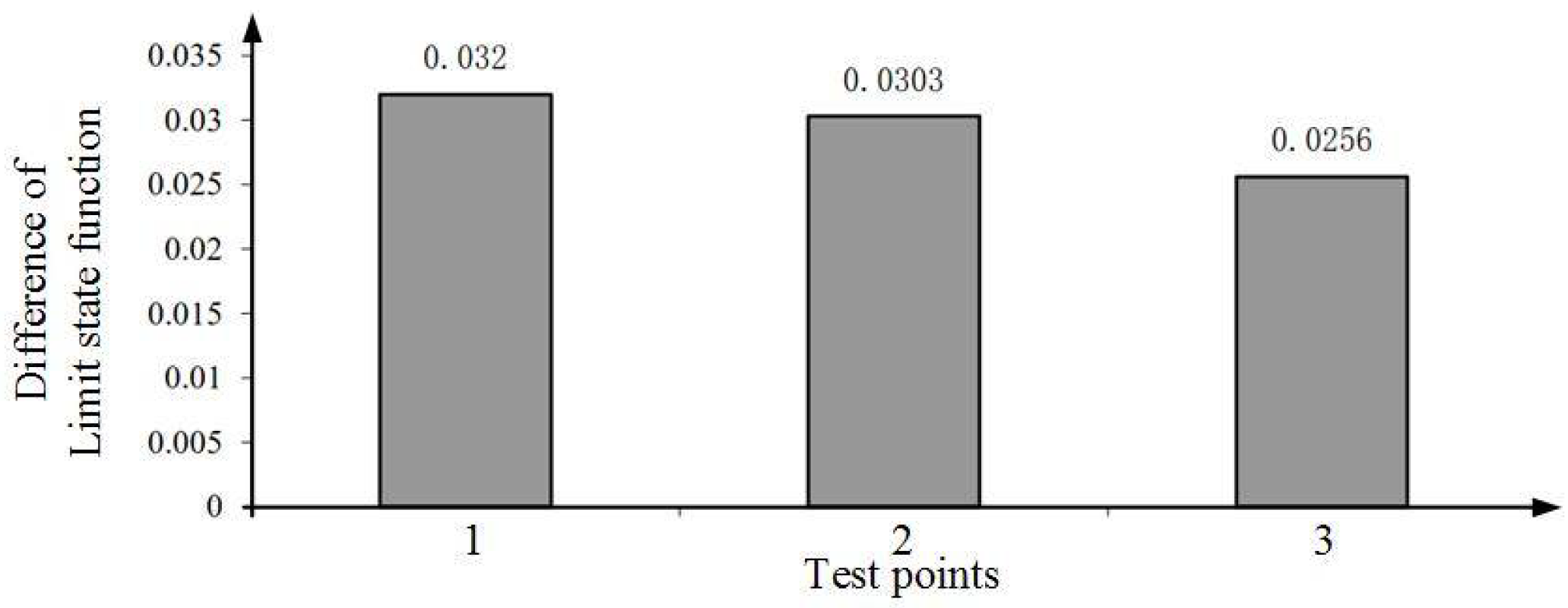

| Test Point | Method | xMPP = {x1, x2, x3, x4, x5} | Limi-State Function Value | Iteration Times |
|---|---|---|---|---|
| Case 1 | SMPRA | (1.1726, 1.1726, 1.1726, 1.0017, 1.0017) | g1(x) = 0.0323 | 232 |
| Case2: Test point 1 | MU-DBMRA | (1.1933, 1.1620, 1.1625, 1.0036, 0.9931) | g1(x,v)min = 0.0111 | 258 |
| (1.1937, 1.1623, 1.1617, 0.9964, 1.0069) | g1(x,v)max = 0.0431 | 258 | ||
| MCs | (1.2014, 1.1872, 1.1359, 1.0763, 1.0018) | g1(x,v)min = 0.0092 | 296,000 | |
| (1.2143, 1.1924, 1.1427, 1.0914, 1.0067) | g1(x,v)max = 0.0513 | 296,000 | ||
| MDF + SQP | (1.2212, 1.1812, 1.0906, 1.0000, 1.0000) | g1(x,v) = 0.0429 | 304 | |
| IDF + SQP | (1.2209, 1.1816, 1.0951, 1.0000, 1.0000) | g1(x,v) = 0.0172 | 276 | |
| Case2: Test point 2 | MU-DBMRA | (1.1933, 1.1620, 1.1624, 1.0023, 0.9912) | g1(x,v)min = 0.0120 | 258 |
| (1.1936, 1.1622, 1.1618, 0.9977, 1.0088) | g1(x,v)max = 0.0423 | 258 | ||
| MCs | (1.1879, 1.1564, 1.1607, 1.0008, 0.9847) | g1(x,v)min = 0.0021 | 296,000 | |
| (1.1952, 1.1693, 1.1684, 1.0042, 1.0106) | g1(x,v)max = 0.0657 | 296,000 | ||
| Case2: Test point 3 | MU-DBMRA | (1.1932, 1.1619, 1.1627, 1.0050, 0.9988) | g1(x,v)min = 0.0143 | 258 |
| (1.1938, 1.1623, 1.1615, 0.9950, 1.0012) | g1(x,v)max = 0.0399 | 258 | ||
| MCs | (1.1884, 1.1579, 1.1631, 1.0021, 0.9864) | g1(x,v)min = 0.0074 | 296,000 | |
| (1.1804, 1.1672, 1.1616, 1.0032, 1.0094) | g1(x,v)max = 0.0362 | 296,000 |
| Constraints | Specification | Expression |
|---|---|---|
| Bending stress constraint of gear | ||
| Contact stress constraint of gear | ||
| Dimensional constraints 1 | ||
| Dimensional constraints 2 | ||
| Dimensional constraints 3 | ||
| Small shaft lateral displacement constraint | ||
| Large shaft lateral displacement constraint | ||
| Minor shaft stress constraint | ||
| Major shaft stress constraint | ||
| Dimensional constraints 4 | ||
| Dimensional constraints 5 |
| Limit State Function Value | MPP | ||||
|---|---|---|---|---|---|
| x1 | x2 | x3 | x5 | x7 | |
| g1 = 0.4915 | 2.9916 | 0.6755 | 22.9989 | 7.8000 | 5.2500 |
| g2 = 0.4414 | 2.9916 | 0.6755 | 22.9978 | 7.8000 | 5.2500 |
| g3 = −0.2752 | 2.9801 | 0.8223 | 23.0000 | 7.8000 | 5.2500 |
| g4 = 1.6925 | 3.0164 | 0.6768 | 23.0000 | 7.8000 | 5.2500 |
| g5 = 1.1079 | 3.0000 | 0.8250 | 23.0027 | 7.8000 | 5.2500 |
| g7 = 11.6888 | 3.0000 | 0.6854 | 22.9981 | 7.8170 | 5.2160 |
| g9 = −0.0617 | 3.0000 | 0.7499 | 23.0000 | 7.8000 | 5.1750 |
| g11 = 0.0017 | 3.0000 | 0.7500 | 23.0000 | 7.7496 | 5.3055 |
| Test Points | Method | Value of Functons | Iteration Times |
|---|---|---|---|
| 1 | SMPRA | g6(x) = 6.341 | 124 |
| 2 | MU-DBMRA | g6(x,v)min = 1.1816 | 163 |
| g6(x,v)max = 1.3631 | 163 | ||
| MCs | g6(x) = 0.416 | 18,000 | |
| MDF + SQP | g6(x) = 1.622 | 231 | |
| IDF + SQP | g6(x) = 1.431 | 192 |
| Test Points | Value of Functions | Iteration Times |
|---|---|---|
| 1 | g8(x) = 0.003 | 154 |
| 2 | g8(x,v)min = −0.055 | 188 |
| g8(x,v)max = 0.076 | 188 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Liu, J.; Xu, W. A Decoupling Strategy for Reliability Analysis of Multidisciplinary System with Aleatory and Epistemic Uncertainties. Appl. Sci. 2021, 11, 7008. https://doi.org/10.3390/app11157008
Fu C, Liu J, Xu W. A Decoupling Strategy for Reliability Analysis of Multidisciplinary System with Aleatory and Epistemic Uncertainties. Applied Sciences. 2021; 11(15):7008. https://doi.org/10.3390/app11157008
Chicago/Turabian StyleFu, Chao, Jihong Liu, and Wenting Xu. 2021. "A Decoupling Strategy for Reliability Analysis of Multidisciplinary System with Aleatory and Epistemic Uncertainties" Applied Sciences 11, no. 15: 7008. https://doi.org/10.3390/app11157008
APA StyleFu, C., Liu, J., & Xu, W. (2021). A Decoupling Strategy for Reliability Analysis of Multidisciplinary System with Aleatory and Epistemic Uncertainties. Applied Sciences, 11(15), 7008. https://doi.org/10.3390/app11157008







