Installation of Bored Piles with a Protective Silicate Shell of a New Design in Saline Silty-Clayey Soils
Abstract
:1. Introduction
- -
- Formation of a protective corrosion-resistant “shell” around the pile;
- -
- Formation of a compacted or ground-improved soil layer around the pile by increasing its strength and deformation properties, structural and suffusion resistance, and water resistance and waterproofness;
- -
- Increasing the strength and corrosion resistance of the concrete of the structure by using modifiers, etc.
2. Materials and Methods
2.1. Design of the Protective Case
- -
- The rate of coagulation of silicate solutions and the formation of SiO₂ gel films on salts depend on three factors: the concentration of the sodium silicate solution, and the amount and quality of salts present in the salt waste. Film formation during the interaction of a sodium silicate solution with calcium sulfate slows down with an increase in the concentration of the silicate solution, which is explained by a decrease in the solubility of the reacting salt with the increase in the concentration of silicate. The film thicknesses when using sodium silicate of 10%, 20%, and 30% concentrations were, respectively, 40, 20, and 10 microns.
- -
- With regard to the coagulation of silicate solutions in the soil, the sulfuric acid salts of Ca+2; and Mg+2 are of the greatest importance as the most soluble compounds, in comparison with carbon dioxide Ca, which is almost inert.
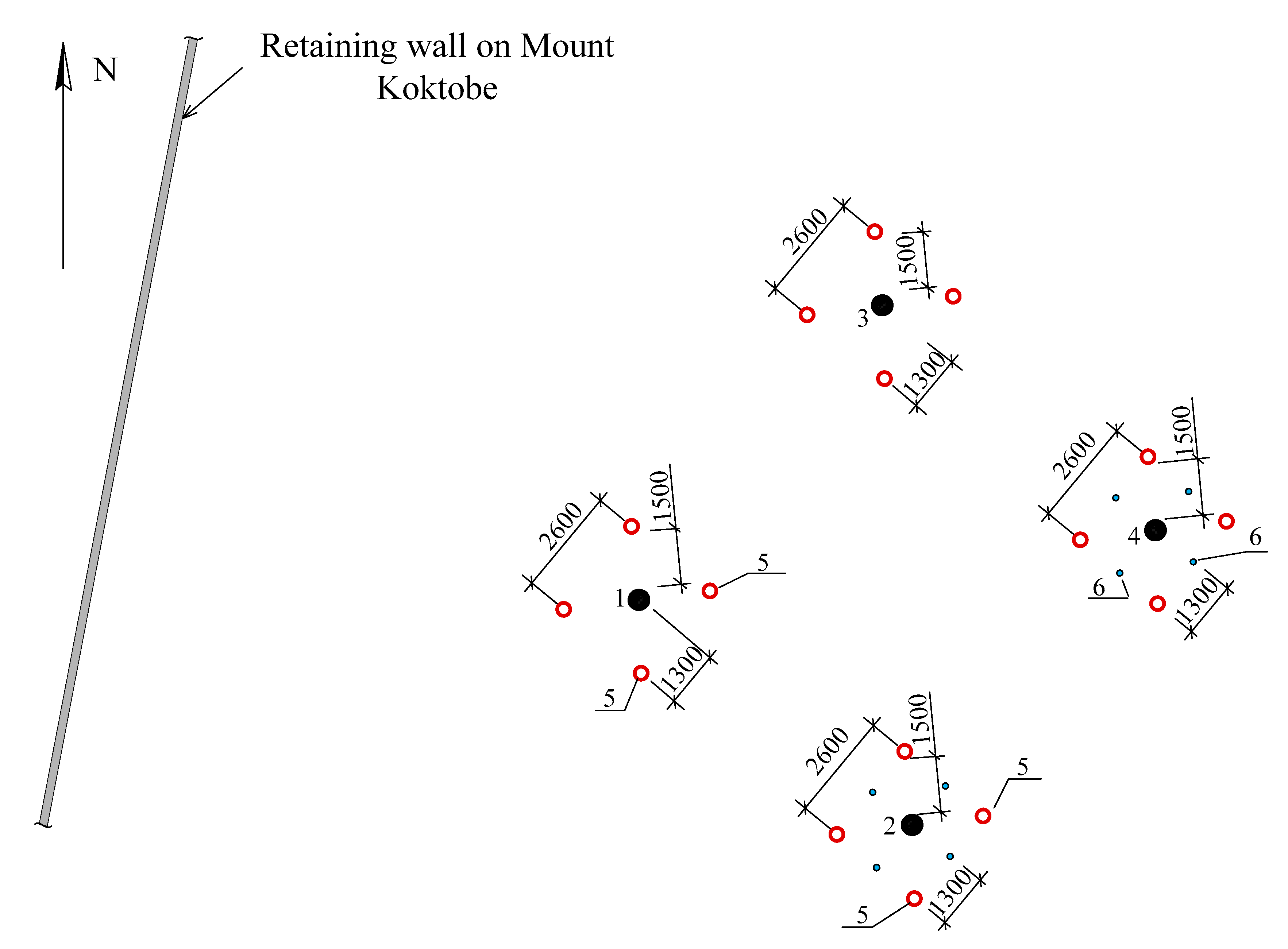
2.2. Field Tests
- -
- Six bored piles with a protective shell, without soil wetting;
- -
- Six ordinary bored piles, without soil wetting;
- -
- Six bored piles with a protective shell, after wetting the soil;
- -
- Six ordinary bored piles, after wetting the soil.
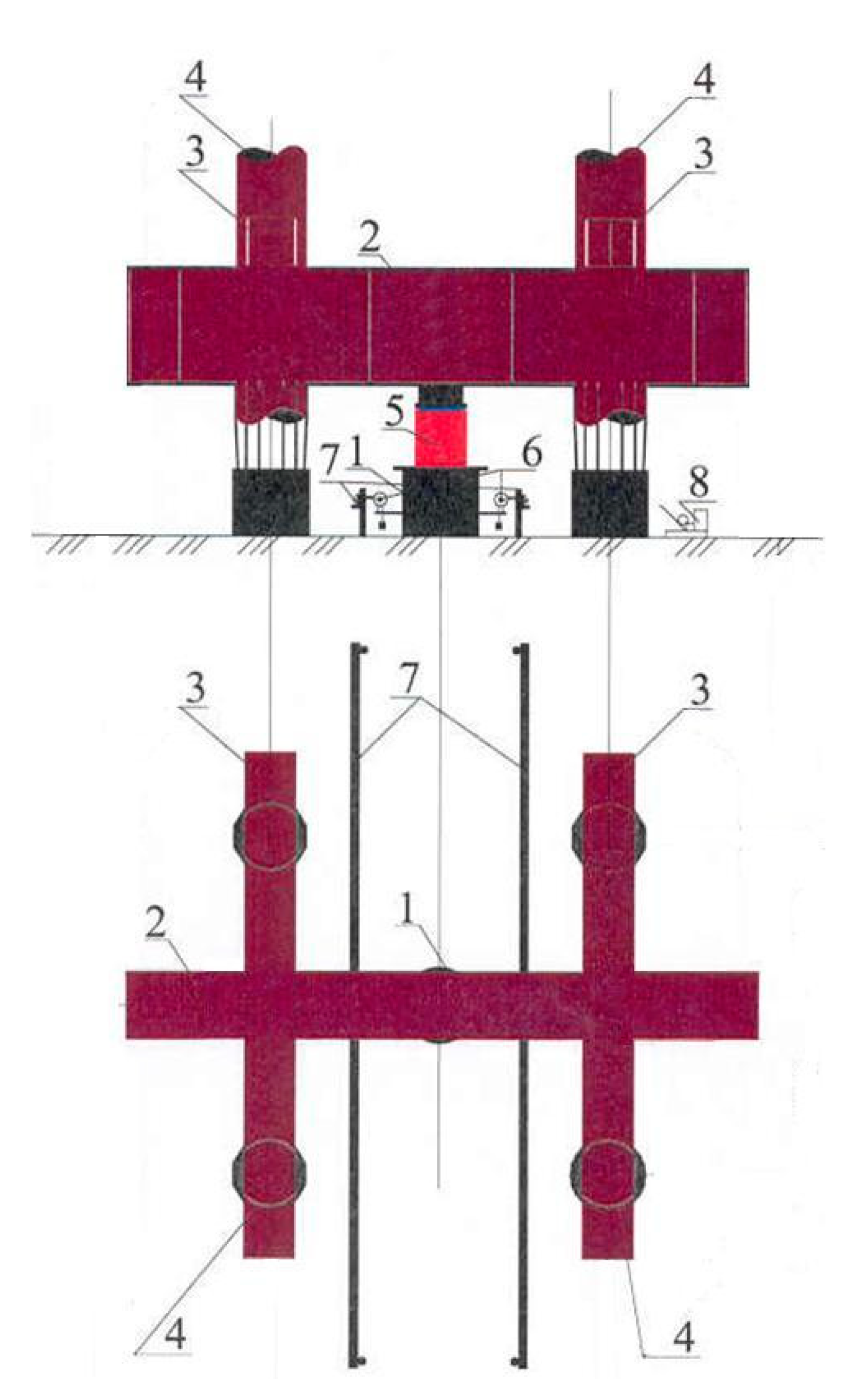
2.3. Site Testing Procedure
- -
- Hydraulic jack of the SMZh-158A brand with a lifting capacity of 2000 kN;
- -
- Manual pumping station MNSR-400 with pressure gauge MTP-160, with a capacity of 785 MPa;
- -
- Two deflection indicators 6PAO (for determining the settlement of the pile).
- -
- The piles were maintained for 7–10 days from the moment of their installation (until the concrete of the pile reached more than 80% of the design strength);
- -
- Loading of the pile was implemented by a vertical-compressing multiple-increasing load and held constant until the rate of settlement fell below 0.1 mm per hour;
- -
- Pile settlement was recorded using electrical displacement transducers according to the standard;
- -
- Unloading of the tested piles was carried out in steps equal to double loading steps;
- -
- Readings of the elastic deformation of the soil and concrete pile during unloading were registered at each stage every 15 min.
3. Results
4. Numerical Modeling of a Bored Pile with a Protective Shell in the Plaxis 2D Discussion
5. Discussion
6. Conclusions
- A method for the construction of a bored pile with a protective shell cast from a silicate solution was developed. The copyright, novelty, and efficiency of the proposed technology were confirmed by a patent [34] and by the results of experimental approbation.
- The physicochemical processes of the formation of a protective shell around a bored pile was described in the process of the interaction of a silicate solution with salts present in saline soils, as a result of the crystallization of acidic silica gel films on soil particles and capillaries.
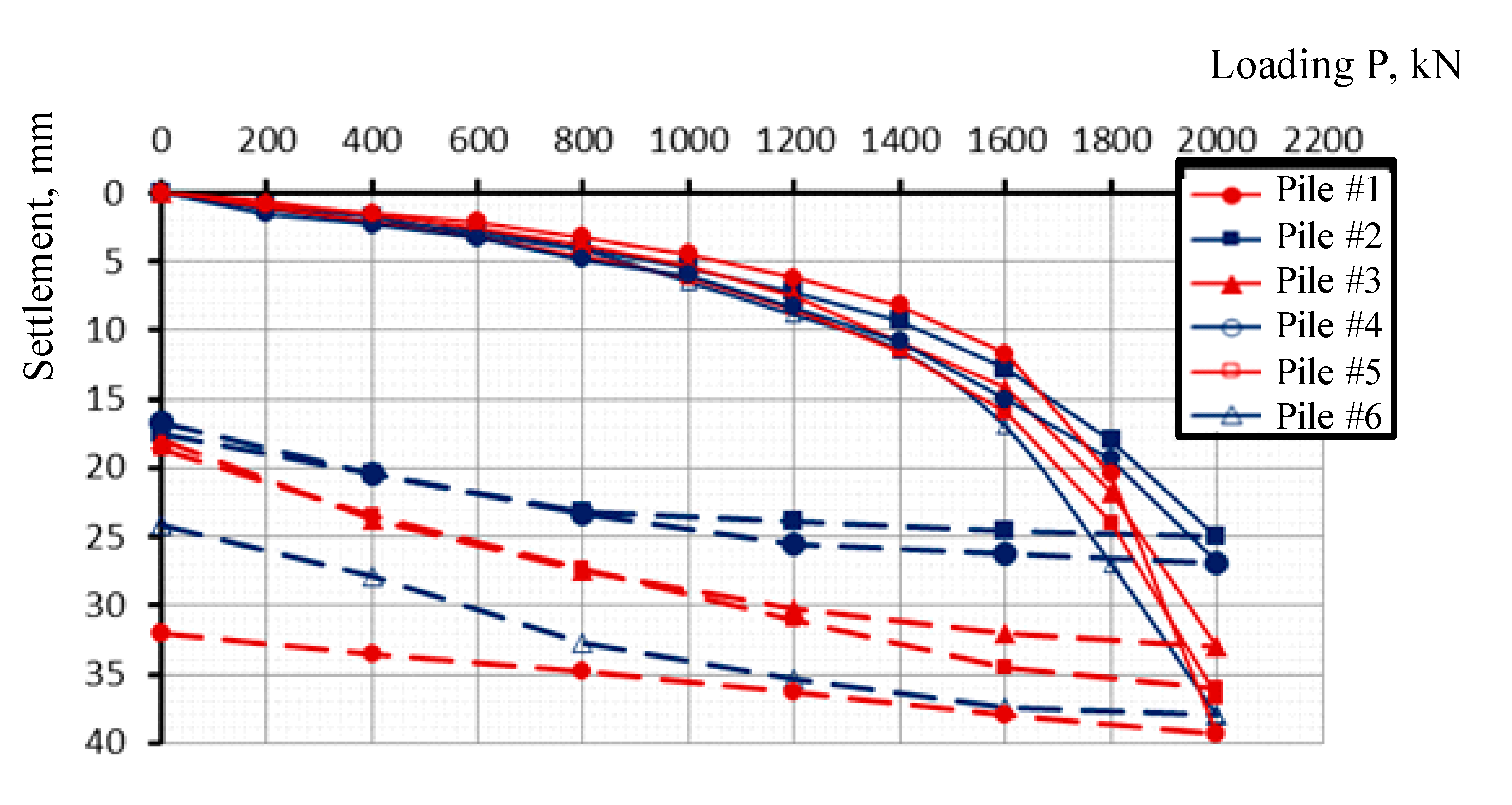
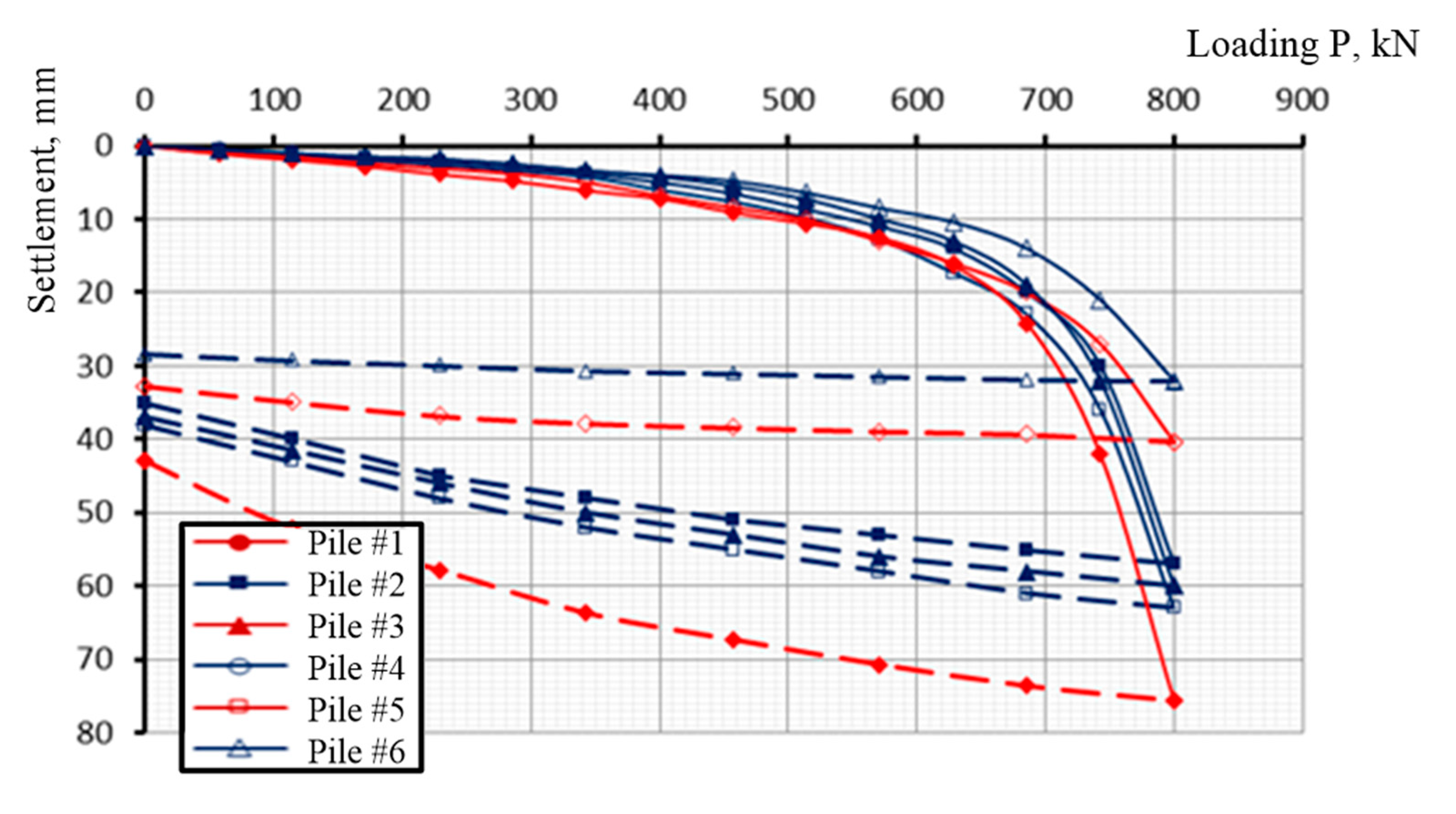
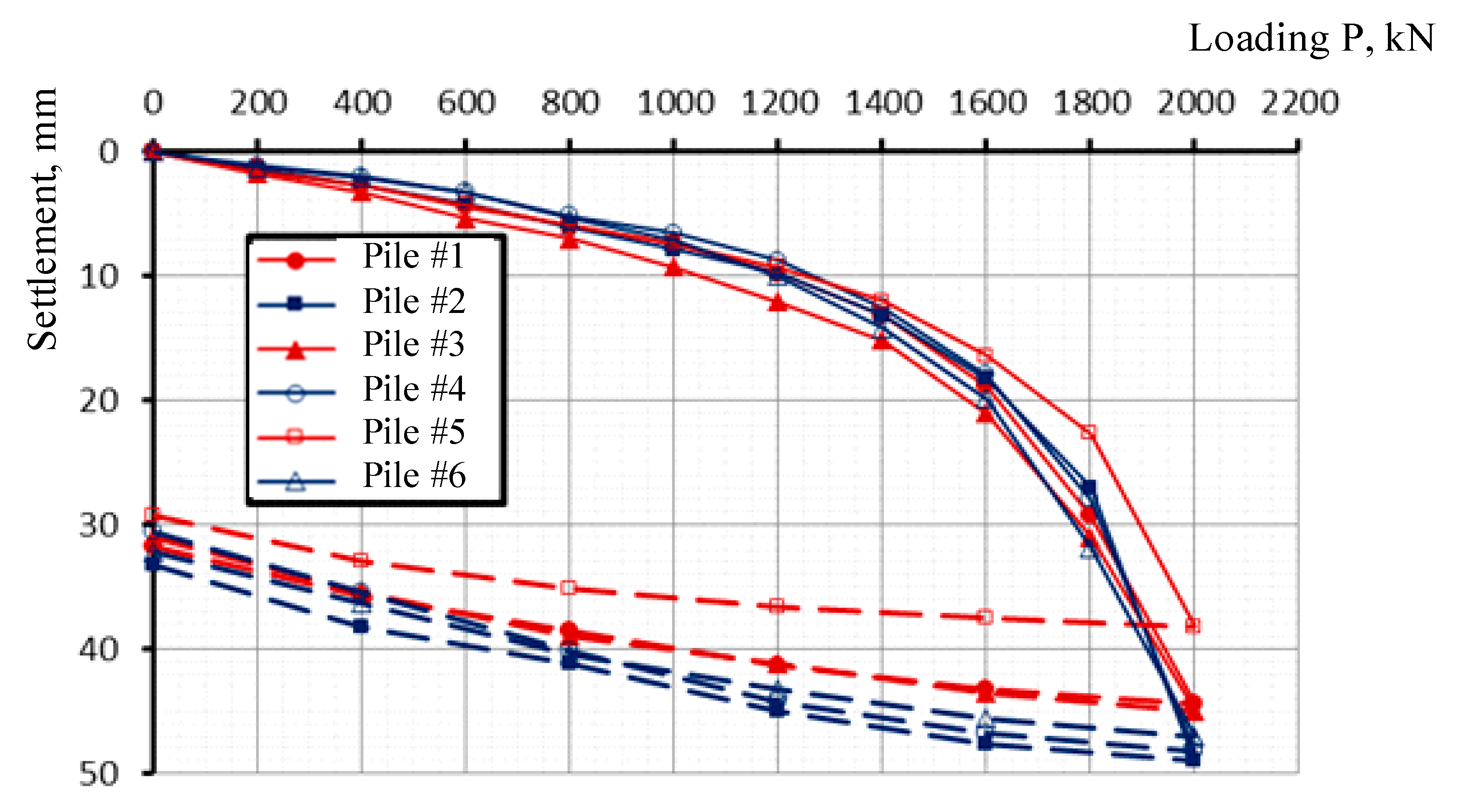
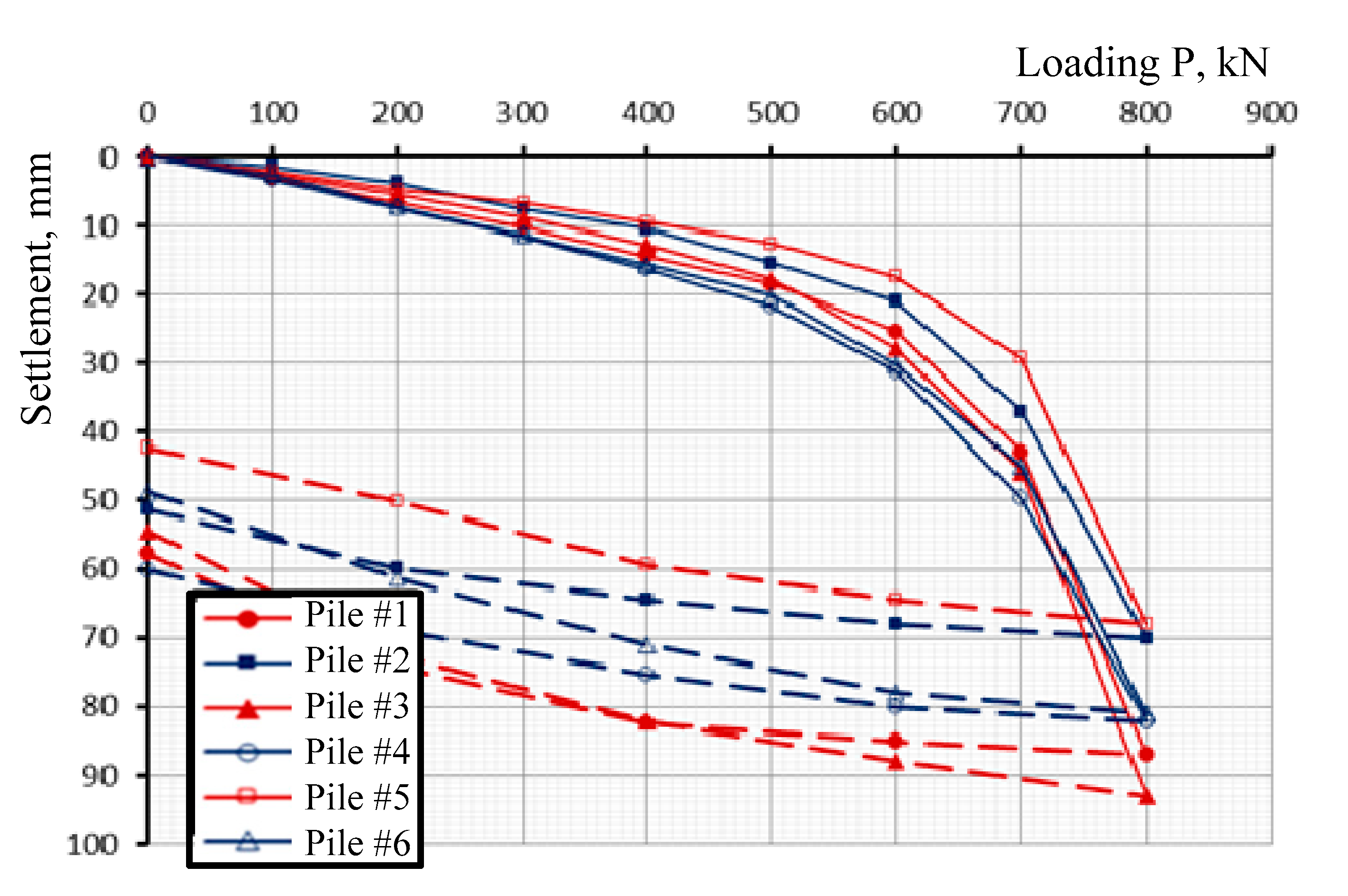
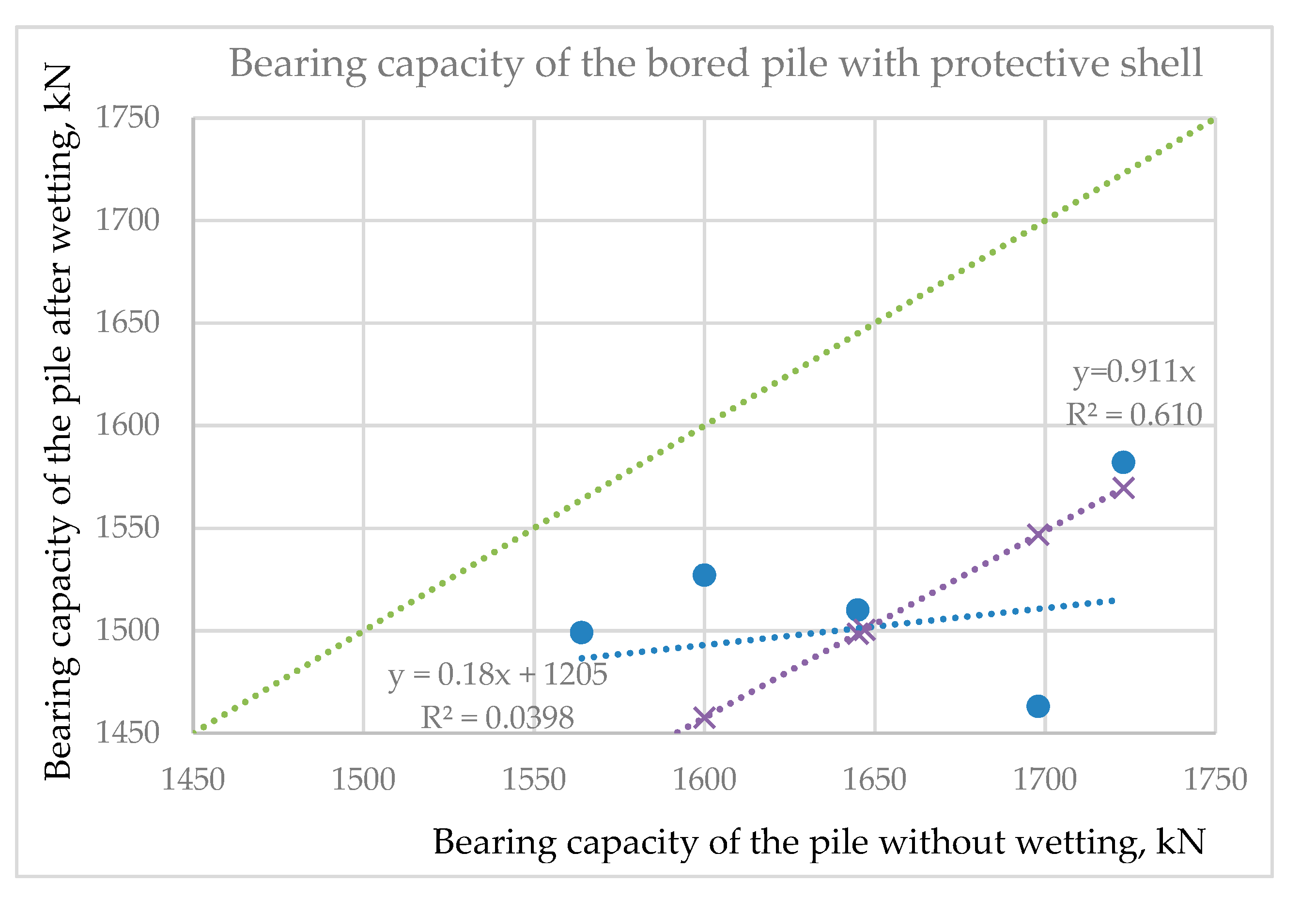
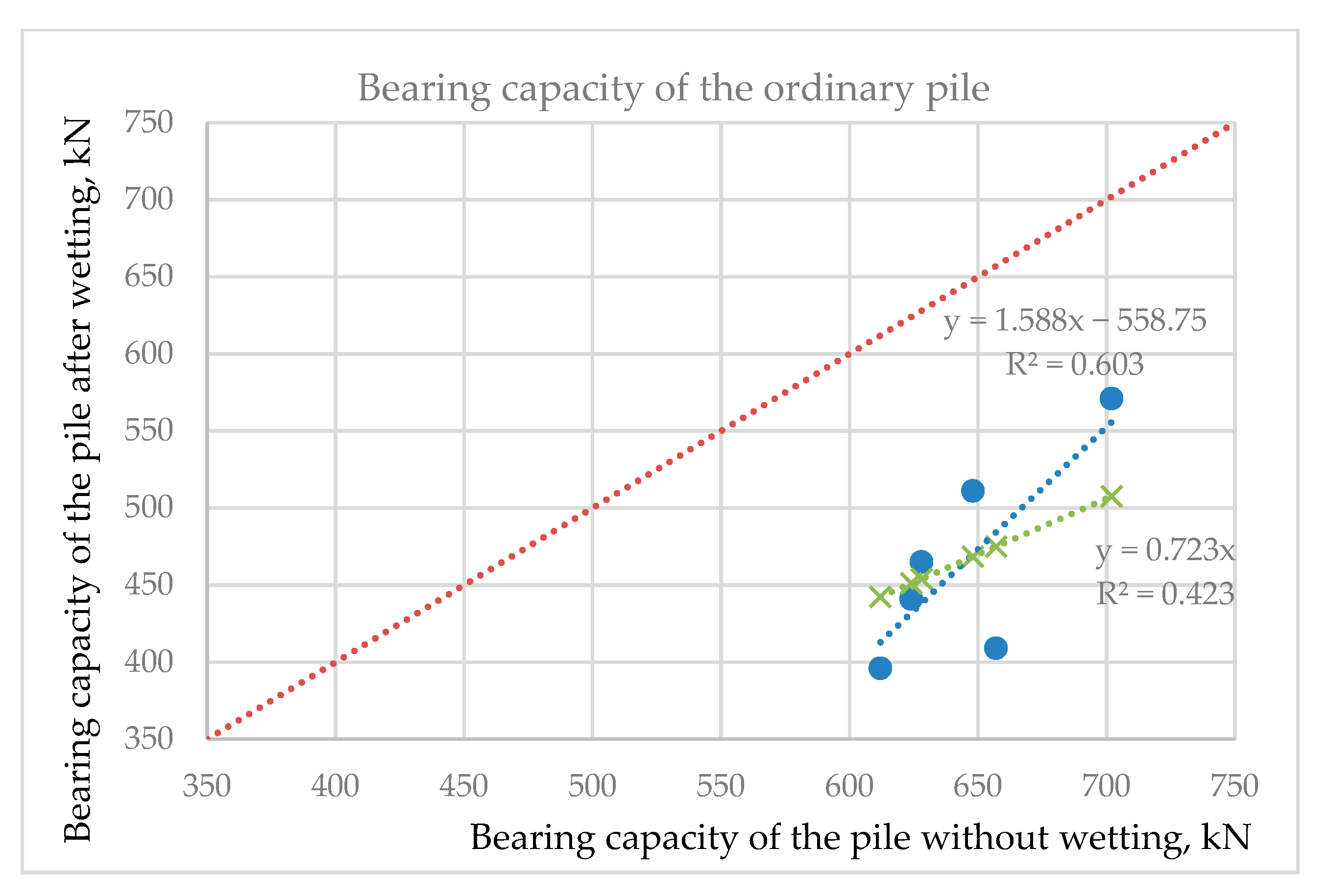
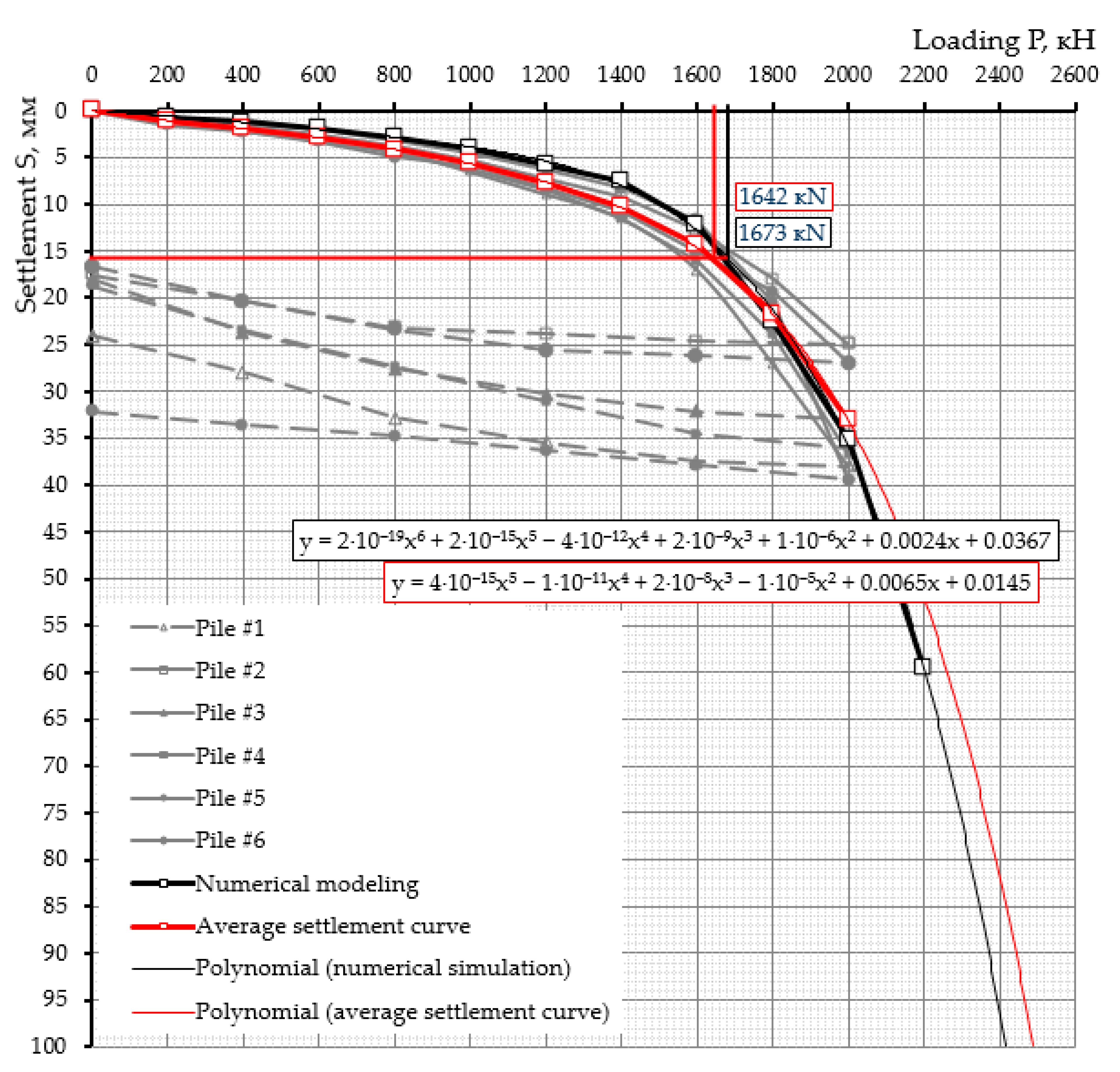
- According to the results of static pile load (SLT) tests of ordinary piles and piles with a protective and bearing shell of the new design, the bearing capacity of the casts exceeded the bearing capacity of ordinary piles, without soil wetting, by 2.5 times on average, and after soil wetting—by 3.2 times.
- According to the SLT results, soil wetting greatly affected the bearing capacity of ordinary piles, while piles with protective silicate shells were more stable due to the increased cross-section of the support area. It was determined that soil wetting decreased the bearing capacity of the ordinary pile by 27.7% on average, and by 8.9% in the case of a pile with protective and the load-bearing silicate shell.
- Numerical modeling of the piles with a protective shell showed a great convergence of the results of modeling and static pile load tests results. The polynomial functional dependence of the load–settlement was obtained, with which a prediction of the numerical and averaged experimental curve “load–settlement” was made with an accuracy of 99.9%.
- An economic comparison of the costs of the material and construction of ordinary piles and piles with a protective and load-bearing shell confirmed an extended economic effect of the developed technology of piling in a protective silicate shell with a significant reduction in the cost of piling, equal to 27.85%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adikov, M.T.; Podkolzin, V.V. Experience in Studying the Building Properties of Saline Soils in South Kazakhstan; Express Information: Alma-Ata, Kazakhstan, 1976. (In Russian) [Google Scholar]
- Ministry of National Economy of the Republic of Kazakhstan. Design of Buildings on Salt Soils: Regulatory-Technical Guide; NTP RK 07-01.1-2011; Office of Technical Regulation and Rationing of the Construction Committee, Housing and Communal Services and Management Land Resources of the Ministry of National Economy of the Republic of Kazakhstan: Astana, Kazakhstan, 2011. Available online: https://online.zakon.kz/Document/?doc_id=34440425 (accessed on 21 July 2021). (In Russian)
- Ministry of National Economy of the Republic of Kazakhstan. Foundations of Buildings and Structures; SP RK 5.01-102-2013; Office of Technical Regulation and Rationing of the Construction Committee, Housing and Communal Services and Management Land Resources of the Ministry of National Economy of the Republic of Kazakhstan: Astana, Kazakhstan, 2013. Available online: https://online.zakon.kz/Document/?doc_id=39343712 (accessed on 21 July 2021). (In Russian)
- Pan, X.; Shi, Z.; Shi, C.; Ling, T.-C.; Li, N. A review on concrete surface treatment Part I: Types and mechanisms. Constr. Build. Mater. 2017, 132, 578–590. [Google Scholar] [CrossRef]
- De Brito, J.; Kurda, R. The past and future of sustainable concrete: A critical review and new strategies on cement-based materials. J. Clean. Prod. 2021, 281, 123558. [Google Scholar] [CrossRef]
- Zerda, A.S.; Lesser, A.J. Intercalated clay nanocomposites: Morphology, mechanics, and fracture behavior. J. Polym. Sci. B Polym. Phys. 2001, 39, 1137–1146. [Google Scholar] [CrossRef]
- Wang, W.; Lockwood, K.; Boyd, L.M.; Davidson, M.D.; Movafaghi, S.; Vahabi, H.; Khetani, S.R.; Kota, A.K. Super hydrophobic coatings with edible materials. ACS Appl. Mater. Interfaces 2016, 8, 18664–18668. [Google Scholar] [CrossRef]
- Kozak, A. Multi-criteria assessment of an acrylic coating exposed to natural and artificial weathering. Procedia Eng. 2015, 108, 664–672. [Google Scholar] [CrossRef] [Green Version]
- Elnaggar, E.M.; Elsokkary, T.M.; Shohide, M.A.; El-Sabbagh, B.A.; Abdel Gawwad, H.A. Surface protection of concrete by new protective coating. Constr. Build. Mater. 2019, 220, 245–252. [Google Scholar] [CrossRef]
- Scarfato, P.; Di Maio, L.; Fariello, M.L.; Russo, P.; Incarnato, L. Preparation and evaluation of polymer/clay nanocomposite surface treatments for concrete durability enhancement. Cem. Concr. Compos. 2012, 34, 297–305. [Google Scholar] [CrossRef]
- Carmona-Quiroga, P.M.; Martínez-Ramírez, S.; Sobrados, I.; Blanco-Varela, M.T. Interaction between two anti-graffiti treatments and cement mortar (paste). Cem. Concr. Res. 2010, 40, 723–730. [Google Scholar] [CrossRef]
- Peng, C.; Chen, Z.; Tiwari, M.K. All-organic superhydrophobic coatings with mechanochemical robustness and liquid impalement resistance. Nat. Mater. 2018, 17, 355–360. [Google Scholar] [CrossRef]
- Li, G.; Yue, J.; Guo, C.; Ji, Y. Influences of modified nanoparticles on hydro phobicity of concrete with organic film coating. Constr. Build. Mater. 2018, 169, 1–7. [Google Scholar] [CrossRef]
- Esposito Corcione, C.; Striani, R.; Capone, C.; Molfetta, M.; Vendetta, S.; Frigione, M. Preliminary study of the application of a novel hydrophobic photo polymerizable nano-structured coating on concrete substrates. Prog. Org. Coat. 2018, 121, 82–189. [Google Scholar] [CrossRef]
- Mora, E.; Gonzalez, G.; Romero, P.; Castellon, E. Control of water absorption in concrete materials by modification with hybrid hydrophobic silica particles. Constr. Build. Mater. 2019, 221, 210–218. [Google Scholar] [CrossRef]
- Feng, Z.; Wang, F.; Xie, T.; Ou, J.; Xue, M.; Li, W. Integral hydrophobic concrete without using silane. Constr. Build. Mater. 2019, 227, 116678. [Google Scholar] [CrossRef]
- Chen, S.; Li, X.; Li, Y.; Sun, J. Intumescent flame-retardant and self-healing superhydrophobic coatings on cotton fabric. ACS Nano 2015, 9, 4070–4076. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Qiu, J.; Sakai, E.; Kanazawa, N.; Liang, R.; Feng, H. Robust and superhydrophobic surface modification by a “Paintþ Adhesive” method: Applications in self-cleaning after oil contamination and oilewater separation. ACS Appl. Mater. Interfaces 2016, 8, 17659–17667. [Google Scholar] [CrossRef]
- Iqbal, R.; Majhy, B.; Sen, A. Facile fabrication and characterization of a PDMS derived candle soot coated stable biocompatible superhydrophobic and superhemophobic surface. ACS Appl. Mater. Interfaces 2017, 9, 31170–31180. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Li, D.; Tian, H.; Zha, F.; Feng, H.; Guo, L. Smart candle soot coated membranes for on-demand immiscible oil/water mixture and emulsion switchable separation. Nanoscale 2017, 9, 13610–13617. [Google Scholar] [CrossRef]
- Pan, S.; Guo, R.; Bjornmalm, M.; Richardson, J.J.; Li, L.; Peng, C.; Bertleff-Zieschang, N.; Xu, W.; Jiang, J.; Caruso, F. Coatings super-repellent to ultralow surface tension liquids. Nat. Mater. 2018, 17, 1040–1047. [Google Scholar] [CrossRef]
- Husni, H.; Nazari, M.R.; Yee, H.M.; Rohim, R.; Yusuff, A.; Mohd Ariff, M.A.; Ahmad, N.N.R.; Leo, C.P.; Junaidi, M.U.M. Superhydrophobic rice husk ash coating on concrete. Constr. Build. Mater. 2017, 144, 385–391. [Google Scholar] [CrossRef]
- Jia, L.; Shi, C.; Pan, X.; Zhang, J.; Wu, L. Effects of inorganic surface treatment on water permeability of cement-based materials. Cem. Concr. Compos. 2016, 67, 85–92. [Google Scholar] [CrossRef]
- Jiang, L.; Xue, X.; Zhang, W.; Yang, J.; Zhang, H.; Li, Y.; Zhang, R.; Zhang, Z.; Xu, L.; Qu, J.; et al. The investigation of factors affecting the water impermeability of inorganic sodium silicate-based concrete sealers. Constr. Build. Mater. 2015, 93, 729–736. [Google Scholar] [CrossRef]
- Moon, H.Y.; Shin, D.G.; Choi, D.S. Evaluation of the durability of mortar and concrete applied with inorganic coating material and surface treatment system. Constr. Build. Mater. 2007, 21, 362–369. [Google Scholar] [CrossRef]
- Xu, J.; Li, Y.; Wang, S.; Ren, J.; Ding, J.; Wang, Q.; Cheng, D.; Yu, F. Cement-Improved Wetting Resistance of Coarse Saline Soils in Northwest China. J. Test. Eval. 2021, 49, 229–254. [Google Scholar] [CrossRef]
- Yaghoubi, M.; Arulrajah, A.; Disfani, M.M.; Horpibulsuk, S.; Bo, M.W.; Darmawan, S. Effects of industrial by-product based geopolymers on the strength development of a soft soil. Soils Found. 2018, 58, 716–728. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, W.; Zhao, L.; Peng, Z. Field in-situ stabilization of bored pile mud: Engineering properties and application for pavement. Constr. Build. Mater. 2018, 165, 541–547. [Google Scholar] [CrossRef]
- Unaibayev, B.B.; Unaibayev, B.Z.; Andreyachshenko, V. Cast-in-situ piles encasements based on oil-bituminous rocks (kirs) in saline soils. Sci. Rev. Eng. Environ. Sci. 2021, 30, 51–61. [Google Scholar] [CrossRef]
- Ministry of National Economy of the Republic of Kazakhstan. Construction Structures Corrosion Protection; SP RK 2.01-101-2013; Office of Technical Regulation and Rationing of the Construction Committee, Housing and Communal Services and Management Land Resources of the Ministry of National Economy of the Republic of Kazakhstan: Astana, Kazakhstan, 2013. Available online: https://online.zakon.kz/Document/?doc_id=33796763 (accessed on 21 July 2021). (In Russian)
- Karimov, Y.L.; Latipov, Z.Y.; Kayumov, O.A.; Boimurodov, N.A. Development of the technology for fixing salt waste from the mine of the Tyubegatan mining complex. Univers. Tech. Sci. Electron. Sci. J. 2020, 12, 81. Available online: https://7universum.com/ru/tech/archive/item/11071 (accessed on 23 March 2021).
- Ministry of National Economy of the Republic of Kazakhstan. Pile Foundations; SP RK 5.01-103-2013; Office of Technical Regulation and Rationing of the Construction Committee, Housing and Communal Services and Management Land Resources of the Ministry of National Economy of the Republic of Kazakhstan: Astana, Kazakhstan, 2013. Available online: https://online.zakon.kz/Document/?doc_id=38144008 (accessed on 21 July 2021). (In Russian)
- State Standard GOST 5686-2012; Soils Field Test: Methods for Piles; Standartinform: Moscow, Russian, 2012. (In Russian)
- A Method of Erecting a Bored Pile in Saline Loess Subsidence Soils. Innovative Patent for Invention No. 22796, Bulletin No. 8. 16 August 2010. (In Russian).
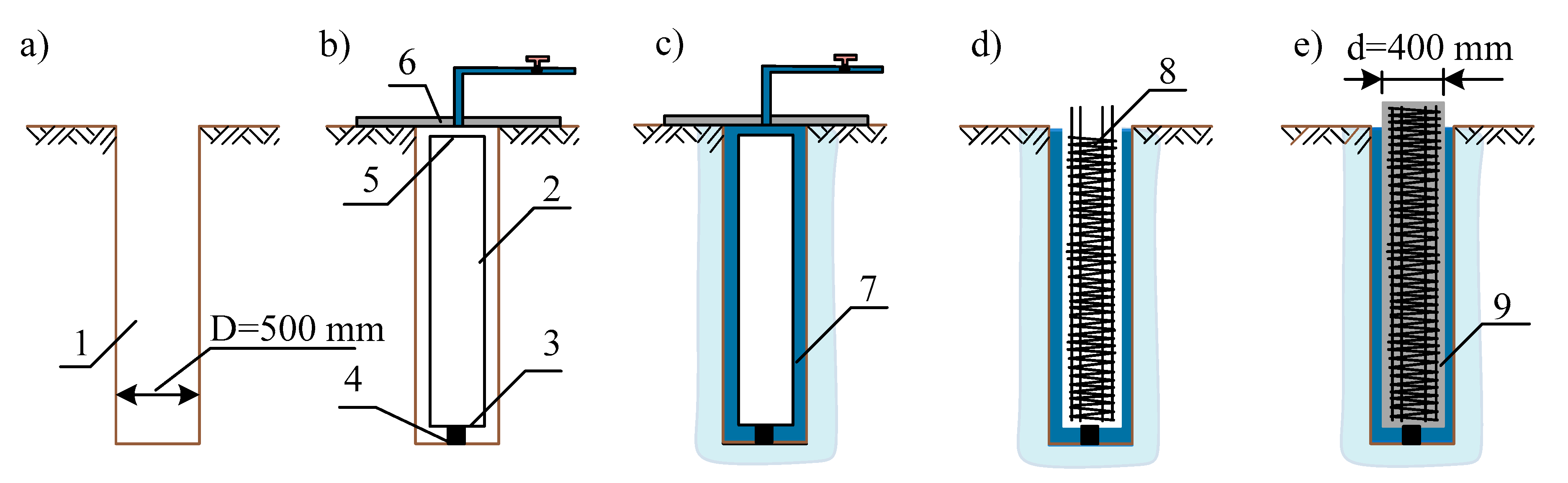
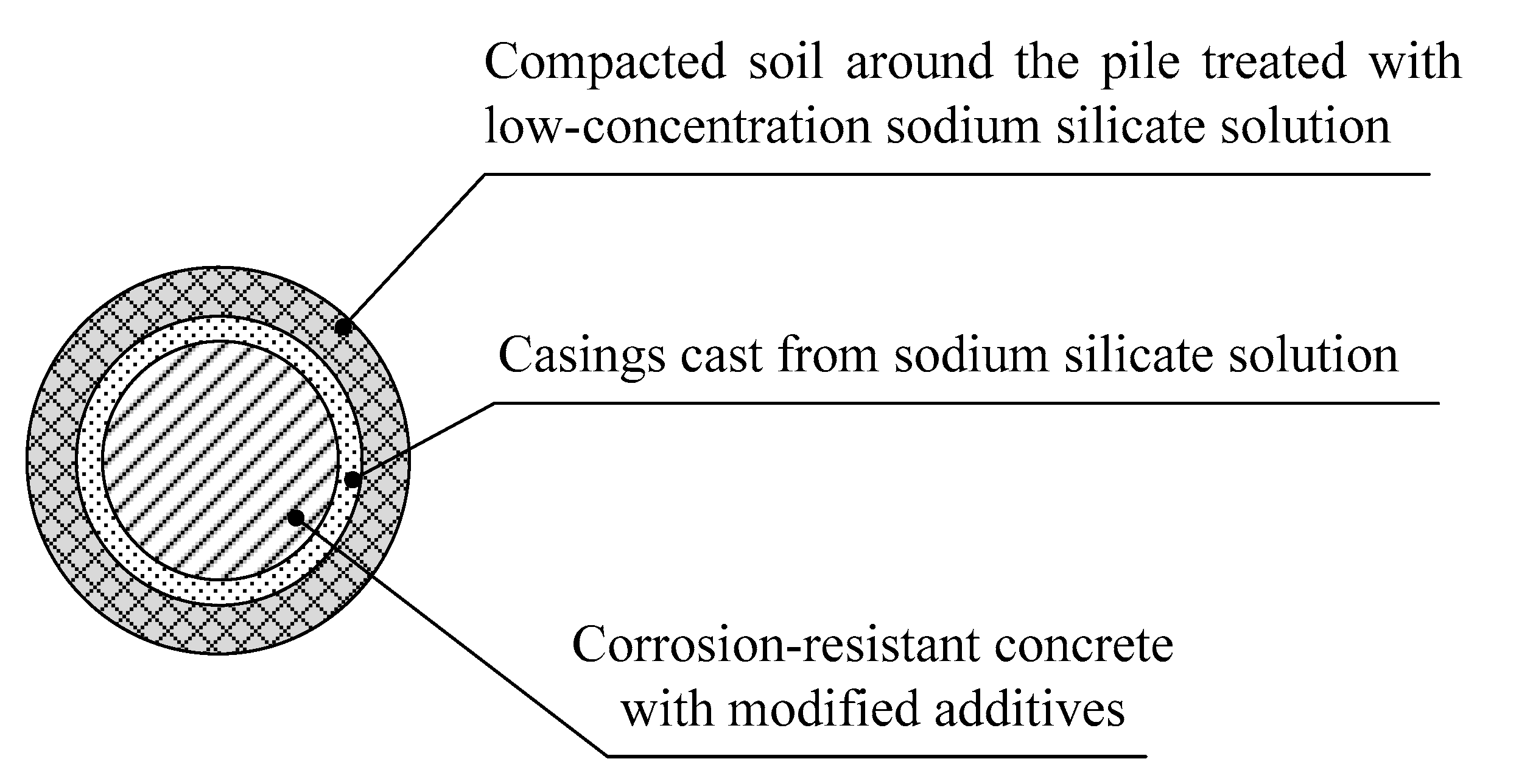
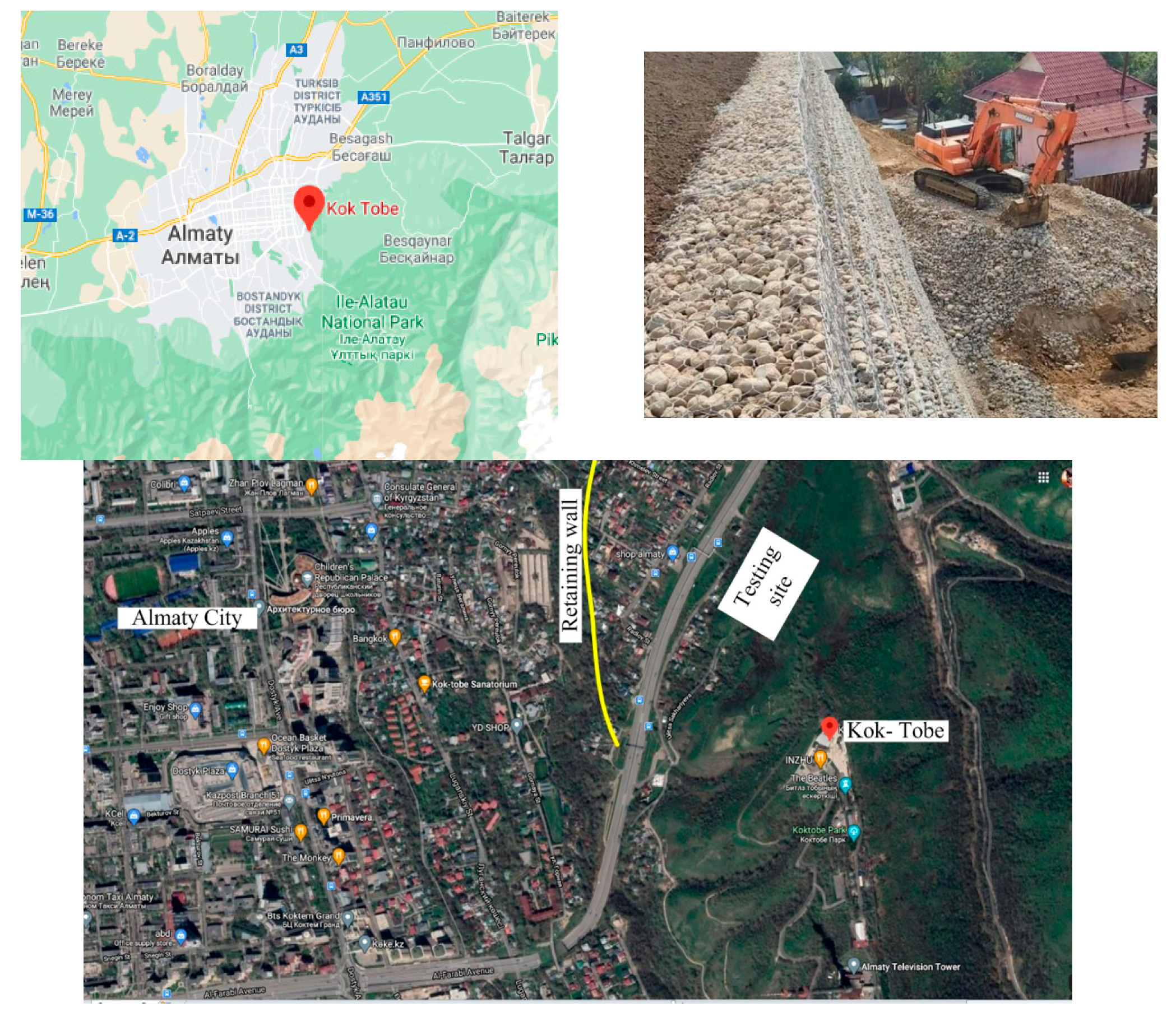
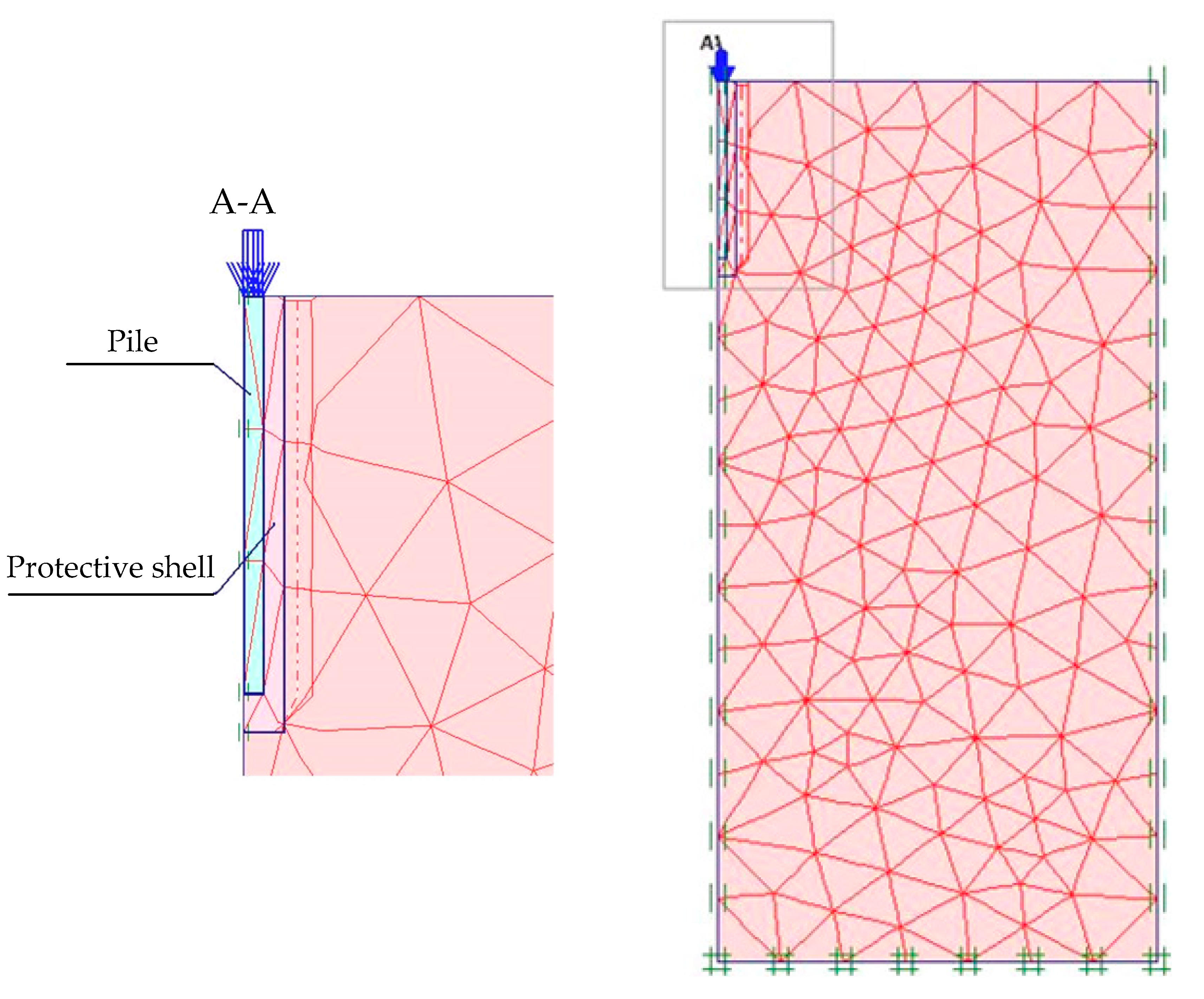
| Engineering—Geological Element | Description of Soils | Layer Thickness, m | Soil Properties | |||
|---|---|---|---|---|---|---|
| E, MPa | C, kPa | φ, Degrees | ρ, g/cm3 | |||
| 1 | Silty clays (with soil wetting) | 20 | 10.8 | 21 | 26 | 1.98 |
| Pile # | Pile Characteristics of | |||
|---|---|---|---|---|
| Bored Pile with Protective Shell, without Soil Wetting, kN | Ordinary Bored Pile, without Soil Wetting, kN | Bored Pile with Protective Shell, after Soil Wetting, kN | Ordinary Bored Pile, after Soil Wetting, kN | |
| pile #1 | 1564 | 648 | 1499 | 511 |
| pile #2 | 1723 | 702 | 1582 | 571 |
| pile #3 | 1647 | 657 | 1427 | 409 |
| pile #4 | 1600 | 612 | 1527 | 396 |
| pile #5 | 1645 | 628 | 1510 | 465 |
| pile #6 | 1698 | 624 | 1463 | 441 |
| Arithmetic mean, | 1646 | 645 | 1501 | 466 |
| Mean square deviation, Sn | 59 | 32 | 53 | 66 |
| Statistical criteria, v | 2.07 | |||
| Coefficient of variation, V 1 | 0.036 | 0.051 | 0.035 | 0.12 |
| Accuracy index, | 0.029 | 0.041 | 0.029 | 0.12 |
| Reliability factor, | 1.03 | 1.04 | 1.03 | 1.13 |
| Calculated values of F, kN | 1598 | 619 | 1458 | 411 |
| n | F`u | Fu | k | b | kx | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 1564 | 1499 | 2,446,096 | 2,247,001 | 2,344,436 | 0.180 | 1205.000 | 0.911 |
| 2 | 1723 | 1582 | 2,968,729 | 2,502,724 | 2,725,786 | |||
| 3 | 1647 | 1427 | 2,712,609 | 2,036,329 | 2,350,269 | |||
| 4 | 1600 | 1527 | 2,560,000 | 2,331,729 | 2,443,200 | |||
| 5 | 1645 | 1510 | 2,706,025 | 2,280,100 | 2,483,950 | |||
| 6 | 1698 | 1463 | 2,883,204 | 2,140,369 | 2,484,174 | |||
| 9877 | 9008 | 14,831,815 | 16,276,663 | 13,538,252 |
| n | F`u | Fu | k | b | kx | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 648 | 511 | 419,904 | 261,121 | 331,128 | 1.586 | −558.755 | 0.723 |
| 2 | 702 | 571 | 492,804 | 326,041 | 400,842 | |||
| 3 | 657 | 409 | 431,649 | 167,281 | 268,713 | |||
| 4 | 612 | 396 | 374,544 | 156,816 | 242,352 | |||
| 5 | 628 | 465 | 394,384 | 216,225 | 292,020 | |||
| 6 | 624 | 441 | 389,376 | 194,481 | 275,184 | |||
| 3871 | 2793 | 1,810,239 | 2,502,661 | 1,321,965 |
| Parameter Name | Designation | Unit | Values for | ||
|---|---|---|---|---|---|
| Soil | Silicate Shell | Pile | |||
| Calculation model | - | - | Coulomb–Mohr | Linear-elastic | Linear-elastic |
| Soil behavior type | - | - | drained | undrained | undrained |
| Specific gravity of dry soil/dry unit weight | ϒdry | kN/m3 | 18.0 | 21.6 | 24.0 |
| Specific gravity of saturated soil/saturated unit weight | ϒwet | kN/m3 | 20.0 | 23.2 | 24.0 |
| Soil permeability in horizontal direction | kx | m/day | 1 × 10−5 | 1 × 10−9 | - |
| Soil permeability in vertical direction | ky | m/day | 1 × 10−5 | 1 × 10−9 | - |
| Deformation modulus for soil/elastic modulus for pile or shell | E | kN/m2 | 10.8 | 530,000 | 3 × 107 |
| Poisson’s ratio | v | - | 0.35 | 0.25 | 0.1 |
| Cohesion | c | kN/m2 | 21 | 27.3 | - |
| Angle of internal friction | φ | grad. | 26 | 27 | - |
| Dilatancy angle | ψ | grad. | 0 | 0 | - |
| Name | Construction Cost for 1 m3 of Piles, USD | Pile Volume, m3 | The cost of Building of 1 m3 Shell, USD | Volume of the Shell, m3 | Cost of Material for 1m3 of Pile, USD | Cost of Material for 1m3 of Shell, USD | The Volume of the Shell Material per 1 Pile, m3 | Total Costs, USD | % |
|---|---|---|---|---|---|---|---|---|---|
| Piles with protective shell (2 x 4 m piles) | 48 | 10.05 | 72 | 8.44 | 36 | 8.5 | 8.44 | 1513 | - |
| Ordinary pile (5 pcs of 4 m piles) | 48 | 25.12 | - | - | 36 | - | - | 2097 | - |
| Economic efficiency | 584 | 28% | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unaibayev, B.B.; Unaibayev, B.Z.; Alibekova, N.; Sarsembayeva, A. Installation of Bored Piles with a Protective Silicate Shell of a New Design in Saline Silty-Clayey Soils. Appl. Sci. 2021, 11, 6935. https://doi.org/10.3390/app11156935
Unaibayev BB, Unaibayev BZ, Alibekova N, Sarsembayeva A. Installation of Bored Piles with a Protective Silicate Shell of a New Design in Saline Silty-Clayey Soils. Applied Sciences. 2021; 11(15):6935. https://doi.org/10.3390/app11156935
Chicago/Turabian StyleUnaibayev, Bulat B., Bulat Zh. Unaibayev, Nurgul Alibekova, and Assel Sarsembayeva. 2021. "Installation of Bored Piles with a Protective Silicate Shell of a New Design in Saline Silty-Clayey Soils" Applied Sciences 11, no. 15: 6935. https://doi.org/10.3390/app11156935
APA StyleUnaibayev, B. B., Unaibayev, B. Z., Alibekova, N., & Sarsembayeva, A. (2021). Installation of Bored Piles with a Protective Silicate Shell of a New Design in Saline Silty-Clayey Soils. Applied Sciences, 11(15), 6935. https://doi.org/10.3390/app11156935








