Imperfections of Scalar Approximation in Calibration of Computer-Generated Holograms for Optical Surface Measurements
Abstract
:1. Introduction
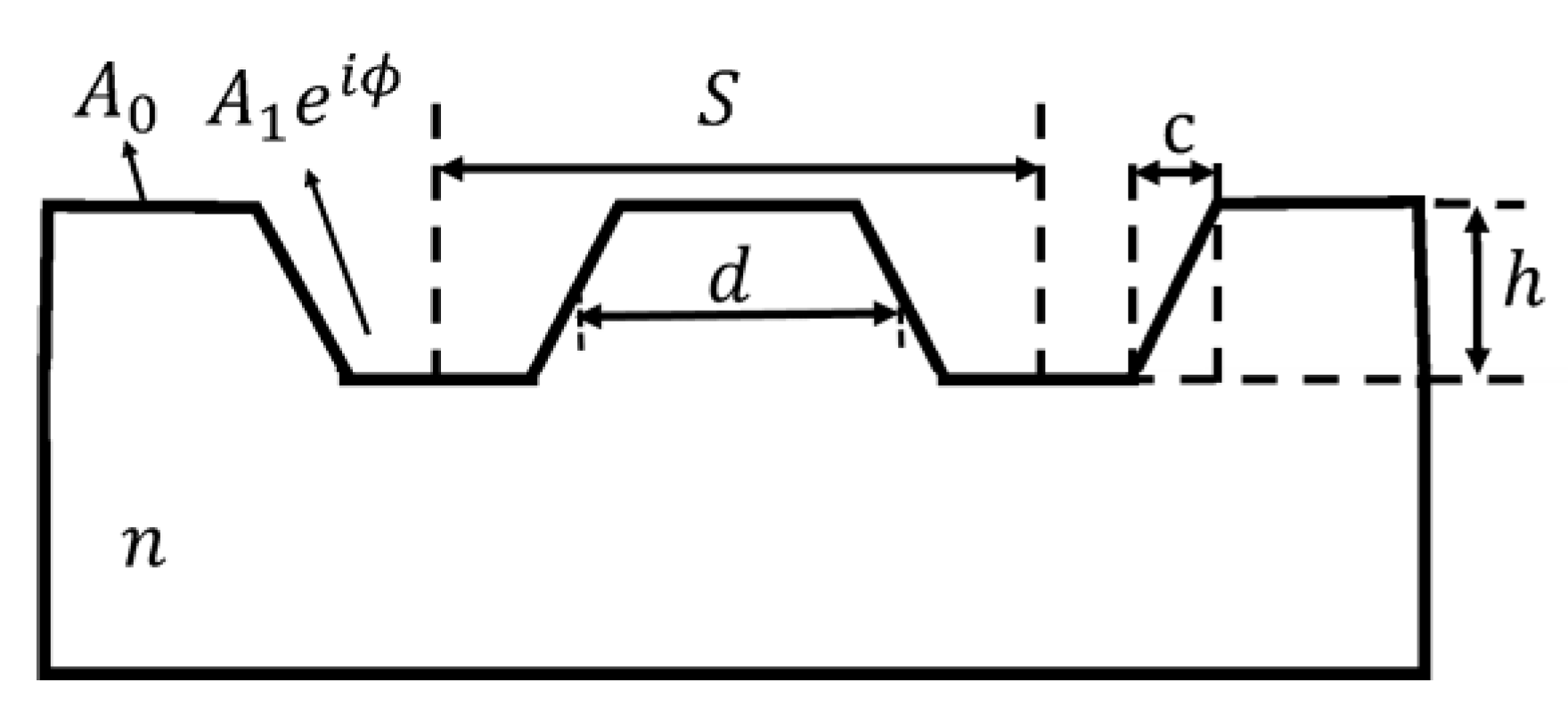
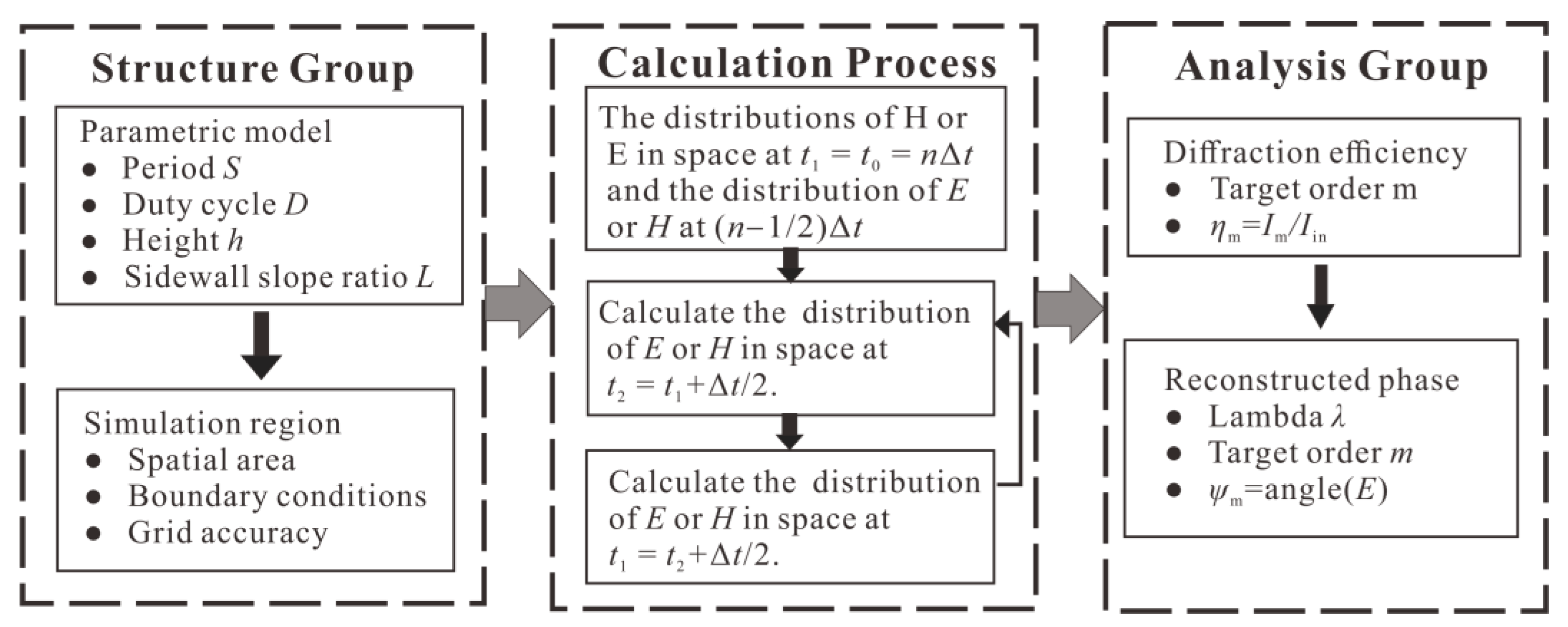
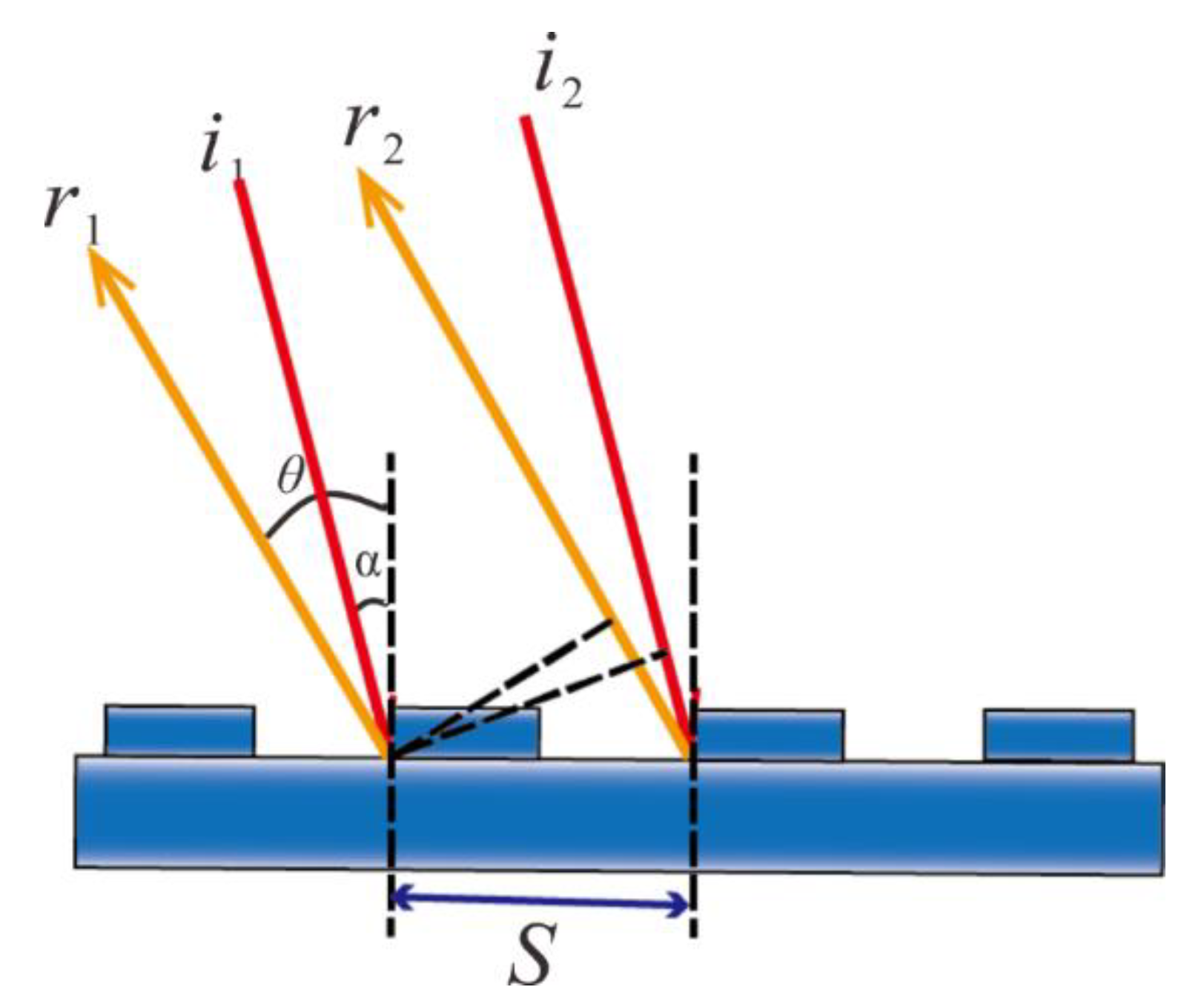
2. Parametric Model and Methods
3. Imperfections of Scalar Approximation
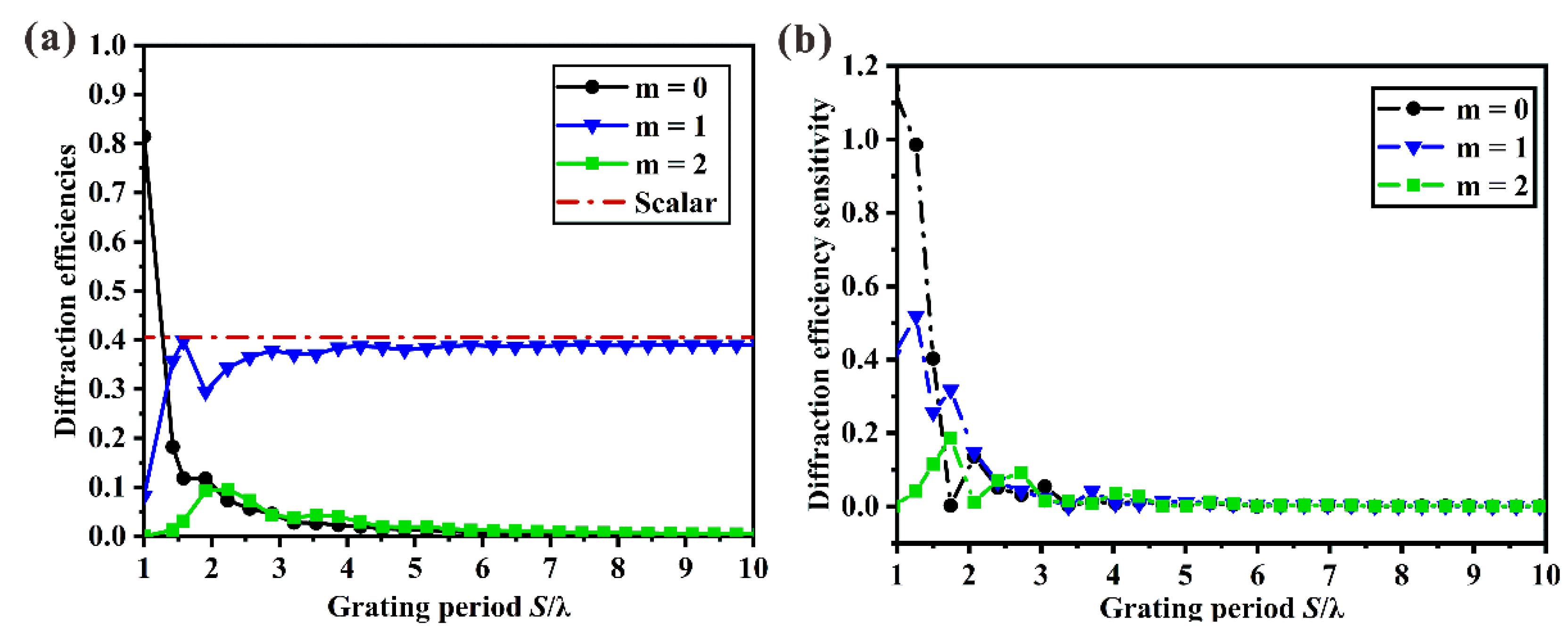
3.1. Threshold Value
3.2. Phase Sensitivity
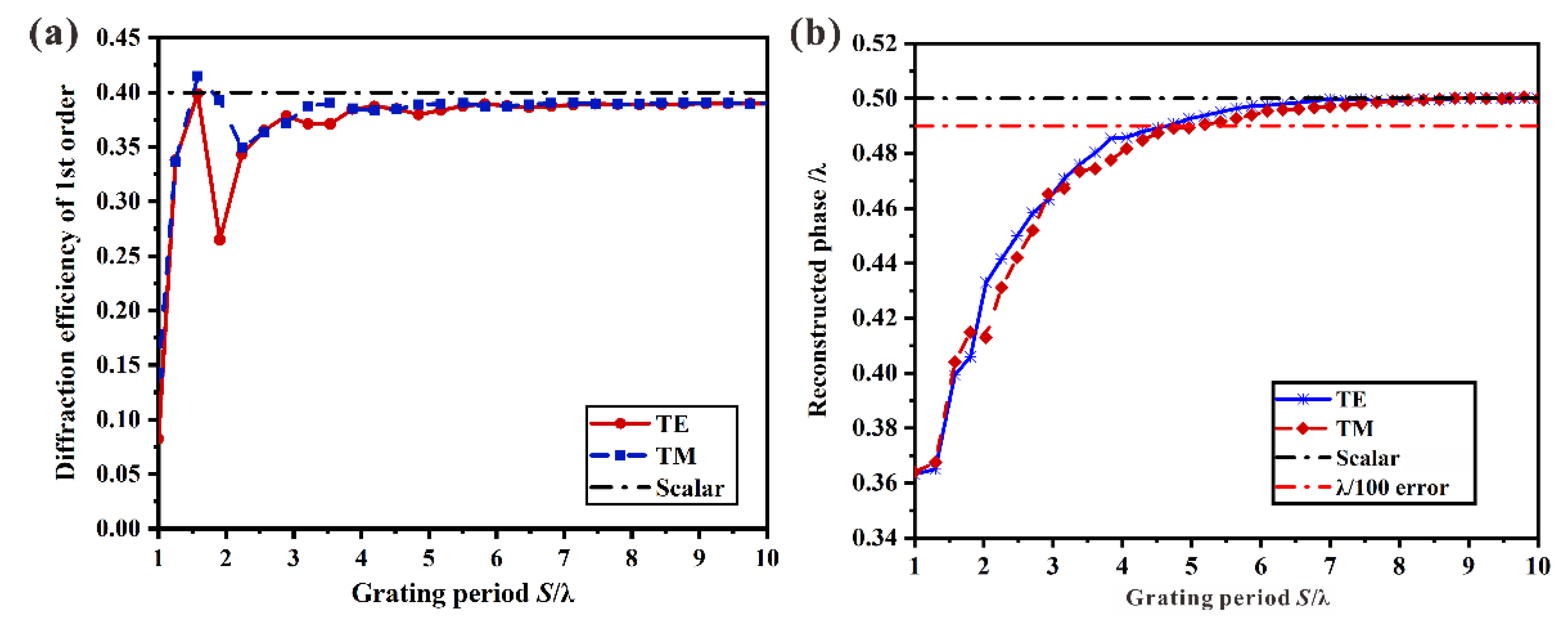
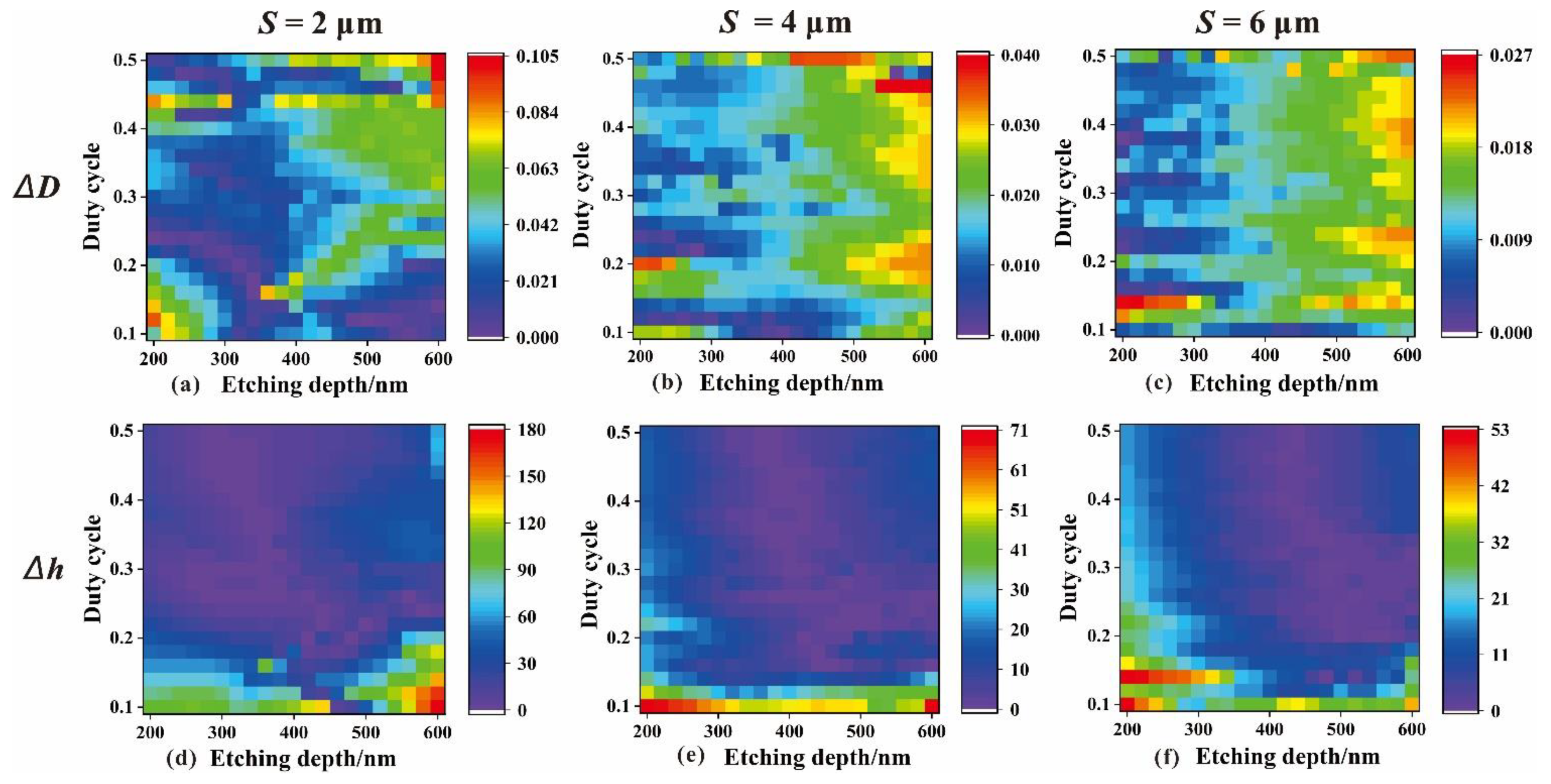
3.3. Reconstruction Errors
4. Experimental Verification and Discussion
4.1. Profile Consistency of Gratings
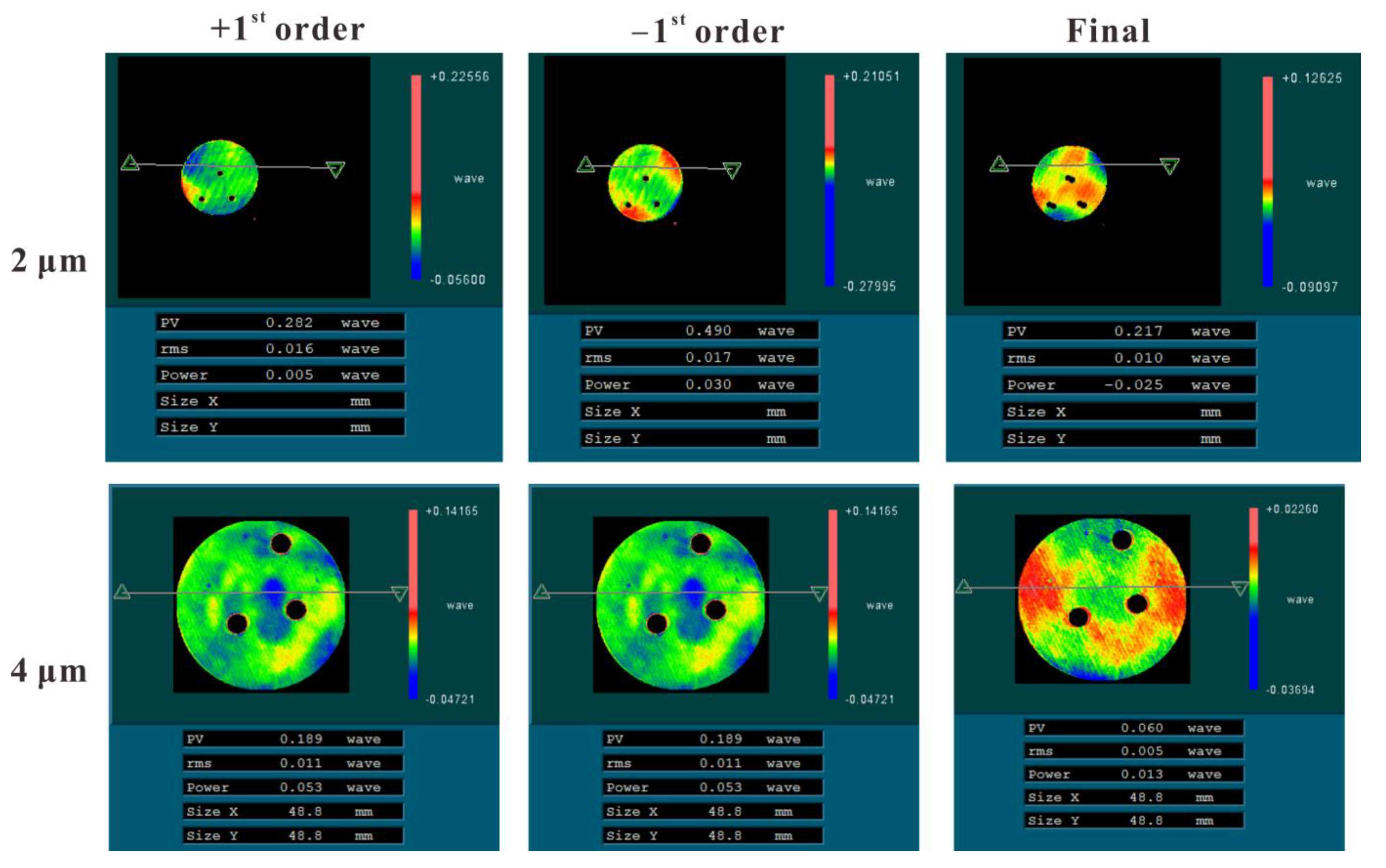
4.2. Wavefront Aberrations Evaluation
5. Conclusions
- (1)
- When the grating period is less than 5λ, the scalar approximation fails to accurately describe the characteristics of CGH by diffractive optics calibrators.
- (2)
- Reconstruction geometric errors are concentrated in cases in which the period is small and the depth is large. For example, a 10% error for the duty cycle and a 180 nm error for the depth are introduced owing to the imperfections of scalar approximation in the 2 μm grating case.
- (3)
- Wavefront aberration is more sensitive to fabrication errors in small-period regions of a CGH, and the effect of the duty cycle error on the wavefront cannot be ignored.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Wang, L.; Yu, J.; Yu, B.; Jin, C. Design method for off-axis aspheric reflective optical system with extremely low aberration and large field of view. Appl. Opt. 2020, 59, 10185–10193. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.; Congcong, C.; Binchao, D.; Qi, C.; Jianxun, B. Fabricating of Φ4m CIOMP-SiC mirror blank. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Large Mirrors and Telescopes. International Society for Optics and Photonics, Chengdu, China, 26–28 June 2018. [Google Scholar] [CrossRef]
- Bai, Y.; Li, L.; Xue, D.; Zhang, X. Rapid fabrication of a silicon modification layer on silicon carbide substrate. Appl. Opt. 2016, 55, 5814–5820. [Google Scholar] [CrossRef]
- Malacara, D. Optical Shop Testing, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Mohammad, N.; Meem, M.; Shen, B.; Wang, P.; Menon, R. Broadband imaging with one planar diffractive lens. Sci. Rep. 2018, 8, 2799. [Google Scholar] [CrossRef] [Green Version]
- Sasa, B.; Mauro, P.; Holger, F.; Martin, D.; Chapman, H.N.; Morgan, A.J. X-ray focusing with efficient high-NA multilayer Laue lenses. Light Sci. Appl. 2018, 7, 1–9. [Google Scholar] [CrossRef]
- Feng, W.; Zhiyu, Z.; Ruoqiu, W.; Xuefeng, Z.; Xu, Y.; Shiliang, L.; Feng, Z. Distortion measurement of optical system using phase diffractive beam splitter. Opt. Express 2019, 27, 29803–29816. [Google Scholar] [CrossRef]
- Peng, J.; Chen, X.; Zhang, X.; Fu, T.; Ren, J. Optimal design of tilt carrier frequency computer-generated holograms to measure aspherics. Appl. Opt. 2015, 54, 7433–7441. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Chen, S.; Shuai, X. Characterization of the contribution of CGH fabrication error to measurement uncertainty in null test. In Proceedings of the AOPC 2017: Optoelectronics and Micro/Nano-Optics. International Society for Optics and Photonics, Beijing, China, 4–6 June 2017. [Google Scholar] [CrossRef]
- Gan, Z.; Peng, X.; Chen, S.; Guan, C. Evaluation of wavefront errors introduced by pattern distortion of computer-generated holograms. Optik 2019, 185, 699–706. [Google Scholar] [CrossRef]
- Cai, W.; Zhou, P.; Zhao, C.; Burge, J.H. Diffractive optics calibrator: Measurement of etching variations for binary computer-generated holograms. Appl. Opt. 2014, 53, 2477–2486. [Google Scholar] [CrossRef] [PubMed]
- Korolkov, V.P.; Konchenko, A.S.; Poleshchuk, A.G. Application of fiber spectrometers for etch depth measurement of binary computer-generated holograms. In Proceedings of the Application of fiber spectrometers for etch depth measurement of binary computer-generated hologram, Chengdu, China, 31 January 2013. [Google Scholar] [CrossRef]
- Korolkov, V.P.; Konchenko, A.S.; Cherkashin, V.V. Etch depth mapping of phase binary computer-generated holograms by means of specular spectroscopic scatterometry. Opt. Eng. 2013, 52, 72. [Google Scholar] [CrossRef]
- Cai, W.; Zhou, P.; Zhao, C.; Burge, J.H. Diffractive optics calibrator: Design and construction. Opt. Eng. 2013, 52, 124101. [Google Scholar] [CrossRef]
- Zhou, P.; Burge, J.H. Optimal design of computer-generated holograms to minimize sensitivity to fabrication errors. Opt. Express 2007, 15, 15410–15417. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.C.; Zhou, P.; Burge, J.H. Analysis of phase sensitivity for binary computer-generated holograms. Appl. Opt. 2006, 45, 4223–4234. [Google Scholar] [CrossRef] [PubMed]
- Stuerwald, S. Error compensation in computer generated hologram-based form testing of aspheres. Appl. Opt. 2014, 53, 8249–8255. [Google Scholar] [CrossRef] [PubMed]
- Changqing, W.; Xili, Z. Finite Difference Time Domain Method in Electromagnetic Field Calculation; Peking University Press: Beijing, China, 2014. [Google Scholar]
- Wang, R.; Zhang, Z.; Bai, Z.; Wang, Z.; Yin, X.; Kong, L.; Deng, W.; Xue, D.; Zhang, X. Scanning ion beam etching: A method for the fabrication of computer-generated hologram with nanometric accuracy for aspherical testing. Opt. Lasers Eng. 2021, 139, 106503. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Z.; Wang, X.; Ji, S.; Zhang, C.; Li, J.; Zhu, W.; Wu, D.; Chu, J. Efficient full-path optical calculation of scalar and vector diffraction using the Bluestein method. Light Sci. Appl. 2020, 9, 119. [Google Scholar] [CrossRef] [PubMed]


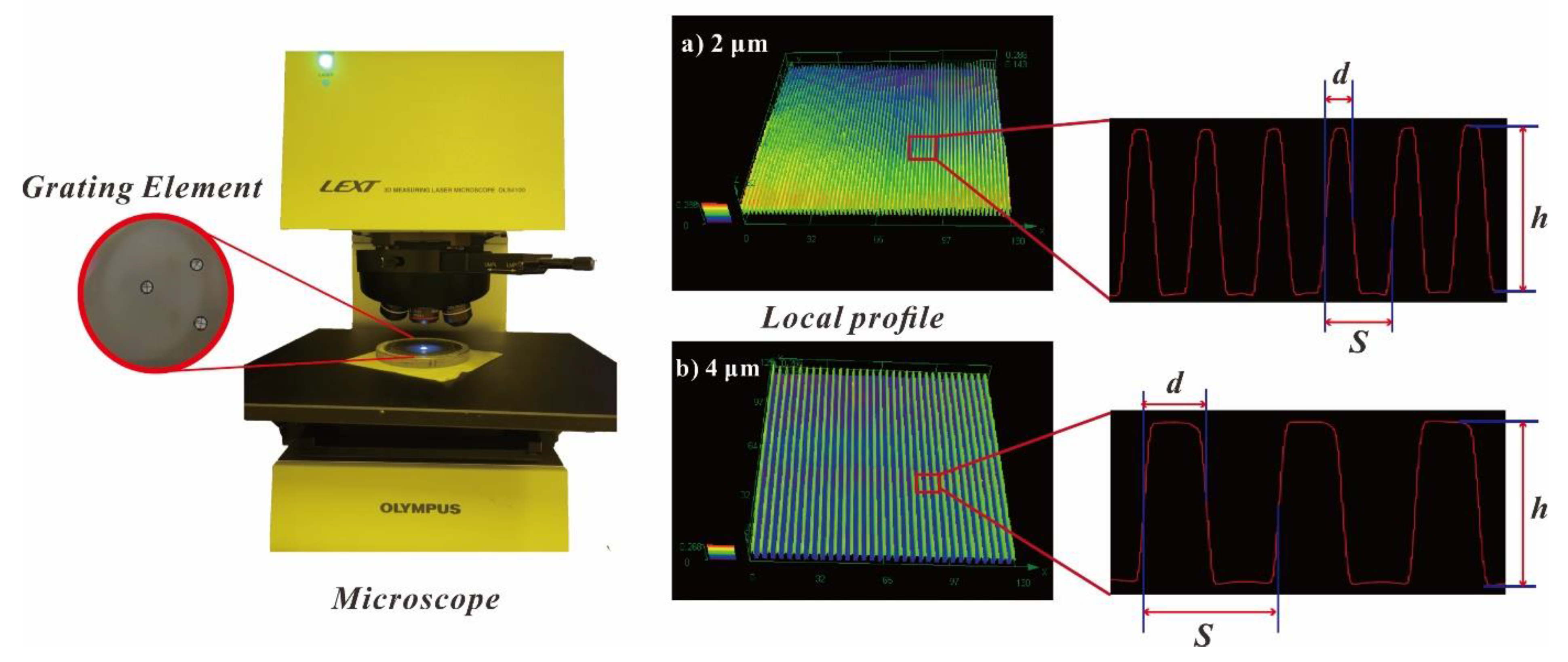

| Points | S = 2 μm | S = 4 μm | ||||||
|---|---|---|---|---|---|---|---|---|
| S [μm] | d [μm] | h [nm] | D | S [μm] | d [μm] | h [nm] | D | |
| 1 | 2.032 | 0.904 | 390 | 0.4449 | 4.064 | 1.829 | 392 | 0.4500 |
| 2 | 1.905 | 0.850 | 389 | 0.4462 | 3.937 | 1.772 | 390 | 0.4501 |
| 3 | 2.032 | 0.904 | 388 | 0.4449 | 4.064 | 1.829 | 393 | 0.4500 |
| 4 | 2.032 | 0.902 | 390 | 0.4439 | 4.064 | 1.832 | 391 | 0.4508 |
| 5 | 2.032 | 0.904 | 391 | 0.4449 | 4.064 | 1.829 | 391 | 0.4500 |
| 6 | 2.032 | 0.904 | 389 | 0.4449 | 3.937 | 1.772 | 390 | 0.4501 |
| 7 | 1.905 | 0.850 | 389 | 0.4462 | 4.064 | 1.829 | 392 | 0.4500 |
| 8 | 2.032 | 0.904 | 390 | 0.4449 | 4.064 | 1.832 | 392 | 0.4508 |
| 9 | 2.032 | 0.902 | 390 | 0.4439 | 3.937 | 1.772 | 391 | 0.4501 |
| 10 | 2.032 | 0.902 | 388 | 0.4439 | 4.064 | 1.829 | 393 | 0.4500 |
| AVG | 2.007 | 0.893 | 389 | 0.4448 | 4.026 | 1.812 | 391 | 0.4502 |
| STD | 0.054 | 0.022 | 1 | 0.0008 | 0.061 | 0.028 | 1 | 0.0003 |
| +1st Order/λ | −1st Order/λ | Final Result/λ | |
|---|---|---|---|
| S = 2 μm | 0.016 | 0.017 | 0.010 |
| S = 4 μm | 0.011 | 0.011 | 0.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Zhang, Z.; Wang, R.; Chen, T.; Wang, X.; Zhang, X. Imperfections of Scalar Approximation in Calibration of Computer-Generated Holograms for Optical Surface Measurements. Appl. Sci. 2021, 11, 6897. https://doi.org/10.3390/app11156897
Bai Y, Zhang Z, Wang R, Chen T, Wang X, Zhang X. Imperfections of Scalar Approximation in Calibration of Computer-Generated Holograms for Optical Surface Measurements. Applied Sciences. 2021; 11(15):6897. https://doi.org/10.3390/app11156897
Chicago/Turabian StyleBai, Yingying, Zhiyu Zhang, Ruoqiu Wang, Tianbao Chen, Xu Wang, and Xuejun Zhang. 2021. "Imperfections of Scalar Approximation in Calibration of Computer-Generated Holograms for Optical Surface Measurements" Applied Sciences 11, no. 15: 6897. https://doi.org/10.3390/app11156897
APA StyleBai, Y., Zhang, Z., Wang, R., Chen, T., Wang, X., & Zhang, X. (2021). Imperfections of Scalar Approximation in Calibration of Computer-Generated Holograms for Optical Surface Measurements. Applied Sciences, 11(15), 6897. https://doi.org/10.3390/app11156897






