Shape and Weighting Optimization of a Subarray for an mm-Wave Phased Array Antenna

Abstract

This paper discusses how to optimize the weighting of individual subarrays to derive the low sidelobe level (SLL) based on quadratic programming (QP) and how to derive QP parameters to ensure that the objective function is composed of the quadratic function form, with the actual number identical to the standard objective function of QP. Next, in order to analyze the SLL, a 24 × 24 phased array antenna was compared with 96 transmit–receive modules (TRMs) attached only to the subarray stage and a phased array antenna with 576 TRMs attached to all radiating elements without a subarray. Optimized weighting was applied to the array antennas with a subarray, and Taylor weighting was applied to the array antennas without a subarray. The number of TRMs used in the phased array antenna with the optimized weighting was reduced by 83.3% compared to the phased array antenna in which TRMs were attached to all radiating elements. The SLL and the half-power beamwidths (HPBWs) of the two antennas were practically identical in a narrow beam-scanning environment. Finally, an array pattern (AP) in which mutual coupling between the radiating elements was considered was calculated to verify the optimized weighting. Moreover, the optimized weighting was applied to CST Microwave Studio (an EM full-wave simulation) to compare the results from the AP calculation and a simulation. It was confirmed that the two results above are largely indistinguishable. The analysis found that the HPBW is 3.6${}^{\circ }$ × 3.6${}^{\circ }$ and the SLL is −26.18 dB from AP calculations in the boresight direction. When each 5${}^{\circ }$ beam was scanned at the azimuth and elevation, the corresponding HPBW values were 3.7${}^{\circ }$ × 3.7${}^{\circ }$ and 3.7${}^{\circ }$ × 3.7${}^{\circ }$ and the SLLs were −22.70 dB and −24.44 dB according to the AP calculations.

1. Introduction

An active phased array antenna is composed of hundreds or thousands of radiating elements. The weighting and phase of the input signal are controlled with transmit–receive modules (TRMs) attached to each radiating element, and digital signal processing is performed through an analog-to-digital converter (ADC). However, due to the increased signals transmitted/received from numerous radiating elements, the computational speed of signal processing has been reduced [1]. In addition, given the significant number of TRMs, system construction costs have increased [2]. A subarray technique for grouping radiating elements has been applied to overcome these shortcomings. However, when the subarray is applied to an array antenna, problems can occur, such as the generation of a grating lobe or high sidelobe level (SLL). Therefore, various methods have been studied to solve these problems. In a previous study [3], a low SLL was achieved by using an overlapped subarray using a Butler matrix or a lens feed, and through various methods based on subarray rotation, the SLL was minimized [4]. In addition, the target SLL was achieved by applying an aperiodic space to individual subarrays [5]. In [6], a study of the optimization of subarray weighting and size levels to achieve a target SLL using a hybrid genetic algorithm (GA) was performed. A GA was also utilized to optimize excitation amplitude and phase to increase transmission efficiency and to derive optimal antenna design parameters to increase gain [7,8]. The particle swarm optimization (PSO) has been utilized to reduce beam scattering by optimizing the radome design parameters and to estimate the unknown parameters of the one-dimensional micro-Doppler frequency trajectories as a field of radar signal processing [9,10]. Recently, a modified form of PSO was used to optimize the subarray weighting and achieve a low SLL [11]. In [12,13], in order to reduce the SLL and form a narrow beam, linear programming was used. A radiation pattern with a low SLL was obtained by optimizing the shape of the subarray and the weighting applied to each subarray utilizing an excitation matching method [14]. In [15], the phase center of the subarray was irregular to achieve a low SLL by making the shape of subarrays tetromino and octomino. Additionally, how the shape of the subarray affects the gain was also investigated. The authors of [16] introduce the various methods to reduce the SLL regarding an unconventional phased array antenna. The SLL could be reduced by optimizing the subarray configuration and subarray excitation to a phased array antenna with subarrays applied. In [17], the characteristics of an array antenna including a low SLL were improved by designing a passive coherent location system with a non-uniform array environment of a space tapering. In this paper, we introduce a method by which to optimize the weighting of each subarray based on quadratic programming (QP) to acquire a low SLL. QP is a type of mathematical programming that determines an optimal value when a mathematical model defined as a quadratic function is given [18], and an optimization technique for the feeding signal of an array antenna using QP has been devised [19]. The subarray shape should be irregular to avoid the grating lobe when scanning [20,21]. However, it is not easy to apply Taylor/Chebyshev weighting to an array antenna to which a non-periodic subarray is applied. Hence, weighting optimization for each subarray to secure a low SLL in an aperiodic array environment was conducted using QP. The array antenna configuration is a 24 × 24 rectangular lattice, the distance between the radiating elements operating at 30 GHz is $0.72\lambda$ and the number of radiating elements is 576. This paper is organized as follows: Section 2 introduces the method to optimize the subarray shape and weighting to each subarray using genetic swarm optimization (GSO) and QP, respectively. Firstly, in order to achieve a low SLL and avoid a grating lobe, the shapes of 96 subarrays were optimized by GSO. Therefore, the single subarray consisted of six radiating elements. Secondly, we performed weighting optimization of each subarray to achieve an SLL below −22 dB by the QP when steering the 5${}^{\circ }$ beam. Lastly, the beam characteristics of an array antenna with TRMs in all 576 radiating elements and an array antenna with TRMs in only 96 subarrays were compared. Optimized weighting was applied to the array antenna with the subarray, and −25 dB Taylor weighting was applied to the array antenna without a subarray. In Section 3, the beam-scanning characteristics are predicted by applying optimized weighting to AP calculations considering the presence of mutual coupling. By applying the optimized weighting to an EM full-wave simulation, the beam characteristics in a simulated environment were compared with the characteristics according to AP calculations. The conclusion is presented in Section 4.

2. Weighting Optimization for Individual Subarrays by Quadratic Programming

2.1. Array Factor Definition of the Subarray

Figure 1 shows the structure of a phased array antenna with an attenuator and a phase shifter positioned at the subarray stage. Accordingly, the weighting of the radiating elements belonging to the same subarray is identical, and the phases are also in phase with each other. In order to implement the phased array antenna system applied to the subarray as shown in Figure 1, the excitation amplitude and phase of the radiating elements belonging to the same subarray must be equal. The amplitude and phase of the radiating elements in the subarray can be made the same by using feeding coaxial lines with an identical electrical length, power divider and various calibration methods for phased array antennas [22]. Figure 1 is expressed as Equations (1)–(3) [1,23].

$$AF(\theta ,\varphi )\approx \left({\displaystyle \sum _{k=1}^K{f}_k(\theta ,\varphi )}\right)f_{super}(\theta ,\varphi )$$

(1)

$${\displaystyle f_k(\theta ,\varphi )=\sum _{n=1}^{N_k}{e}^{j\frac{2\pi }{\lambda }(x_{k,n}u+y_{k,n}v)}}$$

(2)

$$\begin{array}{c}\hfill {\displaystyle f_{super}(\theta ,\varphi )=\sum _{k=1}^K{w}_k{e}^{j\frac{2\pi }{\lambda }({\rho }_{k,x}(u-u_0)+{\rho }_{k,y}(v-v_0))}}\end{array}$$

(3a)

$$\begin{array}{c}\hfill u=sin(\theta )cos(\varphi )(-{90}^{\circ }\le \theta \le {90}^{\circ },0^{\circ }\le \varphi \le {360}^{\circ })\end{array}$$

(3b)

$$\begin{array}{c}\hfill v=sin(\theta )sin(\varphi )(-{90}^{\circ }\le \theta \le {90}^{\circ },0^{\circ }\le \varphi \le {360}^{\circ })\end{array}$$

(3c)

$$\begin{array}{c}\hfill u_0=sin({\theta }_0)cos({\varphi }_0)(-{90}^{\circ }\le {\theta }_0\le {90}^{\circ },0^{\circ }\le {\varphi }_0\le {360}^{\circ })\end{array}$$

(3d)

$$\begin{array}{c}\hfill v_0=sin({\theta }_0)sin({\varphi }_0)(-{90}^{\circ }\le {\theta }_0\le {90}^{\circ },0^{\circ }\le {\varphi }_0\le {360}^{\circ })\end{array}$$

(3e)

Figure 1. Phased array antenna with a subarray.

Here, $AF(\varphi ,\theta )$ is the average subarray pattern and determined by $f_k(\theta ,\varphi )$ and $f_{super}(\theta ,\varphi )$ [1]. $f_k(\theta ,\varphi )$ is the array factor of the kth subarray and is defined by the location at which the radiating elements are positioned. In addition, the weighting and phase value of the radiating element in kth subarray are identical because each attenuator and phase shifter is located in each subarray stage, as shown in Figure 1. $f_{super}(\theta ,\varphi )$ is the array factor when each subarray is assumed to be one radiator, and this is defined as a superarray. The superarray is determined by the position of the phase center $({\rho }_{k,x},{\rho }_{k,y})$ of the subarray, $u_0,v_0$ applied from the phase shifter located at the subarray and the weighting $(w_k)$ applied from the attenuator, which control the amplitude of the feed signal, located at the subarray. The phase center of the subarray is determined by the position of the radiating element in the subarray and the applied weighting through Equation (4) [23]. If the same weighting is applied to the radiating elements in the subarray as in the proposed structure, the phase center of the subarray is determined by the location of the radiating elements and the number of radiating elements in the subarray.

$${\rho }_{k,p}=\frac{{\displaystyle \sum _{n=1}^{N_k}{w}_{k,n}{p}_{k,n}}}{{\displaystyle \sum _{n=1}^{N_k}{w}_{k,n}}}(p=xory)=\frac{{\displaystyle \sum _{n=1}^{N_k}{p}_{k,n}}}{N_k}(w_k=1)$$

(4)

In this study, before weighting optimization, the subarray shape was optimized into 96 subarrays by GSO of a rectangular lattice array (24 × 24) antenna initially with 576 radiating elements. Using Equation (1) as a cost function of GSO, the subarray shape was optimized to avoid grating lobes when scanning on the condition of uniform weighting ($w_k=1$). Equation (5) shows that the grating lobe (${\theta }_{GL}$) is not a function of weighting, which is the amplitude of the feed signal [24]. It is a function of the distance (d) between radiating elements, the number of radiating elements (n) and beam-scanning angle (${\theta }_0$). Therefore, prior to performing subarray weighting optimization, optimization for subarray shapes should be performed to prevent the grating lobe from occurring when the beam is steered.

$$\frac{d}{\lambda }=\frac{n}{sin{\theta }_0-sin{\theta }_{GL}}$$

(5)

The optimization of subarray shape was conducted so that the numbers of radiating elements in each subarray were identical, using a form with origin symmetry. The procedures of optimization for subarray shape and weighting are as below:

Step1.

Design of a 24 × 24 phased array antenna with uniform weighting.

Step2.

Arbitrarily allocate the phase centers to any points on the array antenna in the first quadrant.

Step3.

Shape the subarray by clustering the radiating elements based on the assigned phase centers.

Step4.

Place an origin symmetry on the optimized subarray formed in the first quadrant of the array antenna.

Step5.

Check the grating lobe by calculating $AF(\varphi ,\theta )$ (Equation (1)) on the condition of uniform weighting ($w_k=1$).

Step6.

If grating lobe takes place, repeat Step 2–5.

Step7.

If completing optimization of subarray shape, such as in Figure 2b, weighting optimization of each subarray is performed by using Equations (22) and (23), which are the objective function of QP and derived by Equations (8)–(21).

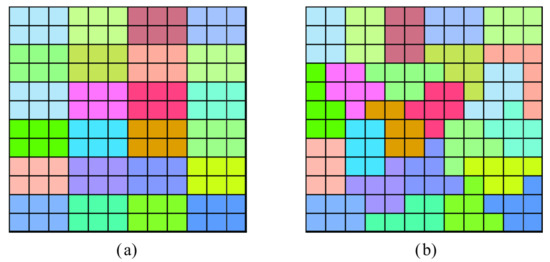Figure 2. Comparison of the subarray shape: (a) first quadrant array structure before optimizing the subarray shape (regular shape), and (b) first quadrant array structure after optimizing the subarray shape (aperiodic shape).

Step8.

Calculate the SLL from $AF(\varphi ,\theta )$ (Equation (1)), applying optimized weighting derived by QP.

Step9.

If the SLL is not satisfied, repeat Step 2–8 by reshaping the subarray or updating phase centers until the last iteration of GSO.

In the next section, the weighting optimization method by QP on the optimized subarray shape, which is an aperiodic environment, is introduced.

2.2. Weighting Optimized by Quadratic Programming

QP is a mathematical program that determines the global optimal value given by a mathematical model defined as a quadratic function composed by a real number. The standard objective function of QP is defined as shown in Equations (6) and (7).

$$minimize\frac{1}{2}{x}^{T}Qx+c^{T}x$$

(6)

$$subjectto\left\{\begin{array}{c}Ax\le b\hfill \\ Cx=f\hfill \end{array}\right.$$

(7)

Here, T is the vector transpose operator, with lowercase letters used to express vectors and capital letters used to express matrices. QP is an optimization method that finds the minimum or maximum value of a quadratic objective function when linear equality and inequality limits are given. Therefore, the weighting of the feed signal that minimizes the SLL can be obtained by QP [19]. In the proposed phased array antenna, the weighting of the radiating elements in each subarray should be identical; thus, the objective function ($Ob{j}_{fnc}$) is defined by Equation (8).

$${\displaystyle Ob{j}_{fnc}=\sum _{k=1}^K{\displaystyle w_k\sum _{n=1}^{N_k}{e}^{j\frac{2\pi }{\lambda }(x_{k,n}u+y_{k,n}v)}}}$$

(8)

Equation (8) cannot be immediately utilized as the objective function for QP because it has both real and imaginary parts according to Euler’s formula and does not have a quadratic form. Therefore, in order to formulate the $Ob{j}_{fnc}$ quadratic function, it was divided into real and imaginary parts. The real part and the imaginary part were substituted with s and t, as shown in Equations (9) and (10).

$${\displaystyle Real(Ob{j}_{fnc})=\sum _{k=1}^K{w}_k\sum _{n=1}^{N_k}cos(\frac{2\pi }{\lambda }(x_{k,n}u+y_{k,n}v))=s}$$

(9)

$${\displaystyle Imag(Ob{j}_{fnc})=\sum _{k=1}^K{w}_k\sum _{n=1}^{N_k}sin(\frac{2\pi }{\lambda }(x_{k,n}u+y_{k,n}v))=t}$$

(10)

As the objective function should be a quadratic function composed of real numbers for optimization by QP, it was expressed as the sum of the square of the maximum value s of the real part of $Ob{j}_{fnc}$ and the square of the maximum value t of the imaginary part of $Ob{j}_{fnc}$, as in Equation (11). In addition, when the beam is in the boresight direction, $Ob{j}_{fnc}$ should reach its maximum value. Accordingly, the optimization condition was set as shown in Equation (12) such that the SLL in a direction other than the front is the minimum (where $u_{SLL}$ and $v_{SLL}$ are sample regions of the SLL) [25].

$$minimize{s}^2+t^2$$

(11)

$$subjectto\left\{\begin{array}{c}Ob{j}_{fnc}(u=0,v=0)=1\hfill \\ \left|\begin{array}{c}Real(Ob{j}_{fnc}(u=u_{SLL},v=v_{SLL}))|\le s\\ Imag(Ob{j}_{fnc}(u=u_{SLL},v=v_{SLL}))|\le t\end{array}\right.\end{array}\right.$$

(12)

.

In order to substitute Equations (11) and (12) into the standard objective functions (6) and (7), QP parameters were derived, as shown in Equations (14)–(21). In these equations, the QP parameters make the objective function composed of the quadratic function and the real number identical to the standard objective function of QP.

$$s^2+t^2=\frac{1}{2}{x}^{T}Qx+c^{T}x$$

(13)

$$x={[w_1,w_2,w_3,···,w_K,s,t]}^T$$

(14)

$$Q=\left[\begin{array}{cccccc}0& 0& \cdots & 0& 0& 0\\ 0& 0& \cdots & 0& 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& \cdots & 0& 0& 0\\ 0& 0& \cdots & 0& 2& 0\\ 0& 0& \cdots & 0& 0& 2\end{array}\right] ((K+2)\times (K+2) matrix)$$

(15)

$$c^T=[0,0,···,0,0,0]((K+2)\times 1vector)$$

(16)

$$[1,1,···,1,0,0]{[w_1,w_2,···,w_K,s,t]}^T={a_0}^{T}x=1$$

(17)

$$\begin{array}{c}{\displaystyle [\sum _{n=1}^{N_1}cos(\frac{2\pi }{\lambda }(x_{1,n}{u}_i+y_{1,n}{v}_i)),\sum _{n=1}^{N_2}cos(\frac{2\pi }{\lambda }(x_{2,n}{u}_i+y_{2,n}{v}_i)),\cdots ,\sum _{n=1}^{N_k}cos(\frac{2\pi }{\lambda }(x_{K,n}{u}_i+y_{K,n}{v}_i)),-1,0]}\hfill \\ \hfill [w_1,w_2,\cdots ,w_K{,s,t]}^T={A_i}^{T}x\le 0\end{array}$$

(18)

$$\begin{array}{c}{\displaystyle [-\sum _{n=1}^{N_1}cos(\frac{2\pi }{\lambda }(x_{1,n}{u}_i+y_{1,n}{v}_i)),-\sum _{n=1}^{N_2}cos(\frac{2\pi }{\lambda }(x_{2,n}{u}_i+y_{2,n}{v}_i)),\cdots ,-\sum _{n=1}^{N_k}cos(\frac{2\pi }{\lambda }(x_{K,n}{u}_i+y_{K,n}{v}_i)),-1,0]}\hfill \\ \hfill [w_1,w_2,\cdots ,w_K{,s,t]}^T={B_i}^{T}x\le 0\end{array}$$

(19)

$$\begin{array}{c}{\displaystyle [\sum _{n=1}^{N_1}sin(\frac{2\pi }{\lambda }(x_{1,n}{u}_i+y_{1,n}{v}_i)),\sum _{n=1}^{N_2}sin(\frac{2\pi }{\lambda }(x_{2,n}{u}_i+y_{2,n}{v}_i)),\cdots ,\sum _{n=1}^{N_k}sin(\frac{2\pi }{\lambda }(x_{K,n}{u}_i+y_{K,n}{v}_i)),0,-1]}\hfill \\ \hfill [w_1,w_2,\cdots ,w_K{,s,t]}^T={C_i}^{T}x\le 0\end{array}$$

(20)

$$\begin{array}{c}{\displaystyle [-\sum _{n=1}^{N_1}sin(\frac{2\pi }{\lambda }(x_{1,n}{u}_i+y_{1,n}{v}_i)),-\sum _{n=1}^{N_2}sin(\frac{2\pi }{\lambda }(x_{2,n}{u}_i+y_{2,n}{v}_i)),\cdots ,-\sum _{n=1}^{N_k}sin(\frac{2\pi }{\lambda }(x_{K,n}{u}_i+y_{K,n}{v}_i)),0,-1]}\hfill \\ \hfill [w_1,w_2,\cdots ,w_K{,s,t]}^T={D_i}^{T}x\le 0\end{array}$$

(21)

Equation (14) shows the subarray weighting optimized by QP and Equation (13) is the objective function converted to the standard objective function of QP. In order to substitute Equations (11) and (12) into the objective functions (6) and (7) of QP, the matrix Q and vector c are defined via Equations (15) and (16), respectively. Equations (17)–(21) represent equality and inequality conditions that minimize the SLL in sections other than the main beam. In Equations (13)–(21), the QP parameters for subarray weighting optimization are reorganized as Equations (22) and (23) (where I denotes the number of maximum sample regions of the SLL). MATLAB’s active set/interior-point convex, which is a type of QP algorithm, was used to optimize the weighting of each subarray [26].

$$minimize\frac{1}{2}{x}^T{Q}_x+c^{T}x$$

(22)

$$subjectto\left\{\begin{array}{c}{a_0}^{T}x=1\hfill \\ {A_i}^{T}x\le 0\hfill \\ {B_i}^{T}x\le 0\hfill \\ {C_i}^{T}x\le 0\hfill \\ {D_i}^{T}x\le 0\hfill \\ i=1,2,···,I\hfill \end{array}\right.$$

(23)

2.3. Analysis of Subarray Weighting Optimization

Figure 3 shows the distribution of the optimized weighting assigned to the first quadrant of the array antenna. The optimized weighting was derived using QP and was conducted via origin symmetry. Figure 4 shows the radiation pattern of the array antenna with optimized weighting applied. In addition, a single element pattern was applied with $co{s}^{1.5}\theta$. When the beam is in the boresight direction, the HPBW and PSL values are 3.6${}^{\circ }$ and −26.16 dB at the azimuth cut and 3.6${}^{\circ }$ and −27.36 dB at the elevation cut, respectively.

Figure 3. Distribution of optimization weighting assigned to each subarray (1st quadrant): (a) distribution of the optimized weighting of the subarray (3-D), and (b) distribution of the optimized weighting of the subarray (top view).

Figure 4. Radiation pattern in which optimized weighting is applied: (a) boresight direction in the 3-D plot, (b) boresight direction in the UV plot, (c) boresight direction at the azimuth cut, and (d) boresight direction at the elevation cut.

In Figure 5, Figure 6 and Figure 7, the beam-scanning characteristics of the array antenna with TRMs in all 576 radiating elements and the array antenna with TRMs in only 96 subarrays are compared. Here, optimized weighting below a −26 dB SLL was applied to the array antenna with the subarray, and −25 dB Taylor weighting was applied to the array antenna without the subarray. The number of TRMs used in the proposed phased array antenna with a subarray was reduced by 83.3% compared to the phased array antenna in which TRMs were attached to all radiating elements. In a narrow-angle beam-scanning system, the SLLs and HPBWs in the two set of results above were similar. For the radiation patterns, a $co{s}^{1.5}\theta$ single element pattern was applied. Table 1 shows that qualitative results, i.e., the difference between the above two results, can be confirmed.

Figure 5. Radiation pattern about the boresight direction at 30 GHz (w/a subarray (96 TRMs) vs. w/o a subarray (576 TRMs)): (a) azimuth cut, and (b) elevation cut.

Figure 6. Radiation pattern when scanning the azimuth at 30 GHz (w/a subarray (96 TRMs) vs. w/o a subarray (576 TRMs)): (a) 1${}^{\circ }$ scanning, (b) 3${}^{\circ }$ scanning and (c) 5${}^{\circ }$ scanning.

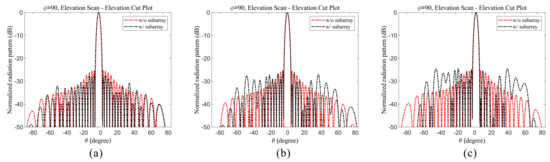
Figure 7. Radiation pattern when scanning the elevation at 30 GHz (w/a subarray (96 TRMs) vs. w/o a subarray (576 TRMs)): (a) 1${}^{\circ }$ scanning, (b) 3${}^{\circ }$ scanning and (c) 5${}^{\circ }$ scanning.

Table 1. Comparative analysis of SLL/HPBW changes according to the beam-steering angle at 30 GHz (w/a subarray (96 TRMs) vs. w/o a subarray (576 TRMs)).

	Azimuth Scan (Azimuth Cut Plot)		Elevation Scan (Elevation Cut Plot)
	w/a Subarray	w/o a Subarray	w/a Subarray	w/o a Subarray
Boresight	−26.18 dB/3.6${}^{\circ }$	−25.38 dB/3.6${}^{\circ }$	−27.36 dB/3.6${}^{\circ }$	−25.38 dB/3.6${}^{\circ }$
1${}^{\circ }$ scanning	−25.68 dB/3.6${}^{\circ }$	−25.19 dB/3.6${}^{\circ }$	−26.58 dB/3.6${}^{\circ }$	−25.19 dB/3.6${}^{\circ }$
3${}^{\circ }$ scanning	−24.83 dB/3.6${}^{\circ }$	−25.36 dB/3.6${}^{\circ }$	−25.42 dB/3.6${}^{\circ }$	−25.36 dB/3.6${}^{\circ }$
5${}^{\circ }$ scanning	−22.87 dB/3.7${}^{\circ }$	−25.17 dB/3.7${}^{\circ }$	−24.50 dB/3.7${}^{\circ }$	−25.17 dB/3.7${}^{\circ }$

3. Calculation of the Array Pattern with Optimized Weighting Applied to Each Subarray Considering Mutual Coupling

3.1. Cavity-Backed Type Single Radiating Element Design and mm-Wave Analysis

Figure 8 shows a cavity-backed patch antenna designed to operate at 30 GHz. This antenna has a radiator on the front, and a cavity filled with air is located on the rear. Power is supplied through a metal post connected to a feeder. The substrate of the radiator is the TLE-95 type ($ϵ=2.95$) with a thickness of 0.127 mm and loss tangent of 0.003. The cavity-backed patch antenna is fed by coupling feeding technique by using a metal post with a diameter of 0.31 mm and positioned at a distance of 0.9 mm in the −y axis direction in the middle of the air-filled cavity. Table 2 presents the parameters used to design the cavity-backed patch antenna. Figure 9 shows the characteristics of $S_{11}$ on the 30 GHz band, and the bandwidth that meets the requirement of −10 dB or less is 27–36 GHz. The maximum realized gain of the antenna is 7.34 dBi at 30 GHz, and it has a unidirectional pattern.

Figure 8. Configuration of the cavity-backed patch antenna: (a) overall view, (b) side-cut view.

Table 2. Design parameters for a cavity-backed patch antenna (unit: mm).

Parameter	Value	Parameter	Value
dx	7.2	cavh	2.12
dy	7.2	cavdx	4.11
patdx	2.9	cavdy	5.31
patdy	2.8	airh	1.21

Figure 9. Simulated $S_{11}$ and 3-D radiation pattern of a cavity-backed patch antenna: (a) $S_{11}$, (b) 3-D radiation pattern.

3.2. Array Antenna Design and Calculation of an Array Pattern Considering Mutual Coupling

Using the designed single antenna, a 24 × 24 array antenna was designed as shown in Figure 10. In addition, the AP was calculated by applying the optimized weighting scheme in Figure 3 to the designed array antenna. In order to calculate the AP considering mutual coupling, the calculation applied an active element pattern (AEP). The AEP is defined as the radiation pattern by the center element when radiating elements other than the center radiating element of a large array antenna are matched in terms of the impedance. In [27], the characteristics of the AEP according to the location of the radiating element were explained as follows: in a large array, most radiating elements are in a similar coupling environment (except for the edge radiating elements). Therefore, there is a similar radiation pattern for each radiating element. However, the edge radiating elements have somewhat different radiation patterns. In a typical phased array antenna, the amplitude of the edge radiating elements is 10–15 dB lower than the amplitude of the central elements. For this reason, the AEP is used for the radiation pattern of the central radiating element. Using the AEP, the array pattern of a finite array in which the effect of mutual coupling between array elements is considered can be calculated through Equation (24) [27]. In order to derive the AEP, only the central element (port 300) was fed while the other radiating elements were impedance matched (termination 50-$\Omega$).

$$AP=AEP\times AF$$

(24)

Figure 10. A 24 × 24 rectangular lattice array antenna: (a) cavity-type array antenna structure, (b) port definition from a front view (z-axis).

Figure 11 shows the radiation pattern according to the AP calculation to which the AEP is applied when the beam direction is the boresight direction. It was confirmed that the SLL was −26.18 dB through AP calculations considering the presence of mutual coupling. Figure 4 shows the radiation pattern without considering mutual coupling. It was confirmed that the radiation pattern is slightly different from AP considering the influence of mutual coupling and AP when ignoring the mutual coupling effect. Figure 11, Figure 12 and Figure 13 show the radiation pattern applied with the AEP when the beam is scanned at the azimuth and elevation. Each 5${}^{\circ }$ beam was scanned at an azimuth elevation, and through AP calculations, it was confirmed that the SLLs were −22.70 dB and −24.44 dB. In addition, it was confirmed that the radiation pattern derived through the AP calculations and the radiation pattern obtained using the EM full-wave simulation are practically equal. Table 3 quantitatively summarizes the beam characteristics shown in Figure 11, Figure 12 and Figure 13. As the beam scanning angle increases, it can be seen that the SLL and HPBW both increase.

Figure 11. Radiation pattern in the boresight direction at 30 GHz (calculation vs. EM full-wave simulation): (a) azimuth cut and (b) elevation cut.

Figure 12. Radiation pattern when scanning the azimuth at 30 GHz (calculation vs. EM full-wave simulation): (a) 1${}^{\circ }$ scanning, (b) 3${}^{\circ }$ scanning and (c) 5${}^{\circ }$ scanning.

Figure 13. Radiation pattern with the scanning elevation at 30 GHz (calculation vs. EM full-wave simulation): (a) 1${}^{\circ }$ scanning, (b) 3${}^{\circ }$ scanning and (c) 5${}^{\circ }$ scanning.

Table 3. Comparative analysis of the SLL/HPBW changes according to the beam-steering angle at 30 GHz (calculation vs. EM full-wave simulation).

	Azimuth Scan (Azimuth Cut Plot)		Elevation Scan (Elevation Cut Plot)
	Calc.	EM-Sim.	Calc.	EM-Sim.
Boresight	−26.21 dB/3.6${}^{\circ }$	−25.38 dB/3.6${}^{\circ }$	−27.39 dB/3.6${}^{\circ }$	−25.38 dB/3.6${}^{\circ }$
1${}^{\circ }$ scanning	−25.68 dB/3.6${}^{\circ }$	−25.61 dB/3.6${}^{\circ }$	−26.58 dB/3.6${}^{\circ }$	−26.51 dB/3.6${}^{\circ }$
3${}^{\circ }$ scanning	−24.87 dB/3.6${}^{\circ }$	−24.78 dB/3.6${}^{\circ }$	−25.40 dB/3.6${}^{\circ }$	−25.33 dB/3.6${}^{\circ }$
5${}^{\circ }$ scanning	−22.70 dB/3.7${}^{\circ }$	−22.86 dB/3.7${}^{\circ }$	−24.44 dB/3.7${}^{\circ }$	−24.49 dB/3.7${}^{\circ }$

4. Conclusions

In this study, QP is used to perform weighting optimization for individual subarrays in an aperiodic array environment. First, the AF was transformed into a quadratic function composed of real numbers to apply QP to the array environment, and QP parameters were derived so that the AF could conform to the QP objective function. Through these procedures, the optimized weighting of each subarray was derived to achieve a low SLL. Secondly, the beam-scanning characteristics of an array antenna with TRMs in all 576 radiating elements and an array antenna with TRMs in only 96 subarrays were compared. It was confirmed that the beam-scanning performance metrics of the SLL and HPBW when applying optimized weighting to the array antenna composed of 96 TRM subarrays and the beam-scanning performance of the array antenna composed of 576 TRMs in a narrow beam-scanning system are identical. Finally, AP calculations with optimized weighting applied to each subarray were solved while taking into account mutual coupling. In order to verify the beam characteristics from the AP calculations, a cavity-backed antenna operating in the mm-wave was designed and configured in a 24 × 24 array. Applying optimized weighting to the array antenna, the beam characteristics from the simulation and from the AP calculations were compared. It was confirmed that these two results were almost identical. Hence, the proposed optimization method is expected to be applicable to radar systems and communication systems based on a phased array antenna using a subarray.