Geometric Deep Lean Learning: Evaluation Using a Twitter Social Network
Abstract
:1. Introduction
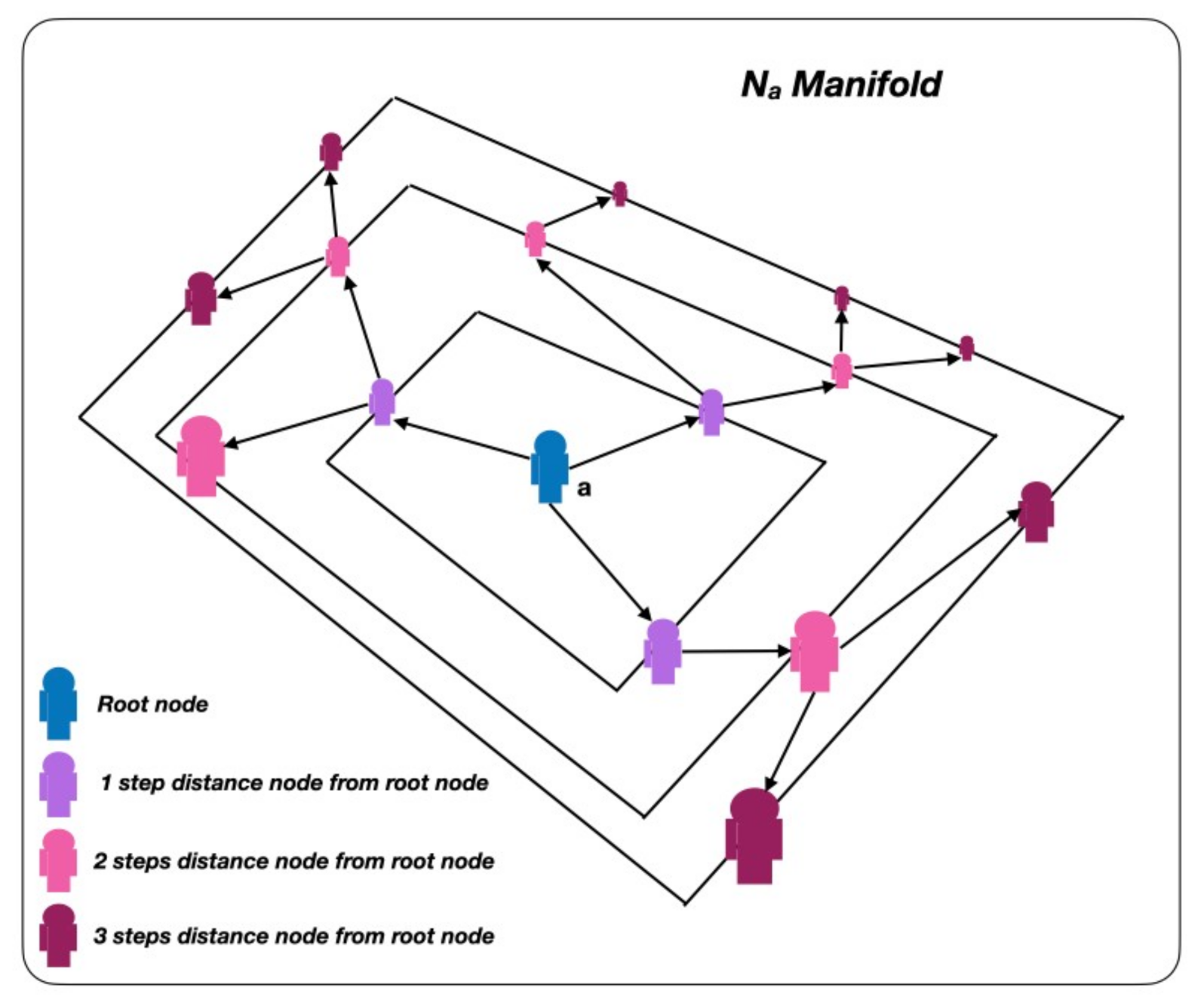
2. Summary of Geometric Deep Lean Learning Algorithm
- The structure of the graph is described by its adjacency matrix, the Laplacian of the graph , or any other normalisation of it, as a linear transformation to encode the structure of a graph. As described in [42], its topology is typically featured by a log–log long-tailed degree distribution, a degree exponent , an average path length in the range and high clustering coefficients.
- Each node and edge can be characterised by a series of signals expressed in the form of tensors for the nodes and for the edges. If these tensors are empty, i.e., formed by zeros, the node or edge would be considered nonexistent for our purposes. Subsequently, these signals are described by given by Equation (1).The information contained in both in the nodes and in the edges is usually structured information which almost always, depending on its nature, needs to be treated with appropriate data preprocessing techniques [13,14,43].
3. Data Mining on Twitter
3.1. Experimental Setup
- Programming language: Python 3.7.6 [58];
- Python wrapper for the Twitter API: Tweepy 3.8.0;
- Python package for the creation and study of complex networks: NetworkX 2.4 [59];
- Python plotting library: Matplotlib 3.1.3;
- Python package for data analysis and manipulation: Pandas 1.0.1;
- Network visualisation and exploration: Gephi 0.9.2 [60].
3.2. Specification of Population and Sampling
3.3. Data Collection
3.4. Standardisation Procedure
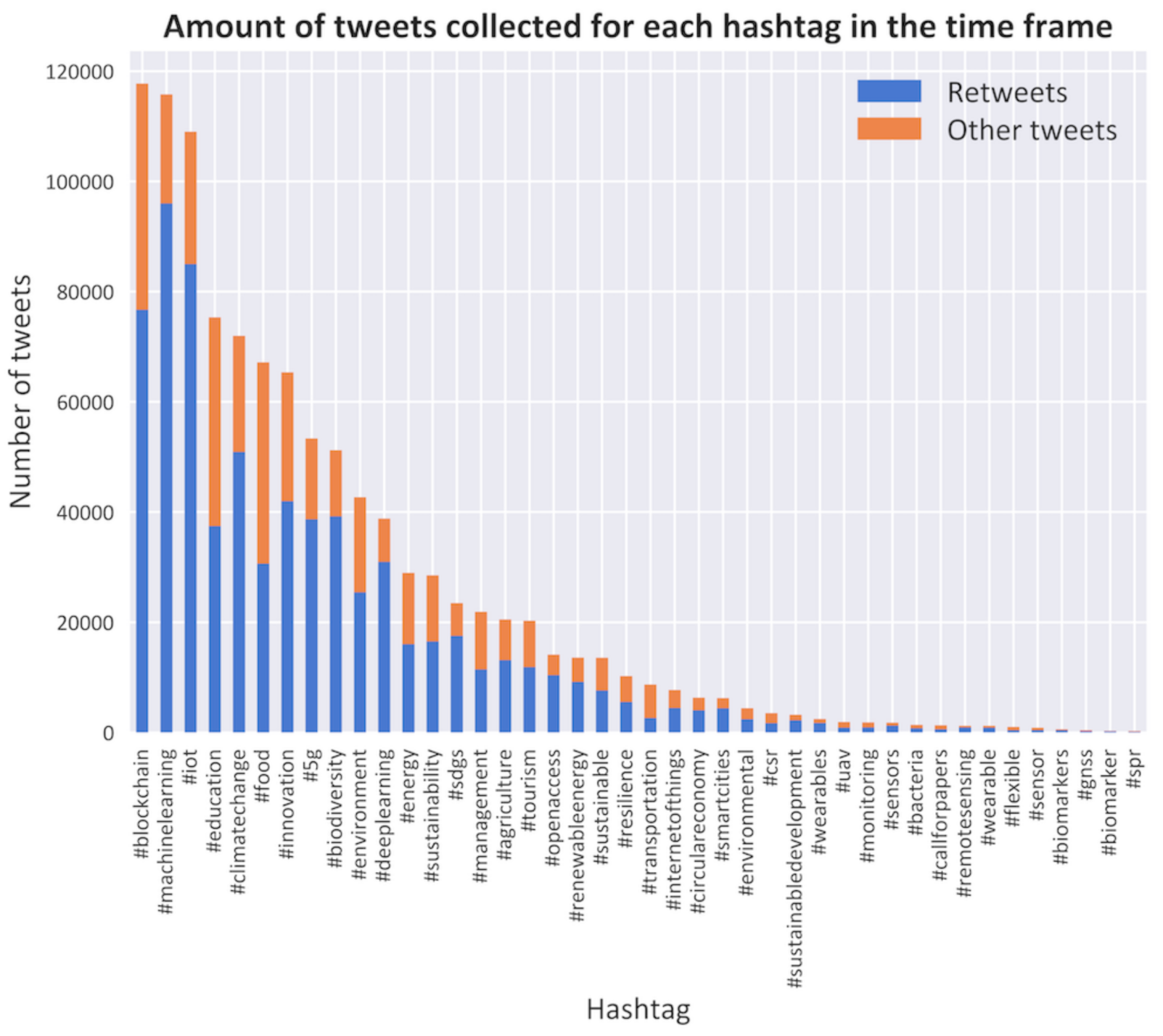
3.5. Data Analysis
- For most tweets of the dominant hashtags, distinct communities are formed that mostly have interactions with users that also use that hashtag. The strength of the interconnection can be seen by the density of the communities. Users with the #machinelearning tweets are at close distance, which indicates a high level of connectedness. This, in turn, is a sign that a low average path length and a high clustering coefficient exists within this group. On the other hand, #blockchain has a further stretched the patch, which indicates a higher average path length and lower clustering coefficient. These differences can be seen for all dominant tweets.
- Strong points of contact and overlap can be seen between some groups. As could be expected, one of the strongest can be seen between the tweets of #climatechange and #biodiversity, but also between #machinelearning and #blockchain, although the connection is weaker and limited to specific parts of the network, which is probably due to the users discussing the technical side of both. Strong connections can also be seen in other parts. This demonstrates the overlap of some communities.
- Although clear communities for #5g are visible, these are separated. This can be traced to the fact that it can be used in different contexts. More importantly, it can be used in tweets that are written in different languages, which is rarely the case with other hashtags, as they most often have a translation for that language.
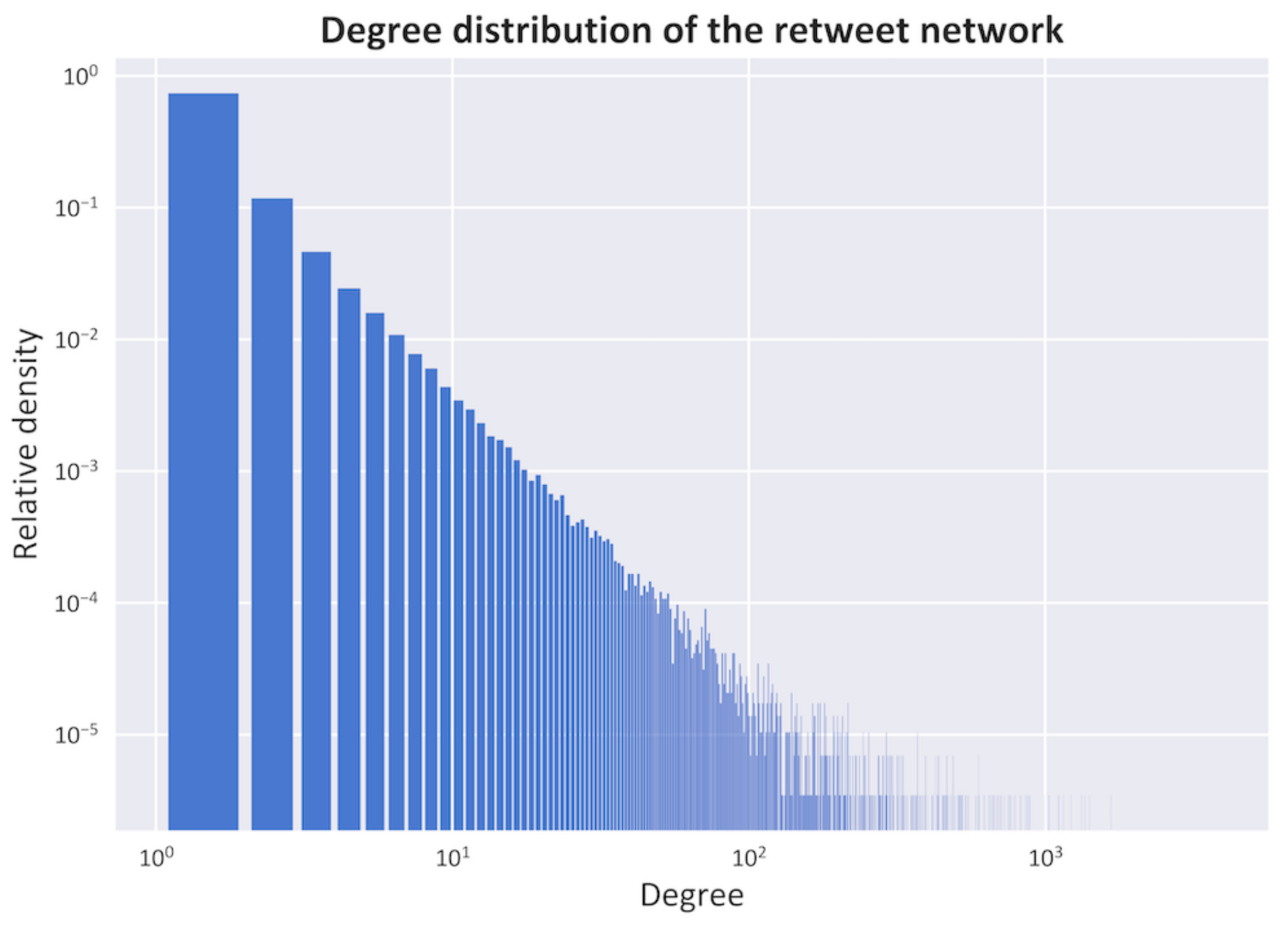
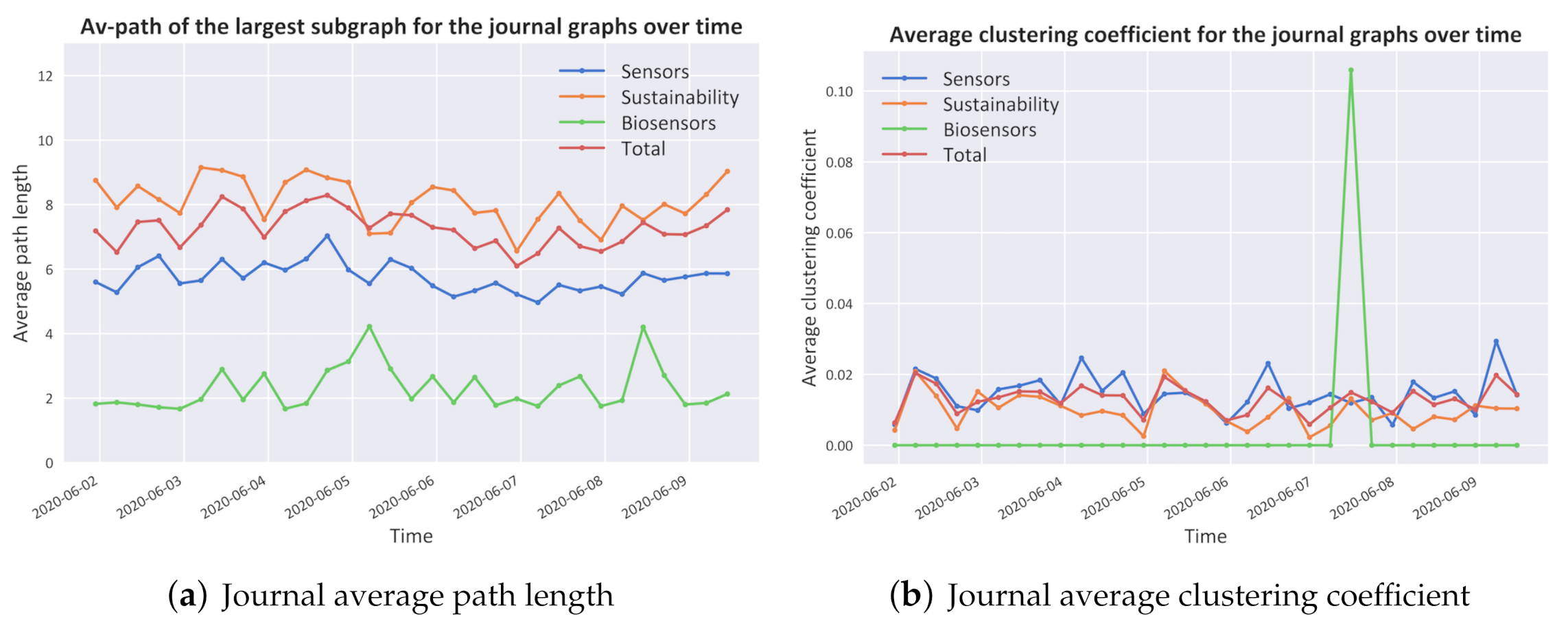
- Network StructureAs shown in Figure 6, the dataset presents a typical log–log long-tailed degree distribution which is typical of small-world/scale-free networks with a degree exponent of [41].In Figure 7, several other network metrics are shown. Specifically, in Figure 7a, the average path length, which is defined as the average number of steps along the shortest paths for all possible pairs of network nodes of all journals, is proved to be in the range which, together with the representation in Figure 7b of the high clustering coefficients, which is a measure of the degree to which nodes in a graph tend to cluster together, show a typical behaviour of small-world networks evolving towards a scale-free network topology [41].
- Network SignalsThe information contained in each retweet network about the nodes and edges can be mined in a semi-structured standard given by the platform. A truncated for our purposes example of a retweet is shown in Table 2.After this inspection, it will be easy for the reader to recognise that all information, both for the nodes and for the edges, except the text field, is structured. The information contained in the text field, which is the content of the retweet, can be considered as unstructured since it is given by the user who composes it.
4. Geometric Deep Lean Learning Evaluation
4.1. Experimental Setup
- Programming language: Python 3.7.6 [58];
- Python plotting library: Matplotlib 3.1.3;
- Python package for data analysis and manipulation: Pandas 1.0.1;
- Python package for scientific computing and array calculation: Numpy 1.18.0.
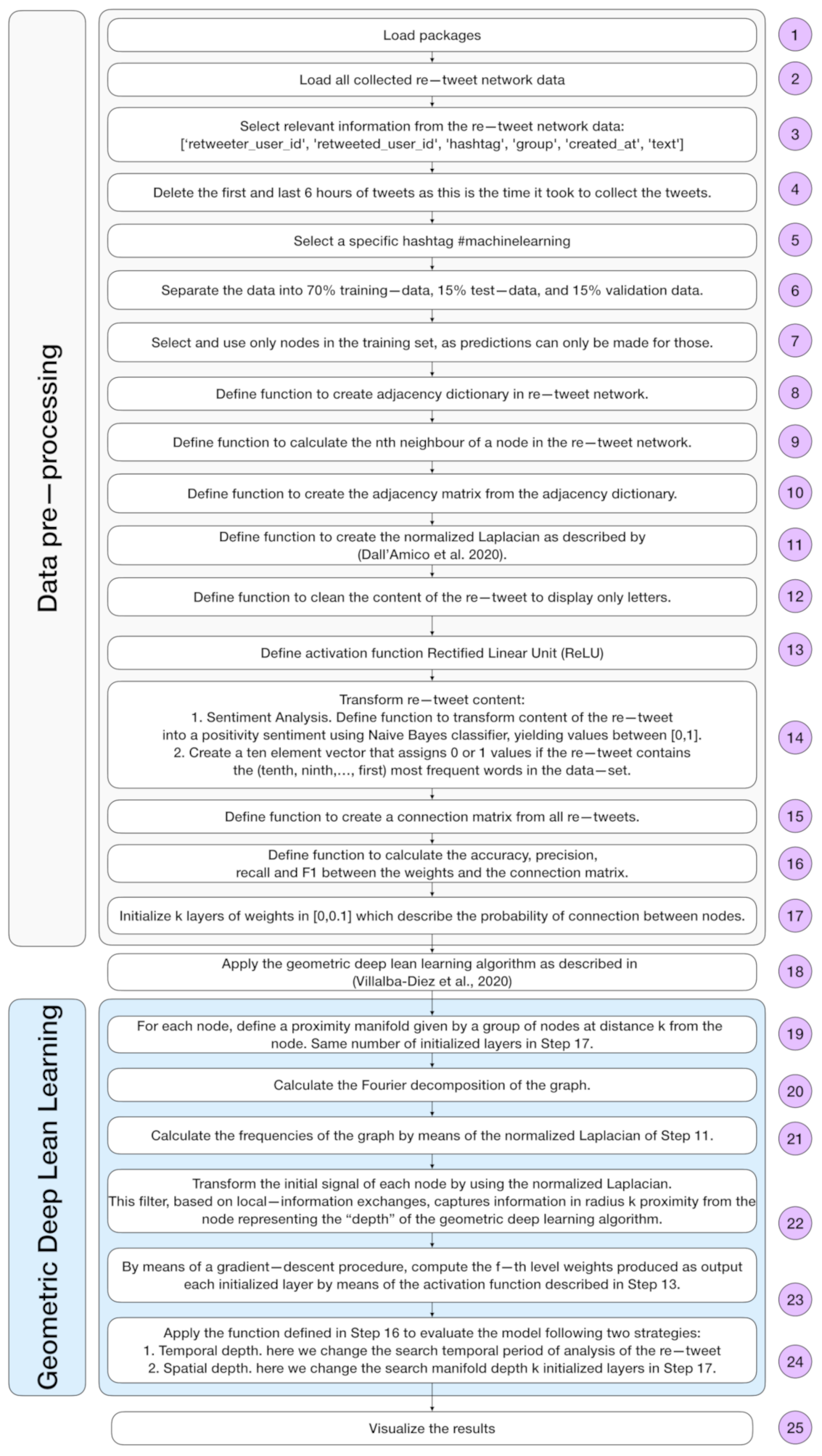
4.2. Data Preprocessing
4.3. Geometric Deep Lean Learning Hyperparameters
4.4. Data Analysis and Results
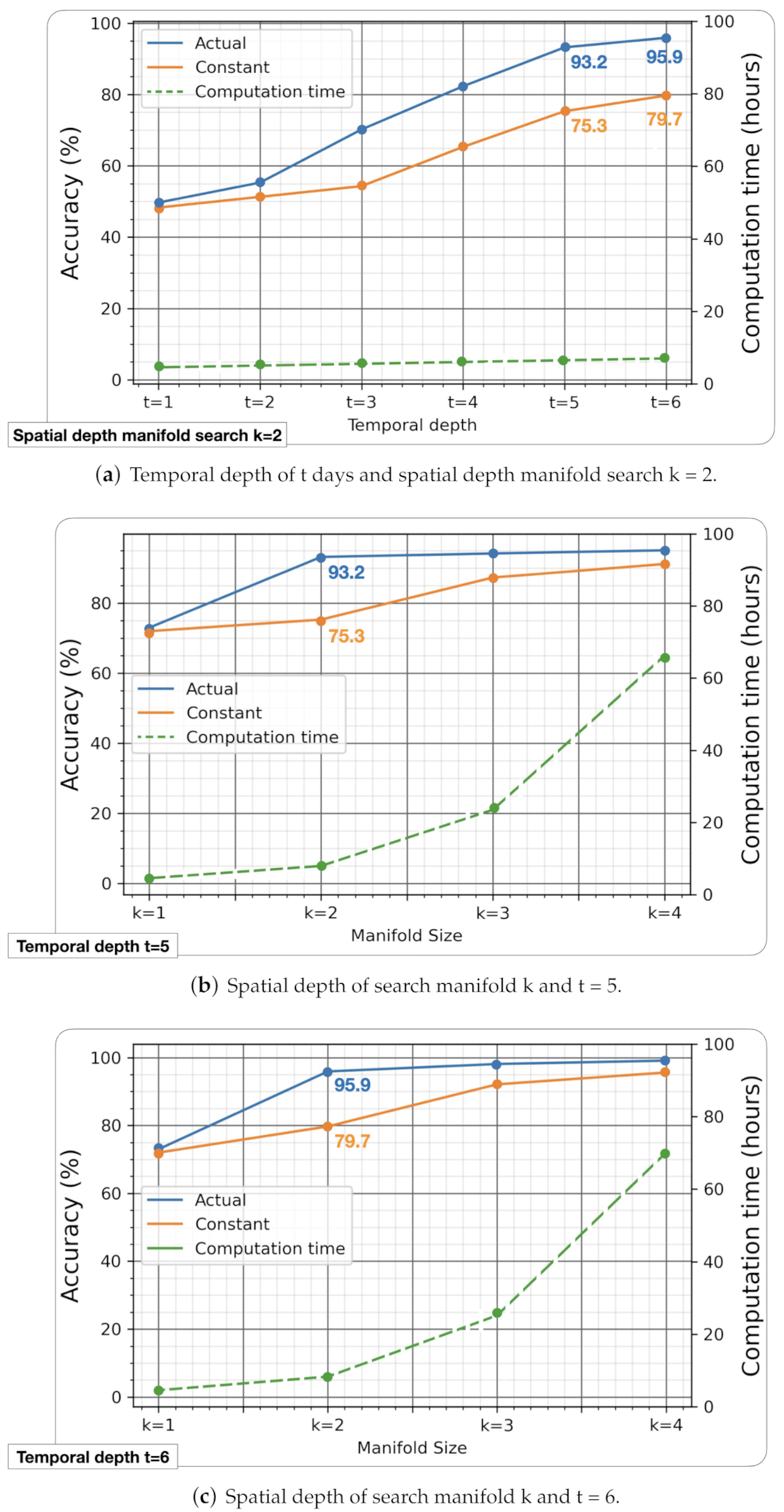
- As shown in Figure 8a we perform several experiments for different temporal depth with a constant spatial depth of the search manifold of .
- As shown in Figure 8b,c, we performed several experiments for different spatial depths of the search manifold with a constant temporal depth of and , respectively.
5. Discussion
5.1. Variation of Temporal Depth with Constant Spatial Depth
5.2. Variation of Spatial Depth with Constant Temporal Depth
6. Conclusions and Management Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| API | Application programming interface |
| AUC | Area under the receiver operating characteristic curve |
| MDPI | Multidisciplinary Digital Publishing Institute |
References
- Reinsel, D.; Gantz, J.; Rydning, J. The Digitization of the World. From Edge to Core. 2018. Available online: https://resources.moredirect.com/white-papers/idc-report-the-digitization-of-the-world-from-edge-to-core (accessed on 2 April 2021).
- Froelicher, D.; Troncoso-Pastoriza, J.R.; Sousa, J.S.; Hubaux, J. Drynx: Decentralized, Secure, Verifiable System for Statistical Queries and Machine Learning on Distributed Datasets. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3035–3050. [Google Scholar] [CrossRef]
- Verbraeken, J.; Wolting, M.; Katzy, J.; Kloppenburg, J.; Verbelen, T.; Rellermeyer, J.S. A Survey on Distributed Machine Learning. ACM Comput. Surv. 2020, 53. [Google Scholar] [CrossRef] [Green Version]
- Diène, B.; Rodrigues, J.J.; Diallo, O.; Ndoye, E.H.M.; Korotaev, V.V. Data management techniques for Internet of Things. Mech. Syst. Signal Process. 2020, 138, 106564. [Google Scholar] [CrossRef]
- Savaglio, C.; Ganzha, M.; Paprzycki, M.; Bădică, C.; Ivanović, M.; Fortino, G. Agent-based Internet of Things: State-of-the-art and research challenges. Future Gener. Comput. Syst. 2020, 102, 1038–1053. [Google Scholar] [CrossRef]
- Ordieres-Mere, J.; Villalba-Diez, J.; Zheng, X. Challenges and Opportunities for Publishing IIoT Data in Manufacturing as a Service Business. Procedia Manuf. 2019, 39, 185–193. [Google Scholar] [CrossRef]
- Khan, W.; Rehman, M.; Zangoti, H.; Afzal, M.; Armi, N.; Salah, K. Industrial internet of things: Recent advances, enabling technologies and open challenges. Comput. Electr. Eng. 2020, 81, 106522. [Google Scholar] [CrossRef]
- Evjemo, L.D.; Gjerstad, T.; Grøtli, E.I.; Sziebig, G. Trends in Smart Manufacturing: Role of Humans and Industrial Robots in Smart Factories. Curr. Robot. Rep. 2020, 1, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Jardim-Goncalves, R.; Romero, D.; Grilo, A. Factories of the future: Challenges and leading innovations in intelligent manufacturing. Int. J. Comput. Integr. Manuf. 2017, 30, 4–14. [Google Scholar] [CrossRef]
- Huang, Q.; He, H.; Singh, A.; Lim, S.N.; Benson, A.R. Combining Label Propagation and Simple Models Out-performs Graph Neural Networks. arXiv 2020, arXiv:2010.13993. [Google Scholar]
- Frasca, F.; Rossi, E.; Eynard, D.; Chamberlain, B.; Bronstein, M.; Monti, F. SIGN: Scalable Inception Graph Neural Networks. arXiv 2020, arXiv:2004.11198. [Google Scholar]
- Löwe, S.; Madras, D.; Zemel, R.; Welling, M. Amortized Causal Discovery: Learning to Infer Causal Graphs from Time-Series Data. arXiv 2020, arXiv:2006.10833. [Google Scholar]
- Johnson, D.D.; Larochelle, H.; Tarlow, D. Learning Graph Structure With A Finite-State Automaton Layer. arXiv 2020, arXiv:2007.04929. [Google Scholar]
- Rossi, E.; Chamberlain, B.; Frasca, F.; Eynard, D.; Monti, F.; Bronstein, M. Temporal Graph Networks for Deep Learning on Dynamic Graphs. arXiv 2020, arXiv:2006.10637. [Google Scholar]
- Kumar, S.; Zhang, X.; Leskovec, J. Predicting Dynamic Embedding Trajectory in Temporal Interaction Networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Volume 2019, pp. 1269–1278. [Google Scholar] [CrossRef]
- Noorshams, N.; Verma, S.; Hofleitner, A. TIES: Temporal Interaction Embeddings for Enhancing Social Media Integrity at Facebook. arXiv 2020, arXiv:2002.07917. [Google Scholar]
- Wang, X.; Lyu, D.; Li, M.; Xia, Y.; Yang, Q.; Wang, X.; Wang, X.; Cui, P.; Yang, Y.; Sun, B.; et al. APAN: Asynchronous Propagation Attention Network for Real-time Temporal Graph Embedding. arXiv 2020, arXiv:2011.11545. [Google Scholar]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef] [Green Version]
- Monti, F.; Otness, K.; Bronstein, M.M. Motifnet: A Motif-Based Graph Convolutional Network for Directed Graphs. In Proceedings of the 2018 IEEE Data Science Workshop (DSW), Lausanne, Switzerland, 4–6 June 2018; pp. 225–228. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Cui, P.; Zhu, W. Deep Learning on Graphs: A Survey. IEEE Trans. Knowl. Data Eng. 2020. [Google Scholar] [CrossRef] [Green Version]
- Mayer, R.; Jacobsen, H.A. Scalable Deep Learning on Distributed Infrastructures: Challenges, Techniques, and Tools. ACM Comput. Surv. 2020, 53, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Lei, N.; An, D.; Guo, Y.; Su, K.; Liu, S.; Luo, Z.; Yau, S.T.; Gu, X. A Geometric Understanding of Deep Learning. Engineering 2020, 6, 361–374. [Google Scholar] [CrossRef]
- Villalba-Diez, J.; Molina, M.; Ordieres-Mere, J.; Sun, S.; Schmidt, D.; Wellbrock, W. Geometric Deep Lean Learning: Deep Learning in Industry 4.0 Cyber–Physical Complex Networks. Sensors 2020, 20, 763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duvenaud, D.; Maclaurin, D.; Aguilera-Iparraguirre, J.; Gómez-Bombarelli, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional Networks on Graphs for Learning Molecular Fingerprints. arXiv 2015, arXiv:1509.09292. [Google Scholar]
- Stankovic, L.; Mandic, D.; Dakovic, M.; Brajovic, M.; Scalzo, B.; Li, S.; Constantinides, A.G. Graph Signal Processing—Part III: Machine Learning on Graphs, from Graph Topology to Applications. arXiv 2020, arXiv:2001.00426. [Google Scholar]
- Chen, L.C.; Barron, J.T.; Papandreou, G.; Murphy, K.; Yuille, A.L. Semantic Image Segmentation with Task-Specific Edge Detection Using CNNs and a Discriminatively Trained Domain Transform. arXiv 2015, arXiv:1511.03328. [Google Scholar]
- Velardi, P.; Navigli, R.; Cucchiarelli, A.; D’Antonio, F. A New Content-Based Model for Social Network Analysis. In Proceedings of the 2008 IEEE International Conference on Semantic Computing, Santa Clara, CA, USA, 4–7 August 2008; pp. 18–25. [Google Scholar] [CrossRef]
- Stilo, G.; Velardi, P. Time Makes Sense: Event Discovery in Twitter Using Temporal Similarity. In Proceedings of the 2014 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT), Warsaw, Poland, 11–14 August 2014; Volume 2, pp. 186–193. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Xu, X.; Fu, C.; Zhang, D.; Zhang, Q.; Xuan, Q. E-LSTM-D: A Deep Learning Framework for Dynamic Network Link Prediction. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3699–3712. [Google Scholar] [CrossRef] [Green Version]
- Yao, L.; Wang, L.; Pan, L.; Yao, K. Link Prediction Based on Common-Neighbors for Dynamic Social Network. Procedia Comput. Sci. 2016, 83, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Evci, U.; Pedregosa, F.; Gomez, A.; Elsen, E. The Difficulty of Training Sparse Neural Networks. arXiv 2020, arXiv:1906.10732. [Google Scholar]
- Zhang, M.; Chen, Y. Link Prediction Based on Graph Neural Networks. arXiv 2018, arXiv:1802.09691. [Google Scholar]
- Shang, K.K.; Li, T.C.; Small, M.; Burton, D.; Wang, Y. Link prediction for tree-like networks. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 061103. [Google Scholar] [CrossRef]
- Zhou, L.K.; Yang, Y.; Ren, X.; Wu, F.; Zhuang, Y. Dynamic Network Embedding by Modeling Triadic Closure Process. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th Innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, LA, USA, 2–7 February 2018; pp. 571–578. [Google Scholar]
- Keller, M. Curvature, Geometry and Spectral Properties of Planar Graphs. Discret. Comput. Geom. 2011, 46, 500–525. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Menichetti, G.; Rahmede, C.; Bianconi, G. Emergent complex network geometry. Sci. Rep. 2015, 5, 10073. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, G.; Rahmede, C.; Wu, Z. Complex quantum network geometries: Evolution and phase transitions. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 92, 022815. [Google Scholar] [CrossRef] [Green Version]
- Bianconi, G.; Rahmede, C. Complex Quantum Network Manifolds in Dimension d > 2 are Scale-Free. Sci. Rep. 2015, 5, 13979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saleh, M.; Esa, Y.; Mohamed, A. Applications of Complex Network Analysis in Electric Power Systems. Energies 2018, 11, 1381. [Google Scholar] [CrossRef] [Green Version]
- Villalba-Diez, J.; Ordieres-Mere, J. Improving manufacturing operational performance by standardizing process management. Trans. Eng. Manag. 2015, 62, 351–360. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Villalba-Diez, J. The Lean Brain Theory. Complex Networked Lean Strategic Organizational Design; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group LLC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Dall’Amico, L.; Couillet, R.; Tremblay, N. A unified framework for spectral clustering in sparse graphs. arXiv 2020, arXiv:2003.09198. [Google Scholar]
- Harris, K.D.; Aravkin, A.; Rao, R.; Brunton, B.W. Time-varying Autoregression with Low Rank Tensors. arXiv 2019, arXiv:1905.08389. [Google Scholar]
- Wang, Y.; Yuan, Y.; Ma, Y.; Wang, G. Time-Dependent Graphs: Definitions, Applications, and Algorithms. Data Sci. Eng. 2019, 4, 352–366. [Google Scholar] [CrossRef] [Green Version]
- Borgatti, S.P.; Everett, M.G.; Johnson, J.C. Analyzing Social Networks; Sage: London, UK, 2018. [Google Scholar]
- Kim, J.; Hastak, M. Social network analysis: Characteristics of online social networks after a disaster. Int. J. Inf. Manag. 2018, 38, 86–96. [Google Scholar] [CrossRef]
- Arafeh, M.; Ceravolo, P.; Mourad, A.; Damiani, E.; Bellini, E. Ontology based recommender system using social network data. Future Gener. Comput. Syst. 2021, 115, 769–779. [Google Scholar] [CrossRef]
- Centola, D. The spread of behavior in an online social network experiment. Science 2010, 329, 1194–1197. [Google Scholar] [CrossRef] [PubMed]
- Arafeh, M.; Ceravolo, P.; Mourad, A.; Damiani, E. Sampling Online Social Networks with Tailored Mining Strategies. In Proceedings of the 2019 Sixth International Conference on Social Networks Analysis, Management and Security (SNAMS), Granada, Spain, 22–25 October 2019; pp. 217–222. [Google Scholar] [CrossRef]
- Ovadia, S. Exploring the potential of Twitter as a research tool. Behav. Soc. Sci. Libr. 2009, 28, 202–205. [Google Scholar] [CrossRef]
- Sloan, L.; Morgan, J.; Burnap, P.; Williams, M. Who tweets? Deriving the demographic characteristics of age, occupation and social class from Twitter user meta-data. PLoS ONE 2015, 10, e0115545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cherepnalkoski, D.; Mozetic, I. A retweet network analysis of the European Parliament. In Proceedings of the 2015 11TH International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Bangkok, Thailand, 23–27 November 2015; pp. 350–357. [Google Scholar]
- Stewart, L.G.; Arif, A.; Starbird, K. Examining trolls and polarization with a retweet network. In Proceedings of the ACM WSDM, Workshop on Misinformation and Misbehavior Mining on the Web, Los Angeles, CA, USA, 9 February 2018. [Google Scholar]
- Byrd, T.; Turner, D. Measuring the flexibility of information technology infrastructure: Exploratory analysis of a construct. J. Manag. Inf. Syst. 2000, 17, 167–208. [Google Scholar]
- Eisenhardt, K. Building theories from case study research. Acad. Manag. Rev. 1989, 14, 532–550. [Google Scholar] [CrossRef]
- Morstatter, F.; Pfeffer, J.; Liu, H.; Carley, K.M. Is the sample good enough? Comparing data from twitter’s streaming api with twitter’s firehose. arXiv 2013, arXiv:1306.5204. [Google Scholar]
- van Rossum, G. Python Tutorial, Technical Report CS-R9526; Centrum voor Wiskunde en Informatica (CWI): Amsterdam, The Netherlands, 1995. [Google Scholar]
- Hagberg, A.; Swart, P.; Chult, D.S. Exploring Network Structure, Dynamics, and Function Using NetworkX; Technical Report; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2008.
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the Third International AAAI Conference on Weblogs and Social Media, San Jose, CA, USA, 17–20 May 2009; Volume 8, pp. 361–362. [Google Scholar]
- Freeman, L.C. Visualizing social networks. J. Soc. Struct. 2000, 1, 4. [Google Scholar]
- Bi, B.; Cho, J. Modeling a retweet network via an adaptive bayesian approach. In Proceedings of the 25th International Conference on World Wide Web, Montreal, QC, Canada, 11–15 April 2016; pp. 459–469. [Google Scholar]
- Jacomy, M.; Venturini, T.; Heymann, S.; Bastian, M. ForceAtlas2, a continuous graph layout algorithm for handy network visualization designed for the Gephi software. PLoS ONE 2014, 9, e98679. [Google Scholar] [CrossRef] [PubMed]
- Wali, M. Learn Microsoft Azure: Build, Manage, and Scale Cloud Applications Using the Azure Ecosystem; Packt Publishing: Birmingham, UK, 2018. [Google Scholar]
- Loria, S. Textblob Documentation. 2020. Available online: https://buildmedia.readthedocs.org/media/pdf/textblob/latest/textblob.pdf (accessed on 3 April 2021).
- Sheridan, R.P. Time-Split Cross-Validation as a Method for Estimating the Goodness of Prospective Prediction. J. Chem. Inf. Model. 2013, 53, 783–790. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Manning Publications Co.: Shelter Island, NY, USA, 2018. [Google Scholar]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef] [Green Version]
- Jiménez-Valverde, A. Insights into the area under the receiver operating characteristic curve (AUC) as a discrimination measure in species distribution modelling. Glob. Ecol. Biogeogr. 2012, 21, 498–507. [Google Scholar] [CrossRef]


| Sensors | Sustainability | Biosensors | |
|---|---|---|---|
| 1. | #mdpisensors | #mdpisustainability | #mdpibiosensors |
| 2. | #sensors | #sustainability | #biosensors |
| 3. | #iot | #sustainable | #sers |
| 4. | #deeplearning | #sushighlycitedpaper | #electrochemical |
| 5. | #biosensors | #climatechange | #fret |
| 6. | #machinelearning | #susinterestingpaper | #spr |
| 7. | #internetofthings | #energy | #biomarkers |
| 8. | #sensor | #sdgs | #i3s2017 |
| 9. | #wearable | #circulareconomy | #biomarker |
| 10. | #remotesensing | #sustainabledevelopment | #raman |
| 11. | #uav | #tourism | #biosensor |
| 12. | #structuralhealthmonitoring | #callforpapers | #immunoassay |
| 13. | #wearablesensors | #agriculture | #microfluidic |
| 14. | #wirelesssensornetworks | #transportation | #i3s2019 |
| 15. | #i3s2019 | #biodiversity | #microfluidics |
| 16. | #sensornetworks | #environment | #wearables |
| 17. | #sensing | #csr | #microarray |
| 18. | #5g | #management | #bacteria |
| 19. | #monitoring | #food | #aptamer |
| 20. | #smartcities | #renewableenergy | #sensors |
| 21. | #gnss | #openaccess | #flexible |
| 22. | #biosensor | #innovation | #bret |
| 23. | #blockchain | #education | #lab_on_chip |
| 24. | #sensorfusion | #resilience | #immunosensors |
| 25. | #highlyaccessedpaper | #environmental | #openaccess |
| ’created at:’ | Tue Jun 09 14:42:30 +0000 2020, |
| ’id’: | ’1270365661215240192’, |
| ’username’: | ’MedGIFT group’, |
| ’user id’: | ’1012268385789513729’, |
| ’text’: | ’We are hiring! |
| ’quoted user’: | ’id’: ’1270359799201443840’, ... |
| ...’user id’: ’2163570636’,... | |
| ...’username’: ’adepeursinge’ |
| Sender | retweeted_user_id |
| Receiver | retweeter_user_id |
| Evolution | created_at |
| Content | hashtag, group and retweet text |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villalba-Diez, J.; Molina, M.; Schmidt, D. Geometric Deep Lean Learning: Evaluation Using a Twitter Social Network. Appl. Sci. 2021, 11, 6777. https://doi.org/10.3390/app11156777
Villalba-Diez J, Molina M, Schmidt D. Geometric Deep Lean Learning: Evaluation Using a Twitter Social Network. Applied Sciences. 2021; 11(15):6777. https://doi.org/10.3390/app11156777
Chicago/Turabian StyleVillalba-Diez, Javier, Martin Molina, and Daniel Schmidt. 2021. "Geometric Deep Lean Learning: Evaluation Using a Twitter Social Network" Applied Sciences 11, no. 15: 6777. https://doi.org/10.3390/app11156777
APA StyleVillalba-Diez, J., Molina, M., & Schmidt, D. (2021). Geometric Deep Lean Learning: Evaluation Using a Twitter Social Network. Applied Sciences, 11(15), 6777. https://doi.org/10.3390/app11156777







