Trigonometric Inference Providing Learning in Deep Neural Networks
Abstract
:1. Introduction
- We propose a novel training and inference method that utilizes trigonometric approximations. To the best of our knowledge, this is the first work that shows trigonometric inference can provide learning in deep neural networks;
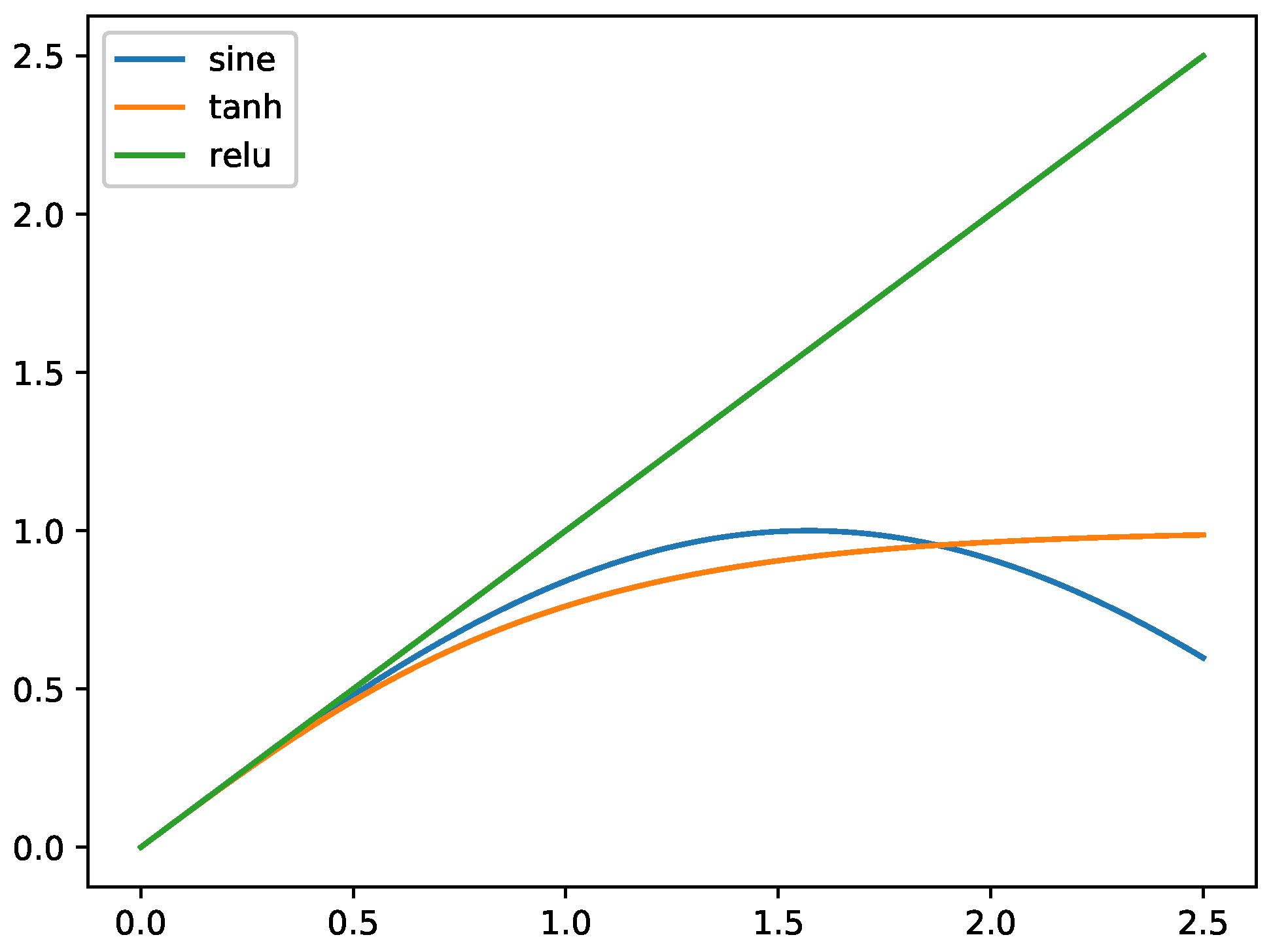
- By replacing the model parameters and activations with their sine value, we analyze that multiplications could be transferred to shift-and-add operations in training and inference. To achieve this, a rectified sine activation function is proposed;
- We evaluate trigonometric inference on several models and shows that it can achieve performance that is close to conventional CNNs on MNIST, Cifar10, and Cifar100 datasets.
2. Related Work
2.1. Training with Low Precision
2.2. Training with Add or Shift Operations
2.3. Hardware Optimization for Hyperbolic Functions with CORDIC
3. Methodology
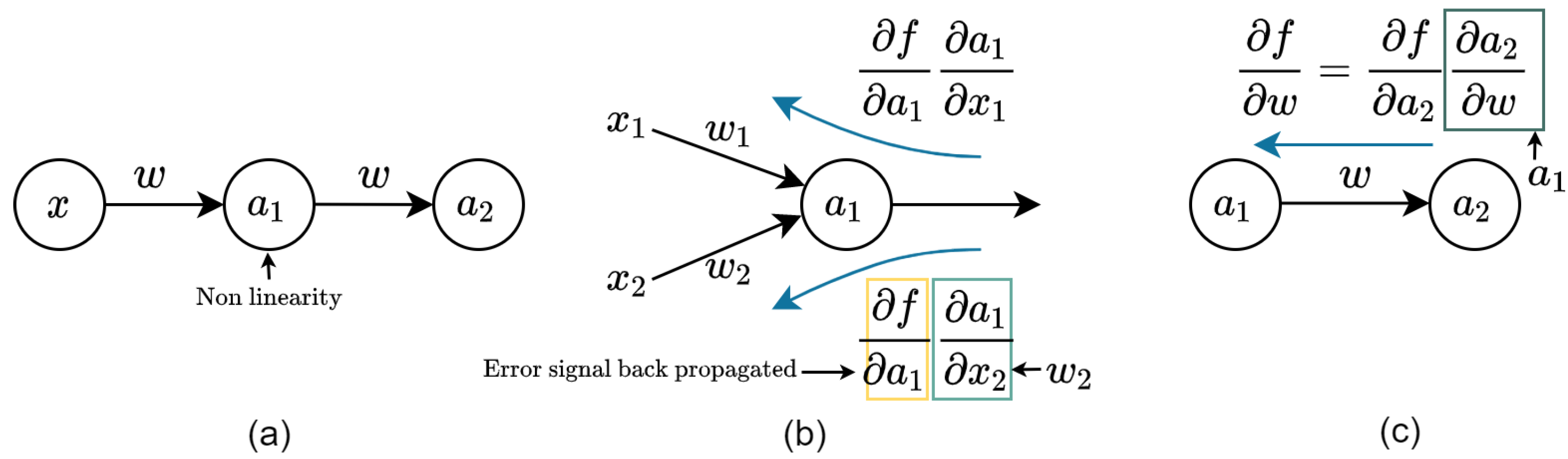
3.1. Forward and Backward Inference
3.1.1. Forward Inference
3.1.2. Backward Inference
3.1.3. Weight Update
3.2. Precision Analysis
3.3. A Toy Example
3.4. Suitable Scenarios
4. Evaluation
4.1. Experiments on MNIST
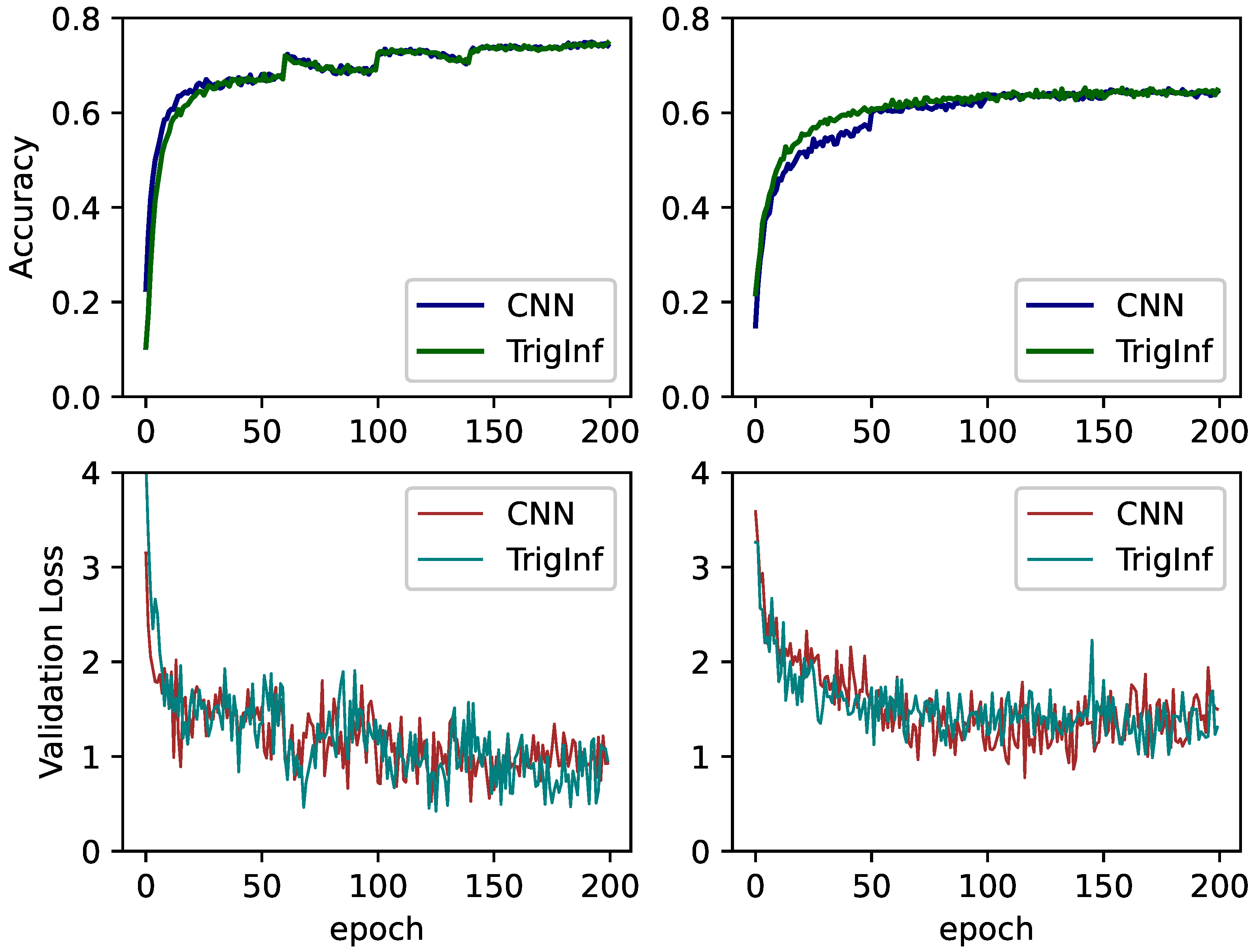
4.2. Experiments on CIFAR
4.3. Narrowing the Accuracy Loss
4.4. Compatibility with Other Optimizers
5. Future Research and Challenges
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Volder, J. The CORDIC computing technique. IRE Trans. Electron. Comput. 1959, EC-8, 330–334. [Google Scholar] [CrossRef]
- Tiwari, V.; Khare, N. Hardware implementation of neural network with Sigmoidal activation functions using CORDIC. Microprocess. Microsyst. 2015, 39, 373–381. [Google Scholar] [CrossRef]
- Chen, Y.H.; Chen, S.W.; Wei, M.X. A VLSI Implementation of Independent Component Analysis for Biomedical Signal Separation Using CORDIC Engine. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 373–381. [Google Scholar] [CrossRef]
- Koyuncu, I. Implementation of high speed tangent sigmoid transfer function approximations for artificial neural network applications on FPGA. Adv. Electr. Comput. Eng. 2018, 18, 79–86. [Google Scholar] [CrossRef]
- Shomron, G.; Weiser, U. Spatial correlation and value prediction in convolutional neural networks. IEEE Comput. Archit. Lett. 2018, 18, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Shomron, G.; Banner, R.; Shkolnik, M.; Weiser, U. Thanks for nothing: Predicting zero-valued activations with lightweight convolutional neural networks. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 234–250. [Google Scholar]
- Shomron, G.; Weiser, U. Non-blocking simultaneous multithreading: Embracing the resiliency of deep neural networks. In Proceedings of the 2020 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Athens, Greece, 17–21 October 2020; pp. 256–269. [Google Scholar]
- Cai, J.; Takemoto, M.; Nakajo, H. A deep look into logarithmic quantization of model parameters in neural networks. In Proceedings of the 10th International Conference on Advances in Information Technology, Bangkok, Thailand, 10–13 December 2018; pp. 1–8. [Google Scholar]
- Sanyal, A.; Beerel, P.A.; Chugg, K.M. Neural Network Training with Approximate Logarithmic Computations. In Proceedings of the ICASSP 2020 IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020; pp. 3122–3126. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks. Adv. Neural Inf. Process. Syst. 2016, 29, 4107–4115. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-net: Imagenet classification using binary convolutional neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 525–542. [Google Scholar]
- Banner, R.; Hubara, I.; Hoffer, E.; Soudry, D. Scalable methods for 8-bit training of neural networks. arXiv 2018, arXiv:1805.11046. [Google Scholar]
- Bhandare, A.; Sripathi, V.; Karkada, D.; Menon, V.; Choi, S.; Datta, K.; Saletore, V. Efficient 8-bit quantization of transformer neural machine language translation model. arXiv 2019, arXiv:1906.00532. [Google Scholar]
- Shomron, G.; Gabbay, F.; Kurzum, S.; Weiser, U. Post-Training Sparsity-Aware Quantization. arXiv 2021, arXiv:2105.11010. [Google Scholar]
- Chen, H.; Wang, Y.; Xu, C.; Shi, B.; Xu, C.; Tian, Q.; Xu, C. AdderNet: Do We Really Need Multiplications in Deep Learning? arXiv 2019, arXiv:1912.13200. [Google Scholar]
- Miyashita, D.; Lee, H.E.; Murmann, B. Convolutional Neural Networks using Logarithmic Data Representation. arXiv 2016, arXiv:1603.01025. [Google Scholar]
- Elhoushi, M.; Shafiq, F.; Tian, Y.; Li, J.Y.; Chen, Z. DeepShift: Towards Multiplication-Less Neural Networks. arXiv 2019, arXiv:1905.13298. [Google Scholar]
- Jaime, F.J.; Sánchez, M.A.; Hormigo, J.; Villalba, J.; Zapata, E.L. Enhanced scaling-free CORDIC. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 1654–1662. [Google Scholar] [CrossRef]
- Mokhtar, A.; Reaz, M.; Chellappan, K.; Ali, M.M. Scaling free CORDIC algorithm implementation of sine and cosine function. In Proceedings of the World Congress on Engineering (WCE’13), London, UK, 3–5 July 2013; Volume 2. [Google Scholar]
- Chen, K.T.; Fan, K.; Han, X.; Baba, T. A CORDIC algorithm with improved rotation strategy for embedded applications. J. Ind. Intell. Inf. 2015, 3, 274–279. [Google Scholar] [CrossRef]
- Tiwari, V.; Mishra, A. Neural network-based hardware classifier using CORDIC algorithm. Mod. Phys. Lett. B 2020, 34, 2050161. [Google Scholar] [CrossRef]
- Heidarpur, M.; Ahmadi, A.; Ahmadi, M.; Azghadi, M.R. CORDIC-SNN: On-FPGA STDP Learning with Izhikevich Neurons. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2651–2661. [Google Scholar] [CrossRef]
- Hao, X.; Yang, S.; Wang, J.; Deng, B.; Wei, X.; Yi, G. Efficient Implementation of Cerebellar Purkinje Cell with CORDIC Algorithm on LaCSNN. Front. Neurosci. 2019, 13, 1078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sopena, J.M.; Romero, E.; Alquezar, R. Neural networks with periodic and monotonic activation functions: A comparative study in classification problems. In Proceedings of the 9th International Conference on Artificial Neural Networks, Edinburgh, UK, 7–10 September 1999; pp. 323–328. [Google Scholar]
- Parascandolo, G.; Huttunen, H.; Virtanen, T. Taming the Waves: Sine as Activation Function in Deep Neural Networks. 2016. Available online: https://openreview.net/pdf?id=Sks3zF9eg (accessed on 18 July 2021).
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Zhang, Y.; Qu, L.; Liu, J.; Guo, D.; Li, M. Sine neural network (SNN) with double-stage weights and structure determination (DS-WASD). Soft Comput. 2016, 20, 211–221. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Cownden, D.; Tweed, D.B.; Akerman, C.J. Random synaptic feedback weights support error backpropagation for deep learning. Nat. Commun. 2016, 7, 13276. [Google Scholar] [CrossRef]
- Crafton, B.A.; Parihar, A.; Gebhardt, E.; Raychowdhury, A. Direct feedback alignment with sparse connections for local learning. Front. Neurosci. 2019, 13, 525. [Google Scholar] [CrossRef]
- Nøkland, A. Direct feedback alignment provides learning in deep neural networks. arXiv 2016, arXiv:1609.01596. [Google Scholar]
- Heidarpour, M.; Ahmadi, A.; Rashidzadeh, R. A CORDIC based digital hardware for adaptive exponential integrate and fire neuron. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1986–1996. [Google Scholar] [CrossRef]
- Chetlur, S.; Woolley, C.; Vandermersch, P.; Cohen, J.; Tran, J.; Catanzaro, B.; Shelhamer, E. cudnn: Efficient primitives for deep learning. arXiv 2014, arXiv:1410.0759. [Google Scholar]
- Tokui, S.; Oono, K.; Hido, S.; Clayton, J. Chainer: A next-generation open source framework for deep learning. In Proceedings of the Workshop on Machine Learning Systems (LearningSys) in the Twenty-Ninth Annual Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 October 2015; Volume 5, pp. 1–6. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]



| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | Layer 8 | |
|---|---|---|---|---|---|---|---|---|
| 0.3985 | 0.3994 | 0.4015 | 0.8437 | 0.4036 | 0.6533 | 0.4101 | 0.3984 | |
| 0.3411 | 0.3411 | 0.3376 | 0.5188 | 0.3360 | 0.4836 | 0.3312 | 0.3410 | |
| Initials | a | b | c | d |
|---|---|---|---|---|
| 0.5 | 0.43 | −0.78 | 0 | |
| 0.1 | 500 | −0.07 | 1.83 | |
| (0.03, 0.3) | (0.3, 0.3) | (0.03, 0.3) | (0.03, 2) | |
| m | 0.07 | −0.61 | 1.73 | −0.54 |
| Model | ||||
|---|---|---|---|---|
| layer 1 | 1000 | 1000 | 100 | 10,000 |
| layer 2 | 1000 | 1000 | 100 | 10,000 |
| layer 3 | 1000 | 100 | 1000 | 10,000 |
| 0.9827 | 0.9832 | 0.9802 | 0.9833 | |
| 0.9239 | 0.1087 | 0.9221 | 0.9241 | |
| 0.9832 | 0.1153 | 0.9289 | 0.9836 |
| VGG | WideResNet |
|---|---|
| 1024-linear × 2 | |
| avg-pool | |
| 640-linear |
| Model and Dataset | CIFAR 10 | CIFAR 100 |
|---|---|---|
| VGG Stdandard | 0.9309 | 0.7158 |
| VGG TrigInf 1 | 0.9192 | 0.7009 |
| VGG TrigInf 2 | 0.9213 | 0.6957 |
| WRN Stdandard | 0.9564 | 0.7861 |
| WRN TrigInf 1 | 0.9537 | 0.7759 |
| WRN TrigInf 2 | 0.9334 | 0.7053 |
| Model (ResNet50) and Result | Accuracy | Training Loss | Validation Loss |
|---|---|---|---|
| CNN () | 0.7171 | 0.0582 | 1.0614 |
| TrigInf () | 0.7058 | 0.0701 | 1.2853 |
| TrigInf () | 0.7124 | 0.0644 | 1.6003 |
| TrigInf () | 0.7205 | 0.0577 | 0.9063 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, J.; Takemoto, M.; Qiu, Y.; Nakajo, H. Trigonometric Inference Providing Learning in Deep Neural Networks. Appl. Sci. 2021, 11, 6704. https://doi.org/10.3390/app11156704
Cai J, Takemoto M, Qiu Y, Nakajo H. Trigonometric Inference Providing Learning in Deep Neural Networks. Applied Sciences. 2021; 11(15):6704. https://doi.org/10.3390/app11156704
Chicago/Turabian StyleCai, Jingyong, Masashi Takemoto, Yuming Qiu, and Hironori Nakajo. 2021. "Trigonometric Inference Providing Learning in Deep Neural Networks" Applied Sciences 11, no. 15: 6704. https://doi.org/10.3390/app11156704
APA StyleCai, J., Takemoto, M., Qiu, Y., & Nakajo, H. (2021). Trigonometric Inference Providing Learning in Deep Neural Networks. Applied Sciences, 11(15), 6704. https://doi.org/10.3390/app11156704






