Echo State Network Based Model Predictive Control for Active Vibration Control of Hybrid Electric Vehicle Powertrains
Abstract
:1. Introduction
2. Related Work
- A novel control scheme based on an ESN and MPC is developed to improve the control performance in cases involving highly irregular disturbances.
- The proposed MPC control scheme can be applied even if the optimization calculation does not finish within the control period.
- The predictive model for the HEV system is based on the state-space representation to understand the relationship between the model parameters and output.
- The proposed method can be applied to several other control targets apart from the active vibration control of HEV powertrains.
3. Control Method
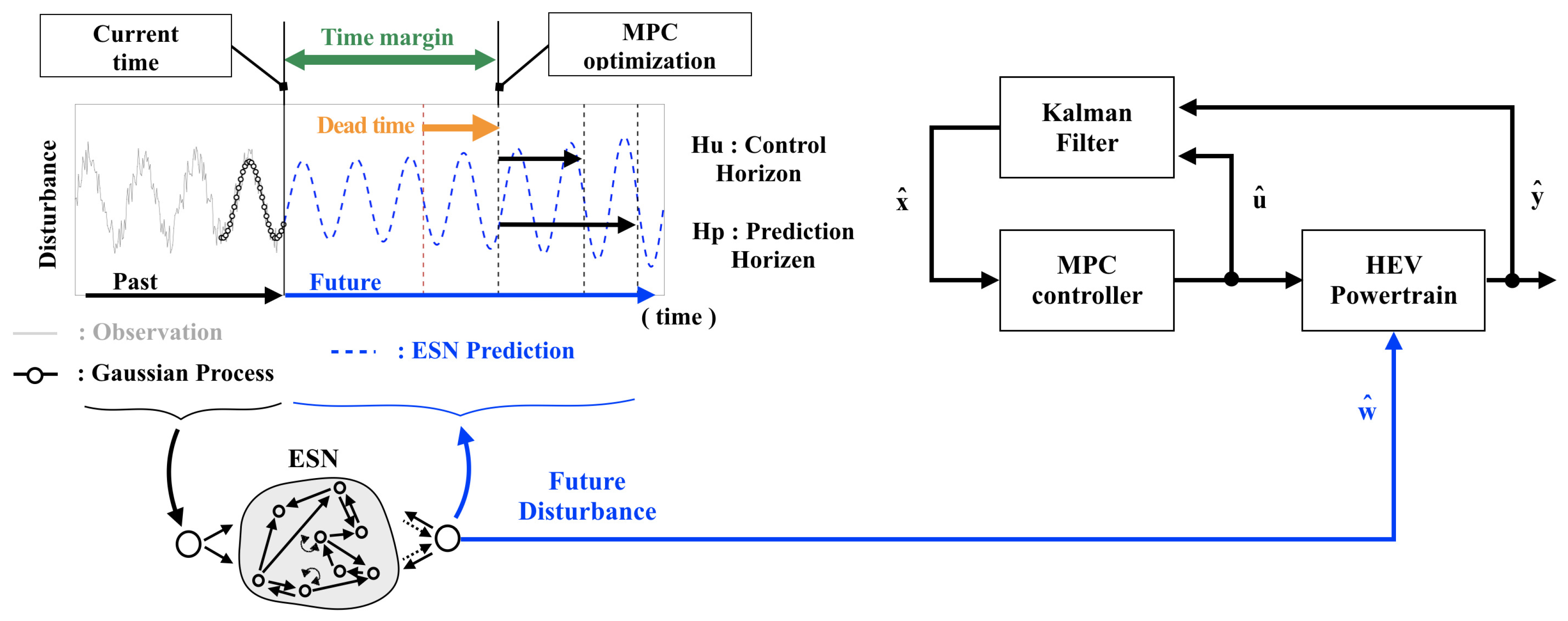
3.1. Concept of ESN-MPC
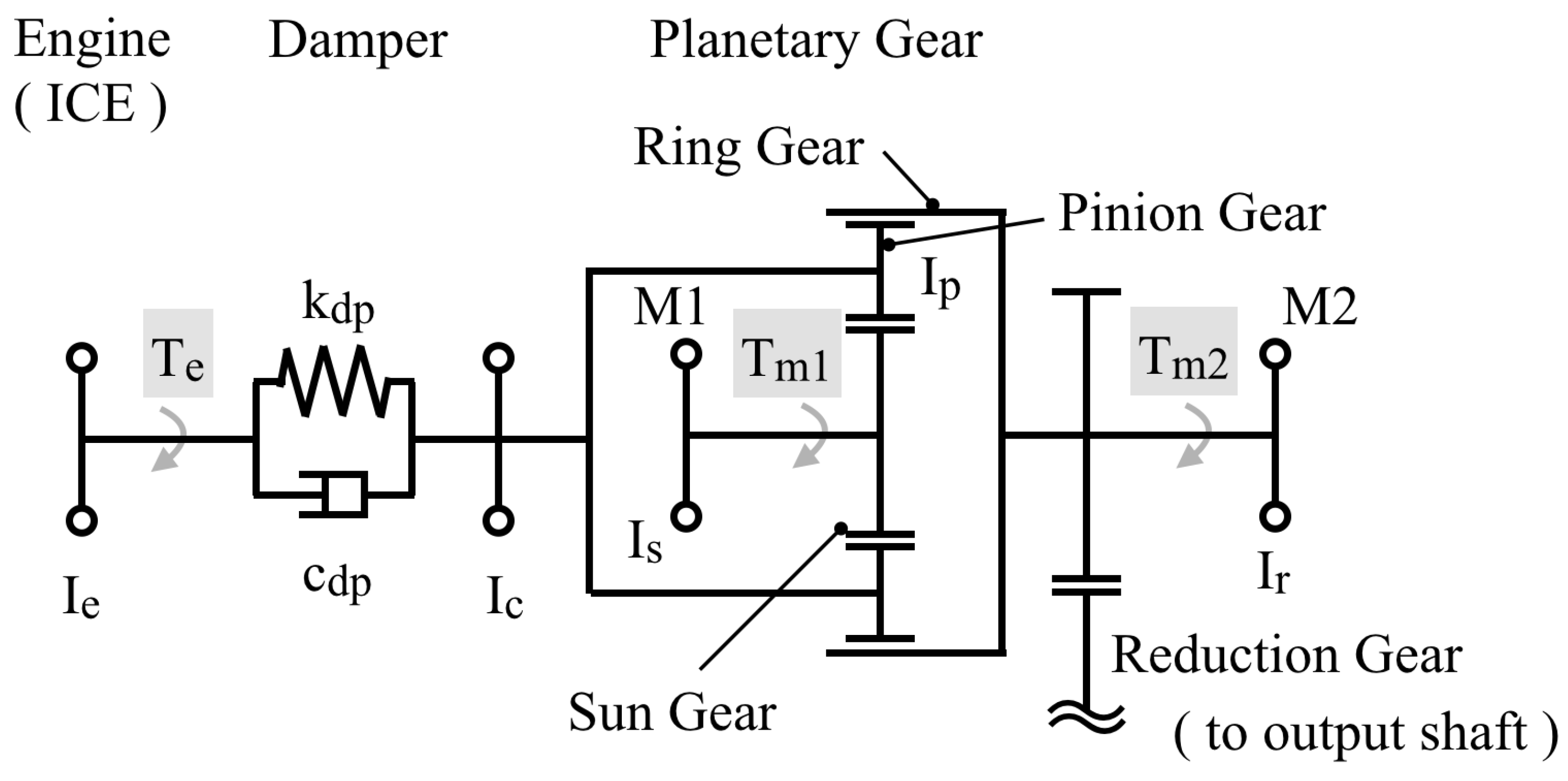
3.2. Basic Equations for the HEV Powertrain
3.3. State-Space Representation and Kalman Filter
3.4. Solving the Predictive Control Problem
3.5. Explicit Dead-Time Compensation-Based MPC (EDT-MPC)
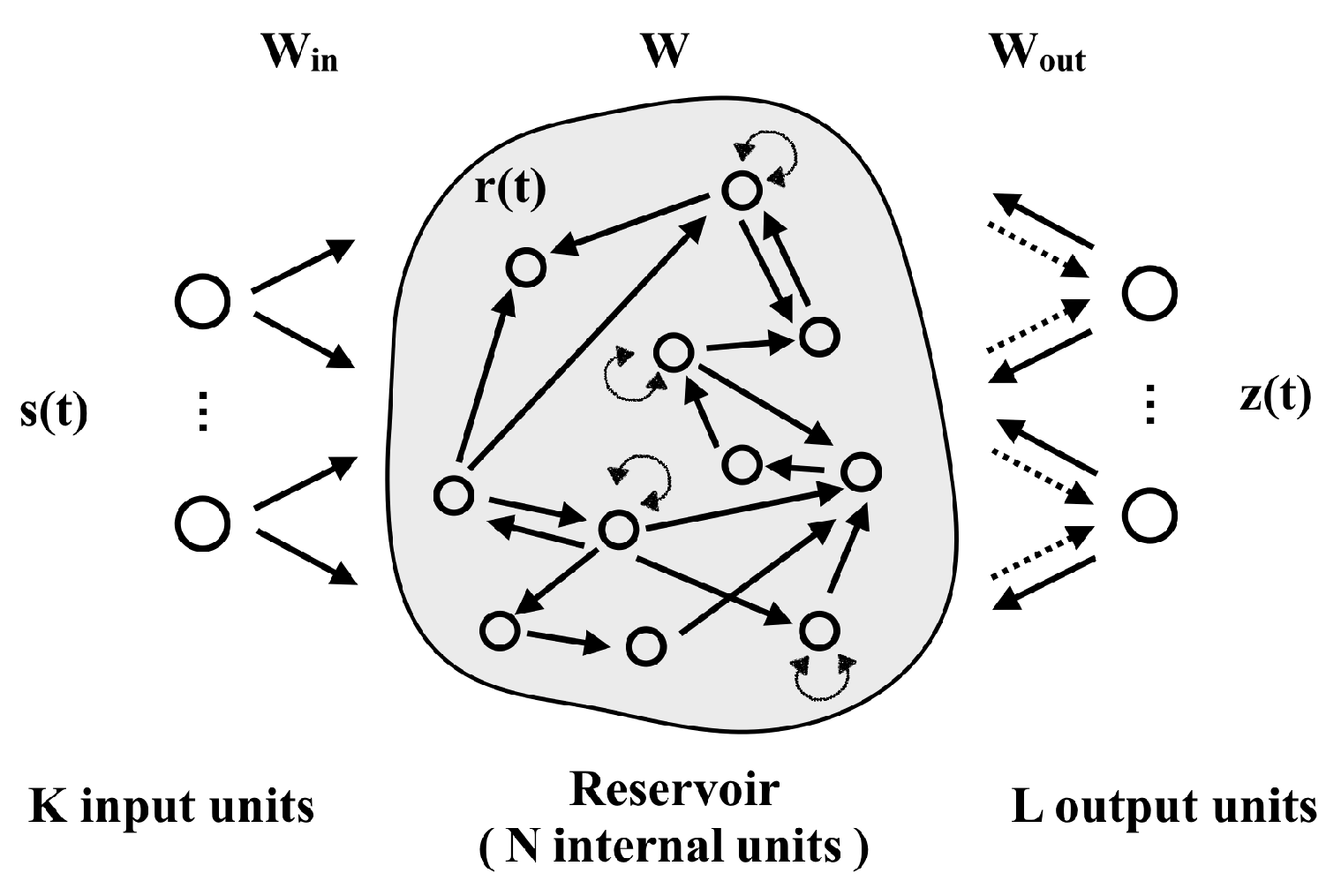
3.6. ESN with Gaussian Process Regression (GPR)
4. Simulation
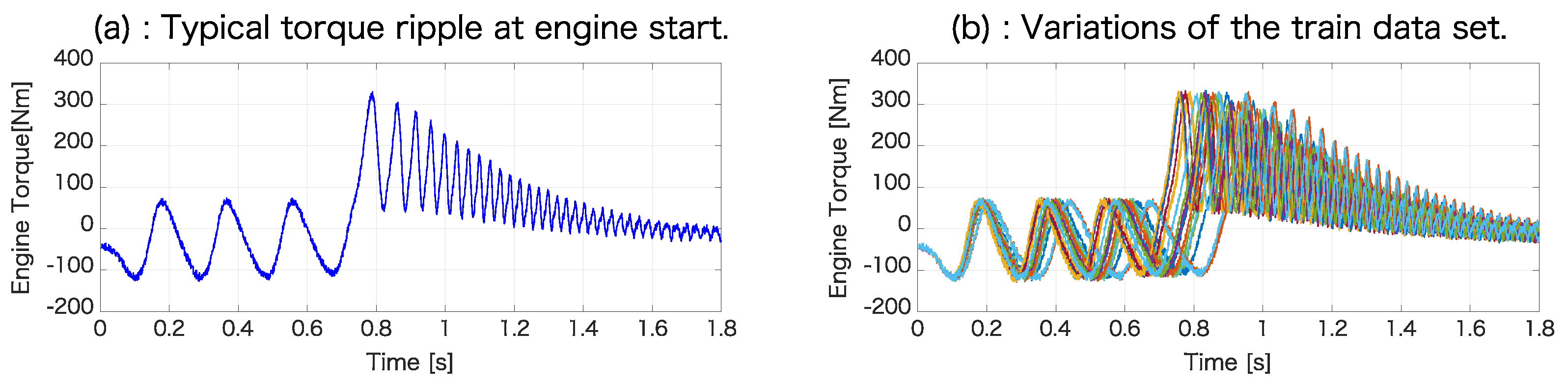
4.1. Numerical Conditions
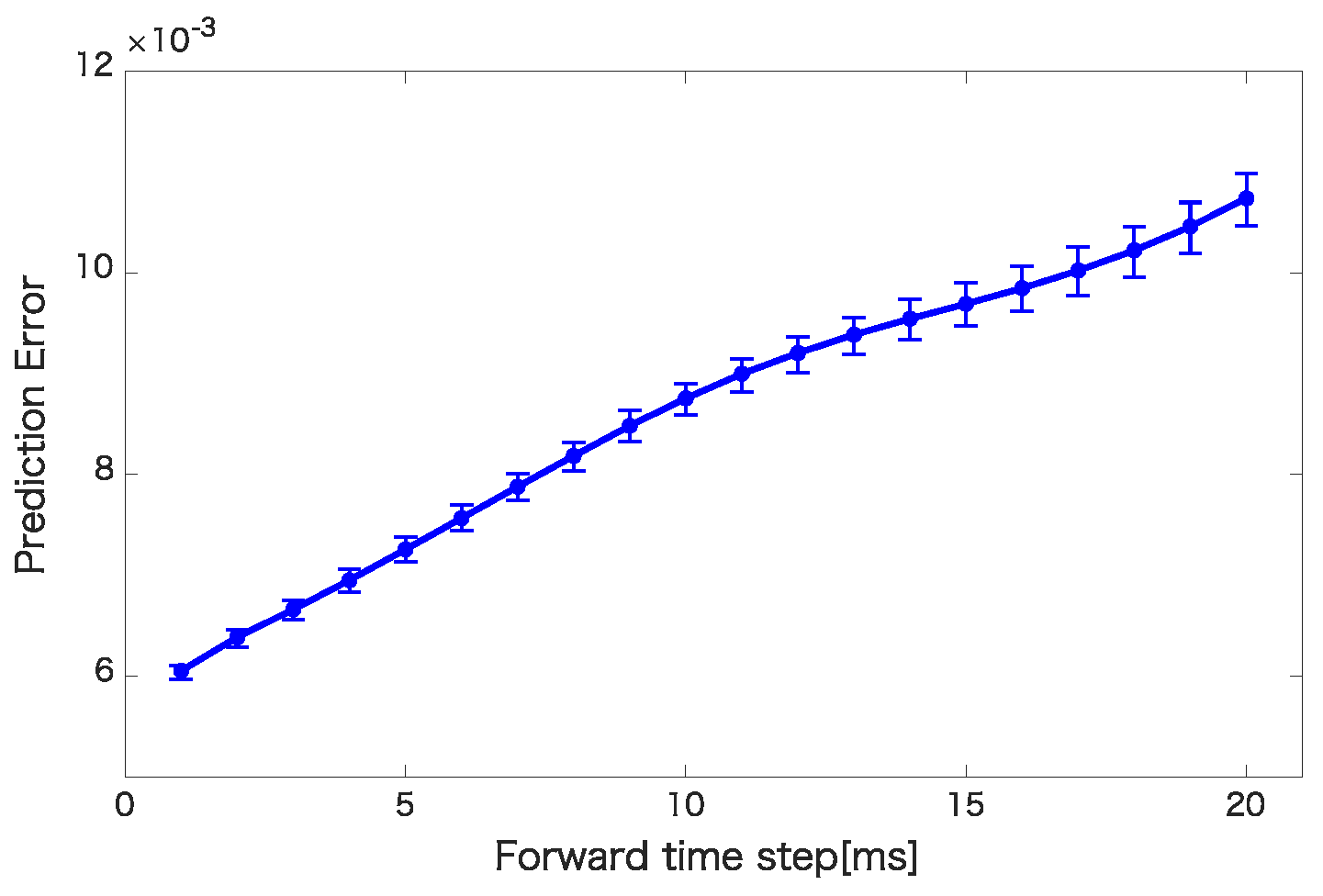
4.2. ESN Prediction Results
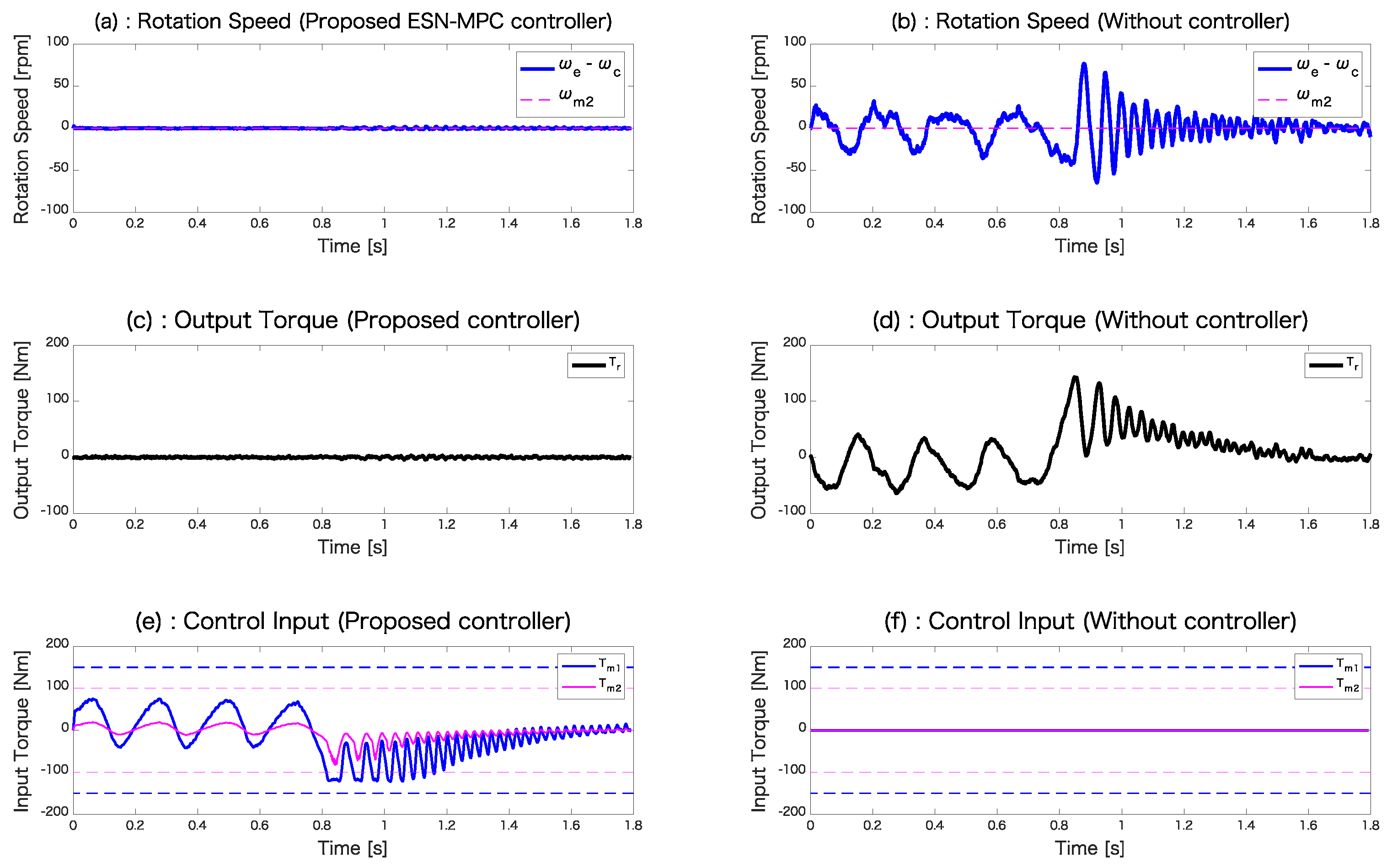
4.3. ESN-Based MPC Results
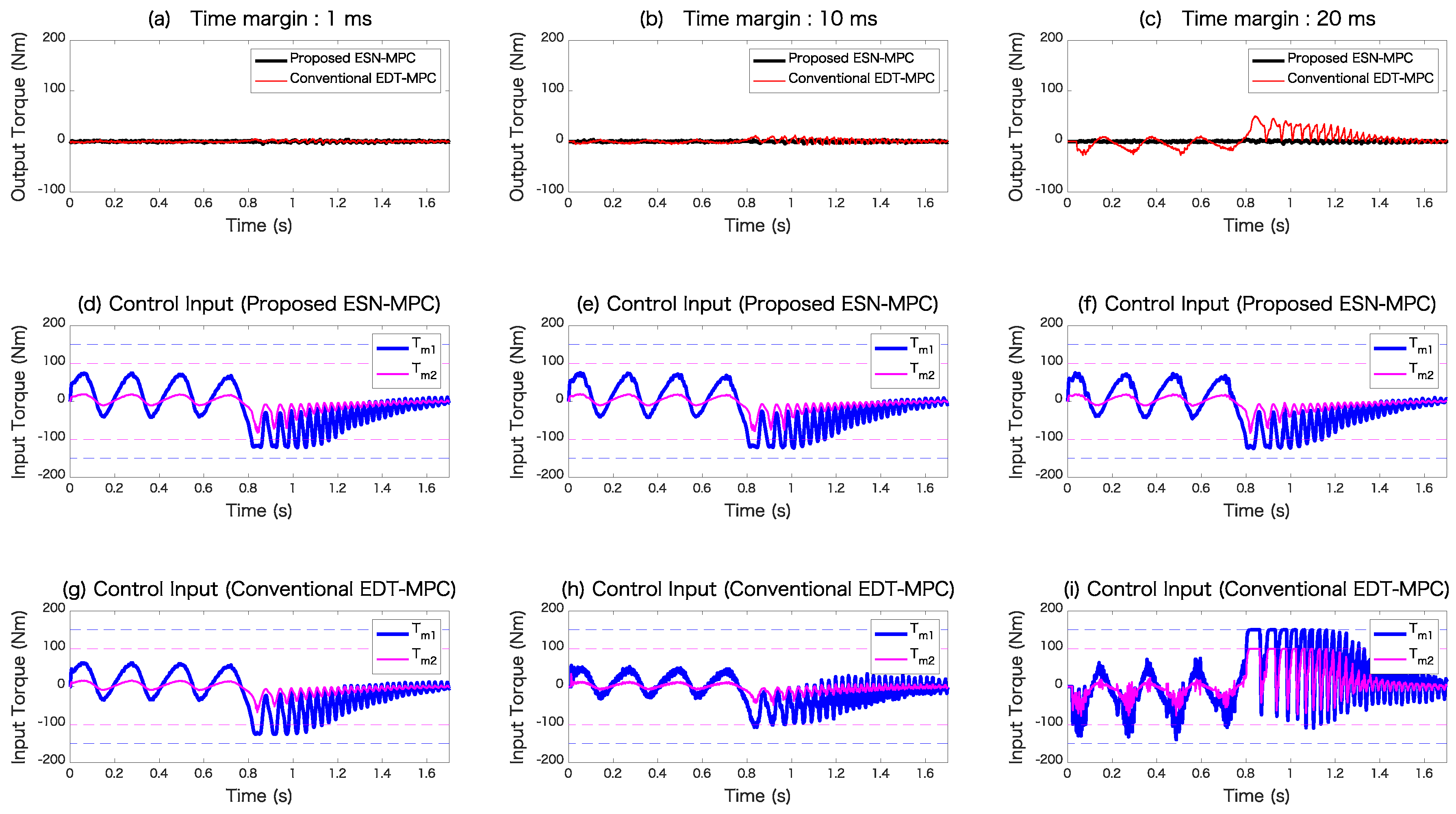
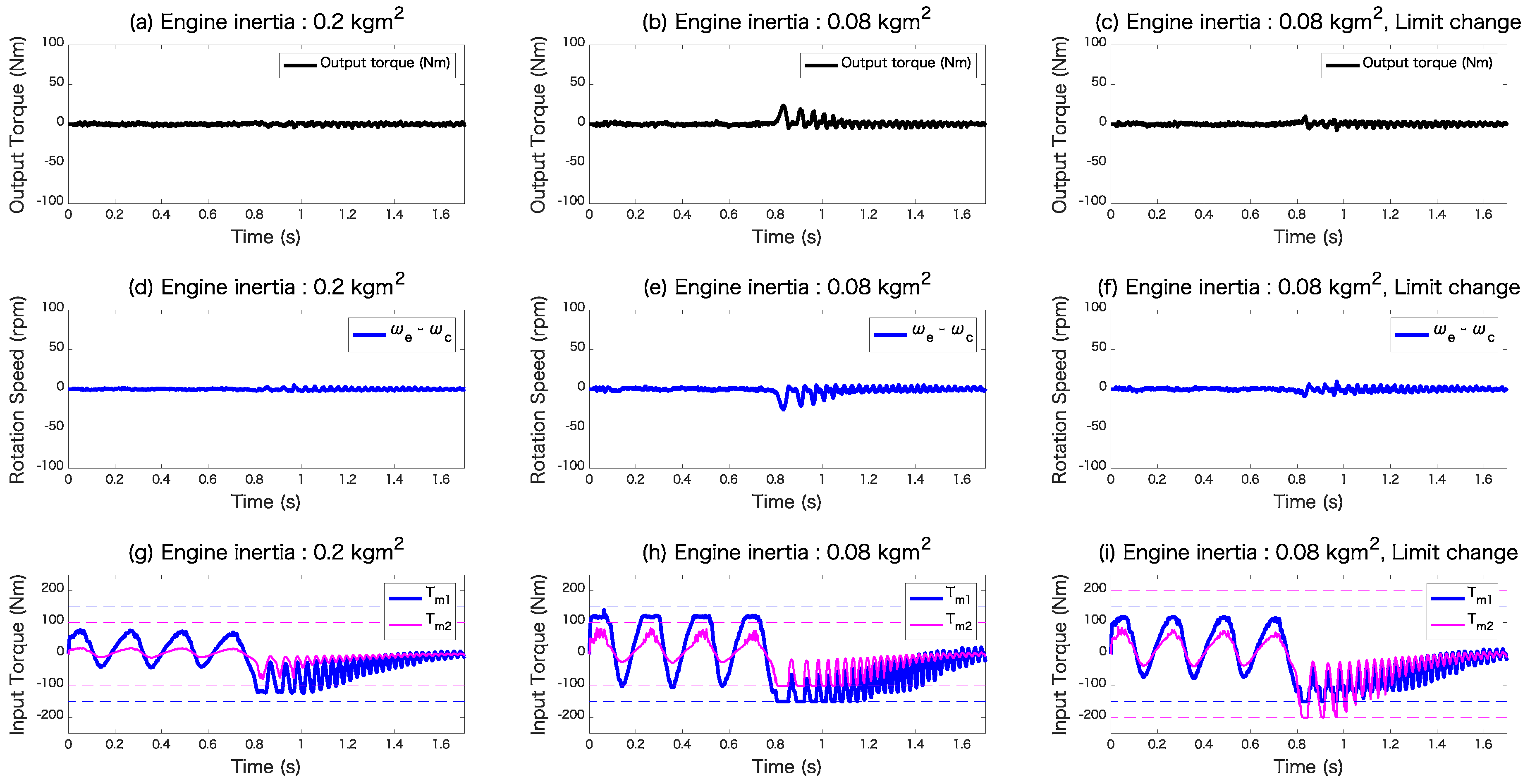
4.4. Case Study for the Design Variables
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ohtsuka, T. Concept and Applications of Real-Time Optimization. In Proceedings of the Conference of Transdisciplinary Federation of Science and Technology, Kyoto, Japan, 2–3 December 2017; p. B-4-5. (In Japanese). [Google Scholar]
- Kooy, A.; Seebacher, R. Best-in-Class Dampers for Every Driveline Concept. In Proceedings of the Schaeffler Kolloqu, Baden-Baden, Germany, 11–13 April 2018; pp. 146–160. [Google Scholar]
- Gusev, S.V.; Johnson, W.; Miller, J. Active flywheel control based on the method of moment restrictions. Proc. Am. Control. Conf. 1997, 5, 3426–3430. [Google Scholar]
- Beuschel, M.; Rau, M.; Schroder, D. Adaptive damping of torque pulsation using a starter generator-opportunities and boundaries. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference, Rome, Italy, 8–12 October 2000. [Google Scholar]
- Santos, T.L.; Limon, D.; Normey-Rico, J.E.; Alamo, T. On the explicit dead-time compensation for robust model predictive control. J. Process Control 2012, 22, 236–246. [Google Scholar] [CrossRef]
- Pham, T.; Seifried, R.; Scholz, C. Anti-Jerk Control of a Parallel Hybrid Electrified Vehicle with Dead Time. IFAC-PapersOnLine 2017, 50, 966–971. [Google Scholar] [CrossRef]
- Vadamalu, R.S.; Beidl, C. MPC for Active Torsional Vibration Reduction of Hybrid Electric Powertrains. IFAC-PapersOnLine 2016, 49, 756–761. [Google Scholar] [CrossRef]
- Draeger, A.; Engell, S.; Ranke, H. Model predictive control using neural networks. IEEE Control Syst. Mag. 1995, 15, 61–66. [Google Scholar]
- Lanzetti, N.; Lian, Y.Z.; Cortinovis, A.; Dominguez, L.; Mercangöz, M.; Jones, C. Recurrent Neural Network based MPC for Process Industries. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 1005–1010. [Google Scholar]
- Zhang, B.; Sun, X.; Liu, S.; Deng, X. Recurrent Neural Network-Based Model Predictive Control for Multiple Unmanned Quadrotor Formation Flight. Int. J. Aerosp. Eng. 2019, 2019, 7272387. [Google Scholar] [CrossRef] [Green Version]
- Pan, Y.; Wang, J. Model Predictive Control of Unknown Nonlinear Dynamical Systems Based on Recurrent Neural Networks. IEEE Trans. Ind. Electron. 2012, 59, 3089–3101. [Google Scholar] [CrossRef]
- Xiang, K.; Li, B.N.; Zhang, L.; Pang, M.; Wang, M.; Li, X. Regularized Taylor Echo State Networks for Predictive Control of Partially Observed Systems. IEEE Access 2016, 4, 3300–3309. [Google Scholar] [CrossRef]
- Jordanou, J.P.; Camponogara, E.; Antonelo, E.A.; Aguiar, M.A.S. Nonlinear Model Predictive Control of an Oil Well with Echo State Networks. IFAC-PapersOnLine 2018, 51, 13–18. [Google Scholar] [CrossRef]
- Plucenio, A.; Pagano, D.J.; Bruciapaglia, A.; Normey-Rico, J.E. A Practical Approach to Predictive Control for Nonlinear Processes. IFAC Proc. Vol. 2007, 40, 210–215. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.; Su, H.; Zhang, K. Echo State Network-Based Decentralized Control of Continuous-Time Nonlinear Large-Scale Interconnected Systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 1–11. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, H.; Luo, Y.; Su, H. Dual Heuristic Programming for Optimal Control of Continuous-Time Nonlinear Systems Using Single Echo State Network. IEEE Trans. Cybern. 2020, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Shen, T.; Ohata, A. Modeling and Control Design for Automotive Engines; Corona Publishing: Tokyo, Japan, 2011. (In Japanese) [Google Scholar]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Technical Report; University of North Carolina: Chapel Hill, NC, USA, 2001. [Google Scholar]
- Maciejowski, J. Predictive Control With Constraints; Pearson Education Limited: Hoboken, NJ, USA, 2002. [Google Scholar]
- Diehl, M.; Bock, H.G.; Schöder, J.P.; Findeisen, R.; Nagy, Z.; Allgöwer, F. Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations. J. Process Control 2002, 12, 577–585. [Google Scholar] [CrossRef]
- Jaeger, H. The ”echo state” approach to analysing and training recurrent neural networks. Ger. Natl. Res. Cent. Inf. Technol. 2001, 148, 43. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication. Science 2004, 304, 78–79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006. [Google Scholar]
- Wiseman, Y. “Autonomous Vehicles”, Encyclopedia of Information Science and Technology, 5th ed.; Information Resources Management Association: Hershey, PA, USA, 2020; Volume 1, pp. 1–11. [Google Scholar] [CrossRef]

| Symbol | Parameter | Value |
|---|---|---|
| M1 inertia | 0.0265 kg m | |
| M2 inertia | 0.035 kg m | |
| Engine inertia | 0.20 (0.08) kg m | |
| Carrier inertia | 0.01 kg m | |
| Sun gear inertia | 0.01 kg m | |
| Ring gear inertia | 0.005 kg m | |
| Pinion gear inertia | 0.001 kg m | |
| Sun radius | 0.0477 m | |
| Pinion radius | 0.0382 m | |
| Number of pinions | 4 | |
| Planetary gear ratio | 0.3846 | |
| Damper stiffness | 700 Nm/rad | |
| Damping coefficient | 10 Nm s/rad | |
| Sampling time | 1 ms | |
| Control horizon | 5 steps | |
| Prediction horizon | 6 steps | |
| , | M1 torque limitation | −150, +150 Nm |
| , | M2 torque limitation | −100, +100 (−200, +200) Nm |
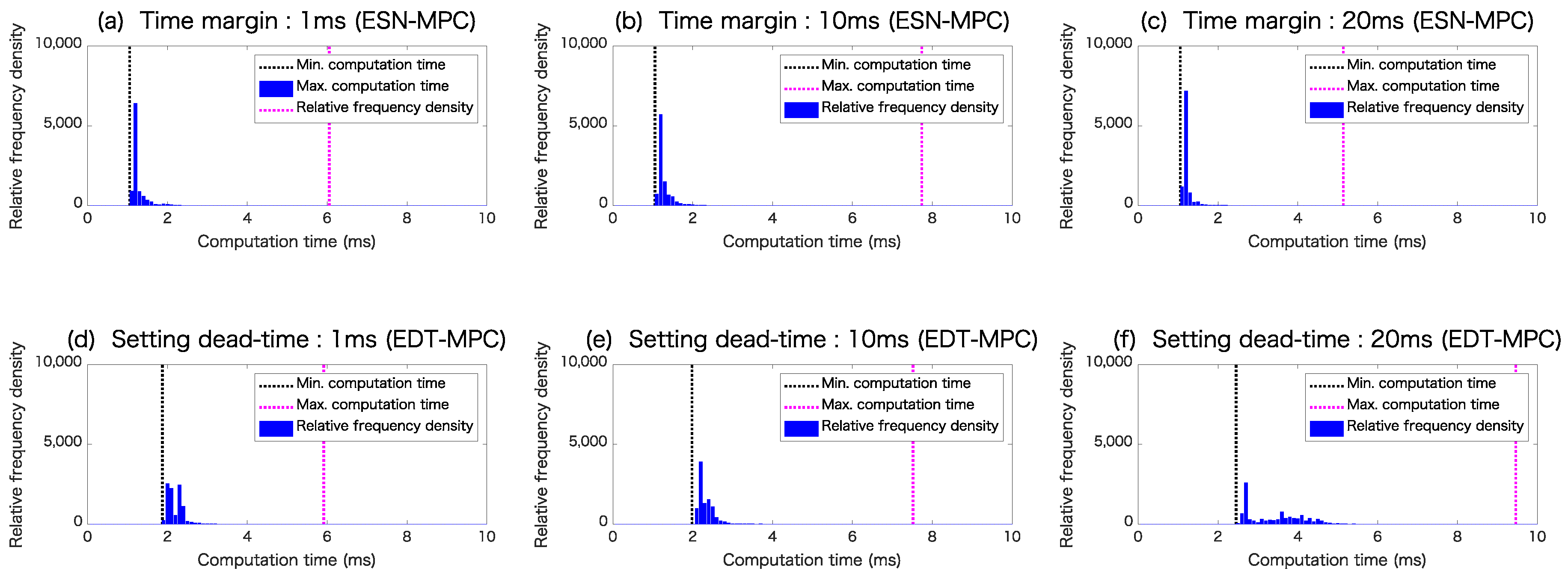
| CPU Time (ms) | ||||
|---|---|---|---|---|
| Model | Simulation Condition | Ave. | Max. | |
| ESN-MPC | Time margin | 1 ms | 1.2 | 6.1 |
| 10 ms | 1.2 | 7.7 | ||
| 20 ms | 1.2 | 5.1 | ||
| EDT-MPC | Setting dead-time | 1 ms | 2.2 | 5.9 |
| 10 ms | 2.3 | 7.5 | ||
| 20 ms | 3.4 | 9.5 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogawa, H.; Takahashi, Y. Echo State Network Based Model Predictive Control for Active Vibration Control of Hybrid Electric Vehicle Powertrains. Appl. Sci. 2021, 11, 6621. https://doi.org/10.3390/app11146621
Ogawa H, Takahashi Y. Echo State Network Based Model Predictive Control for Active Vibration Control of Hybrid Electric Vehicle Powertrains. Applied Sciences. 2021; 11(14):6621. https://doi.org/10.3390/app11146621
Chicago/Turabian StyleOgawa, Hideki, and Yasutake Takahashi. 2021. "Echo State Network Based Model Predictive Control for Active Vibration Control of Hybrid Electric Vehicle Powertrains" Applied Sciences 11, no. 14: 6621. https://doi.org/10.3390/app11146621
APA StyleOgawa, H., & Takahashi, Y. (2021). Echo State Network Based Model Predictive Control for Active Vibration Control of Hybrid Electric Vehicle Powertrains. Applied Sciences, 11(14), 6621. https://doi.org/10.3390/app11146621





