Lp-Norm Inversion of Gravity Data Using Adaptive Differential Evolution

Abstract

As a popular population based heuristic evolutionary algorithm, differential evolution (DE) has been widely applied in various science and engineering problems. Similar to other global nonlinear algorithms, such as genetic algorithm, simulated annealing, particle swarm optimization, etc., the DE algorithm is mostly applied to resolve the parametric inverse problem, but has few applications in physical property inversion. According to our knowledge, this is the first time DE has been applied in obtaining the physical property distribution of gravity data due to causative sources embedded in the subsurface. In this work, the search direction of DE is guided by better vectors, enhancing the exploration efficiency of the mutation strategy. Besides, to reduce the over-stochastic of the DE algorithm, the perturbation directions in mutation operations are smoothed by using a weighted moving average smoothing technique, and the Lp-norm regularization term is implemented to sharpen the boundary of density distribution. Meanwhile, in the search process of DE, the effect of Lp-norm regularization term is controlled in an adaptive manner, which can always have an impact on the data misfit function. In the synthetic anomaly case, both noise-free and noisy data sets are considered. For the field case, gravity anomalies originating from the Shihe iron ore deposit in China were inverted and interpreted. The reconstructed density distribution is in good agreement with the one obtained by drill-hole information. Based on the tests in the present study, one can conclude that the Lp-norm inversion using DE is a useful tool for physical property distribution using gravity anomalies.

1. Introduction

As an important geophysical approach, gravity surveying is an effective tool for explorations dealing with mineral deposits, oil and gas, and environmental problems [1,2,3,4,5]. Over the past decades, despite substantial progress having been made in the interpretation of gravity data, the identification and characterization of field sources remain a challenging task due to several limitations: the inherent non-uniqueness of the gravity inverse problem and the limited and inaccurate discrete data sets [6,7]. To deal with the non-uniqueness issue, some kinds of regularizations and/or constraint(s) integrating with other available geologic or geophysical information, such as subsurface structure, borehole data, and prior models, etc. are taken into account in the inversion process.

Generally, according to the kind of model parameters selected, there are two basic approaches to gravity inversion—parametric inversion (e.g., [7,8,9,10]) and physical property inversion (e.g., [2,3,11,12,13]). The methods of parametric inversion determine the geometrical properties of unknown density sources with a fixed density contrast, and offer a homogeneous body of the postulated density. Compared with parametric inversion, the physical property inversion methods allow the densities of the elements of a regular subsurface partition to vary. In this case, the solution can give great flexibility to recover the depths and complex shape of sources. Therefore, the inversion for physical properties is currently important and prevalent. As we know, inversion methods search for the possible solutions employing optimization techniques with linearly iterative approaches such as steepest descent method, conjugate gradients, etc. These optimization techniques have traditionally proven very difficult to solve the highly non-linear mathematical formulation since the iteration process can be prone to fall into the local minima. Moreover, considering the inherent ambiguity of inverse problem for the potential field, it is necessary to choose an appropriate starting model and add regularization constraints (see [2,14]). To avoid the weak points of the linearly iterative optimization procedures, global optimization techniques, such as genetic algorithm (GA), simulated annealing (SA), particle swarm optimization (PSO), differential evolution (DE), etc., are considered appropriate to solve the inverse problems [6,7,15,16,17]. Among them, genetic algorithms have been successfully used for physical property inversion of gravity data (e.g., [6,18]).

Differential evolution, which has been illustrated as a simple but efficient evolution algorithm, was first proposed by Storn and Price to solve Chebyshev polynomial problems [19]. In recent years, it has been verified that DE provides better accuracy, more robustness, and fast convergence speed than other evolution algorithms, such as GA and PSO [20,21,22]. Hence, it has attracted great attention in many scientific and engineering fields, such as neural network training [23,24,25,26], data mining [27,28], and image processing [29,30,31,32], etc. With regards to geophysical inverse problems, the applications of DE are mainly non-gravity methods. Balkaya [33] implemented an inversion program for self-potential (SP) and vertical electrical sounding (VES) by DE; the synthetic data and field data demonstrate the effectiveness of DE in geoelectrical inversion. Li et al. [34] proposed a modified Boltzmann Annealing Differential Evolution (BADE) algorithm, which uses an annealing strategy to avoid the local minima and solve the inversion problem in the directional resistivity logging-while-drilling (DRLWD) measurements; the results also show robustness and immunity to the non-uniqueness inversion problem of their method. Ekinci et al. [17,35] applied DE to both inverting model parameters from residual gravity anomalies and amplitude of the 2D analytic signal of magnetic anomalies. Their works show the applicability and effectiveness of this algorithm on both synthetic and field anomalies, but they mainly focus on the basic parameters of the field source. Balkaya et al. [36] achieved a DE inversion for total field magnetic anomalies caused by vertical-sided prismatic bodies, and they mainly focus on geometric structure inversion. Recently, Du et al. [37] reconstructed magnetic susceptibility by using an improved adaptive DE. According to the inverted results, their inversion methods can help maintain the sharp boundary of magnetic sources.

Apart from the above-mentioned studies, DE has few applications in physical property inversion, although this method has become popular for geophysical inversion. The main reason is that in DE iteration, the smooth constraint is difficult to apply directly to physical property parameters. Here, we present a DE algorithm incorporated with the $lp$ regularization technique to resolve the inversion problem by determining the 2-D distribution of the subsurface density distribution in the mineral exploration. Our gravity inversion method is tested with synthetic examples, and then applied to an iron ore deposit. Finally, we briefly discuss the application of $lp$ norm gravity inversion using DE.

2. Differential Evolution

2.1. Standard Differential Evolution Algorithm

DE is a population-based heuristic search method suitable for solving numerical optimization problems. Its search process includes four parts: initialization, mutation, crossover, and selection. Without loss of generality, let the optimization problem in D-dimensional space be $f\left(x\right),x\in {ℝ}^D$. For the G-th iteration, any i-th vector in the population can be expressed as $m_i^G=\left(m_{i,1}^G,m_{i,2}^G,\cdots ,m_{i,D}^G\right)$, in which $i=1,2,3\cdots ,NP$, NP is the population size. The evolution of these vectors is accomplished by repeatedly performing mutation, crossover, and selection operations.

(1)

Initialization

In order to establish a starting point for the optimization process, the DE randomly generates the decision parameter in every vector of initial population according to the given range. Therefore, the j-th variable of the i-th vector can be defined as:

$$m_{ij}^0=L_j+rand\left(0,1\right)·\left(U_j-L_j\right),j\in \left[1,D\right]$$

(1)

In which, $rand\left(0,1\right)$ represents a uniformly distributed random number in the range of ($0,1$), the lower and upper bounds of the j-th variable is expressed as $L_j$ and $U_j$ respectively. Generally, the upper and lower bounds of variables can be expressed as vectors, such as $L=(L_1,L_2,\dots ,L_D)$, $U=(U_1,U_2,\dots ,U_D)$.

(2)

Mutation

After initialization, the mutation vector ${\mathit{v}}_i^G$ is generated for each target vector ${\mathit{m}}_i^G$ in the current population with a suitable mutation strategy. In essence, the mutation strategy of differential evolution can be regarded as a linear combination of multiple vectors. The widely used strategies are as follows (see [38]):

“DE/rand/1”:

$${\mathit{v}}_i^G={\mathit{m}}_{r1}^G+F\left({\mathit{m}}_{r2}^G-{\mathit{m}}_{r3}^G\right)$$

(2)

“DE/rand/2”:

$${\mathit{v}}_i^G={\mathit{m}}_{r1}^G+F\left({\mathit{m}}_{r2}^G-{\mathit{m}}_{r3}^G\right)+F\left({\mathit{m}}_{r4}^G-{\mathit{m}}_{r5}^G\right)$$

(3)

“DE/best/1”:

$${\mathit{v}}_i^G={\mathit{m}}_{best}^G+F\left({\mathit{m}}_{r1}^G-{\mathit{m}}_{r2}^G\right)$$

(4)

“DE/best/2”:

$${\mathit{v}}_i^G={\mathit{m}}_{best}^G+F\left({\mathit{m}}_{r1}^G-{\mathit{m}}_{r2}^G\right)+F\left({\mathit{m}}_{r3}^G-{\mathit{m}}_{r4}^G\right)$$

(5)

“DE/current-to-best/1”:

$${\mathit{v}}_i^G={\mathit{m}}_i^G+F\left({\mathit{m}}_{best}^G-{\mathit{m}}_i^G\right)+F\left({\mathit{m}}_{r1}^G-{\mathit{m}}_{r2}^G\right)$$

(6)

“DE/current-to-pbest/1”:

$${\mathit{v}}_i^G={\mathit{m}}_{r1}^G+F\left({\mathit{m}}_{pbest}^G-{\mathit{m}}_{r1}^G\right)+F\left({\mathit{m}}_{r2}^G-{\mathit{m}}_{r3}^G\right)$$

(7)

In which, $r1, r2, r3, r4$, and $r5$ are random integers that are different from each other in the range of $\left[1, NP\right]$, and all of them are not equal to $i$. The coefficient $F\left(F>0\right)$ is called the scaling factor, which is used to control the size of the difference direction. ${\mathit{m}}_{best}^G$ represents the best vector in the population and also has the optimal function value in the G generation. For more details on the differential evolutionary mutation strategy, please refer to the work of Das et al. [39].

(3)

Crossover

The purpose of the crossover is to replace some variables in the target vector ${\mathit{m}}_i^G$ with variables in the mutation vector ${\mathit{v}}_i^{G+1}$, thereby the trial vector ${\mathit{m}}_i^{G+1}$ is obtained. Both binomial crossover and exponential crossover are commonly used crossover mechanisms. Here, the binomial crossover is explained, in which at least one variable in the trial vector is inherited from the mutation vector, and can be expressed as:

$$\begin{array}{c}{u}_{ij}^G=\{\begin{array}{l}{v}_{ij}^G,\mathrm{if}rand\left(0,1\right)\le CR or j=jrand \\ m_{ij}^G,\mathrm{otherwise}\end{array}\end{array}$$

(8)

Here, $CR\in (0,1)$ is the crossover probability, which is used to control the number of variables inherited from the mutation vector in the trial vector. $jrand$ is an integer randomly selected in the range of $\left[1,D\right]$.

(4)

Selection

In DE, a greedy mechanism is employed to select a better one between the trial vector ${\mathit{u}}_i^G$ and the target vector ${\mathit{m}}_i^G$ according to their function values. The selection operation is as follows (for a minimization problem):

$${\mathit{m}}_i^{G+1}=\{\begin{array}{l}{\mathit{u}}_i^G,\mathrm{if}f\left({\mathit{u}}_i^G\right)\le f\left({\mathit{x}}_i^G\right)\\ {\mathit{m}}_i^G,\mathrm{otherwise}\end{array}$$

(9)

where $f(·)$ is the fitness value of the target and the trial vector.

2.2. Improved Differential Evolution Algorithm

(1)

Improvement of Mutation Strategy

When conducting gravity inversion, to obtain a smooth density model, it is necessary to use a proper smoothing technique to process the disturbance direction. For the disturbance direction $d_{i,j}$ of variable $m_{i,j}$, the adjacent variables and weights information are represented as shown in Figure 1. Assuming the weight of each adjacent point is $W_{s,i,j}$, then the smoothed $d_{s, i,j}$ can be calculated by:

$$d_{s, i,j}=\frac{{\sum }_{l=-1}^1{\sum }_{m=-1}^1{W}_{s,i+l,j+m}{d}_{i+l,j+m}}{{\sum }_{l=-1}^1{\sum }_{m=-1}^1{W}_{s,i+l,j+m}}$$

(10)

In order to use the above formula repeatedly, the coefficients associated with all $d_{ij}$ can be converted into a sparse matrix $\mathit{S}$, in which the k-th row stores the weight information of direction $k$ and its adjacent elements. Finally, the smooth matrix is expressed as:

$$\mathit{S}={\mathit{S}}^{f_s}$$

(11)

where the parameter $f_s$ is the times of applying the smooth filter. Usually, we use $f_s=2,$ implying that the density of each $k$-element is calculated taking into account the values of the adjacent 18 elements. Obviously, A greater value of $f_s$ increases the scope used for the smoothing around the $k$-element.

Here, the adaptive differential evolution algorithm (JADE) proposed by Zhang and Sanderson [40] is used, in which the mutation strategy is “current-to-pbest/1”, showed in:

$${\mathit{v}}_i^G={\mathit{m}}_i^G+F_i\left({\mathit{m}}_{pbest}^G-{\mathit{m}}_i^G\right)+F_i\left({\mathit{m}}_{ r1}^G-{\mathit{m}}_{r2}^G\right)$$

(12)

where ${\mathit{m}}_{pbest}^G$ is randomly selected from the top $p_b\ast 100\%$ vectors in the G-th generation $\left(p_b\in \left[0,1\right]\right)$. $F_i$ is the scale factor related to the vector ${\mathit{x}}_i$. $r1,r2$ used to construct the disturbance direction $d_i$ for each mutant vector are mutually different random integers in the range of $\left[1,NP\right]$. Applying the smooth matrix to the perturbation direction formed by vectors r1 and r2, the new mutation strategy is:

$${\mathit{v}}_i^G={\mathit{m}}_i^G+F_i\left({\mathit{m}}_{pbest}^G-{\mathit{m}}_i^G\right)+F_i\mathit{S}\left({\mathit{m}}_{ r1}^G-{\mathit{m}}_{r2}^G\right)$$

(13)

In which, the difference vector part formed by the $pbest$ vector ${\mathit{m}}_{pbest}^G$ and the target vector ${\mathit{m}}_i^G$ is not smoothed, because smoothing will destroy the convex combination of ${\mathit{m}}_{pbest}^G$ and ${\mathit{m}}_i^G$.

(2)

Adaptive Guided Evolution

In JADE, the parameter $p_b$ in the “current-to-pbest” mutation strategy is fixed throughout the evolution process and needs to be manually set according to the problem. Then, in order to improve the exploration ability of mutation mechanism, Tamabe and Fukunaga [41] assigned an independent $p_{b,i}$ to each target vector ${\mathit{m}}_i$ by applying a uniform distribution. Here, the value of $p_{b,i}$ is adaptively and independently generated for each vector ${\mathit{x}}_i$ based on the gaussian perturbation scheme. And $p_{b,i}$ is defined as:

$$\begin{array}{c}{p}_{b,i}=rand{n}_i\left({\mu }_{p_b},0.1\right) \end{array}$$

(14)

The average value ${\mu }_{p_b}$ is initialized to 0.5. If $p_{b,i}$ is not in the interval $\left[2/NP,0.5\right]$, it will be truncated. At the end of each search, ${\mu }_{p_b}$ is updated as follows:

$$\begin{array}{c}{\mu }_{p_b}=\left(1-c_p\right){\mu }_{p_b}+c_p·{\mathrm{mean}}_A\left(S_p\right) \end{array}$$

(15)

Here, $S_p$ is the set of successful $p_b$ values in each iteration, $c_p\in \left(0,1\right)$ is the learning rate of ${\mu }_{p_b}$, ${\mathrm{mean}}_A$ represents the arithmetic mean. According to the above formula, it can be seen that the greedy here is controlled by ${\mu }_{p_b}$, unlike in JADE, which is controlled by $p_b$. Therefore, ${\mu }_p$ can be set to a larger value at the beginning of the evolution process, such as ${\mu }_p=0.5$, to maintain the diversity of the population.

The update method of ${\mu }_{p_b}$ in the above equation is an arithmetic average, which makes ${\mu }_p$ converge to a smaller value. In other words, as the search progresses, the parameter ${\mu }_p$ will decrease, thereby improving local exploitation capabilities.

2.3. Control Parameters Adaptation of DE Algorithm

Experimental results conducted by Wu et al. [38] have shown that parameter adaptation schemes in JADE [40] is the most effective. As a result, its procedures are extended here to adapt the parameters of gravity inversion.

In JADE, for each vector, the parameters $F_i$ and $C{R}_i$ are independently generated according to the successful $F$ and $CR$ values in last generation. The formula of generating $C{R}_i$ can be expressed as follows:

$$C{R}_i=rand{n}_i\left({\mu }_{CR},0.1\right)$$

(16)

where $rand{n}_i\left({\mu }_{CR},0.1\right)$ returns a random value with a gaussian distribution. 0.1 is standard deviation; ${\mu }_{CR}$ is initialized to 0.5 and calculated using the following formula:

$${\mu }_{CR}=\left(1-c_{CR}\right){\mu }_{CR}+c_{CR} mea{n}_A\left(S_{CR}\right)$$

(17)

where $c_{CR}\in \left(0,1\right)$ is a constant, $S_{CR}$ is the set of all successful $CR$ values in last generation; $mea{n}_A(·)$ is the usual arithmetic mean.

Similarly, the adaptation of $F_i$ is as follows:

$$\{\begin{array}{l}{F}_i=ran{d}_{ci}\left({\mu }_F,0.1\right)\\ {\mu }_F=\left(1-c\right){\mu }_F+c mea{n}_L\left(S_F\right)\\ mea{n}_L=\frac{{\sum }_{F\in S_F}{F}^2}{{\sum }_{F\in S_F}F}\end{array}$$

(18)

where $ran{d}_{ci}\left({\mu }_F,0.1\right)$ means Cauchy distribution with location parameter ${\mu }_F$ and scale parameter 0; $mea{n}_L(·)$ is the Lehmer mean; and $S_F$ is the set of successful scale factors.

3. Lp-Norm Gravity Inversion Based on Adaptive Differential Evolution

3.1. Forward Modeling

Assuming that the observed gravity data is a vector written as $\mathit{d}$, whose length is N. The underground model is represented by $\mathit{m}$, whose length is M. Then the forward modeling problem can be expressed as:

$$\begin{array}{c}\mathit{d}=\mathit{G}\left(\mathit{m}\right) \end{array}$$

(19)

where $\mathit{G}$ is the forward operator. In the traditional gravity inversion method, $\mathit{G}$ is the linear forward matrix, but here $\mathit{G}$ is no longer a linear matrix, while the finite volume method is adopted in the forward modeling [42].

3.2. Inversion Method

The objective function of Lp-norm gravity inversion can be expressed as:

$$\begin{array}{c}\min \mathsf{\Phi }\left(\mathit{m}\right)={\mathsf{\Phi }}_d\left(\mathit{m}\right)+\lambda {\mathsf{\Phi }}_m\left(\mathit{m}\right),\\ s.t. {\mathit{m}}_a\le \mathit{m}\le {\mathit{m}}_b\end{array}$$

(20)

In which $\lambda$ denotes the regularization factor, ${\mathit{m}}_a,{\mathit{m}}_b$ are the search range of the parameters, while there are M parameters need to be inverted, then the upper and lower bounds of the model parameters are constrained as ${\mathit{m}}_a={\left(m_{a,1}, m_{a,2},\cdots ,m_{a,D}\right)}^T$, ${\mathit{m}}_b={\left(m_{b,1}, m_{b,2},\cdots ,m_{b,D}\right)}^T$. ${\mathsf{\Phi }}_d\left(\mathit{m}\right)$ is the misfit function of gravity data, which is defined as:

$${\mathsf{\Phi }}_d\left(\mathit{m}\right)=\frac{\Vert {\mathit{W}}_d{\left({\mathit{d}}^{obs}-G\left(\mathit{m}\right)\right)\Vert }_2^2}{{\Vert {\mathit{W}}_d{\mathit{d}}^{obs}\Vert }_2^2}$$

(21)

where ${\mathit{W}}_d$ is the weight to the observed data, and determined by the followed equation [43,44]:

$$W_{d,i}=\frac{1}{\left|d_i^{obs}\right|+0.5\left(d_{max}^{obs}-d_{min}^{obs}\right)}, i\in \left[1,N\right]$$

(22)

In which, $d_{max}^{obs}$ and $d_{min}^{obs}$ denote the maximum and minimum data among the observed data, respectively. In Equation (21), the normalization process is carried out, and the purpose is to weaken the influence of the observation data error on the misfit function [45]. ${\mathsf{\Phi }}_m\left(\mathit{m}\right)$ is regularization term of Lp $(1\le p<\infty )$, and expressed as:

$${\mathsf{\Phi }}_m\left(\mathit{m}\right)={\displaystyle \sum }{W}_{m,}{\left|m_i-m_{0,i}\right|}^p$$

(23)

$W_{m,i}$ is the weight coefficient of parameter $m_i$, and it is the empirical information of the model, such as depth weighting value (see [2]). The notation $m_{0,i}$ denotes the reference model or 0 model. While the model distribution is known, $m_0$ can be used to strengthen the constraints on the inversion. Combining (21) and (23), the objective function of Lp-norm gravity inversion can be written as:

$$\begin{array}{c}\min \mathsf{\Phi }\left(\mathit{m}\right)=\frac{\Vert {\mathit{W}}_d{({\mathit{d}}^{obs}-G\left(\mathit{m}\right))\Vert }_2^2}{{\Vert {\mathit{W}}_d{\mathit{d}}^{obs}\Vert }_2^2}+\lambda \sum W_{m,i}{\left|m_i-m_{0,i}\right|}^p,\\ s.t.{\mathit{m}}_a\le \mathit{m}\le {\mathit{m}}_b\end{array}$$

(24)

3.3. Adaptive Adjustment of Regularization Factor

The regularization factor $\lambda$ determines the main fitting object in the inversion process. While $\lambda \to 0$, the observation data is mainly fitted; on the contrary, the model regularization term is mainly fitted. Chen et al. [45] and Zhdanov [46] have presented some adaptive techniques to adjust the regularization factor, but these methods are only suitable for conventional gradient-based iterative search algorithm, and are not suitable for global nonlinear DE algorithms. In order to fit DE algorithms, Du et al. [37] combined the ideas of Zhdanov [46] and Lu [47], then proposed the following update method:

$$\begin{array}{c}{\lambda }^{G+1}=\{\begin{array}{l}\xi {\lambda }^G if {\mathsf{\Phi }}_{d, mean}^G>{\mathsf{\Phi }}_{d, mean}^{G-1}\\ {\lambda }^G otherwise\end{array},\\ {\mathsf{\Phi }}_{d, mean}^G=\frac{1}{NP}\sum {\mathsf{\Phi }}_{d, i}^G,\end{array}$$

(25)

where ${\mathsf{\Phi }}_{d, mean}^G$ denotes the average misfit function value, $\xi \in \left(0,1\right)$ is attenuation coefficient, and equal to 0.65. At the 0-th iteration, the regularization factor is defined as:

$${\lambda }^0=10\frac{\sum {\mathsf{\Phi }}_{d,i}^0}{\sum {\mathsf{\Phi }}_{m,i}^0},i\in \left[1,NP\right]$$

(26)

The above method is successfully used for the inversion of the magnetic method, but this updated method ignores the phenomenon that the ratio of ${\mathsf{\Phi }}_d$ and ${\mathsf{\Phi }}_m$ is constantly changing during the search process. Therefore, in order to enable $\lambda$ to balance the effects of ${\mathsf{\Phi }}_d$ and ${\mathsf{\Phi }}_m$ throughout the inversion process, the following updated method is proposed:

$$\begin{array}{c}{\lambda }^{G+1}=\{\begin{array}{l}\xi {\lambda }^G if {\mathsf{\Phi }}_{d, mean}^G\ge {\mathsf{\Phi }}_{d, mean}^{G-1}\\ \left(1-c_{\lambda }\right){\lambda }^G+c_{\lambda }\max \left({\lambda }^G,{\lambda }^t\right), elseif {\mathsf{\Phi }}_{d, mean}^G\le {\delta }_{\lambda }\\ {\lambda }^G otherwise\end{array},\\ {\lambda }_t=\frac{\sum {\mathsf{\Phi }}_{d,i}^G}{\sum {\mathsf{\Phi }}_{m,i}^G},\end{array}$$

(27)

In which, $c_{\lambda }\in \left(0,1\right)$ denotes the learning rate, and is set at 0.8 based on the experimental results. ${\lambda }_t$ is the ratio of ${\mathsf{\Phi }}_{d, mean}^G$ and ${\mathsf{\Phi }}_{m, mean}^G$ in the current population, ${\delta }_{\lambda }$ is a given threshold and is defined as follows:

$${\delta }_{\lambda }=\frac{1}{2NP}{\displaystyle \sum }{\mathsf{\Phi }}_{d,i}^0$$

(28)

Compared with Equation (25), it can be found that the new update method of regularization factor is more complicated. At the same time, the new adjustment method is more reasonable due to the influence of ${\lambda }_t$.

3.4. Implement of Inversion Algorithm

The detailed implementation process of the inversion algorithm is shown in Algorithm 1.

Algorithm 1. Lp-norm inversion of gravity based on an improved adaptive differential evolution.

1: $G$ = 1  2: Set $NP$ = 100, ${\mu }_{CR}$ = 0.5, ${\mu }_F$ = 0.5, ${\mu }_{p_b}$ = 0.5, $c$ = 0.1, $c_p$ = 0.05, initialize population $\mathit{m}=\left({\mathit{m}}_{0,1},\cdots ,{\mathit{m}}_{0,NP}\right)$, initialize the regularity coefficient ${\lambda }^0$, evaluation the population $\mathit{m}$.  3: While termination conditions are not met do  4:  $G=G+1$  5:  For $i=1$ to $NP$ do  6:    $C{R}_i^G=rand{n}_i\left({\mu }_{CR},0.1\right)$;  7:    $F_i^G=rand{c}_i\left({\mu }_F,0.1\right)$;  8:    $p_b{}_i^G=rand{n}_i\left({\mu }_{p_b},0.1\right)$  9:  End For  10:  For $i=1toNP$ do  11:   Generate mutation vector according to mutation strategy (12)  12:   Generate trial vector ${\mathit{u}}_i^G$ from (8)  13:  End For  14:  Evaluation test vector ${\mathit{u}}^G$  15:  Form a new population ${\mathit{m}}^{G+1}$ according to Equation (9)  16:  Update ${\mu }_{CR}$ and ${\mu }_F$ according to Equations (16)–(18), update ${\mu }_{p_b}$ according to (14), update $\lambda$ by (27).  17. End While

In Algorithm 1, the termination condition is that the data fitting error reaches 5% or the maximum number of iterations is reached. And the maximum number of iterations is set to 100 M, M denotes the number of parameters to be inverted.

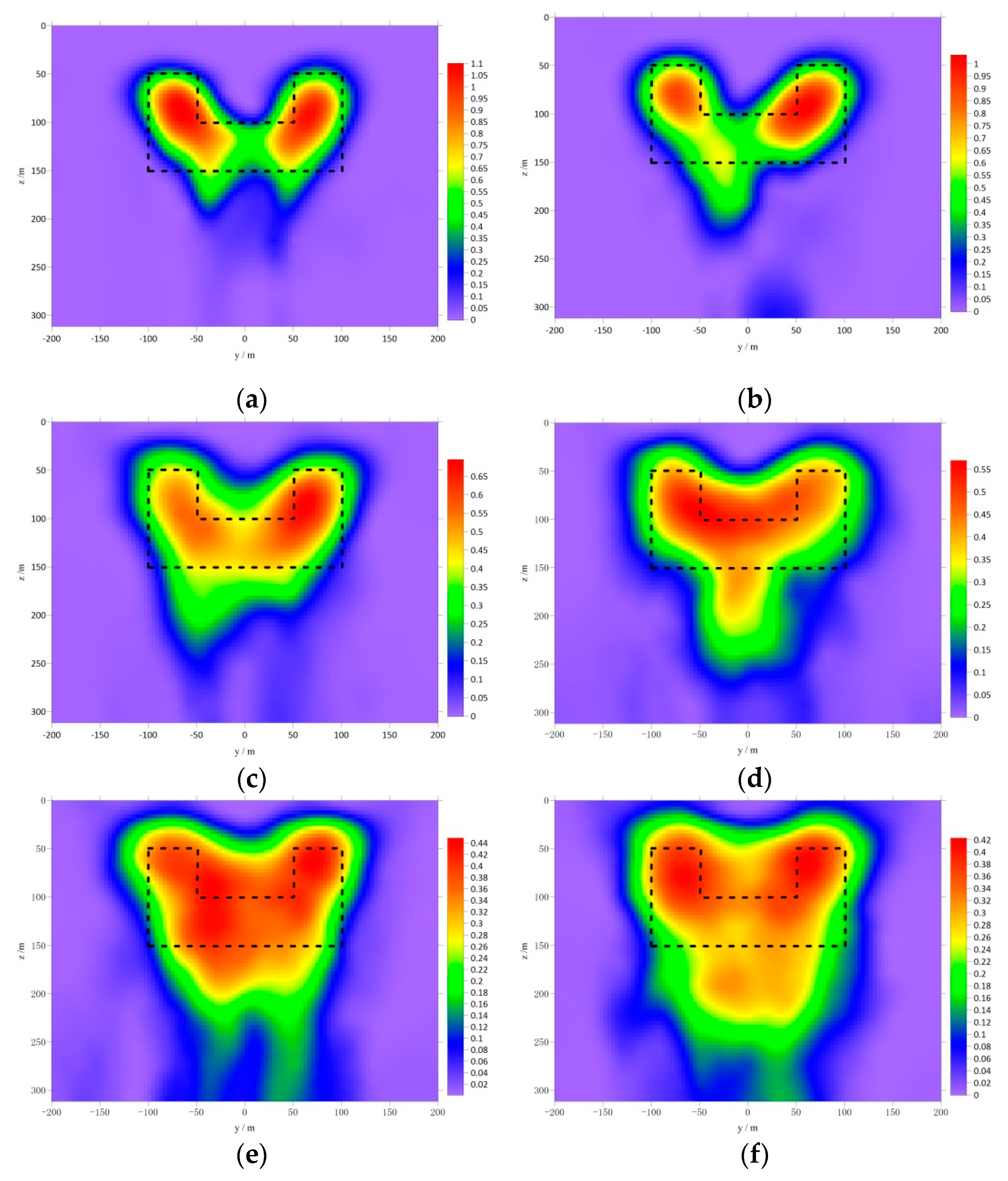
4. Simulation Tests

To illustrate the effectiveness and flexibility of the proposed inversion approach, four types of 2D single or combined prism models are set to test the DE algorithm used in this section, including (a) rectangular prism, (b) dipping prism, (c) parallel prism, and (d) U prism. All test models are list in Figure 2. The conclusion of the test results show that the method provides us with better resolution and can be used for interpreting the real geological case.

4.1. Parameter Setting

As mentioned before, three main control parameters ($NP, F \mathrm{and}CR$) are used to adjust the search process of DE. Actually, when implementing the improved JADE for gravity inversion, corresponding parameters are set as: $NP=100$; ${\mu }_{CR}=0.9$; ${\mu }_F=0.9$; ${\mu }_{pb}=0.5$. And the density bound constraints for synthetic models are $0\le m\le 1.1 \mathrm{g}/{\mathrm{cm}}^3$ for all variables in the DE population. When inverting the gravity data of the synthetic models, the initial model of the density distribution is created randomly from 0 to 10⁻². Besides, crossover rate sorting proposed by Zhou et al. is used to maintain the exploration ability of algorithm further [48]. The key idea of CR sorting mechanism is to assign a smaller CR to a vector with better fitness.

4.2. The Impact of Weighted Moving Average Smoothing

Here, the rectangular (Figure 2a) and dipping (Figure 2b) prism are adopted to verify the effectiveness of smoothing. To simplify the discussion, the norm of regularization term is set to 2 for two type of prism models. Additionally, considering that the smoothness of obtained models is controlled by the values of $s_f$ factor, the different $s_f$ values will be selected. In this part, $s_f$ is set as 0, 1, 2 and 3, while $s_f=0$ means no smoothness is applied in the inversion process. The inverted results for these two models are shown in Figure 3 and Figure 4, respectively. Obviously, according to the models obtained with different $s_f$ values, incorporating the smoothness technique with mutation strategy of DE can help strengthen the continuity among the variables.

The fitting process to each $s_f$ for the rectangular and dipping prism is shown in Figure 5.

Obviously from Figure 5 when $s_f\ne 0$, which mean smoothness is applied in the inversion process, the inversion can be significantly accelerated.

4.3. The Effect of $p$ Value

For the Lp-norm based gravity inversion, the value of $p$ actually plays a key role in determining the density distribution and shape of density source. To get a proper $p$ value, the U prism model is selected to conduct the inversion with different $p$ values. In this paper, the candidate values of $p$ are 1, 1.1, 1.3, 1.5, 1.7, and 2, respectively. The inverted results are shown in Figure 6. We can observe that the density obtained by a larger $p$ value is lower than the one with a smaller $p$. Besides, by comparing with the designed model, the large $p$ values, especially when the $p$ is close to 2, will increase the range of the predicted density model, and make the boundaries of model blur. On the contrary, a smaller $p$ is helpful in describing the shape of the density model accurately, but it may weaken the continuity of the obtained model. Overall, in our opinion, it is appropriate to set $p$ less than 1.5.

4.4. Gravity Data with Gaussian Noise

To prove that a new method works correctly, it is essential to test it on data with noise since actual gravity data may be contaminated by noise. Here, Gaussian white noise with a mean value 0 and a standard deviation equal to 10% of the maximum value of synthetic data are added. By using the proposed inversion method, fittings between the observed and model response for these noisy data are shown in Figure 7. The inversion results of noise data are shown in Figure 8. According to the results, one can conclude that the Lp-norm inversion of gravity is robust, and capable of reflecting the real shape of the field source from the noisy data.

5. Field Example

The Shihe iron ore deposit is located in the northern part of the Hengshan-Wutaishan dome in the Lvliang-Taihang fault block, North China. The main exposed strata are the Paleoproterozoic Jingangku Formation, the Mesoproterozoic Changcheng System, the Cambrian, and Quaternary. The Jingangku Formation is the ore-bearing unit that comprises metamorphic amphibolite-like rocks. The density of rock and mineral in this area is shown in

Table 1. Density parameters of minerals and rocks in the Shihe area.

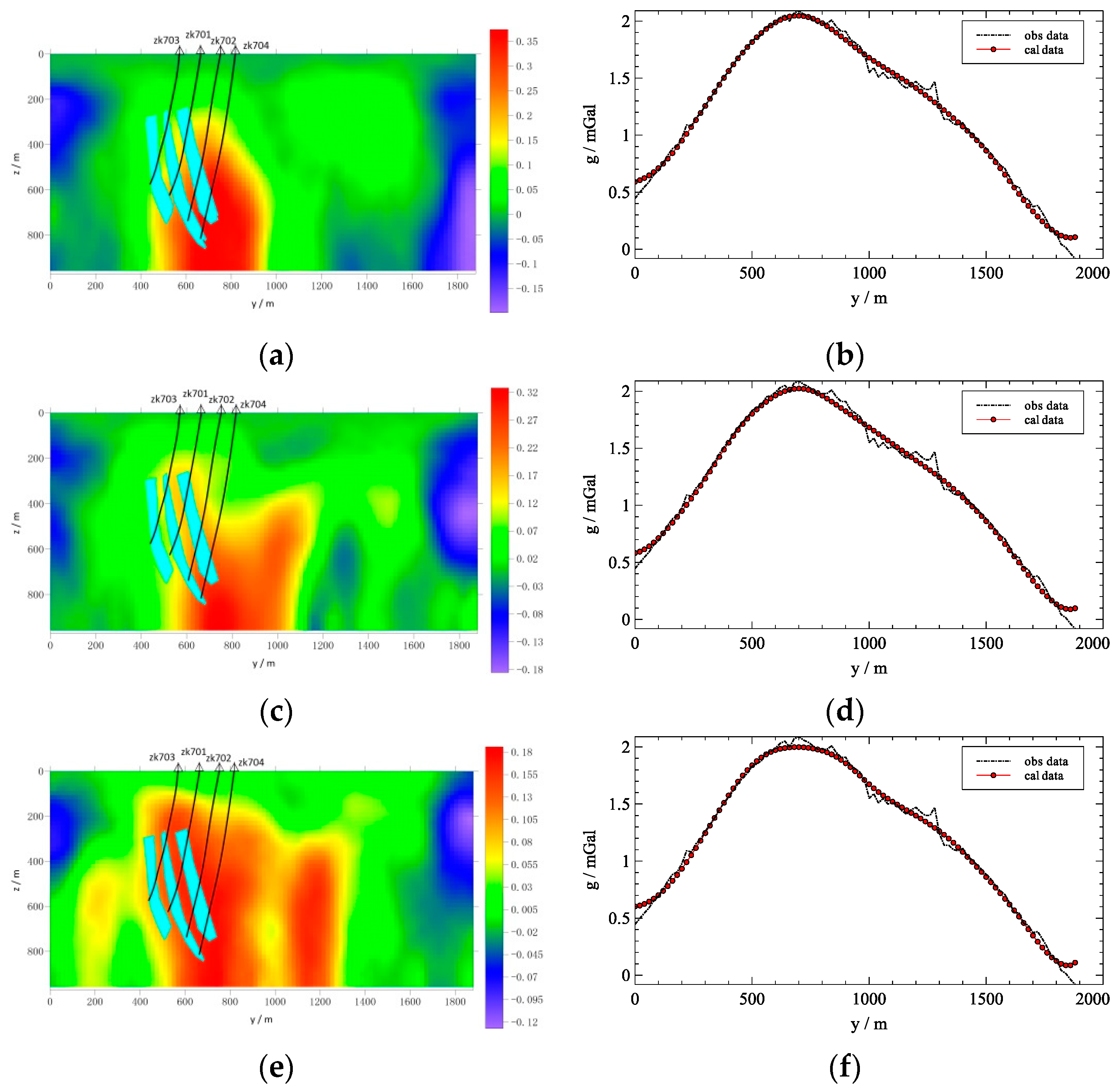
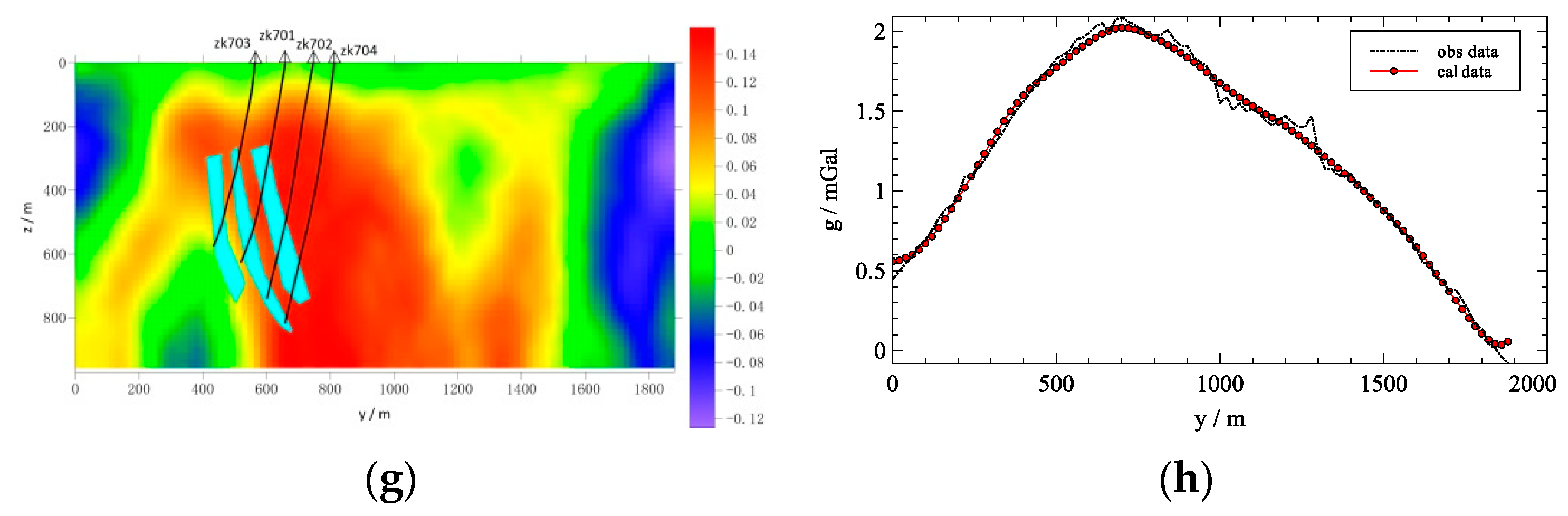
Mineral	Number of Specimens	Arithmetic Mean (g/cm3)
PlagioclAse amphibolite	41	2.78
Garnet Magnetite Quartzite	30	3.16
Biotite Granulite	27	2.88
Amphibole Plagioclase	7	2.65
Layer	Number of specimens	Arithmetic mean (g/cm3)
Quaternary system	6	1.53
Jingangku formation	106	2.78

. The garnet magnetite quartzite has the highest average density, and the difference between its density and the one of surrounding rock amphibolite has reached 0.38 g/cm³.

Since there are negative residual anomalies in the original data, in order to fit this part of the data, the search range of Lp-norm gravity inversion in this area is set to [−0.5, 0.5] g/cm³. The horizontal cell size for subsurface space is set to 20 m during the inversion process, and the vertical cell size changes proportionally. The results with different $p$ values are shown in Figure 9; it can be concluded that the top buried depth of the iron ore is about 400 m, and the depth of the ore body extends more than 400 m.

Observed from Figure 9, the density distribution results obtained by Lp-norm regularization inversion with different $p$ values are similar, and are in good agreement with the one obtained by drill-hole information. In Figure 9, the relation between the three inversion results and the geological interpretation of the ore body is also shown. Obviously, the inversion results Lp-norm with $p\le 1.5$ are reliable, which shows that the Lp-norm inversion algorithm in this paper can improve the quality of inversion and bring the restored model closer to the real situation. Additionally, by comparing the L2-norm regularization results shown in Figure 9 with L1, L1.1, and L1.5, it is easy to see that the L2-norm inversion technique failed to draw the real shape of the ore deposit.

6. Conclusions

In this work, an attempt was made to test the applicability and effectiveness of adaptive DE on Lp-norm gravity inversion. As far as this work is concerned, this is the first attempt at applying DE for physical property inversion using gravity data. In the application of this stochastic search algorithm, to further improve the exploration ability, the evolved direction of the DE population in this paper is guided adaptively. Besides, in order to maintain the physical property to distribute in a continuous space, the perturbation direction in the mutation operation is smoothed by using the weighted moving average smooth technique. In addition, adaptive adjustment of the regularization factor is proposed to balance the effect of data misfit and Lp-norm regularization term. In the present algorithm, synthetic data experiments are performed using noise free and noisy data sets calculated from simple-shaped causative bodies. From the example of synthetic models, the adaptive DE algorithm with improved mechanisms shows favorable results and is capable of achieving a density distribution with sharp boundary by setting a proper $p$ value. In addition, the proposed algorithm was also tested on a field data from the Shihe iron deposit; the predicted density distribution was verified by drill-hole information. Finally, in this work, we discussed the application of an improved JADE version in Lp-norm gravity inversion. Some recent DE variants demonstrated excellent performance for single objective optimization problems. Their application in geophysical inversion will be done in future research.