Spectral-Element Simulation of the Turbulent Flow in an Urban Environment
Abstract
:1. Introduction to Urban Flows
1.1. Structure of the Flow above the Urban Canopy
1.2. Influence of an Urban Obstacle
1.3. Description of the Flow Inside the Urban Roughness Sublayer
2. Governing Equations and Numerical Simulations
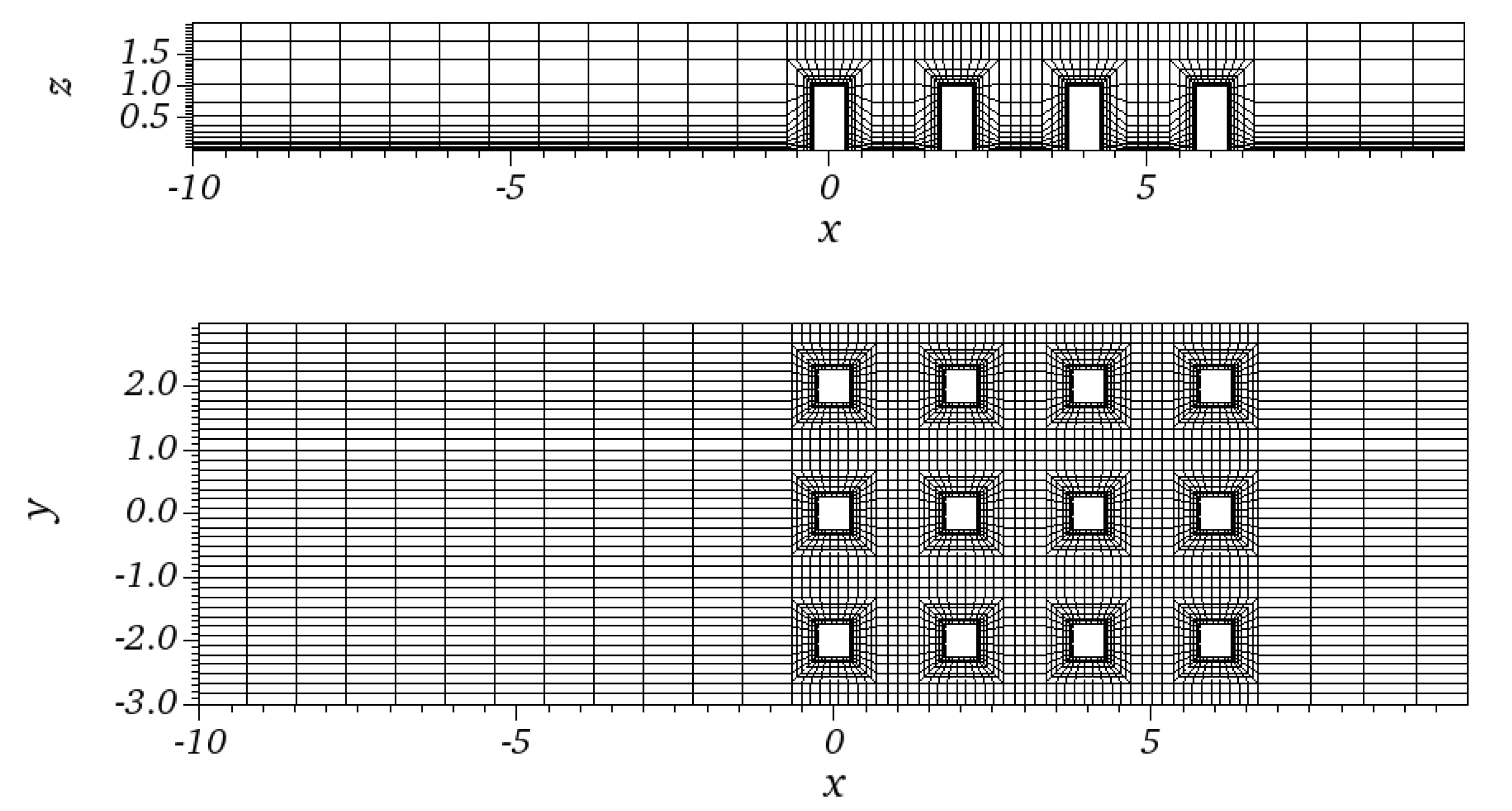
Mesh Design
3. Analysis of the Well-Resolved LES
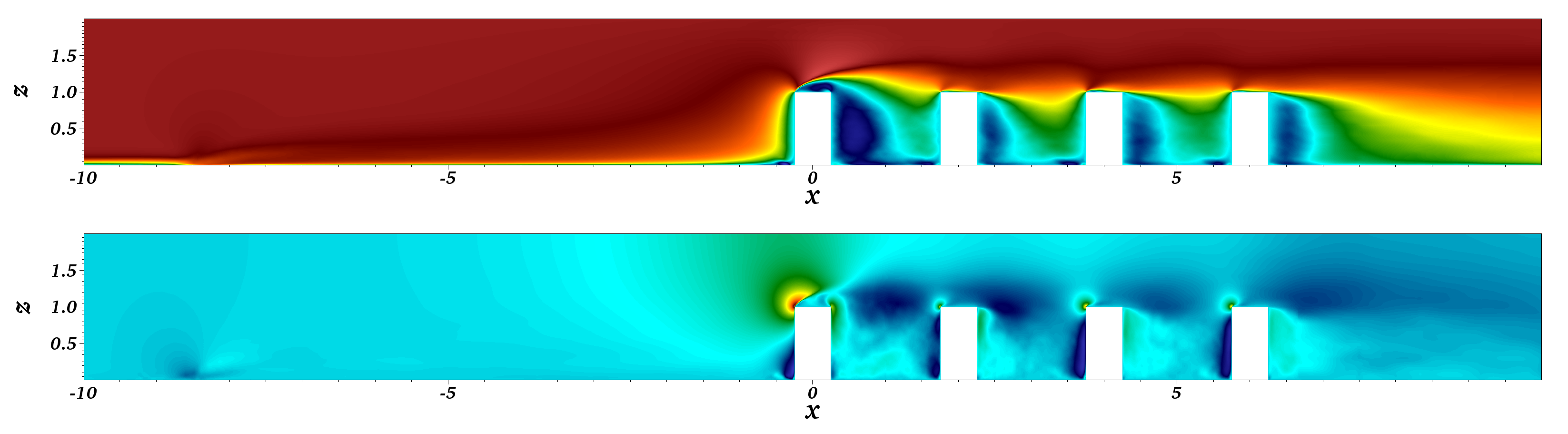
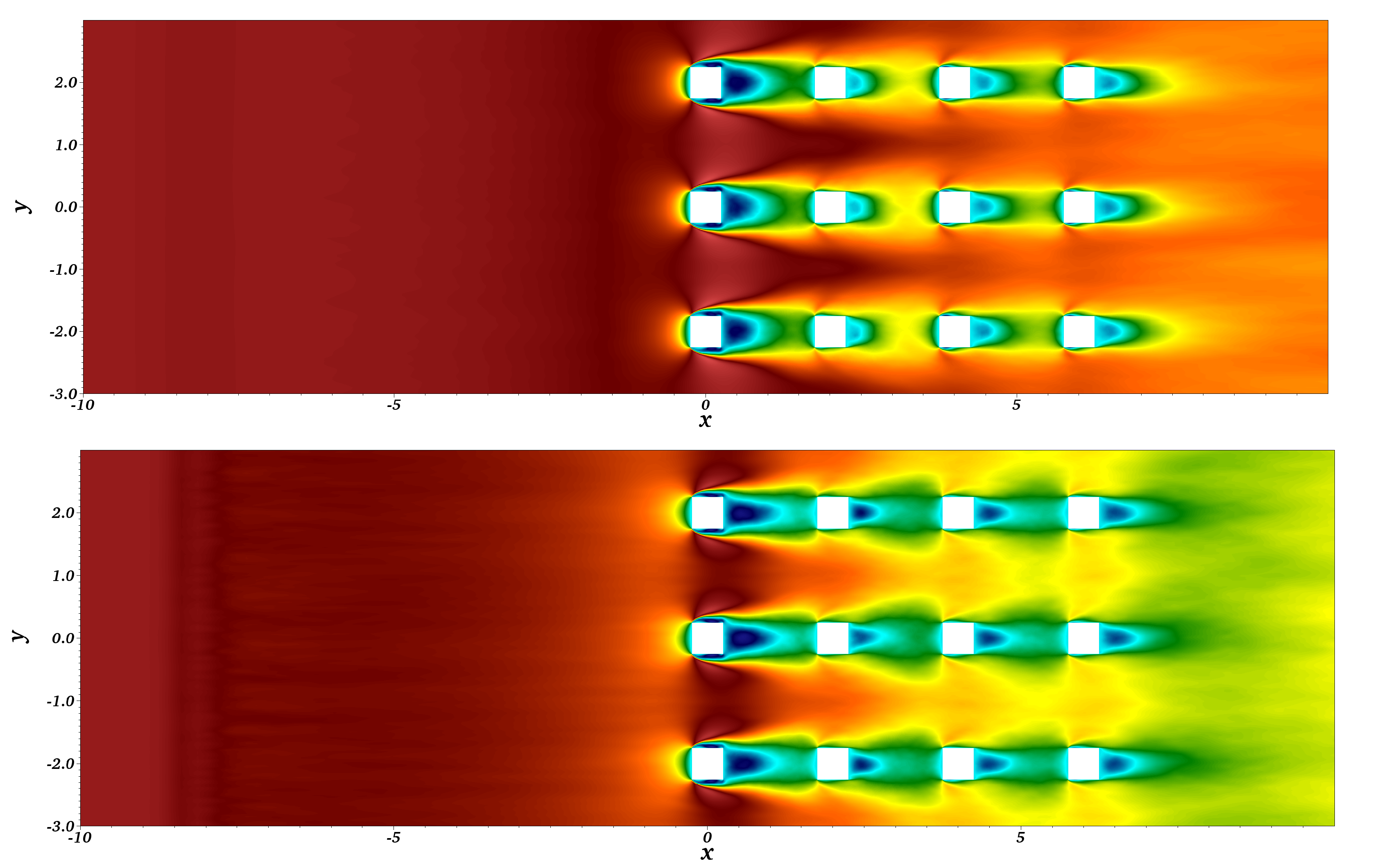
3.1. Analysis of the Mean Flow
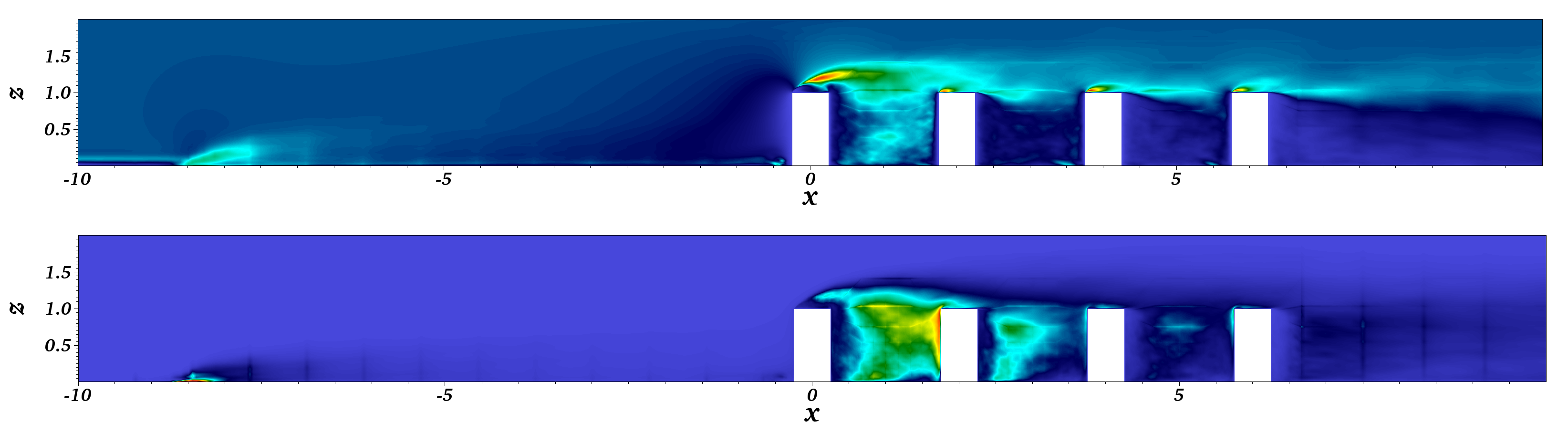
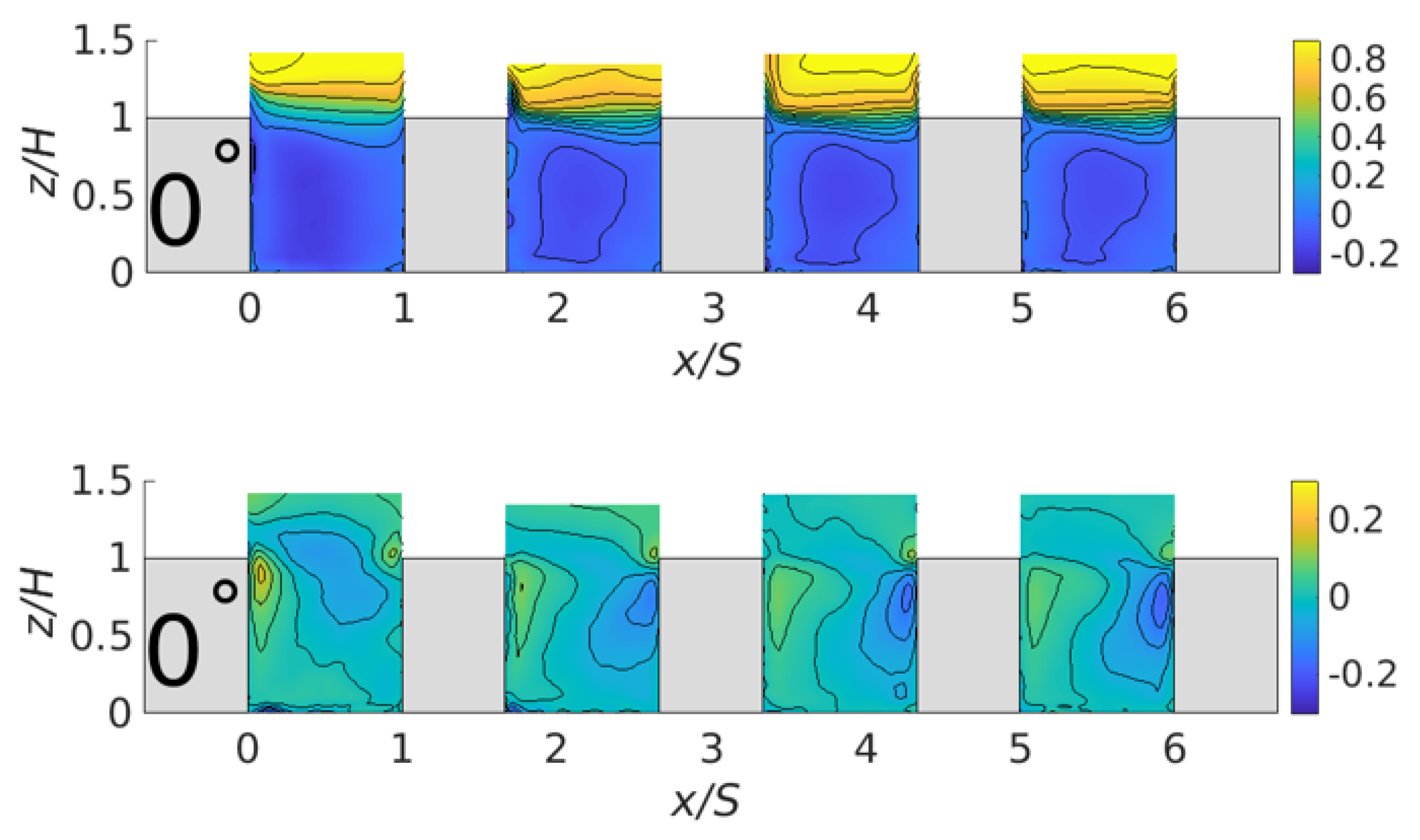
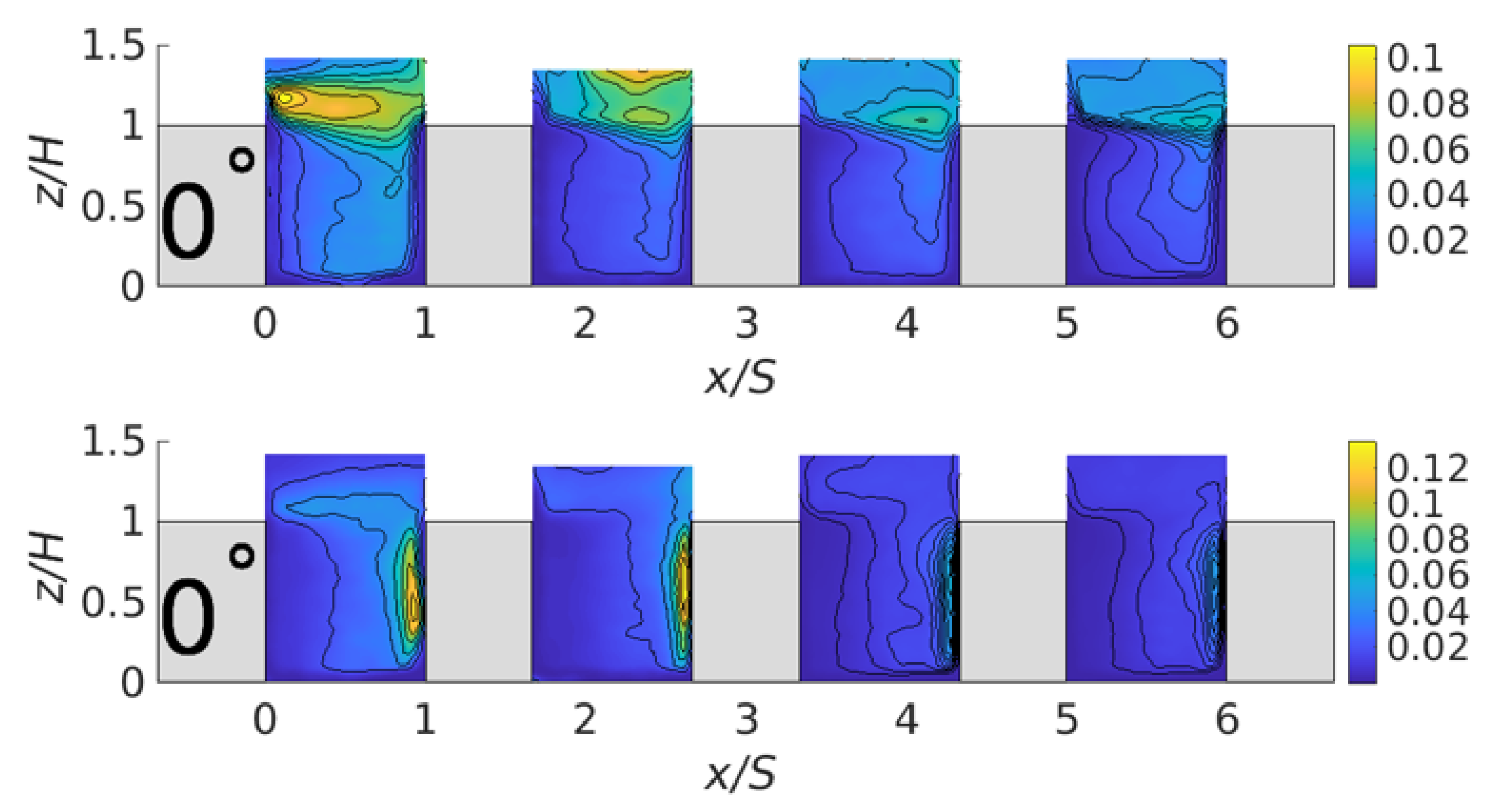
3.2. Analysis of the Turbulent Fluctuations
4. Comparison with Experimental Data
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Torres, P.; Le Clainche, S.; Vinuesa, R. On the experimental, numerical and data-driven methods to study urban flows. Energies 2021, 14, 1310. [Google Scholar] [CrossRef]
- Britter, R.; Hanna, S. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Stathopoulos, T. Pedestrian level winds and outdoor human comfort. J. Wind Eng. Ind. Aerodyn. 2006, 94, 769–780. [Google Scholar] [CrossRef]
- Garbero, V.; Salizzoni, P.; Soulhac, L. Experimental study of pollutant dispersion within a network of streets. Bound.-Layer Meteorol. 2010, 136, 457–487. [Google Scholar] [CrossRef]
- Belcher, S. Mixing and transport in urban areas. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 363, 2947–2968. [Google Scholar] [CrossRef]
- Baik, J.; Kim, J. A numerical study of flow and pollutant dispersion characteristics in urban street canyons. J. Appl. Meteorol. 1999, 38, 1576–1589. [Google Scholar] [CrossRef]
- Vinuesa, R.; Schlatter, P.; Malm, J.; Mavriplis, C.; Henningson, D. Direct numerical simulation of the flow around a wall-mounted square cylinder under various inflow conditions. J. Turbul. 2015, 16, 555–587. [Google Scholar] [CrossRef]
- Nagib, H.; Corke, T. Wind microclimate around buildings: Characteristics and control. J. Wind Eng. Ind. Aerodyn. 1984, 16, 1–15. [Google Scholar] [CrossRef]
- Monnier, B.; Goudarzi, S.; Vinuesa, R.; Wark, C. Turbulent structure of a simplified urban fluid flow studied through stereoscopic particle image velocimetry. Bound.-Layer Meteorol. 2018, 166, 239–268. [Google Scholar] [CrossRef]
- Fischer, P.F.; Lottes, J.W.; Kerkemeier, S.G. Nek5000: Open Source Spectral Element CFD Solver. 2008. Available online: https://nek5000.mcs.anl.gov (accessed on 12 July 2021).
- Vinuesa, R.; Fick, L.; Negi, P.; Marin, O.; Merzari, E.; Schlatter, P. Turbulence Statistics in a Spectral Element Code: A Toolbox for High-Fidelity Simulations; Technical Report; Argonne National Lab (ANL): Argonne, IL, USA, 2017. [Google Scholar]
- Kastner-Klein, P.; Rotach, M. Mean flow and turbulence characteristics in an urban roughness sublayer. Bound.-Layer Meteorol. 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Reynolds, R.; Castro, I. Measurements in an urban-type boundary layer. Exp. Fluids 2008, 45, 141–156. [Google Scholar] [CrossRef] [Green Version]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Belcher, S.; Harman, I.; Finnigan, J. The wind in the willows: Flows in forest canopies in complex terrain. Annu. Rev. Fluid Mech. 2012, 44, 479–504. [Google Scholar] [CrossRef]
- Stull, R. Mean boundary layer characteristics. In An Introduction to Boundary Layer Meteorology; Springer: Berlin/Heidelberg, Germany, 1988; pp. 1–27. [Google Scholar]
- Dupont, S.; Brunet, Y. Edge flow and canopy structure: A large-eddy simulation study. Bound.-Layer Meteorol. 2008, 126, 51–71. [Google Scholar] [CrossRef]
- Liakos, A.; Malamataris, N. Direct numerical simulation of steady state, three dimensional, laminar flow around a wall mounted cube. Phys. Fluids 2014, 26, 053603. [Google Scholar] [CrossRef]
- Sousa, J. Turbulent flow around a surface-mounted obstacle using 2D-3C DPIV. Exp. Fluids 2002, 33, 854–862. [Google Scholar] [CrossRef]
- Hussein, H.; Martinuzzi, R. Energy balance for turbulent flow around a surface mounted cube placed in a channel. Phys. Fluids 1996, 8, 764–780. [Google Scholar] [CrossRef]
- Becker, S.; Lienhart, H.; Durst, F. Flow around three-dimensional obstacles in boundary layers. J. Wind Eng. Ind. Aerodyn. 2002, 90, 265–279. [Google Scholar] [CrossRef]
- Monnier, B.; Neiswander, B.; Wark, C. Stereoscopic particle image velocimetry measurements in an urban-type boundary layer: Insight into flow regimes and incidence angle effect. Bound.-Layer Meteorol. 2010, 135, 243–268. [Google Scholar] [CrossRef]
- Hwang, J.; Yang, K. Numerical study of vortical structures around a wall-mounted cubic obstacle in channel flow. Phys. Fluids 2004, 16, 2382–2394. [Google Scholar] [CrossRef] [Green Version]
- Schenk, F.; Vinuesa, R. Enhanced large-scale atmospheric flow interaction with ice sheets at high model resolution. Results Eng. 2019, 3, 100030. [Google Scholar] [CrossRef]
- Martinuzzi, R.; Havel, B. Turbulent flow around two interfering surface-mounted cubic obstacles in tandem arrangement. J. Fluids Eng. 2000, 122, 24–31. [Google Scholar] [CrossRef]
- Oke, T. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.; Castro, I.; Belcher, S. Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Bound.-Layer Meteorol. 2006, 121, 491–519. [Google Scholar] [CrossRef]
- Xing, F.; Mohotti, D.; Chauhan, K.A. Experimental and numerical study on mean pressure distributions around an isolated gable roof building with and without openings. Build. Environ. 2018, 132, 30–44. [Google Scholar] [CrossRef]
- Fernando, H.; Zajic, D.; Di Sabatino, S.; Dimitrova, R.; Hedquist, B.; Dallman, A. Flow, turbulence, and pollutant dispersion in urban environments. Phys. Fluid 2010, 22, 051301. [Google Scholar] [CrossRef]
- Pol, S.; Brown, M. Flow patterns at the ends of a street canyon: Measurements from the Joint Urban 2003 field experiment. J. Appl. Meteorol. Climatol. 2008, 47, 1413–1426. [Google Scholar] [CrossRef] [Green Version]
- Hamlyn, D.; Britter, R. A numerical study of the flow field and exchange processes within a canopy of urban-type roughness. Atmos. Environ. 2005, 39, 3243–3254. [Google Scholar] [CrossRef]
- Assimakopoulos, V.; Georgakis, C.; Santamouris, M. Experimental validation of a computational fluid dynamics code to predict the wind speed in street canyons for passive cooling purposes. Sol. Energy 2006, 80, 423–434. [Google Scholar] [CrossRef]
- Jones, W.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Yamartino, R.; Wiegand, G. Development and evaluation of simple models for the flow, turbulence and pollutant concentration fields within an urban street canyon. Atmos. Environ. (1967) 1986, 20, 2137–2156. [Google Scholar] [CrossRef]
- Boddy, J.; Smalley, R.; Dixon, N.; Tate, J.; Tomlin, A. The spatial variability in concentrations of a traffic-related pollutant in two street canyons in York, UK—Part I: The influence of background winds. Atmos. Environ. 2005, 39, 3147–3161. [Google Scholar] [CrossRef]
- Louka, P.; Belcher, S.; Harrison, R. Modified street canyon flow. J. Wind Eng. Ind. Aerodyn. 1998, 74, 485–493. [Google Scholar] [CrossRef]
- Patera, A. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Vinuesa, R.; Hosseini, S.; Hanifi, A.; Henningson, D.; Schlatter, P. Pressure-gradient turbulent boundary layers developing around a wing section. Flow Turbul. Combust. 2017, 99, 613–641. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Karniadakis, G.; Chryssostomidis, C. A robust and accurate outflow boundary condition for incompressible flow simulations on severely-truncated unbounded domains. J. Comput. Phys. 2014, 261, 83–105. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Schlatter, P.; Stolz, S.; Kleiser, L. LES of transitional flows using the approximate deconvolution model. Int. J. Heat Fluid Flow 2004, 25, 549–558. [Google Scholar]
- Vinuesa, R.; Negi, P.S.; Atzori, M.; Hanifi, A.; Henningson, D.S.; Schlatter, P. Turbulent boundary layers around wing sections up to Rec = 1,000,000. Int. J. Heat Fluid Flow 2018, 72, 86–99. [Google Scholar] [CrossRef] [Green Version]
- Negi, P.S.; Vinuesa, R.; Hanifi, A.; Schlatter, P.; Henningson, D.S. Unsteady aerodynamic effects in small-amplitude pitch oscillations of an airfoil. Int. J. Heat Fluid Flow 2018, 71, 378–391. [Google Scholar] [CrossRef] [Green Version]
- Bobke, A.; Vinuesa, R.; Örlü, R.; Schlatter, P. History effects and near-equilibrium in adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 2017, 820, 667–692. [Google Scholar] [CrossRef]
- Vinuesa, R.; Azizpour, H.; Leite, I.; Balaam, M.; Dignum, V.; Domisch, S.; Felländer, A.; Langhans, S.D.; Tegmark, M.; Fuso Nerini, F. The role of artificial intelligence in achieving the Sustainable Development Goals. Nat. Commun. 2020, 11, 233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gupta, S.; Langhans, S.D.; Domisch, S.; Fuso-Nerini, F.; Felländer, A.; Battaglini, M.; Tegmark, M.; Vinuesa, R. Assessing whether artificial intelligence is an enabler or an inhibitor of sustainability at indicator level. Transp. Eng. 2021, 4, 100064. [Google Scholar] [CrossRef]
- Torres, P. High-Order Spectral Simulations of the Flow in a Simplified Urban Environment. Bachelor’s Thesis, Polytechnic University of Valencia, Valencia, Spain, 2020. [Google Scholar]
- Vinuesa, R.; Prus, C.; Schlatter, P.; Nagib, H. Convergence of numerical simulations of turbulent wall-bounded flows and mean cross-flow structure of rectangular ducts. Meccanica 2016, 51, 3025–3042. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, P.A.; Guastoni, L.; Azizpour, H.; Schlatter, P.; Vinuesa, R. Predictions of turbulent shear flows using deep neural networks. Phys. Rev. Fluids 2019, 4, 054603. [Google Scholar] [CrossRef] [Green Version]
- Guastoni, L.; Güemes, A.; Ianiro, A.; Discetti, S.; Schlatter, P.; Azizpour, H.; Vinuesa, R. Convolutional-network models to predict wall-bounded turbulence from wall quantities. arXiv 2020, arXiv:2006.12483. [Google Scholar]
- Vinuesa, R.; Schlatter, P.; Nagib, H.M. Role of data uncertainties in identifying the logarithmic region of turbulent boundary layers. Exp. Fluids 2014, 55, 1751. [Google Scholar] [CrossRef]
- Vinuesa, R.; Nagib, H.M. Enhancing the accuracy of measurement techniques in high Reynolds number turbulent boundary layers for more representative comparison to their canonical representations. Eur. J. Mech.-B/Fluids 2016, 55, 300–312. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stuck, M.; Vidal, A.; Torres, P.; Nagib, H.M.; Wark, C.; Vinuesa, R. Spectral-Element Simulation of the Turbulent Flow in an Urban Environment. Appl. Sci. 2021, 11, 6472. https://doi.org/10.3390/app11146472
Stuck M, Vidal A, Torres P, Nagib HM, Wark C, Vinuesa R. Spectral-Element Simulation of the Turbulent Flow in an Urban Environment. Applied Sciences. 2021; 11(14):6472. https://doi.org/10.3390/app11146472
Chicago/Turabian StyleStuck, Maxime, Alvaro Vidal, Pablo Torres, Hassan M. Nagib, Candace Wark, and Ricardo Vinuesa. 2021. "Spectral-Element Simulation of the Turbulent Flow in an Urban Environment" Applied Sciences 11, no. 14: 6472. https://doi.org/10.3390/app11146472
APA StyleStuck, M., Vidal, A., Torres, P., Nagib, H. M., Wark, C., & Vinuesa, R. (2021). Spectral-Element Simulation of the Turbulent Flow in an Urban Environment. Applied Sciences, 11(14), 6472. https://doi.org/10.3390/app11146472






