Few-Cycle, μJ-Class, Deep-UV Source from Gas Media
Abstract
:1. Introduction
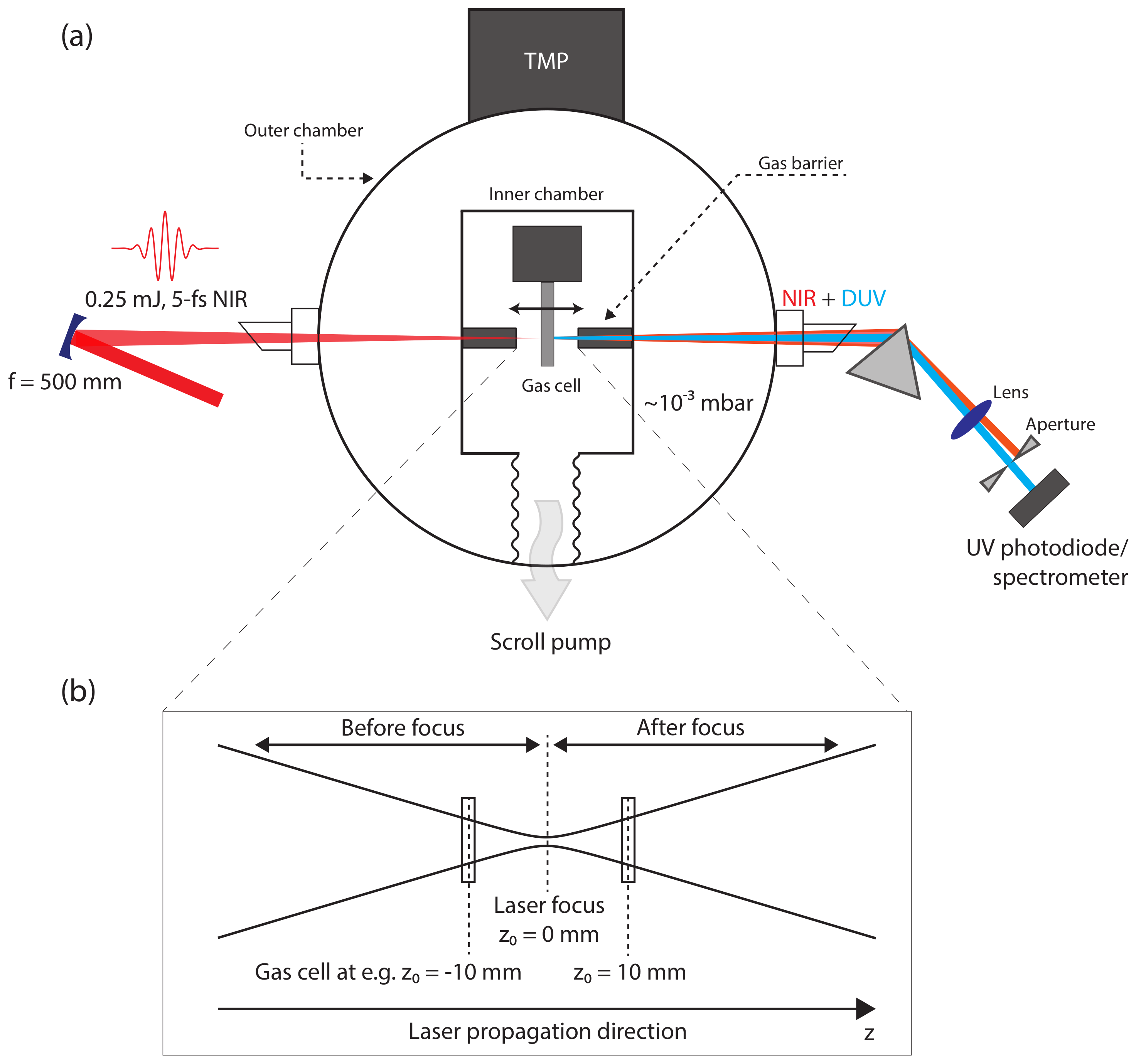
2. Experimental Setup and Methods
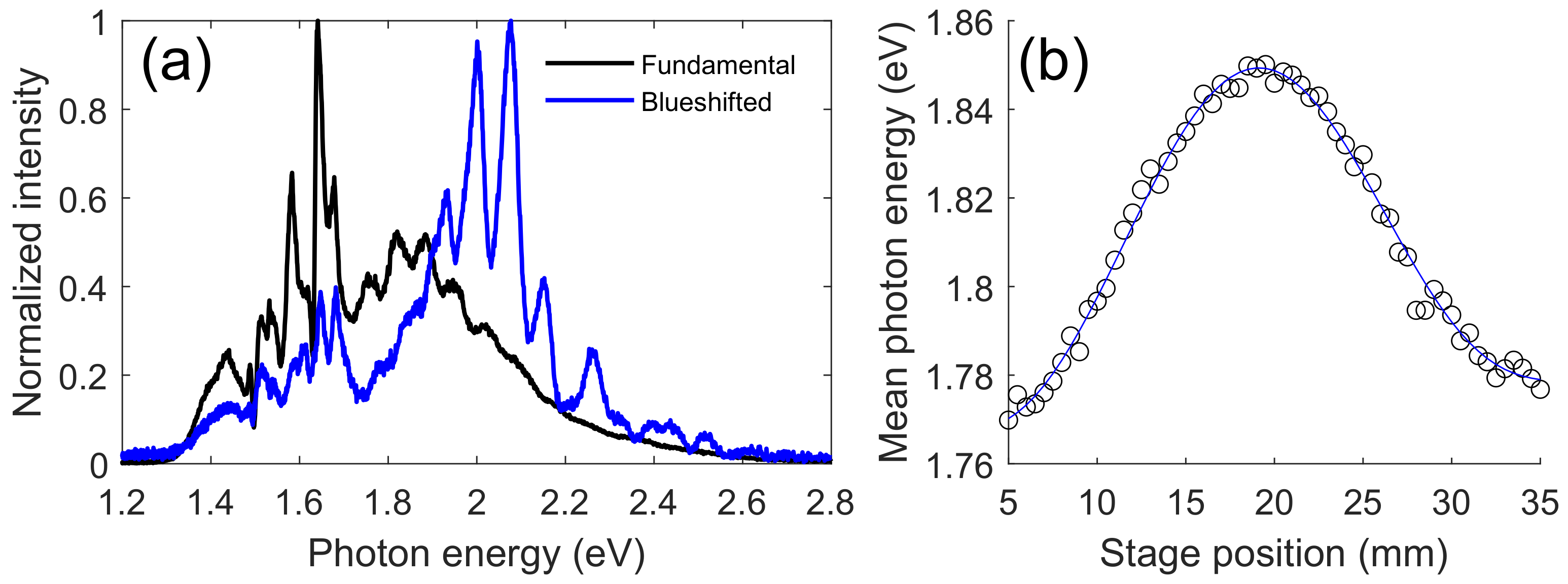
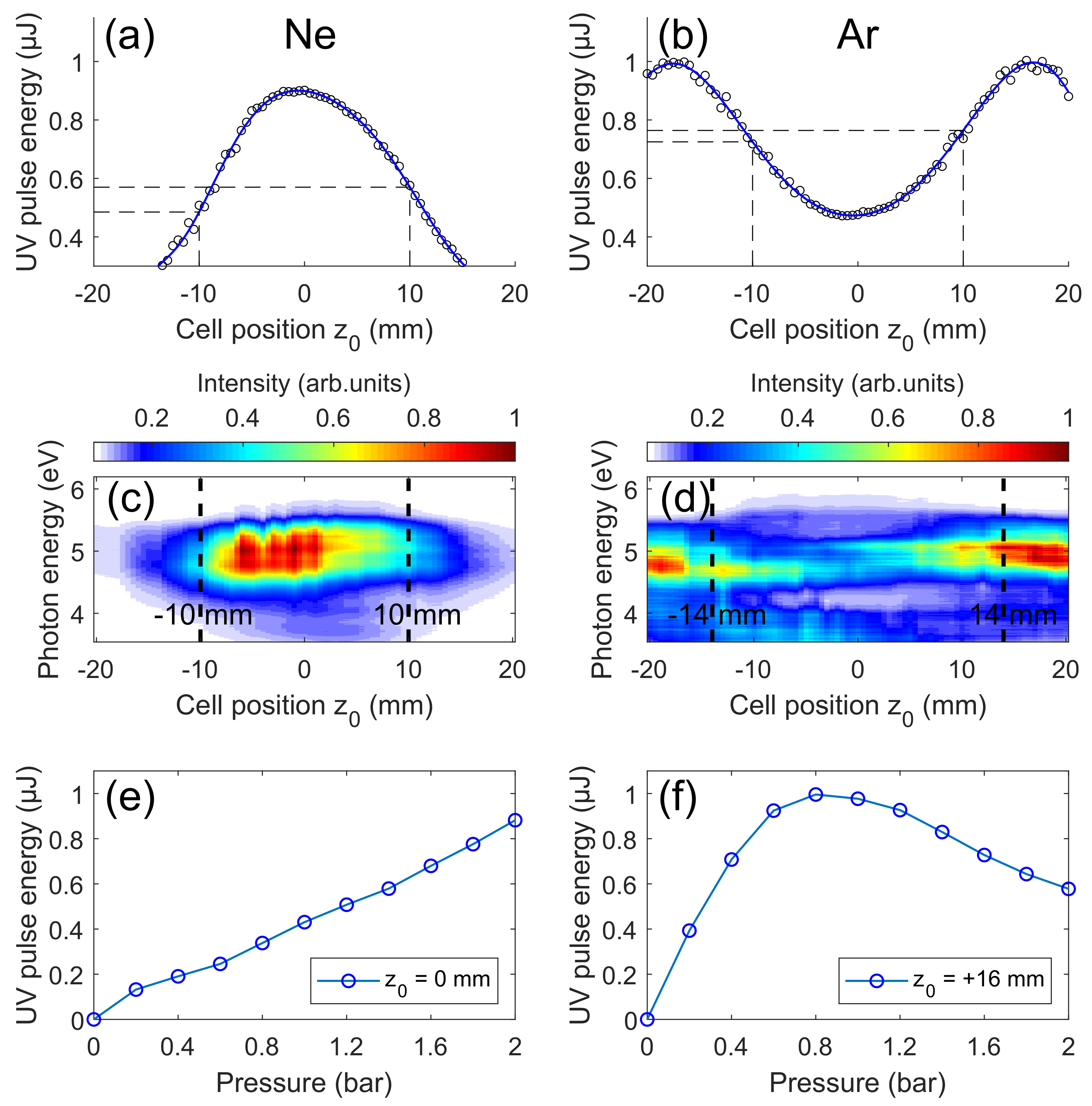
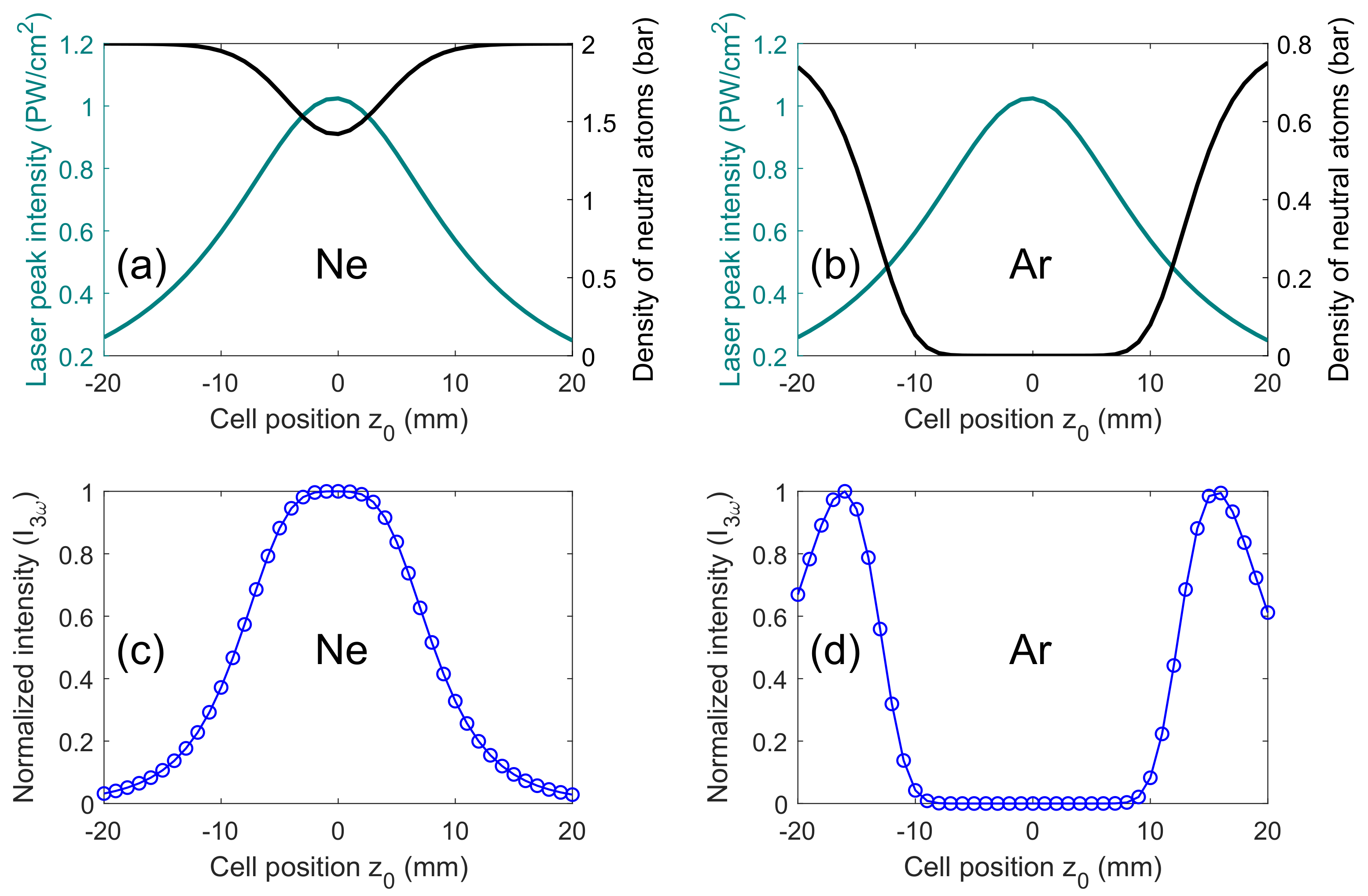
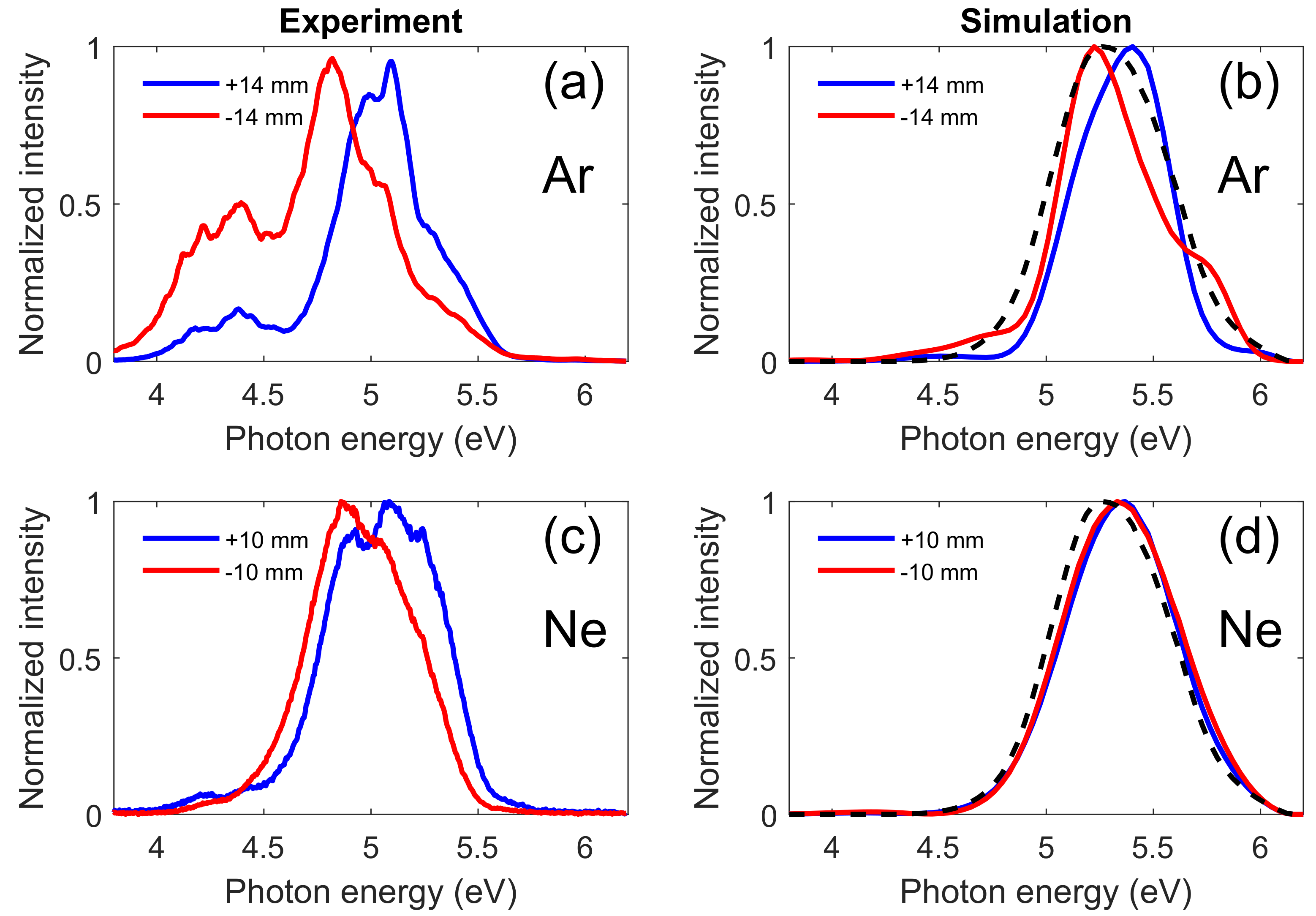
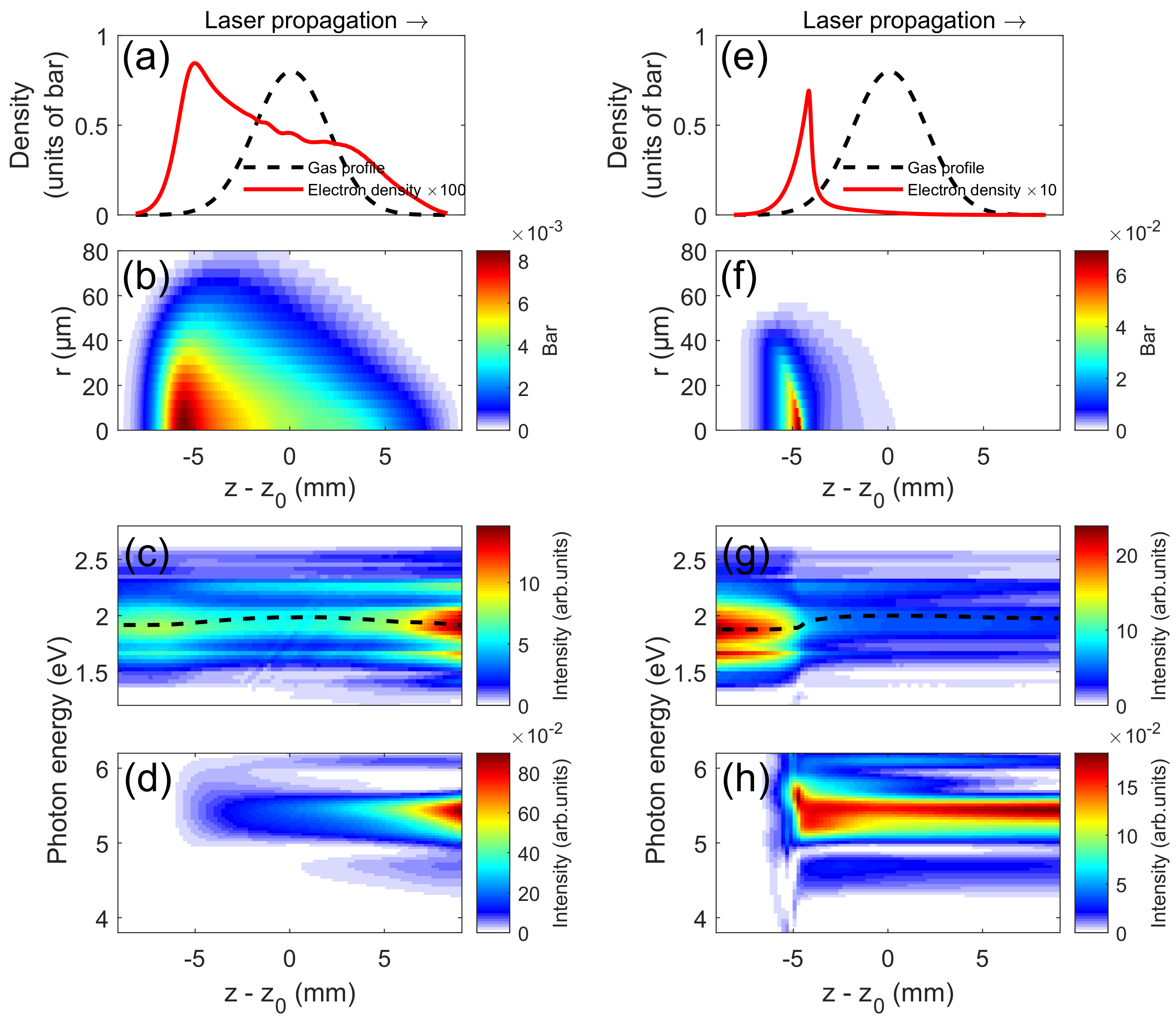
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HHG | High-order harmonic generation |
| THG | Third-order harmonic generation |
| NIR | Near infrared |
| Dscan | Dispersion scan |
| SEWA | Slowly evolving wave approximation |
References
- Crespo-Hernández, C.E.; Cohen, B.; Hare, P.M.; Kohler, B. Ultrafast Excited-State Dynamics in Nucleic Acids. Chem. Rev. 2004, 104, 1977–2020. [Google Scholar] [CrossRef]
- Gustavsson, T.; Improta, R.; Markovitsi, D. DNA/RNA: Building Blocks of Life Under UV Irradiation. J. Phys. Chem. Lett. 2010, 1, 2025–2030. [Google Scholar] [CrossRef] [Green Version]
- Wirth, A.; Hassan, M.T.; Grguraš, I.; Gagnon, J.; Moulet, A.; Luu, T.T.; Pabst, S.; Santra, R.; Alahmed, Z.A.; Azzeer, A.M.; et al. Synthesized Light Transients. Science 2011, 334, 195–200. [Google Scholar] [CrossRef] [Green Version]
- Reiter, F.; Graf, U.; Serebryannikov, E.E.; Schweinberger, W.; Fiess, M.; Schultze, M.; Azzeer, A.M.; Kienberger, R.; Krausz, F.; Zheltikov, A.M.; et al. Route to Attosecond Nonlinear Spectroscopy. Phys. Rev. Lett. 2010, 105, 243902. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a Train of Attosecond Pulses from High Harmonic Generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef]
- Chini, M.; Zhao, K.; Chang, Z. The generation, characterization and applications of broadband isolated attosecond pulses. Nat. Photonics 2014, 8, 178–186. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.C.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright Coherent Ultrahigh Harmonics in the keV X-ray Regime from Mid-Infrared Femtosecond Lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef]
- Teichmann, S.M.; Silva, F.; Cousin, S.L.; Hemmer, M.; Biegert, J. 0.5-keV Soft X-ray attosecond continua. Nat. Commun. 2016, 7, 11493. [Google Scholar] [CrossRef] [Green Version]
- Fuji, T.; Suzuki, T. Generation of sub-two-cycle mid-infrared pulses by four-wave mixing through filamentation in air. Opt. Lett. 2007, 32, 3330–3332. [Google Scholar] [CrossRef]
- Ghotbi, M.; Beutler, M.; Noack, F. Generation of 2.5 μJ vacuum ultraviolet pulses with sub-50 fs duration by noncollinear four-wave mixing in argon. Opt. Lett. 2010, 35, 3492–3494. [Google Scholar] [CrossRef]
- Aközbek, N.; Iwasaki, A.; Becker, A.; Scalora, M.; Chin, S.L.; Bowden, C.M. Third-Harmonic Generation and Self-Channeling in Air Using High-Power Femtosecond Laser Pulses. Phys. Rev. Lett. 2002, 89, 143901. [Google Scholar] [CrossRef]
- Durfee, C.G.; Backus, S.; Kapteyn, H.C.; Murnane, M.M. Intense 8-fs pulse generation in the deep ultraviolet. Opt. Lett. 1999, 24, 697–699. [Google Scholar] [CrossRef]
- Baum, P.; Lochbrunner, S.; Riedle, E. Tunable sub-10-fs ultraviolet pulses generated by achromatic frequency doubling. Opt. Lett. 2004, 29, 1686–1688. [Google Scholar] [CrossRef]
- Graf, U.; Fieß, M.; Schultze, M.; Kienberger, R.; Krausz, F.; Goulielmakis, E. Intense few-cycle light pulses in the deep ultraviolet. Opt. Express 2008, 16, 18956–18963. [Google Scholar] [CrossRef]
- Reiter, F.; Graf, U.; Schultze, M.; Schweinberger, W.; Schröder, H.; Karpowicz, N.; Azzeer, A.M.; Kienberger, R.; Krausz, F.; Goulielmakis, E. Generation of sub-3 fs pulses in the deep ultraviolet. Opt. Lett. 2010, 35, 2248–2250. [Google Scholar] [CrossRef] [Green Version]
- Galli, M.; Wanie, V.; Lopes, D.P.; Månsson, E.P.; Trabattoni, A.; Colaizzi, L.; Saraswathula, K.; Cartella, A.; Frassetto, F.; Poletto, L.; et al. Generation of deep ultraviolet sub-2-fs pulses. Opt. Lett. 2019, 44, 1308–1311. [Google Scholar] [CrossRef] [Green Version]
- Belli, F.; Belli, F.; Abdolvand, A.; Abdolvand, A.; Travers, J.C.; Travers, J.C.; Russell, P.S.J.; Russell, P.S.J. Highly efficient deep UV generation by four-wave mixing in gas-filled hollow-core photonic crystal fiber. Opti. Lett. 2019, 44, 5509–5512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Travers, J.C.; Grigorova, T.F.; Brahms, C.; Belli, F. High-energy pulse self-compression and ultraviolet generation through soliton dynamics in hollow capillary fibres. Nat. Photonics 2019, 13, 547–554. [Google Scholar] [CrossRef] [Green Version]
- Brahms, C.; Belli, F.; Travers, J.C. Infrared attosecond field transients and UV to IR few-femtosecond pulses generated by high-energy soliton self-compression. Phys. Rev. Res. 2020, 2, 043037. [Google Scholar] [CrossRef]
- L’Huillier, A.; Balcou, P.; Lompré, L.A. Coherence and resonance effects in high-order harmonic generation. Phys. Rev. Lett. 1992, 68, 166–169. [Google Scholar] [CrossRef] [PubMed]
- Balcou, P.; L’Huillier, A. Phase-matching effects in strong-field harmonic generation. Phys. Rev. A 1993, 47, 1447–1459. [Google Scholar] [CrossRef]
- Salières, P.; L’Huillier, A.; Lewenstein, M. Coherence Control of High-Order Harmonics. Phys. Rev. Lett. 1995, 74, 3776–3779. [Google Scholar] [CrossRef] [Green Version]
- Gaarde, M.B.; Tate, J.L.; Schafer, K.J. Macroscopic aspects of attosecond pulse generation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 132001. [Google Scholar] [CrossRef]
- Miranda, M.; Arnold, C.L.; Fordell, T.; Silva, F.; Alonso, B.; Weigand, R.; L’Huillier, A.; Crespo, H. Characterization of broadband few-cycle laser pulses with the d-scan technique. Opt. Express 2012, 20, 18732. [Google Scholar] [CrossRef]
- Larochelle, S.F.J.; Talebpour, A.; Chin, S.L. Coulomb effect in multiphoton ionization of rare-gas atoms. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 1215–1224. [Google Scholar] [CrossRef]
- Weber, M.J. Handbook of Optical Materials; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Brée, C.; Demircan, A.; Steinmeyer, G. Saturation of the All-Optical Kerr Effect. Phys. Rev. Lett. 2011, 106, 183902. [Google Scholar] [CrossRef] [Green Version]
- Couairon, A.; Brambilla, E.; Corti, T.; Majus, D.; Ramírez-Góngora, O.D.J.; Kolesik, M. Practitioner’s guide to laser pulse propagation models and simulation. Eur. Phys. J. Spec. Top. 2011, 199, 5–76. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khurelbaatar, T.; Mun, J.-H.; Heo, J.; Lee, Y.; Kim, D.-E. Few-Cycle, μJ-Class, Deep-UV Source from Gas Media. Appl. Sci. 2021, 11, 6440. https://doi.org/10.3390/app11146440
Khurelbaatar T, Mun J-H, Heo J, Lee Y, Kim D-E. Few-Cycle, μJ-Class, Deep-UV Source from Gas Media. Applied Sciences. 2021; 11(14):6440. https://doi.org/10.3390/app11146440
Chicago/Turabian StyleKhurelbaatar, Tsendsuren, Je-Hoi Mun, Jaeuk Heo, Yunman Lee, and Dong-Eon Kim. 2021. "Few-Cycle, μJ-Class, Deep-UV Source from Gas Media" Applied Sciences 11, no. 14: 6440. https://doi.org/10.3390/app11146440
APA StyleKhurelbaatar, T., Mun, J.-H., Heo, J., Lee, Y., & Kim, D.-E. (2021). Few-Cycle, μJ-Class, Deep-UV Source from Gas Media. Applied Sciences, 11(14), 6440. https://doi.org/10.3390/app11146440





