Safe Vehicle Trajectory Planning in an Autonomous Decision Support Framework for Emergency Situations
Abstract
:1. Introduction
1.1. Problem Description
- Constraints on the initial state (position, orientation, etc.) and the final state (location of the target point);
- Staying within the boundaries and avoiding collisions with obstacles ;
- Geometric constraints on the path, typically a maximum curvature.
- Constraints on the initial state and the sub-goal state, considering the time dimension.
- Constraints on staying within the boundaries and avoiding moving obstacles;
- Differential constraints on the trajectory, typically upper bounds for speed, acceleration, steering, and steering rate.
1.2. Literature Review
1.2.1. Decision Making
1.2.2. Path and Trajectory Planning Algorithm
1.2.3. Vehicle Control
1.3. Contribution
- A general decision-support framework for autonomous driving is introduced, which uses a combination of two different algorithms for trajectory planning (“autonomous mode” and “emergency mode” algorithms). This expanded framework keeps the efficiency of the previous algorithm but improves its robustness in emergency situation.
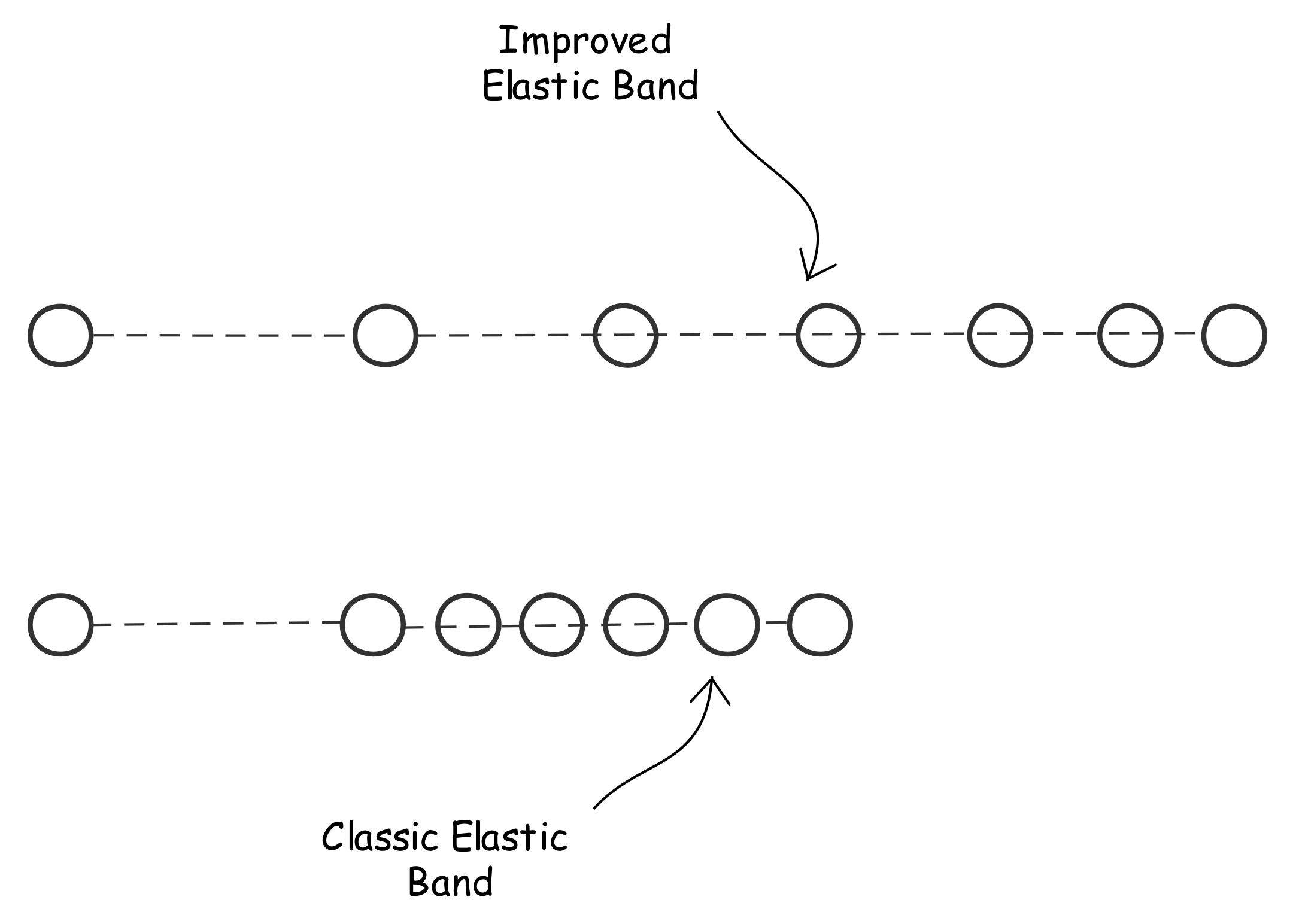
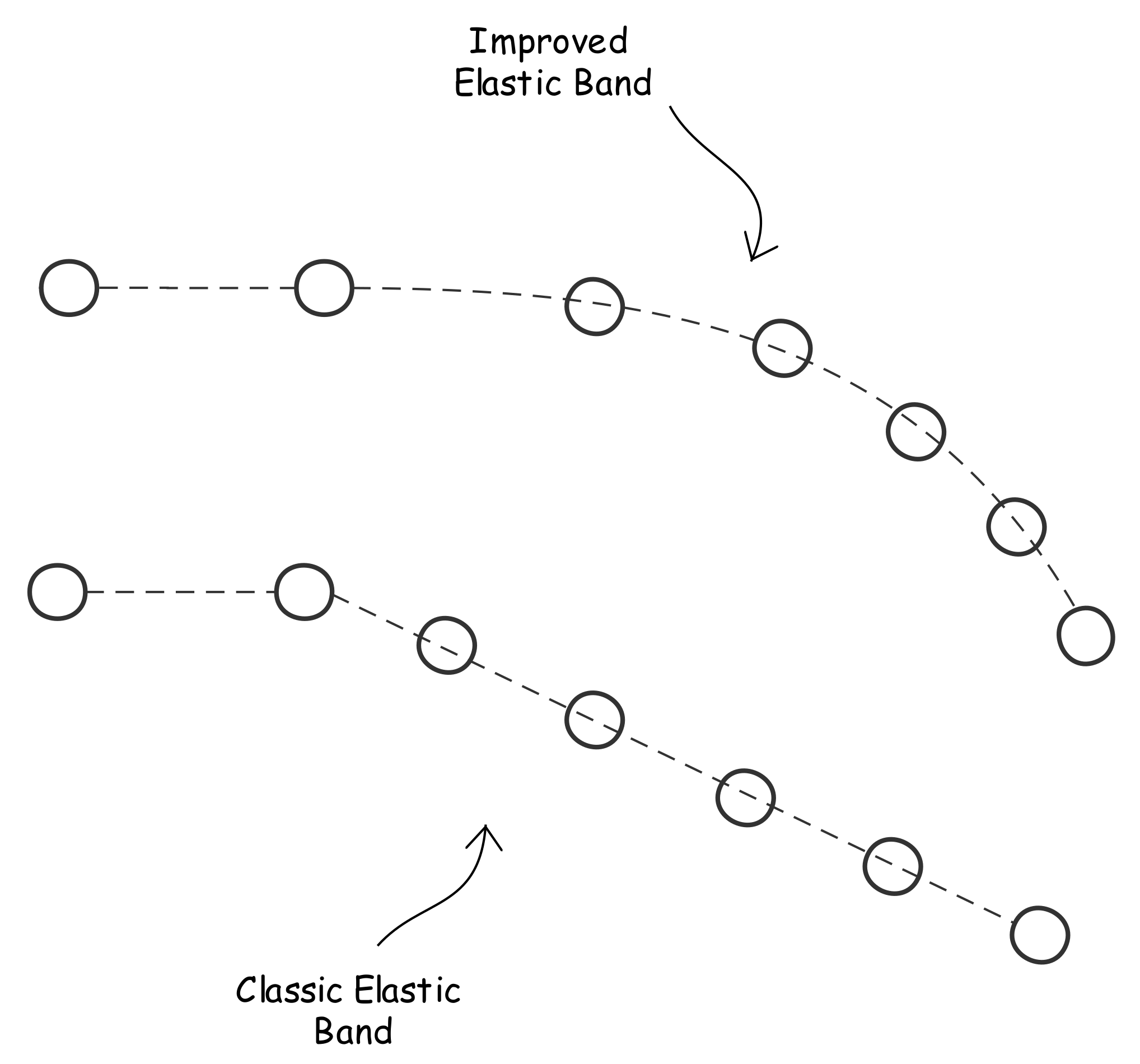
- An emergency trajectory planning algorithm was developed, based on elastic bands. The following improvements are presented:
- –
- A new internal force is proposed, to ensure the steering and acceleration of the vehicle stay bounded (kinematic constraints);
- –
- The last point of the trajectory is not fixed, but instead is subject to specific internal and external forces, to give more flexibility;
- –
- The final trajectory is a linear combination of the solution at different iterations, and is therefore guaranteed to be within the (static) boundaries of the road.
- The new framework was implemented and validated using Matlab and Pro-SiVIC simulations in different emergency scenarios, using both algorithms. The corresponding performance results are evaluated.
1.4. Organization
2. Autonomous Decision Support Framework
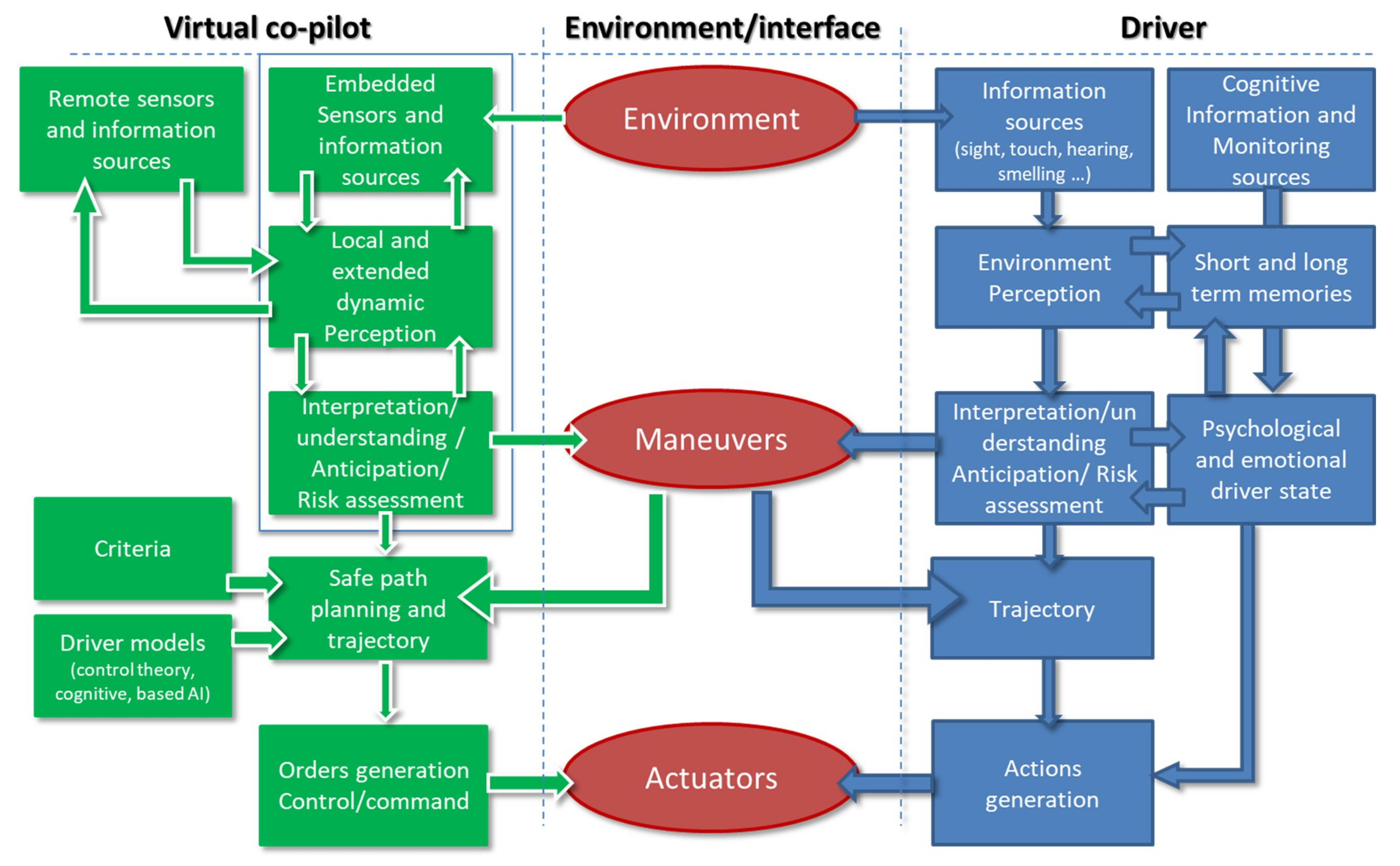
2.1. Autonomous Driving and Virtual Co-Pilot
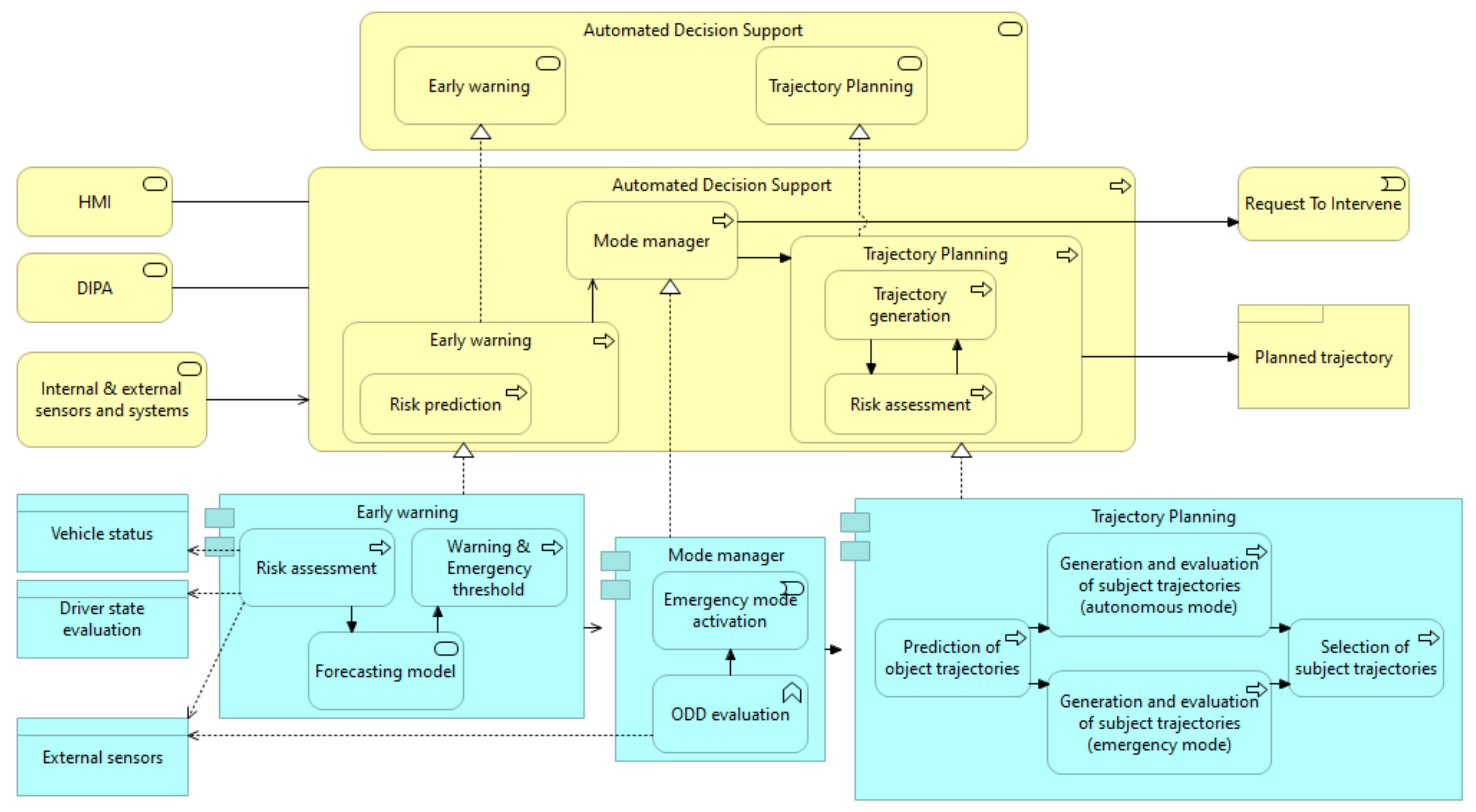
2.2. New Framework Design
2.3. Component Overview
- Early warning:
- The role of this component is to monitor and forecast different risk levels and indicators. Those risks are relative to the main road key components (obstacles, road attributes, ego-vehicle, environment, driver). Each calculated risk depends not only on the current state of the component itself but also on a forecast of its evolution. Thus, each risk has two thresholds (warning and emergency) and three driving states (regular, cautious/degraded, and emergency/critical). When a risk is higher than the warning threshold, the associated warning is sent to the driver via the HMI, whereas the emergency threshold is used directly by the Mode manager. This component is presented in details in [68].
- Mode manager:
- This component decides which driving mode should be adopted, depending on the current and short time predicted situations, the driver’s wish (input from HMI), and the combination of the different risk levels (input from Early warning). The ODD establishes conditions under which the vehicle may operate in autonomous mode. The Mode manager is also responsible for starting the emergency mode and issuing a request to intervene to the human driver.
- Trajectory planning:
- This module generates the trajectories, which the vehicle tracks in autonomous and emergency modes. It uses inputs from the perception module to predict the trajectories of the different objects/obstacles in its environment. It then generates, evaluates and selects the best trajectory for the ego-vehicle. This trajectory must respect a set of constraints (traffic, system, driver rules) relative to safety. Depending on the mode, it uses either the classical Co-Pilot algorithm (see Appendix A) or the new emergency algorithm (see Section 3).
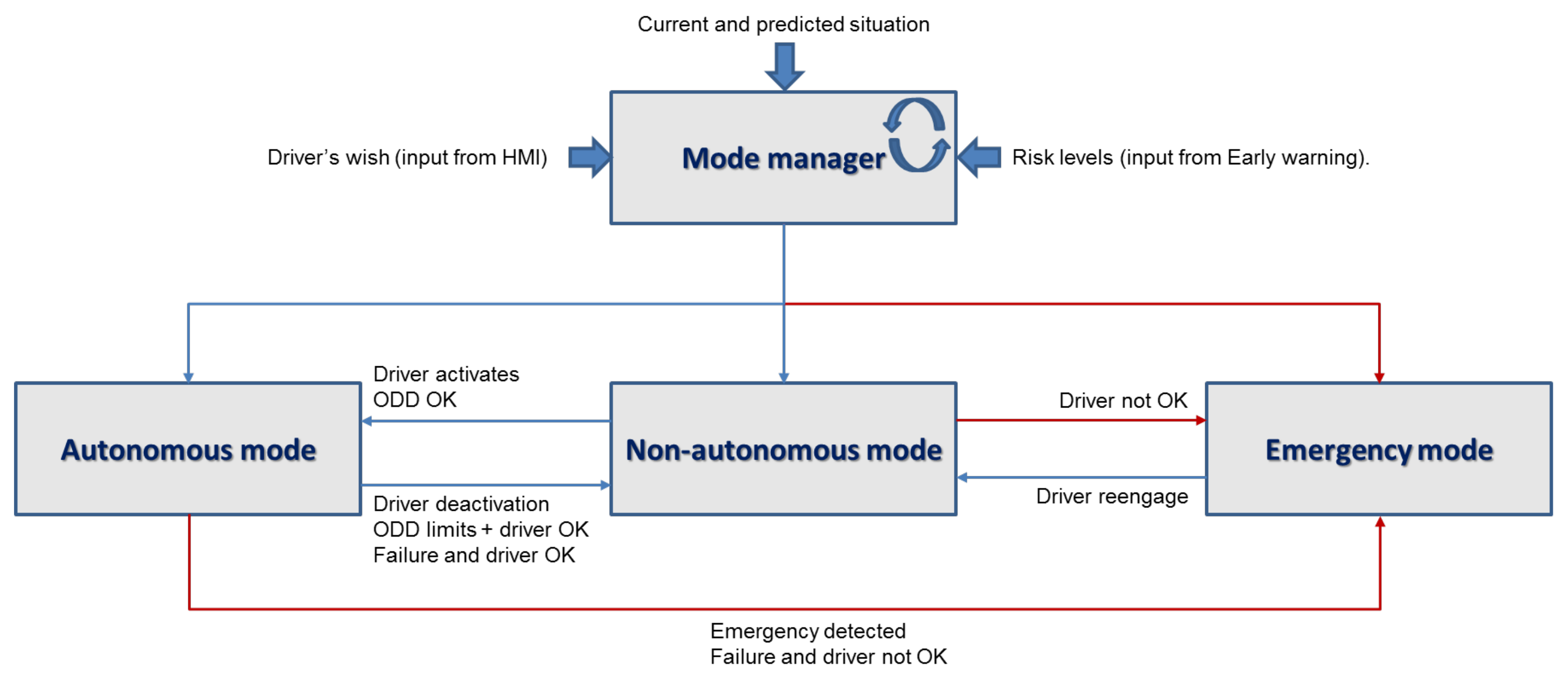
2.4. Mode Transitions
3. Emergency Trajectory Planning Algorithm
3.1. New Emergency Mode
- In this model, the only option proposed in case of emergencies (no collision-free solution found) is an emergency braking to mitigate the collision. Although this answer can work in certain low-speed driving situations, we cannot expect the vehicle to have sufficient braking distance to avoid a collision when entering emergency mode even at medium speed. Meanwhile, a different decision, such as steering rapidly to avoid an obstacle instead of braking, may allow to avoid collisions altogether. It follows that this single option (safe braking) makes the Vanholme’s model less adaptable in emergency situations.
- The Vanholme’s model was designed to react to emergency situations while driving in autonomous mode. The ego vehicle takes the corresponding actions based on certain rules, and all the decisions are made in a fully autonomous driving environment. However, when the emergency mode is force switched from manual mode because of unsafe behavior or visual constraints of the driver (e.g., following with high speed and close distance, invisible obstacles), preconditions in emergency mode will be uncertain for the vehicle and namely lead to Vanholme’s model going to an unknown state, then fails in reducing the risk of collision.
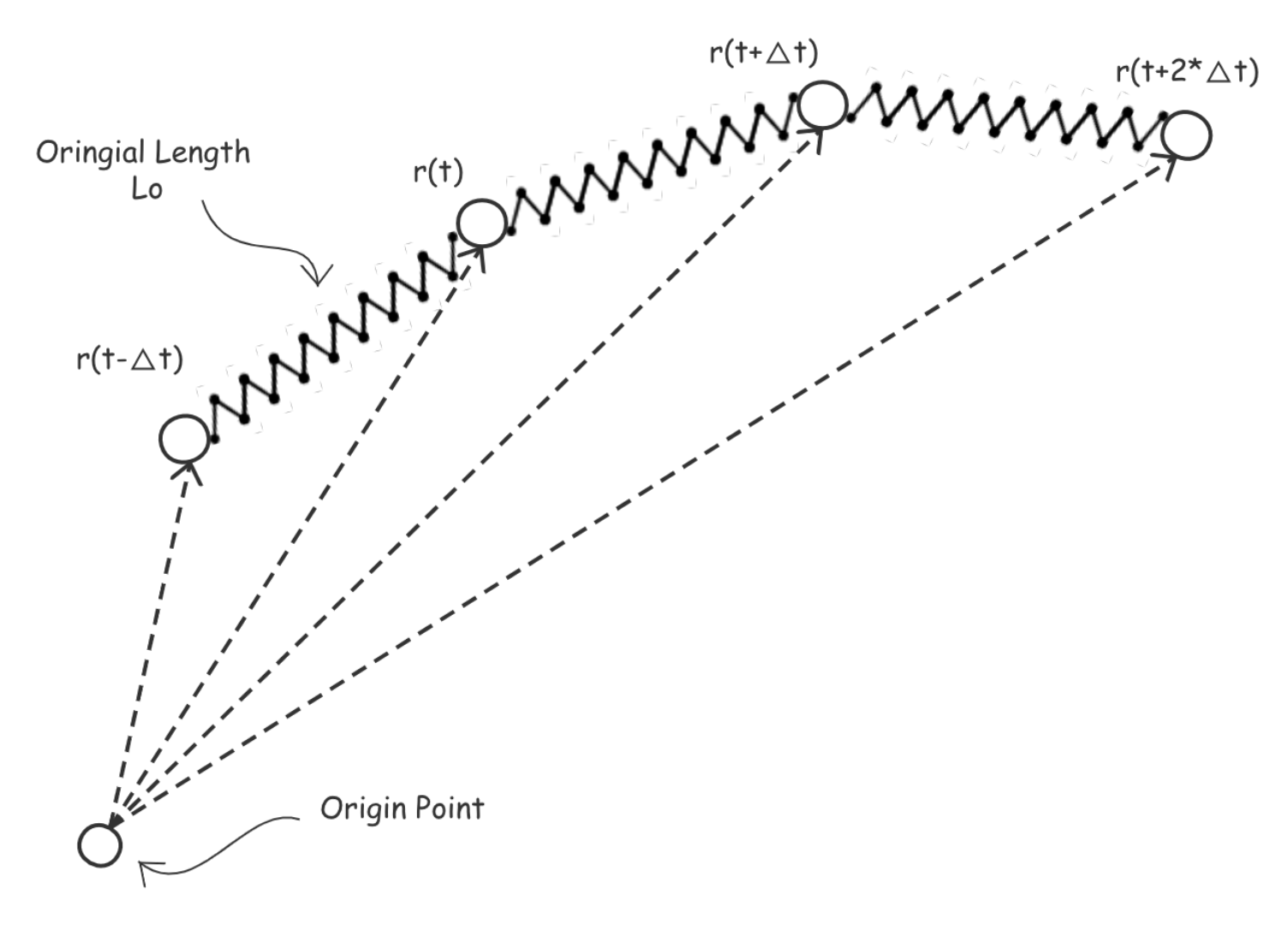
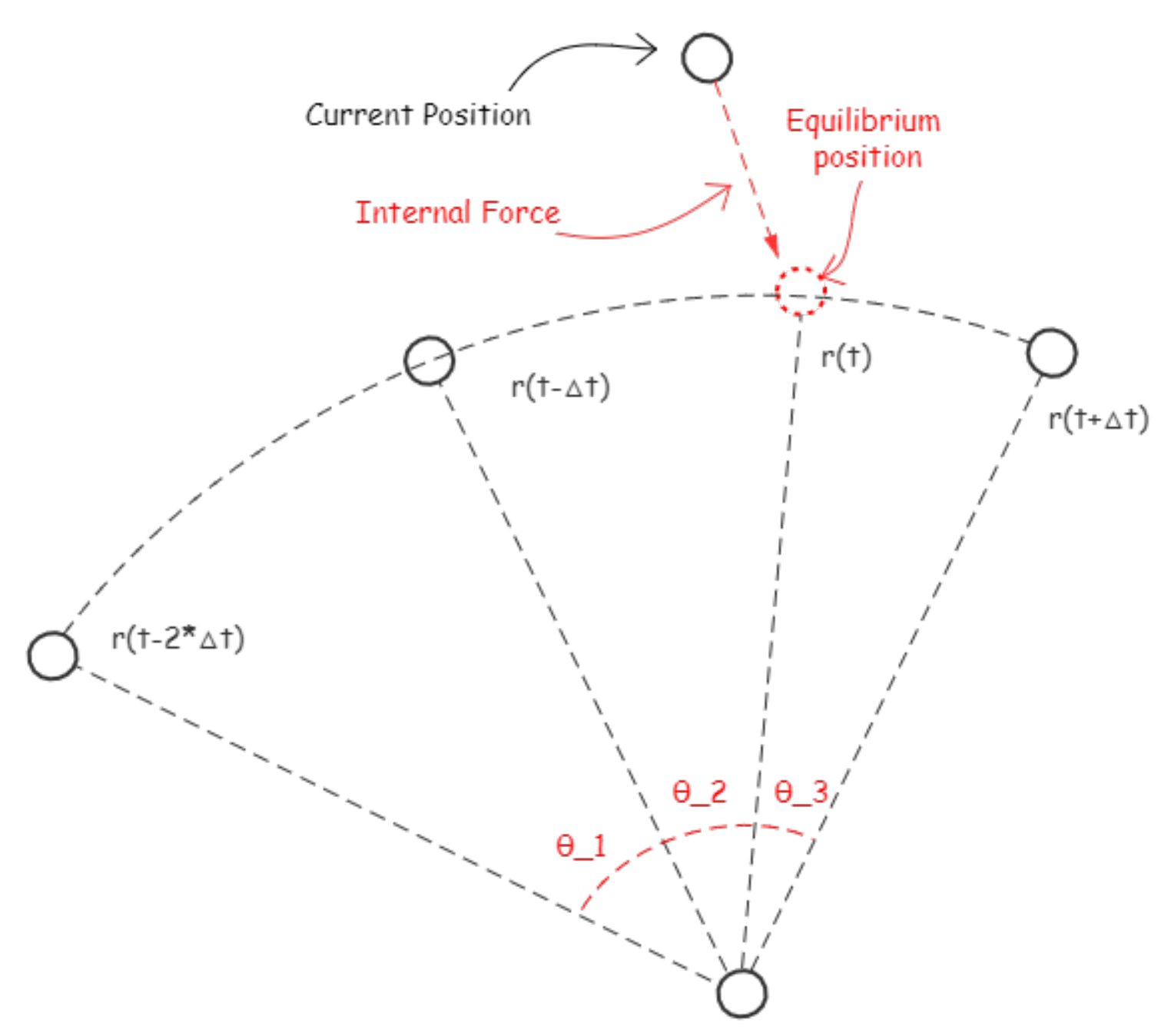
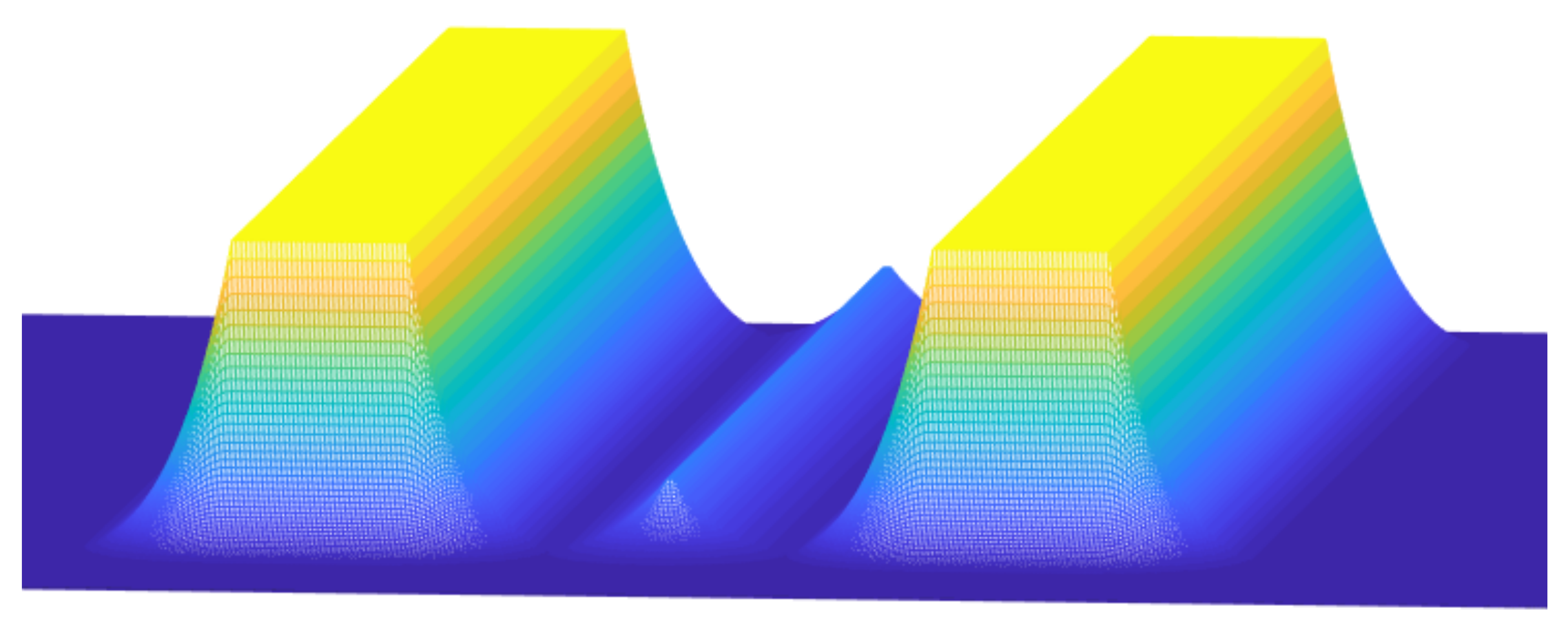
3.2. Internal Force
3.3. External Force
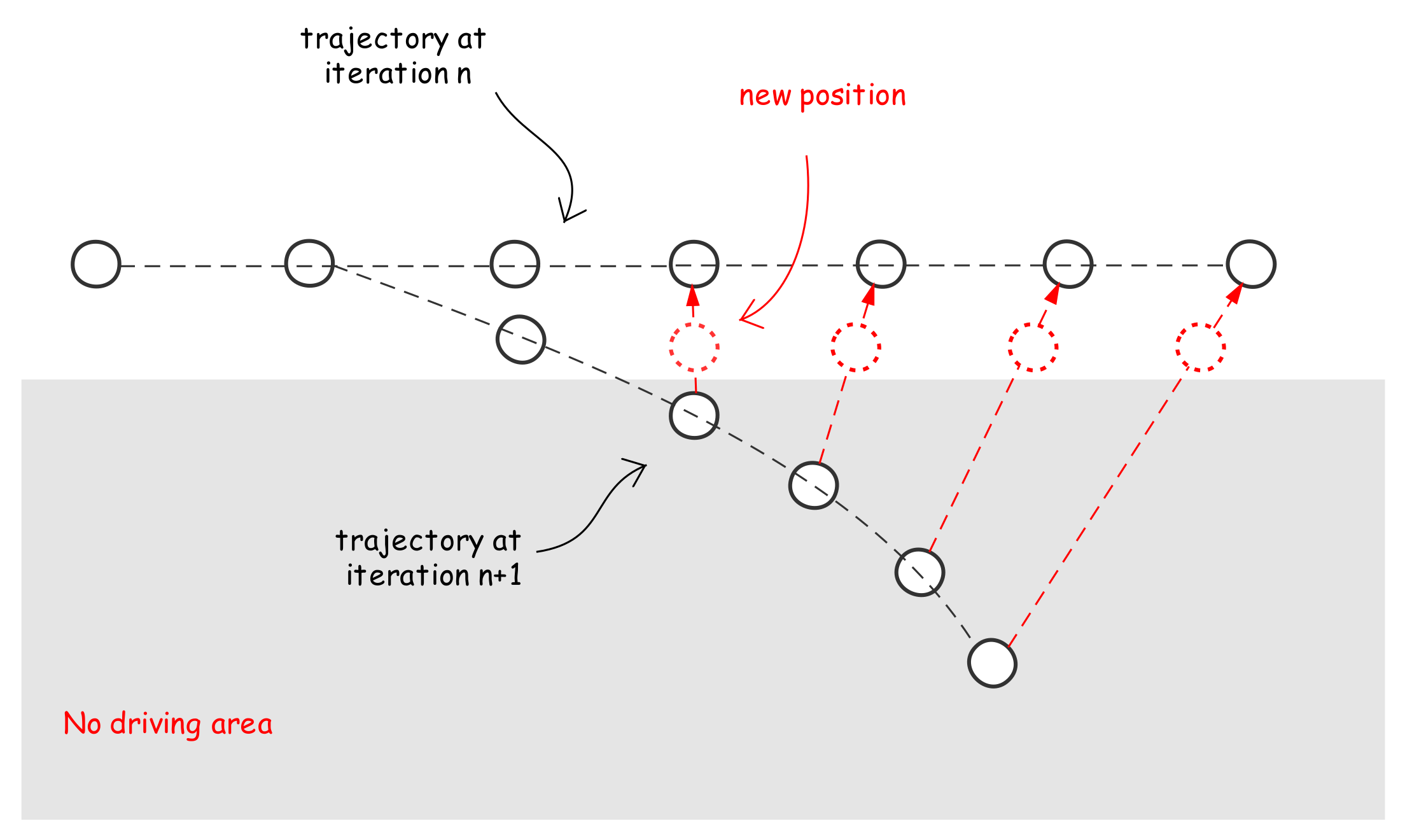
3.4. Dynamic Process
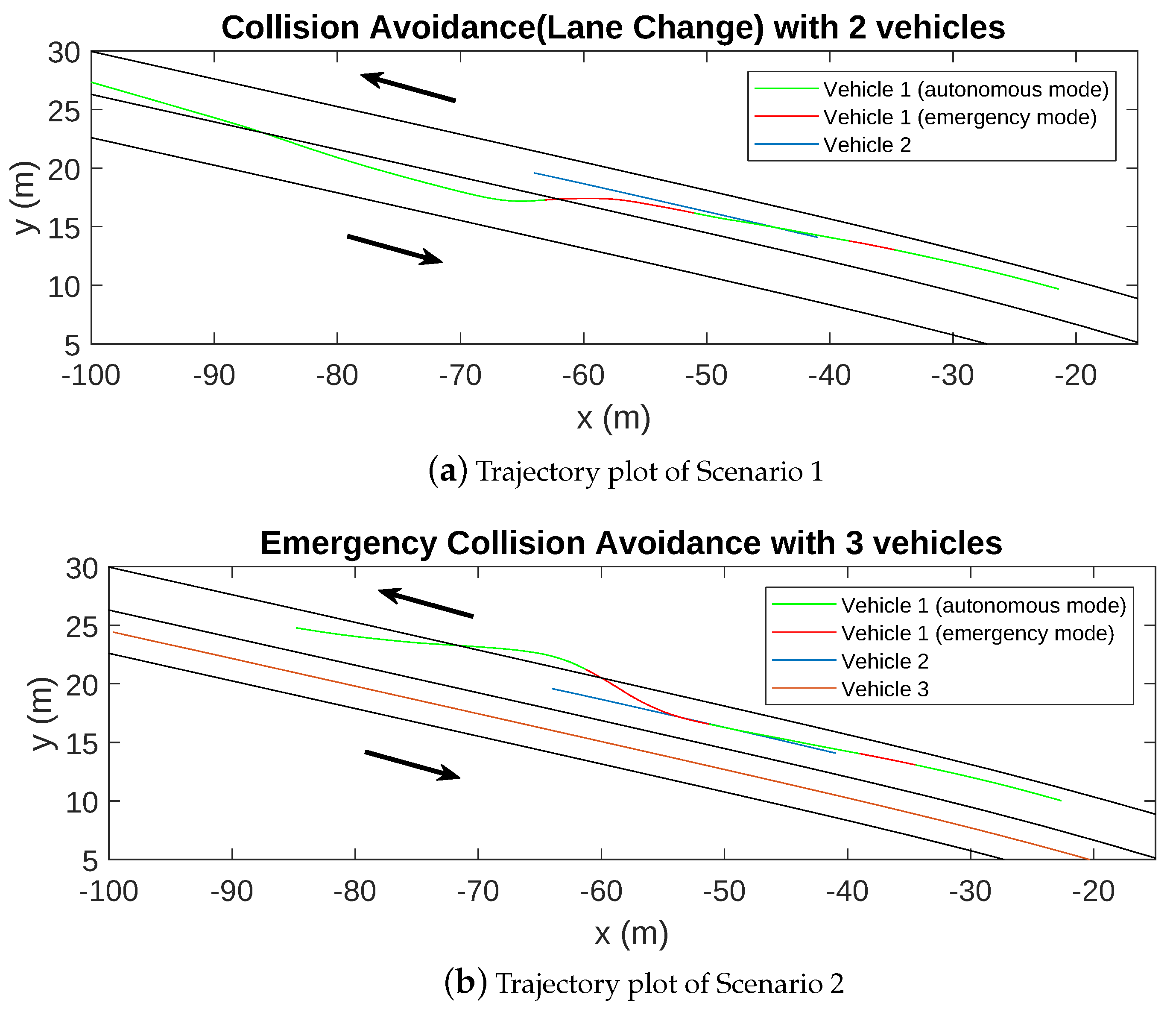
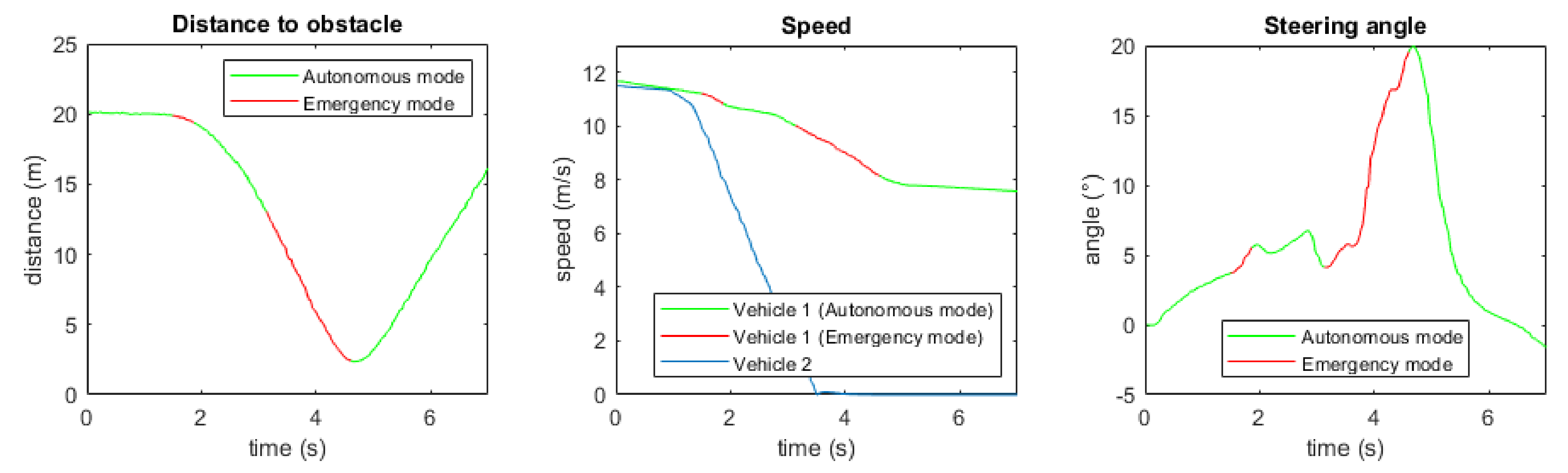
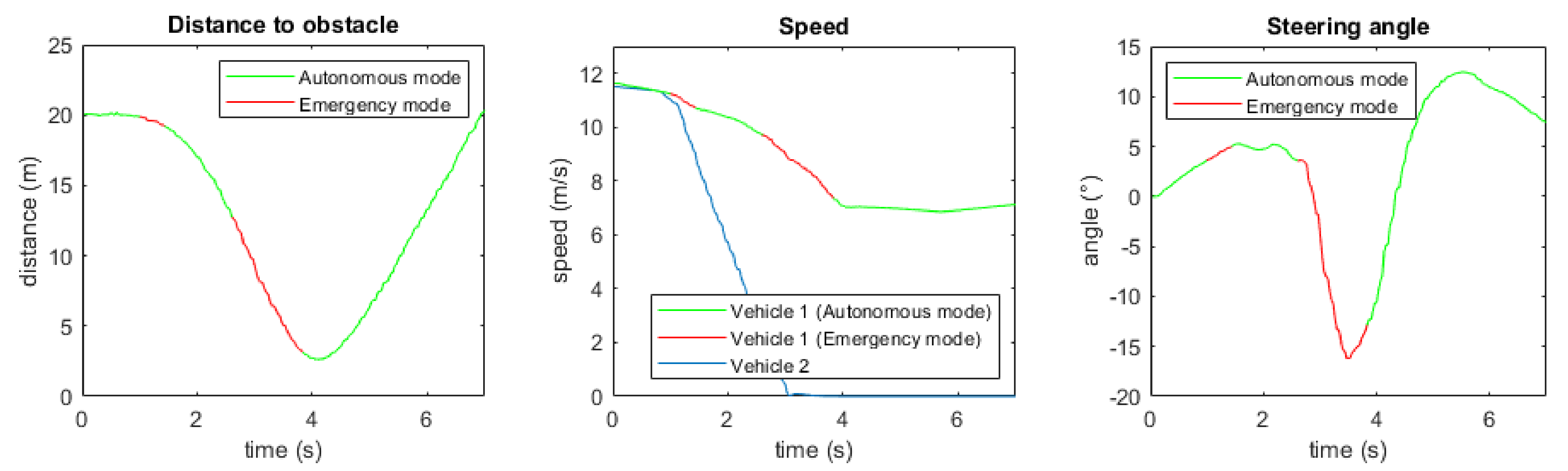
4. Results
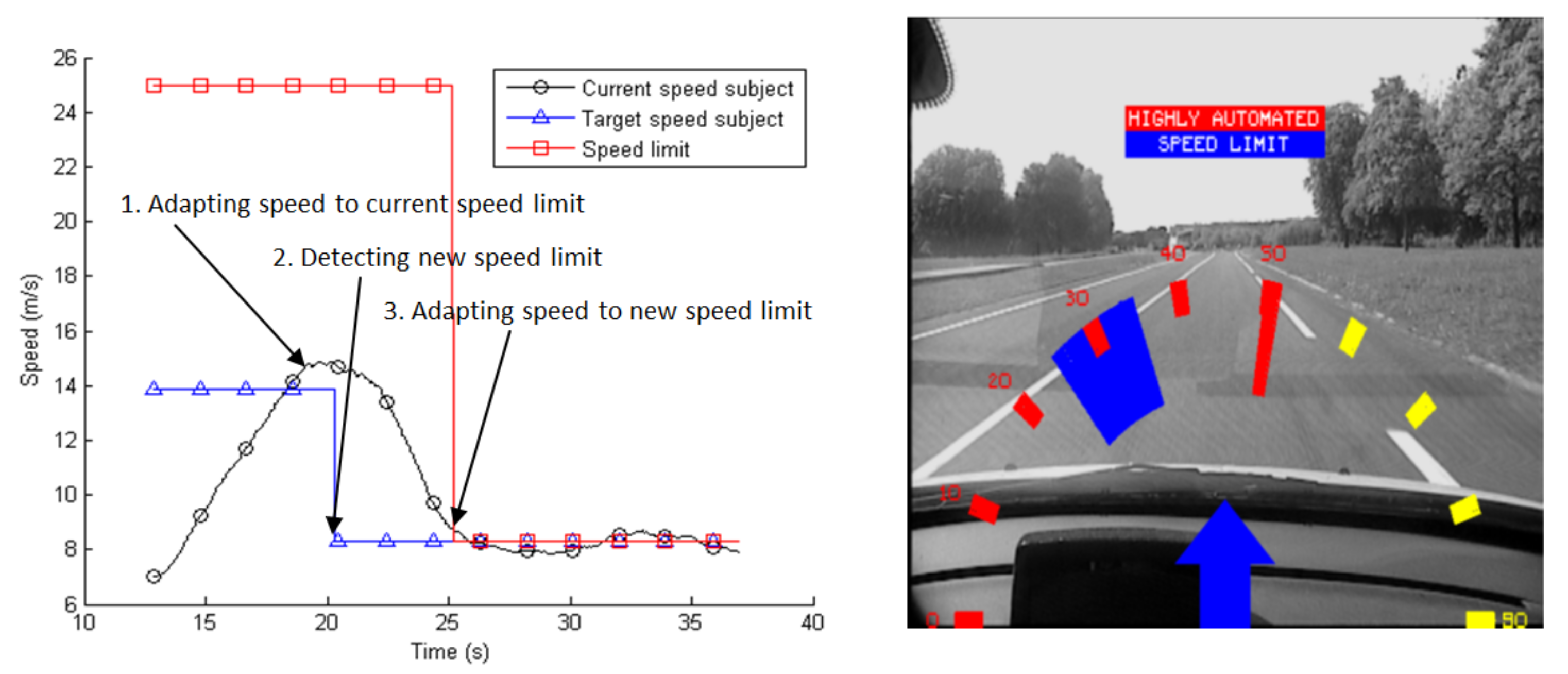
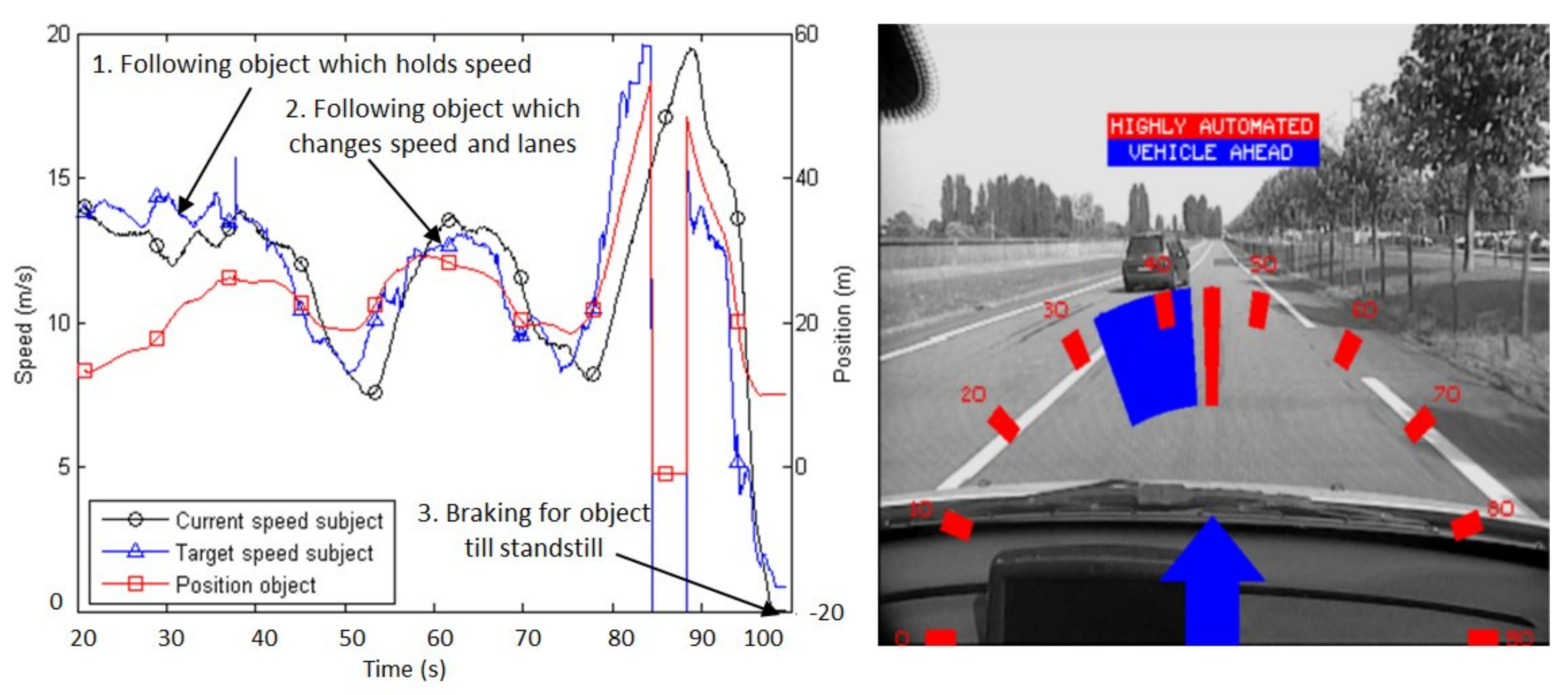
4.1. Results in Normal Driving Conditions
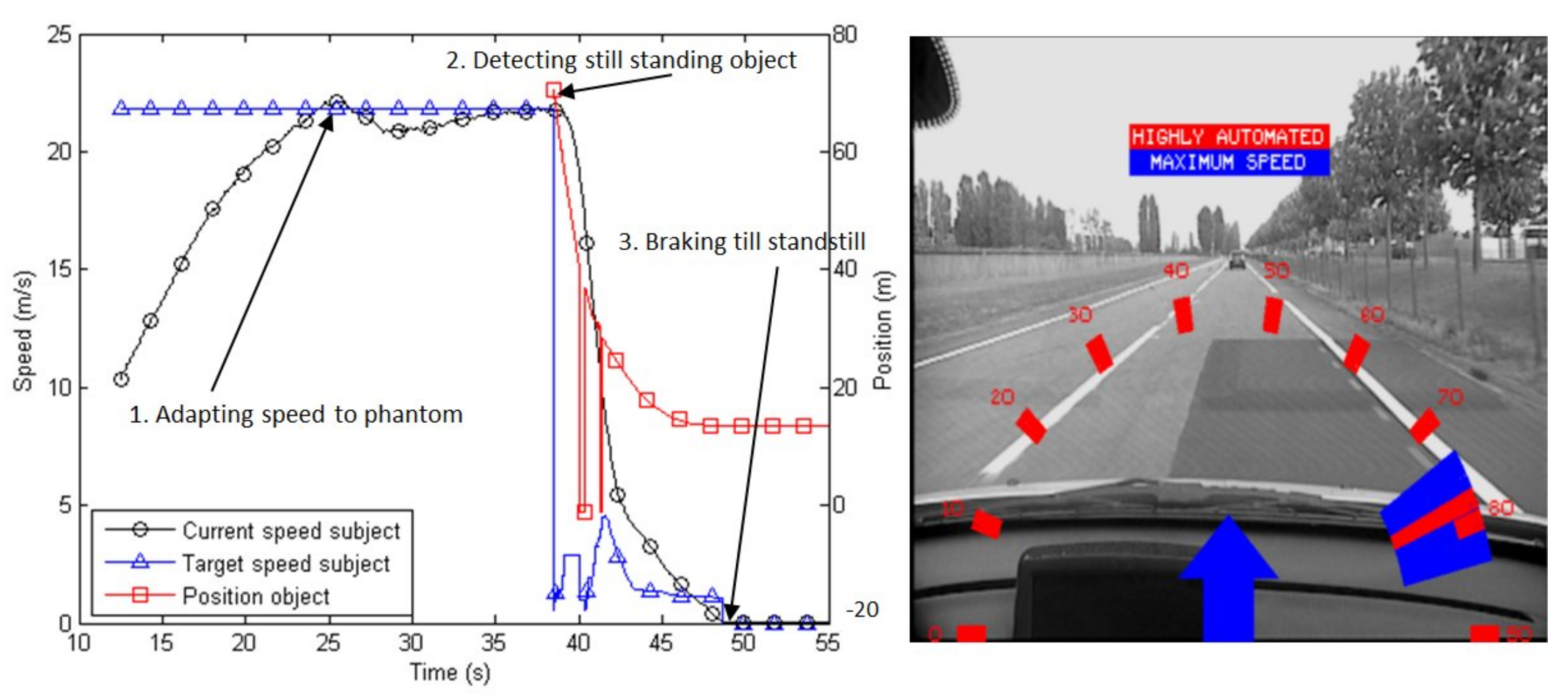
4.2. Results in Emergency Driving Mode
4.2.1. Parameters Values
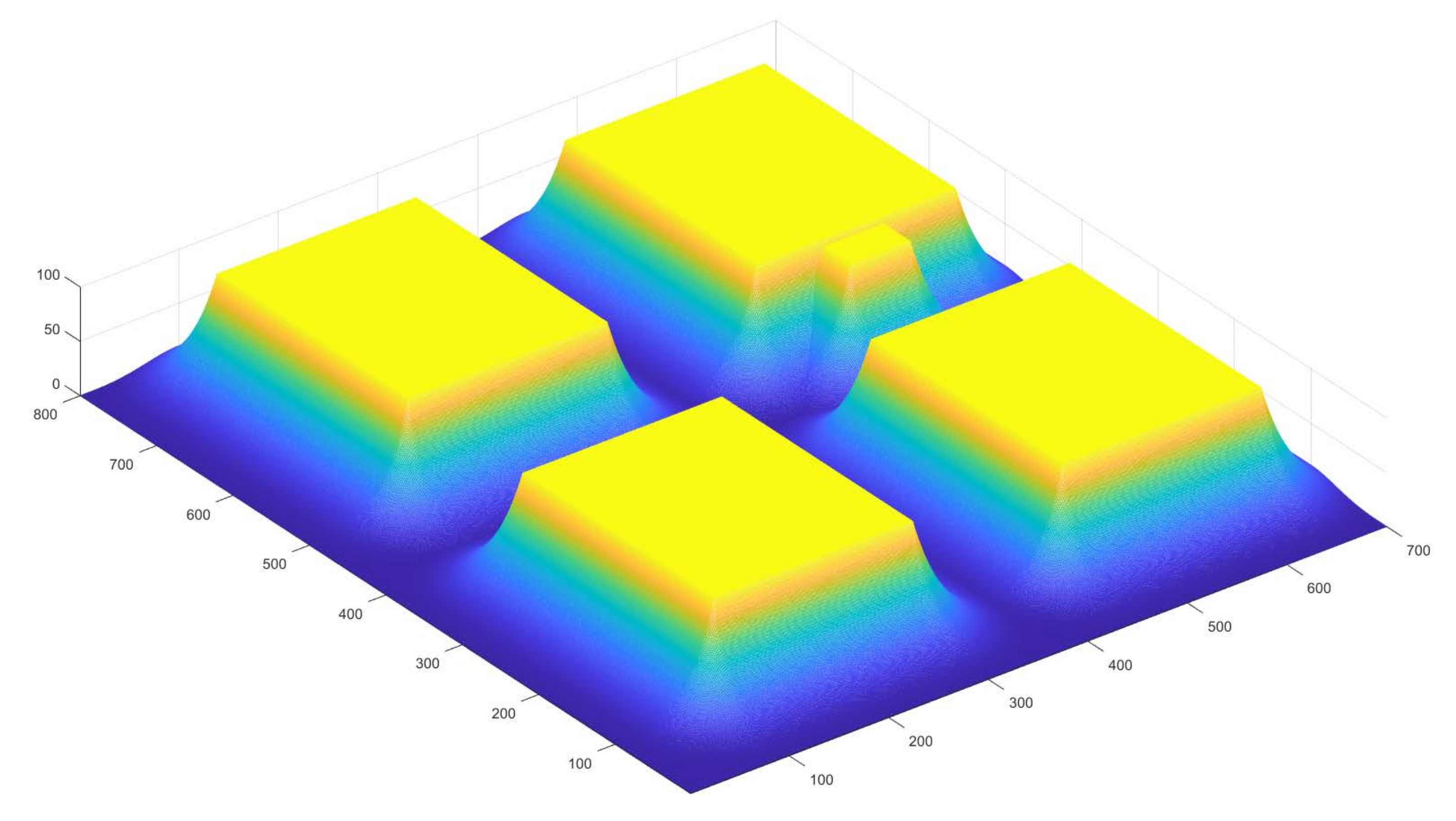
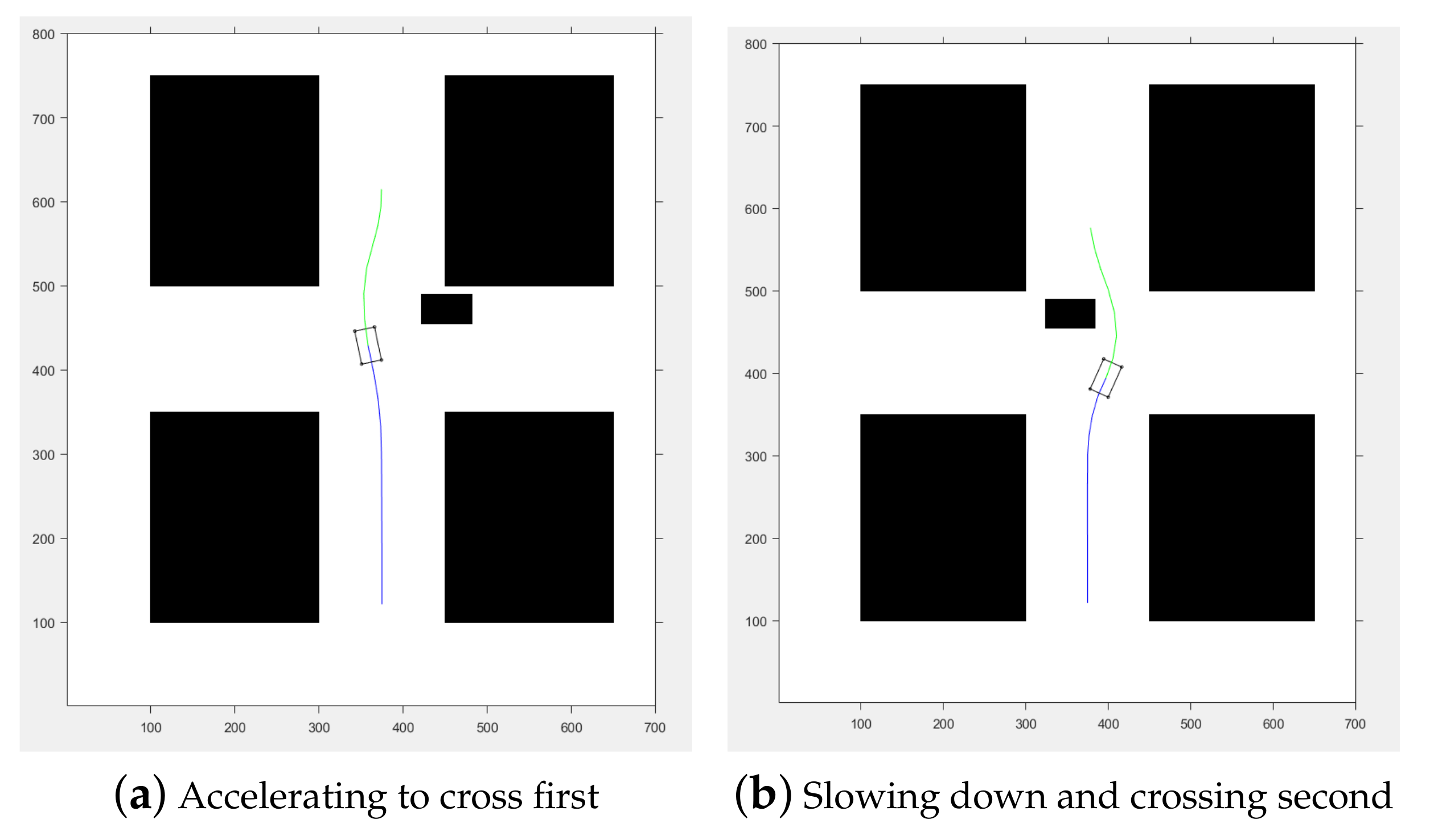
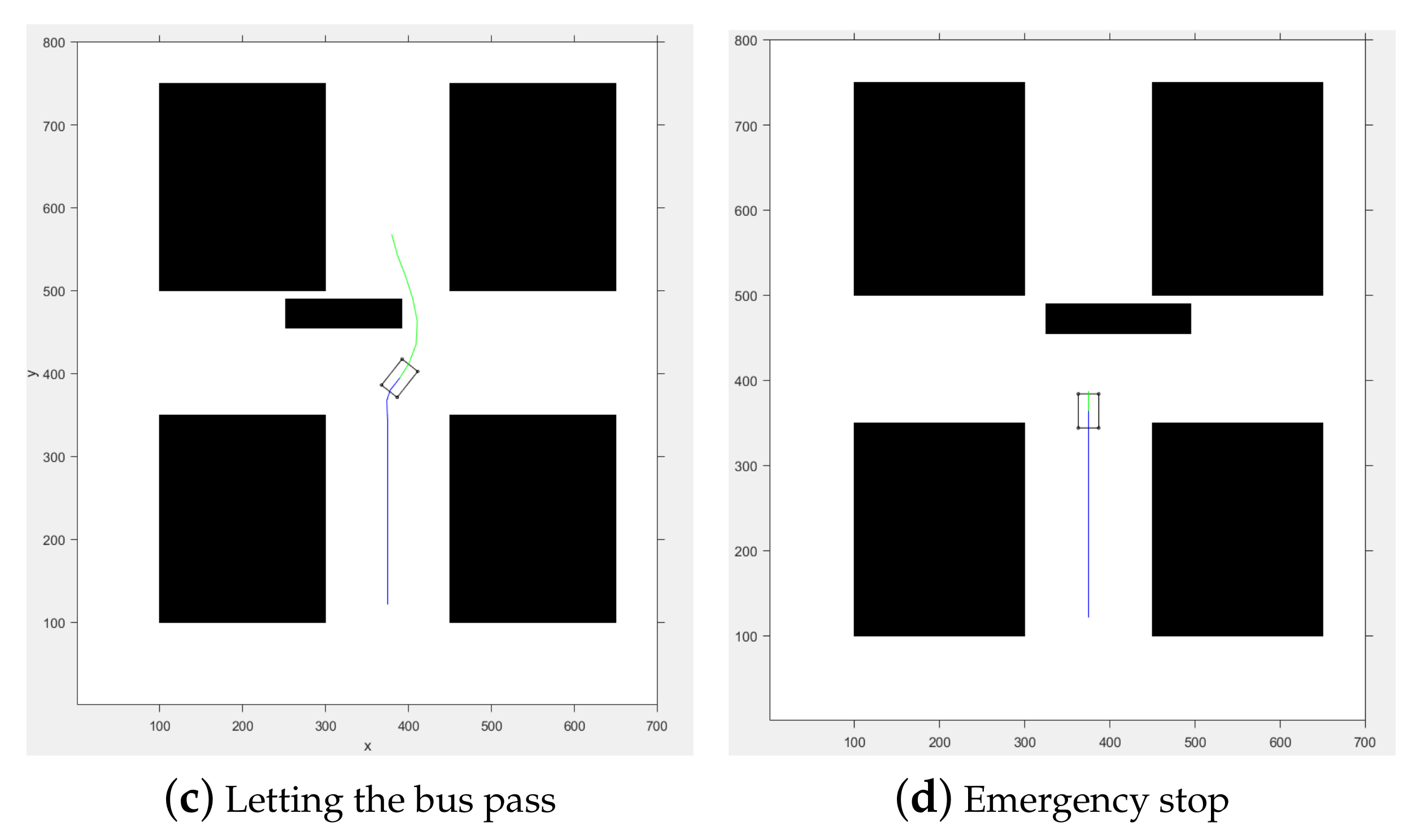
4.2.2. Simulation in Matlab
4.2.3. Simulation in Pro-SiVIC
5. Discussion and Conclusions
- It is based on EB’s trajectory generation, for fast computation.
- Unlike in classical methods, the last point of the trajectory is not fixed, but simply attracted to the general direction of motion, to give more flexibility in different emergency situations.
- The current orientation and speed of the vehicle are taken into account using additional ad hoc forces during the trajectory generation, to ensure mechanical feasibility even when obstacles are very close.
- Calibration and testing of the Emergency trajectory planning algorithm will be continued in different scenarios (urban, scenarios with multiple vehicles, pedestrians, etc).
- The current algorithms will be included in the general ADSF framework, which includes a Driver State Monitoring system and a Driver Intervention Performance Assessment (DIPA) module to monitor mode transitions and driver-related risk management at all times.
- The general framework will be tested on a new real vehicle in 2021 in France, possibly using virtual obstacles generated from Pro-SiVIC platform (Vehicle in the Loop architecture with communication means).
- Different perception architectures and perception data will be used in order to assess the capability of the full ADS in adverse and degraded conditions involving possible sensor failures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADS | Autonomous Driving System |
| ADSF | Autonomous Decision Support Framework |
| AI | Artificial Intelligence |
| APF | Artificial Potential Field |
| AV | Automated Vehicles |
| Co-Pilot | Cooperative Pilot |
| DIPA | Driver Intervention Performance Assessment |
| DSM | Driver Status Monitor |
| EB | Elastic Band |
| ESI | Engineering System International |
| HMI | Human-Machine Interface |
| IEEE | Institute of Electrical and Electronics Engineers |
| IMM | Interacting Multiple Model |
| ODD | Operational Design Domain |
| Pro-SiVIC | Vehicle, Infrastructure and Sensors Simulation Platform (French acronym) |
| RRT | Rapidly-Exploring Random Tree |
| RTMaps | Real-Time Multisensor Applications |
| SAE | Society of Automotive Engineers |
Appendix A. Cooperative Pilot
Appendix A.1. Computation of a Reference Space and Lane Coordinate System

Appendix A.2. Computation of Trajectories for Both Objects and “Ghost” Vehicles

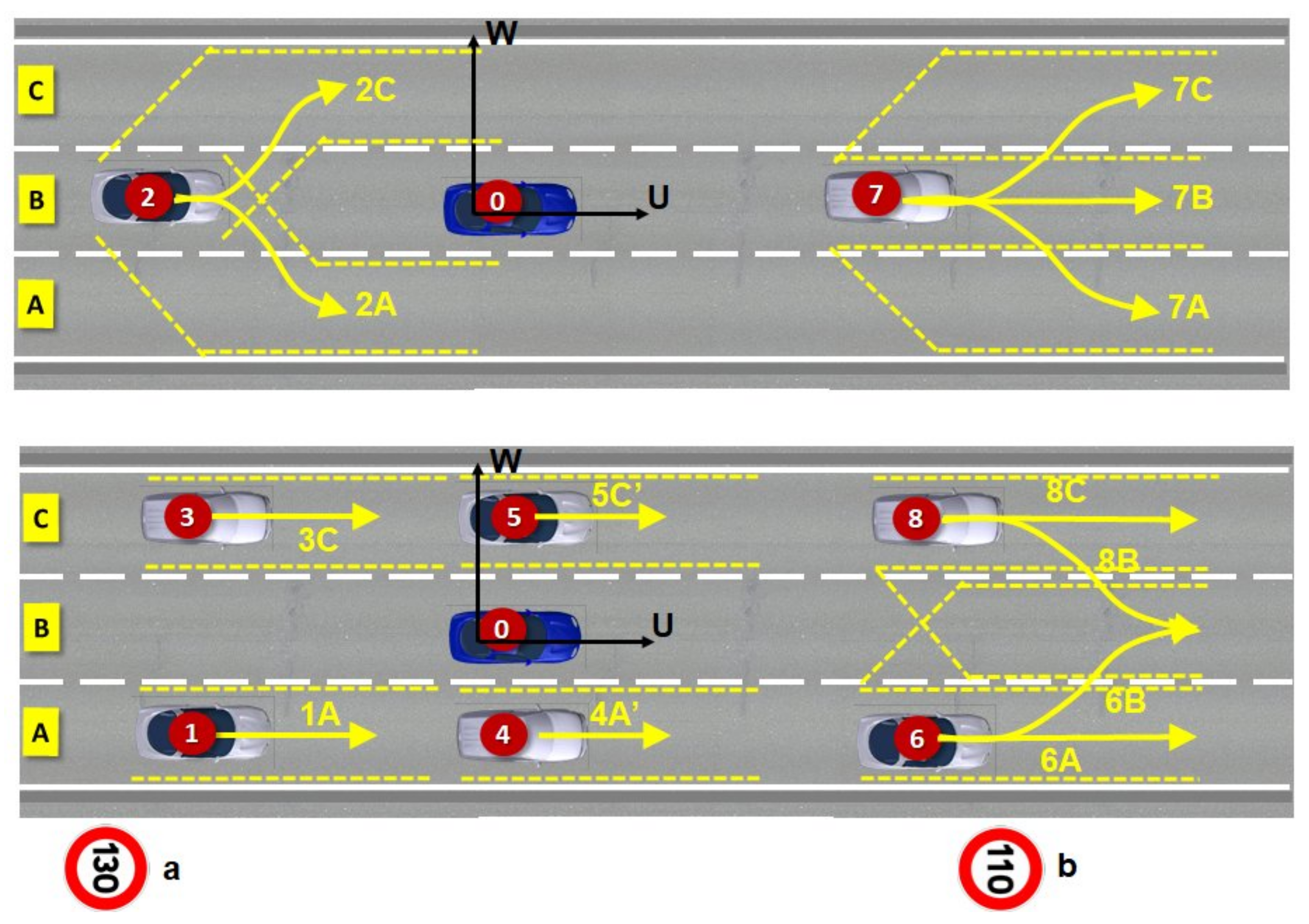
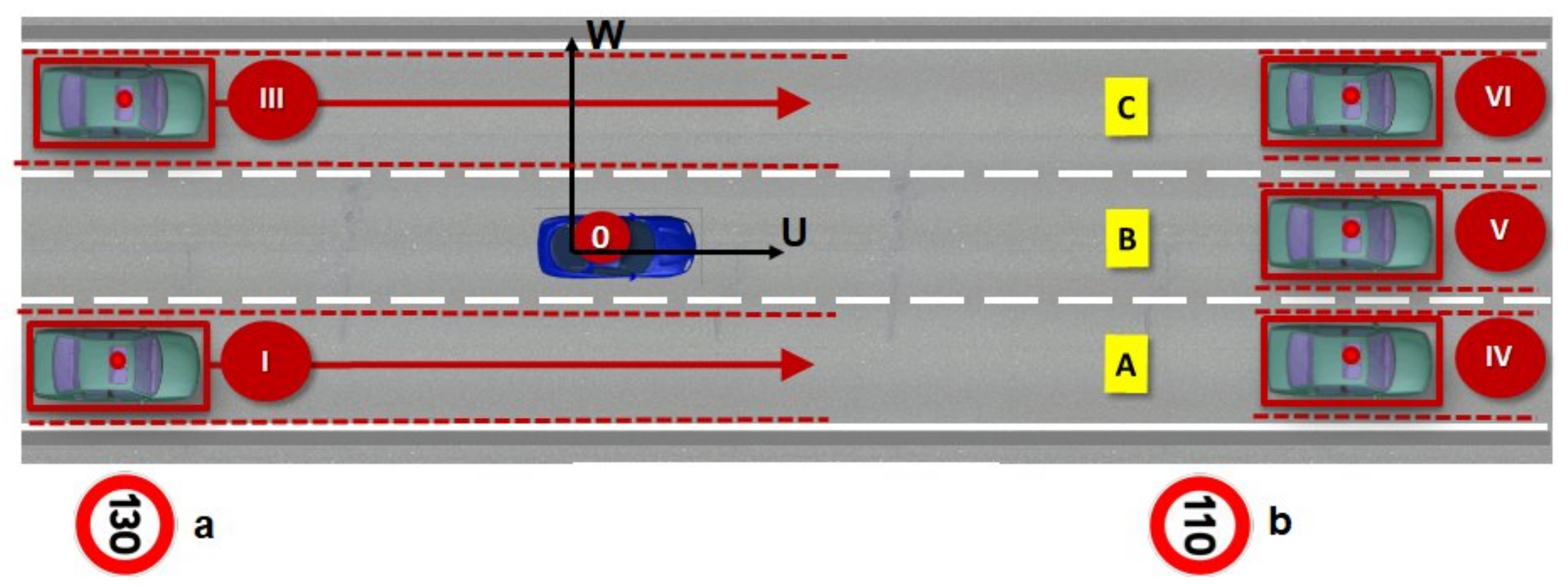
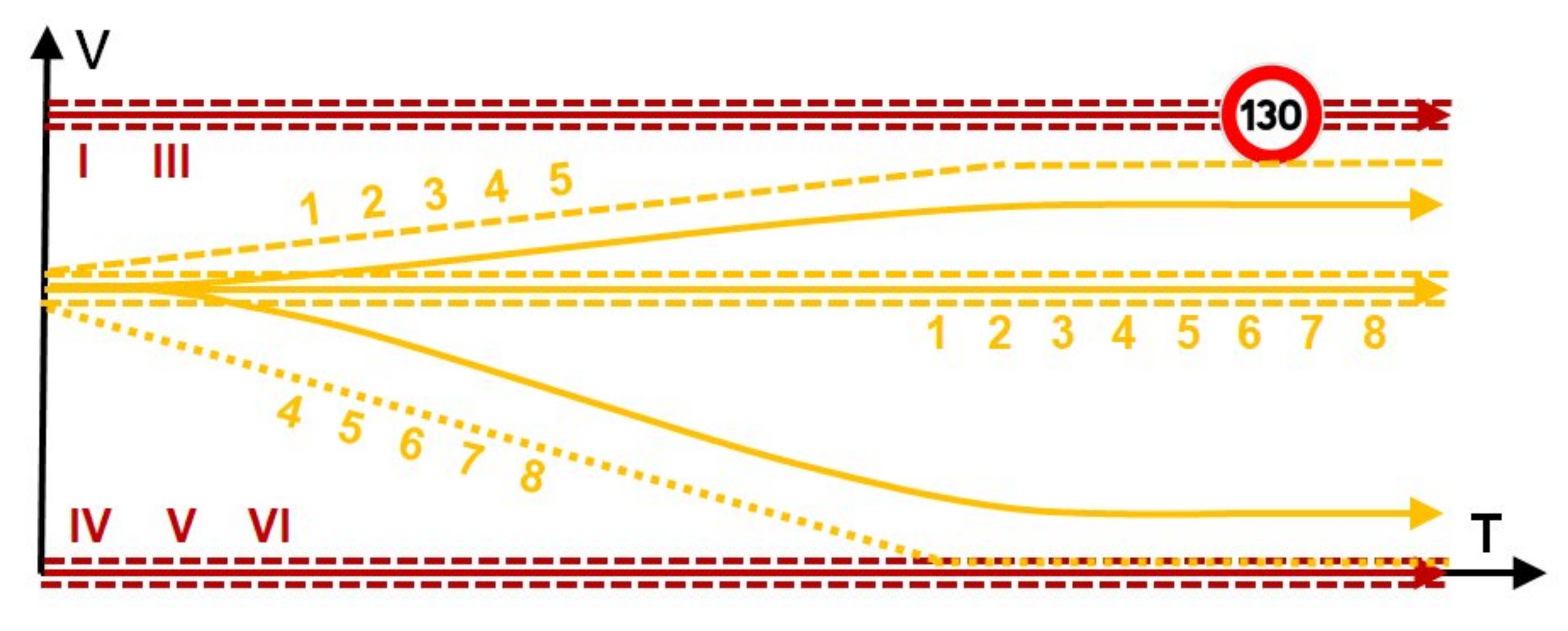
Appendix A.3. Prediction of Speed Profiles and Trajectories for the Ego-Vehicle
- The first corresponds to normal vehicle operation (0A, 0B, 0C).
- The second takes into account the singular situations of breakdown and failure of an ego-vehicle embedded system (FA, FB, FC). The safety speed profiles generated in this case (F for failure) must allow stopping safely the ego-vehicle taking into account all the users.
- The last category corresponds to a situation of safe reaction to a dangerous event requiring the use of a safety braking system or a collision requiring an emergency braking system (JB). This can occur when an unequipped vehicle does not respect traffic and human rules.
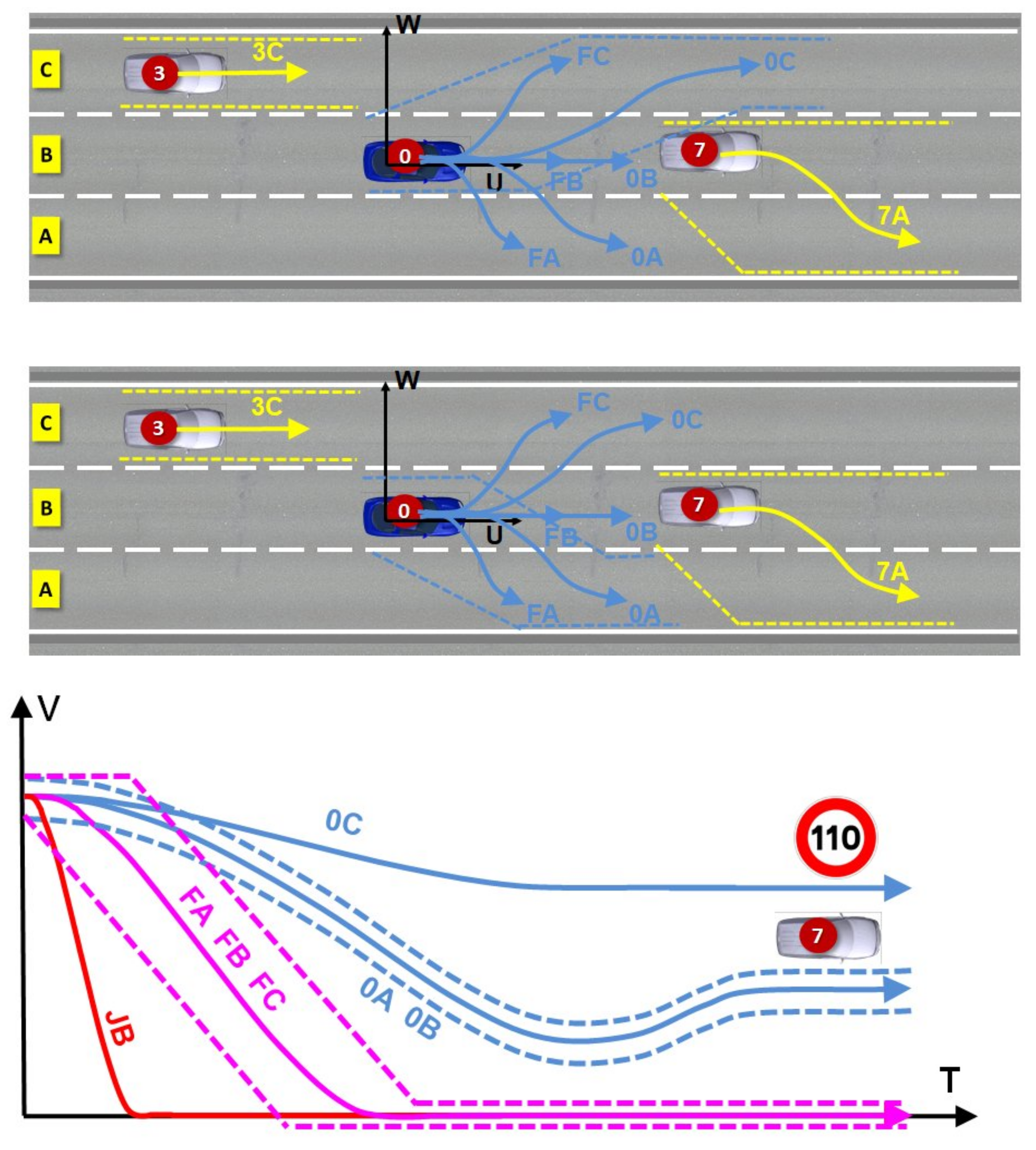
Appendix A.4. Evaluation and Selection of Trajectories for ADS
References
- Tsugawa, S.; Kitoh, K.; Fujii, H.; Koide, K.; Harada, T.; Miura, K.; Yasunobu, S.; Wakabayashi, Y. Info-Mobility: A Concept for Advanced Automotive Functions toward the 21st Century; Technical Report; SAE Technical Paper; SAE International: Pittsburgh, PA, USA, 1991. [Google Scholar]
- Maurer, M.; Christian Gerdes, J.; Lenz, B.; Winner, H. Autonomous Driving: Technical, Legal and Social Aspects; Springer Nature: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Dickmann, J.; Klappstein, J.; Hahn, M.; Appenrodt, N.; Bloecher, H.L.; Werber, K.; Sailer, A. Automotive radar the key technology for autonomous driving: From detection and ranging to environmental understanding. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 1–6 May 2016; pp. 1–6. [Google Scholar]
- Wu, B.F.; Lee, T.T.; Chang, H.H.; Jiang, J.J.; Lien, C.N.; Liao, T.Y.; Perng, J.W. GPS navigation based autonomous driving system design for intelligent vehicles. In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montréal, QC, Canada, 7–10 October 2007; pp. 3294–3299. [Google Scholar]
- Baber, J.; Kolodko, J.; Noel, T.; Parent, M.; Vlacic, L. Cooperative autonomous driving: Intelligent vehicles sharing city roads. IEEE Robot. Autom. Mag. 2005, 12, 44–49. [Google Scholar] [CrossRef] [Green Version]
- Schwarting, W.; Alonso-Mora, J.; Rus, D. Planning and decision-making for autonomous vehicles. Annu. Rev. Control. Robot. Auton. Syst. 2018, 1, 187–210. [Google Scholar] [CrossRef]
- Canny, J.; Reif, J. New lower bound techniques for robot motion planning problems. In Proceedings of the 28th Annual Symposium on Foundations of Computer Science (sfcs 1987), Los Angeles, CA, USA, 12–14 October 1987; pp. 49–60. [Google Scholar]
- DARPA. Darpa Urban Challenge. 2007. Available online: http://archive.darpa.mil/grandchallenge/ (accessed on 7 July 2021).
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the urban challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef] [Green Version]
- Bacha, A.; Bauman, C.; Faruque, R.; Fleming, M.; Terwelp, C.; Reinholtz, C.; Hong, D.; Wicks, A.; Alberi, T.; Anderson, D.; et al. Odin: Team victortango’s entry in the darpa urban challenge. J. Field Robot. 2008, 25, 467–492. [Google Scholar] [CrossRef]
- Hülsen, M.; Zöllner, J.M.; Weiss, C. Traffic intersection situation description ontology for advanced driver assistance. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 993–999. [Google Scholar]
- Zhao, L.; Ichise, R.; Yoshikawa, T.; Naito, T.; Kakinami, T.; Sasaki, Y. Ontology-based decision making on uncontrolled intersections and narrow roads. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 83–88. [Google Scholar]
- Kohlhaas, R.; Hammann, D.; Schamm, T.; Zöllner, J.M. Planning of high-level maneuver sequences on semantic state spaces. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 2090–2096. [Google Scholar]
- Kochenderfer, M.J. Decision Making Under Uncertainty: Theory and Application; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Brechtel, S.; Gindele, T.; Dillmann, R. Probabilistic decision-making under uncertainty for autonomous driving using continuous POMDPs. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), The Hague, The Netherlands, 24–26 September 2014; pp. 392–399. [Google Scholar]
- Liu, W.; Kim, S.W.; Pendleton, S.; Ang, M.H. Situation-aware decision making for autonomous driving on urban road using online POMDP. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 1126–1133. [Google Scholar]
- Hubmann, C.; Becker, M.; Althoff, D.; Lenz, D.; Stiller, C. Decision making for autonomous driving considering interaction and uncertain prediction of surrounding vehicles. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1671–1678. [Google Scholar]
- Werling, M.; Ziegler, J.; Kammel, S.; Thrun, S. Optimal trajectory generation for dynamic street scenarios in a frenet frame. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–8 May 2010; pp. 987–993. [Google Scholar]
- Xu, W.; Pan, J.; Wei, J.; Dolan, J.M. Motion planning under uncertainty for on-road autonomous driving. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 2507–2512. [Google Scholar]
- Damerow, F.; Eggert, J. Risk-aversive behavior planning under multiple situations with uncertainty. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas de Gran Canaria, Spain, 15–18 September 2015; pp. 656–663. [Google Scholar]
- Codevilla, F.; Müller, M.; López, A.; Koltun, V.; Dosovitskiy, A. End-to-end driving via conditional imitation learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4693–4700. [Google Scholar]
- Chen, J.; Yuan, B.; Tomizuka, M. Deep imitation learning for autonomous driving in generic urban scenarios with enhanced safety. arXiv 2019, arXiv:1903.00640. [Google Scholar]
- Hoel, C.J.; Driggs-Campbell, K.; Wolff, K.; Laine, L.; Kochenderfer, M.J. Combining planning and deep reinforcement learning in tactical decision making for autonomous driving. IEEE Trans. Intell. Veh. 2019, 5, 294–305. [Google Scholar] [CrossRef] [Green Version]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Practical search techniques in path planning for autonomous driving. Ann Arbor 2008, 1001, 18–80. [Google Scholar]
- Nash, A.; Daniel, K.; Koenig, S.; Felner, A. Thetaˆ*: Any-Angle Path Planning on Grids; AAAI: Los Angeles, CA, USA, 2007; Volume 7, pp. 1177–1183. [Google Scholar]
- Ferguson, D.; Stentz, A. Using interpolation to improve path planning: The Field D* algorithm. J. Field Robot. 2006, 23, 79–101. [Google Scholar] [CrossRef] [Green Version]
- Koenig, S.; Likhachev, M. D* lite. In Proceedings of the National Conference on Artificial Intelligence (AAAI), Edmonton, AB, Canada, 28 July–1 August 2002. [Google Scholar]
- Artunedo, A.; Villagra, J.; Godoy, J.; del Castillo, M.D. Motion planning approach considering localization uncertainty. IEEE Trans. Veh. Technol. 2020, 69, 5983–5994. [Google Scholar] [CrossRef]
- Lambert, A.; Gruyer, D. Safe path planning in an uncertain-configuration space. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No. 03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 4185–4190. [Google Scholar]
- Kavraki, L.E.; Kolountzakis, M.N.; Latombe, J.C. Analysis of probabilistic roadmaps for path planning. IEEE Trans. Robot. Autom. 1998, 14, 166–171. [Google Scholar] [CrossRef] [Green Version]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Technical Report TR 98-11; Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Ma, L.; Xue, J.; Kawabata, K.; Zhu, J.; Ma, C.; Zheng, N. Efficient sampling-based motion planning for on-road autonomous driving. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1961–1976. [Google Scholar] [CrossRef]
- Feraco, S.; Luciani, S.; Bonfitto, A.; Amati, N.; Tonoli, A. A local trajectory planning and control method for autonomous vehicles based on the RRT algorithm. In Proceedings of the 2020 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 18–20 November 2020; pp. 1–6. [Google Scholar]
- Ferguson, D.; Stentz, A. Anytime rrts. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5369–5375. [Google Scholar]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA, Millennium Conference. IEEE International Conference on Robotics and Automation, Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Ferguson, D.; Kalra, N.; Stentz, A. Replanning with rrts. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 1243–1248. [Google Scholar]
- Karaman, S.; Frazzoli, E. Optimal kinodynamic motion planning using incremental sampling-based methods. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 7681–7687. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Volpe, R.; Khosla, P. Manipulator control with superquadric artificial potential functions: Theory and experiments. IEEE Trans. Syst. Man Cybern. 1990, 20, 1423–1436. [Google Scholar] [CrossRef] [Green Version]
- Vadakkepat, P.; Tan, K.C.; Ming-Liang, W. Evolutionary artificial potential fields and their application in real time robot path planning. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No. 00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 1, pp. 256–263. [Google Scholar]
- Wolf, M.T.; Burdick, J.W. Artificial potential functions for highway driving with collision avoidance. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 3731–3736. [Google Scholar]
- Xu, Y.; Ma, Z.; Sun, J. Simulation of turning vehicles’ behaviors at mixed-flow intersections based on potential field theory. Transp. Transp. Dyn. 2019, 7, 498–518. [Google Scholar] [CrossRef]
- Koren, Y.; Borenstein, J. Potential field methods and their inherent limitations for mobile robot navigation. In Proceedings of International Conference on Robotics and Automation, Sacramento, CA, USA, 7–12 April 1991; pp. 1398–1404. [Google Scholar]
- Caijing, X.; Hui, C. A research on local path planning for antonomous vehicles based on improved APF method. Automot. Eng. 2013, 35, 808. [Google Scholar]
- Park, M.G.; Lee, M.C. A new technique to escape local minimum in artificial potential field based path planning. KSME Int. J. 2003, 17, 1876–1885. [Google Scholar] [CrossRef]
- Wang, P.; Gao, S.; Li, L.; Sun, B.; Cheng, S. Obstacle avoidance path planning design for autonomous driving vehicles based on an improved artificial potential field algorithm. Energies 2019, 12, 2342. [Google Scholar] [CrossRef] [Green Version]
- Le Gouguec, A.; Kemeny, A.; Berthoz, A.; Merienne, F. Artificial Potential Field Simulation Framework for Semi-Autonomous Car Conception. In Proceedings of the Driving Simulation Conference, Stuttgart, Germany, 6–8 September 2017; pp. 20–22. [Google Scholar]
- Quinlan, S.; Khatib, O. Elastic bands: Connecting path planning and control. In Proceedings of the IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; pp. 802–807. [Google Scholar]
- Hilgert, J.; Hirsch, K.; Bertram, T.; Hiller, M. Emergency path planning for autonomous vehicles using elastic band theory. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 2, pp. 1390–1395. [Google Scholar]
- Ararat, Ö.; Güvenç, B.A. Development of a collision avoidance algorithm using elastic band theory. IFAC Proc. Vol. 2008, 41, 8520–8525. [Google Scholar] [CrossRef]
- Song, X.; Cao, H.; Huang, J. Influencing factors research on vehicle path planning based on elastic bands for collision avoidance. SAE Int. J. Passeng.-Cars-Electron. Electr. Syst. 2012, 5, 625–637. [Google Scholar] [CrossRef]
- Song, X.; Cao, H.; Huang, J. Vehicle path planning in various driving situations based on the elastic band theory for highway collision avoidance. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2013, 227, 1706–1722. [Google Scholar] [CrossRef]
- Polack, P.; Altché, F.; d’Andréa Novel, B.; de La Fortelle, A. The kinematic bicycle model: A consistent model for planning feasible trajectories for autonomous vehicles? In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–17 June 2017; pp. 812–818. [Google Scholar]
- Normey-Rico, J.E.; Alcalá, I.; Gómez-Ortega, J.; Camacho, E.F. Mobile robot path tracking using a robust PID controller. Control. Eng. Pract. 2001, 9, 1209–1214. [Google Scholar] [CrossRef]
- Samuel, M.; Hussein, M.; Mohamad, M.B. A review of some pure-pursuit based path tracking techniques for control of autonomous vehicle. Int. J. Comput. Appl. 2016, 135, 35–38. [Google Scholar] [CrossRef]
- Buehler, M.; Iagnemma, K.; Singh, S. The 2005 DARPA Grand Challenge: The Great Robot Race; Springer: Berlin/Heidelberg, Germany, 2007; Volume 36. [Google Scholar]
- Hoffmann, G.M.; Tomlin, C.J.; Montemerlo, M.; Thrun, S. Autonomous automobile trajectory tracking for off-road driving: Controller design, experimental validation and racing. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 2296–2301. [Google Scholar]
- Makarem, L.; Gillet, D. Model predictive coordination of autonomous vehicles crossing intersections. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 1799–1804. [Google Scholar]
- Campos, G.R.; Falcone, P.; Wymeersch, H.; Hult, R.; Sjöberg, J. Cooperative receding horizon conflict resolution at traffic intersections. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 2932–2937. [Google Scholar]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path tracking control for autonomous vehicles based on an improved MPC. IEEE Access 2019, 7, 161064–161073. [Google Scholar] [CrossRef]
- Kapania, N.R.; Gerdes, J.C. Design of a feedback-feedforward steering controller for accurate path tracking and stability at the limits of handling. Veh. Syst. Dyn. 2015, 53, 1687–1704. [Google Scholar] [CrossRef] [Green Version]
- Vanholme, B.; Gruyer, D.; Lusetti, B.; Glaser, S.; Mammar, S. Highly automated driving on highways based on legal safety. IEEE Trans. Intell. Transp. Syst. 2012, 14, 333–347. [Google Scholar] [CrossRef]
- Trustonomy Project. 2020. Available online: https://h2020-trustonomy.eu/ (accessed on 7 July 2021).
- Resende, P.; Pollard, E.; Li, H.; Nashashibi, F. ABV-A Low Speed Automation Project to Study the Technical Feasibility of Fully Automated Driving. In Proceedings of the Workshop PAMM, Kumamoto, Japan, 9–10 November 2013. [Google Scholar]
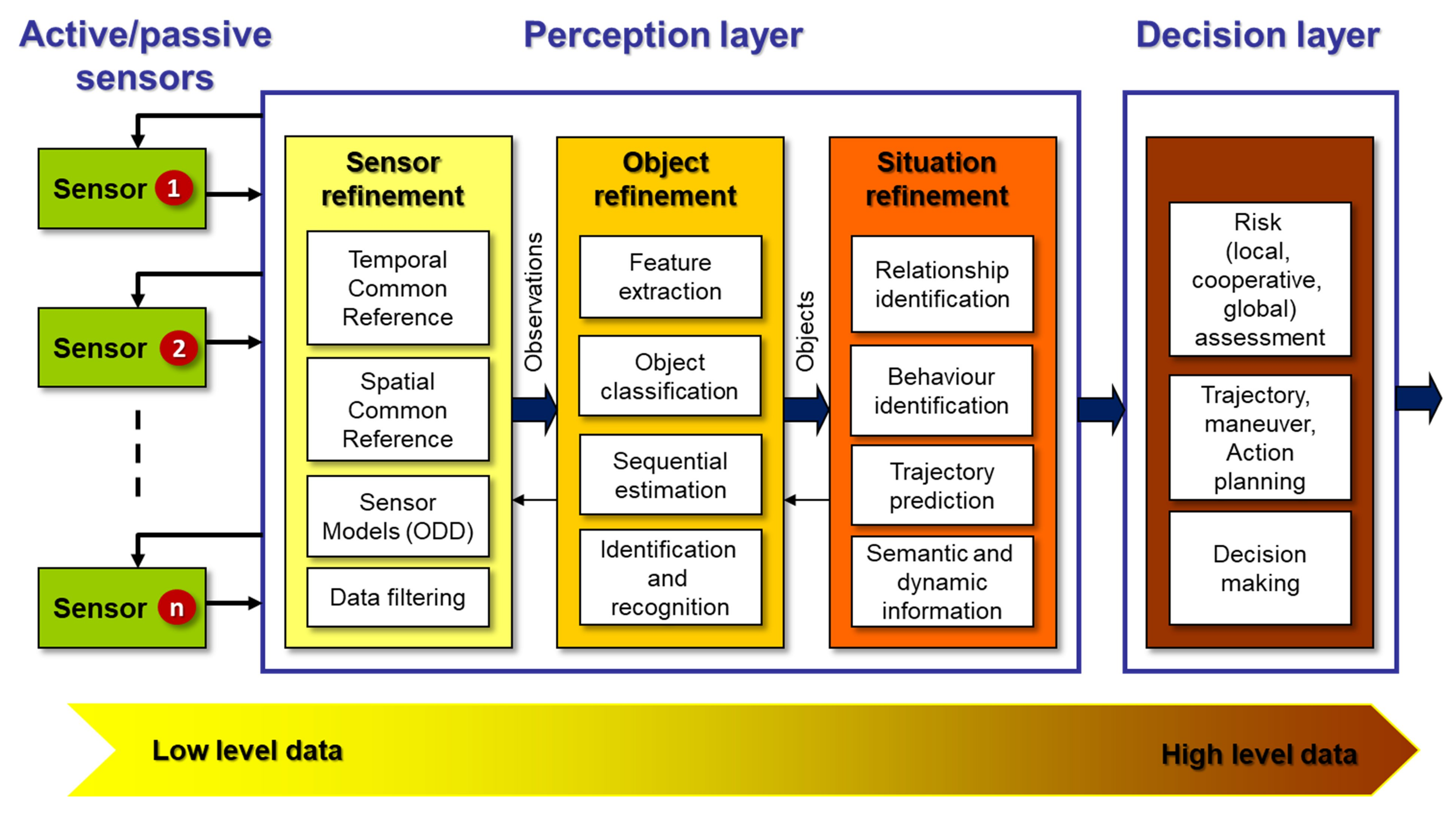
- Gruyer, D.; Magnier, V.; Hamdi, K.; Claussmann, L.; Orfila, O.; Rakotonirainy, A. Perception, information processing and modeling: Critical stages for autonomous driving applications. Annu. Rev. Control. 2017, 44, 323–341. [Google Scholar] [CrossRef]
- Caballero, W.N.; Ríos Insua, D.; Banks, D. Decision support issues in automated driving systems. Int. Trans. Oper. Res. 2021. Available online: http://xxx.lanl.gov/abs/https://onlinelibrary.wiley.com/doi/pdf/10.1111/itor.12936 (accessed on 7 July 2021). [CrossRef]
- The IEEE Global Initiative on Ethics of Autonomous and Intelligent Systems. Available online: https://standards.ieee.org/content/dam/ieee-standards/standards/web/documents/other/ead1e_embedding_values.pdf (accessed on 7 July 2021).
- Sattel, T.; Brandt, T. Ground vehicle guidance along collision-free trajectories using elastic bands. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 10 June 2005; pp. 4991–4996. [Google Scholar]
- Perrollaz, M.; Labayrade, R.; Gruyer, D.; Lambert, A.; Aubert, D. Proposition of generic validation criteria using stereo-vision for on-road obstacle detection. Int. J. Robot. Autom. 2014, 29, 65–87. [Google Scholar] [CrossRef]
- Gruyer, D.; Cord, A.; Belaroussi, R. Vehicle detection and tracking by collaborative fusion between laser scanner and camera. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 5207–5214. [Google Scholar]
- Gruyer, D.; Demmel, S.; Magnier, V.; Belaroussi, R. Multi-hypotheses tracking using the Dempster–Shafer theory, application to ambiguous road context. Inf. Fusion 2016, 29, 40–56. [Google Scholar] [CrossRef] [Green Version]
- Revilloud, M.; Gruyer, D.; Pollard, E. An improved approach for robust road marking detection and tracking applied to multi-lane estimation. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast City, Australia, 23–26 June 2013; pp. 783–790. [Google Scholar]
- Revilloud, M.; Gruyer, D.; Rahal, M.C. A new multi-agent approach for lane detection and tracking. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3147–3153. [Google Scholar]
- Ndjeng, A.N.; Gruyer, D.; Glaser, S.; Lambert, A. Low cost IMU–Odometer–GPS ego localization for unusual maneuvers. Inf. Fusion 2011, 12, 264–274. [Google Scholar] [CrossRef]
- Gruyer, D.; Belaroussi, R.; Revilloud, M. Accurate lateral positioning from map data and road marking detection. Expert Syst. Appl. 2016, 43, 1–8. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A review of motion planning for highway autonomous driving. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1826–1848. [Google Scholar] [CrossRef] [Green Version]
- Kant, K.; Zucker, S.W. Toward efficient trajectory planning: The path-velocity decomposition. Int. J. Robot. Res. 1986, 5, 72–89. [Google Scholar] [CrossRef]




| Notations | Description | Value |
|---|---|---|
| Indices | ||
| interval of time step | 0.25 (s) | |
| w | width of the road | 4 (m) |
| l | length of the vehicle | 4 (m) |
| h | width of the vehicle | 2.5 (m) |
| initial velocity of the vehicle | 10 (m/s) | |
| initial orientation of the vehicle | 0 (°) | |
| strength of internal force | 1 | |
| condition of equilibrium | 1 × 10−3 | |
| Problem parameters | ||
| p | identify the acting area of boundary force | 5 (m) |
| strength of external force from the lane | 0.02 | |
| strength of external force from the boundary | 0.002 | |
| strength of external force from the obstacles | 5 | |
| N | number of the nodes in exploring trajectory | 10 |
| maximal number of iterations | 20 | |
| State variables | ||
| the array of the parameters of the forces in the non-driving area at iteration i | [0,1] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Sainct, R.; Gruyer, D.; Orfila, O. Safe Vehicle Trajectory Planning in an Autonomous Decision Support Framework for Emergency Situations. Appl. Sci. 2021, 11, 6373. https://doi.org/10.3390/app11146373
Xu W, Sainct R, Gruyer D, Orfila O. Safe Vehicle Trajectory Planning in an Autonomous Decision Support Framework for Emergency Situations. Applied Sciences. 2021; 11(14):6373. https://doi.org/10.3390/app11146373
Chicago/Turabian StyleXu, Wei, Rémi Sainct, Dominique Gruyer, and Olivier Orfila. 2021. "Safe Vehicle Trajectory Planning in an Autonomous Decision Support Framework for Emergency Situations" Applied Sciences 11, no. 14: 6373. https://doi.org/10.3390/app11146373
APA StyleXu, W., Sainct, R., Gruyer, D., & Orfila, O. (2021). Safe Vehicle Trajectory Planning in an Autonomous Decision Support Framework for Emergency Situations. Applied Sciences, 11(14), 6373. https://doi.org/10.3390/app11146373








