Performance of Envelope Demodulation for Bearing Damage Detection on CWRU Accelerometric Data: Kurtogram and Traditional Indicators vs. Targeted a Posteriori Band Indicators
Abstract
:Featured Application
Abstract
1. Introduction
2. Methodology and Band Indicators
- Protrusion (protrugram [10]):
- Spectral L2/L1 sparsity (sparsogram [12]):where Lr{y[n]} is the mathematical definition of the r-norm of a signal y[n].
- Spectral Gini sparsity (Gini sparsogram [19]):where is the envelope spectrum ordered from the smallest to the largest value.
- Average negentropy (mean of negentropy and spectral negentropy—infogram [20]):where ne{y[n]} is the generic definition of negentropy of a signal y[n] if the (square of the) instantaneous energy flow in the signal is interpreted as a probability distribution.
- Kurtosis of the autocorrelation of the envelope spectrum (modified protrugram [28]):
3. Brief Description of the CWRU Bearing Data Center Test Rig
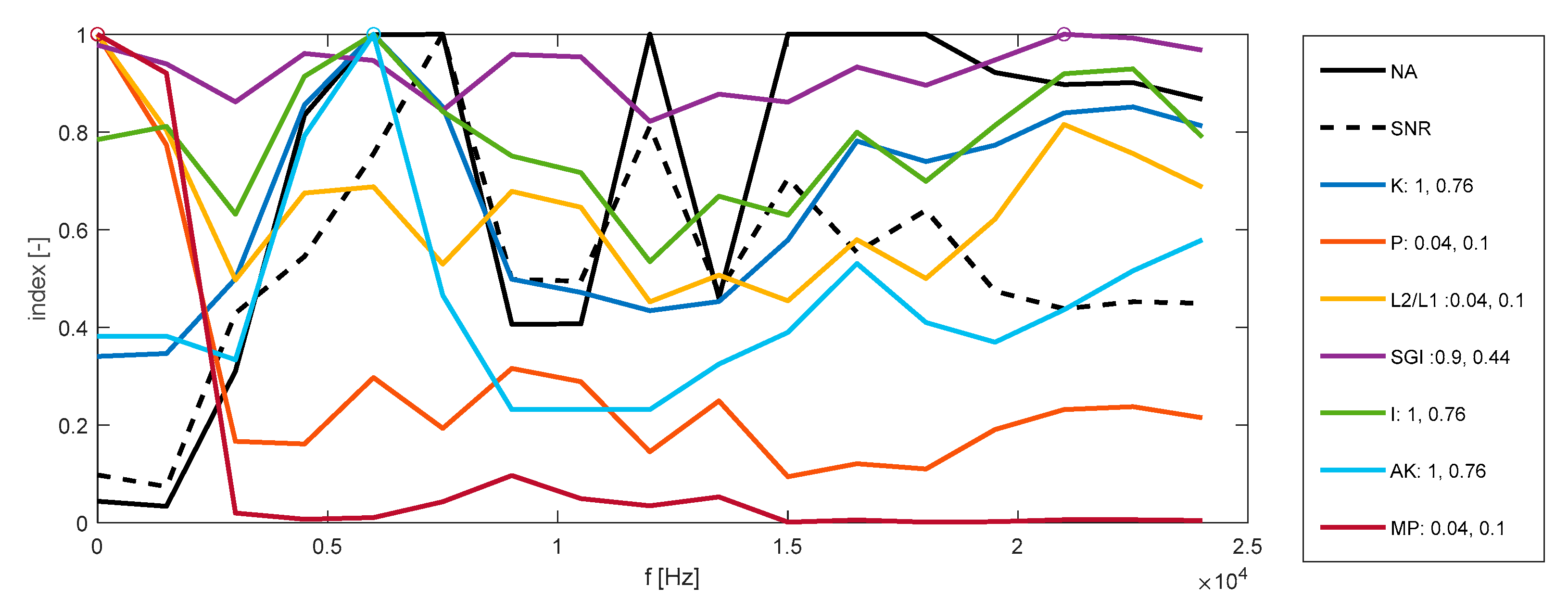
4. Results and Discussion
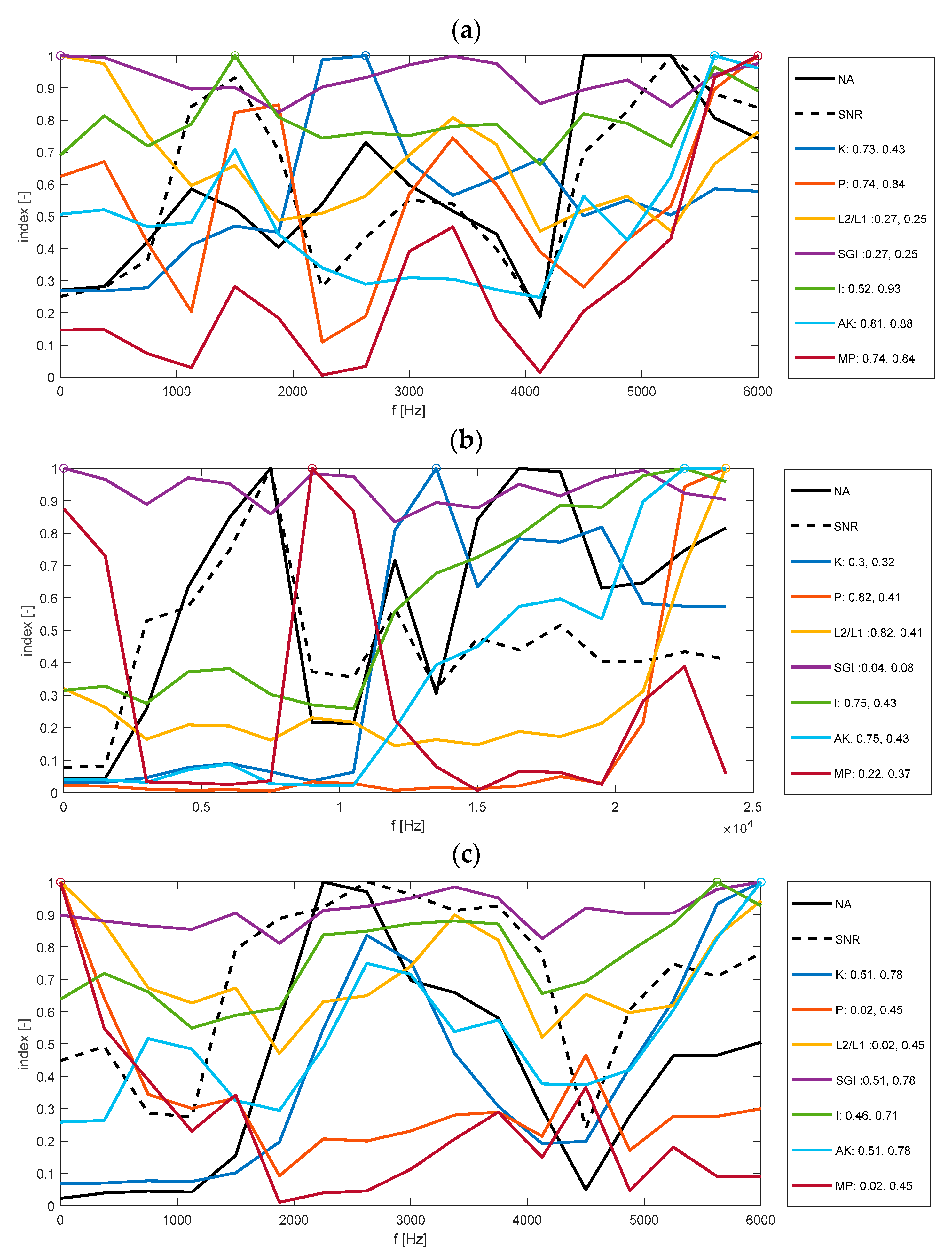
4.1. Acquisition IR014_2 (176FE)
4.2. Acquisition IR014_1 (275DE)
4.3. Acquisition IR014_3 (177FE)
4.4. Acquisition B021_0 (222DE), Fan End Bearing Featuring Ball Fault, Non Periodic Impulses
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Randall, R.B. Vibration-Based Condition Monitoring: Industrial, Aerospace and Automotive Applications, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-0-470-74785-8. [Google Scholar]
- Randall, R.B.; Antoni, J. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal. Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- McFadden, P.D.; Smith, J.D. Vibration monitoring of rolling element bearings by the high frequency resonance technique—A review. Tribol. Int 1984, 17, 3–10. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterizing non-stationary signals. Mech. Syst. Signal. Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal. Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal. Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Zimroz, R. Optimal filter design with progressive genetic algorithm for local damage detection in rolling bearings. Mech. Syst. Signal. Process. 2018, 102, 102–116. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an improved kurtogram method for fault diag-nosis of rolling element bearings. Mech. Syst. Signal. Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Barszcz, T.; JabŁoński, A. Analysis of Kurtogram performance in case of high level non-Gaussian noise. In Proceedings of the 16th International Congress on Sound and Vibration, Krakow, Poland, 5–9 July 2009. [Google Scholar]
- Barszcz, T.; JabŁoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal. Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Wang, D.; Peter, W.T.; Tsui, K.L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal. Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Peter, W.T.; Wang, D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement–Parts 1 and 2”. Mech. Syst. Signal. Process. 2013, 40, 499–519. [Google Scholar]
- Wang, D. Spectral L2/L1 norm: A new perspective for spectral kurtosis for characterizing non-stationary signals. Mech. Syst. Signal. Process. 2018, 104, 290–293. [Google Scholar] [CrossRef]
- Antoni, J. Cyclic spectral analysis of rolling-element bearing signals: Facts and fictions. J. Sound Vib. 2007, 304, 497–529. [Google Scholar] [CrossRef]
- Antoni, J. Cyclic spectral analysis in practice. Mech. Syst. Signal. Process. 2007, 21, 597–630. [Google Scholar] [CrossRef]
- Antoni, J.; Hanson, D. Detection of surface ships from interception of cyclostationary signature with the cyclic modulation coherence. IEEE J. Oceanic Eng. 2012, 37, 478–493. [Google Scholar] [CrossRef]
- Antoni, J.; Xin, G.; Hamzaoui, N. Fast computation of the spectral correlation. Mech. Syst. Signal. Process. 2017, 92, 248–277. [Google Scholar] [CrossRef]
- Wang, D. Some further thoughts about spectral kurtosis, spectral L2/L1 norm, spectral smoothness index and spectral Gini index for characterizing repetitive transients. Mech. Syst. Signal. Process. 2018, 108, 360–368. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal. Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B.; Feng, F.; Jiang, P. Optimal Resonant Band Demodulation Based on an Improved Correlated Kurtosis and Its Application in Bearing Fault Diagnosis. Sensors 2017, 17, 360. [Google Scholar] [CrossRef] [PubMed]
- McDonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal. Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Borghesani, P. The envelope-based cyclic periodogram. Mech. Syst. Signal. Process. 2015, 58, 245–270. [Google Scholar] [CrossRef]
- Smith, W.A.; Borghesani, P.; Ni, Q.; Wang, K.; Peng, Z. Optimal demodulation-band selection for envelope-based diagnostics: A comparative study of traditional and novel tools. Mech. Syst. Signal. Process. 2019, 134, 106303. [Google Scholar] [CrossRef]
- Antoni, J.; Borghesani, P. A statistical methodology for the design of condition indicators. Mech. Syst. Signal. Process. 2019, 114, 290–327. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The Autogram: An effective approach for selecting the opti-mal demodulation band in rolling element bearings diagnosis. Mech. Syst. Signal. Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Daga, A.P.; Fasana, A.; Garibaldi, L.; Marchesiello, S. Fast Computation of the Autogram for the Detection of Transient Faults. In European Workshop on Structural Health Monitoring; Springer International Publishing: Cham, Switzerland, 2020; pp. 469–479. [Google Scholar] [CrossRef]
- Kruczek, P.; Obuchowski, J. Modified Protrugram Method for Damage Detection in Bearing Operating Under Impulsive Load. In Cyclostationarity: Theory and Methods III; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Ho, D.; Randall, R.B. Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals. Mech. Syst. Signal. Process. 2000, 14, 763–788. [Google Scholar] [CrossRef]
- Kim, S.; An, D.; Choi, J.-H. Diagnostics 101: A Tutorial for Fault Diagnostics of Rolling Element Bearing Using Envelope Analysis in MATLAB. Appl. Sci. 2020, 10, 7302. [Google Scholar] [CrossRef]
- Borghesani, P.; Pennacchi, P.; Chatterton, S. The relationship between kurtosis- and envelope-based indexes for the diagnostic of rolling element bearings. Mech. Syst. Signal. Process. 2014, 43, 25–43. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 15 June 2021).
- Smith, W.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. and Signal. Process. 2015, 64, 100–113. [Google Scholar] [CrossRef]
- Daga, A.P.; Fasana, A.; Marchesiello, S.; Garibaldi, L. Machine Vibration Monitoring for Diagnostics through Hypothesis Testing. Information 2019, 10, 204. [Google Scholar] [CrossRef] [Green Version]
- Castellani, F.; Garibaldi, L.; Daga, A.P.; Astolfi, D.; Natili, F. Diagnosis of Faulty Wind Turbine Bearings Using Tower Vibration Measurements. Energies 2020, 13, 1474. [Google Scholar] [CrossRef] [Green Version]
- Daga, A.P.; Fasana, A.; Marchesiello, S.; Garibaldi, L. The Politecnico di Torino rolling bearing test rig: Description and analysis of open access data. Mech. Syst. Signal. Process. 2019, 120, 252–273. [Google Scholar] [CrossRef]
- Antoni, J.; Griffaton, J.; André, H.; Avendaño-Valencia, L.D.; Bonnardot, F.; Cardona-Morales, O.; Castellanos-Dominguez, G.; Daga, A.P.; Leclère, Q.; Vicuña, C.M.; et al. Feedback on the surveillance 8 challenge: Vibration-based diagnosis of a safran aircraft engine. Mech. Syst. Signal. Process. 2017, 97, 112–144. [Google Scholar] [CrossRef]
- Daga, A.P.; Garibaldi, L. GA-Adaptive Template Matching for Offline Shape Motion Tracking Based on Edge Detection: IAS Estimation from the SURVISHNO 2019 Challenge Video for Machine Diagnostics Purposes. Algorithms 2020, 13, 33. [Google Scholar] [CrossRef] [Green Version]
- André, H.; Leclère, Q.; Anastasio, D.; Benaïcha, Y.; Billon, K.; Birem, M.; Bonnardot, F.; Chin, Z.Y.; Combet, F.; Daems, P.J.; et al. Using a smartphone camera to analyse rotating and vibrating systems: Feedback on the SURVISHNO 2019 contest. Mech. Syst. Signal. Process. 2021, 154, 107553. [Google Scholar] [CrossRef]
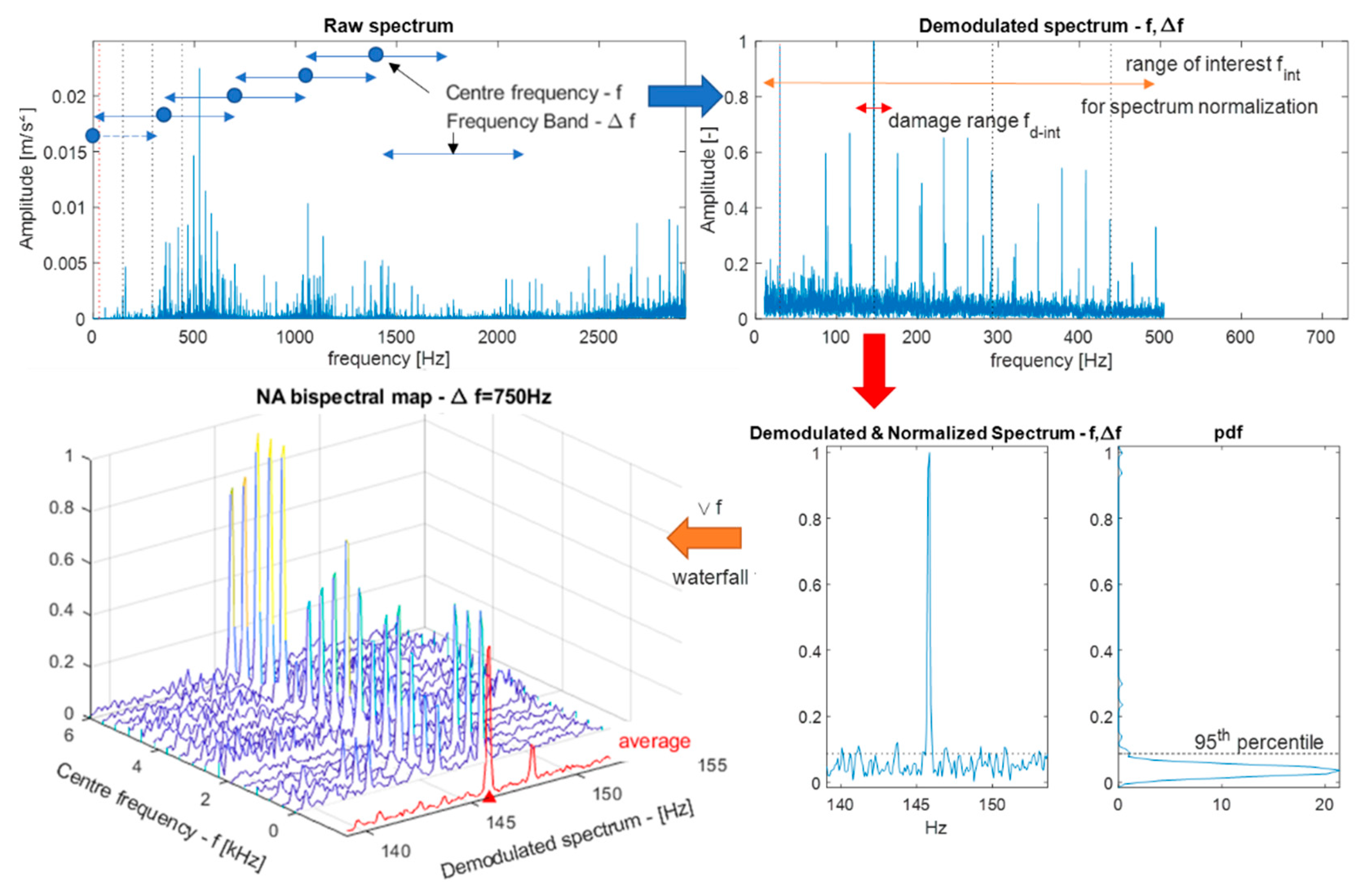
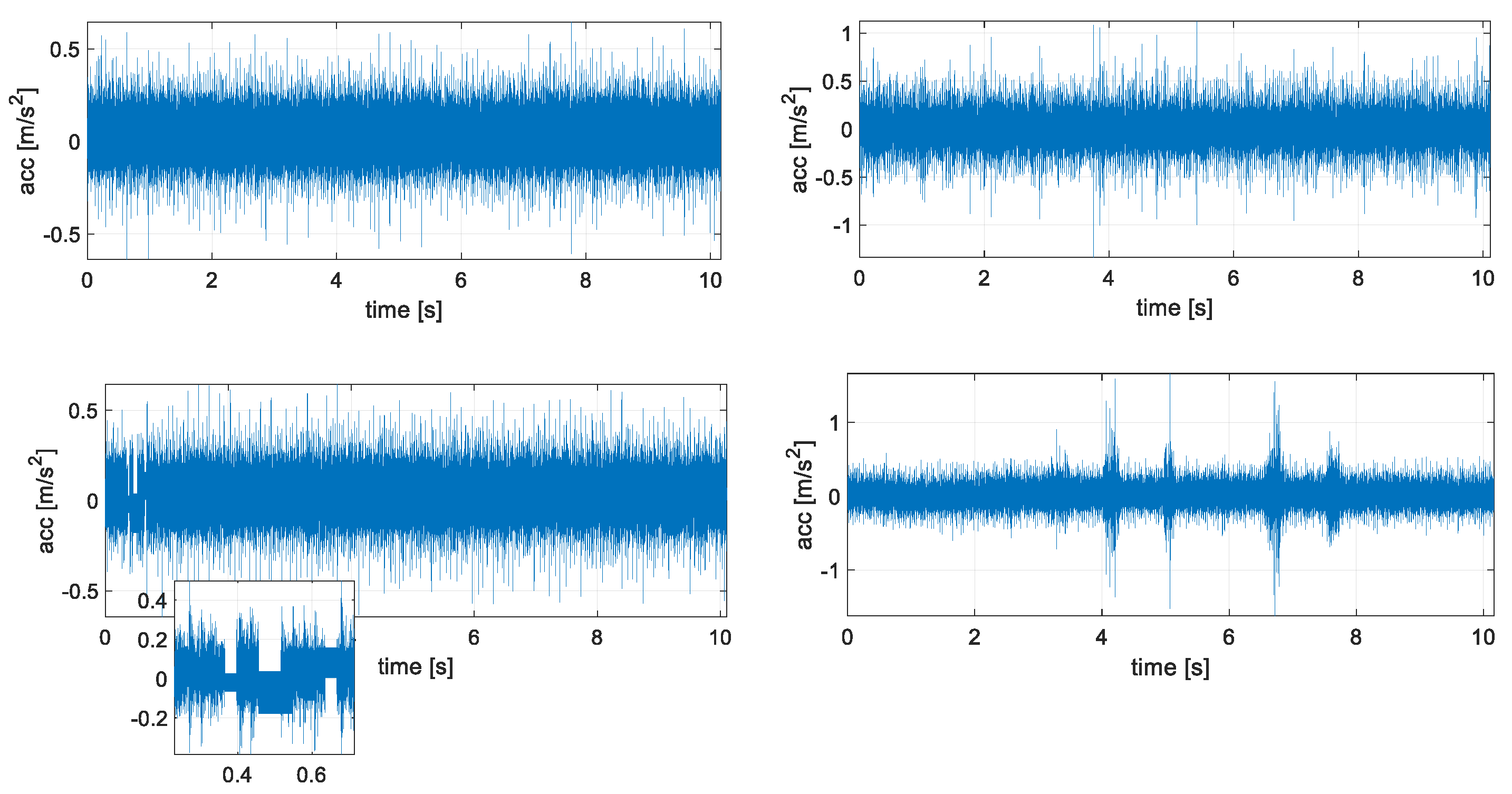
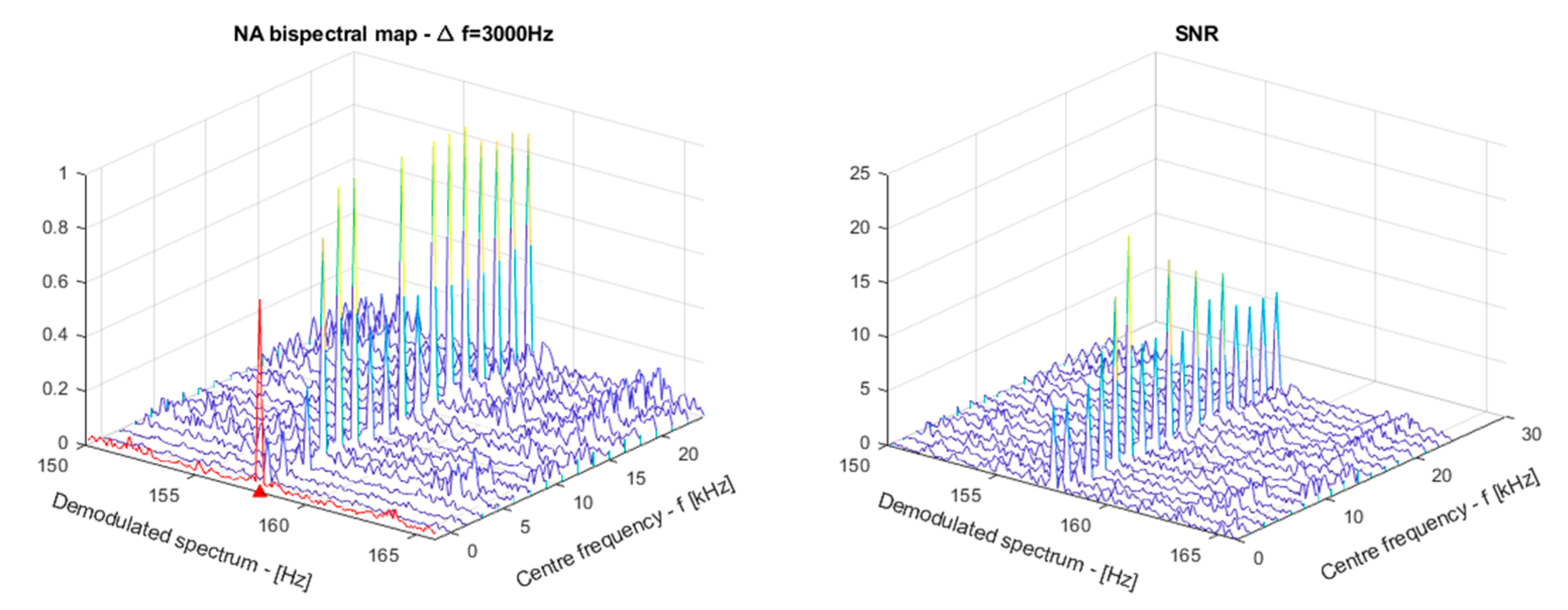
| Location | Name | Fault Frequencies (Multiple of Shaft Speed) | |||
|---|---|---|---|---|---|
| BPFI | BPFO | FTF | BSF | ||
| Drive End | 6205-2RS JEM | 5.415 | 3.585 | 0.3983 | 2.357 |
| Fan End | 6203-2RS JEM | 4.947 | 3.053 | 0.3816 | 1.994 |
| Name | Code | Acc. Location | Damage Location | Damage Size | Fs | Details |
|---|---|---|---|---|---|---|
| IR014_2 | 176 | FE | DE-IR | 0.014″ | 48 ksps | Good Acquisition |
| IR014_1 | 275 | DE | FE-IR | 0.014″ | 12 ksps | Impulsive noise |
| IR014_3 | 177 | FE | DE-IR | 0.014″ | 48 ksps | Electrical noise |
| B021_0 | 222 | DE | DE-B | 0.021″ | 12 ksps | Non-periodic impulses |
| Acquisition: | 176FE | 275DE | 177FE | 222DE | Avg | |
|---|---|---|---|---|---|---|
| dE | 0.71 | 0.59 | 0.58 | 0.18 | - | |
| iE | K | 0.88 | 0.58 | 0.31 | 0.645 | 0.604 |
| P | 0.07 | 0.79 | 0.615 | 0.235 | 0.428 | |
| L2/L1 | 0.07 | 0.26 | 0.615 | 0.235 | 0.295 | |
| SGI | 0.67 | 0.26 | 0.06 | 0.645 | 0.409 | |
| I | 0.88 | 0.725 | 0.59 | 0.585 | 0.695 | |
| AK | 0.88 | 0.845 | 0.59 | 0.645 | 0.740 | |
| MP | 0.07 | 0.79 | 0.295 | 0.235 | 0.348 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alessandro Paolo, D.; Luigi, G.; Alessandro, F.; Stefano, M. Performance of Envelope Demodulation for Bearing Damage Detection on CWRU Accelerometric Data: Kurtogram and Traditional Indicators vs. Targeted a Posteriori Band Indicators. Appl. Sci. 2021, 11, 6262. https://doi.org/10.3390/app11146262
Alessandro Paolo D, Luigi G, Alessandro F, Stefano M. Performance of Envelope Demodulation for Bearing Damage Detection on CWRU Accelerometric Data: Kurtogram and Traditional Indicators vs. Targeted a Posteriori Band Indicators. Applied Sciences. 2021; 11(14):6262. https://doi.org/10.3390/app11146262
Chicago/Turabian StyleAlessandro Paolo, Daga, Garibaldi Luigi, Fasana Alessandro, and Marchesiello Stefano. 2021. "Performance of Envelope Demodulation for Bearing Damage Detection on CWRU Accelerometric Data: Kurtogram and Traditional Indicators vs. Targeted a Posteriori Band Indicators" Applied Sciences 11, no. 14: 6262. https://doi.org/10.3390/app11146262
APA StyleAlessandro Paolo, D., Luigi, G., Alessandro, F., & Stefano, M. (2021). Performance of Envelope Demodulation for Bearing Damage Detection on CWRU Accelerometric Data: Kurtogram and Traditional Indicators vs. Targeted a Posteriori Band Indicators. Applied Sciences, 11(14), 6262. https://doi.org/10.3390/app11146262








