Analysis of the Possibility of Using Various Time-Frequency Transformation Methods to Barkhausen Noise Characterization for the Need of Magnetic Anisotropy Evaluation in Steels
Abstract
1. Introduction
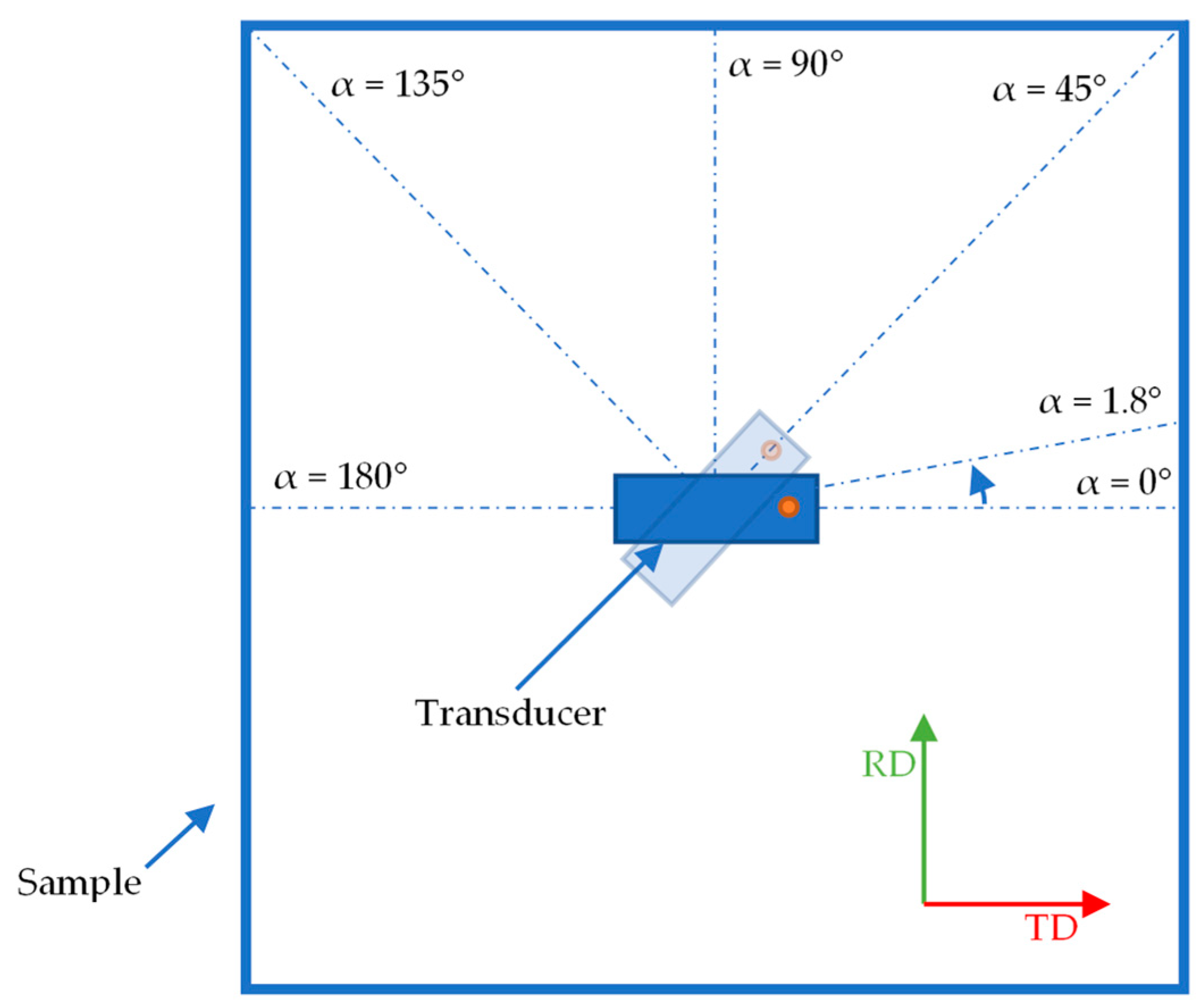
2. Experimental Setup
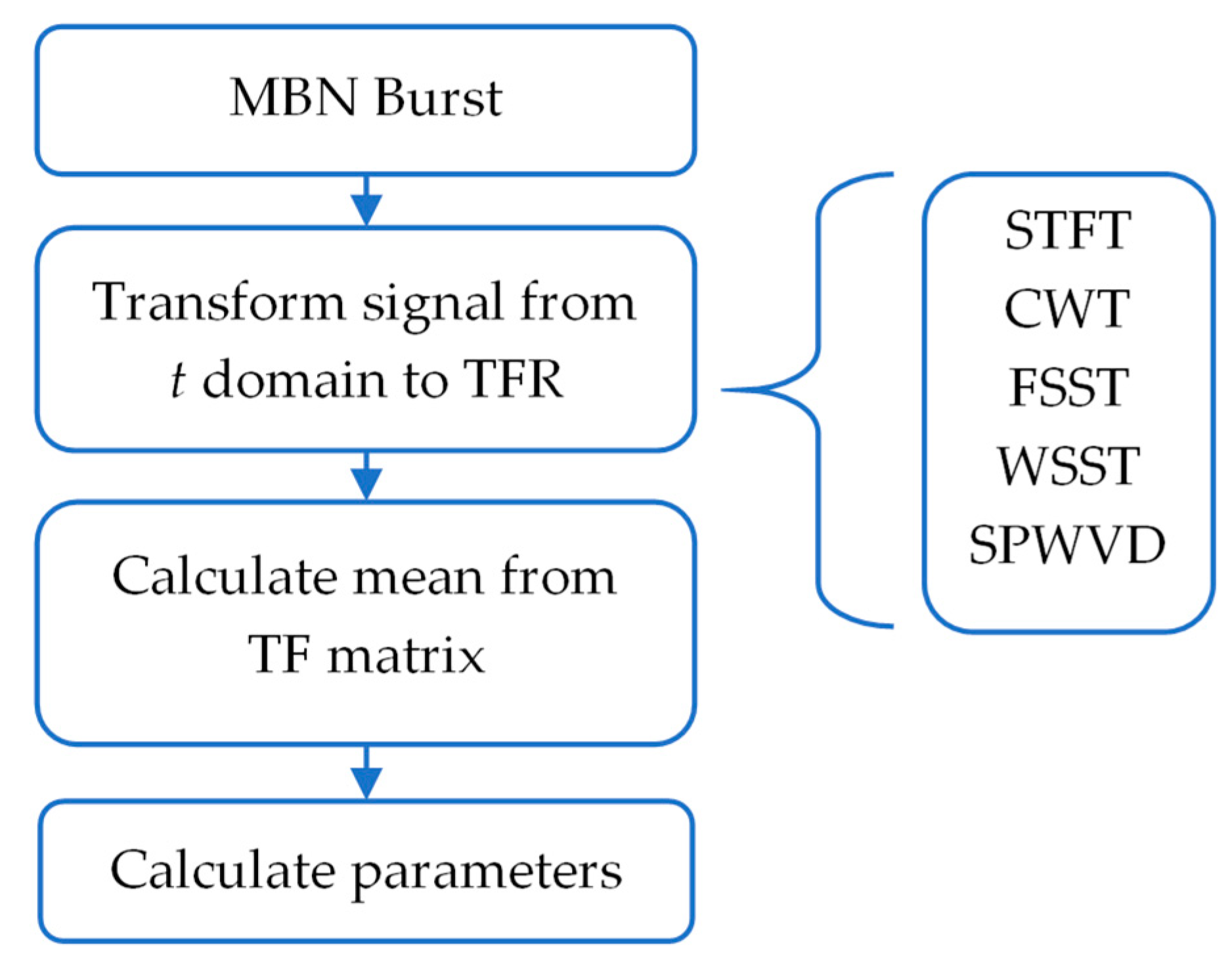
3. TF Transforms and Results
3.1. TF Analysis
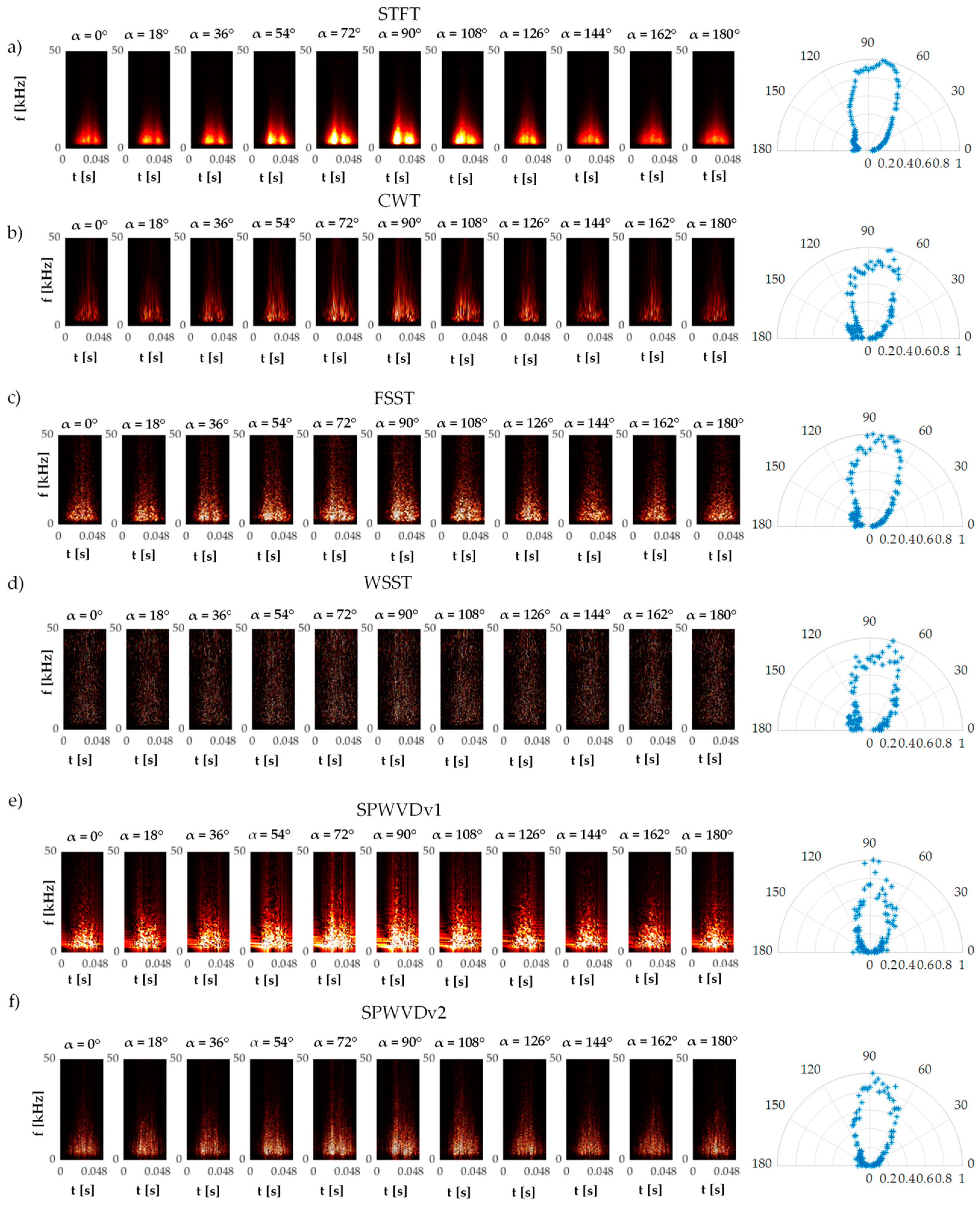
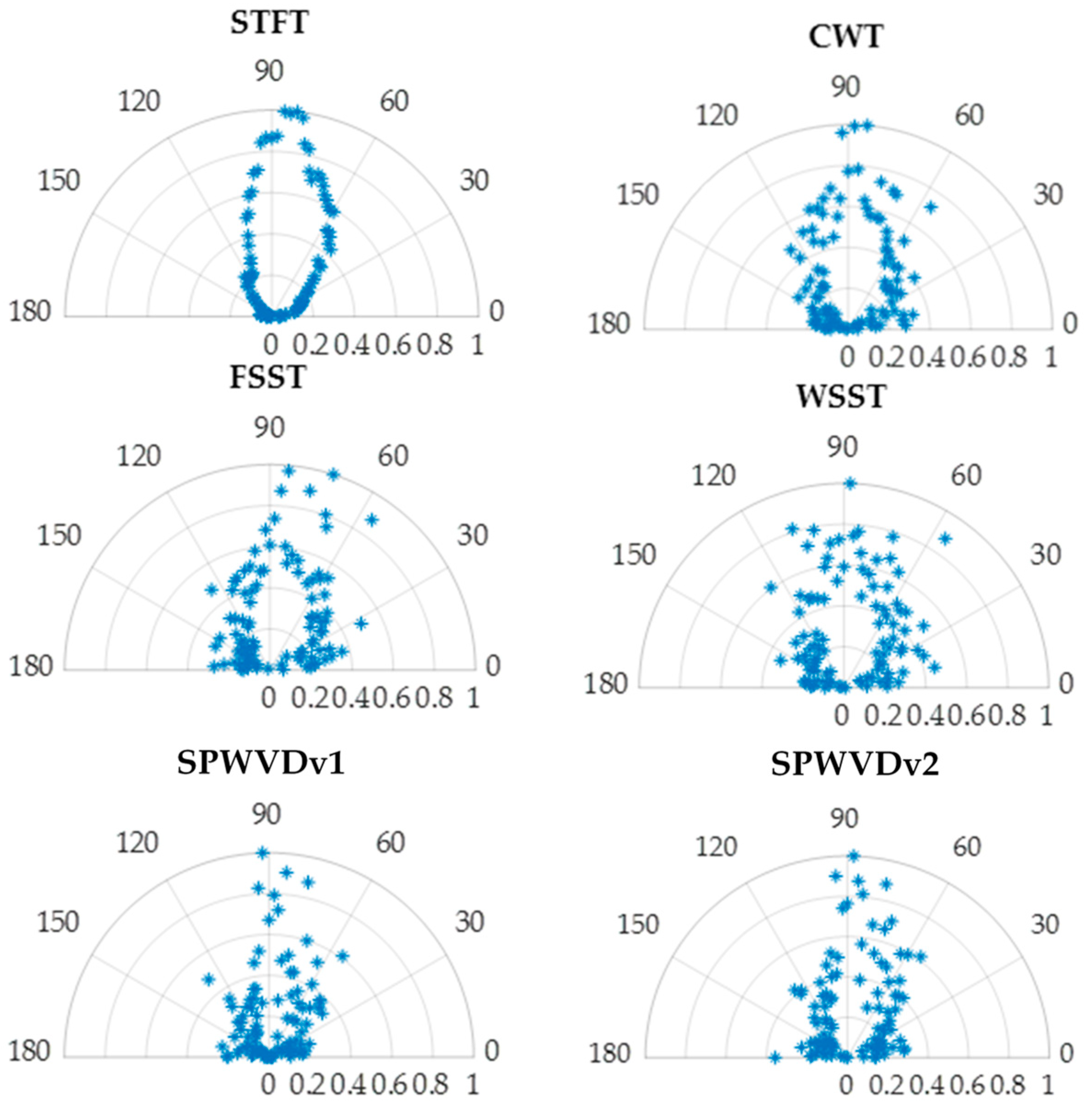
3.2. Qualitative Data Analysis Results
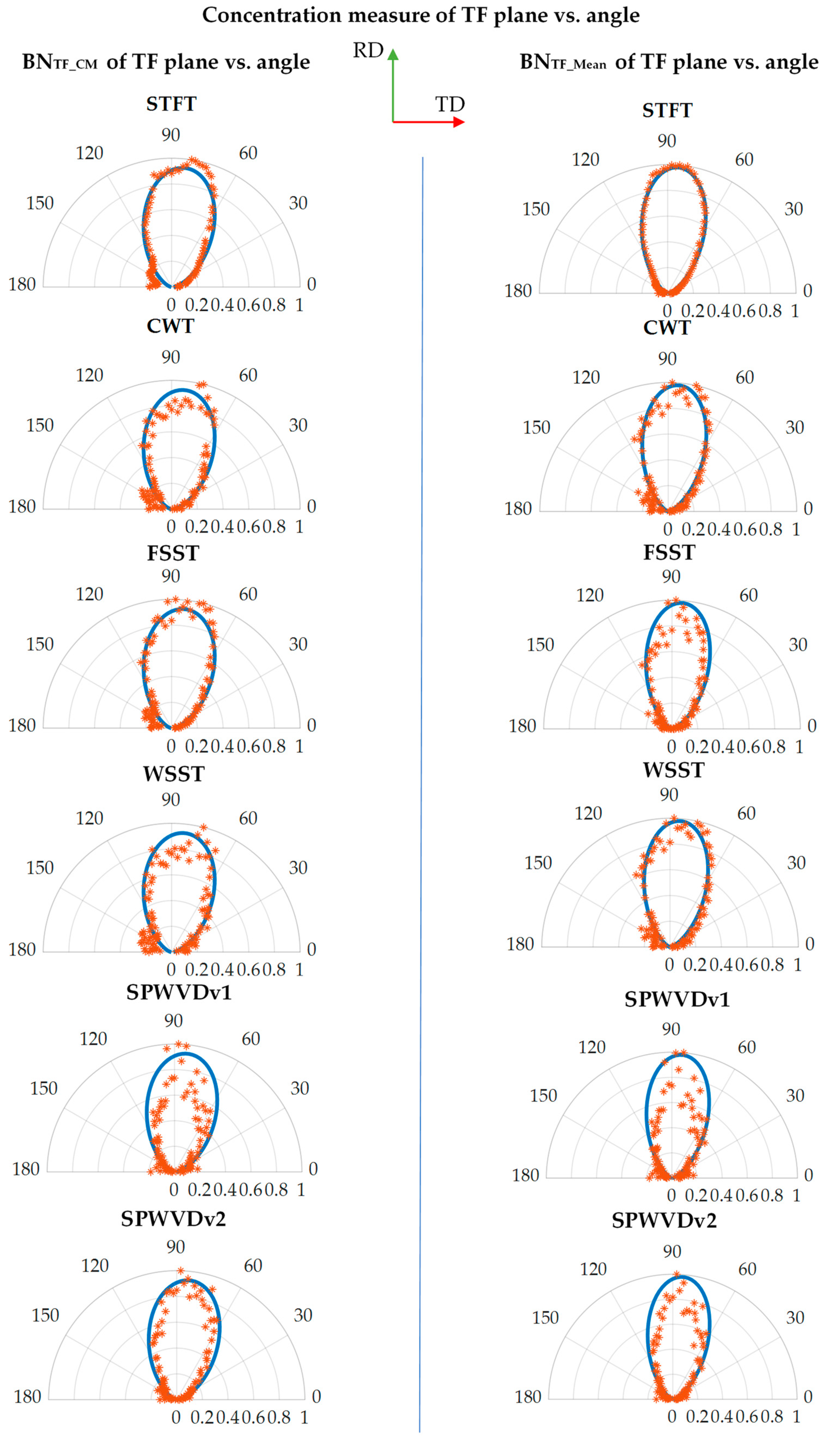
3.3. Qualitative Data Analysis
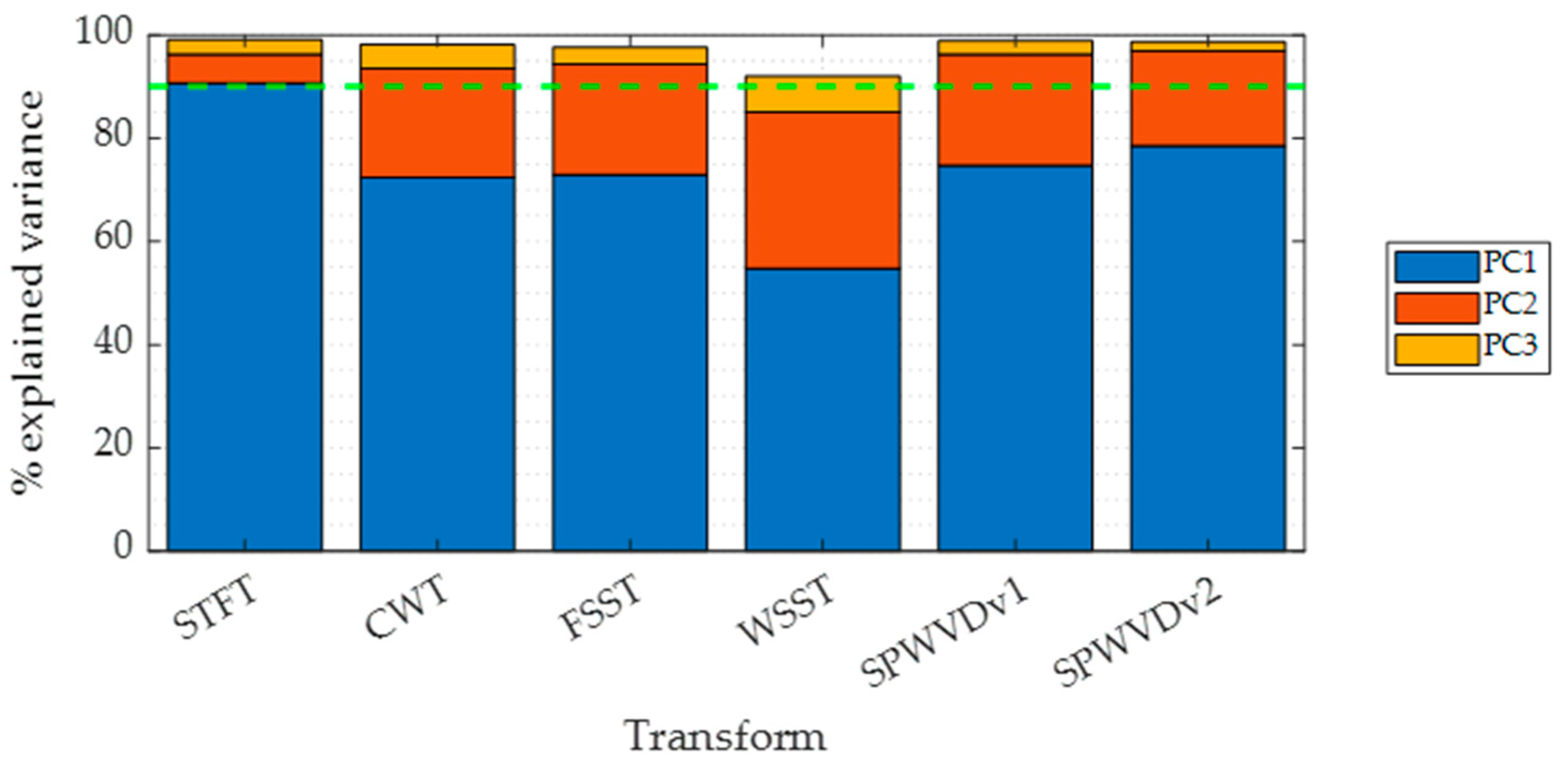
3.4. Time-Frequency Representations Robustness Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shilling, J.; Houze, G. Magnetic Properties and Domain Structure in Grain-Oriented 3% Si-Fe. IEEE Trans. Magn. 1974, 10, 195–223. [Google Scholar] [CrossRef]
- Jiles, D. Introduction to Magnetism and Magnetic Materials, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-1-4822-3887-7. [Google Scholar]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials, 2nd ed.; IEEE: Piscataway Township, NJ, USA; Wiley: Hoboken, NJ, USA, 2009; ISBN 978-0-471-47741-9. [Google Scholar]
- Roskosz, M.; Fryczowski, K.; Tuz, L.; Wu, J.; Schabowicz, K.; Logoń, D. Analysis of the Possibility of Plastic Deformation Characterisation in X2CrNi18-9 Steel Using Measurements of Electromagnetic Parameters. Materials 2021, 14, 2904. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.X.; Yan, R. Wavelets: Theory and Applications for Manufacturing; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-1544-3. [Google Scholar]
- Oberlin, T.; Meignen, S.; Perrier, V. The Fourier-Based Synchrosqueezing Transform. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 315–319. [Google Scholar]
- Meignen, S.; Oberlin, T.; Pham, D.-H. Synchrosqueezing Transforms: From Low- to High-Frequency Modulations and Perspectives. Comptes Rendus Phys. 2019, 20, 449–460. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed Wavelet Transforms: An Empirical Mode Decomposition-like Tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Debnath, L. Wavelet Transforms and Their Applications; Birkhäuser Boston: Boston, MA, USA, 2002; ISBN 978-1-4612-6610-5. [Google Scholar]
- Taebi, A.; Mansy, H.A. Analysis of Seismocardiographic Signals Using Polynomial Chirplet Transform and Smoothed Pseudo Wigner-Ville Distribution. In Proceedings of the 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 2 December 2017; pp. 1–6. [Google Scholar]
- Boashash, B.; Ouelha, S. Automatic Signal Abnormality Detection Using Time-Frequency Features and Machine Learning: A Newborn EEG Seizure Case Study. Knowl. Based Syst. 2016, 106, 38–50. [Google Scholar] [CrossRef]
- Boczar, T.; Zmarzły, D.; Kozioł, M.; Wotzka, D. The Application of Time-Frequency Ridge Transformation for the Analysis of Infrasound Signals Generated by Wind Turbines. Appl. Acoust. 2021, 177, 107961. [Google Scholar] [CrossRef]
- Herrera, R.H.; Han, J. Van Der Baan, M. Applications of the Synchrosqueezing Transform in Seismic Time-Frequency Analysis. Geophysics 2014, 79, V55–V64. [Google Scholar] [CrossRef]
- Gholtashi, S.; Siahsar, M.A.N.; Kahoo, A.R.; Marvi, H.; Ahmadifard, A. Synchrosqueezing-Based Transform and Its Application in Seismic Data Analysis. Iran. J. Oil Gas Sci. Technol. 2015, 4, 14. [Google Scholar]
- Wiciak, P.; Cascante, G.; Polak, M.A. Novel Application of Wavelet Synchrosqueezed Transform (WSST) in Laser-Vibrometer Measurements for Condition Assessment of Cementitious Materials. NDT E Int. 2021, 120, 102424. [Google Scholar] [CrossRef]
- Mostafa, N.; Loendersloot, R.; Maio, D.D.; Tinga, T. Application of Wavelet Synchro-Squeezed Transform (WSST) Method to Railway Bridge Health Monitoring. In Proceedings of the EURODYN 2020—XI International Conference on Structural Dynamics: Proceedings, Athens, Grace, 23–26 November 2020; pp. 1388–1396. [Google Scholar]
- Fryczowski, K.; Roskosz, M. Metody ilościowej analizy szumu napięciowego Barkhausena. Weld. Technol. Rev. 2016, 88. [Google Scholar] [CrossRef]
- Padovese, L.; Martin, N.; Millioz, F. Time-Frequency and Time-Scale Analysis of Barkhausen Noise Signals. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 577–588. [Google Scholar] [CrossRef]
- Maciusowicz, M.; Psuj, G. Use of Time-Dependent Multispectral Representation of Magnetic Barkhausen Noise Signals for the Needs of Non-Destructive Evaluation of Steel Materials. Sensors 2019, 19, 1443. [Google Scholar] [CrossRef] [PubMed]
- Maciusowicz, M.; Psuj, G. Time-Frequency Analysis of Barkhausen Noise for the Needs of Anisotropy Evaluation of Grain-Oriented Steels. Sensors 2020, 20, 768. [Google Scholar] [CrossRef]
- Maciusowicz, M.; Psuj, G. Use of Time-Frequency Representation of Magnetic Barkhausen Noise for Evaluation of Easy Magnetization Axis of Grain-Oriented Steel. Materials 2020, 13, 3390. [Google Scholar] [CrossRef] [PubMed]
- Miesowicz, K.; Staszewski, W.J.; Korbiel, T. Analysis of Barkhausen Noise Using Wavelet-Based Fractal Signal Processing for Fatigue Crack Detection. Int. J. Fatigue 2016, 83, 109–116. [Google Scholar] [CrossRef]
- Maass, P.; Teschke, G.; Willmann, W.; Wollmann, G. Detection and Classification of Material Attributes-a Practical Application of Wavelet Analysis. IEEE Trans. Signal Process. 2000, 48, 2432–2438. [Google Scholar] [CrossRef]
- Kownacki, C. Wavelet Analysis of Barkhausen Noise in Reconstructing Distributions of Residual Stress. Available online: https://www.scientific.net/SSP.144.112 (accessed on 29 March 2019).
- De Campos, M.F.; Campos, M.A.; Landgraf, F.J.G.; Padovese, L.R. Anisotropy Study of Grain Oriented Steels with Magnetic Barkhausen Noise. J. Phys. Conf. Ser. 2011, 303, 012020. [Google Scholar] [CrossRef]
- Espina-Hernández, J.H.; Pérez-Benítez, J.A.; Caleyo, F.; Baudin, T.; Helbert, A.L.; Hallen, J.M. Barkhausen Noise Measurements Give Direct Observation of Magnetocrystalline Anisotropy Energy in Ferromagnetic Polycrystals. J. Phys. D Appl. Phys. 2013, 46, 392001. [Google Scholar] [CrossRef]
- Pérez-Benítez, J.A.; Espina-Hernández, J.H.; Man, T.L.; Caleyo, F.; Hallen, J.M. Identification of Different Processes in Magnetization Dynamics of API Steels Using Magnetic Barkhausen Noise. J. Phys. D Appl. Phys. 2015, 48, 295002. [Google Scholar] [CrossRef]
- Łopato, P.; Psuj, G.; Herbko, M.; Maciusowicz, M. Evaluation of Stress in Steel Structures Using Electromagnetic Methods Based on Utilization of Microstrip Antenna Sensor and Monitoring of AC Magnetization Process. Informatyka Automatyka, Pomiary Gospodarce Ochronie Środowiska 2016, 6, 32–36. [Google Scholar] [CrossRef]
- Boashash, B. Time-Frequency Signal Analysis and Processing—A Comprehensive Reference, 2ed ed.; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-12-398499-9. [Google Scholar]
- Zieliński, T.P. Cyfrowe Przetwarzanie Sygnałów; Wydawnictwa Komunikacji i Łączności sp. z o.o.: Warszawa, Poland, 2014; ISBN 978-83-206-1640-8. [Google Scholar]
- Scholl, S. Fourier, Gabor, Morlet or Wigner: Comparison of Time-Frequency Transforms. arXiv 2021, arXiv:2101.06707 [eess]. [Google Scholar]
- Sandsten, M. Time-Frequency Analysis of Time-Varying Signals and Non-Stationary Processes, an Introduction; Lund University: Lund, Sweden, 2018. [Google Scholar]
- Szmajda, M.; Górecki, K.; Mroczka, J. Gabor transform, spwvd, gabor-wigner transform and wavelet transform—Tools for power quality monitoring. Metrol. Meas. Syst. 2010, 17, 383–396. [Google Scholar] [CrossRef]
- Pérez-Benitez, J.A.; Padovese, L.R.; Capó-Sánchez, J.; Anglada-Rivera, J. Investigation of the Magnetic Barkhausen Noise Using Elementary Signals Parameters in 1000 Commercial Steel. J. Magn. Magn. Mater. 2003, 263, 72–77. [Google Scholar] [CrossRef]


| Steel Parameters | |
|---|---|
| Length/Width | 150 mm |
| Thickness | 0.23 mm |
| Lossiness | 1.10 W/kg |
| Induction | 1.80 T |
| Transformation | Time (s) |
|---|---|
| STFT | 0.005556 |
| Wavelet | 0.073326 |
| FSST | 0.507287 |
| WSST | 0.634261 |
| SPWVDv1 | 0.175987 |
| SPWVDv2 | 0.219765 |
| Component | Model |
|---|---|
| CPU | AMD Ryzen 7 1800X Eight-Core 3.60 Hz |
| RAM | 32 GB 2900 MHz |
| GPU | GeForce GTX 1660 6 GB |
| HDD | ADATA XPG SX 8200PNP M.2 |
| Feature | Formula | |
|---|---|---|
| Concentration Measure | (6) | |
| Mean | (7) | |
| Coefficient of determination | (8) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maciusowicz, M.; Psuj, G. Analysis of the Possibility of Using Various Time-Frequency Transformation Methods to Barkhausen Noise Characterization for the Need of Magnetic Anisotropy Evaluation in Steels. Appl. Sci. 2021, 11, 6193. https://doi.org/10.3390/app11136193
Maciusowicz M, Psuj G. Analysis of the Possibility of Using Various Time-Frequency Transformation Methods to Barkhausen Noise Characterization for the Need of Magnetic Anisotropy Evaluation in Steels. Applied Sciences. 2021; 11(13):6193. https://doi.org/10.3390/app11136193
Chicago/Turabian StyleMaciusowicz, Michal, and Grzegorz Psuj. 2021. "Analysis of the Possibility of Using Various Time-Frequency Transformation Methods to Barkhausen Noise Characterization for the Need of Magnetic Anisotropy Evaluation in Steels" Applied Sciences 11, no. 13: 6193. https://doi.org/10.3390/app11136193
APA StyleMaciusowicz, M., & Psuj, G. (2021). Analysis of the Possibility of Using Various Time-Frequency Transformation Methods to Barkhausen Noise Characterization for the Need of Magnetic Anisotropy Evaluation in Steels. Applied Sciences, 11(13), 6193. https://doi.org/10.3390/app11136193







