Considerations about Parameters Estimation into a Minimum Variance Control System
Abstract
:1. Introduction
2. Analytical Demonstration Based on Minimum Variance Control Law Design
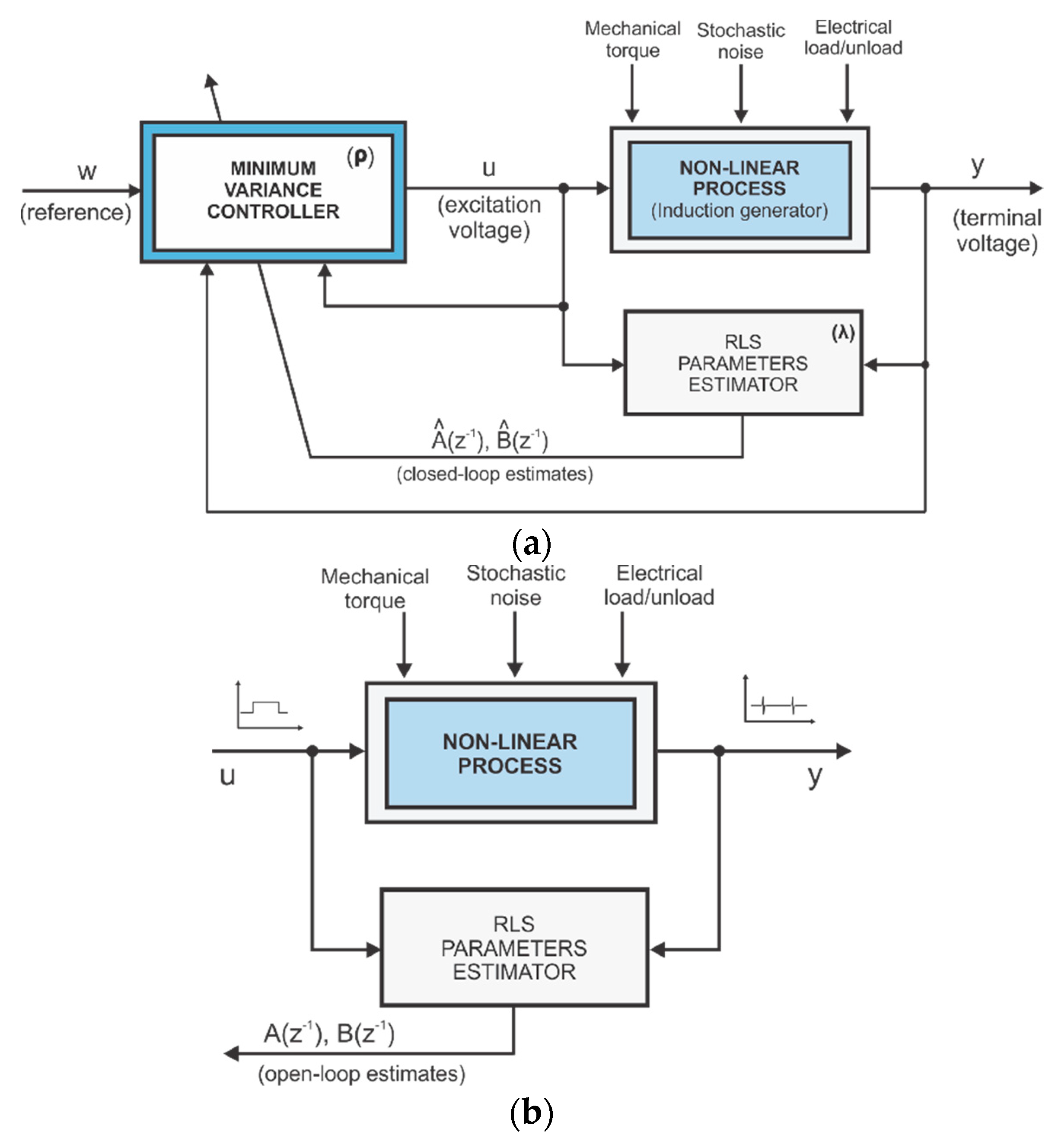
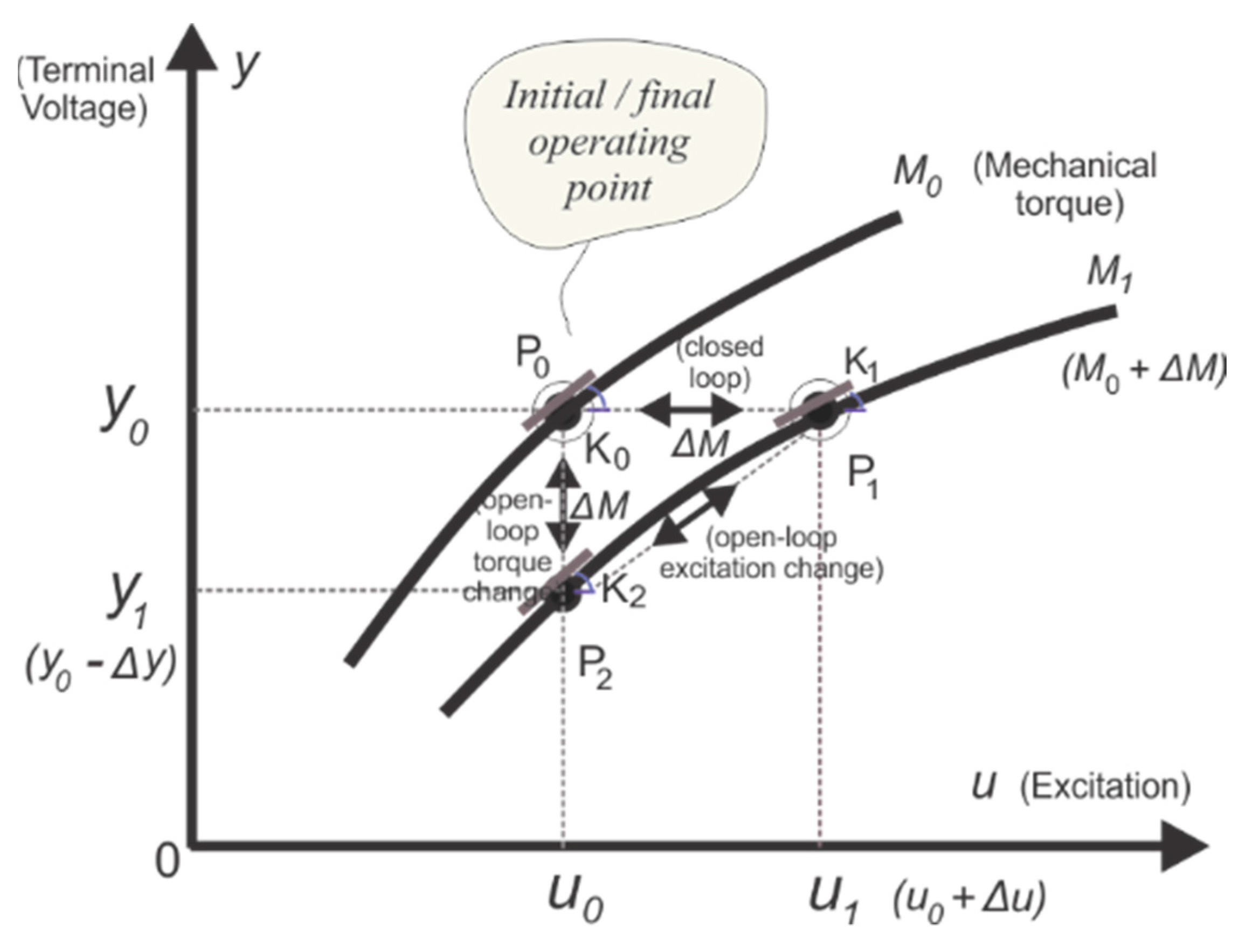
3. Case Studies for Validation
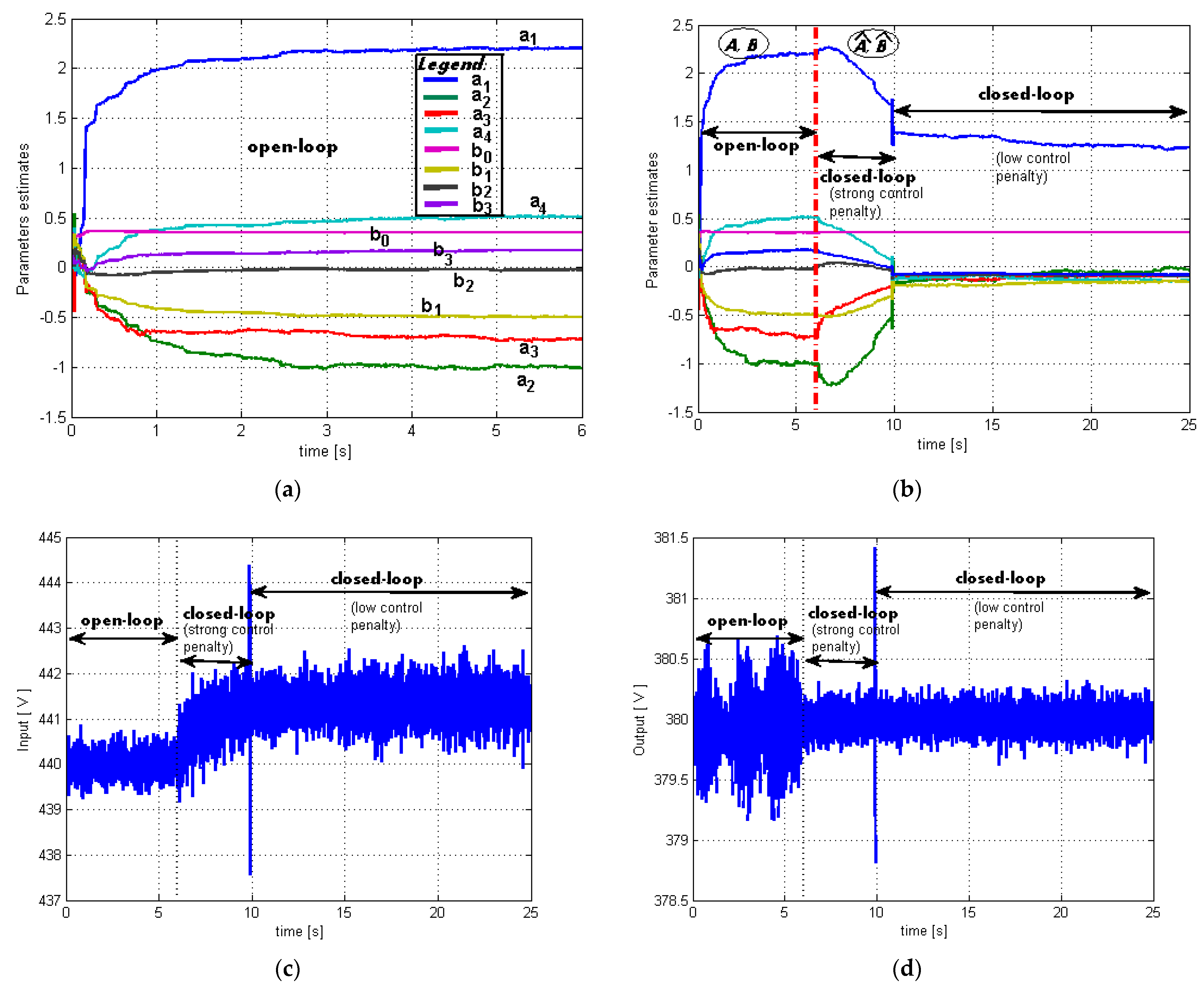
3.1. Case 1. Initialization of the Minimum Variance Control System
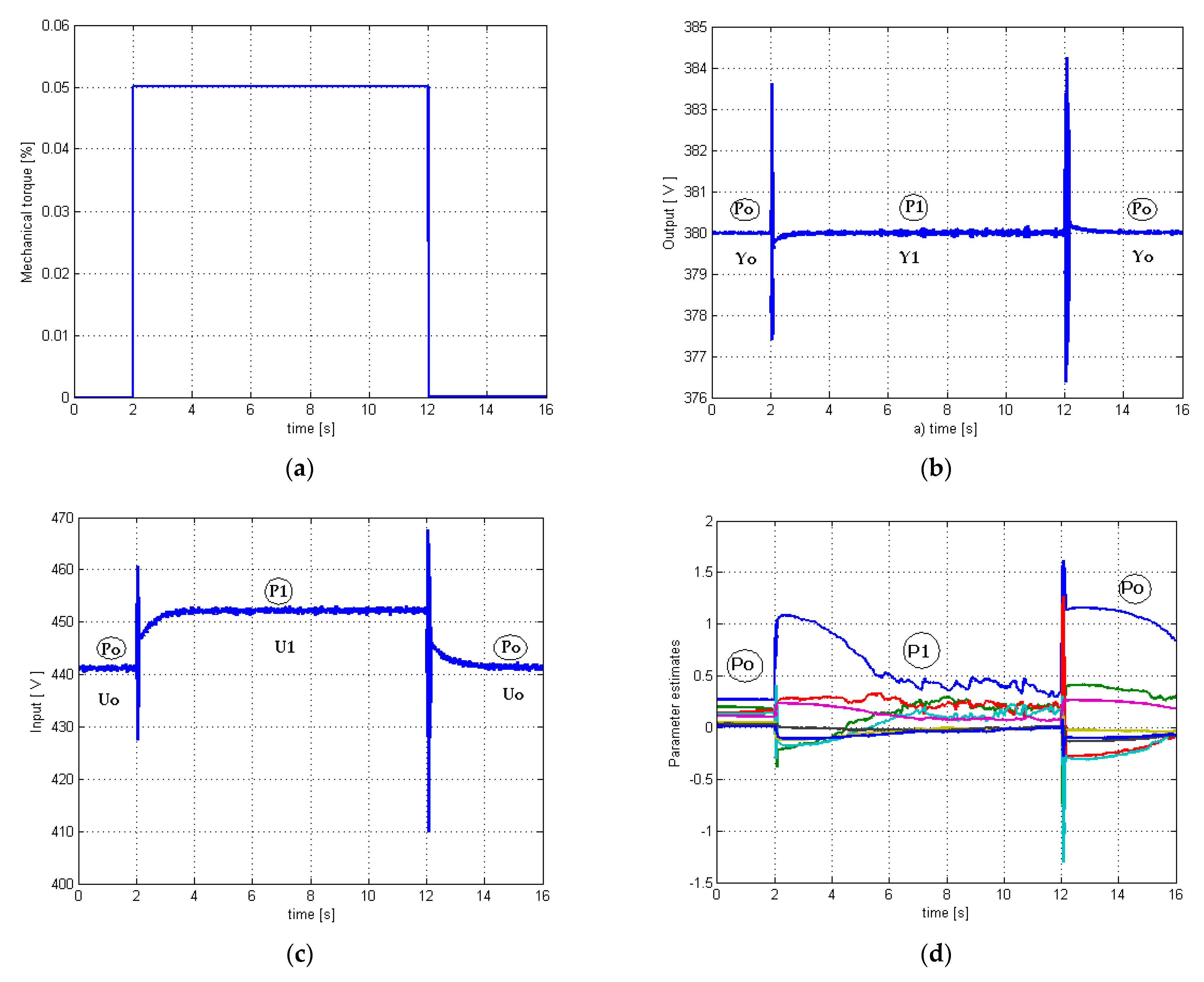
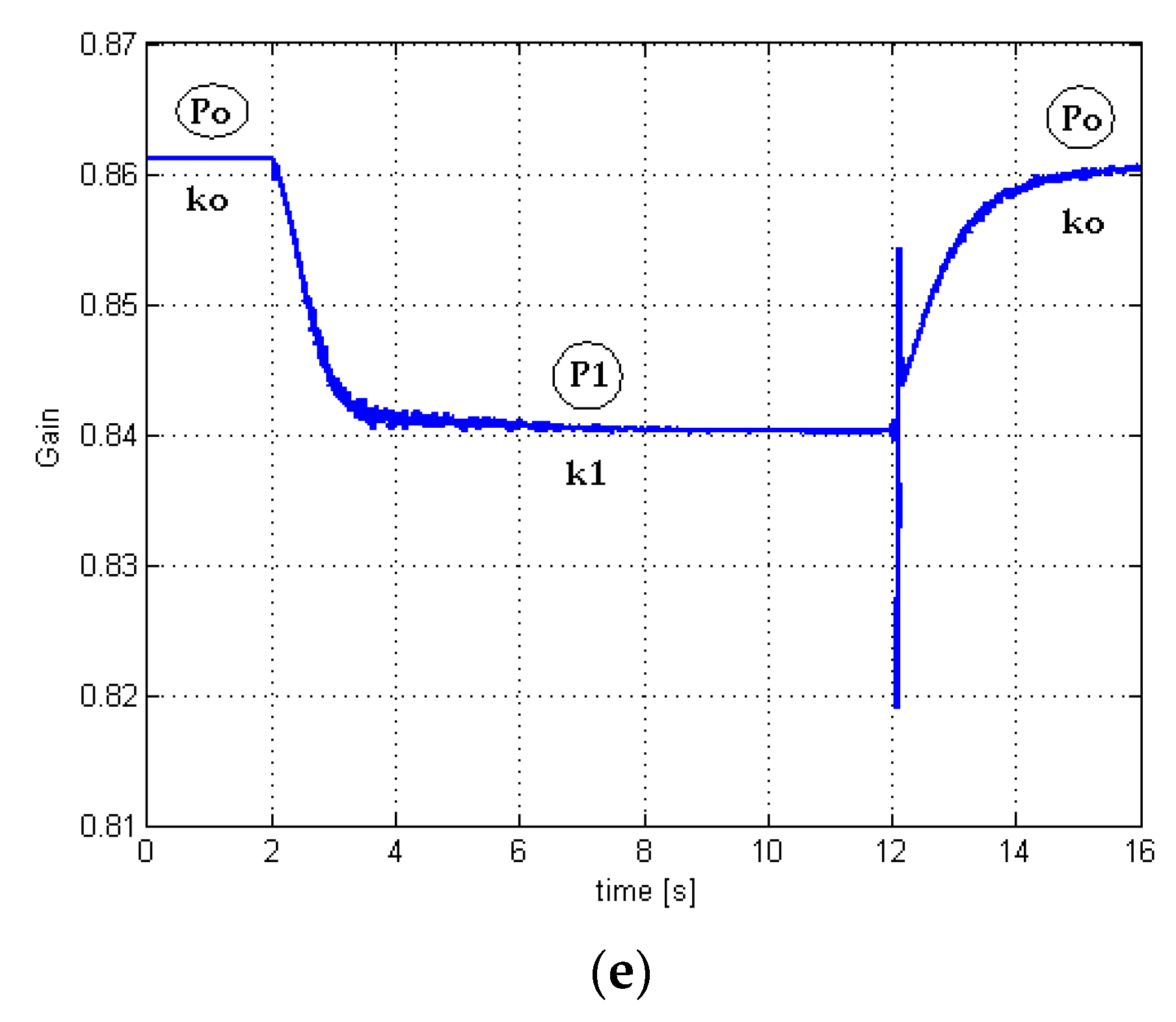
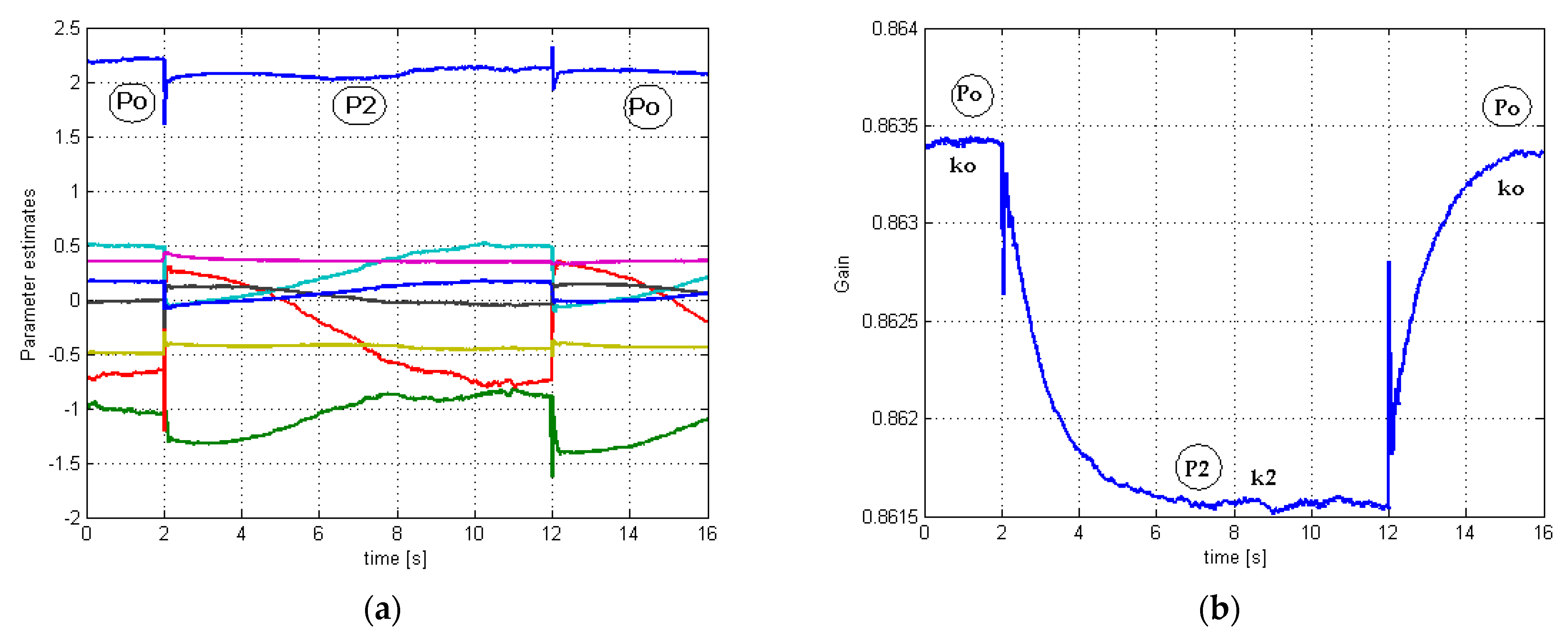
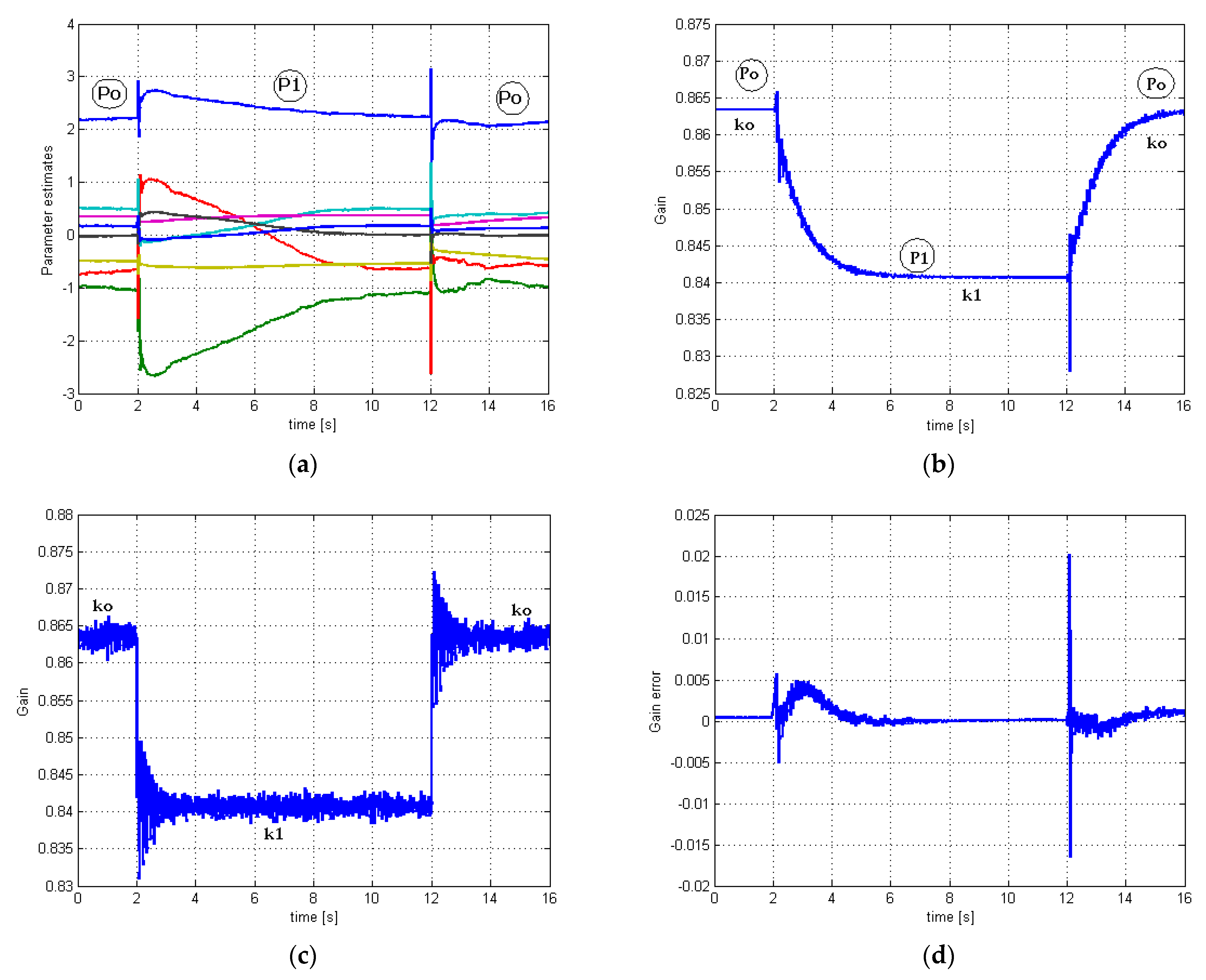
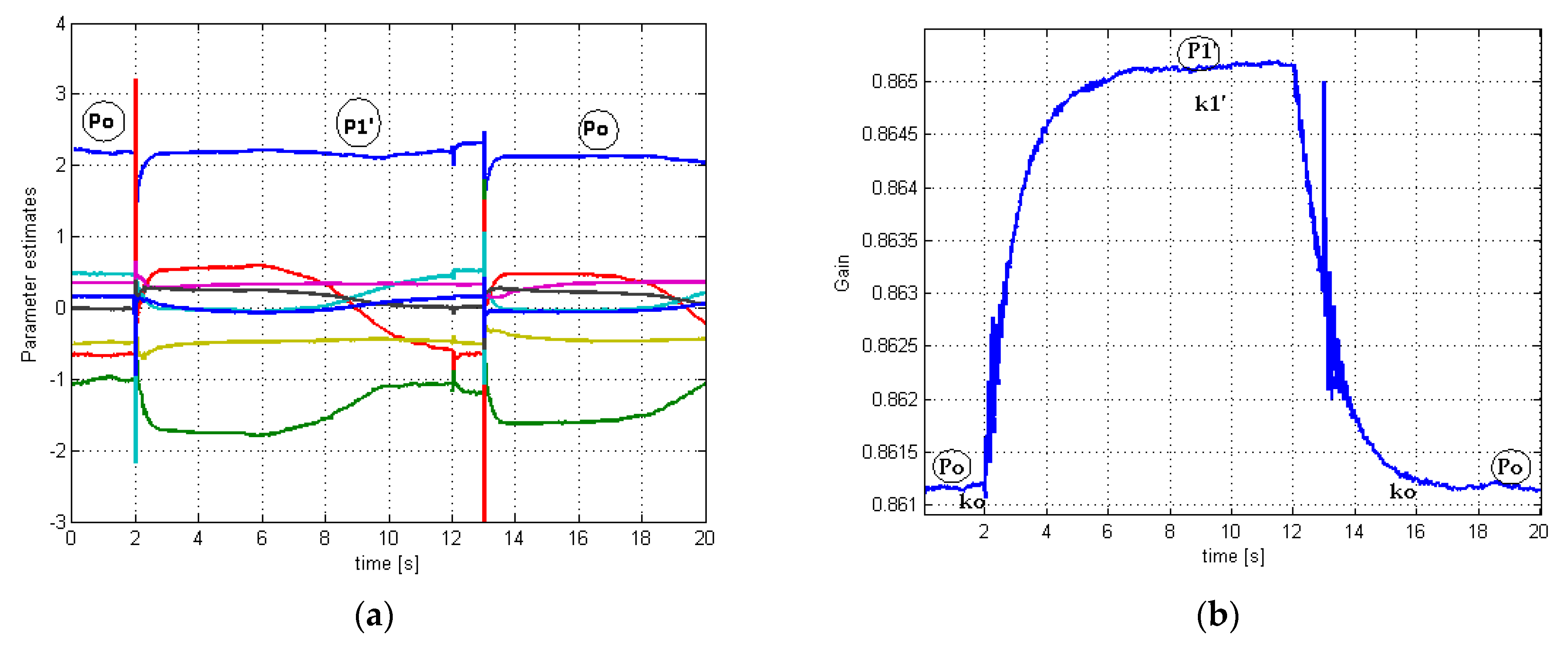
3.2. Case 2. Mechanical Torque Variation
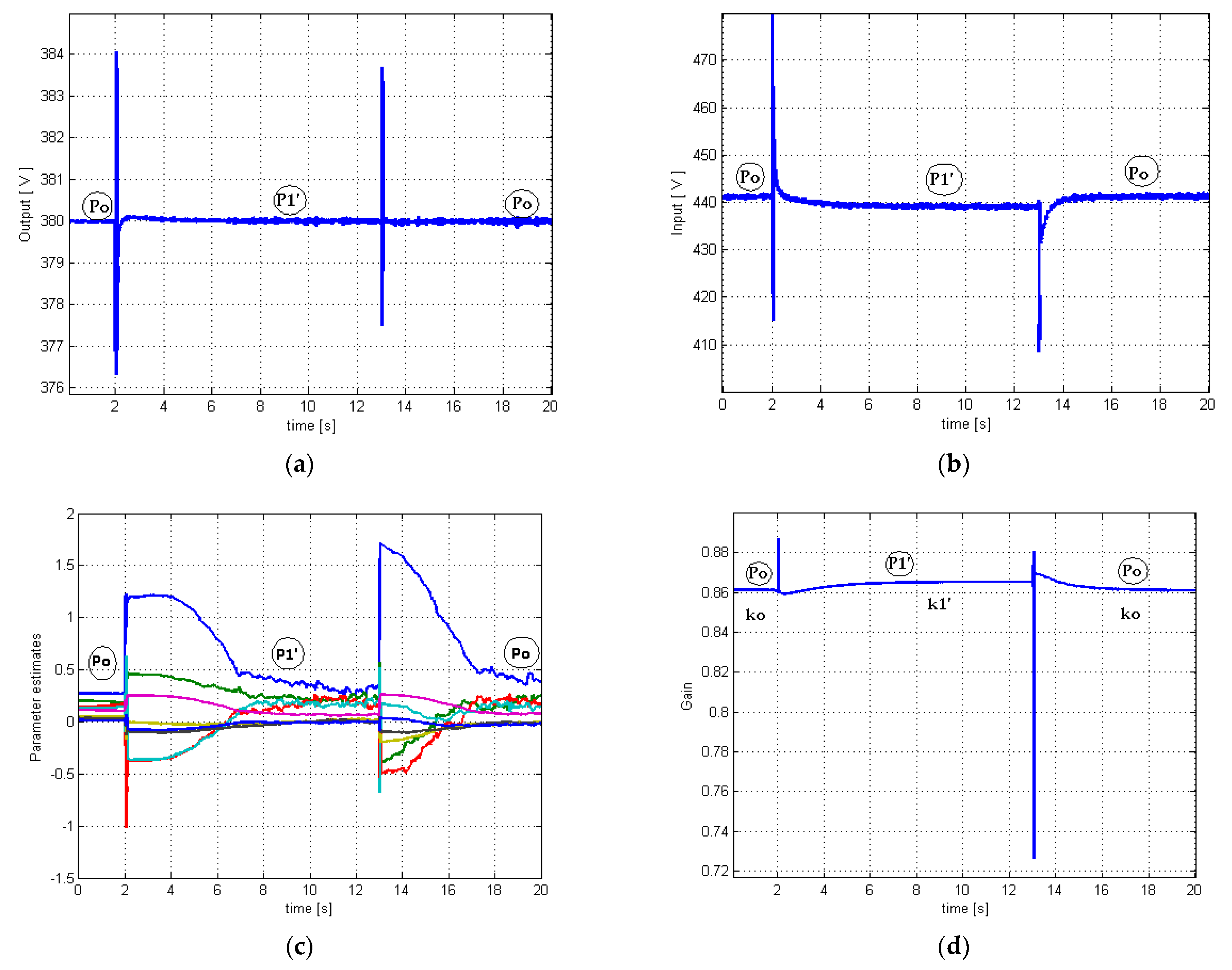
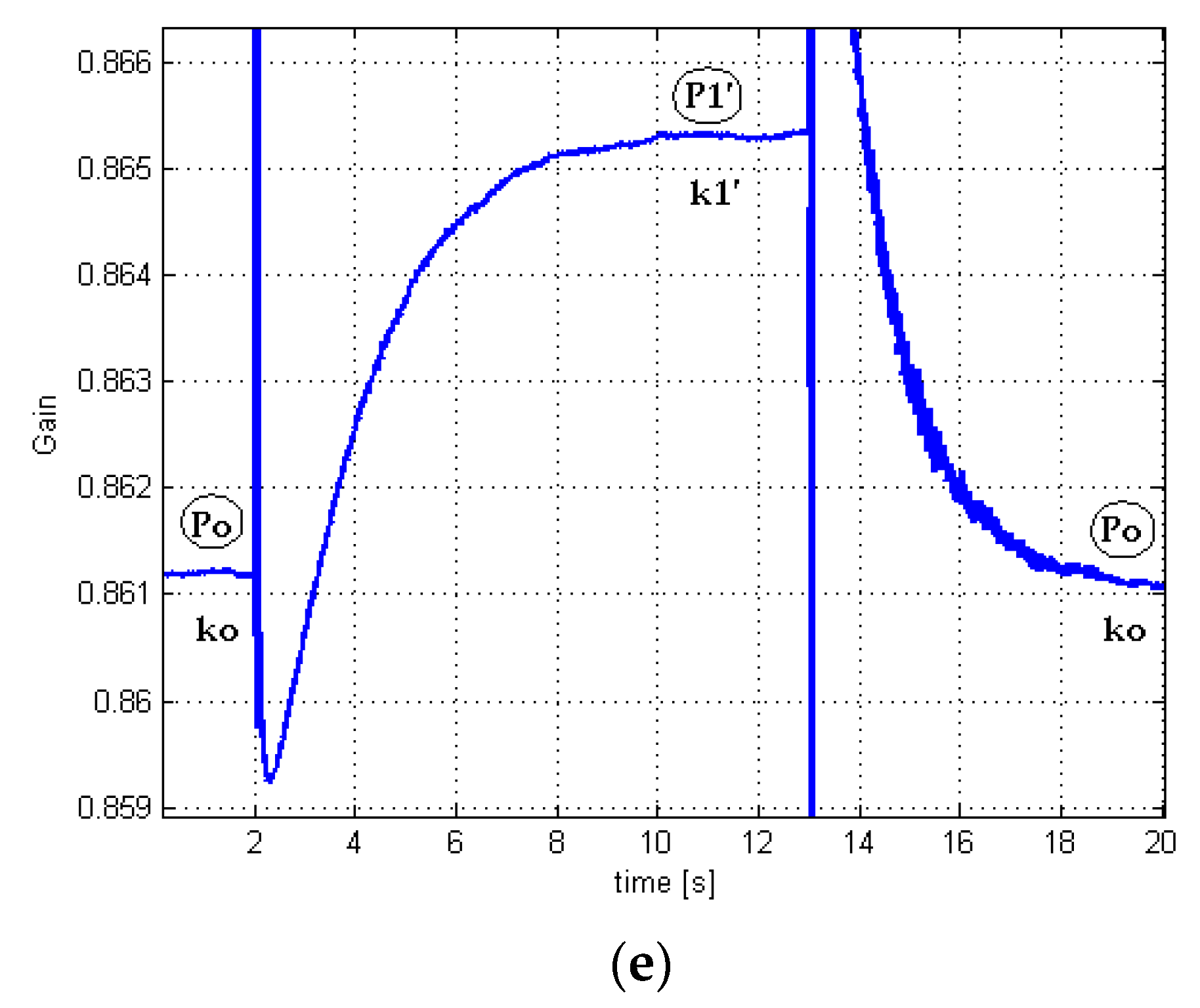
3.3. Case 3. Electrical Load/Unload
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Benosman, M. Learning-Based Adaptive Control. An Extremum Seeking Approach-Theory and Applications, Butterworth-Heinemann; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Aström, K.J.; Kumarb, P.R. Control: A perspective. Automatica 2014, 50, 3–43. [Google Scholar] [CrossRef]
- Clarke, D.W.; Gawthrop, P.J. Self-Tuning Controller. IEE Proc. Part D Control Theory Appl. 1975, 122, 929–934. [Google Scholar] [CrossRef]
- Aström, K.J.; Wittenmark, B. Adaptive Control; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Bobal, V.; Böhm, V.; Fessl, J.; Machácek, J. Digital Self-Tuning Controllers: Algorithms, Implementation and Applications (Advanced Textbooks in Control and Signal Processing); Springer: London, UK, 2005. [Google Scholar]
- Mikles, J.; Fikar, M. Process Modelling, Identification, and Control; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Filip, I.; Prostean, O.; Szeidert, I.; Vasar, C. Consideration regarding the convergence and stability of an adaptive self-tuning control system. In Proceedings of the 5th IEEE International Conference on Computational Cybernetics, Gammarth, Tunisia, 19–21 October 2007; pp. 75–79. [Google Scholar] [CrossRef]
- Filip, I.; Szeidert, I. Tuning the control penalty factor of a minimum variance adaptive controller. Eur. J. Control 2017, 37, 16–26. [Google Scholar] [CrossRef]
- Filip, I.; Vasar, C.; Prostean, O.; Szeidert, I. Self-tuning strategy for a minimum variance control system of a highly disturbed process. Eur. J. Control 2019, 46, 49–62. [Google Scholar] [CrossRef]
- Ishchenko, A.; Myrzik, J.M.A.; Kling, W.L. Linearization of Dynamic Model of Squirrel-Cage Induction Generator Wind Turbine. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Zou, Y.; Elbuluk, M.; Sozer, Y. A Complete Modeling and Simulation of Induction Generator Wind Power Systems. In Proceedings of the IEEE Industry Applications Society Annual Meeting (IAS), Houston, TX, USA, 3–7 October 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Filip, I.; Szeidert, I.; Prostean, O. Mathematical modelling and numerical simulation of the dual winded induction generator’s operating regimes. In Soft Computing Applications, Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2015; Volume 357, pp. 1161–1170. [Google Scholar] [CrossRef]
- Filip, I.; Dragan, F.; Szeidert, I.; Albu, A. Minimum-Variance Control System with Variable Control Penalty Factor. Appl. Sci. 2020, 10, 2274. [Google Scholar] [CrossRef] [Green Version]
- Filip, I.; Mihet-Popa, L.; Vasar, C.; Prostean, O.; Szeidert, I. Considerations Regarding the Design of a Minimum Variance Control System for an Induction Generator. Electronics 2019, 8, 532. [Google Scholar] [CrossRef] [Green Version]
- Filip, I.; Szeidert, I. Givens orthogonal transformation-based estimator versus RLS estimator-Case study for an induction generator model. In Soft Computing Applications, Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2015; Volume 357, pp. 1287–1299. [Google Scholar] [CrossRef]
- Rohwer, C.M.; Angeletti, F.; Touchette, H. Convergence of large-deviation estimators. Phys. Rev. E 2015, 92, 052104. [Google Scholar] [CrossRef] [Green Version]
- Farias, E.R.C.; Cari, E.P.T.; Erlich, I.; Shewarega, F. Online Parameter Estimation of a Transient Induction Generator Model Based on the Hybrid Method. IEEE Trans. Energy Convers. 2018, 33, 1529–1538. [Google Scholar] [CrossRef]
- Wu, D.; Song, J.; Shen, Y. Variable forgetting factor identification algorithm for fault diagnosis of wind turbines. In Proceedings of the Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 1895–1900. [Google Scholar] [CrossRef]
- Huang, X.F.; Tang, X.F.; Deng, X.; Wang, X.J. The large deviation for the least squares estimator of nonlinear regression model based on WOD errors. J. Inequalities Appl. 2016, 125, 2–11. [Google Scholar] [CrossRef] [Green Version]
- Filip, I.; Prostean, O.; Szeidert, I.; Vasar, C. An Improved Structure of an Adaptive Excitation Control System Operating under Short-Circuit. Adv. Electr. Comput. Eng. 2016, 16, 43–50. [Google Scholar] [CrossRef]
- Ni, K.; Hu, Y.; Liu, Y.; Gan, C. Performance Analysis of a Four-Switch Three-Phase Grid-Side Converter with Modulation Simplification in a Doubly-Fed Induction Generator-Based Wind Turbine (DFIG-WT) with Different External Disturbances. Energies 2017, 10, 706. [Google Scholar] [CrossRef]
- Filip, I.; Vasar, C. About Initial Setting of a Self-Tuning Controller. In Proceedings of the 4th International Symposium on Applied Computational Intelligence and Informatics, SACI, Timisoara, Romania, 17–18 May 2007; pp. 251–256. [Google Scholar] [CrossRef]
- Filip, I.; Szeidert, I.; Prostean, O.; Vasar, C. Issues regarding the tuning of a minimum variance adaptive controller. In Soft Computing Applications, Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2018; Volume 633, pp. 70–77. [Google Scholar] [CrossRef]
- Zachariah, K.J.; Finch, J.W.; Farsi, M. Multivariable Self-Tuning Control of a Turbine Generator System. IEEE Trans. Energy Convers. 2009, 24, 406–414. [Google Scholar] [CrossRef]
- Okada, S.; Masuda, S. Data-driven minimum variance control using regulatory closed-loop data based on the FRIT method. Trans. Electron. Inf. Syst. 2019, 138, 1580–1585. [Google Scholar] [CrossRef]
- Saleem, O.; Khalid Mahmood-ul-Hasan, K.; Rizwan, M. Self-Tuning State-Feedback Control of Rotary Pendulum via Online Adaptive Reconfiguration of Control Penalty-Factor. Control Eng. Appl. Inform. 2020, 22, 23–33. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filip, I.; Dragan, F.; Szeidert, I. Considerations about Parameters Estimation into a Minimum Variance Control System. Appl. Sci. 2021, 11, 6165. https://doi.org/10.3390/app11136165
Filip I, Dragan F, Szeidert I. Considerations about Parameters Estimation into a Minimum Variance Control System. Applied Sciences. 2021; 11(13):6165. https://doi.org/10.3390/app11136165
Chicago/Turabian StyleFilip, Ioan, Florin Dragan, and Iosif Szeidert. 2021. "Considerations about Parameters Estimation into a Minimum Variance Control System" Applied Sciences 11, no. 13: 6165. https://doi.org/10.3390/app11136165
APA StyleFilip, I., Dragan, F., & Szeidert, I. (2021). Considerations about Parameters Estimation into a Minimum Variance Control System. Applied Sciences, 11(13), 6165. https://doi.org/10.3390/app11136165






