Advanced Crystal Plasticity Modeling of Multi-Phase Steels: Work-Hardening, Strain Rate Sensitivity and Formability
Abstract
Featured Application
Abstract
1. Introduction
1.1. Modeling of Work Hardening in Steels
1.2. Modeling the Strain Rate Sensitivity of Multiphase Steels
1.3. Modeling of Formability Properties
2. Materials and Methods
2.1. Thermal Processing
2.2. Material Characterization
2.3. Tensile Experiments
3. Modeling
3.1. VPSC Formalism
3.2. VPSC90
3.3. Strain Rate Sensitivity
3.4. Work Hardening
3.5. Modeling of Bainitic Steels
3.6. Parameter Fitting
3.7. Virtual Testing
4. Results
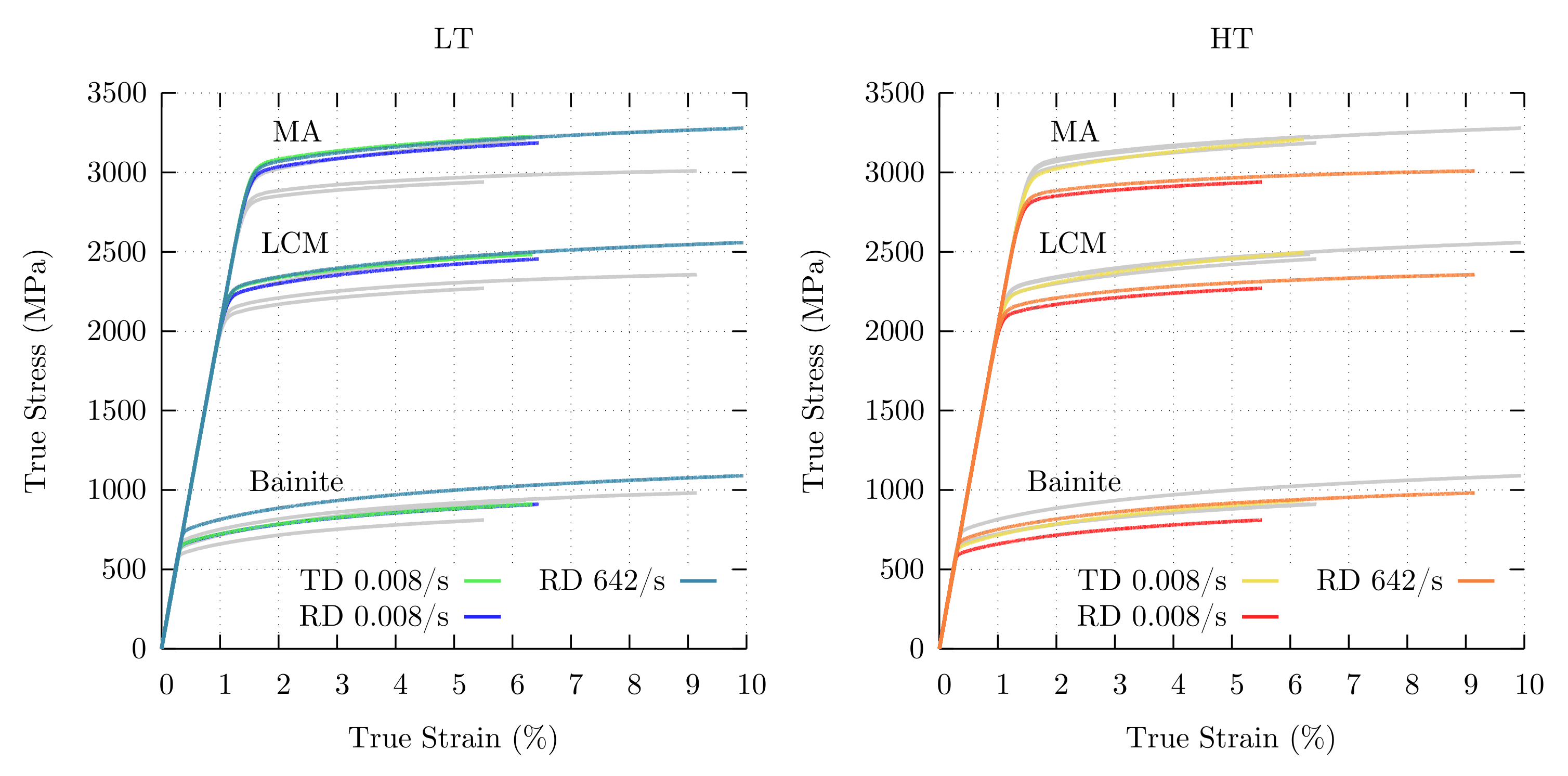
4.1. Material Characterization
4.2. Parameter Fitting
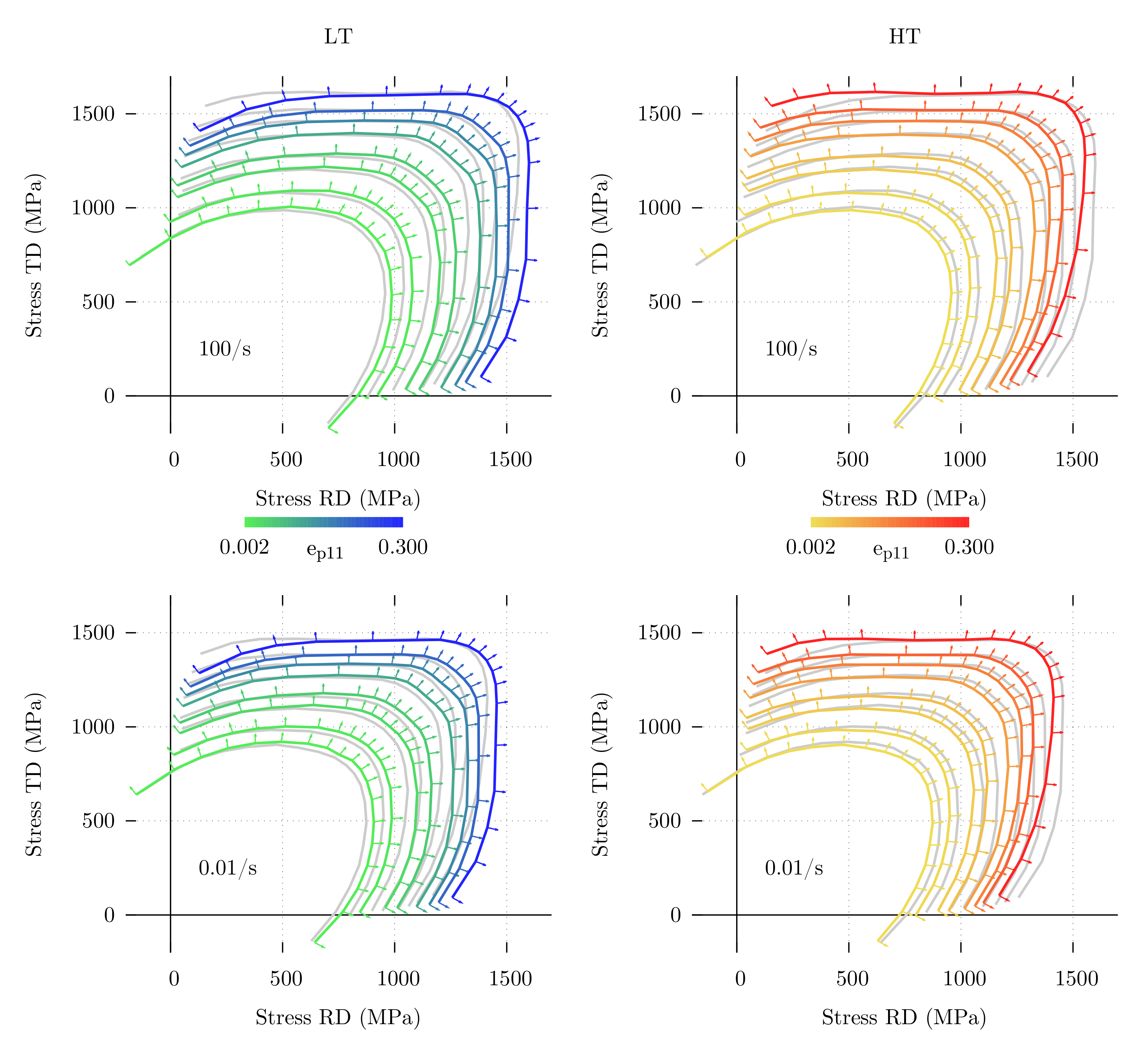
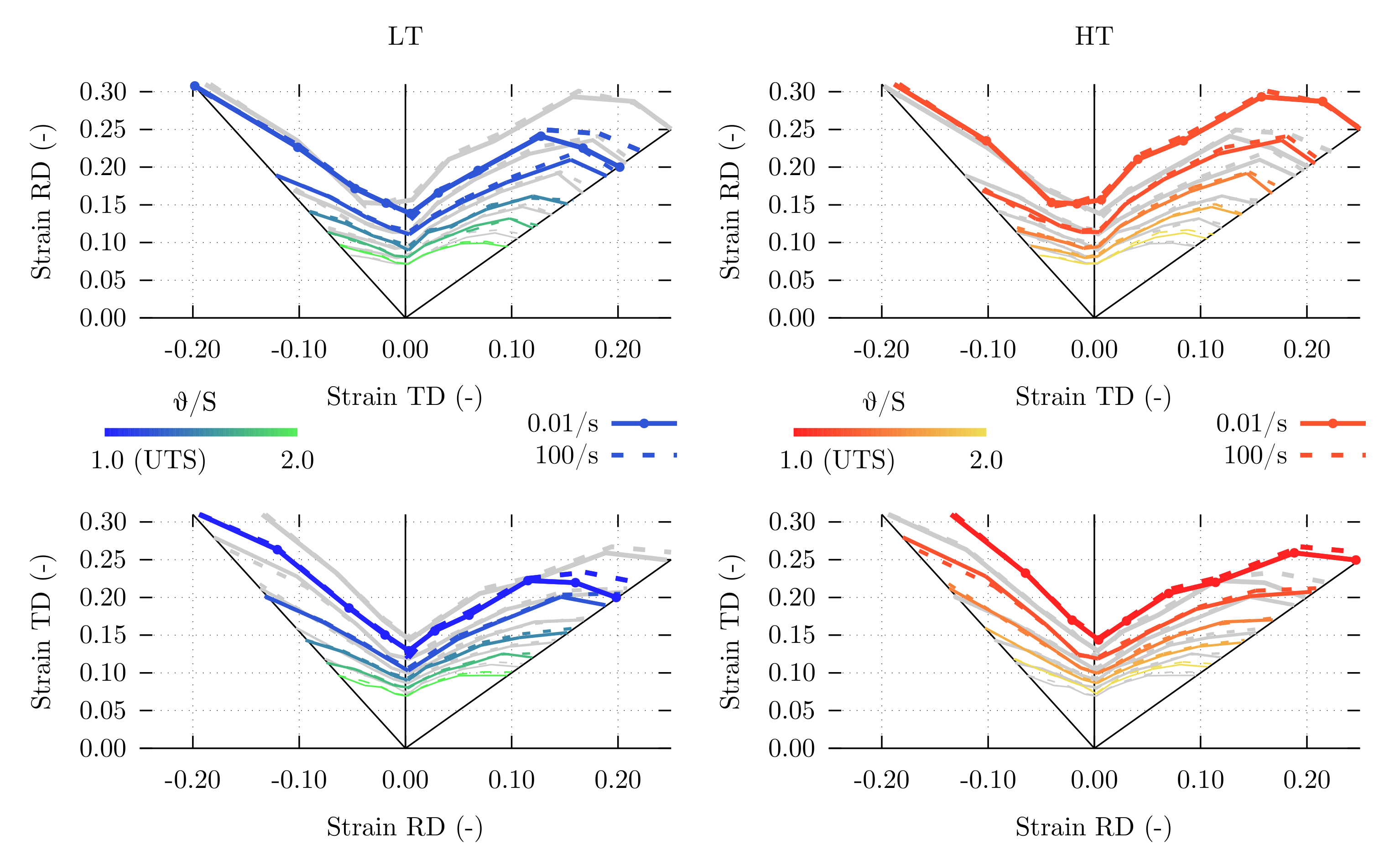
4.3. Formability Properties
5. Discussion
5.1. Experimental Results and Fitted Parameters
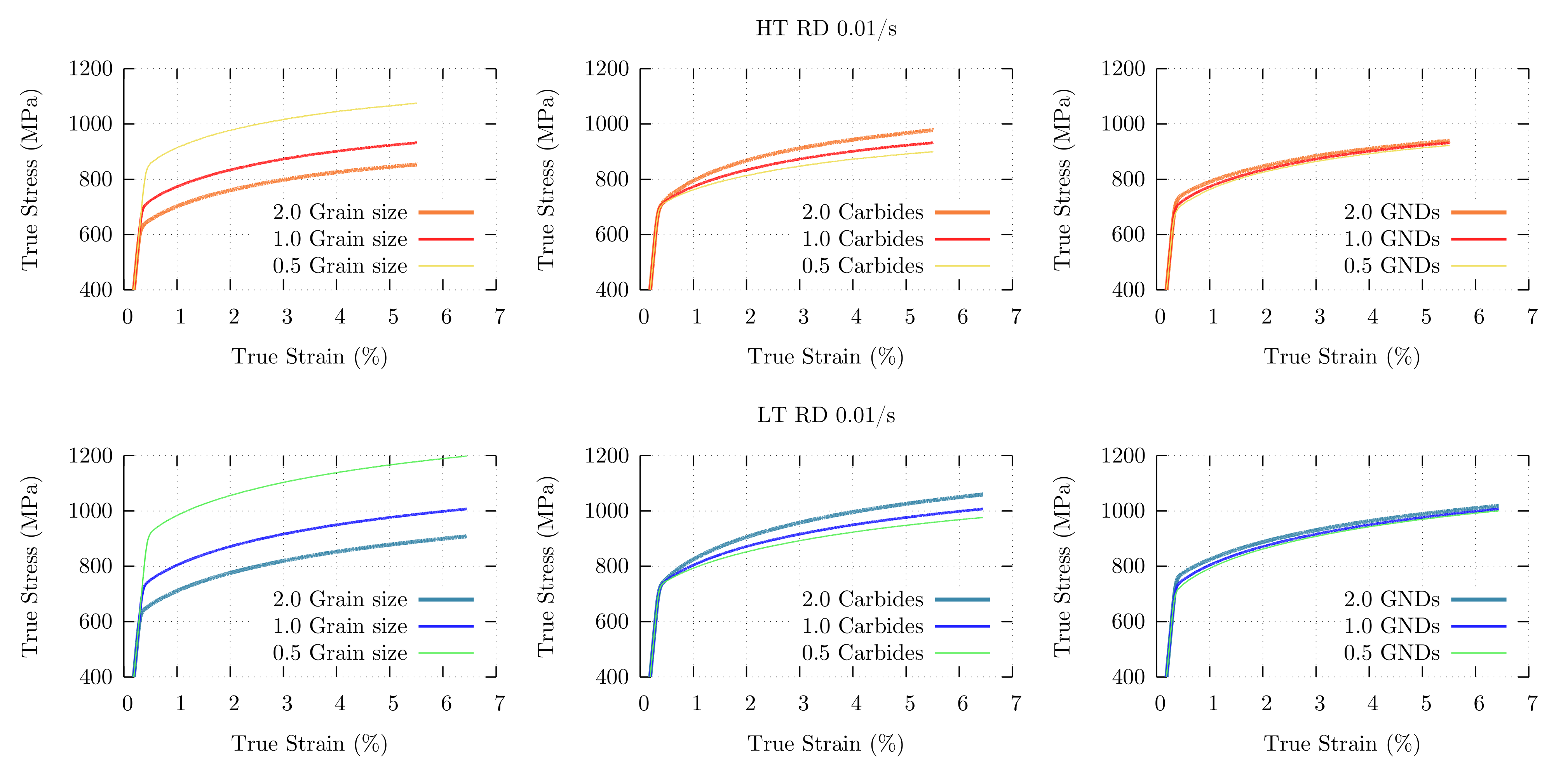
5.2. Role of Microstructural Parameters on Mechanical Behavior
5.3. Formability Properties
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lebensohn, R.A.; Tomé, C. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys. Acta Metall. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Segurado, J.; Lebensohn, R.A.; LLorca, J.; Tomé, C.N. Multiscale modeling of plasticity based on embedding the viscoplastic self-consistent formulation in implicit finite elements. Int. J. Plast. 2012, 28, 124–140. [Google Scholar] [CrossRef]
- Jeong, Y.; Tomé, C.N. An efficient elasto-visco-plastic self-consistent formulation: Application to steel subjected to loading path changes. Int. J. Plast. 2020, 135, 102812. [Google Scholar] [CrossRef]
- Kitayama, K.; Tomé, C.; Rauch, E.; Gracio, J.; Barlat, F. A crystallographic dislocation model for describing hardening of polycrystals during strain path changes. Application to low carbon steels. Int. J. Plast. 2013, 46, 54–69. [Google Scholar] [CrossRef]
- Knezevic, M.; McCabe, R.J.; Lebensohn, R.A.; Tomé, C.N.; Liu, C.; Lovato, M.L.; Mihaila, B. Integration of self-consistent polycrystal plasticity with dislocation density based hardening laws within an implicit finite element framework: Application to low-symmetry metals. J. Mech. Phys. Solids 2013, 61, 2034–2046. [Google Scholar] [CrossRef]
- Knezevic, M.; McCabe, R.J.; Tomé, C.N.; Lebensohn, R.A.; Chen, S.R.; Cady, C.M.; Gray, G.T., III; Mihaila, B. Modeling mechanical response and texture evolution of α-uranium as a function of strain rate and temperature using polycrystal plasticity. Int. J. Plast. 2013, 43, 70–84. [Google Scholar] [CrossRef]
- Zecevic, M.; Knezevic, M. A new visco-plastic self-consistent formulation implicit in dislocation-based hardening within implicit finite elements: Application to high strain rate and impact deformation of tantalum. Comput. Methods Appl. Mech. Eng. 2018, 341, 888–916. [Google Scholar] [CrossRef]
- Galán-López, J.; Verleysen, P. Simulation of the plastic response of Ti–6Al–4V thin sheet under different loading conditions using the viscoplastic self-consistent model. Mater. Sci. Eng. A 2018, 712, 1–11. [Google Scholar] [CrossRef]
- Lebensohn, R.; Tomé, C.; Castaneda, P.P. Self-consistent modelling of the mechanical behaviour of viscoplastic polycrystals incorporating intragranular field fluctuations. Philos. Mag. 2007, 87, 4287–4322. [Google Scholar] [CrossRef]
- Galán, J.; Verleysen, P.; Lebensohn, R. An improved algorithm for the polycrystal viscoplastic self-consistent model and its integration with implicit finite element schemes. Model. Simul. Mater. Sci. Eng. 2014, 22, 055023. [Google Scholar] [CrossRef]
- Bhadeshia, H.K. High Performance Bainitic Steels. In Materials Science Forum; Trans Tech Publ: Baech, Switzerland, 2005; Volume 500, pp. 63–74. [Google Scholar]
- Garcia-Mateo, C.; Caballero, F.G. Design of carbide-free low-temperature ultra high strength bainitic steels. Int. J. Mater. Res. 2007, 98, 137–143. [Google Scholar] [CrossRef]
- Fekete, J. Current challenges in Implementing Advanced High Strength Steels. In Proceedings of the International Conference on Microalloyed Steels: Processing Microstructure, Properties and Peformance, Pittsburgh, PA, USA, 16–19 July 2007; pp. 1–9. [Google Scholar]
- Matlock, D.K.; Speer, J.G.; De Moor, E.; Gibbs, P.J. Recent developments in advanced high strength sheet steels for automotive applications: An overview. Jestech 2012, 15, 1–12. [Google Scholar]
- Kocks, U. Law for Work-Hardening and Low-Temperature Creep. Trans. ASME J. Eng. Mater. Technol. 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Pantleon, W. Stage IV work-hardening related to disorientations in dislocation structures. Mater. Sci. Eng. A 2004, 387, 257–261. [Google Scholar] [CrossRef]
- León García, O. Micromechanisms of Failure under Static Loading in Sheet Metals for Automotive Applications. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Zhu, K.; Bouaziz, O.; Oberbillig, C.; Huang, M. An approach to define the effective lath size controlling yield strength of bainite. Mater. Sci. Eng. A 2010, 527, 6614–6619. [Google Scholar] [CrossRef]
- Ashby, M. The deformation of plastically non-homogeneous materials. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Zuev, L.B. On the waves of plastic flow localization in pure metals and alloys. Ann. Phys. 2007, 16, 286–310. [Google Scholar] [CrossRef]
- Shakerifard, B.; Lopez, J.G.; Legaza, M.C.T.; Verleysen, P.; Kestens, L.A. Strain rate dependent dynamic mechanical response of bainitic multiphase steels. Mater. Sci. Eng. A 2019, 745, 279–290. [Google Scholar] [CrossRef]
- Asaro, R.J.; Needleman, A. Overview no. 42 texture development and strain hardening in rate dependent polycrystals. Acta Metall. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Johnson, G.; Cook, W. A Constitutive modeling and data for metals subjected to large strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–577. [Google Scholar]
- Banabic, D.; Barlat, F.; Cazacu, O.; Kuwabara, T. Advances in anisotropy of plastic behaviour and formability of sheet metals. Int. J. Mater. Form. 2020, 13, 749–787. [Google Scholar] [CrossRef]
- Lankford, W. New criteria for predicting the performance of deep drawing sheets. Trans. ASM 1950, 42, 1197. [Google Scholar]
- Galán-López, J.; Kestens, L.A. Optimization of crystallographic texture for sheet-forming applications using Taylor-based Models. Metall. Mater. Trans. A 2018, 49, 5745–5762. [Google Scholar] [CrossRef]
- Van Houtte, P.; Li, S.; Engler, O. Taylor-Type Homogenization Methods for Texture and Anisotropy. In Continuum Scale Simulation of Engineering Materials: Fundamentals–Microstructures–Process Applications; Wiley: Weinheim, Germany, 2004; pp. 459–472. [Google Scholar]
- Ma, A.; Roters, F.; Raabe, D. Simulation of Textures and Lankford Values for Face Centered Cubic Polycrystaline Metals by Using a Modified Taylor Model; Max-Planck-Institut für Eisenforschung: Düsseldorf, Alemanha, 2004. [Google Scholar]
- Melchior, M.A.; Remacle, J.F.; Delannay, L. Assessment of adaptative meshing in CPFEM simulation of the anisotropy of polycristalline aggregates. In Proceedings of the 8th World Congress on Computational Mechanics, Venice, Italy, 30 June–5 July 2008. [Google Scholar]
- Hammami, W.; Delannay, L.; Habraken, A.M.; Duchêne, L. Crystal plasticity prediction of Lankford coefficients using the MULTISITE model: Influence of the critical resolved shear stresses. Int. J. Mater. Form. 2009, 2, 65–68. [Google Scholar] [CrossRef]
- Min, K.; Jeong, W.; Hong, S.; Lee, C.; Cha, P.R.; Han, H.; Lee, M.G. Integrated crystal plasticity and phase field model for prediction of recrystallization texture and anisotropic mechanical properties of cold-rolled ultra-low carbon steels. Int. J. Plast. 2020, 127, 102644. [Google Scholar] [CrossRef]
- Cazacu, O.; Barlat, F. A criterion for description of anisotropy and yield differential effects in pressure-insensitive metals. Int. J. Plast. 2004, 20, 2027–2045. [Google Scholar] [CrossRef]
- Kuwabara, T.; Ikeda, S.; Kuroda, K. Measurement and analysis of differential work hardening in cold-rolled steel sheet under biaxial tension. J. Mater. Process. Technol. 1998, 80, 517–523. [Google Scholar] [CrossRef]
- Coppieters, S.; Hakoyama, T.; Debruyne, D.; Takahashi, S.; Kuwabara, T. Inverse Yield Locus Identification of Sheet Metal Using a Complex Cruciform in Biaxial Tension and Digital Image Correlation. Proceedings 2018, 2, 382. [Google Scholar] [CrossRef]
- Plunkett, B.; Lebensohn, R.; Cazacu, O.; Barlat, F. Anisotropic yield function of hexagonal materials taking into account texture development and anisotropic hardening. Acta Mater. 2006, 54, 4159–4169. [Google Scholar] [CrossRef]
- Inal, K.; Mishra, R.K.; Cazacu, O. Forming simulation of aluminum sheets using an anisotropic yield function coupled with crystal plasticity theory. Int. J. Solids Struct. 2010, 47, 2223–2233. [Google Scholar] [CrossRef]
- Gawad, J.; Banabic, D.; Van Bael, A.; Comsa, D.S.; Gologanu, M.; Eyckens, P.; Van Houtte, P.; Roose, D. An evolving plane stress yield criterion based on crystal plasticity virtual experiments. Int. J. Plast. 2015, 75, 141–169. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczyński, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Jacques, N. An analytical model for necking strains in stretched plates under dynamic biaxial loading. Int. J. Solids Struct. 2020, 200, 198–212. [Google Scholar] [CrossRef]
- Savoie, J.; Jain, M.; Carr, A.; Wu, P.; Neale, K.; Zhou, Y.; Jonas, J. Predictions of forming limit diagrams using crystal plasticity models. Mater. Sci. Eng. A 1998, 257, 128–133. [Google Scholar] [CrossRef]
- Hajian, M.; Assempour, A. Experimental and numerical determination of forming limit diagram for 1010 steel sheet: A crystal plasticity approach. Int. J. Adv. Manuf. Technol. 2015, 76, 1757–1767. [Google Scholar] [CrossRef]
- Wu, P.; Neale, K.; Van der Giessen, E.; Jain, M.; MacEwen, S.; Makinde, A. Crystal plasticity forming limit diagram analysis of rolled aluminum sheets. Metall. Mater. Trans. A 1998, 29, 527–535. [Google Scholar] [CrossRef][Green Version]
- Shakerifard, B. From Micro-Mechanisms of Damage Initiation to Constitutive Mechanical Behavior of Bainitic Multiphase Steels. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Ruhl, R.; Cohen, M. Splat quenching of iron–carbon alloys. Trans. Metall. Soc. AIME 1969, 245, 241–251. [Google Scholar]
- Van Houtte, P. A new method for the determination of texture functions from incomplete pole figures—Comparison with older methods. Textures Microstruct. 1984, 6, 137–161. [Google Scholar] [CrossRef]
- Verleysen, P.; Degrieck, J.; Verstraete, T.; Van Slycken, J. Influence of specimen geometry on split Hopkinson tensile bar tests on sheet materials. Exp. Mech. 2008, 48, 587. [Google Scholar] [CrossRef]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. Sect. B 1949, 62, 676. [Google Scholar] [CrossRef]
- Peirs, J. Experimental Characterisation and Modelling of the Dynamic Behaviour of the Titanium Alloy Ti6Al4V (’Experimentele Karakterisering en Modellering van het Dynamisch Materiaalgedrag van de Titaniumlegering Ti6Al4V’). Ph.D. Thesis, Ghent University, Ghent, Belgium, 2012. [Google Scholar]
- Tomé, C.; Lebensohn, R. Manual for Code Visco-Plastic Self-Consistent (vpsc); Los Alamos National Laboratory: Los Alamos, NM, USA, 2009. [Google Scholar]
- Schmid, E.; Boas, W. Kristallplastizität: Mit Besonderer Berücksichtigung der Metalle; Springer: Berlin/Heidelberg, Germany, 2013; Volume 17. [Google Scholar]
- Ramazani, A.; Pinard, P.; Richter, S.; Schwedt, A.; Prahl, U. Characterisation of microstructure and modelling of flow behaviour of bainite-aided dual-phase steel. Comput. Mater. Sci. 2013, 80, 134–141. [Google Scholar] [CrossRef]
- He, S.; He, B.; Zhu, K.; Huang, M. Evolution of dislocation density in bainitic steel: Modeling and experiments. Acta Mater. 2018, 149, 46–56. [Google Scholar] [CrossRef]
- Gutierrez, I. Mechanical Property Models for High-Strength Complex Microstructures; Office for Official Publications of the European Communities: Luxembourg, 2008. [Google Scholar]
- Pickering, F.B. Physical Metallurgy and the Design of Steels; Applied Science Publishers Ltd.: London, UK, 1978. [Google Scholar]
- Gutiérrez, I.; Altuna, M.A. Work-hardening of ferrite and microstructure-based modelling of its mechanical behaviour under tension. Acta Mater. 2008, 56, 4682–4690. [Google Scholar] [CrossRef]
- Hall, E. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Petch, N. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Kim, S.A.; Johnson, W.L. Elastic constants and internal friction of martensitic steel, ferritic-pearlitic steel, and α-iron. Mater. Sci. Eng. A 2007, 452, 633–639. [Google Scholar] [CrossRef]
- Franciosi, P. Glide mechanisms in bcc crystals: An investigation of the case of α-iron through multislip and latent hardening tests. Acta Metall. 1983, 31, 1331–1342. [Google Scholar] [CrossRef]
- Pathak, N.; Butcher, C.; Worswick, M.J.; Bellhouse, E.; Gao, J. Damage evolution in complex-phase and dual-phase steels during edge stretching. Materials 2017, 10, 346. [Google Scholar] [CrossRef]
- Smith, D.A. Die Design Handbook; Society of Manufacturing Engineers: Southfield, MI, USA, 1990. [Google Scholar]
- Van Houtte, P. MTM-FHM Software, Ver. 2.; User Manual; Peatix: Tokyo, Japan, 1995. [Google Scholar]
- Kestens, L.; Pirgazi, H. Texture formation in metal alloys with cubic crystal structures. Mater. Sci. Technol. 2016, 32, 1303–1315. [Google Scholar] [CrossRef]
- Hernandez-Duran, E.; Ros-Yanez, T.; Castro-Cerda, F.; Petrov, R. The influence of the heating rate on the microstructure and mechanical properties of a peak annealed quenched and partitioned steel. Mater. Sci. Eng. A 2020, 797, 140061. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, A. Mechanical properties of nanostructured bainitic steels. Materialia 2021, 15, 101034. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Li, W.; Huang, X.; Huang, W. Improved mechanical properties of a quenched and partitioned medium-carbon bainitic steel by control of bainitic isothermal transformation. J. Mater. Eng. Perform. 2020, 29, 32–41. [Google Scholar] [CrossRef]
- Ivaniski, T.M.; Souza, T.F.D.; Épp, J.; Rocha, A.d.S. Constitutive Modelling of High Temperature Flow Behaviour for a Low Carbon High Silicon Bainitic Steel. Mater. Res. 2020, 23. [Google Scholar] [CrossRef]
- Mousalou, H.; Yazdani, S.; Avishan, B.; Ahmadi, N.P.; Chabok, A.; Pei, Y. Microstructural and mechanical properties of low-carbon ultra-fine bainitic steel produced by multi-step austempering process. Mater. Sci. Eng. A 2018, 734, 329–337. [Google Scholar] [CrossRef]
- Fullwood, D.T.; Niezgoda, S.R.; Adams, B.L.; Kalidindi, S.R. Microstructure sensitive design for performance optimization. Prog. Mater. Sci. 2010, 55, 477–562. [Google Scholar] [CrossRef]
- Bhargava, M.; Tewari, A.; Mishra, S.K. Forming limit diagram of Advanced High Strength Steels (AHSS) based on strain-path diagram. Mater. Des. 2015, 85, 149–155. [Google Scholar] [CrossRef]
- Basak, S.; Panda, S.K. Implementation of YLD-96 plasticity theory in formability analysis of Bi-axial pre-strained steel sheets. Procedia Eng. 2017, 173, 1085–1092. [Google Scholar] [CrossRef]
- Bandyopadhyay, K.; Basak, S.; Prasad, K.S.; Lee, M.G.; Panda, S.K.; Lee, J. Improved formability prediction by modeling evolution of anisotropy of steel sheets. Int. J. Solids Struct. 2019, 156, 263–280. [Google Scholar] [CrossRef]
- Achineethongkham, K.; Uthaisangsuk, V. Analysis of forming limit behaviour of high strength steels under non-linear strain paths using a micromechanics damage modelling. Int. J. Mech. Sci. 2020, 183, 105828. [Google Scholar] [CrossRef]
- Shakerifard, B.; Galan Lopez, J.; Kestens, L.A. A New Electron Backscatter Diffraction-Based Method to Study the Role of Crystallographic Orientation in Ductile Damage Initiation. Metals 2020, 10, 113. [Google Scholar] [CrossRef]
- Shakerifard, B.; Lopez, J.G.; Hisker, F.; Kestens, L. Crystallographically resolved damage initiation in advanced high strength steel. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kuala Lumpur, Malaysia, 13–14 August 2018; IOP Publishing: Bristol, UK, 2018; Volume 375, p. 012022. [Google Scholar]
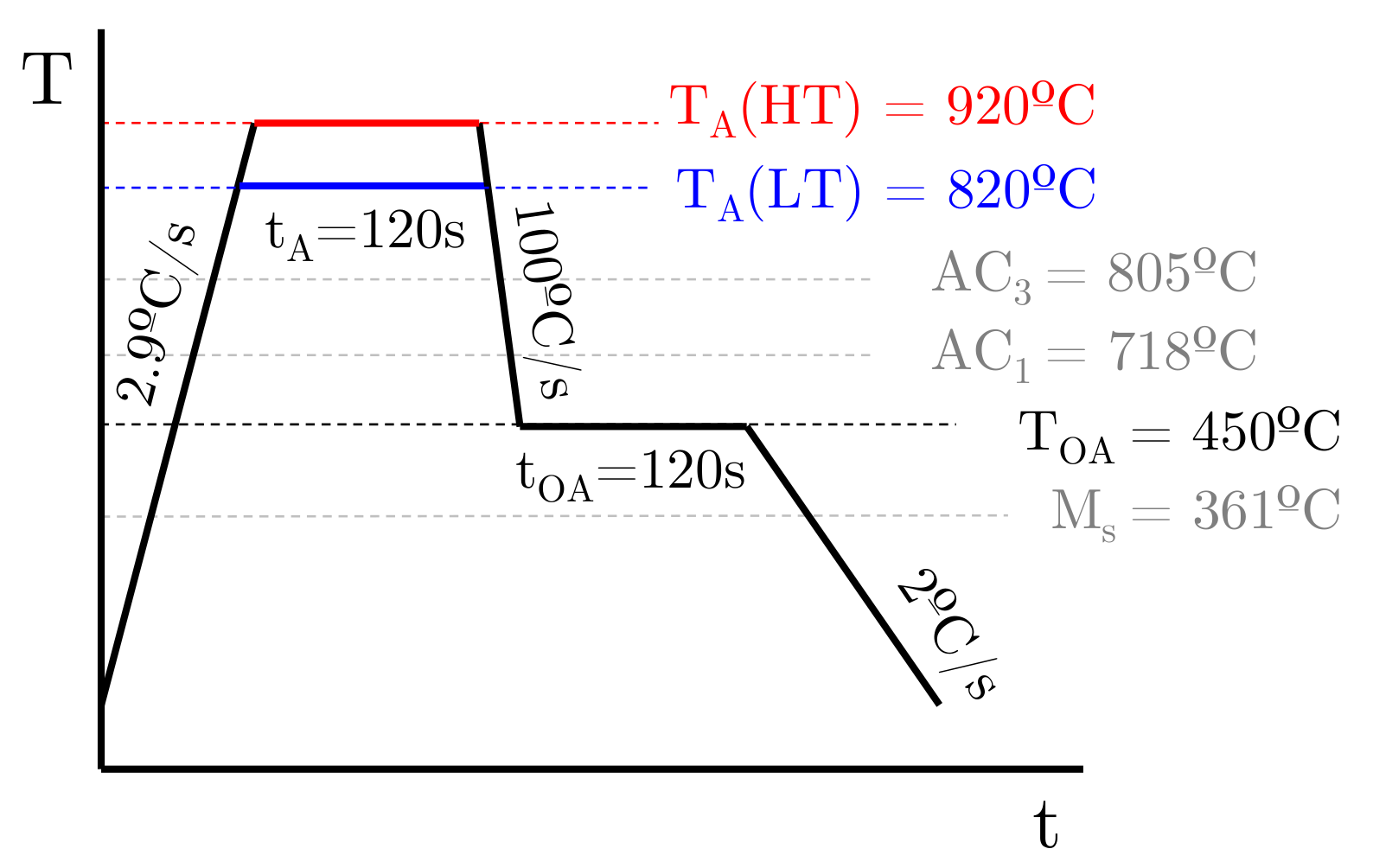

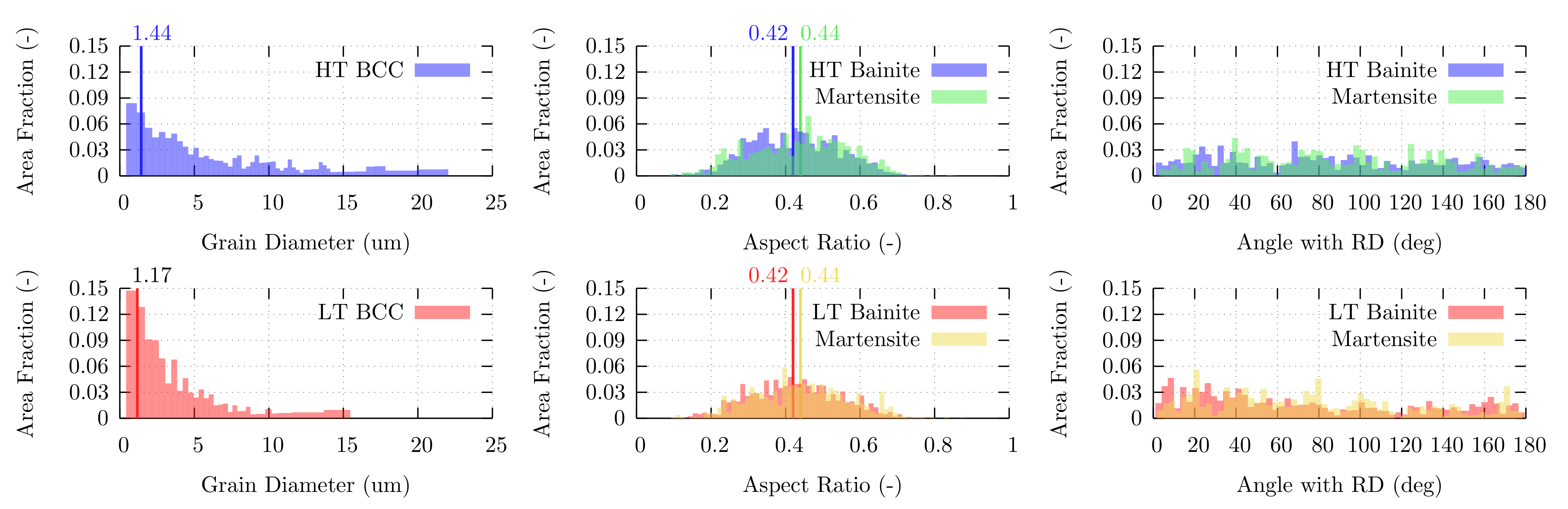

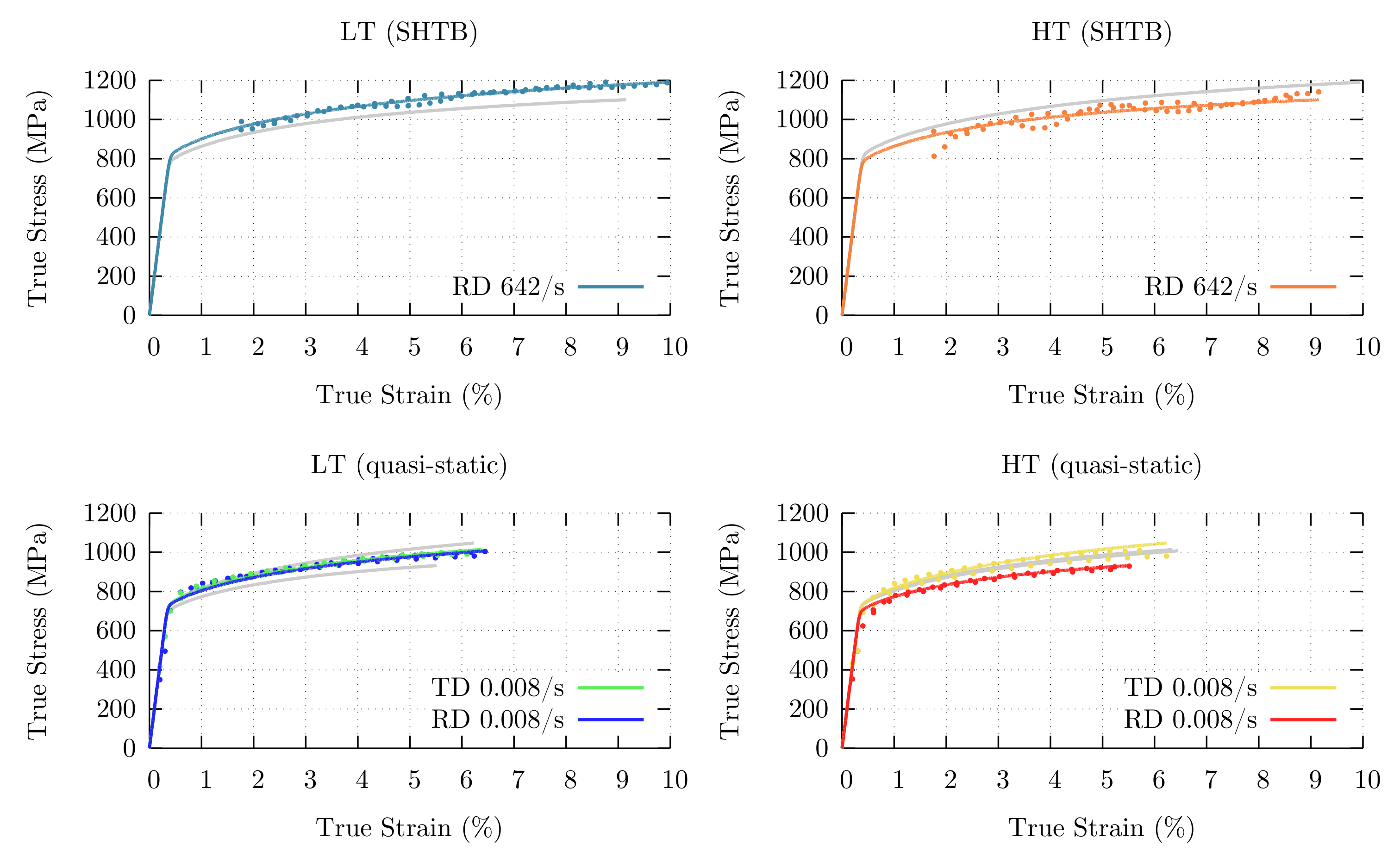
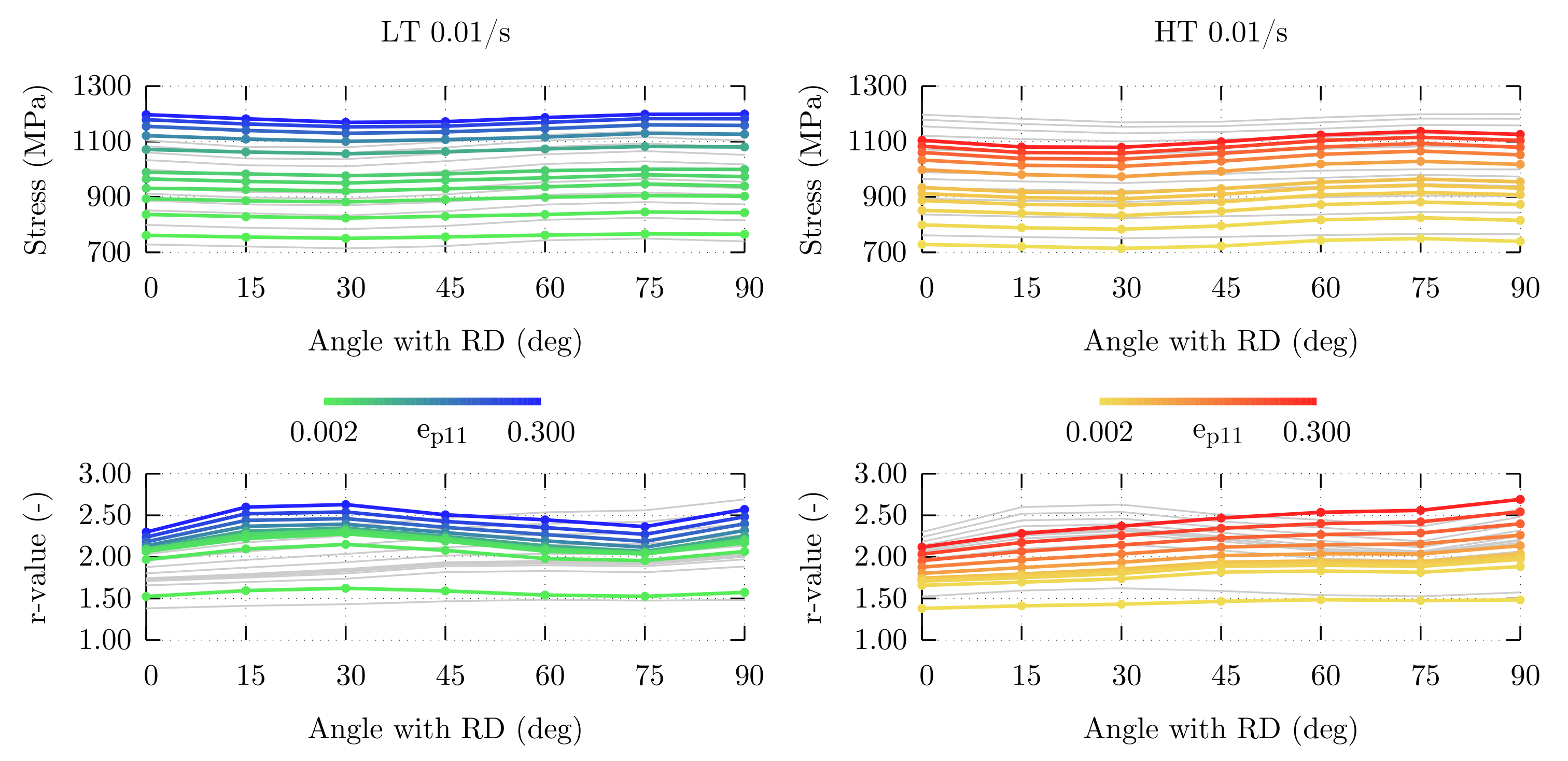
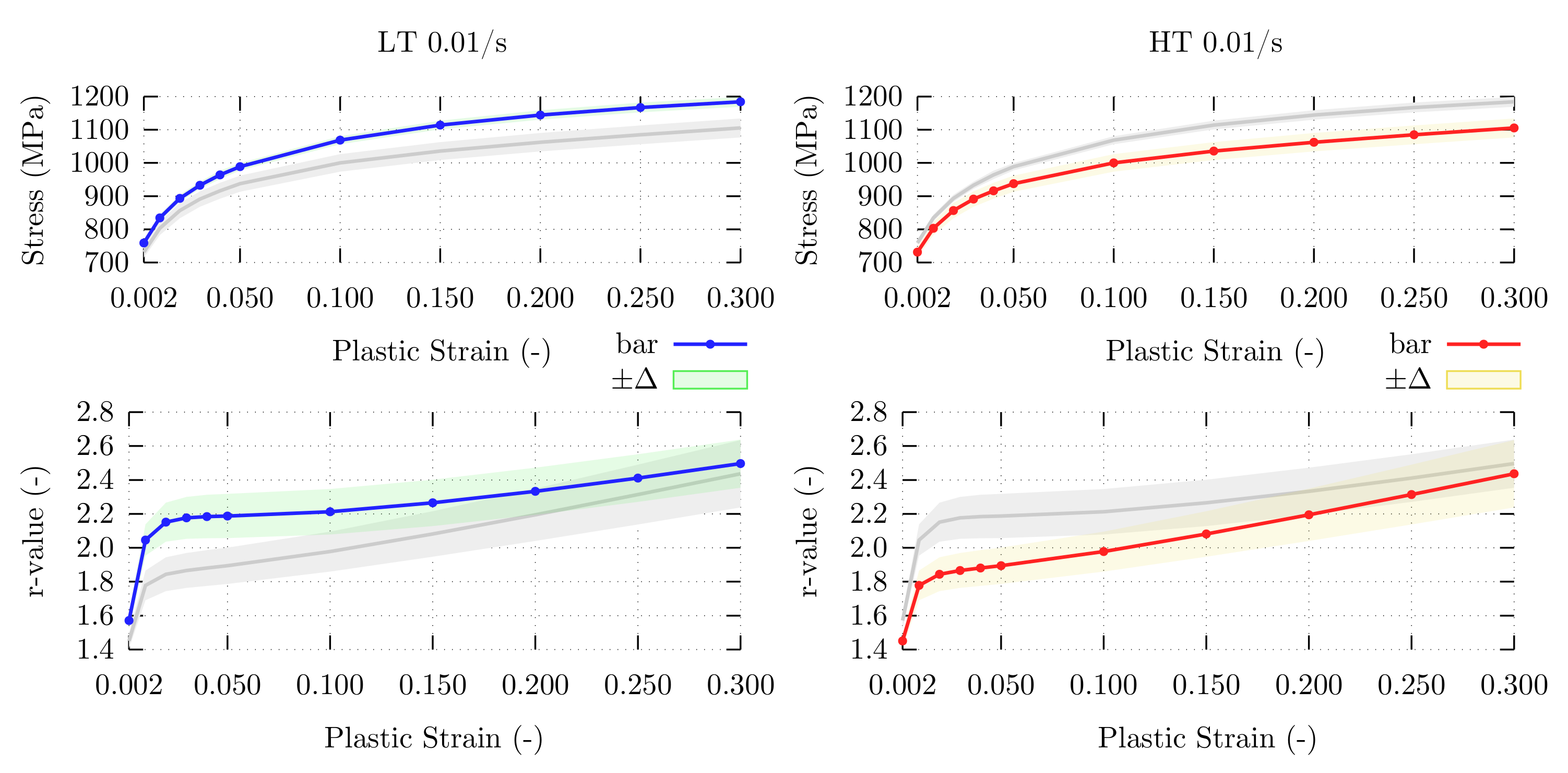
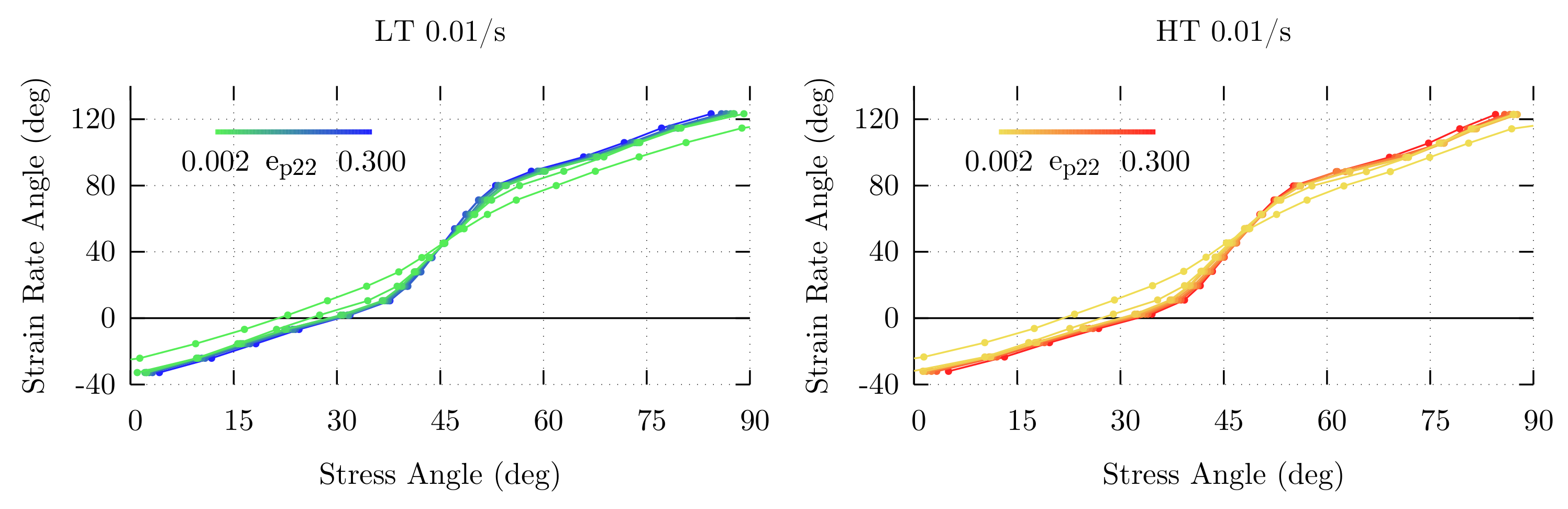
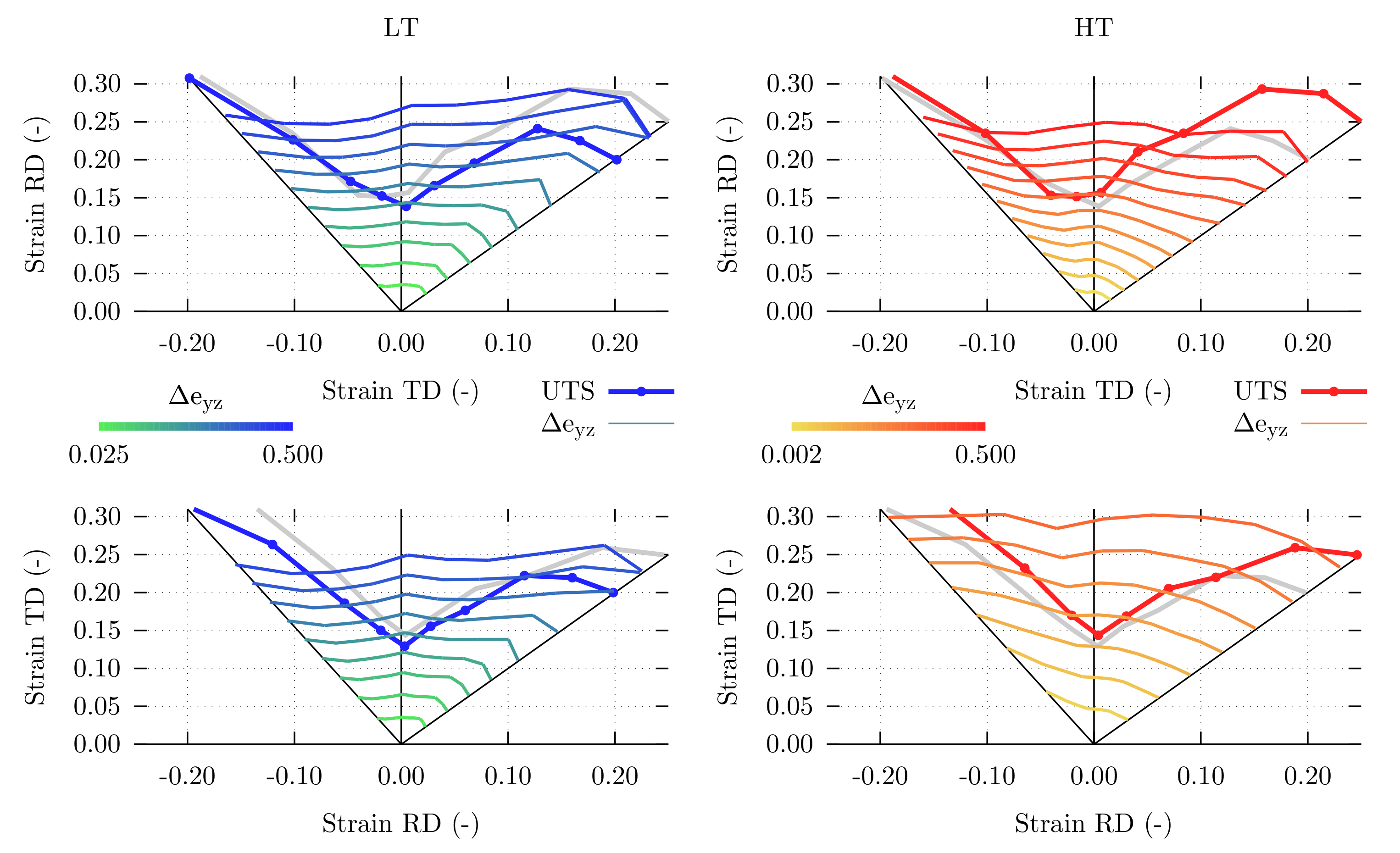
| Element | C | Mn | Si | Cr | Al | P | S | N | Fe |
|---|---|---|---|---|---|---|---|---|---|
| Weight (%) | 0.215 | 1.96 | 0.10 | 0.61 | 0.020 | 0.007 | 0.0027 | 0.005 | Remaining |
| 3.0 | 5.2 | |
| 5.2 | 5.1 |
| Material | Phase | (%) | d (m) | A.R. (-) | () | (%) | (%) | (m) |
|---|---|---|---|---|---|---|---|---|
| HT | Bainite | |||||||
| Martensite (LCM) | ||||||||
| Martensite (MA) | 0 | − | ||||||
| LT | Bainite | |||||||
| Martensite (LCM) | ||||||||
| Martensite (MA) | 0 | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galán-López, J.; Shakerifard, B.; Ochoa-Avendaño, J.; Kestens, L.A.I. Advanced Crystal Plasticity Modeling of Multi-Phase Steels: Work-Hardening, Strain Rate Sensitivity and Formability. Appl. Sci. 2021, 11, 6122. https://doi.org/10.3390/app11136122
Galán-López J, Shakerifard B, Ochoa-Avendaño J, Kestens LAI. Advanced Crystal Plasticity Modeling of Multi-Phase Steels: Work-Hardening, Strain Rate Sensitivity and Formability. Applied Sciences. 2021; 11(13):6122. https://doi.org/10.3390/app11136122
Chicago/Turabian StyleGalán-López, Jesús, Behnam Shakerifard, Jhon Ochoa-Avendaño, and Leo A. I. Kestens. 2021. "Advanced Crystal Plasticity Modeling of Multi-Phase Steels: Work-Hardening, Strain Rate Sensitivity and Formability" Applied Sciences 11, no. 13: 6122. https://doi.org/10.3390/app11136122
APA StyleGalán-López, J., Shakerifard, B., Ochoa-Avendaño, J., & Kestens, L. A. I. (2021). Advanced Crystal Plasticity Modeling of Multi-Phase Steels: Work-Hardening, Strain Rate Sensitivity and Formability. Applied Sciences, 11(13), 6122. https://doi.org/10.3390/app11136122






