Singing Transcription from Polyphonic Music Using Melody Contour Filtering
Abstract
1. Introduction
2. Melody Extraction
2.1. Phase Processing
2.2. Construct Salience Spectrogram
2.3. Singing Voice Detection
2.4. Edge Searching
- Binarization is performed for all peak points and classified as ;
- The distance between two peak points in neighboring frames must not be greater than of that of the continuous contours;
- When two points are discontinuous, the corresponding contour point is generated as a new contour points, and is the end of the previous contour;
- Until the completion of the entire salience graph search, the process is repeated.
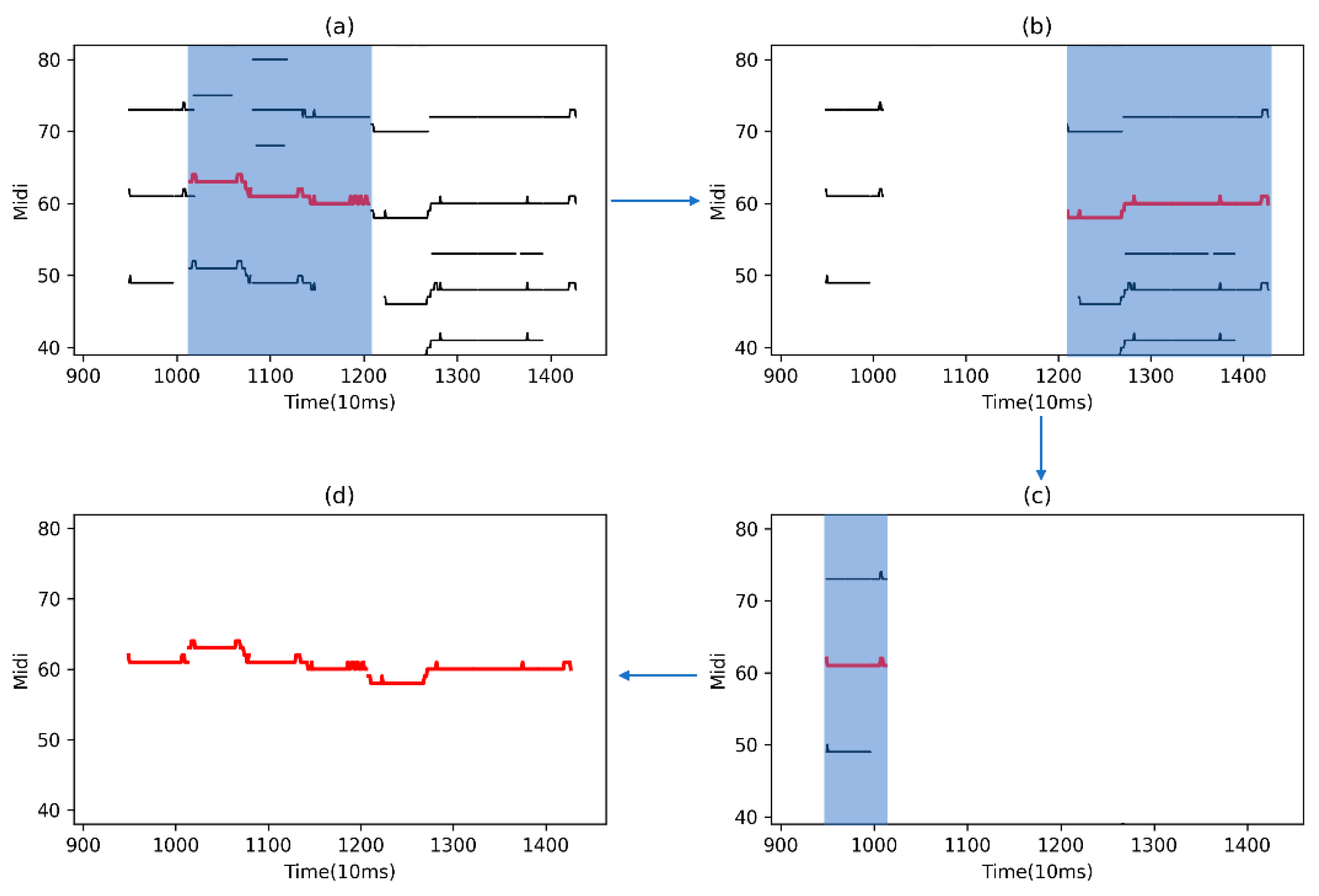
2.5. Melody Contour Filtering
2.5.1. Sliding Window
- (1)
- Superpose the peak points in each frame to obtain the total energy of a frame and create a difference in the energy difference axis, as shown in Figure 3;
- (2)
- Select a window with a specific length, and the hop length is padded with zero, while the length of the tail window is insufficient;
- (3)
- Search in each window and constitute a collection ;
- (4)
- When the same appears in two neighboring windows as the local maximum, all of the set a new collection .
- (5)
- Repeat the above steps (3)–(4) until all searches for the salience graph are completed.
2.5.2. Contour Filtering
- (1)
- Compare the size of each contour in the region to find the contour with the maximum energy (shown in Figure 5, the red lines);
- (2)
- Set the head and the tail from as to filter the remaining peak points in the region ;
- (3)
- If either the head or tail end of their distance between the boundaries is greater than the note threshold , contour filtering will be conducted on the region to find the next largest contour .
- (4)
- Otherwise, the melody contour searching ends in this area and the method proceeds to the next region .
- (5)
- Repeat the above steps until all searches for the entire map are completed.
2.6. Post-Processing
- (1)
- Calculate the average pitch of all current contours;
- (2)
- For the mean pitch of each contour, see Equation (11);
- (3)
- If the number of abnormal contours exceeds 1/4 of the total number, do not perform contour processing.
- (4)
- Repeat the above steps of (2)–(3) until all contours are completed.
3. Note Transcription
3.1. Two Fundamental Frequency Sequences
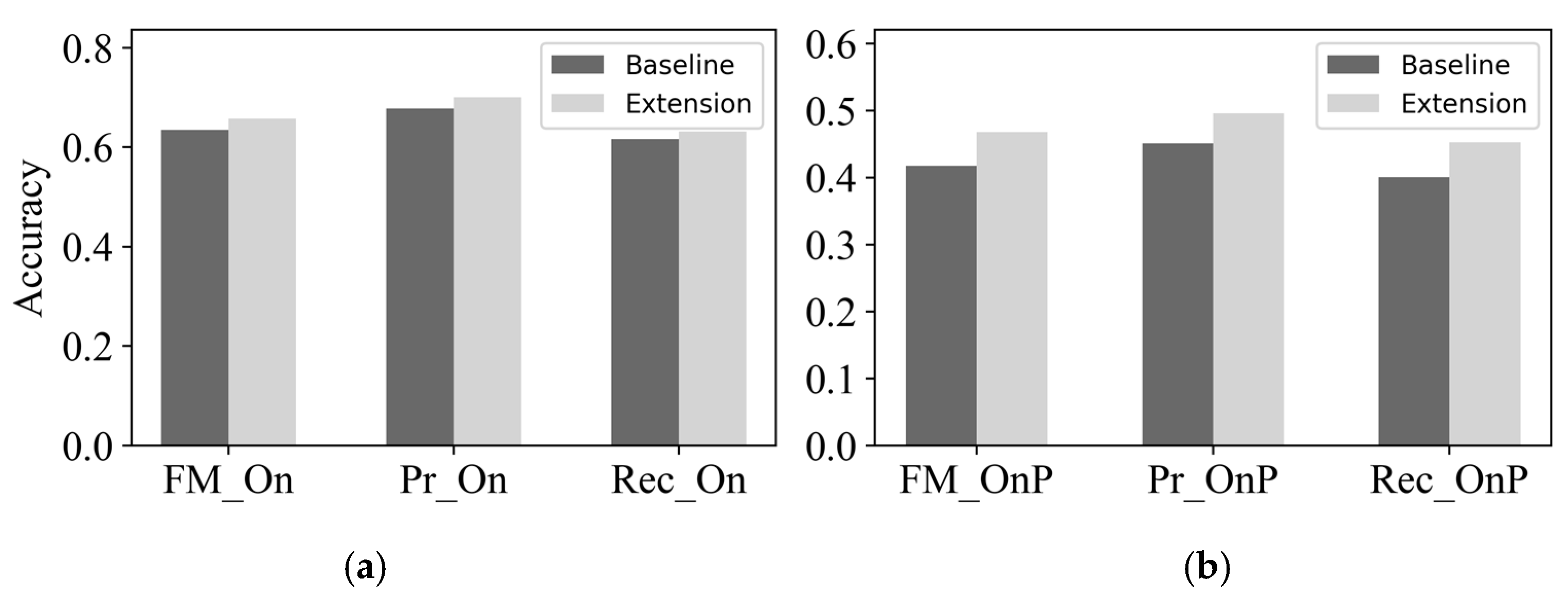
- Baseline: Retain the extracted current integer frequency sequences, which only limits the input for subsequent singing transcription tasks.
- Extension: Readjust the precision of pitch to the accuracy of 10 cents (where 100 cents correspond to a semitone). The basic frequency accuracy error required for the MIREX audio melody extraction competition is within 25 cents. Therefore, we recalculate the salience function using the same instantaneous frequency and amplitude after the phase processing step. The novel pitch frequency conversion formula is as follows:
3.2. Stability Region Division
- (1)
- The initial position of each contour is regarded as an onset. If , the contour is indecomposable, and is regarded as an offset and is transferred to the segmentation of the next contour;
- (2)
- Create a sliding window (as shown in the block in Figure 7), where the initial position is one window length, is the maximum pitch in the window, is the first pitch, and is the last pitch;
- (3)
- For each window, there are following operating conditions:
- (a)
- If , where the subscript of is denoted as , and the hop length is one window length;
- (b)
- If , where the subscript of is denoted as , and the hop length is two window lengths;
- (c)
- If neither of above is true, we consider the window to have attained stability, the hop length is a frame. We then recalculate Step (3) until the distance between and is less than a unit length 12;
- (4)
- Repeat steps (3) until all contour division are completed.
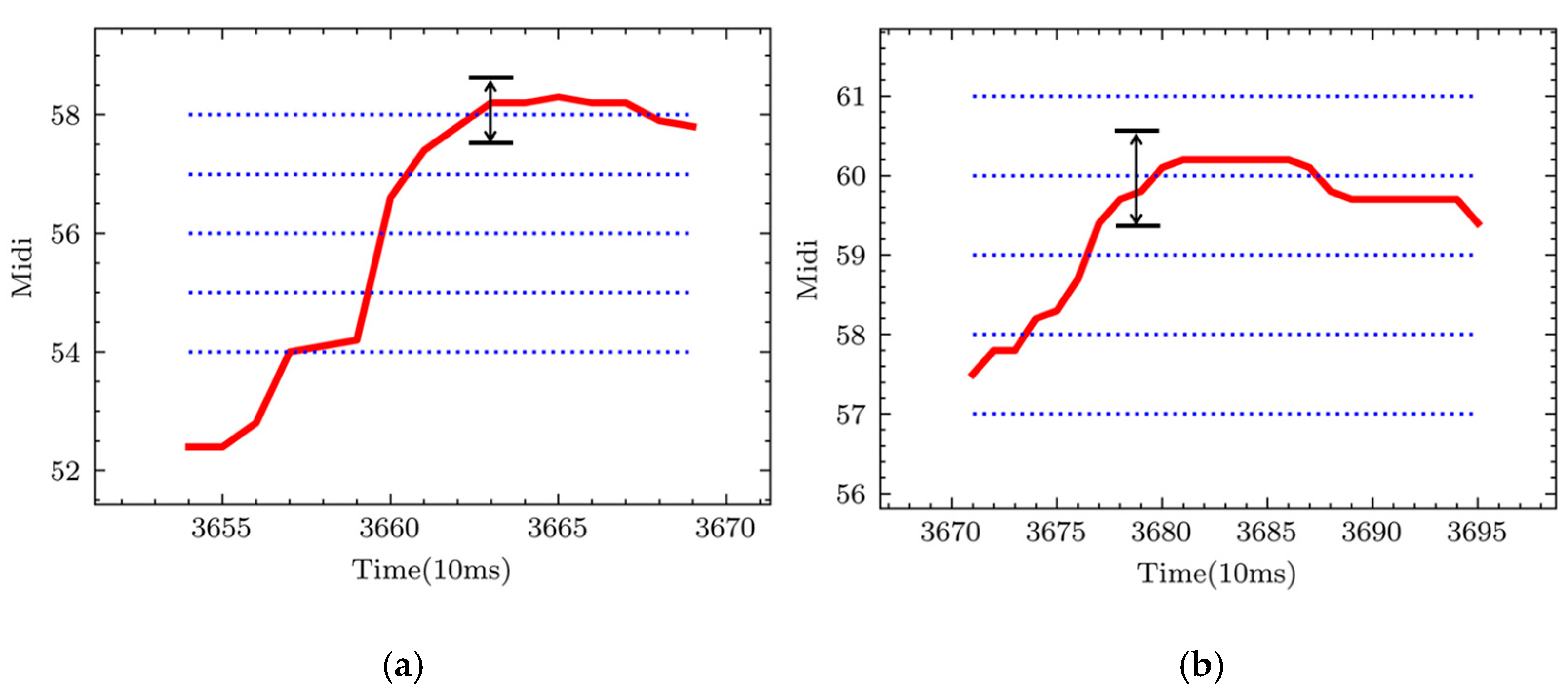
3.3. Pitch Line Matching
- (1)
- Calculate the average pitch of the note and round it to an integer MIDI pitch;
- (2)
- Determine the five pitch lines , , , as shown by the dashed blue line in Figure 8;
- (3)
- For the pitch of each frame, if the interval between a certain pitch line and is less than 50 cents, will be matched to that pitch line. Lastly, the most frequently matched pitches are recorded as the final pitch of the note;
- (4)
- Repeat the above steps to determine the pitch of all notes.
4. Evaluation
4.1. Audio Melody Extraction
4.1.1. Dataset
- MIREX09 database: 374 karaoke recordings of Chinese songs. Each recording was mixed at three different levels of signal-to-accompaniment ratio {−5 dB, 0 dB, +5 dB}, making a total of 1122 audio clips. Total time: 10,022 s.
- MIREX08 database: four excerpts of 1 min from “north Indian classical vocal performances”. There are two different mixtures of each of the four excerpts with differing amounts of accompaniment, making a total of eight audio clips. Total time: 501 s.
- MIREX05 database: 25 phrase excerpts of 10–40 s from the following genres: rock, R&B, pop, jazz, solo classical piano. Total time: 686 s.
- ADC04 database: Dataset from the 2004 Audio Description Contest. A total of 20 excerpts of about 20 s each were used. Total time: 369 s.
4.1.2. Metrics
- TP: true positives. These were frames in which the voicing was correctly detected and where TPC means a correct pitch, TPCch means a chroma correct, and TPI means an incorrect pitch but truly voiced;TP = TPC + TPCch + TPI
- TN: true negative. These were frames in which the nonvoice was correctly detected;
- FP: false positive. These frames were actually unpitched but were detected as pitched;
- FN: false negative. These frames were actually pitched but were detected as unpitched.
4.1.3. Results
4.2. Singing Transcription
4.2.1. Dataset
- Cmedia dataset: This dataset was composed of 200 YouTube links of pop songs (most are Chinese songs), including the ground truth files of the vocal transcription. In total, 100 audio files were released as the open set for training, and the other 100 were kept as the hidden set for testing.
4.2.2. Metrics
- The onset difference was less than 100 ms in this competition;
- The pitch difference was less than 50 cents in this competition.
4.2.3. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klapuri, A.P. Automatic Music Transcription as We Know It Today. J. New Music Res. 2004, 33, 269–282. [Google Scholar]
- Benetos, E.; Dixon, S.; Giannoulis, D.; Kirchhoff, H.; Klapuri, A. Automatic music transcription: Challenges and future directions. J. Intell. Inf. Syst. 2013, 41, 407–434. [Google Scholar] [CrossRef]
- Nishikimi, R.; Nakamura, E.; Fukayama, S.; Goto, M.; Yoshii, K. Automatic singing transcription based on encoder-decoder recurrent neural networks with a weakly-supervised attention mechanism. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 161–165. [Google Scholar]
- Poliner, G.E.; Ellis, D.P.; Ehmann, A.F.; Gómez, E.; Streich, S.; Ong, B. Melody transcription from music audio: Approaches and evaluation. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1247–1256. [Google Scholar] [CrossRef]
- Kroher, N.; Gómez, E. Automatic transcription of flamenco singing from polyphonic music recordings. IEEE Trans. Audio Speech Lang. Process. 2016, 24, 901–913. [Google Scholar] [CrossRef][Green Version]
- Dannenberg, R.B.; Birmingham, W.P.; Pardo, B.; Hu, N.; Meek, C.; Tzanetakis, G. A comparative evaluation of search techniques for query-by-humming using the MUSART testbed. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 687–701. [Google Scholar] [CrossRef]
- Tsai, W.H.; Lee, H.C. Automatic evaluation of karaoke singing based on pitch, volume, and rhythm features. IEEE Trans. Audio Speech Lang. Process. 2011, 20, 1233–1243. [Google Scholar] [CrossRef]
- Foucard, R.; Durrieu, J.L.; Lagrange, M.; Richard, G. Multimodal similarity between musical streams for cover version detection. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, Texas, USA, 15–19 March 2010; pp. 5514–5517. [Google Scholar]
- Kako, T.; Ohishi, Y.; Kameoka, H.; Kashino, K.; Takeda, K. Automatic Identification for Singing Style based on Sung Melodic Contour Characterized in Phase Plane. In Proceedings of the ISMIR, Kobe, Japan, 26–30 October 2009; pp. 393–398. [Google Scholar]
- Dressler, K. An Auditory Streaming Approach for Melody Extraction from Polyphonic Music. In Proceedings of the ISMIR, Miami, FL, USA, 24–28 October 2011; pp. 19–24. [Google Scholar]
- Bittner, R.; Salamon, J.; Essid, S.; Bello, J. Melody extraction by contour classification. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Malaga, Spain, 26–30 October 2015. [Google Scholar]
- Reddy, M.G.; Rao, K.S. Predominant melody extraction from vocal polyphonic music signal by time-domain adaptive filtering-based method. Circuits Syst. Signal Process. 2018, 37, 2911–2933. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Z.; Yin, F.; Zhang, Q. Melody extraction from polyphonic music using particle filter and dynamic programming. IEEE ACM Trans. Audio Speech Lang. Process. 2018, 26, 1620–1632. [Google Scholar] [CrossRef]
- Ikemiya, Y.; Itoyama, K.; Yoshii, K. Singing voice separation and vocal F0 estimation based on mutual combination of robust principal component analysis and subharmonic summation. IEEE ACM Trans. Audio Speech Lang. Process. 2016, 24, 2084–2095. [Google Scholar] [CrossRef]
- Smaragdis, P.; Brown, J.C. Non-negative matrix factorization for polyphonic music transcription. In Proceedings of the 2003 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 19–22 October 2003; pp. 177–180. [Google Scholar]
- Kum, S.; Nam, J. Joint detection and classification of singing voice melody using convolutional recurrent neural networks. Appl. Sci. 2019, 9, 1324. [Google Scholar] [CrossRef]
- Salamon, J.; Gómez, E. Melody extraction from polyphonic music signals using pitch contour characteristics. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1759–1770. [Google Scholar] [CrossRef]
- Cancela, P. Tracking melody in polyphonic audio. In Proceedings of the Mirex 2008. Proc. of Music Information Retrieval Evaluation eXchange, Philadelphia, PA, USA, 14–18 September 2008. [Google Scholar]
- Bittner, R.M.; McFee, B.; Salamon, J.; Li, P.; Bello, J.P. Deep Salience Representations for F0 Estimation in Polyphonic Music. In Proceedings of the ISMIR, Suzhou, China, 23–27 October 2017; pp. 63–70. [Google Scholar]
- Rigaud, F.; Radenen, M. Singing Voice Melody Transcription Using Deep Neural Networks. In Proceedings of the ISMIR, New York City, NY, USA, 7–11 August 2016; pp. 737–743. [Google Scholar]
- Schlüter, J.; Böck, S. Improved musical onset detection with convolutional neural networks. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 6979–6983. [Google Scholar]
- Molina, E.; Tardón, L.J.; Barbancho, A.M.; Barbancho, I. SiPTH: Singing transcription based on hysteresis defined on the pitch-time curve. IEEE Acm Trans. Audio Speech Lang. Process. 2014, 23, 252–263. [Google Scholar] [CrossRef]
- Gómez, E.; Bonada, J.; Salamon, J. Automatic transcription of flamenco singing from monophonic and polyphonic music recordings. In Proceedings of the Interdisciplinary Conference on Flamenco Research (INFLA) and II International Workshop of Folk Music Analysis (FMA), Sevilla, Spain, 19–20 April 2012. [Google Scholar]
- Klapuri, A.; Davy, M. (Eds.) Signal Processing Methods for Music Transcription 2017.
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.; McVicar, M.; Battenberg, E.; Nieto, O. librosa: Audio and music signal analysis in python. In Proceedings of the 14th Python in Science Conference, Austin, TX, USA, 6–12 July 2015; Volume 8, pp. 18–25. [Google Scholar]
- Böck, S.; Korzeniowski, F.; Schlüter, J.; Krebs, F.; Widmer, G. Madmom: A new python audio and music signal processing library. In Proceedings of the 24th ACM international conference on Multimedia, New York, NY, USA, 15–19 October 2016; pp. 1174–1178. [Google Scholar]
- Boashash, B. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Keiler, F.; Marchand, S. Survey on extraction of sinusoids in stationary sounds. In Proceedings of the Digital Audio Effects Conference, Hamburg, Germany, 26–28 September 2002; pp. 51–58. [Google Scholar]
- Salamon, J.; Gómez, E.; Bonada, J. Sinusoid extraction and salience function design for predominant melody estimation. In Proceedings of the 14th International Conference on Digital Audio Effects, Paris, France, 19–23 September 2011; pp. 73–80. [Google Scholar]
- Sundberg, J. The acoustics of the singing voice. Sci. Am. 1977, 236, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- Molina, E.; Barbancho-Perez, A.M.; Tardon-Garcia, L.J.; Barbancho-Perez, I. Evaluation Framework for Automatic Singing Transcription 2014. In Proceedings of the 15th International Society for Music Information Retrieval Conference, ISMIR, Taipei, Taiwan, 27–31 October 2014. [Google Scholar]
- Su, L.; Yang, Y.H. Combining spectral and temporal representations for multipitch estimation of polyphonic music. IEEE ACM Trans. Audio Speech Lang. Process. 2015, 23, 1600–1612. [Google Scholar] [CrossRef]
- Lin, M.; Feng, Y. A post-processing of onset detection based on verification with neural network. In Proceedings of the 7th Conference on Sound and Music Technology (CSMT), Harbin, China, December 2019; pp. 67–80. [Google Scholar]
- Zih-Sing, F.; Su, L. Hierarchical Classification Networks for Singing Voice Segmentation and Transcription. In Proceedings of the ISMIR, Delft, The Netherlands, 4–8 November 2019; pp. 900–907. [Google Scholar]
- McNab, R.J.; Smith, L.A.; Witten, I.H. Signal Processing for Melody Transcription 1995. In Proceedings of the 19th Australasian Computer Science Conf, Melbourne, Australia, 31 January–2 February 1996. [Google Scholar]
- Huang, A.; Li, S.Y.; Dong, Z. Audio Melody Extraction Using Multi-Task Convolutional Recurrent Neural Network. In Proceedings of the MIREX, Delft, The Netherlands, 4–8 November 2019. [Google Scholar]
- Dressler, K. Audio Melody Extraction for MIREX 2020. In Proceedings of the MIREX, Montréal, QC, Canada, 11–15 October 2020. [Google Scholar]
- Cao, Z.; Feng, X.; Li, W. A Multi-task Learning Approach for Melody Extraction. In Proceedings of the 7th Conference on Sound and Music Technology (CSMT), Harbin, China, December 2019; pp. 53–65. [Google Scholar]
- Balhar, J.; Hajic, J., Jr. Melody Extraction Using A Harmonic Convolution Neural Network. In Proceedings of the MIREX, Delft, The Netherlands, 4–8 November 2019. [Google Scholar]
- Raffel, C.; McFee, B.; Humphrey, E.J. mir_eval: A transparent implementation of common MIR metrics. In Proceedings of the 15th International Society for Music Information Retrieval Conference, ISMIR, Taipei, Taiwan, 27–31 October 2014. [Google Scholar]









| Algorithm | OA | RPA | RCA | VR | VFA |
|---|---|---|---|---|---|
| KN4 | 0.724 | 0.698 | 0.702 | 0.764 | 0.124 |
| AH1 | 0.703 | 0.746 | 0.772 | 0.797 | 0.171 |
| HZ4 | 0.701 | 0.721 | 0.751 | 0.879 | 0.32 |
| HLD1 | 0.686 | 0.739 | 0.774 | 0.777 | 0.177 |
| KD1 | 0.681 | 0.749 | 0.767 | 0.832 | 0.373 |
| ZC1 | 0.671 | 0.612 | 0.619 | 0.698 | 0.174 |
| BH2 | 0.657 | 0.734 | 0.774 | 0.714 | 0.292 |
| BH1 | 0.64 | 0.721 | 0.756 | 0.707 | 0.312 |
| HH4 | 0.444 | 0.615 | 0.633 | 0.956 | 0.92 |
| WJH2 | 0.433 | 0.599 | 0.621 | 0.955 | 0.914 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Feng, Y. Singing Transcription from Polyphonic Music Using Melody Contour Filtering. Appl. Sci. 2021, 11, 5913. https://doi.org/10.3390/app11135913
He Z, Feng Y. Singing Transcription from Polyphonic Music Using Melody Contour Filtering. Applied Sciences. 2021; 11(13):5913. https://doi.org/10.3390/app11135913
Chicago/Turabian StyleHe, Zhuang, and Yin Feng. 2021. "Singing Transcription from Polyphonic Music Using Melody Contour Filtering" Applied Sciences 11, no. 13: 5913. https://doi.org/10.3390/app11135913
APA StyleHe, Z., & Feng, Y. (2021). Singing Transcription from Polyphonic Music Using Melody Contour Filtering. Applied Sciences, 11(13), 5913. https://doi.org/10.3390/app11135913





