Light-Induced Ring Pattern in a Dye-Doped Nematic Liquid Crystal
Abstract
1. Introduction
2. Experimental Observations of the Ring Patterns
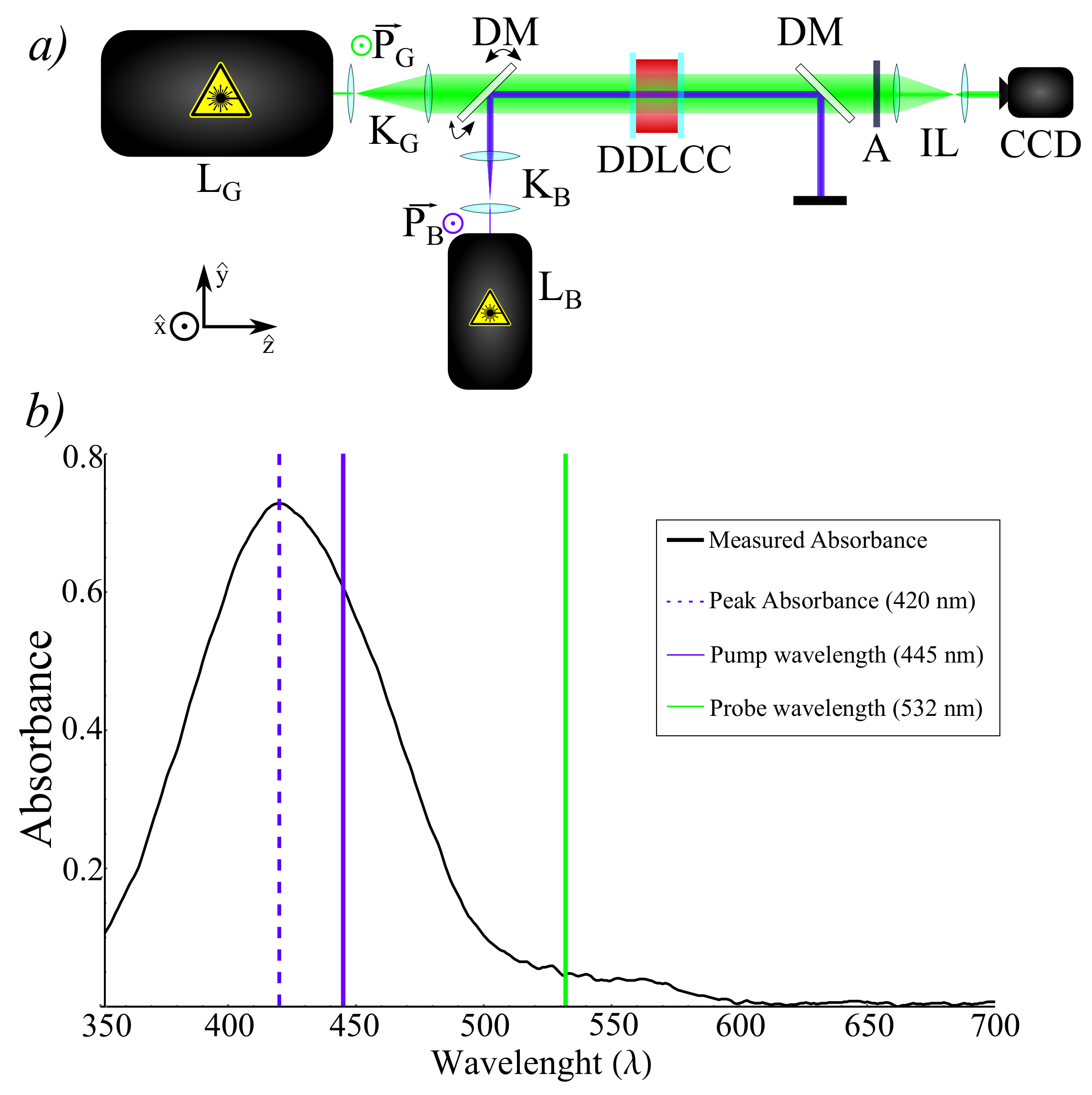
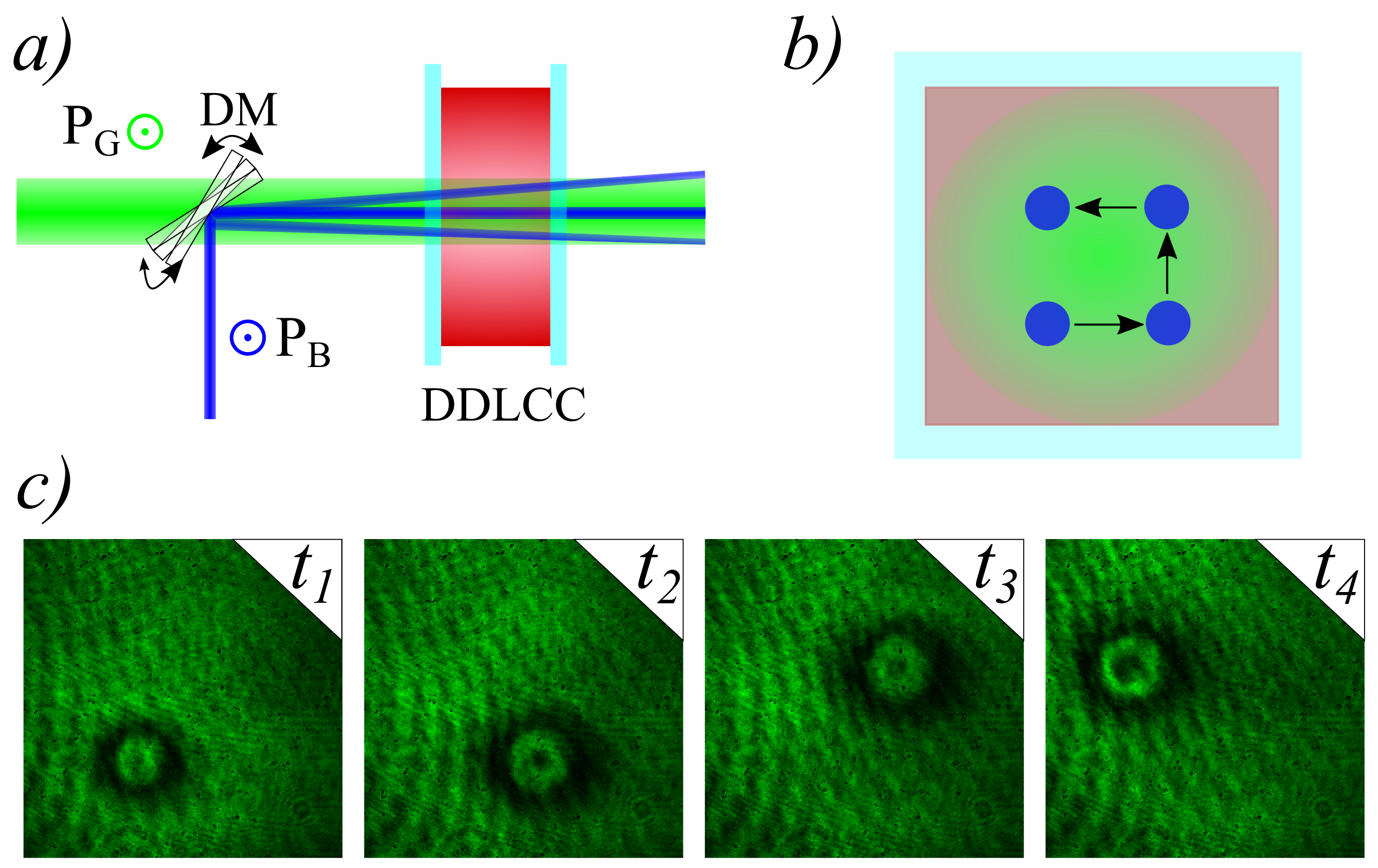
2.1. Experimental Setup
2.2. Synthesis and Preparation of Dye-Dopant and Liquid Crystal Mixture
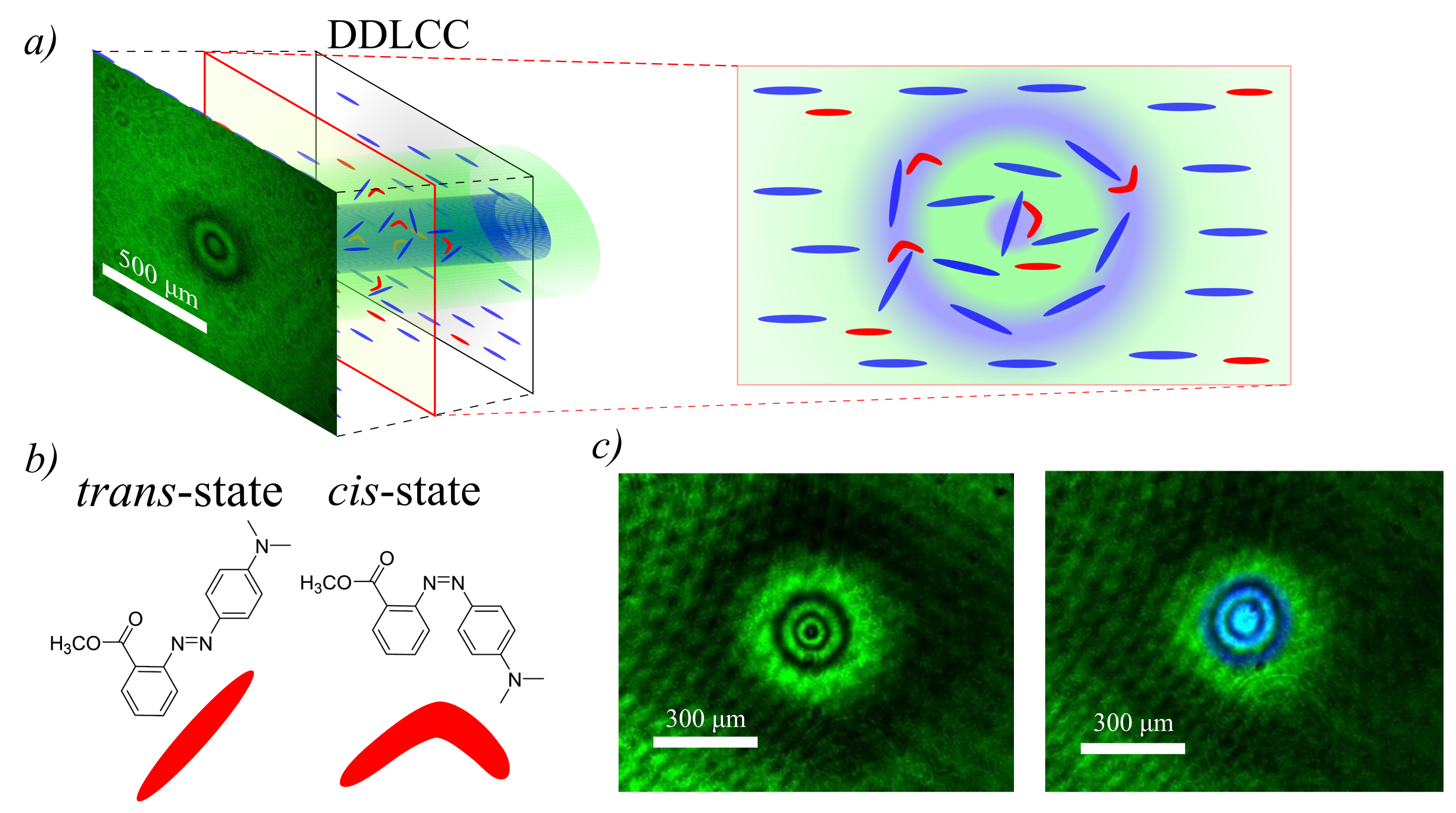
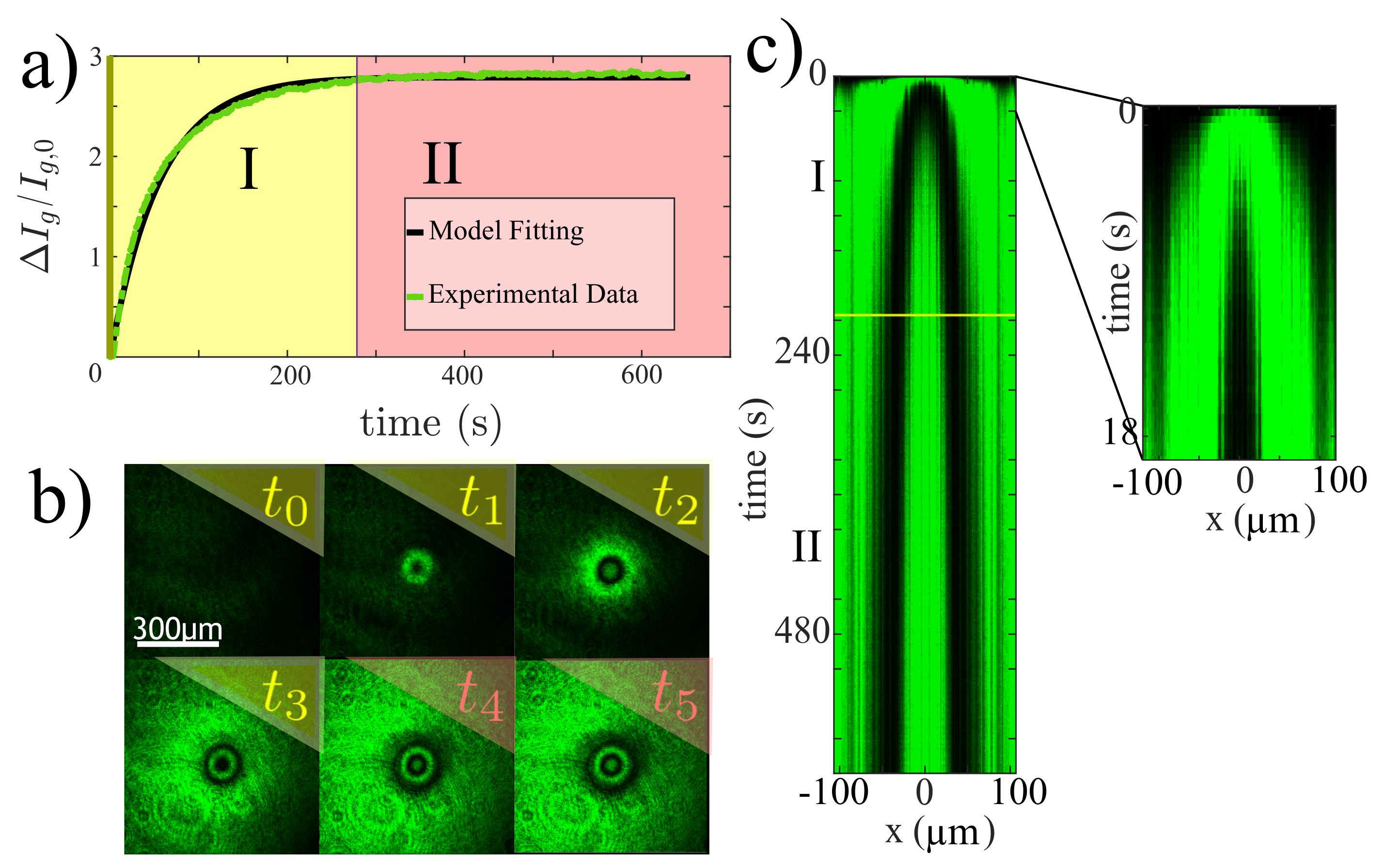
2.3. Light-Induced Ring Patterns
3. Mathematical Modeling for Photo-Isomerization in Dye-Doped Liquid Crystals
3.1. Adiabatic Elimination and Effective Model
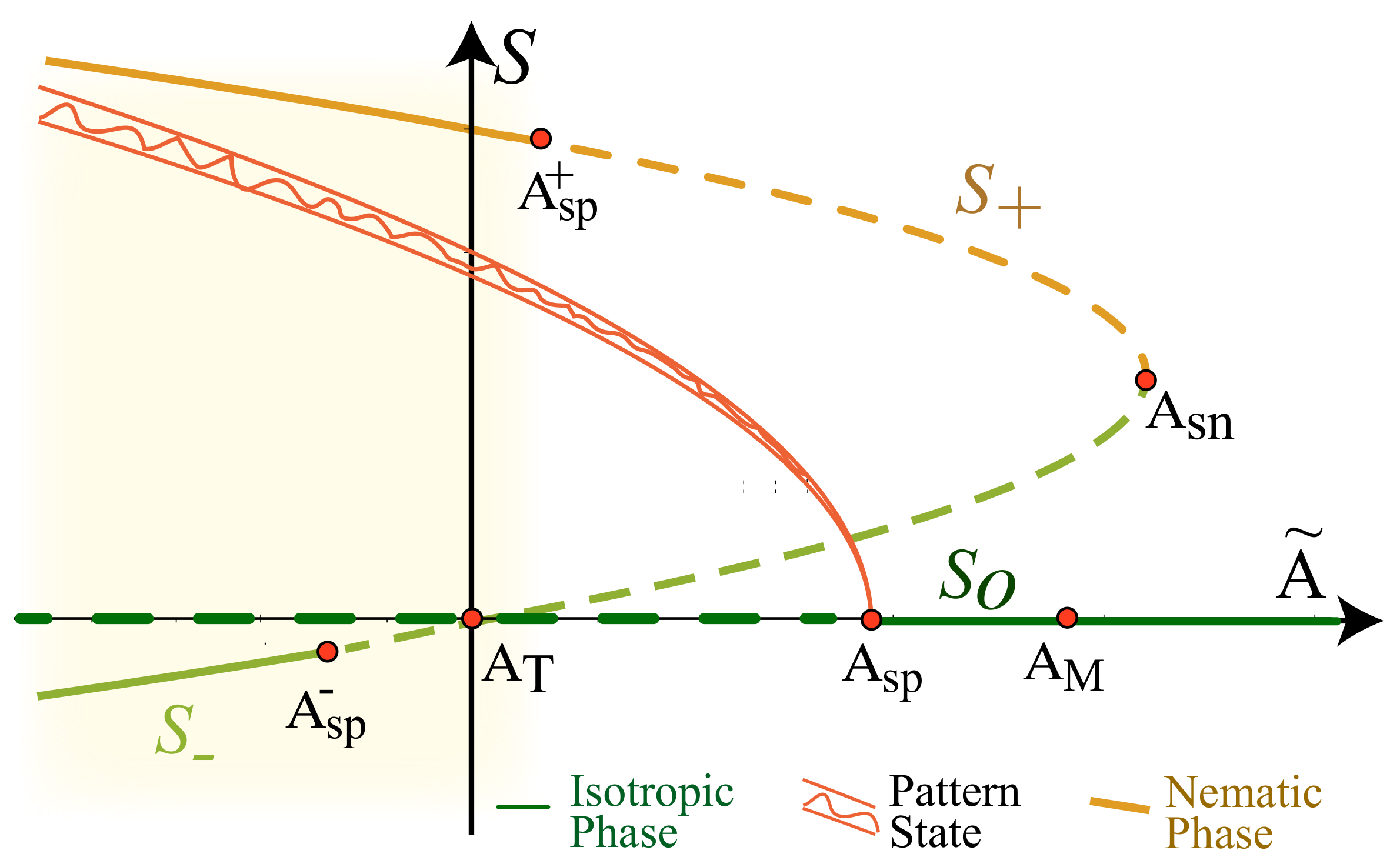
3.2. Homogeneous Illumination and Bifurcation Diagram
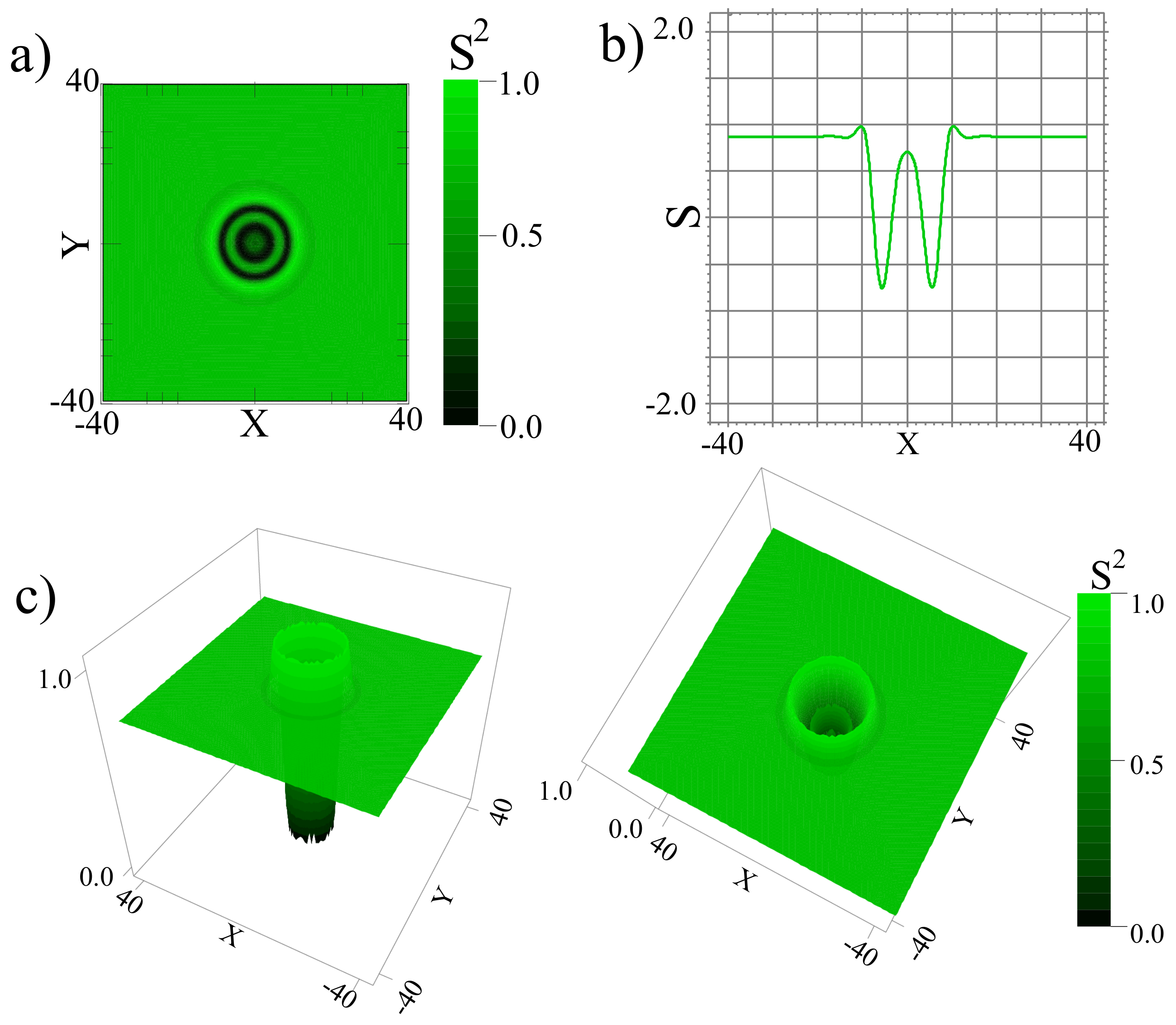
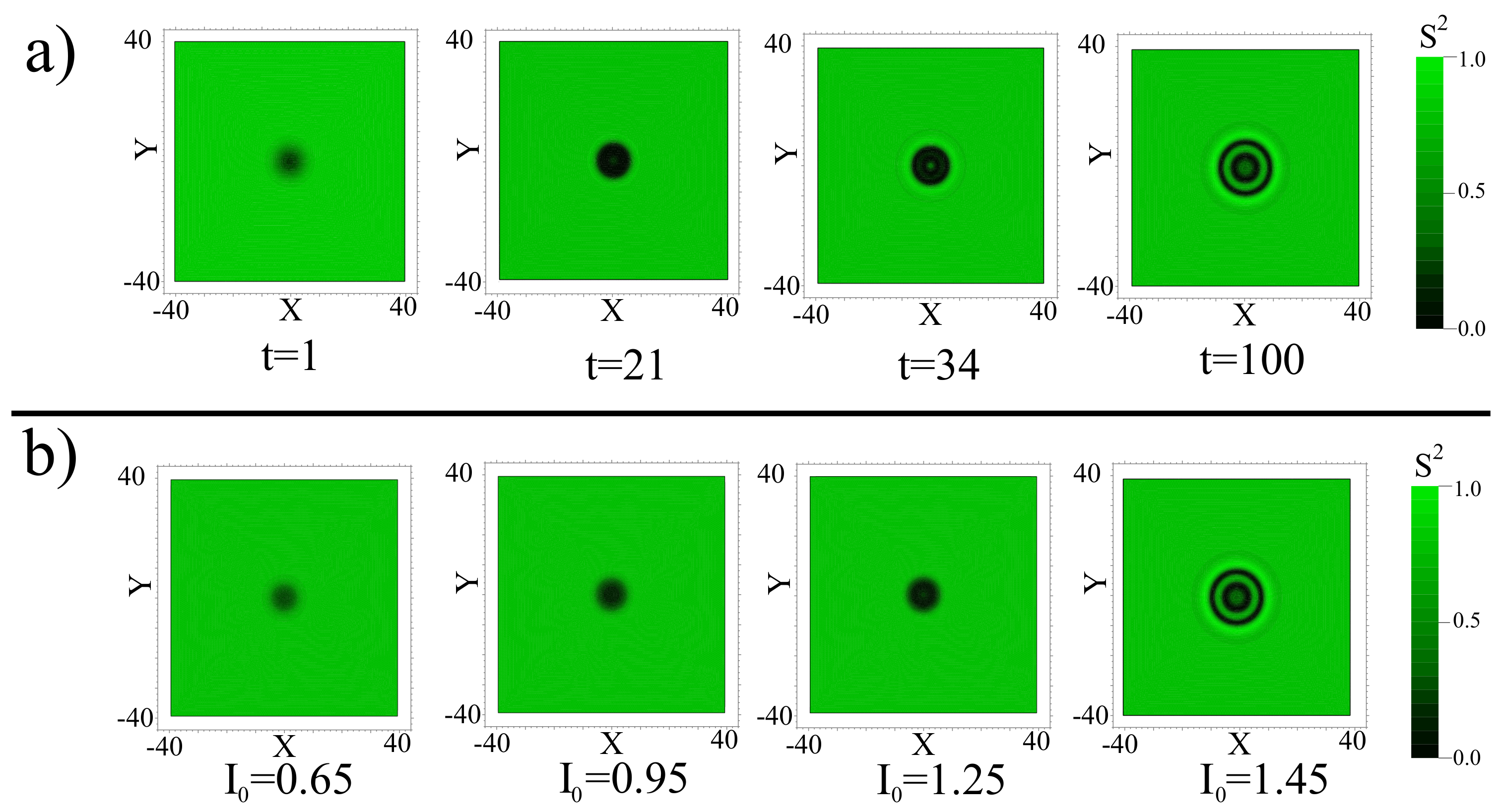
3.3. Light-Induced Ring Pattern
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Newton, I. Opticks, or, a Treatise of the Reflections, Refractions, Inflections & Colours of Light; Sam. Smith and Benj. Walford, Printers to the Royal Society: London, UK, 1704. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Shen, Y.R. The Principles of Nonlinear Optics; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Mills, D.L. Nonlinear Optics: Basic Concepts; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- New, G. Introduction to Nonlinear Optics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Lugiato, L.; Prati, F.; Brambilla, M. Nonlinear Optical Systems; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; Oxford Science Publications, Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Chandrasekhar, S. Liquid Crystal; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Oswald, P.; Pieranski, P. Nematic and Cholesteric Liquid Crystals; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Vertogen, G.; de Jeu, W.H. Thermotropic Liquid Crystals, Fundamentals; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Khoo, I.C. Liquid Crystals; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Takatoh, K.; Sakamoto, M.; Hasegawa, R.; Koden, M.; Itoh, N.; Hasegawa, M. Alignment Technology and Applications of Liquid Crystal Devices; CRC Press: Abingdon, UK, 2005. [Google Scholar]
- Zel’Dovich, B.Y.; Pilipetskii, N.F.; Sukhov, A.V.; Tabiryan, N.V. Giant Optical Nonlinearity in the Mesophase of a Nematic Liquid Crystal. JETP Lett. 1980, 31, 263–267. [Google Scholar]
- Zolot’ko, A.S.; Kitaeva, V.F.; Sobolev, N.K.N.; Chillag, L. The effect of an optical field on the nematic phase of the liquid crystal OCBP. JETP Lett. 1980, 32, 158–162. [Google Scholar]
- Zolot’ko, A.S.; Kitaeva, V.F.; Sobolev, N.N.; Sukhorukov, A.P. Self-focusing of laser radiation in the course of the Fréedericksz transition in the nematic phase of a liquid crystal. Zh. Eksp. Teor. Fiz. 1981, 81, 933–941. [Google Scholar]
- Durbin, S.D.; Arakelian, S.M.; Shen, Y.R. Optical-field-induced birefringence and Freedericksz transition in a nematic liquid crystal. Phys. Rev. Lett. 1981, 47, 1411–1414. [Google Scholar] [CrossRef]
- Frisken, B.J.; Palffy-Muhoray, P. Electric-field-induced twist and bend Freedericksz transitions in nematic liquid crystals. Phys. Rev. A 1989, 39, 1513–1518. [Google Scholar] [CrossRef]
- Khoo, I.C. Nonlinear optics of liquid crystalline materials. Phys. Rep. 2009, 471, 221–267. [Google Scholar] [CrossRef]
- Jánossy, I.; Szabados, L. Photoisomerization of azo-dyes in nematic liquid crystals. J. Nonlinear Opt. Phys. 1998, 7, 539–551. [Google Scholar] [CrossRef]
- Odent, V.; Clerc, M.G.; Falcón, C.; Bortolozzo, U.; Louvergneaux, E.; Residori, S. Photo-isomerization fronts in dye-doped nematic liquid crystals. Opt. Lett. 2014, 39, 1861–1864. [Google Scholar] [CrossRef]
- Andrade-Silva, I.; Bortolozzo, U.; Clerc, M.G.; González-Cortés, G.; Residori, S.; Wilson, M. Spontaneous light-induced Turing patterns in a dye-doped twisted nematic layer. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Andrade-Silva, I.; Bortolozzo, U.; Castillo-Pinto, C.; Clerc, M.G.; González-Cortés, G.; Residori, S.; Wilson, M. Dissipative structures induced by photoisomerization in a dye-doped nematic liquid crystal layer. Phil. Trans. R. Soc. A 2018, 376, 20170382. [Google Scholar] [CrossRef]
- Durbin, S.D.; Arakelian, S.M.; Shen, Y.R. Laser-induced diffraction rings from a nematic-liquid-crystal film. Opt. Lett. 1981, 6, 411–413. [Google Scholar] [CrossRef]
- Assanto, G. Nematicons: Spatial Optical Solitons in Nematic Liquid Crystals; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Barnik, M.I.; Zolot’ko, A.S.; Kitaeva, V.F. Interaction of light with a dye-doped nematic liquid crystal. J. Exp. Theor. Phys. 1997, 84, 1122–1130. [Google Scholar] [CrossRef]
- Deng, L.; He, K.; Su, W.; Sun, H.; Wang, R.; Zhang, H.; Liu, H.K. Optical limiting performances of the methyl-red-dye-doped nematic liquid crystal films. Mater. Devices Syst. Disp. Lighting 2002, 4918, 79–89. [Google Scholar]
- Li, H.; Wang, J.; Wang, C.; Zeng, P.; Cai, P.; Pan, Y.; Yang, Y. Off-resonant nonlinear optical refraction properties of azo dye doped nematic liquid crystals. Opt. Mater. Express 2016, 6, 459–465. [Google Scholar] [CrossRef]
- Serak, S.V.; Tabiryan, N.V.; Assanto, G. Nematicons in azobenzene liquid crystals. Mol. Cryst. Liq. Cryst. 2012, 559, 202–213. [Google Scholar] [CrossRef]
- Park, H.S.; Oh, K.S.; Kim, K.S.; Chang, T.; Spiegel, D.R. Change of internal hydrogen bonding of methyl red upon photoisomerization monitored by Forced Rayleigh Scattering. J. Phys. Chem. B 1999, 103, 2355–2360. [Google Scholar] [CrossRef]
- Castillo-Pinto, C.; Clerc, M.G.; González-Cortés, G. Extended stable equilibrium invaded by an unstable state. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kosa, T.; Sukhomlinova, L.; Su, L.; Taheri, B.; White, T.J.; Bunning, T.J. Light-induced liquid crystallinity. Nature 2012, 485, 347–349. [Google Scholar] [CrossRef]
- Kahl, D.J.; Hutchings, K.M.; Lisabeth, E.M.; Haak, A.J.; Leipprandt, J.R.; Dexheimer, T.; Khanna, D.; Tsou, P.S.; Campbell, P.L.; Fox, D.A.; et al. 5-Aryl-1,3,4-oxadiazol-2-ylthioalkanoic Acids: A Highly Potent New Class of Inhibitors of Rho/Myocardin-Related Transcription Factor (MRTF)/Serum Response Factor (SRF)-Mediated Gene Transcription as Potential Antifibrotic Agents for Scleroderma. J. Med. Chem. 2019, 62, 4350–4369. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics (Course of Theoretical Physics, Volume 5); Pergamon Press: New York, NY, USA, 1993. [Google Scholar]
- Sasaki, T.; Ikeda, T. Photochemical switching of polarization in ferroelectric liquid crystals: Effect of structure of host FLCs. Ferroelectrics 1993, 149, 343–351. [Google Scholar] [CrossRef]
- Bechhoefer, J.; Simon, A.J.; Libchaber, A.; Oswald, P. Destabilization of a flat nematic-isotropic interface. Phys. Rev. A 1989, 40, 2042–2056. [Google Scholar] [CrossRef] [PubMed]
- Haken, H. Synergetics: Introduction and Advanced Topics; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Clerc, M.G.; Petrossian, A.; Residori, S. Bouncing localized structures in a liquid-crystal light-valve experiment. Phys. Rev. E 2005, 71, 015205. [Google Scholar] [CrossRef]
- Kozyreff, G.; Tlidi, M. Nonvariational real Swift-Hohenberg equation for biological, chemical, and optical systems. Chaos 2007, 17, 037103. [Google Scholar] [CrossRef] [PubMed]
- Kozyreff, G.; Chapman, S.J.; Tlidi, M. Interaction of two modulational instabilities in a semiconductor resonator. Phys. Rev. E 2003, 68, 015201. [Google Scholar] [CrossRef] [PubMed]
- Clerc, M.G.; Verschueren, N. Quasiperiodicity route to spatiotemporal chaos in one-dimensional pattern-forming systems. Phys. Rev. E 2013, 88, 052916. [Google Scholar] [CrossRef]
- Burke, J.; Dawes, J.H. Localized states in an extended Swift?Hohenberg equation. SIAM J. Appl. Dyn. Syst. 2012, 11, 261–284. [Google Scholar] [CrossRef]
- Alvarez-Socorro, A.J.; Clerc, M.G.; Tlidi, M. Spontaneous motion of localized structures induced by parity symmetry breaking transition. Chaos 2018, 28, 053119. [Google Scholar] [CrossRef]
- Houghton, S.M.; Knobloch, E. Swift-Hohenberg equation with broken cubic-quintic nonlinearity. Phys. Rev. E 2011, 84, 016204. [Google Scholar] [CrossRef]
- Verschueren, N.; Bortolozzo, U.; Clerc, M.G.; Residori, S. Spatiotemporal chaotic localized state in liquid crystal light valve experiments with optical feedback. Phys. Rev. Lett. 2013, 110, 104101. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. B 1952, 237, 37–72. [Google Scholar]
- Goldstein, R.E.; Gunaratne, G.H.; Gil, L.; Coullet, P. Hydrodynamic and interfacial patterns with broken space-time symmetry. Phys. Rev. A 1991, 43, 6700–6721. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clerc, M.G.; González-Cortés, G.; Hidalgo, P.I.; Letelier, L.A.; Morel, M.J.; Vergara, J. Light-Induced Ring Pattern in a Dye-Doped Nematic Liquid Crystal. Appl. Sci. 2021, 11, 5285. https://doi.org/10.3390/app11115285
Clerc MG, González-Cortés G, Hidalgo PI, Letelier LA, Morel MJ, Vergara J. Light-Induced Ring Pattern in a Dye-Doped Nematic Liquid Crystal. Applied Sciences. 2021; 11(11):5285. https://doi.org/10.3390/app11115285
Chicago/Turabian StyleClerc, Marcel G., Gregorio González-Cortés, Paulina I. Hidalgo, Lucciano A. Letelier, Mauricio J. Morel, and Jorge Vergara. 2021. "Light-Induced Ring Pattern in a Dye-Doped Nematic Liquid Crystal" Applied Sciences 11, no. 11: 5285. https://doi.org/10.3390/app11115285
APA StyleClerc, M. G., González-Cortés, G., Hidalgo, P. I., Letelier, L. A., Morel, M. J., & Vergara, J. (2021). Light-Induced Ring Pattern in a Dye-Doped Nematic Liquid Crystal. Applied Sciences, 11(11), 5285. https://doi.org/10.3390/app11115285






