Quantitative Risk Assessment for Deep Tunnel Failure Based on Normal Cloud Model: A Case Study at the ASHELE Copper Mine, China
Abstract
1. Introduction
2. Normal Cloud Model Theory
2.1. Entropy Weight Method
2.2. Cloud Model
2.2.1. Definition and Numerical Characteristics of the Cloud Model
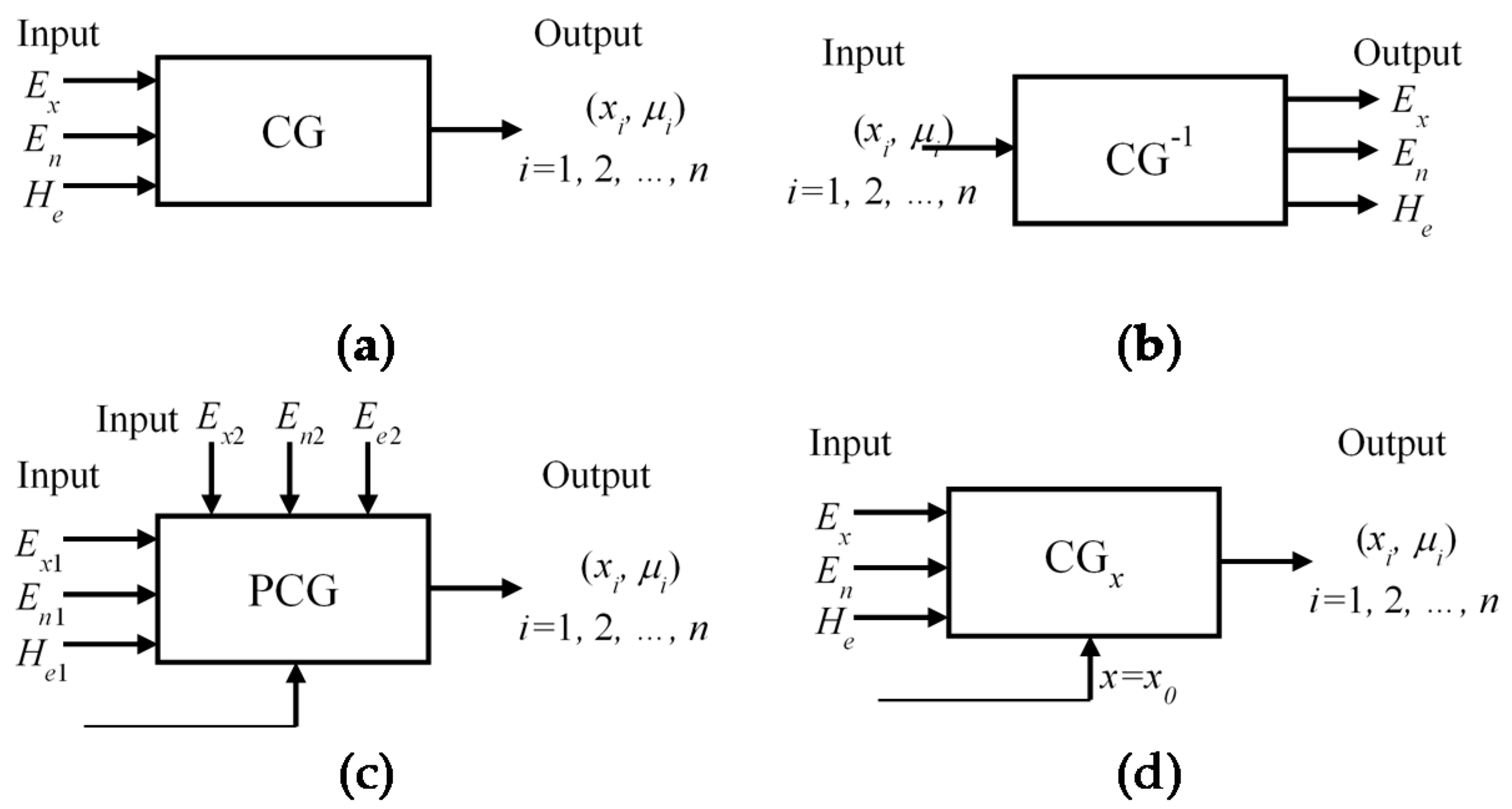
2.2.2. Cloud Generator
2.2.3. Integrated Cloud Model
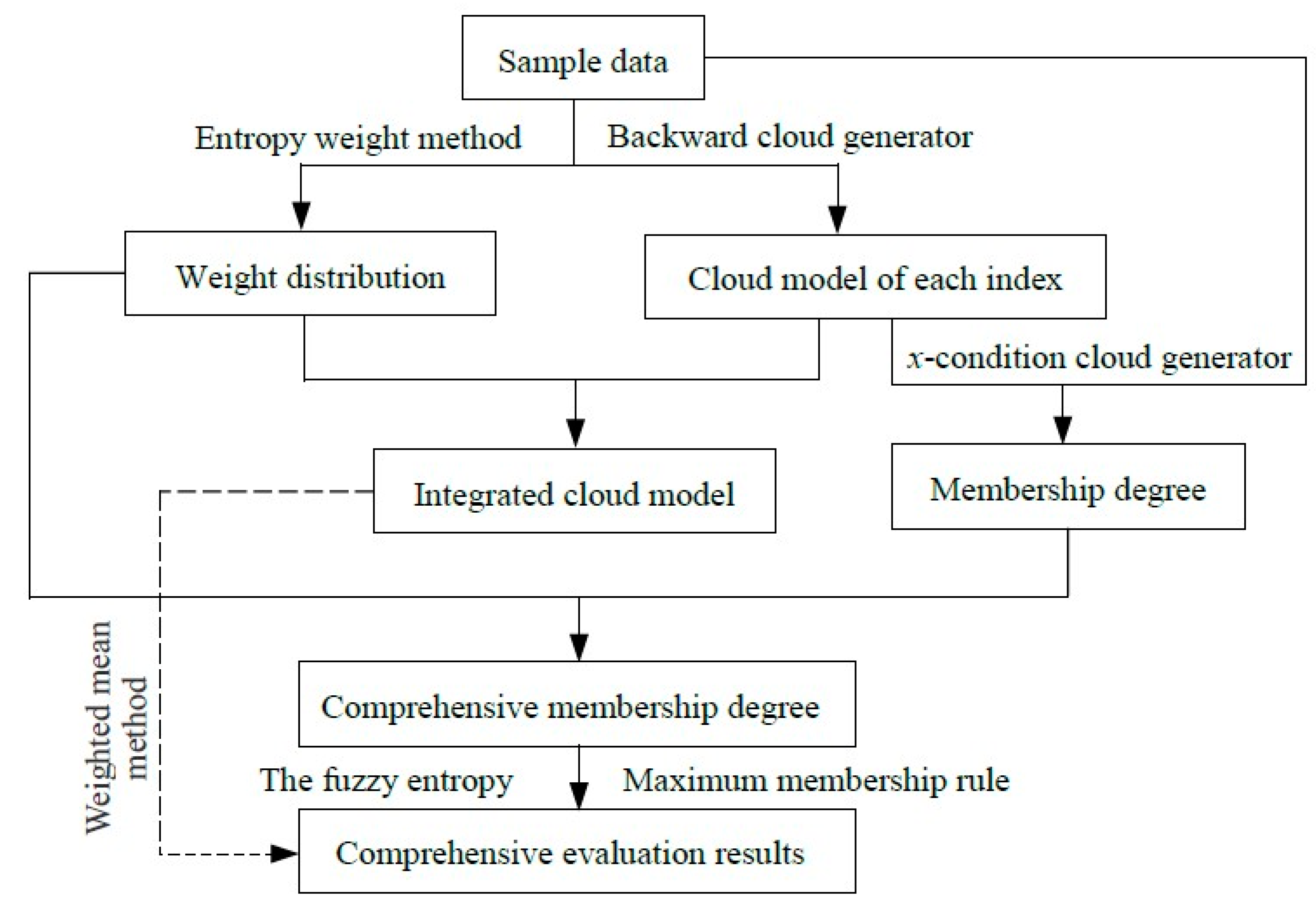
2.3. Calculation Process of Cloud Model
3. The Index System of Risk Assessment for Tunnel Failure
3.1. Damage Level of the Tunnel
3.2. Evaluation Index
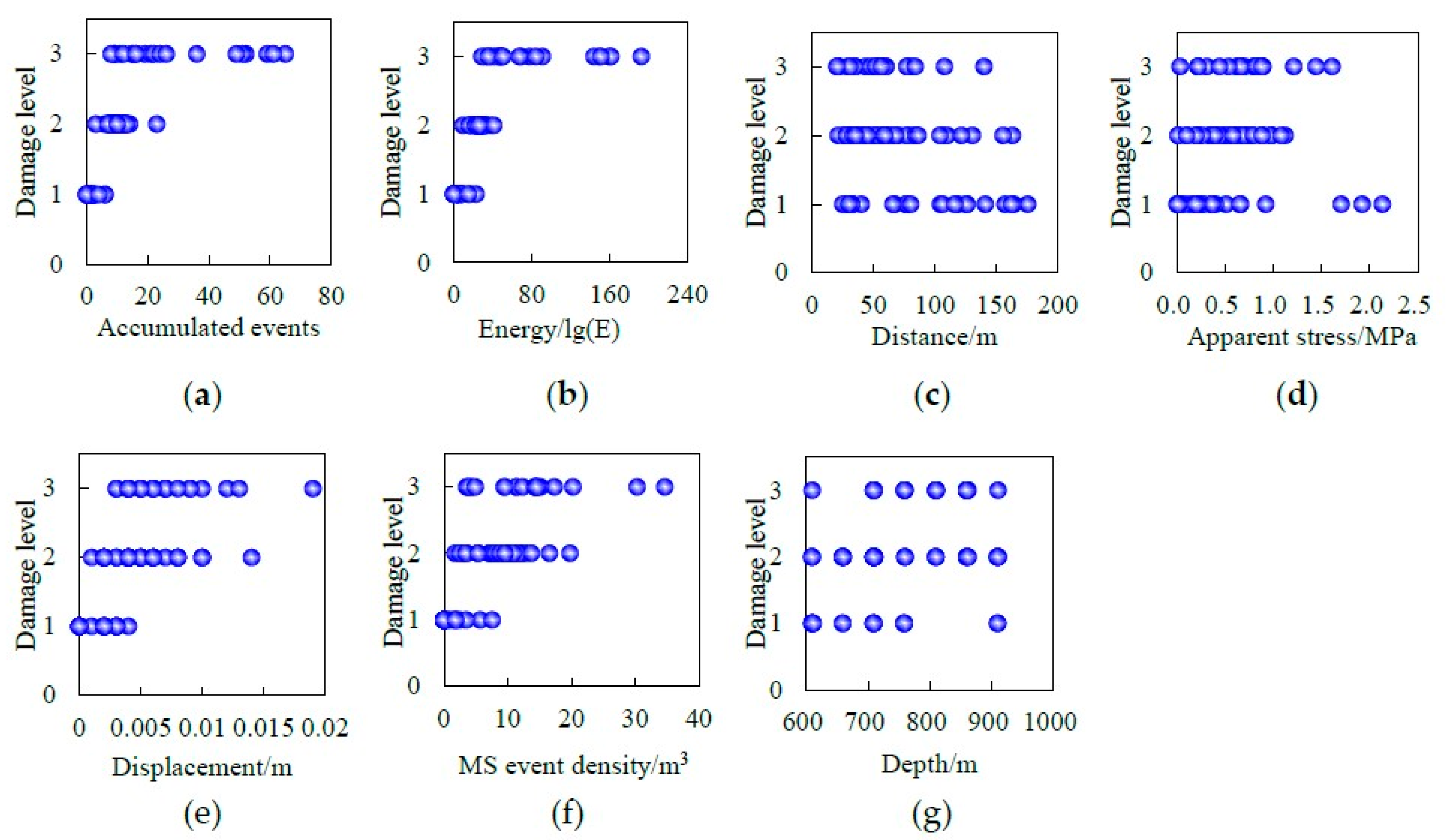
3.3. Correlation Between Evaluation Indicators and Damage Levels
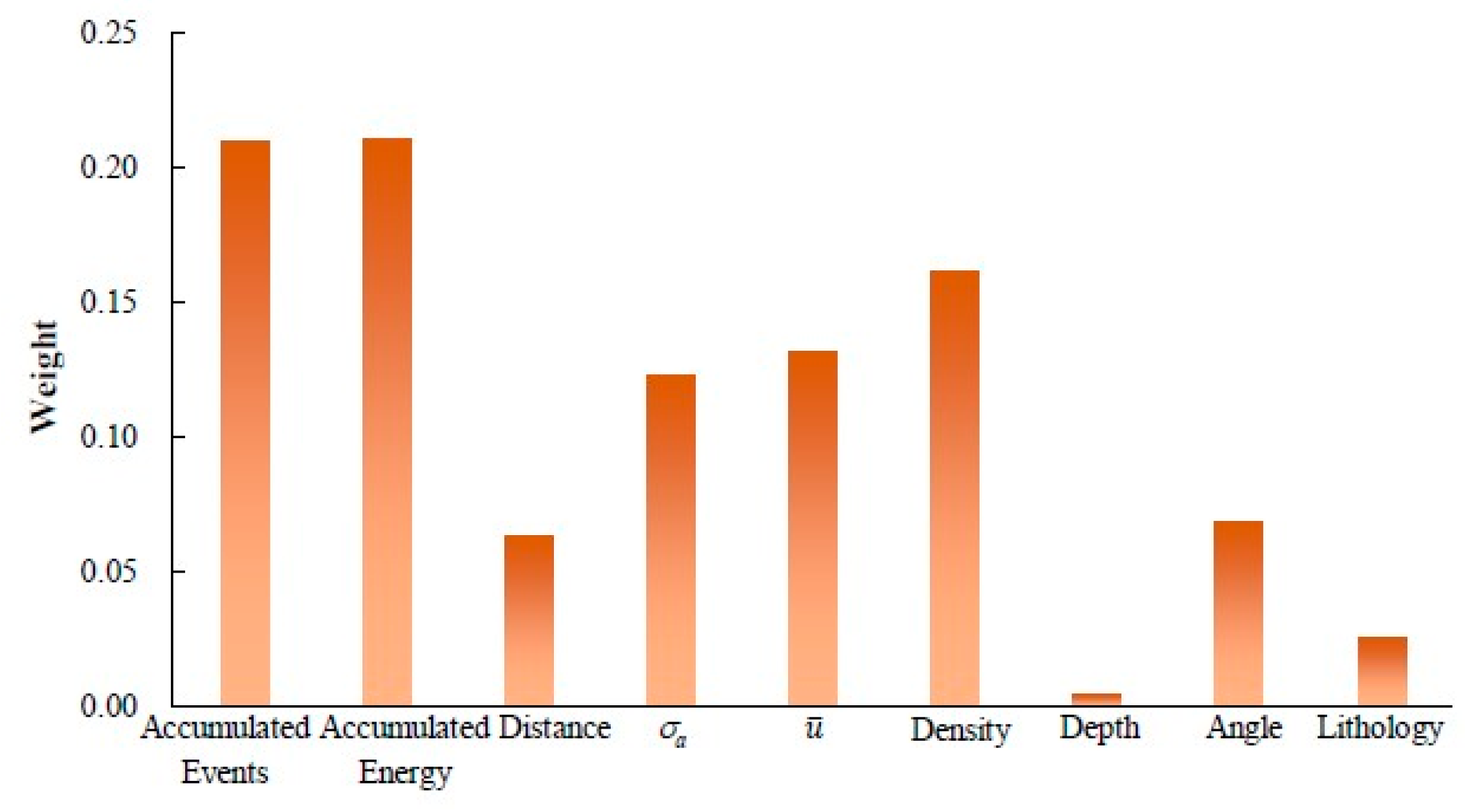
3.4. Weight of Evaluation Indexes
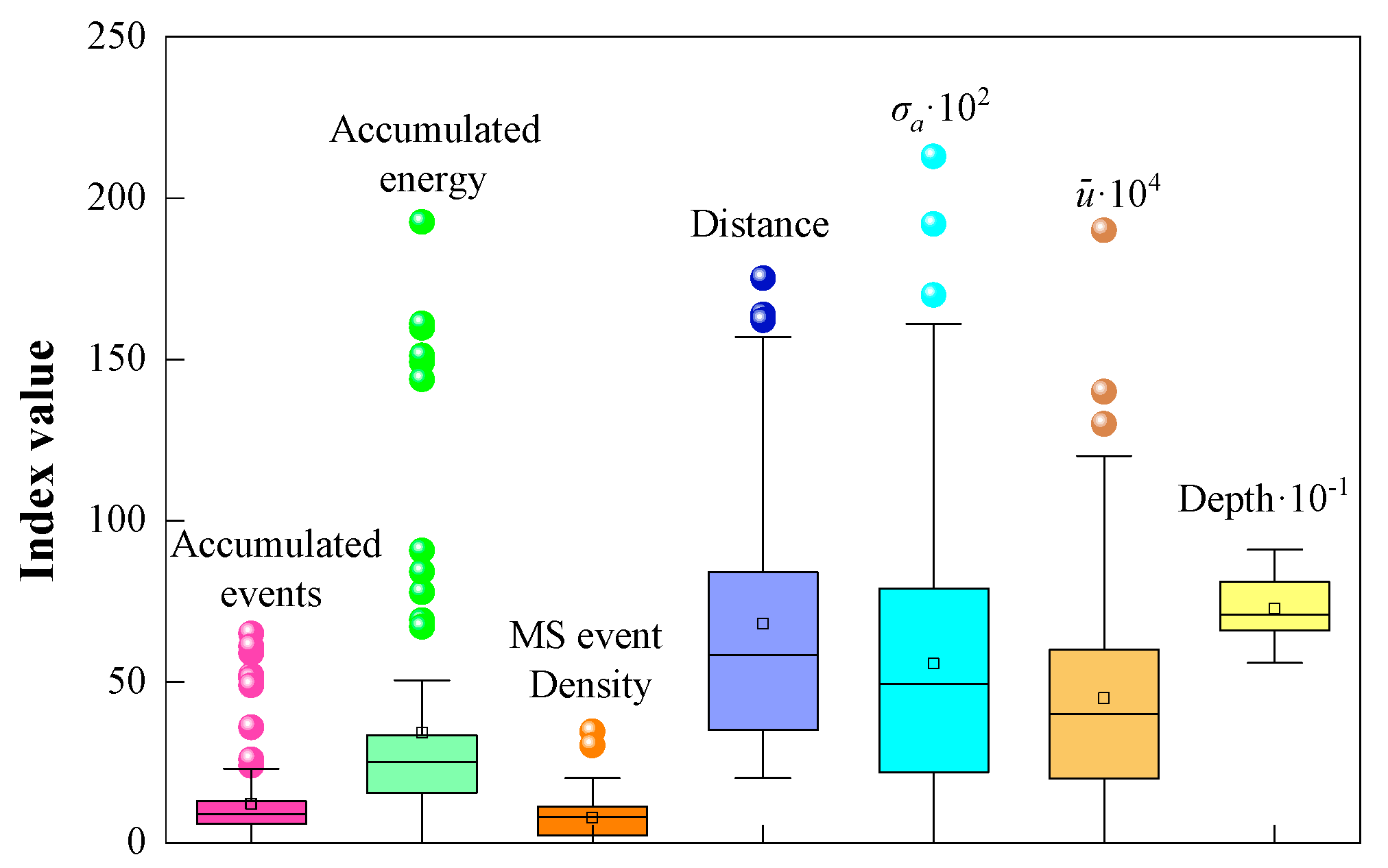
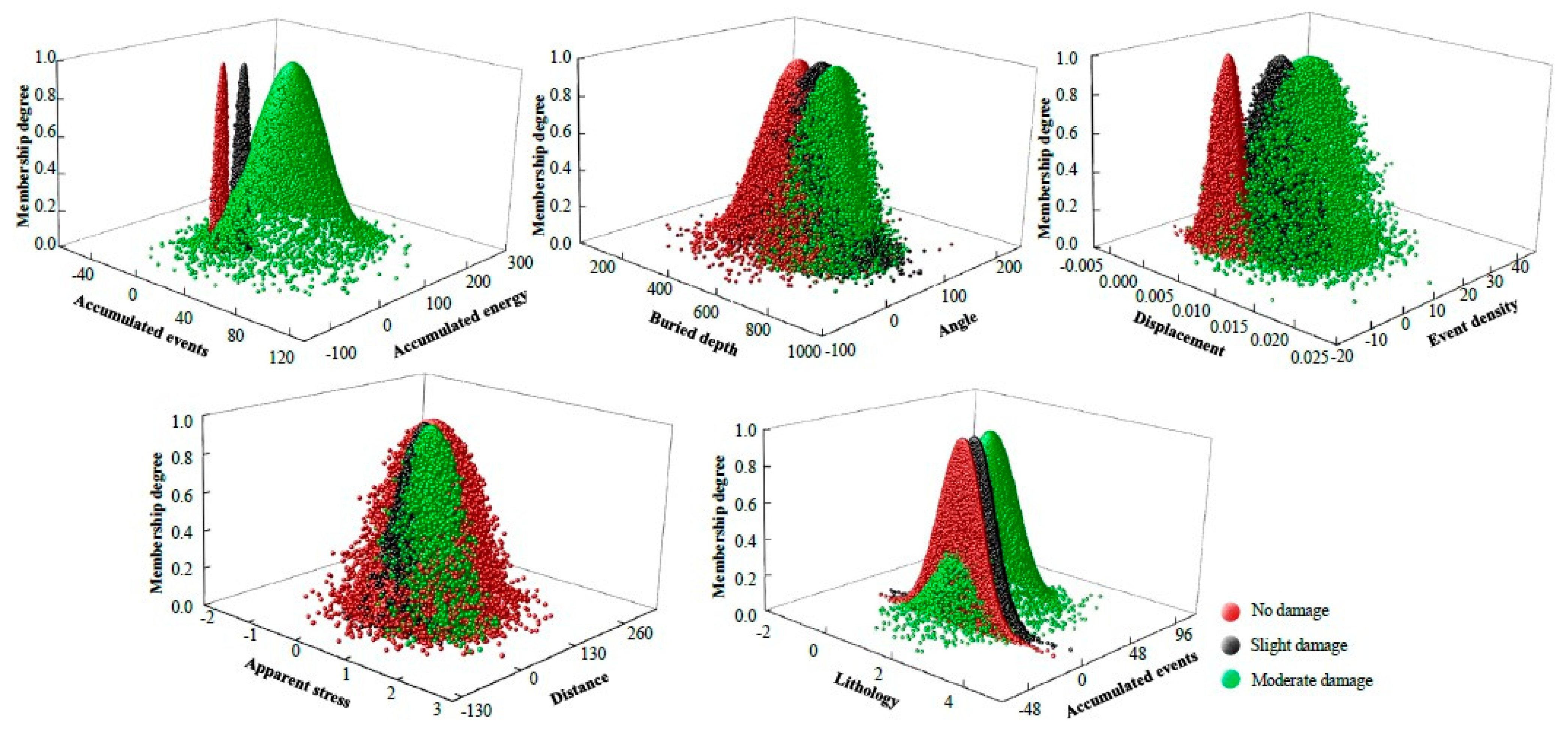
3.5. Numerical Characteristics of Evaluation Indexes
4. Risk Assessment of Rock Mass Failure in Tunnel
4.1. Eigenvalues of Damage Levels
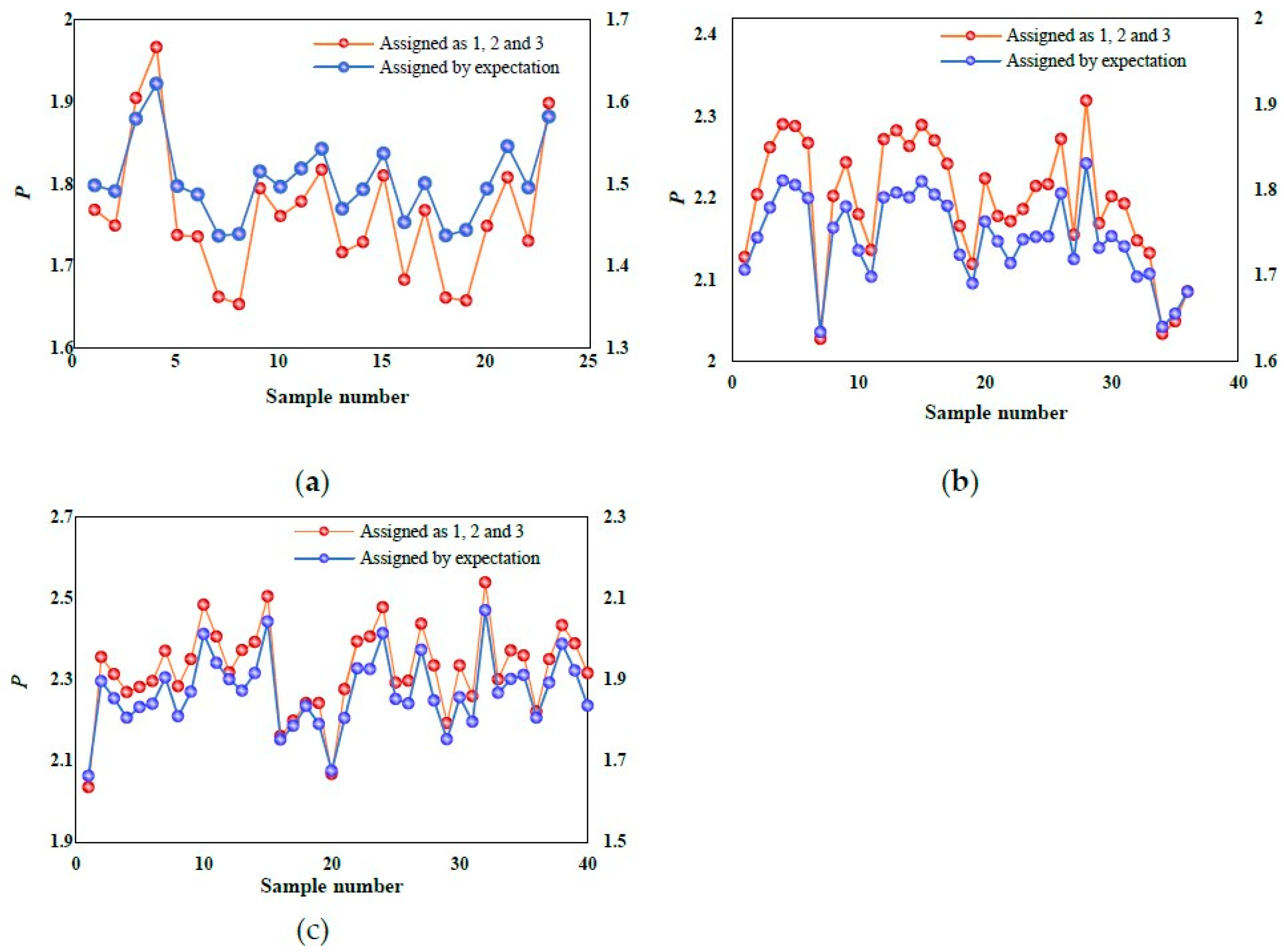
4.2. Determination of the Damage Levels
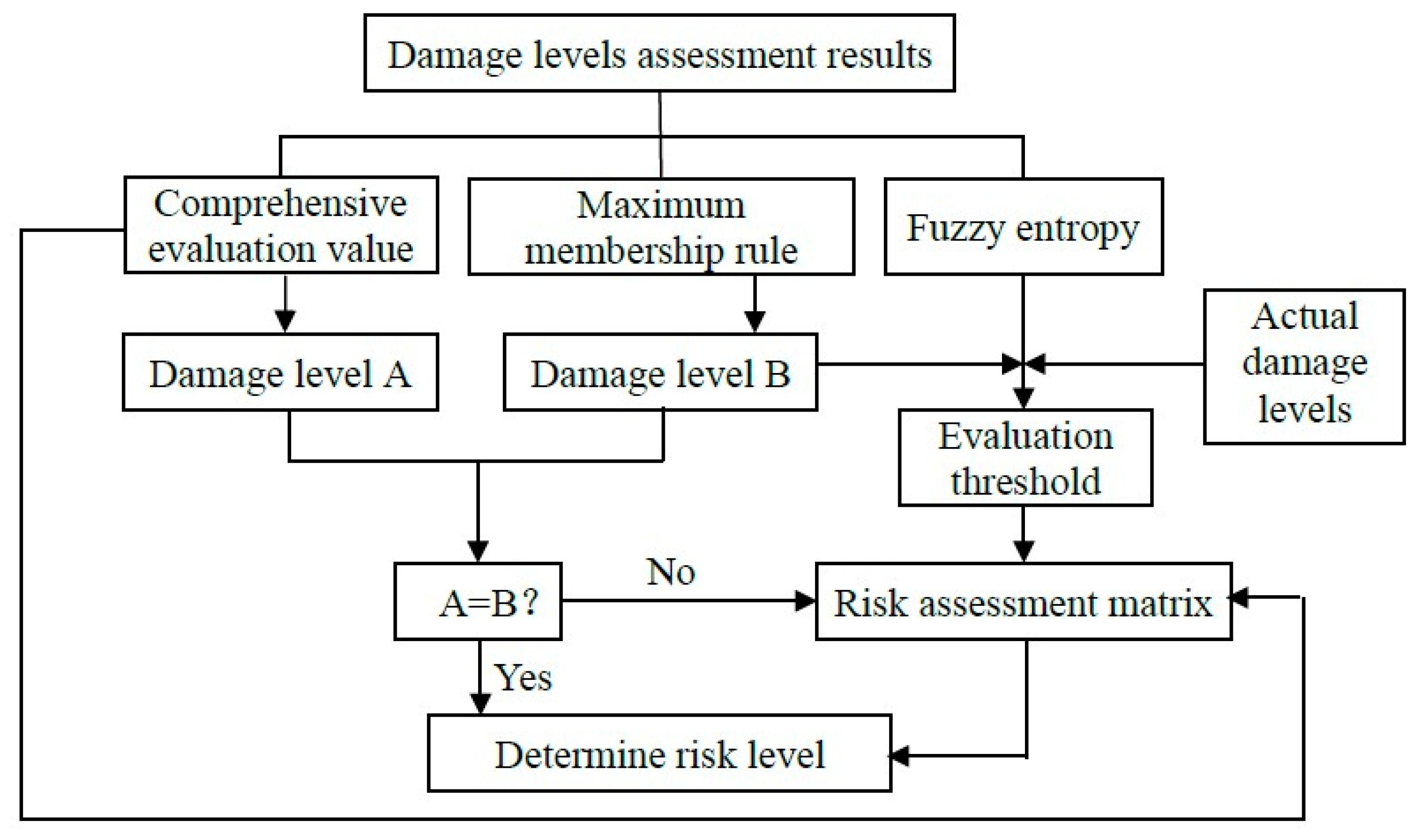
4.3. Tunnel Failure Risk Assessment Method
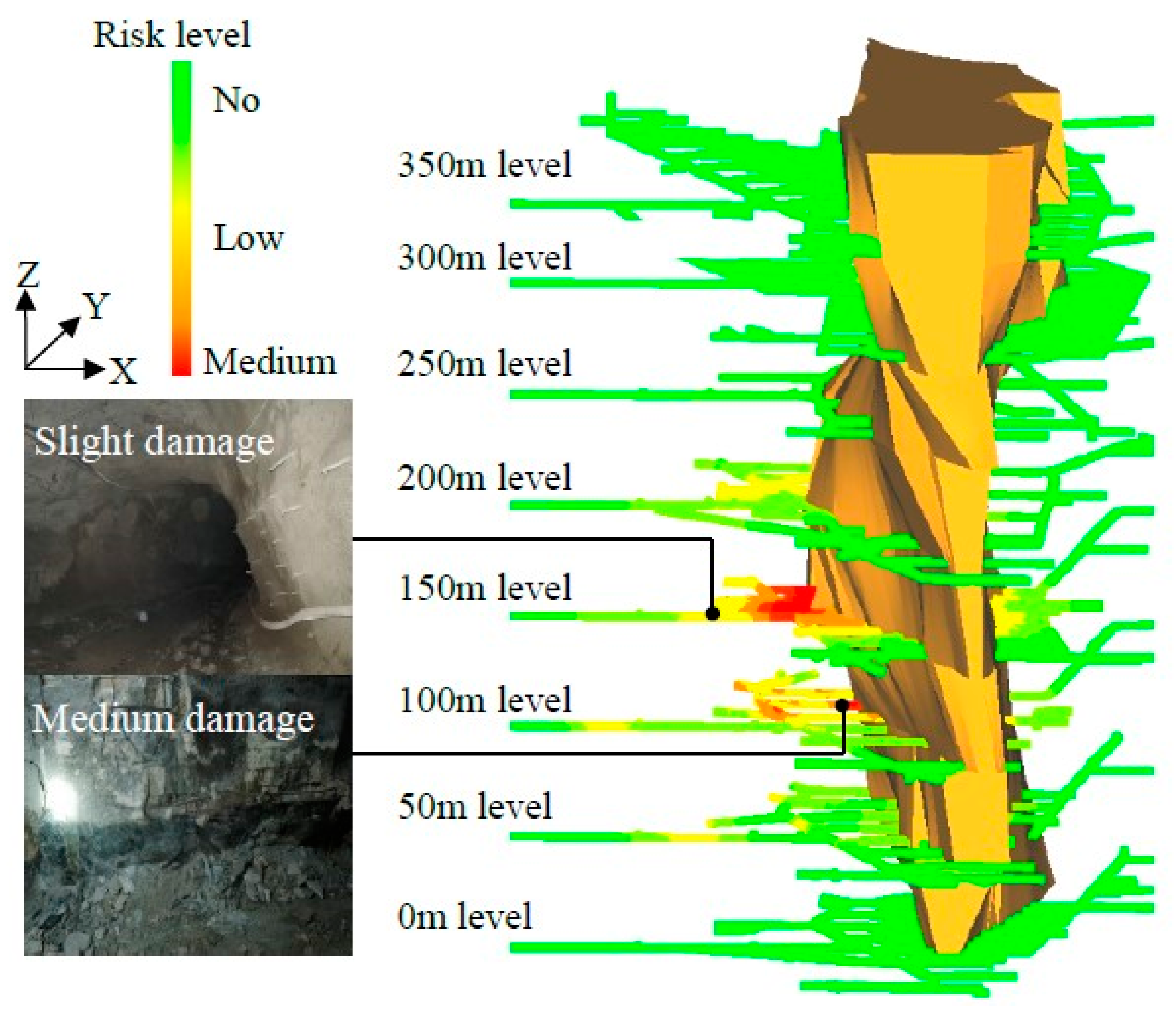
4.4. Application
5. Conclusions
- The evaluation indexes considered here provided different contributions to the tunnel failure model, and any single index did not lead the factor compared to other indexes. Among the nine indexes, the accumulated energy and accumulated events had the largest contributions, while the weight of the buried depth had the smallest contribution. The five largest weights within the model were attributed to MS indexes and accounted for 83.8% of the total weight. This indicates that the MS indexes play a leading role in the risk assessment of tunnel failure.
- The eigenvalues of the three damage levels predicted within the Ashele mine were defined by using the normalized expectations (Ex), which can reduce the range of the comprehensive evaluation value of each damage level and improve the application of the weighted mean method.
- The accuracy rate of damage level classified by the maximum membership rule was 81.1% in the Ashele copper mine. By considering the fuzzy entropy of the sample, the comprehensive application of the maximum membership rule and the comprehensive evaluation value were used to improve the evaluation accuracy of the tunnel damage level to 86%.
- Based on the maximum membership rule, the comprehensive evaluation value, and the fuzzy entropy, a quantitative evaluation method for the tunnel damage risk was established in the Ashele Copper Mine. The application results indicate that the assessment results can provide a basis for the control of ground pressure hazards and the optimization of mining process in deep metal mines.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, X.B.; Zhou, J.; Wang, S.F.; Liu, B. Review and practice of deep mining for solid mineral resources. Chin. J. Nonferrous Met. 2017, 27, 1236–1262. [Google Scholar]
- Cai, M.F.; Xue, D.L.; Ren, F.H. Current status and development strategy of metal mines. Chin. J. Eng. 2019, 41, 417–426. [Google Scholar]
- Xie, H.P. Research review of the state key research development program of China: Deep rock mechanics and mining theory. J. Chin. Coal Soc. 2019, 44, 1283–1305. [Google Scholar]
- Liu, J.P.; Xu, S.D.; Li, Y.H.; Lei, G. Analysis of rock mass stability based on mining-induced seismicity: A case study at the Hongtoushan copper mine in China. Rock Mech. Rock Eng. 2019, 52, 265–276. [Google Scholar] [CrossRef]
- Gao, Q.; Song, J.G.; Yu, W.J.; Wang, Z.H. Design and numerical simulation of rock bolting and shotcrete for deep tunnels with high stress in Jinchuan Mine. Chin. J. Geotech. Eng. 2007, 29, 279–284. [Google Scholar]
- Yang, Z.G.; Yu, R.C.; Guo, R.; Wang, L.H. Research of mining based on microseismic monitoring technology in high-stress area. Chin. J. Rock Mech. Eng. 2009, 28, 3632–3638. [Google Scholar]
- Zhang, R.L.; Luo, Z.Q. Research on Roadway roof fall prediction based on combined weighting and finite interval cloud model. Min. Metall. Eng. 2019, 39, 11–14+19. [Google Scholar]
- Jin, C.Y.; Lu, Y.; Han, T.; Chen, T.Y.; Cui, J.X.; Cheng, D.X. Study on refined back analysis method for stress field based on in situ and disturbed stresses. Int. J. Geomech. 2021, 21, 04021141. [Google Scholar] [CrossRef]
- Gu, J.C.; Chen, A.M.; Xu, J.M.; Zhao, H.L.; Zhang, X.Y.; Gu, L.Y.; Ming, Z.Q. Model test study of failure patterns of anchored tunnel subjected to explosion load. Chin. J. Rock Mech. Eng. 2008, 27, 1315–1320. [Google Scholar]
- Zhu, W.C.; Li, Z.H.; Zhu, L.; Tang, C.A. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance. Tunn. Undergr. Space Technol. 2010, 25, 587–599. [Google Scholar] [CrossRef]
- Li, Y.H.; Peng, J.Y.; Zhang, F.P.; Qiu, Z.G. Cracking behavior and mechanism of sandstone containing a pre-cut hole under combined static and dynamic loading. Eng. Geol. 2016, 213, 64–73. [Google Scholar] [CrossRef]
- Li, X.B.; Li, C.J.; Cao, W.Z.; Tao, M. Dynamic stress concentration and energy evolution of deep-buried tunnels under blasting loads. Int. J. Rock Mech. Min. 2018, 104, 131–146. [Google Scholar] [CrossRef]
- Liu, J.P.; Zhang, C.Y.; Si, Y.T.; Wang, R.; Lei, G.; Xu, S.D. Temporal-spatial evolution of acoustic emission during progressive fracture processes around tunnel triggered by blast-induced disturbances under uniaxial and biaxial compression. Tunn. Undergr. Space Technol. 2020, 96, 103329. [Google Scholar]
- Mendecki, A.J. Seismic Monitoring in Mines; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Poplawski, R.F. Seismic parameters and rockburst hazard at Mt Charlotte mine. Int. J. Rock Mech. Min. 1997, 34, 1213–1228. [Google Scholar] [CrossRef]
- Urbancic, T.I.; Trifu, C.I. Recent advances in seismic monitoring technology at Canadian mines. J. Appl. Geophys. 2000, 45, 225–237. [Google Scholar] [CrossRef]
- Li, S.L.; Yin, X.G.; Zeng, W.D.; Trifu, C.I. Research of multi-channel microseismic monitoring system and its application to Fankou Lead-zinc Mine. Chin. J. Rock Mech. Eng. 2005, 24, 2048–2053. [Google Scholar]
- Tang, L.Z.; Wang, L.H.; Zhang, J.; Li, X.B. Seismic apparent stress and deformation in a deep mine under large-scale mining and areal hazardous seismic prediction. Chin. J. Rock Mech. Eng. 2011, 30, 1168–1178. [Google Scholar]
- Liu, J.P.; Feng, X.T.; Li, Y.H.; Xu, S.D.; Sheng, Y. Studies on temporal and spatial variation of microseismic activities in a deep metal mine. Int. J. Rock Mech. Min. 2013, 60, 171–179. [Google Scholar] [CrossRef]
- Feng, X.T.; Liu, J.P.; Chen, B.R.; Xiao, Y.X.; Feng, G.L.; Zhang, F.P. Monitoring, warning, and control of rockburst in deep metal mines. Engineering 2017, 3, 538–545. [Google Scholar] [CrossRef]
- Mngadi, S.B.; Durrheim, R.J.; Manzi, M.S.D.; Ogasawara, H.; Yabe, Y.; Yilmaz, H.; Wechsler, N.G.; Aswegen, G.V.; Roberts, D.; Ward, A.K.; et al. Integration of underground mapping, petrology, and high-resolution microseismicity analysis to characterise weak geotechnical zones in deep South African gold mines. Int. J. Rock Mech. Min. 2019, 114, 79–91. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, X.; Wang, Z.; Gao, R. High-accuracy location of microseismic events in a strong inhomogeneous mining environment by optimized global full waveform inversion. Appl. Sci. 2020, 10, 7205. [Google Scholar] [CrossRef]
- Hudyma, M.; Potvin, Y.H. An engineering approach to seismic risk management in hardrock mines. Rock Mech. Rock Eng. 2010, 43, 891–906. [Google Scholar] [CrossRef]
- Wu, S.C.; Huang, X.Q.; Chen, F.; Chai, J.F.; Wu, H.Y. Moment tensor inversion of rock failure and its application. Rock Soil Mech. 2016, 37, 1–18. [Google Scholar]
- Liu, J.P.; Si, Y.T.; Zhang, C.Y.; Wang, R. Estimation of fracturing mechanisms by the ratio of radiated energy between S and P waves of microseismic events during mining in metal mines. Appl. Geophys. 2020, 17, 465–474. [Google Scholar] [CrossRef]
- Zhang, P.H.; Yang, T.H.; Yu, Q.L.; Xu, T.; Zhu, W.C.; Liu, H.L.; Zhou, J.R.; Zhao, Y.C. Microseimicity induced by fault activation during the fracture process of a crown pillar. Rock Mech. Rock Eng. 2015, 48, 1673–1682. [Google Scholar] [CrossRef]
- Liu, J.P.; Liu, Z.S.; Wang, S.Q.; Shi, C.Y.; Li, Y.H. Analysis of microseismic activity in rock mass controlled by fault in deep metal mine. Int. J. Min. Sci. Technol. 2016, 26, 235–239. [Google Scholar] [CrossRef]
- Ma, J.; Dong, L.J.; Zhao, G.Y.; Li, X.B. Focal Mechanism of Mining-Induced Seismicity in Fault Zones: A Case Study of Yongshaba Mine in China. Rock Mech. Rock Eng. 2019, 52, 3341–3352. [Google Scholar] [CrossRef]
- Feng, G.L.; Xia, G.Q.; Chen, B.R.; Yao, Y.X.; Zhou, R.C. A method for rockburst prediction in the deep tunnels of hydropower stations based on the monitored microseismicity and an optimized probabilistic neural network model. Sustainability 2019, 11, 3212. [Google Scholar] [CrossRef]
- Ji, B.; Xie, F.; Wang, X.P.; He, S.Q.; Song, D.Z. Investigate contribution of multi-microseismic data to rockburst risk prediction using support vector machine with genetic algorithm. IEEE Access. 2020, 8, 58817–58828. [Google Scholar] [CrossRef]
- Hu, Y.X.; Li, X.B. Bayes discriminant analysis method to identify risky of complicated goaf in mines and its application. Trans. Nonferrous Met. Soc. China 2012, 22, 425–431. [Google Scholar] [CrossRef]
- Liu, Y.C.; Chen, C.S. A new approach for application of rock mass classification on rock slope stability assessment. Eng. Geol. 2007, 89, 129–143. [Google Scholar] [CrossRef]
- Pu, Y.Y.; Apel, D.; Xu, H.W. A principal component analysis/fuzzy comprehensive evaluation for rockburst potential in kimberlite. Pure Appl. Geophys. 2018, 175, 2141–2151. [Google Scholar] [CrossRef]
- Wu, S.C.; Zhang, C.X.; Cheng, Z.Q. Prediction of intensity classification of rockburst based on PCA-PNN principle. J. Chin. Coal Soc. 2019, 44, 2767–2776. [Google Scholar]
- Gao, C.L.; Li, S.C.; Wang, J.; Li, L.P.; Lin, P. The Risk Assessment of Tunnels Based on Grey Correlation and Entropy Weight Method. Geotech. Geol. Eng. 2018, 36, 1621–1631. [Google Scholar] [CrossRef]
- Gong, J.; Hu, N.L.; Cui, X.; Wang, X.D. Rockburst tendency prediction based on AHP-TOPSIS evaluation model. Chin. J. Rock Mech. Eng. 2014, 33, 1442–1448. [Google Scholar]
- Xue, Y.G.; Bai, C.H.; Kong, F.M.; Qiu, D.H.; Li, L.P.; Su, M.X.; Zhao, Y. A two-step comprehensive evaluation model for rockburst prediction based on multiple empirical criteria. Eng. Geol. 2020, 268, 105515. [Google Scholar] [CrossRef]
- Cai, W.; Dou, L.M.; Zhang, M.; Cao, W.Z.; Shi, J.Q.; Feng, L.F. A fuzzy comprehensive evaluation methodology for rock burst forecasting using microseismic monitoring. Tunn. Undergr. Space Technol. 2018, 80, 232–245. [Google Scholar] [CrossRef]
- Wang, Y.C.; Shang, Y.Q.; Sun, H.Y.; Yan, X.S. Study of prediction of rockburst intensity based on efficacy coefficient method. Rock Soil Mech. 2010, 31, 529–534. [Google Scholar]
- Qiu, D.H.; Li, S.C.; Zhang, L.W. Study on rockburst intensity prediction based on efficacy coefficient method. Appl. Mech. Mater. 2013, 353–356, 1277–1280. [Google Scholar] [CrossRef]
- Jia, Q.J.; Wu, L.; Li, B.; Chen, C.H.; Peng, Y.X. The comprehensive prediction model of rockburst tendency in tunnel based on optimized unascertained measure theory. Geotech. Geol. Eng. 2019, 37, 3399–3411. [Google Scholar] [CrossRef]
- Jiao, S.H.; Wang, J.A.; Zhou, H.L. Comprehensive evaluation of bolt and wire mesh support scheme of roadway based on set pair analysis. Adv. Mater. Res. 2014, 838–841, 1250–1255. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, C.Y.; Gan, W.Y. A new cognitive model: Cloud model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Wu, S.L.; Yang, S.; Du, X.D. A model for evaluation of surrounding rock stability based on D-S evidence theory and error-eliminating theory. Bull. Eng. Geol. Environ. 2021, 80, 2237–2248. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Meng, Y.D. Prediction of rock burst classification using the technique of cloud models with attribution weight. Nat. Hazards. 2013, 68, 549–568. [Google Scholar] [CrossRef]
- Lin, Y.; Zhou, K.P.; Li, J.L. Application of cloud model in rock burst prediction and performance comparison with three machine learning algorithms. IEEE Access 2018, 6, 30958–30968. [Google Scholar] [CrossRef]
- Li, D.Y.; Meng, H.J.; Shi, X.M. Membership clouds and membership cloud generator. J. Res. Dev. 1995, 32, 15–20. [Google Scholar]
- Li, D.Y.; Liu, C.Y.; Liu, L.Y. Study on the universality of the normal cloud. Eng. Sci. 2005, 3, 18–24. [Google Scholar]
- Ding, S.F.; Zhu, H.; Xu, X.Z.; Shi, Z.Z. Entropy-based fuzzy information measures. Chin. J. Comput. 2012, 35, 796–801. [Google Scholar] [CrossRef]
- Ke, J.K. Blasting Vibration Failure Criterion of Granite Body and Rock Cave. Combust. Explos. Shock Waves. 1987, 02, 117–122. [Google Scholar]
- Tian, C.G.; Chen, S.H. Application of standard for engineering classification of rock masses in underground mining engineering. Min. Tech. 2005, 5, 90–93. [Google Scholar]
- Feng, X.T.; Chen, B.R.; Zhang, C.Q.; Li, S.J.; Wu, S.Y. Mechanism, Warning and Dynamic Control of Rockburst Development Processes; Science Press: Beijing, China, 2013. [Google Scholar]

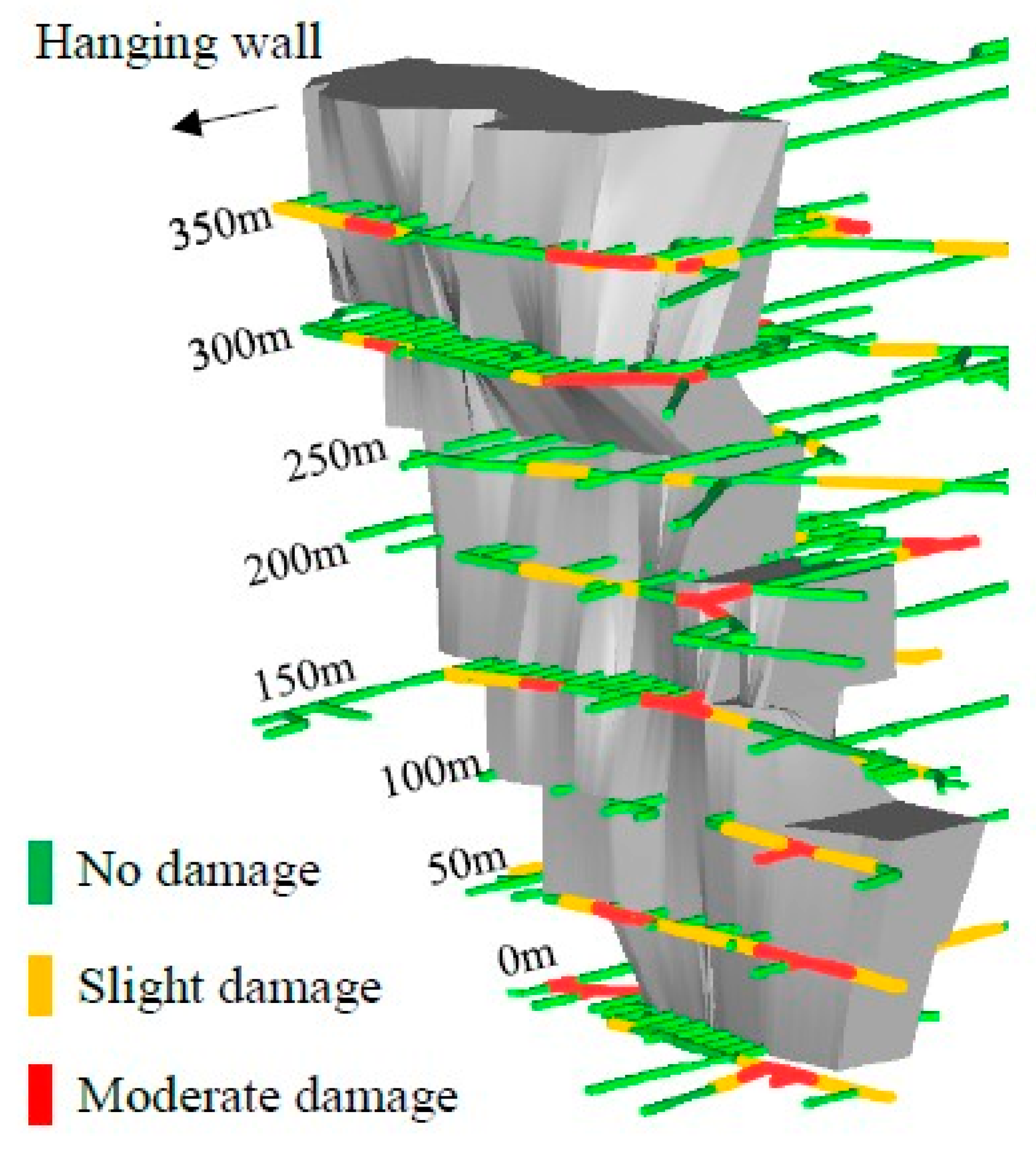



| Damage Level | Description |
|---|---|
| No damage | There is no damage or only slight deformation in the tunnel. The current support is able to keep the rock mass stable. |
| Slight damage | The deformation of rock mass in the tunnel can be observed by the naked eye. A small range of rock mass has fallen or is bulking. Parts of the support appear damaged but can keep being used after small repairs. |
| Moderate damage | The support and rock mass in the tunnel appear to be damaged and fall in a range greater than a meter in length. Secondary support should be put in place. |
| Serious damage | The integrity of the support and rock mass in tunnel is severely damaged along several meters and has had serious impact on the normal production work. It is difficult to clean up the collapsed rock. Secondary reinforcement or support should be put in place. |
| Evaluation Index | Description |
|---|---|
| Angle | Defined as the angle between the tunnel and the maximum principal stress. The majority of the damage occurred in the strike-drift that, which is oriented perpendicular to the maximum principal stress. |
| Depth | The deeper the tunnels are buried, the greater the vertical stress and the more serious damage that occurs. |
| Lithology | The lithology and the development of joints and fractures have an important influence on the damage of tunnel. |
| Distance | Rock mass is inevitably subjected to changes in stress field after the ore is mined and during blasting disturbances. The closer the tunnel is to the stope, the more the mining disturbances and unloading effects affect the tunnel stability. |
| Accumulated events | Total number of MS events generated within a certain time period and region. The number of accumulated events is used to evaluate the change in regional fracture activities. |
| Accumulated energy | Total energy released by MS events within a certain time period and region. The accumulated energy is used to reflect the degree of energy released by cracks generated inside the rock mass. |
| Event density | Number of MS events per unit volume of rock mass. The event density is used to describe the cluster extent of MS events. |
| Apparent stress σa | The apparent stress is the ratio of the total radiated seismic energy to the seismic moment. It assesses the amount of energy released per unit of deformation and is defined as: σa = μ/M0, where u is the modulus of rigidity of the source and M0 is the seismic moment. |
| Displacement | It is the average displacement of the source, where r0 is the source radius and is defined as: |
| Accumulated MS Events | Accumulated Energy/lgE(J) | Distance/m | σa/MPa | /m | Density/m3 | Depth/m | Angle/° | Lithology | Damage Level |
|---|---|---|---|---|---|---|---|---|---|
| 8 | 23.6 | 35.3 | 0.20 | 0.002 | 11.79 | 709 | 90 | Pyrite | Slight |
| 1 | 4.35 | 105.88 | 0.02 | 0.002 | 0.32 | 609 | 90 | Tuff | No |
| 2 | 7.15 | 76.35 | 0.36 | 0.003 | 2.47 | 758 | 0 | Pyrite | No |
| 16 | 50.5 | 83.95 | 0.44 | 0.008 | 4.89 | 759 | 0 | Pyrite | Moderate |
| 10 | 25 | 58.91 | 0.26 | 0.003 | 13.68 | 659 | 90 | Pyrite | Slight |
| 11 | 32.4 | 60.28 | 0.22 | 0.004 | 8 | 908 | 0 | Tuff | Slight |
| 13 | 29.8 | 85.98 | 0.39 | 0.005 | 3.42 | 659 | 90 | Pyrite | Slight |
| 22 | 69.1 | 55.3 | 0.87 | 0.007 | 20.26 | 810 | 90 | Tuff | Moderate |
| 7 | 23.4 | 121.37 | 0.20 | 0.004 | 8.79 | 709 | 90 | Tuff | Slight |
| 10 | 25.8 | 155.1 | 0.10 | 0.002 | 9.55 | 910 | 90 | Pyrite | Slight |
| Damage Level | Pyrite | Tuff | Angle/0° | Angle/90° |
|---|---|---|---|---|
| No damage | 13 | 11 | 5 | 19 |
| Slight damage | 21 | 23 | 5 | 39 |
| Moderate damage | 13 | 9 | 3 | 19 |
| Damage Level | Statistical Parameters | Accumulated Events | Accumulated Energy | Distance | σa | Density | Depth | |
|---|---|---|---|---|---|---|---|---|
| No damage (n = 24) | Minimum value | 0 | 0 | 24.95 | 0 | 0 | 0 | 559 |
| Maximum value | 6 | 22.7 | 175.2 | 2.13 | 0.004 | 7.58 | 909 | |
| Truncation mean | 1.43 | 4.5 | 88.87 | 0.42 | 0.0013 | 0.82 | 650.9 | |
| Standard deviation | 1.72 | 5.82 | 49.07 | 0.6 | 0.0014 | 1.97 | 103.95 | |
| Slight damage (n = 44) | Minimum value | 3 | 9.08 | 21.24 | 0.01 | 0.001 | 1.73 | 558 |
| Maximum value | 23 | 40.8 | 162.74 | 1.12 | 0.014 | 19.78 | 910 | |
| Truncation mean | 9.8 | 25.67 | 58.85 | 0.52 | 0.0047 | 8.75 | 730.49 | |
| Standard deviation | 2.96 | 5.67 | 34.34 | 0.29 | 0.0027 | 3.54 | 104.44 | |
| Moderate damage (n = 22) | Minimum value | 8 | 28.8 | 20.11 | 0.03 | 0.003 | 3.58 | 609 |
| Maximum value | 65 | 192.7 | 139.83 | 1.61 | 0.019 | 34.63 | 910 | |
| Truncation mean | 26.52 | 79 | 53.91 | 0.69 | 0.0067 | 12.21 | 797.32 | |
| Standard deviation | 19.35 | 51.93 | 29.5 | 0.39 | 0.0038 | 8.05 | 73.46 |
| Evaluation Indexes | Numerical Characteristics (Expectation Ex, Entropy En, Hyper Entropy He) | ||
|---|---|---|---|
| No Damage | Slight Damage | Moderate Damage | |
| Angle | (71.25, 37.21, 3.10) | (79.77, 22.72, 17.85) | (77.72, 26.57, 17.13) |
| Depth | (659.27, 103.99, 0) | (730.96, 105.85, 0) | (793.64, 75.24, 0) |
| Lithology | (1.45, 0.62, 0) | (1.52, 0.63, 0) | (1.4, 0.61, 0) |
| Distance | (89.92, 52.85, 0) | (62.00, 32.63, 10.69) | (56.37, 26.86, 12.19) |
| Accumulated events | (1.58, 1.58, 0.66) | (10.18, 2.40, 1.42) | (27.5, 20.57, 0) |
| Accumulated energy | (5.14, 5.22, 2.58) | (26.22, 4.93, 1.56) | (82.05, 54.28, 0) |
| Event density | (1.10, 1.75, 0.91) | (9.05, 3.11, 1.55) | (12.88, 7.16, 3.68) |
| Apparent stress | (0.48, 0.53, 0.28) | (0.52, 0.31, 0) | (0.70, 0.36, 0.15) |
| Displacement | (0.0013, 0.0016, 0) | (0.0049, 0.0025, 0.00094) | (0.0071, 0.0035, 0.0016) |
| Damage Level | Expectation Ex | Entropy En | Hyper Entropy He | Eigenvalues |
|---|---|---|---|---|
| No damage | 15.46 | 18.19 | 1.08 | 1.00 |
| Slight damage | 22.17 | 12.84 | 2.78 | 1.43 |
| Moderate damage | 38.03 | 28.99 | 2.56 | 2.46 |
| Sample Number | Comprehensive Membership Degree B | Fuzzy Entropy H | Maximum Membership b | Comprehensive Evaluation Value p | ||
|---|---|---|---|---|---|---|
| No Damage | Slight Damage | Moderate Damage | ||||
| 1 | 0.21 | 0.40 | 0.38 | 0.97 | 0.40 (Slight damage) | 1.73 |
| 2 | 0.59 | 0.15 | 0.25 | 0.87 | 0.59 (No damage) | 1.44 |
| 3 | 0.54 | 0.18 | 0.29 | 0.92 | 0.54 (No damage) | 1.49 |
| 4 | 0.24 | 0.20 | 0.56 | 0.91 | 0.56 (Moderate damage) | 1.90 |
| 5 | 0.18 | 0.44 | 0.38 | 0.95 | 0.44 (Slight damage) | 1.75 |
| 6 | 0.17 | 0.41 | 0.42 | 0.95 | 0.42 (Moderate damage) | 1.80 |
| 7 | 0.21 | 0.39 | 0.40 | 0.97 | 0.40 (Moderate damage) | 1.75 |
| 8 | 0.15 | 0.22 | 0.63 | 0.84 | 0.63 (Moderate damage) | 2.01 |
| 9 | 0.18 | 0.46 | 0.37 | 0.95 | 0.46 (Slight damage) | 1.73 |
| 10 | 0.19 | 0.46 | 0.34 | 0.96 | 0.46 (Slight damage) | 1.70 |
| Damage Level | Data Category | Results by the Maximum Membership Rule | Results by Comprehensive Application of the Maximum Membership Rule and the Comprehensive Evaluation Value | ||||
|---|---|---|---|---|---|---|---|
| No Damage | Slight Damage | Moderate Damage | No Damage | Slight Damage | Moderate Damage | ||
| No damage | Modeling data (24) | 22 | 1 | 1 | 22 | 1 | 1 |
| Test data (0) | 0 | 0 | 0 | 0 | 0 | 0 | |
| Slight damage | Modeling data (44) | 1 | 30 | 13 | 1 | 34 | 9 |
| Test data (4) | 0 | 4 | 0 | 0 | 4 | 0 | |
| Moderate damage | Modeling data (22) | 0 | 1 | 21 | 0 | 1 | 21 |
| Test data (6) | 0 | 0 | 6 | 0 | 0 | 6 | |
| Accuracy | Modeling data | 81.1% | 86% | ||||
| Test data | 100% | 100% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shi, H.; Wang, R.; Si, Y.; Wei, D.; Wang, Y. Quantitative Risk Assessment for Deep Tunnel Failure Based on Normal Cloud Model: A Case Study at the ASHELE Copper Mine, China. Appl. Sci. 2021, 11, 5208. https://doi.org/10.3390/app11115208
Liu J, Shi H, Wang R, Si Y, Wei D, Wang Y. Quantitative Risk Assessment for Deep Tunnel Failure Based on Normal Cloud Model: A Case Study at the ASHELE Copper Mine, China. Applied Sciences. 2021; 11(11):5208. https://doi.org/10.3390/app11115208
Chicago/Turabian StyleLiu, Jianpo, Hongxu Shi, Ren Wang, Yingtao Si, Dengcheng Wei, and Yongxin Wang. 2021. "Quantitative Risk Assessment for Deep Tunnel Failure Based on Normal Cloud Model: A Case Study at the ASHELE Copper Mine, China" Applied Sciences 11, no. 11: 5208. https://doi.org/10.3390/app11115208
APA StyleLiu, J., Shi, H., Wang, R., Si, Y., Wei, D., & Wang, Y. (2021). Quantitative Risk Assessment for Deep Tunnel Failure Based on Normal Cloud Model: A Case Study at the ASHELE Copper Mine, China. Applied Sciences, 11(11), 5208. https://doi.org/10.3390/app11115208





