Comparison of Six Machine-Learning Methods for Predicting the Tensile Strength (Brazilian) of Evaporitic Rocks
Abstract
:Featured Application
Abstract
1. Introduction
2. Sampling, Experimental Work, and Data Collection
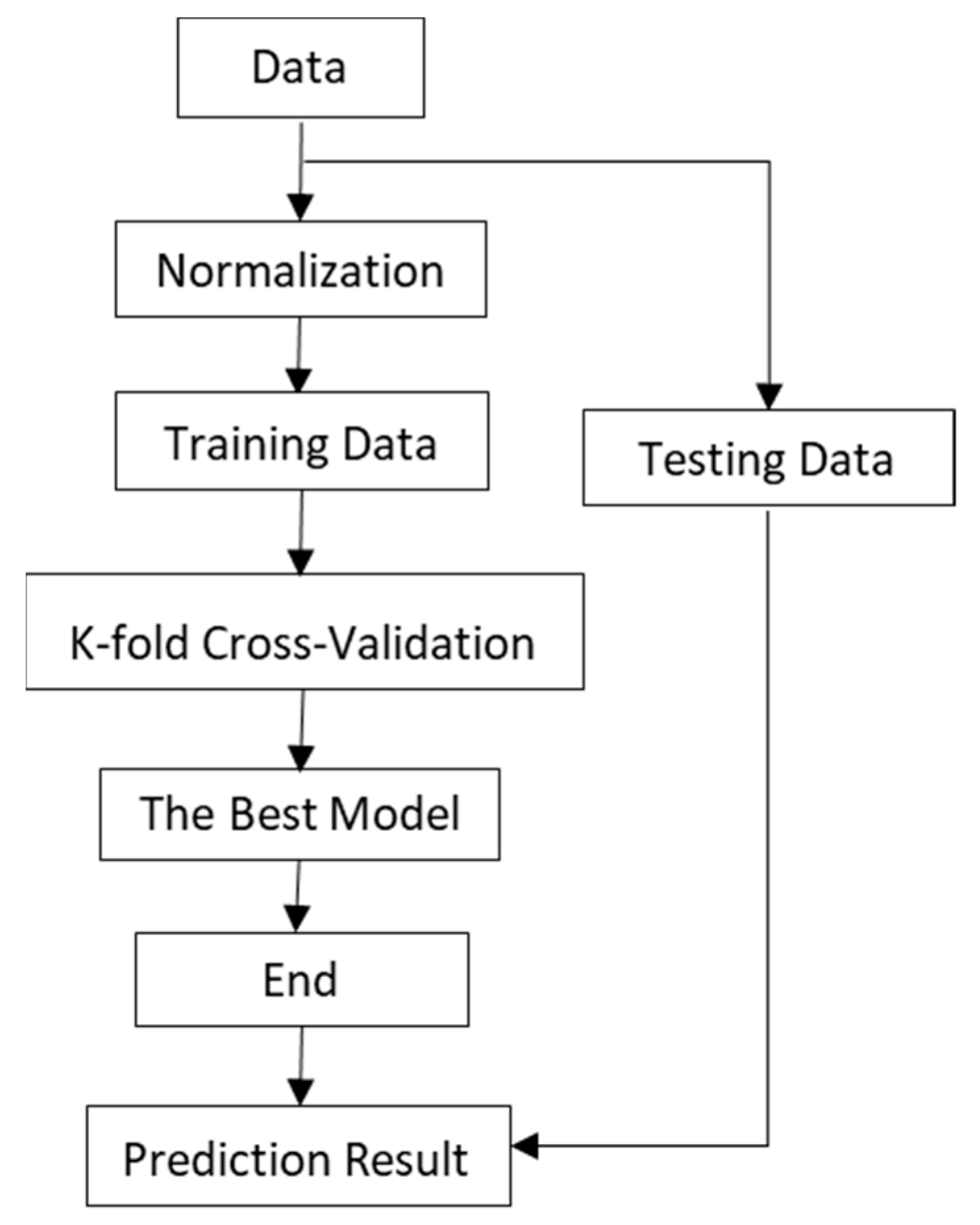
3. Methodology
4. Model Development
4.1. A. ANN
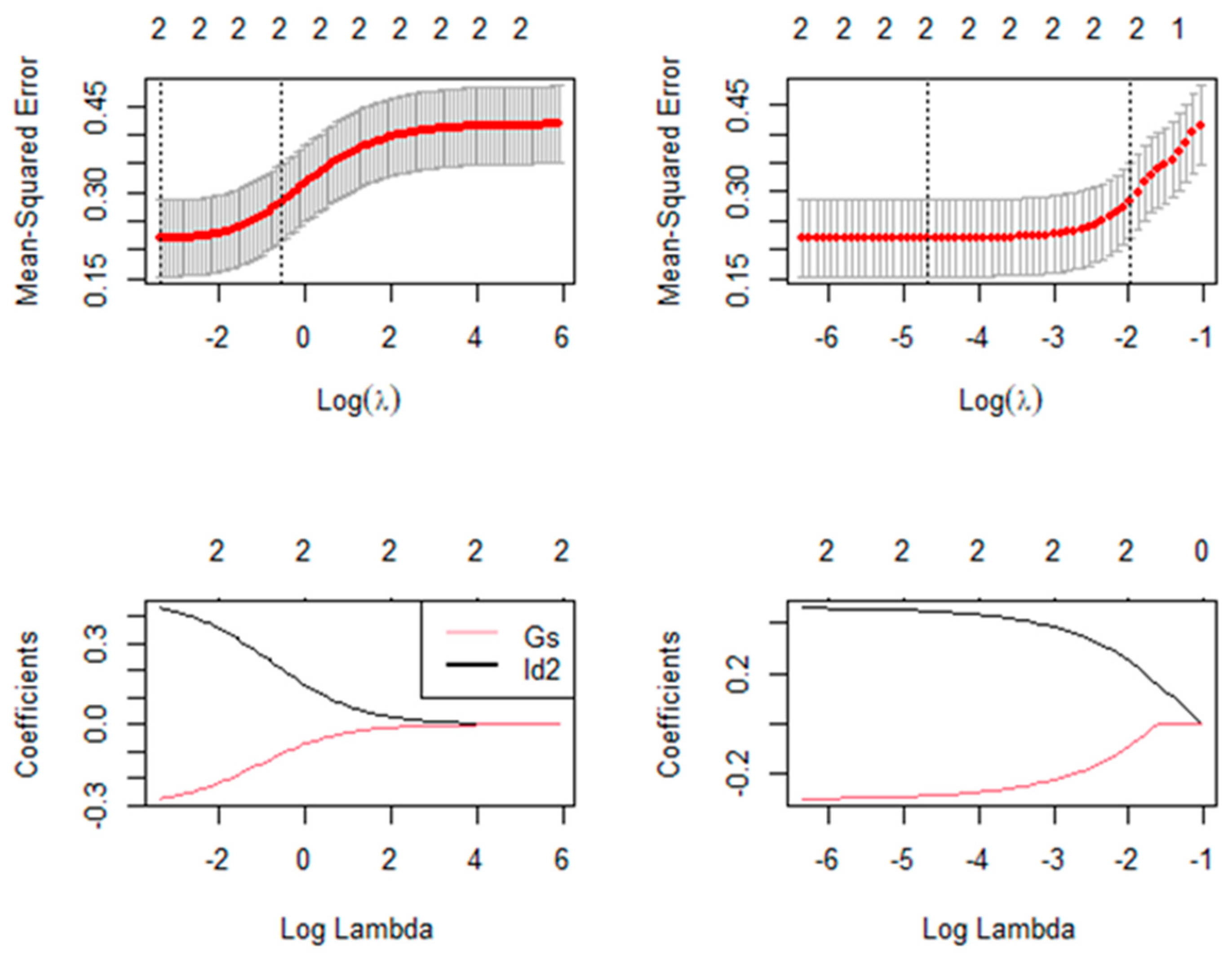
4.2. B. Regularization
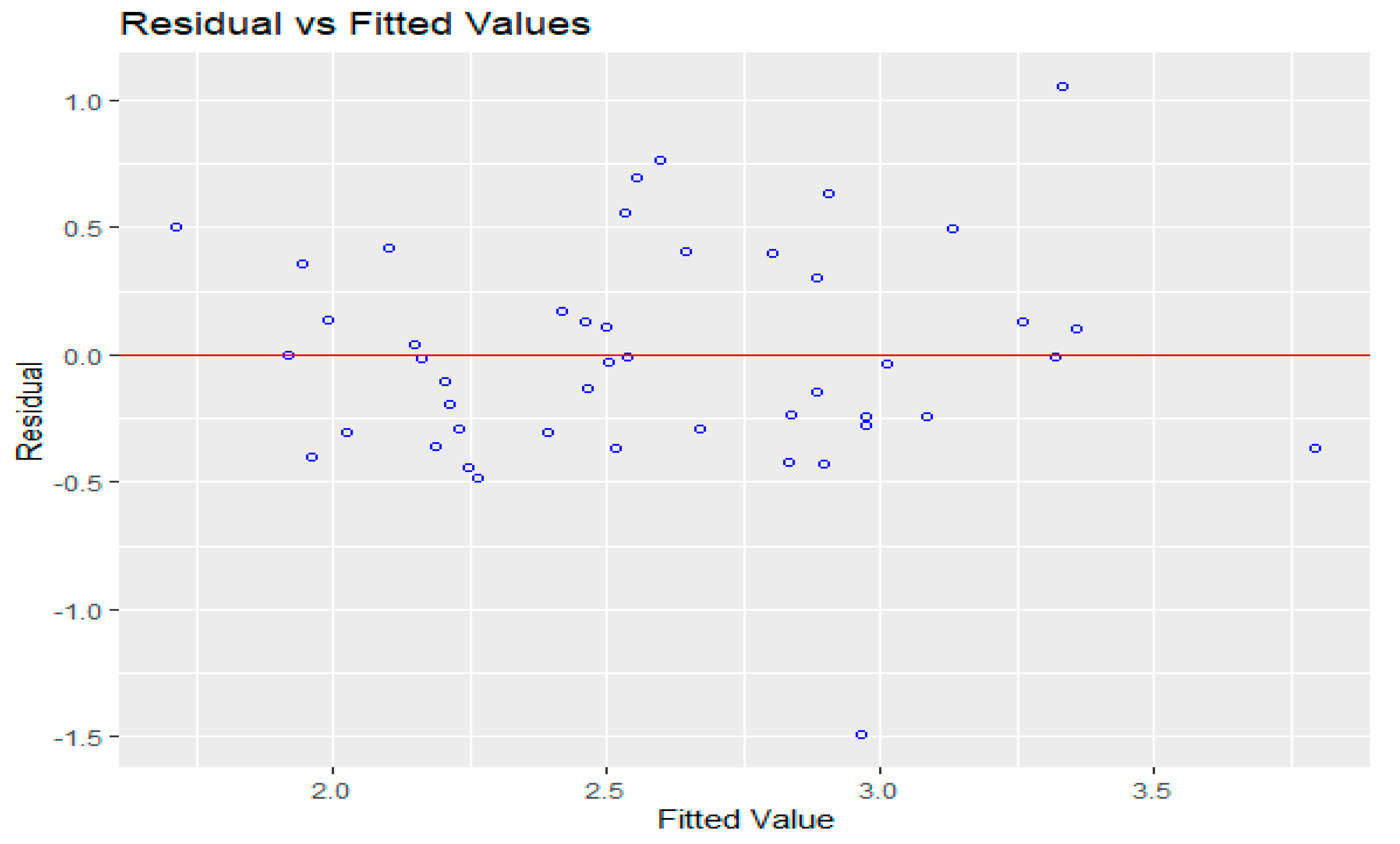
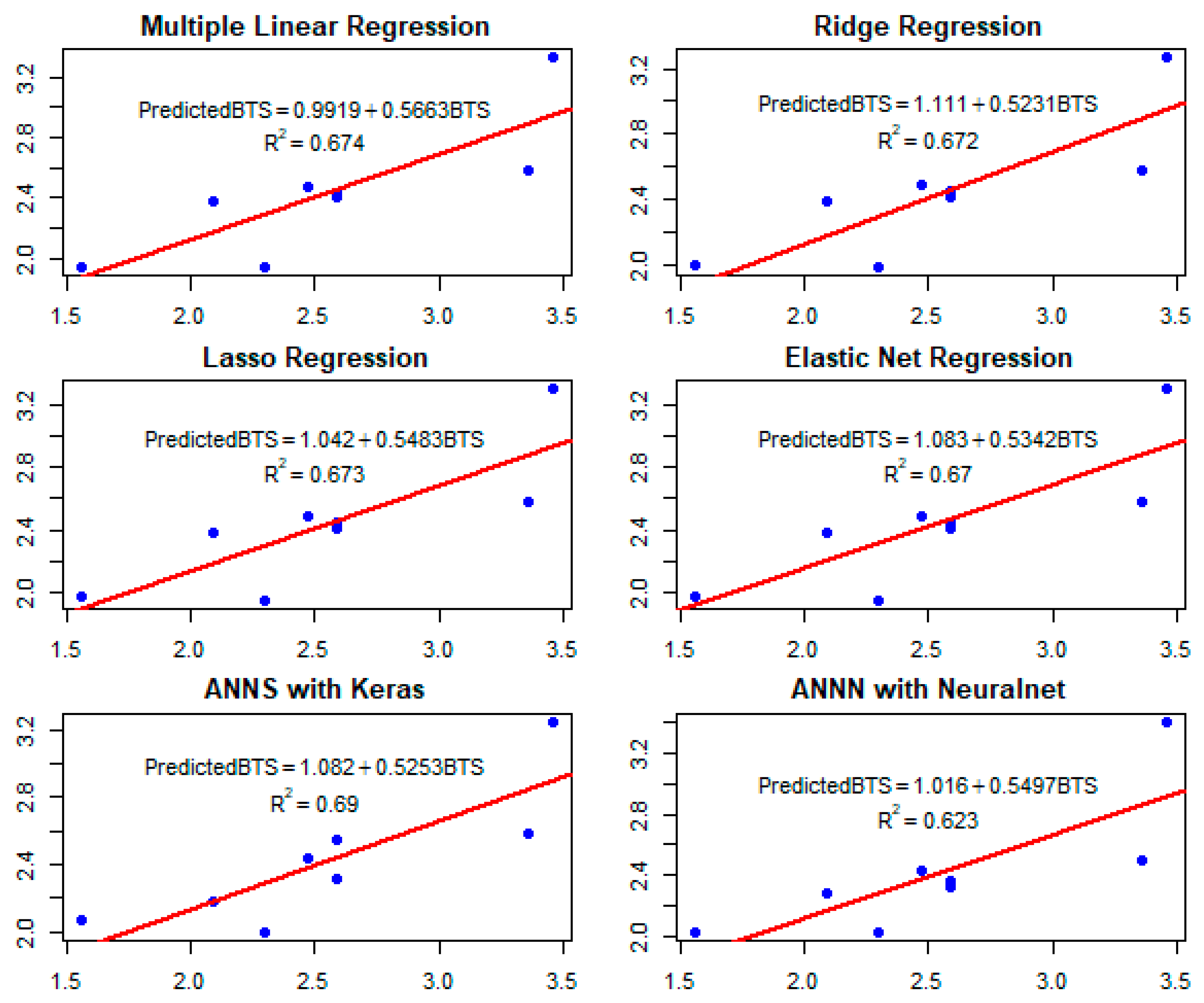
5. Results and Discussion
5.1. A. ANN Model
5.2. B. Regression Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baykasoglu, A.; Güllü, H.; Çanakçi, H.; Özbakir, L. Prediction of compressive and tensile strength of limestone via genetic programming. Expert Syst. Appl. 2008, 35, 111–123. [Google Scholar] [CrossRef]
- Arman, H.; Abdelghany, O.; Saima, M.A.; Aldahan, A.; Mahmoud, B.; Hussein, S.; Fowler, A.; AlRashdi, S. Strength estimation of evaporitic rocks using different testing methods. Arab. J. Geosci. 2019, 12, 1–9. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Zhang, W.; Armaghani, D.J.; Rad, H.N. The potential application of a new intelligent based approach in predicting the tensile strength of rock. IEEE Access 2020, 8, 57148–57157. [Google Scholar] [CrossRef]
- Arman, H. Correlation of uniaxial compressive strength with indirect tensile strength (Brazilian) and 2nd cycle of slake durability index for evaporitic rocks. Geotech. Geol. Eng. 2021, 39, 1583–1590. [Google Scholar] [CrossRef]
- Altindag, R.; Guney, A. Predicting the relationships between brittleness and mechanical properties (UCS, TS and SH) of rocks. Sci. Res. Essays 2010, 5, 2107–2118. [Google Scholar]
- Farah, R. Correlations between index properties and unconfined compressive strength of weathered Ocala limestone. Univ. Tech. Rep. Master’s Thesis, University of North Florida, Jacksonville, FL, USA, 2011; p. 142.
- Kahraman, S.; Fener, M.; Kozman, E. Predicting the compressive and tensile strength of rocks from indentation hardness index. J. S. Afr. Inst. Min. Metall. 2012, 112, 331–339. [Google Scholar]
- Nazir, R.; Momeni, E.; Armaghani, D.J.; Amin, M.F.M. Correlation between unconfined compressive strength and indirect tensile strength of limestone rock samples. Electron. J. Geotech. Eng. 2013, 18, 1737–1746. [Google Scholar]
- Kallu, R.; Roghanchi, P. Correlations between direct and indirect strength test methods. Int. J. Min. Sci. Technol. 2015, 25, 355–360. [Google Scholar] [CrossRef]
- ISRM. Suggested Methods, Rock characterization testing and monitoring. In International Society of Rock Mechanics. Commission on Testing Methods; Brown, E.T., Ed.; Pergamon Press: Oxford, UK, 1981; pp. 113–114. [Google Scholar]
- Kilic, A.; Teymen, A. Determination of mechanical properties of rocks using simple methods. Bull. Eng. Geol. Environ. 2008, 67, 237–244. [Google Scholar] [CrossRef]
- Heidari, M.; Khanlari, G.R.; Torabi Kaveh, M.; Kargarian, S. Predicting the uniaxial compressive and tensile strengths of gypsum rock by point load testing. Rock Mech. Rock Eng. 2012, 45, 265–273. [Google Scholar] [CrossRef]
- Arman, H.; Hashem, W.; El Tokhi, M.; Abdelghany, O.; El Saiy, A. Petrographical and geomechanical properties of the Lower Oligocene Limestones from Al Ain city, United Arab Emirates. Arab. J. Sci. Eng. 2014, 39, 261–271. [Google Scholar] [CrossRef]
- Karaman, K.; Kesimal, A.; Ersoy, H. A comparative assessment of indirect methods for estimating the uniaxial compressive and tensile strength of rocks. Arab. J. Geosci. 2015, 8, 2393–2403. [Google Scholar] [CrossRef]
- ASTM D Standards. 3967–08, Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Singh, T.N.; Verma, A.K.; Sharma, P.K. A neuro-genetic approach for prediction of time dependent deformational characteristic of rock and its sensitivity analysis. Geotech. Geol. Eng. 2007, 25, 395–407. [Google Scholar] [CrossRef]
- Yilmaz, I.; Yuksek, A.G. An example of artificial neural network (ANN) application for indirect estimation of rock parameters. Rock Mech. Rock Eng. 2008, 41, 781–795. [Google Scholar] [CrossRef]
- Yilmaz, I.; Yuksek, G. Prediction of the strength and elasticity modulus of gypsum using multiple regression, ANN, and ANFIS models. Int. J. Rock Mech. Min. Sci. 2009, 46, 803–810. [Google Scholar] [CrossRef]
- Majdi, A.; Beiki, M. Evolving neural network using a genetic algorithm for predicting the deformation modulus of rock masses. Int. J. Rock Mech. Min. Sci. 2010, 47, 246–253. [Google Scholar] [CrossRef]
- Rajesh Kumar, B.; Vardhan, H.; Govindaraj, M. Prediction of uniaxial compressive strength, tensile strength and porosity of sedimentary rocks using sound level produced during rotary drilling. Rock Mech. Rock Eng. 2011, 44, 613–620. [Google Scholar] [CrossRef]
- Monjezi, M.; Khoshalan, H.A.; Razifard, M. A neuro-genetic network for predicting uniaxial compressive strength of rocks. Geotech. Geol. Eng. 2012, 30, 1053–1062. [Google Scholar] [CrossRef]
- Momeni, E.; Jahed Armaghani, D.; Hajihassani, M.; Mohd Amin, M.F. Prediction of uniaxial compressive strength of rock samples using hybrid particle swarm optimization-based artificial neural networks. Measurement 2015, 60, 50–63. [Google Scholar] [CrossRef]
- Hajihassani, M.; Armaghani, D.J.; Marto, A.; Mohamad, E.T. Ground vibration prediction in quarry blasting through an artificial neural network optimized by imperialist competitive algorithm. Bull. Eng. Geol. Environ. 2015, 74, 873–886. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Jahed Armaghani, D.; Momeni, E.; Alavi Nezhad Khalil Abad, S.V. Prediction of the unconfined compressive strength of soft rocks: A PSO-based ANN approach. Bull. Eng. Geol. Environ. 2015, 74, 745–757. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Armaghani, D.J.; Monjezi, M. Development of a new model for predicting fly rock distance in quarry blasting: A genetic programming technique. Bull. Eng. Geol. Environ. 2016, 75, 993–1006. [Google Scholar] [CrossRef]
- Khandelwal, M.; Armaghani, D.J. Prediction of drillability of rocks with strength properties using a hybrid GA-ANN technique. Geotech. Geol. Eng. 2016, 34, 605–620. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Noorian-Bidgoli, M.; Jahed Armaghani, D.; Khamesi, H. Feasibility of PSO-ANN model for predicting surface settlement caused by tunneling. Eng. Comput. 2016, 32, 705–715. [Google Scholar] [CrossRef]
- Gordan, B.; Jahed Armaghani, D.; Hajihassani, M.; Monjezi, M. Prediction of seismic slope stability through combination of particle swarm optimization and neural network. Eng. Comput. 2016, 32, 85–97. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Jahed Armaghani, D.; Bakhshandeh Amnieh, H.; AbdMajid, M.Z.; Tahir, M.M.D. Application of PSO to develop a powerful equation for prediction of fly rock due to blasting. Neural Comput. Appl. 2017, 28, 1043–1050. [Google Scholar] [CrossRef]
- Guha Roy, D.; Singh, T.N. Regression and soft computing models to estimate Young’s modulus of CO2 saturated coals. Measurement 2018, 129, 91–101. [Google Scholar] [CrossRef]
- Bejarbaneh, B.Y.; Bejarbaneh, E.Y.; Amin, M.F.M.; Fahimifar, A.; Armaghani, D.J.; Majid, M.Z. Intelligent modelling of sandstone deformation behavior using fuzzy logic and neural network systems. Bull. Eng. Geol. Environ. 2018, 77, 345–361. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Faradonbeh, R.S.; Rezaei, H.; Rashid, A.S.; Amnieh, H.B. Settlement prediction of the rock-socketed piles through a new technique based on gene expression programming. Neural Comput. Appl. 2018, 29, 1115–1125. [Google Scholar] [CrossRef]
- Alavi Nezhad Khalil Abad, S.V.; Yilmaz, M.; Jahed Armaghani, D.; Tugrul, A. Prediction of the durability of limestone aggregates using computational techniques. Neural Comput. Appl. 2018, 29, 423–433. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Armaghani, D.J.; Momeni, E.; Yazdavar, A.H.; Ebrahimi, M. Rock strength estimation: A PSO-based BP approach. Neural Comput. Appl. 2018, 30, 1635–1646. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Jahed Armaghani, D.; Haghighi, M.; Ghaleini, E.N. A neuro-genetic predictive model to approximate over break induced by drilling and blasting operation in tunnels. Bull. Eng. Geol. Environ. 2019, 78, 981–990. [Google Scholar] [CrossRef]
- Mahdiyar, A.; Armaghani, D.J.; Marto, A.; Nilashi, M.; Ismail, S. Rock tensile strength prediction using empirical and soft computing approaches. Bull. Eng. Geol. Environ. 2019, 78, 4519–4531. [Google Scholar] [CrossRef]
- Saedi, B.; Mohammadi, S.D.; Shahbazi, H. Prediction of uniaxial compressive strength and elastic modulus of migmatites using various modeling techniques. Arab. J. Geosci. 2018, 11, 574. [Google Scholar] [CrossRef]
- Saedi, B.; Mohammadi, S.D.; Shahbazi, H. Application of fuzzy inference system to predict uniaxial compressive strength and elastic modulus of migmatites. Environ. Earth Sci. 2019, 78, 208. [Google Scholar] [CrossRef]
- ASTM. D4644–16, Standard Test Method for Slake Durability of Shales and Other Similar Weak Rocks; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- ASTM. C97–2, Standard Test Method for Absorption and Bulk Specific Gravity of Dimension Stone; ASTM International: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Chester, D.L. Why two hidden layers are better than one. In Proceedings of the International Joint Conference on Neural Networks, San Diego, CA, USA, 17-21 June 1990; CRC Press: Boca Raton, FL, USA, 1990; Volume 1, pp. 265–268. [Google Scholar]
- Lippmann, R.P. An introduction to computing with neural nets. IEEE ASSP Mag. 1987, 4–22. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Sontag, E.D. Feedback stabilization using two-hidden-layernets. IEEE Trans. Neural Netw. 1992, 3, 981–990. [Google Scholar] [CrossRef] [PubMed]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Applications to Nonorthogonal Problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Santosa, F.; Symes, W. Linear inversion of band-limited reflection seismograms. SIAM J. Sci. Stat. Comp. 1986, 7, 1307–1330. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Tibshirani, R. The Lasso Method for Variable Selection in the Cox Model. Stat. Med. 1997, 16, 385–395. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Better Subset Regression Using the Nonnegative Garrote. Technometrics 1995, 37, 373–384. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Swingler, K. Applying Neural Networks: A Practical Guide; Academic Press: New York, NY, USA, 1996. [Google Scholar]
- LeCun, Y.; Bottou, L.; Genevieve, O.; Klaus-Robert, M. Efficient backprop in neural networks: Tricks of the trade. Lect. Notes Comput. Sci. 1998, 1524. [Google Scholar]
- Santurkar, S.; Tsipras, D.; Ilyas, A.; Madry, A. How does batch normalization help optimization? Adv. Neural Inf. Process. Syst. 2018, 31, 2488–2498. [Google Scholar]
- Jayalakshmi, T.; Santhakumaran, A. Statistical normalization and back propagation for classification. Int. J. Comput. Theory Eng. 2011, 3, 89–93. [Google Scholar] [CrossRef]

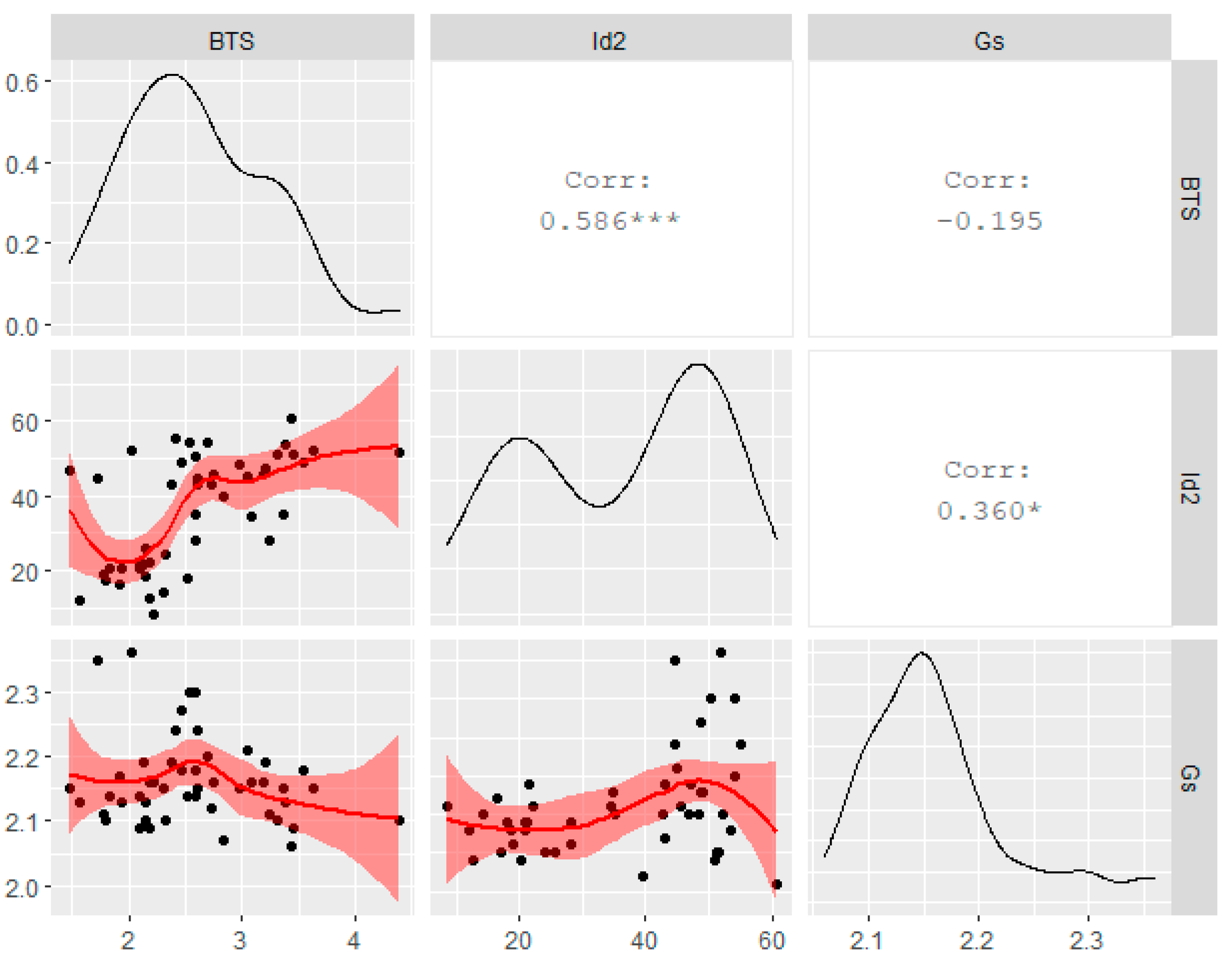

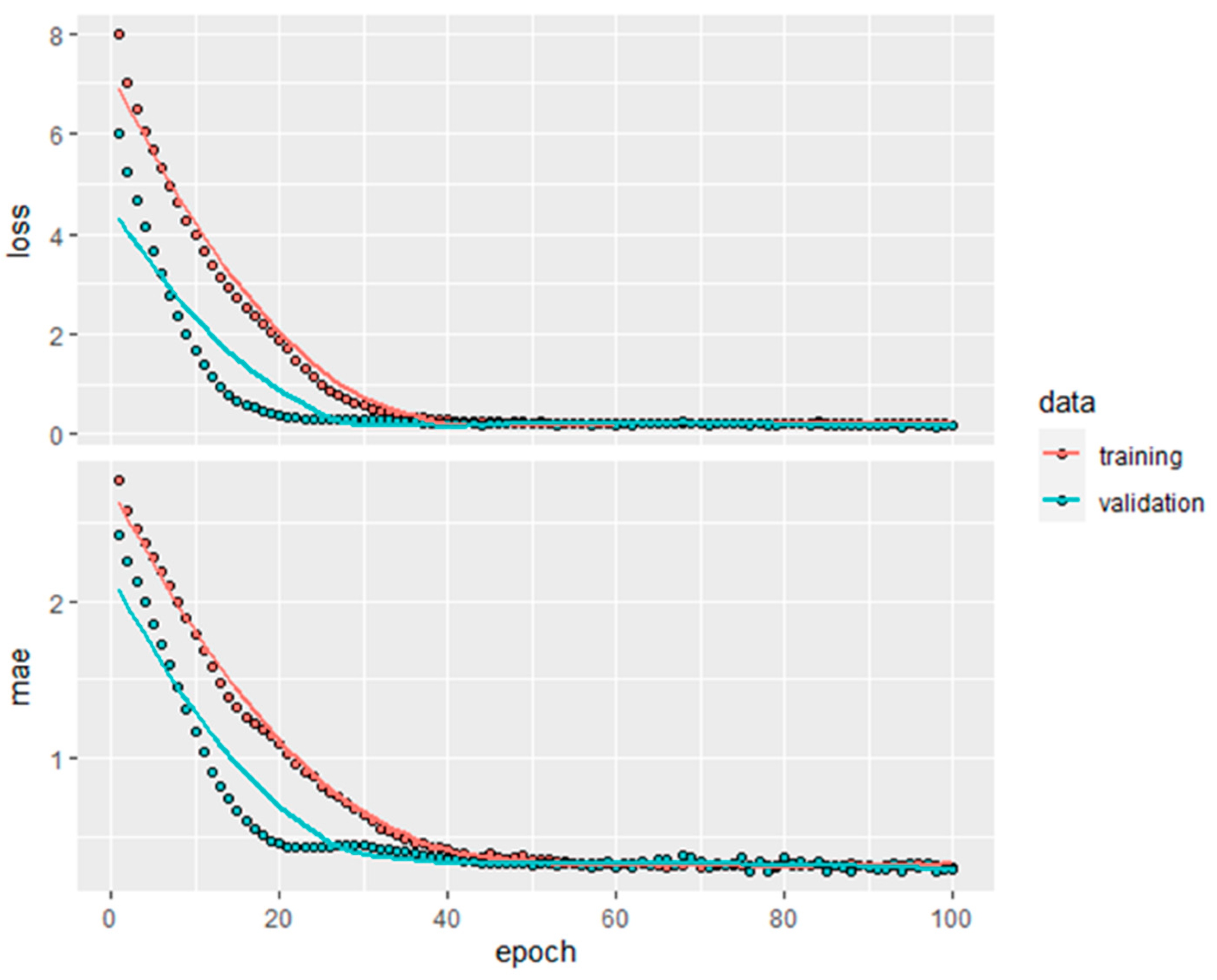
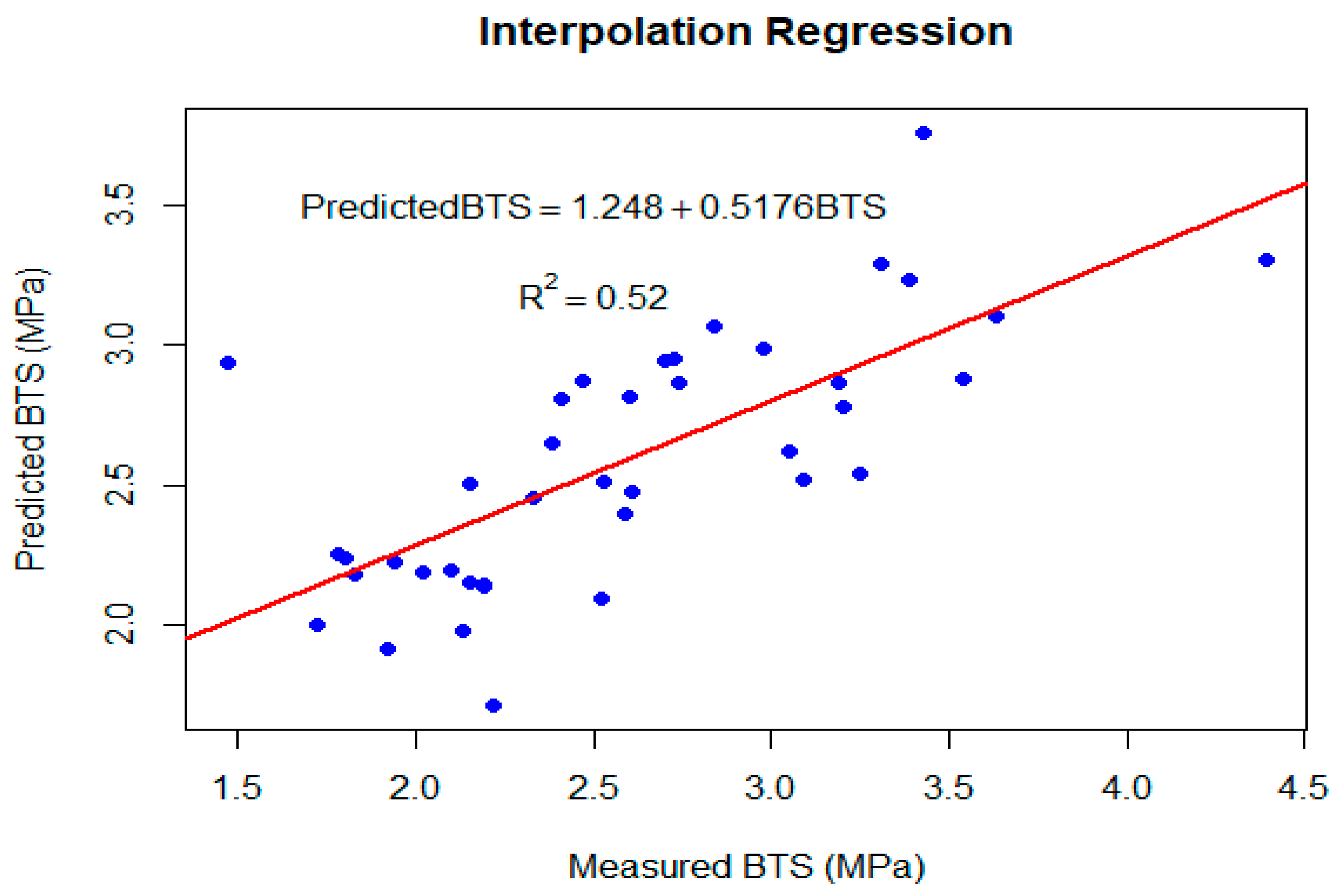
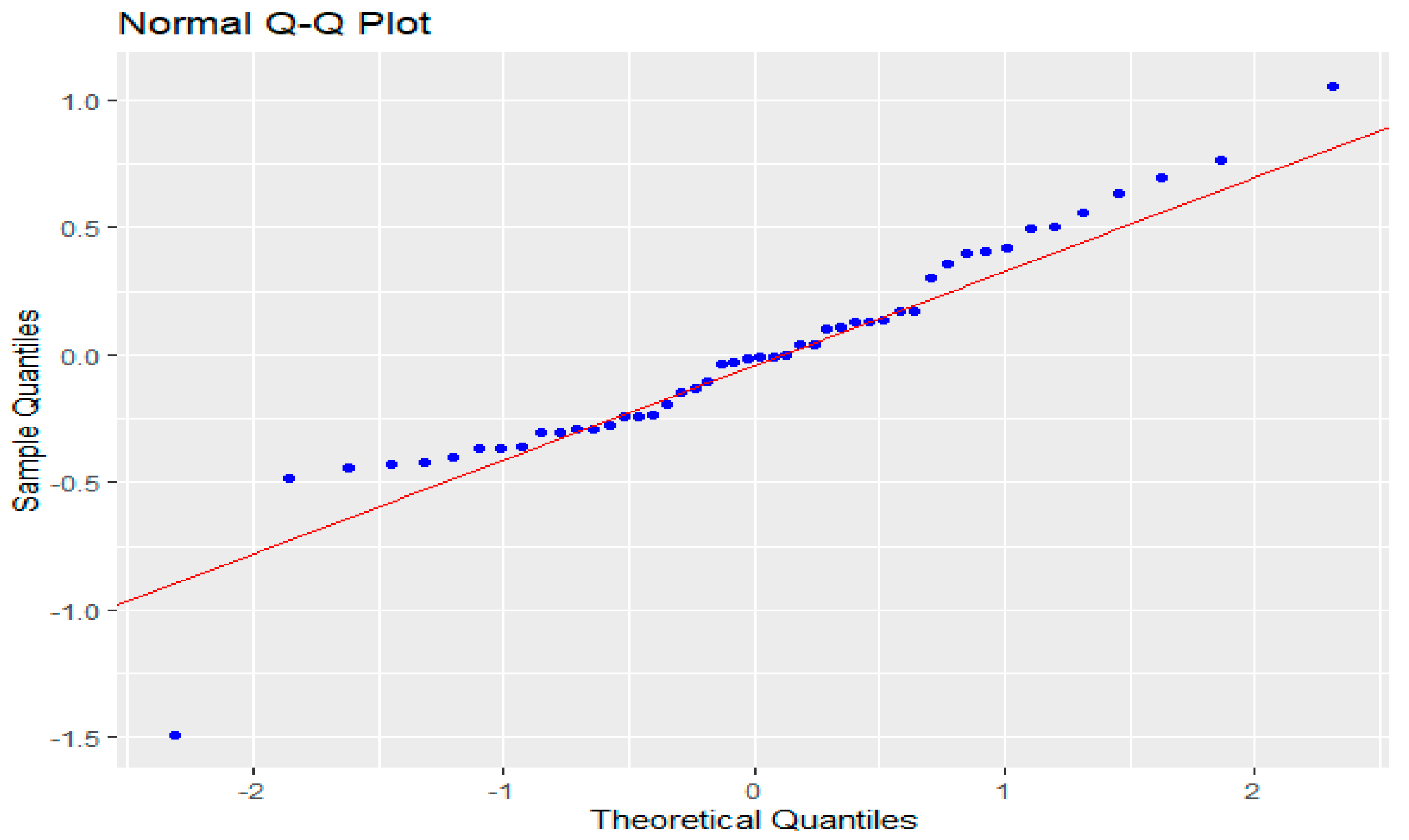
| Id2 (%) | Gs | BTS (MPa) |
|---|---|---|
| 34.9 | 2.18 | 2.59 |
| 19.0 | 2.11 | 1.78 |
| 28.0 | 2.14 | 2.59 |
| 17.0 | 2.10 | 1.80 |
| 54.1 | 2.20 | 2.70 |
| 51.9 | 2.36 | 2.02 |
| 20.3 | 2.09 | 2.09 |
| 44.6 | 2.35 | 1.72 |
| 48.8 | 2.18 | 2.47 |
| 8.4 | 2.16 | 2.22 |
| 35.1 | 2.15 | 3.36 |
| 51.1 | 2.09 | 3.46 |
| 53.5 | 2.13 | 3.39 |
| 20.7 | 2.13 | 1.94 |
| 45.7 | 2.16 | 3.19 |
| Variable | Mean | Median | Range | 95% CI for M |
|---|---|---|---|---|
| BTS (MPa) | 2.5819 | 2.5250 | 2.9200 | (2.40, 2.762) |
| Gs | 2.1619 | 2.1500 | 0.3000 | (2.142, 2.181) |
| Id2 (%) | 36.29 | 42.90 | 52.40 | (31.93, 40.64) |
| Variable | Coeff. | T-Value | p-Value | VIF |
|---|---|---|---|---|
| Constant | 2.5878 | 36.39 | p < 0.001 | |
| Id2 | 0.4622 | 6.00 | p < 0.001 | 1.14 |
| Gs | 0.3006 | −3.91 | p < 0.001 | 1.14 |
| Model | RMSE | ||
|---|---|---|---|
| MLR | 0 | 0 | 0.435 |
| Ridge | 0.035 | 1 | 0.434 |
| Lasso | 0.009 | 0 | 0.435 |
| Elastic Net | 0.007 | 0.1 | 0.435 |
| Model | R2 | MAE | RMSE |
|---|---|---|---|
| MLR | 0.669 | 0.351 | 0.435 |
| Ridge | 0.670 | 0.348 | 0.434 |
| Lasso | 0.670 | 0.349 | 0.435 |
| Elastic Net | 0.670 | 0.348 | 0.435 |
| Model | R2 | MAE | RMSE |
|---|---|---|---|
| ANNS | 0.689 | 0.281 | 0.370 |
| ANNN | 0.623 | 0.300 | 0.388 |
| MLR | 0.674 | 0.288 | 0.364 |
| Ridge | 0.672 | 0.295 | 0.368 |
| Lasso | 0.673 | 0.291 | 0.365 |
| Elastic Net | 0.670 | 0.294 | 0.367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, M.Y.; Arman, H. Comparison of Six Machine-Learning Methods for Predicting the Tensile Strength (Brazilian) of Evaporitic Rocks. Appl. Sci. 2021, 11, 5207. https://doi.org/10.3390/app11115207
Hassan MY, Arman H. Comparison of Six Machine-Learning Methods for Predicting the Tensile Strength (Brazilian) of Evaporitic Rocks. Applied Sciences. 2021; 11(11):5207. https://doi.org/10.3390/app11115207
Chicago/Turabian StyleHassan, Mohamed Yusuf, and Hasan Arman. 2021. "Comparison of Six Machine-Learning Methods for Predicting the Tensile Strength (Brazilian) of Evaporitic Rocks" Applied Sciences 11, no. 11: 5207. https://doi.org/10.3390/app11115207
APA StyleHassan, M. Y., & Arman, H. (2021). Comparison of Six Machine-Learning Methods for Predicting the Tensile Strength (Brazilian) of Evaporitic Rocks. Applied Sciences, 11(11), 5207. https://doi.org/10.3390/app11115207







