Numerical Study of the Influence of the Inlet Turbulence Length Scale on the Turbulent Boundary Layer
Abstract
:1. Introduction
2. Numerical Analysis
2.1. Governing Equation
2.2. Modeling of the Inflow Generator
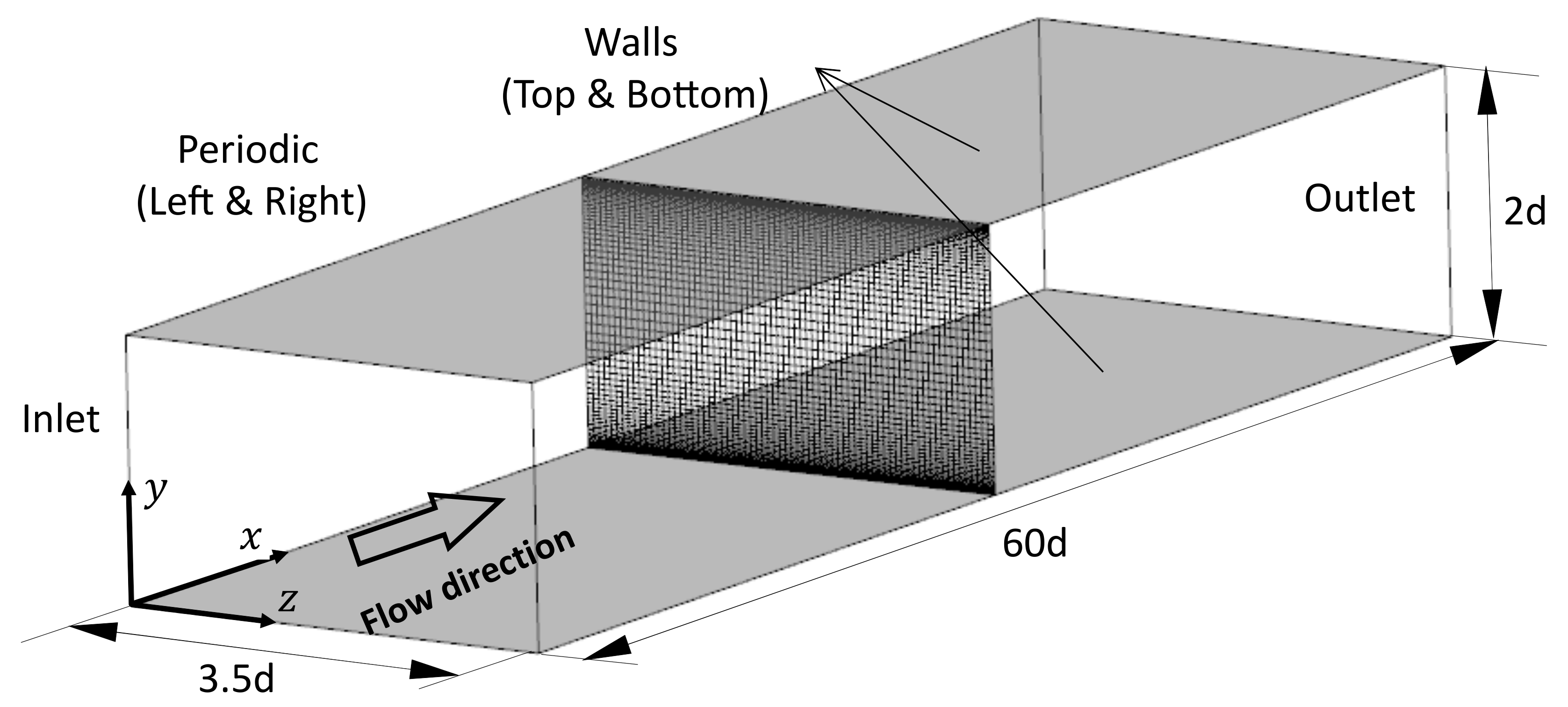
2.3. Implementation of the Boundary Condition and Inflow Length Scale
2.4. Variation of Inflow Length Scale
2.5. Filtering Process and Correlation
3. Results and Discussion
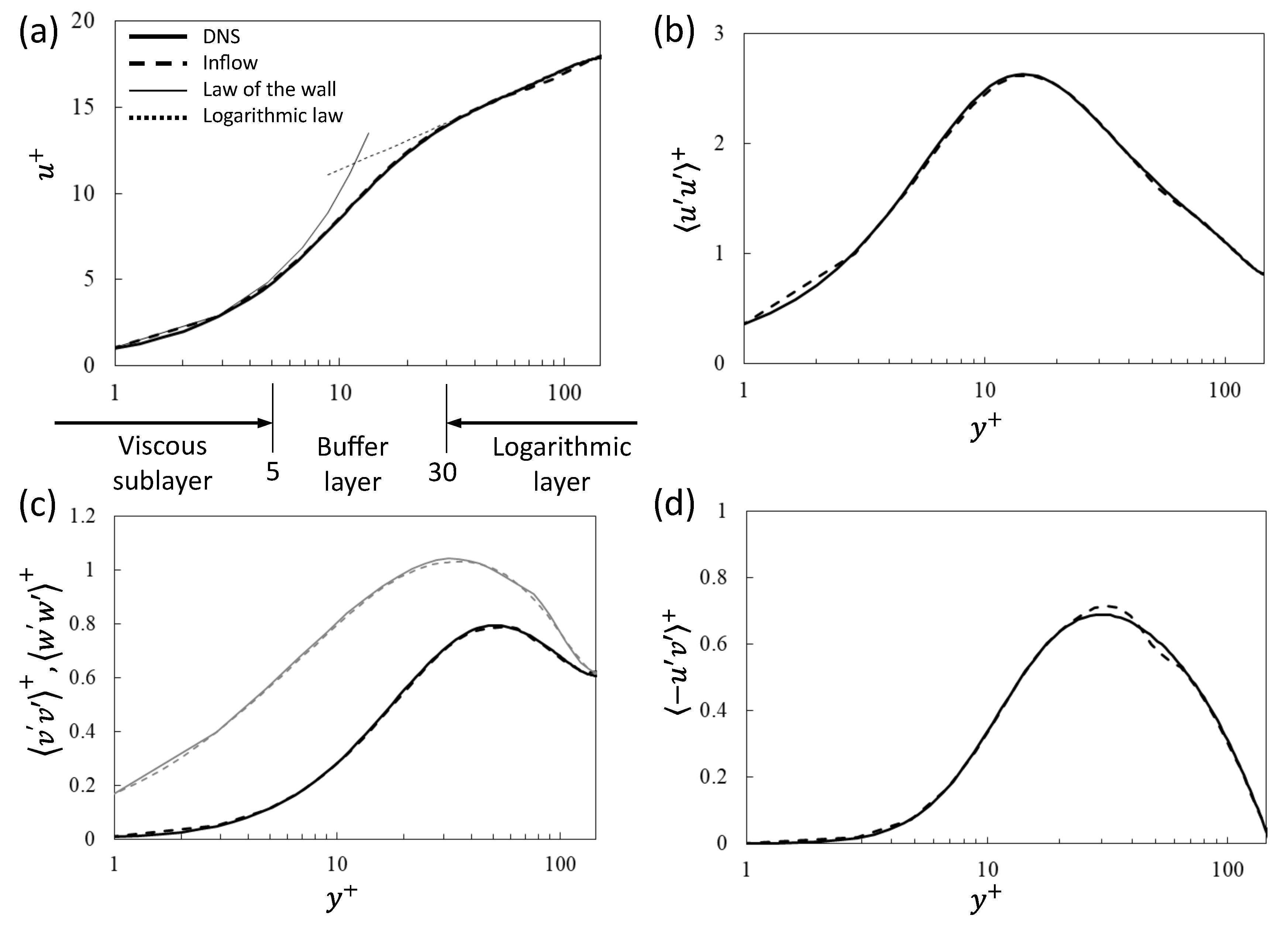
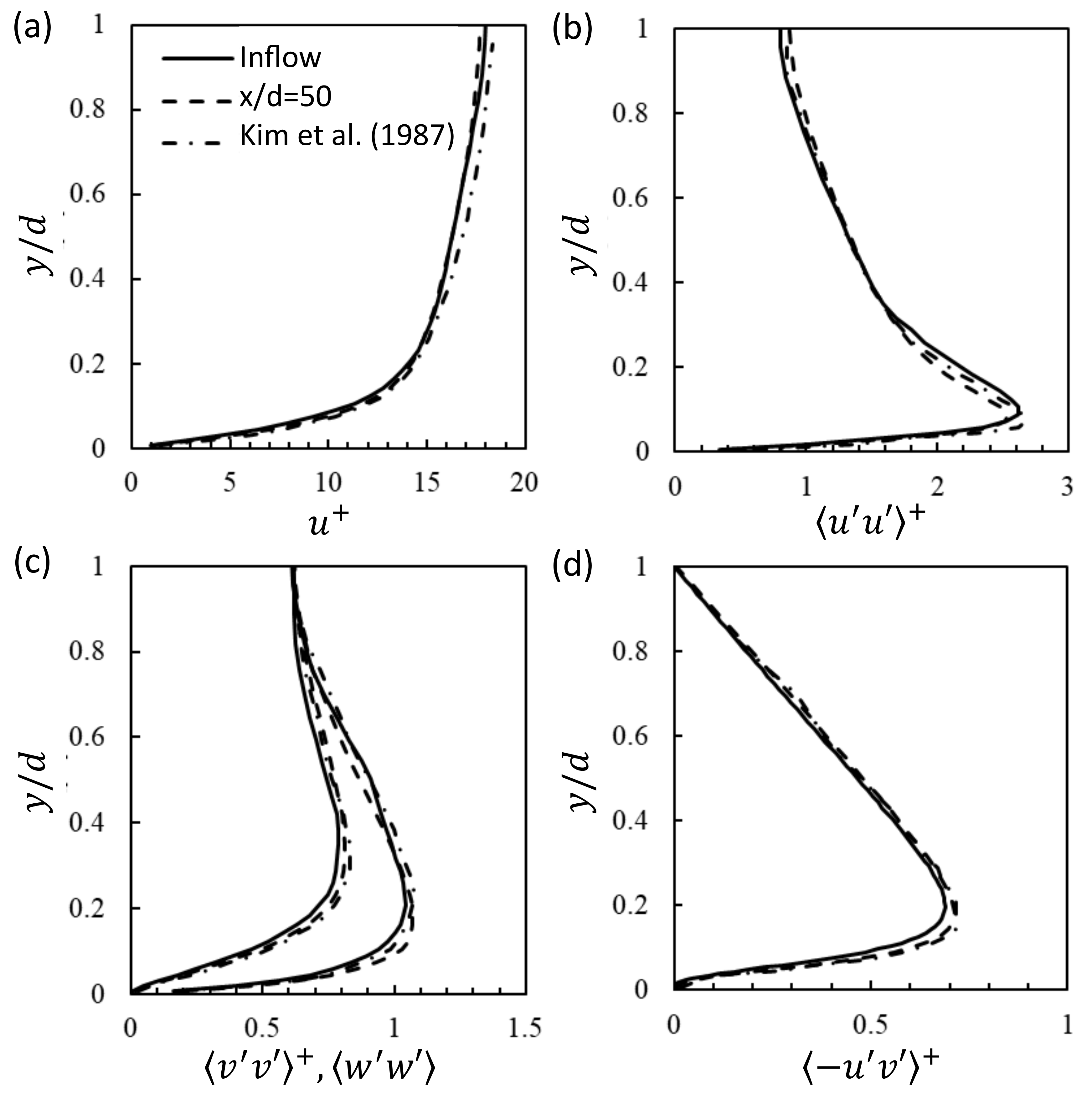
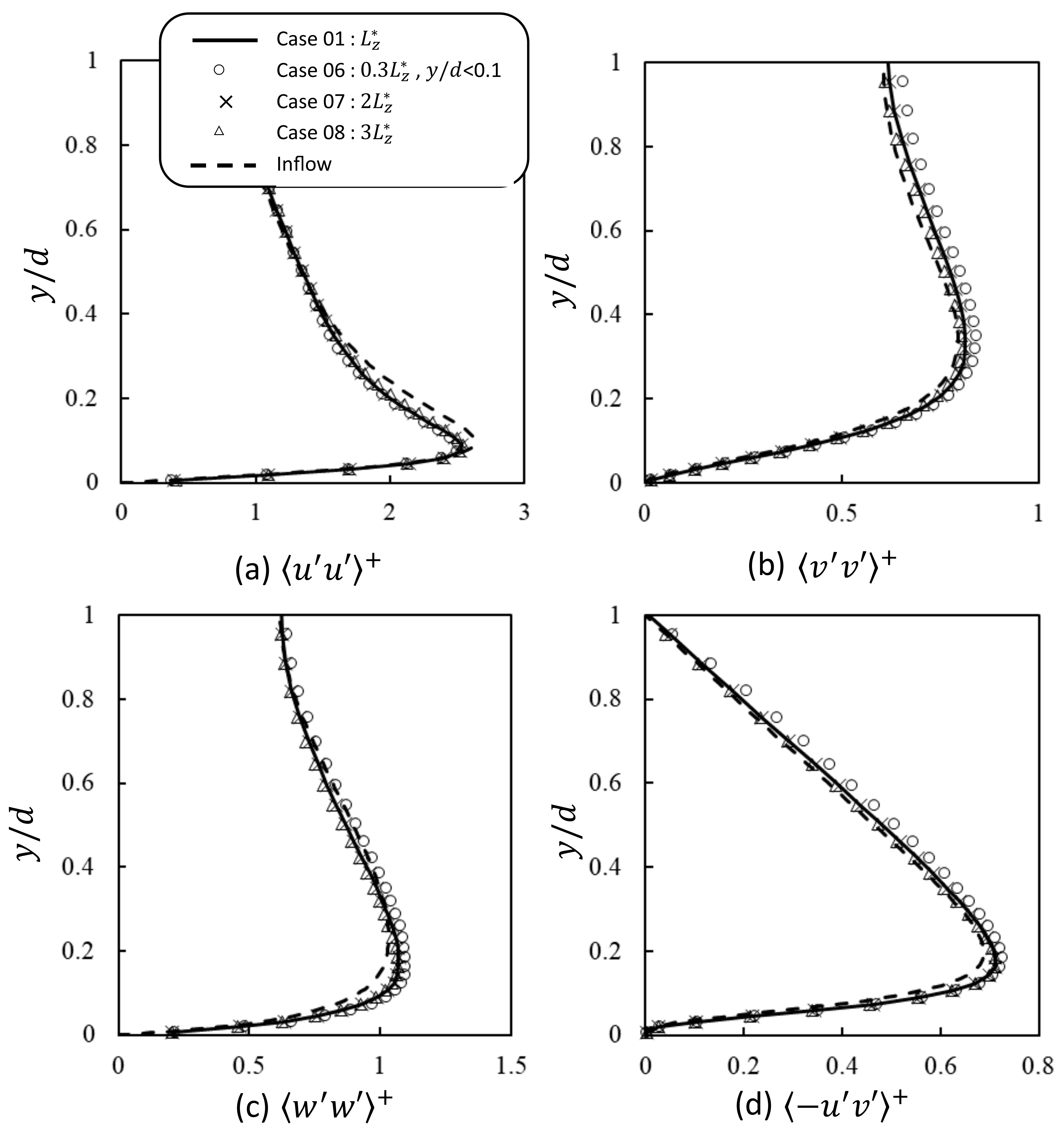
3.1. Channel Flow Simulation Using the Synthetic Inflow Generator
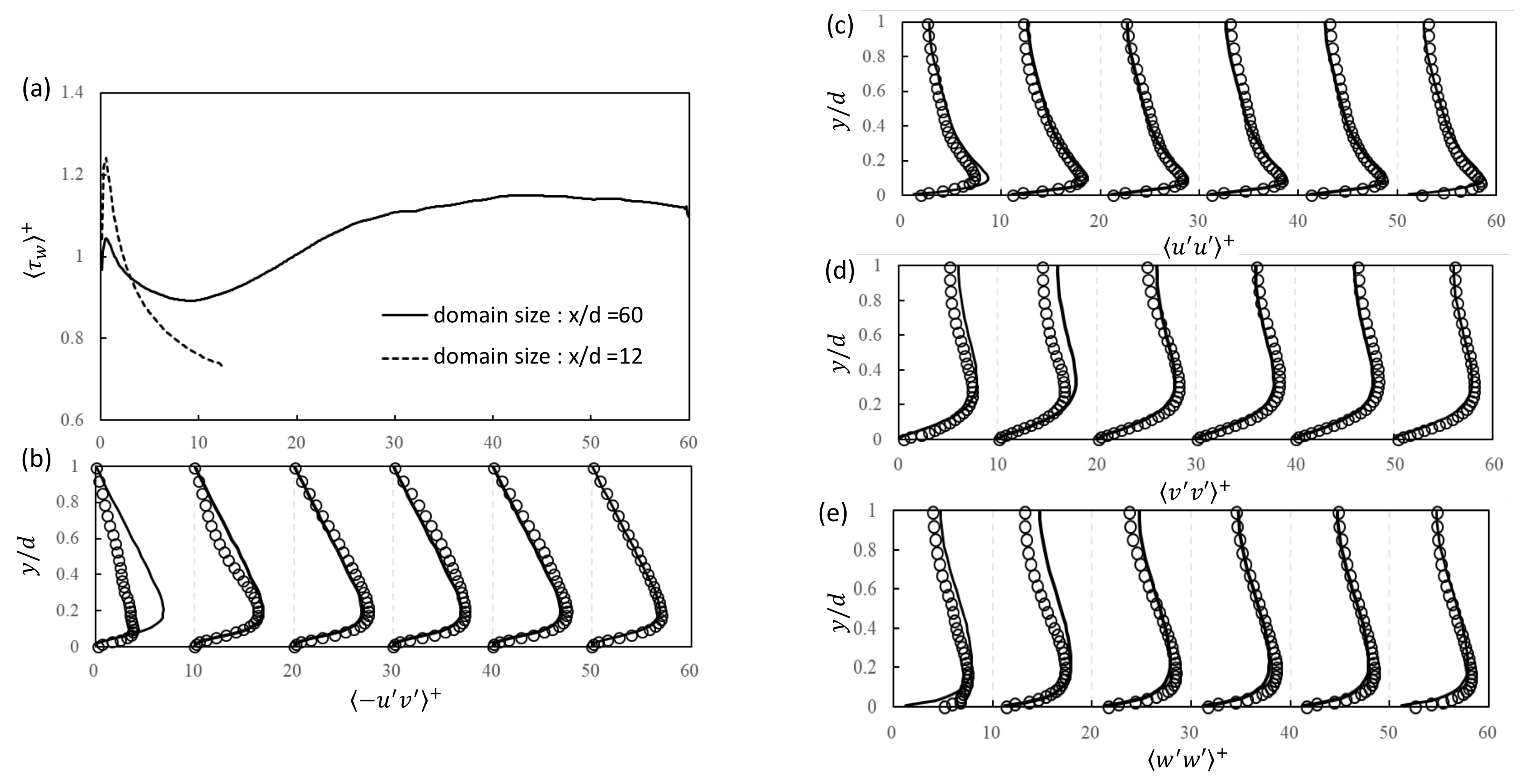
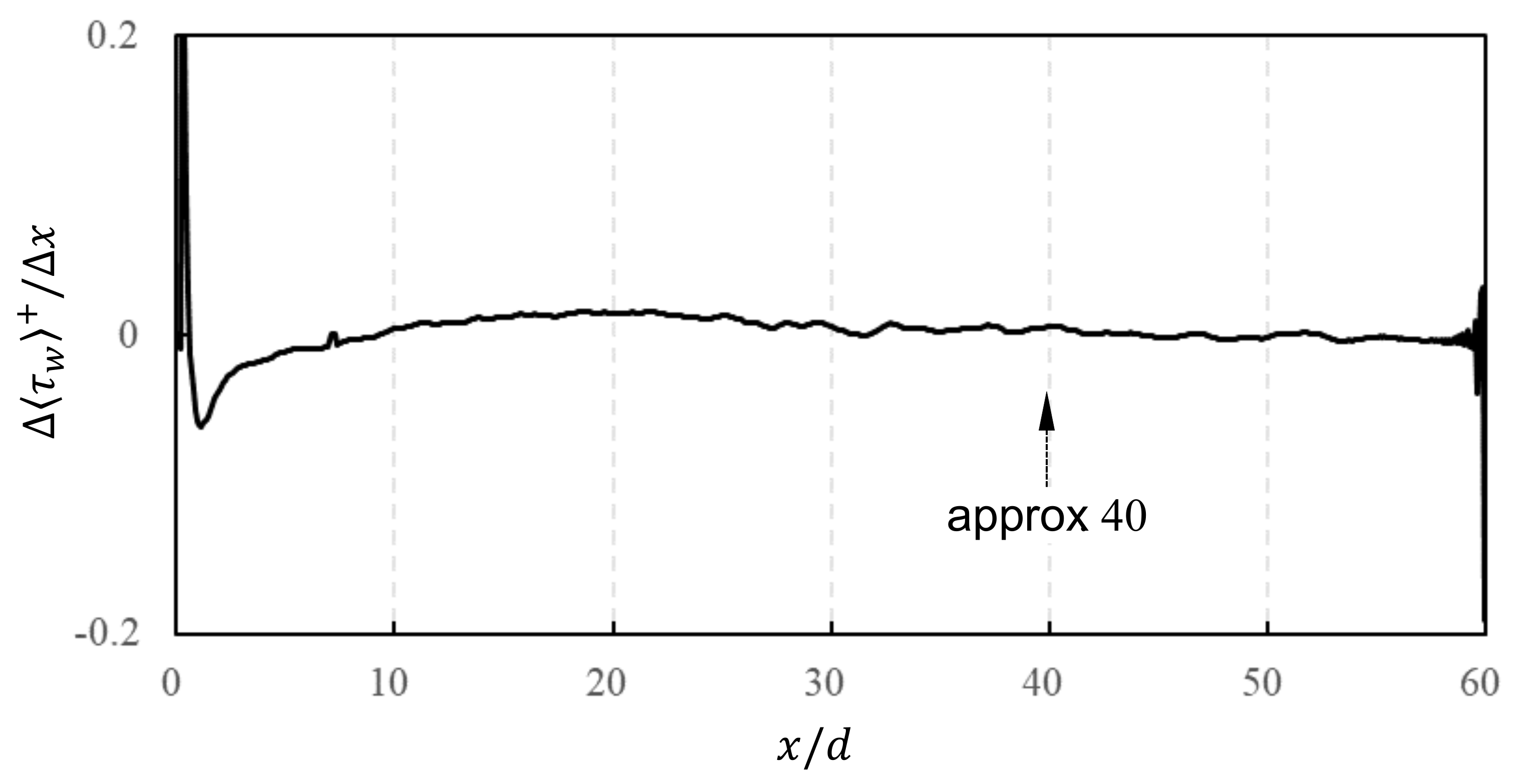
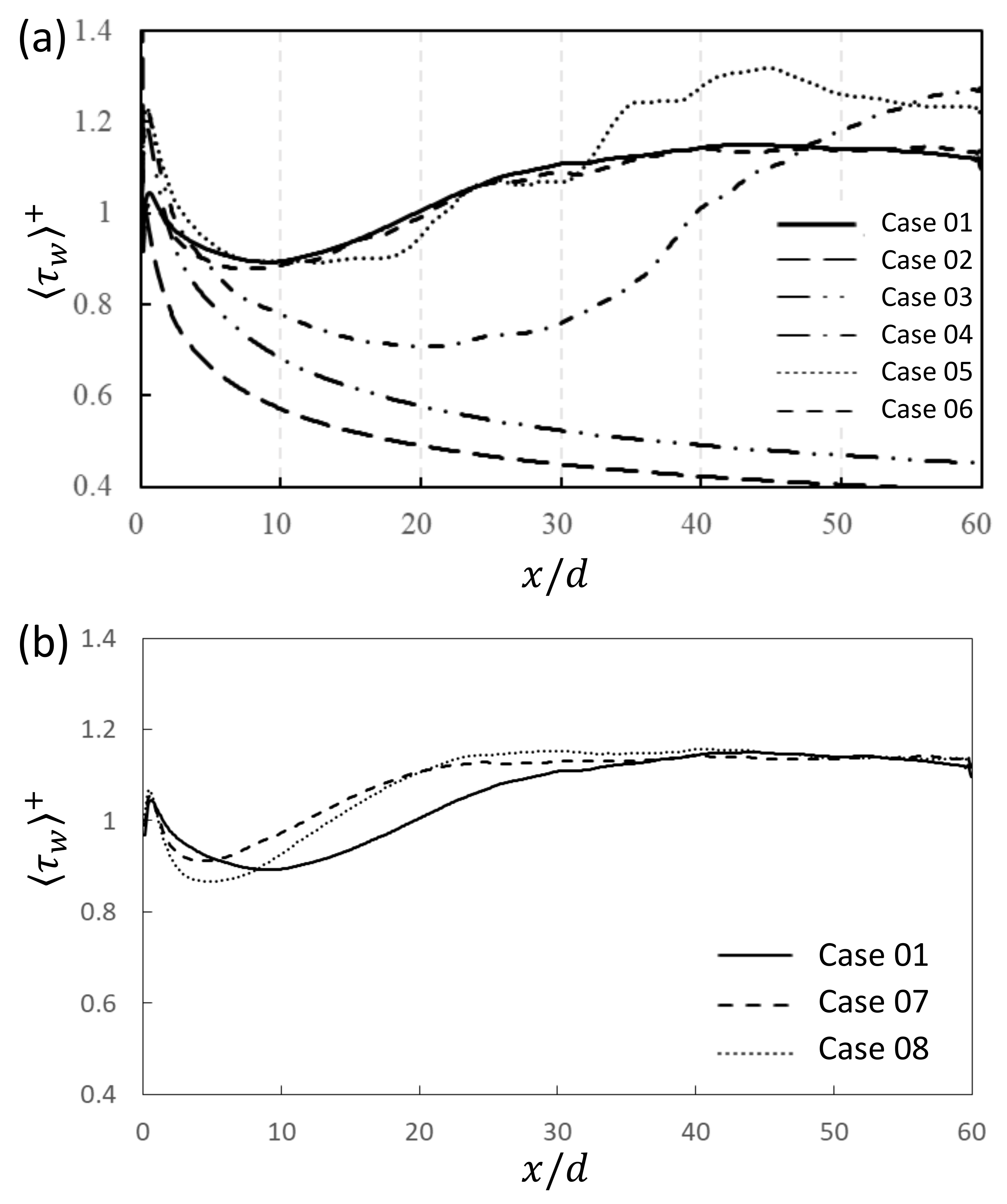
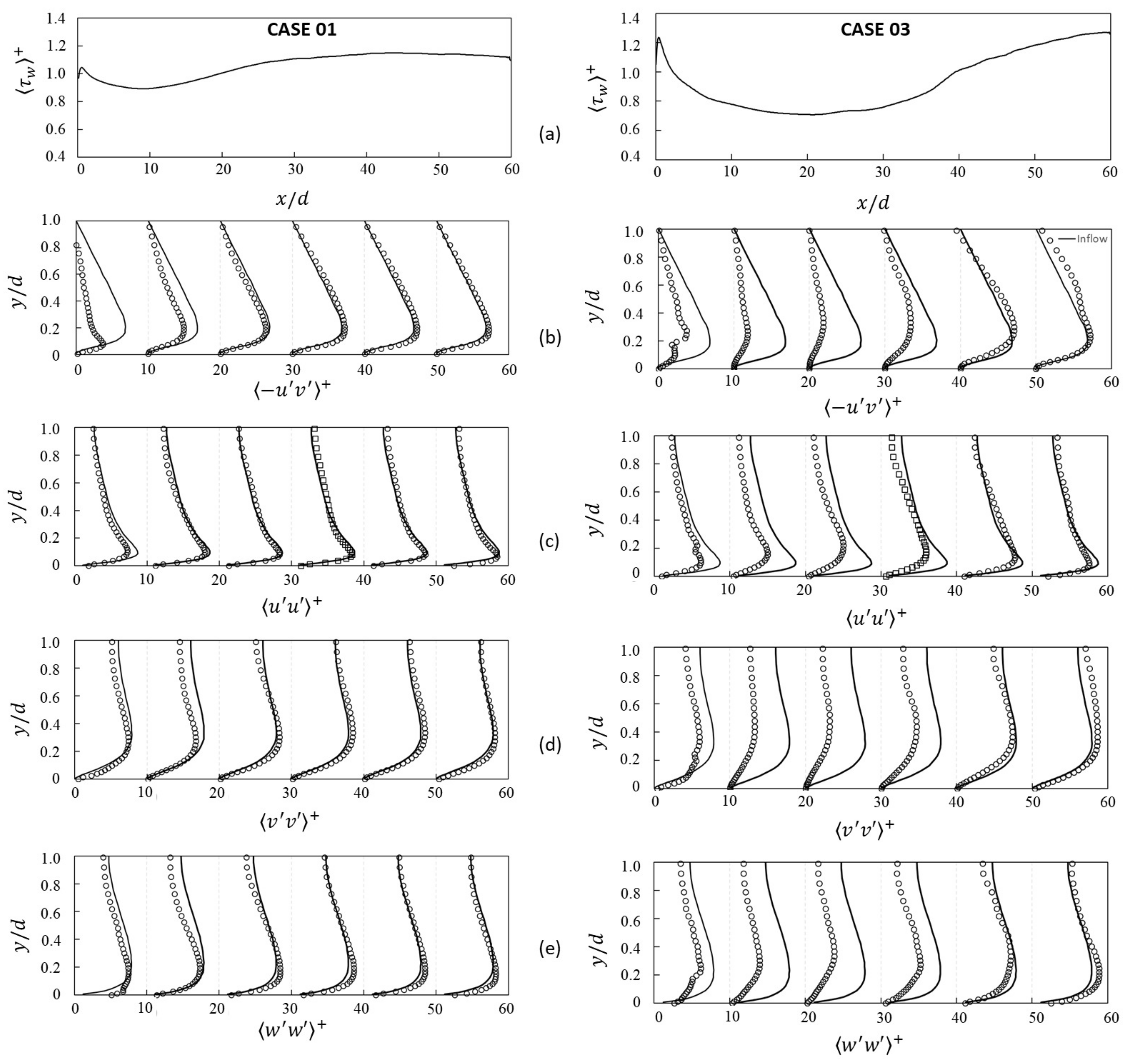
3.2. Effect of Inlet Length Scale on Wall Shear Stress
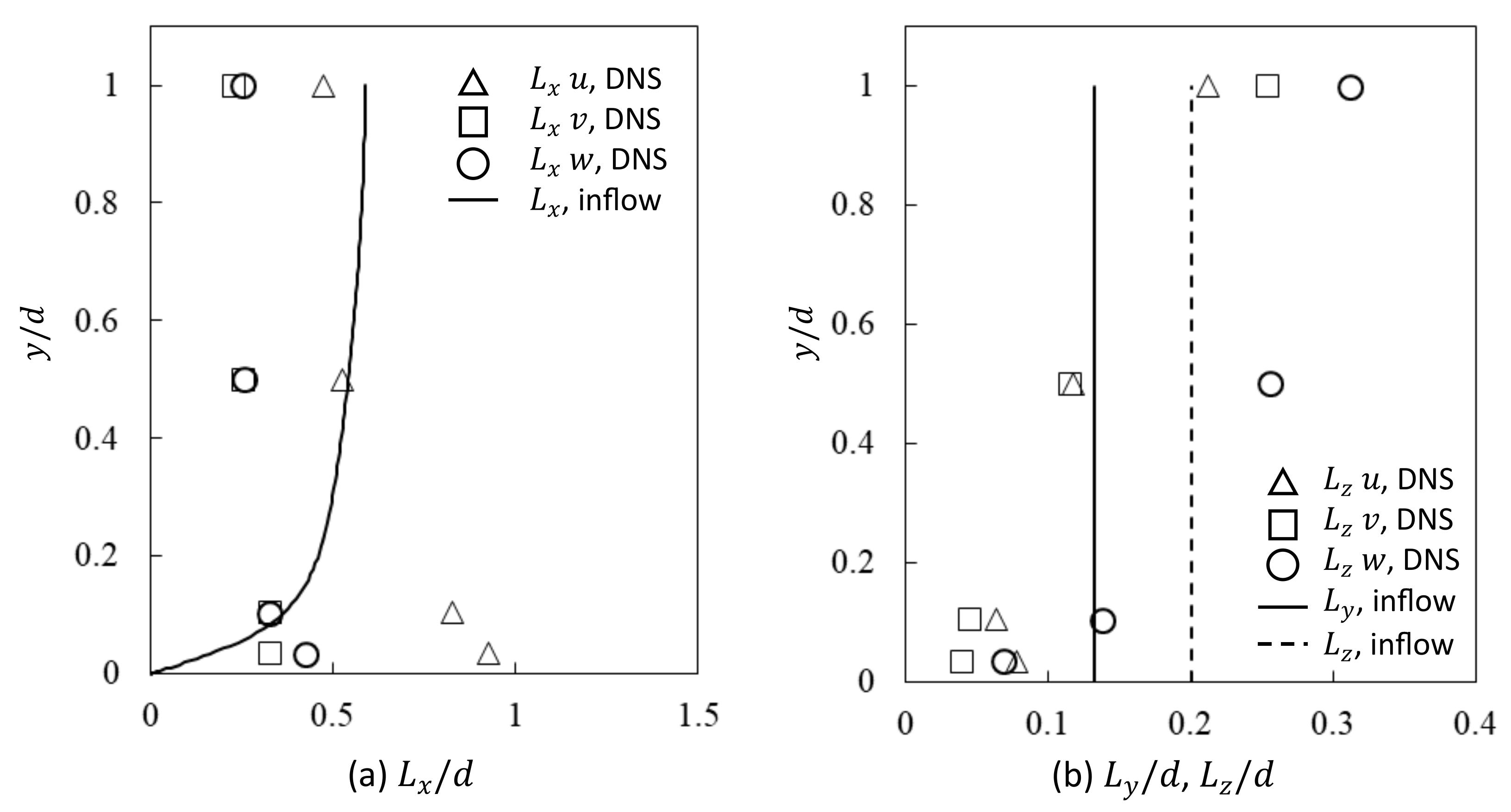
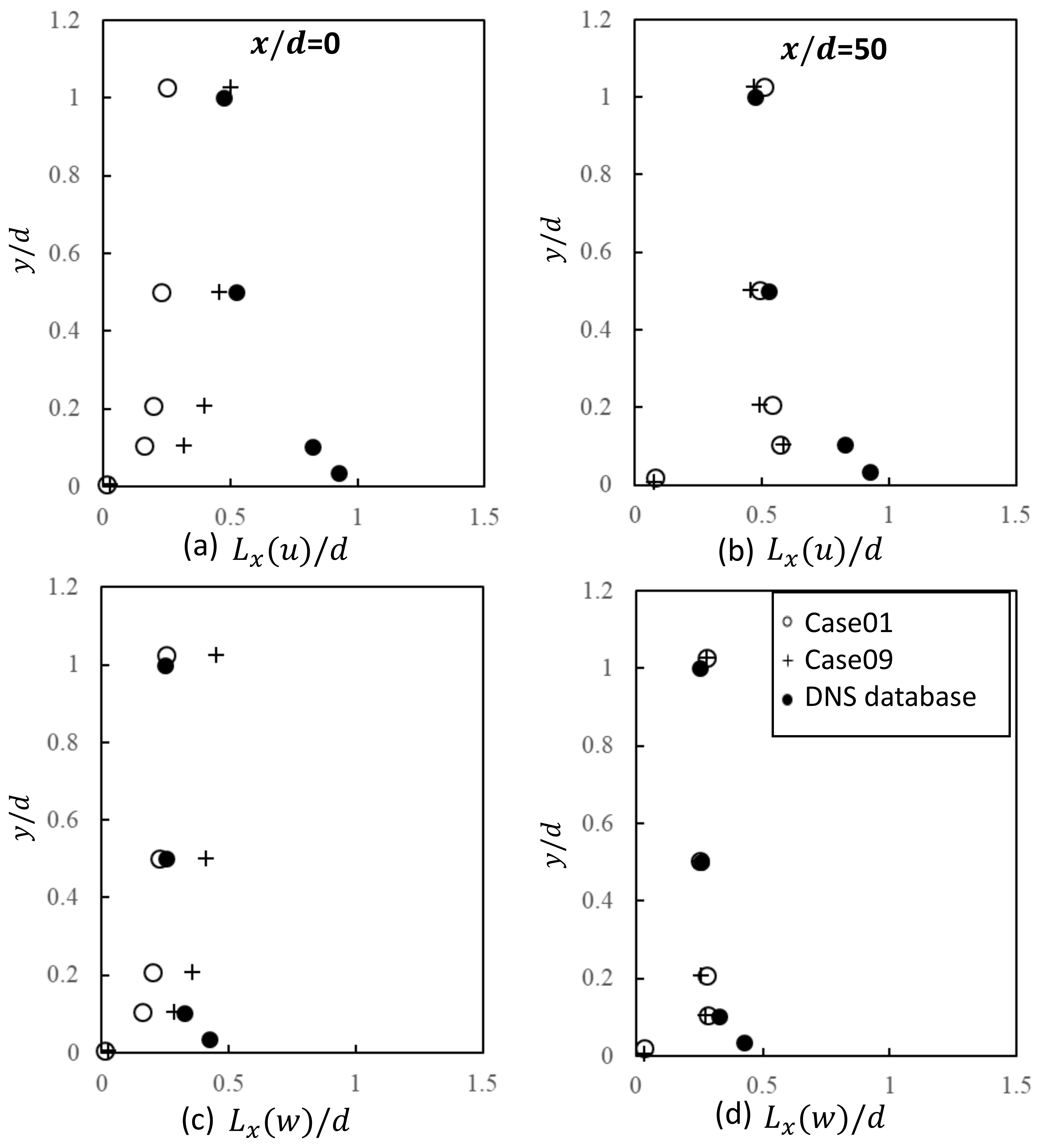
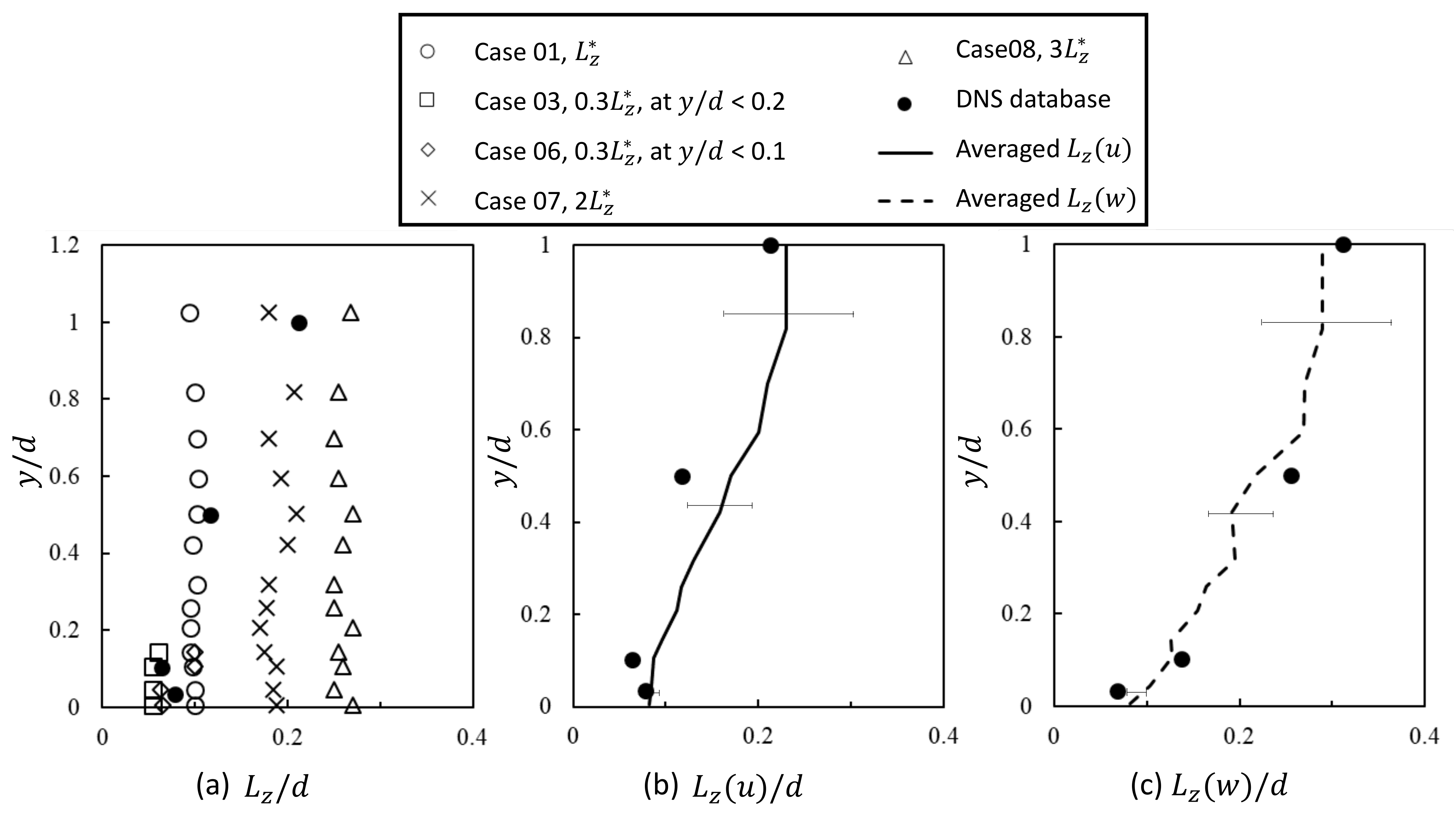
3.3. Effect of Inlet Length Scale on the Integral Length Scale in the Domain
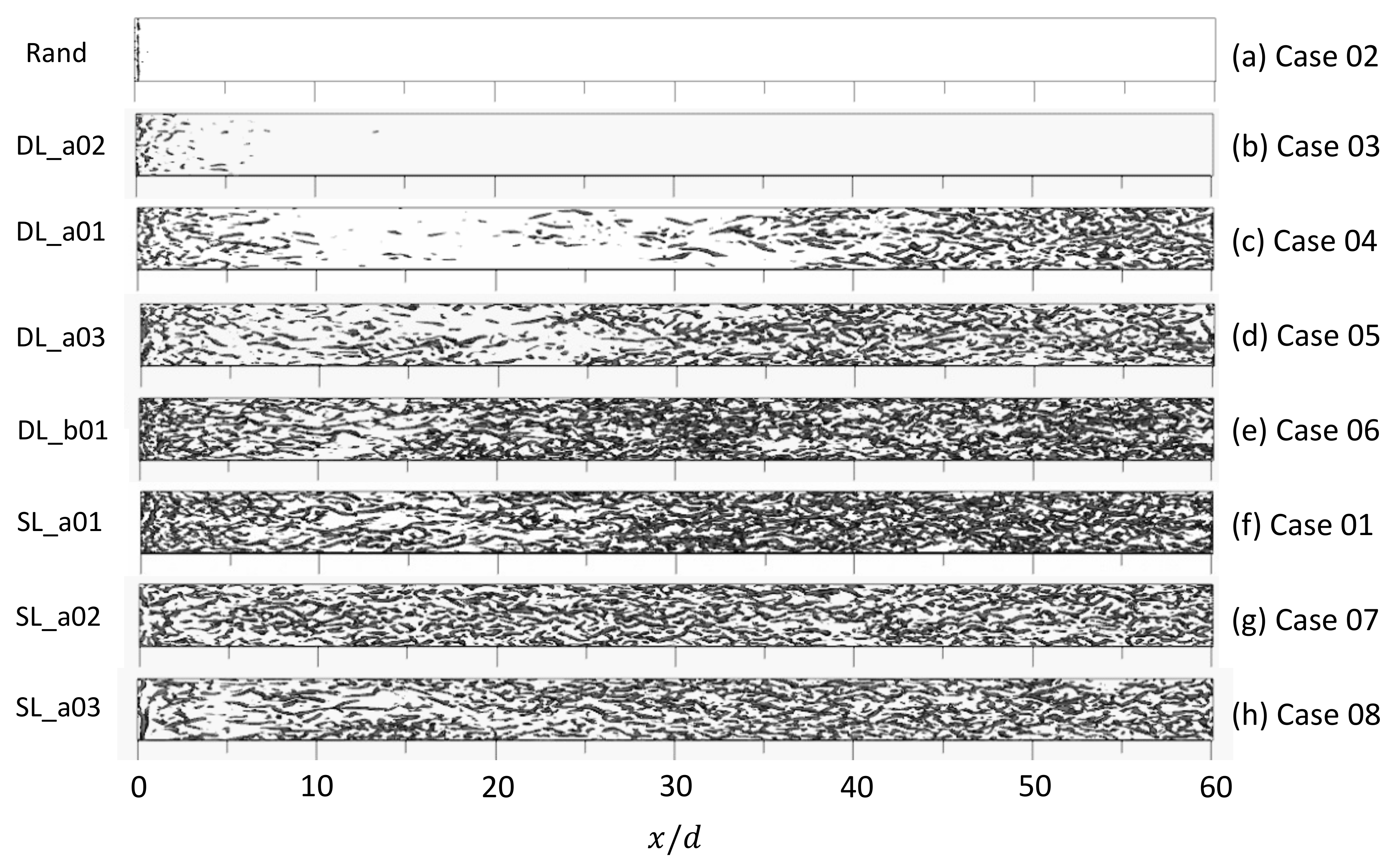
3.4. Second Invariant Flow Structure near the Wall
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kovasznay, L.S. Turbulent boundary layer. Annu. Rev. Fluid Mech. 1970, 2, 95–112. [Google Scholar] [CrossRef]
- Willmarth, W.W. Pressure-fluctuations beneath turbulent boundary-layers. Annu. Rev. Fluid Mech. 1975, 7, 13–38. [Google Scholar] [CrossRef]
- Kline, S.J.; Reynolds, W.C.; Schraub, F.A.; Runstadler, P.W. The structure of turbulent boundary-layers. J. Fluid Mech. 1967, 30, 741–773. [Google Scholar] [CrossRef] [Green Version]
- Sreenivasan, K.R. The turbulent boundary layer. Front. Exp. Fluid Mech. 1989, 46, 159–210. [Google Scholar]
- Kline, S.J.; Robinson, S.K. Quasi-Coherent Structures in the Turbulent Boundary Layer. Part I: Status Report on a Community-Wide Summary of the Data. In Near Wall Turbulence; Hemisphere Publishing Corp: New York, NY, USA, 1990; pp. 200–217. [Google Scholar]
- Cermak, J.E.; Cochran, L.S. Physical modeling of the atmospheric surface-layer. J. Wind Eng. Ind. Aero. 1992, 42, 935–946. [Google Scholar] [CrossRef]
- Rachele, H.; Tunick, A.; Hansen, F.V. Mariah—A similarity-based method for determining wind, temperature, and humidity profile structure in the atmospheric surface-Layer. J. Appl. Meteorol. 1995, 34, 1000–1005. [Google Scholar] [CrossRef] [Green Version]
- Rachele, H.; Tunick, A.; Hansen, F.V. Reply to Arya, S.P. Comments on “Mariah—A similarity-based method for determining wind, temperature, and humidity profile structure in the atmospheric surface”. J. Appl. Meteorol. 1996, 35, 613–614. [Google Scholar] [CrossRef] [Green Version]
- Raupach, M.R.; Antonia, R.A.; Rajagopalan, S. Rough-wall turbulent boundary layers. Appl. Mech. Rev. 1991, 44, 1–25. [Google Scholar] [CrossRef]
- Meroney, R.N. Wind-tunnel modeling of the flow about bluff-Bodies. J. Wind Eng. Ind. Aero. 1988, 29, 203–223. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Cr. Acad. Sci. URSS 1941, 30, 301–305. [Google Scholar]
- Prandtl, L. On fluid motions with very small friction. Verhldg 1904, 3, 484–491. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972; 300p. [Google Scholar]
- Hunt, A. Wind-tunnel measurements of surface pressures on cubic building models at several scales. J. Wind Eng. Ind. Aero. 1982, 10, 137–163. [Google Scholar] [CrossRef]
- Sun, J.; Mahrt, L. Determination of surface fluxes from the surface radiative temperature. J. Atmos. Sci. 1995, 52, 1096–1106. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lele, S.K.; Moin, P. Simulation of spatially evolving turbulence and the applicability of Taylor hypothesis in compressible flow. Phys. Fluids 1992, 4, 1521–1530. [Google Scholar] [CrossRef]
- Keating, A.; Piomelli, U.; Balaras, E.; Kaltenbach, H. A priori and a posteriori tests of inflow conditions for large-eddy simulation. Phys. Fluids 2004, 16, 4696–4712. [Google Scholar] [CrossRef]
- Lim, H.C.; Thomas, T.G.; Castro, I.P. Flow around a cube in a turbulent boundary layer: LES and experiment. J. Wind. Eng. Ind. Aero. 2009, 97, 96–109. [Google Scholar] [CrossRef] [Green Version]
- Lim, H.C.; Castro, I.P.; Hoxey, R.P. Bluff bodies in deep turbulent boundary layers: Reynolds-number issues. J. Fluid Mech. 2007, 571, 97–118. [Google Scholar] [CrossRef] [Green Version]
- Lund, T.S.; Wu, X.H.; Squires, K.D. Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 1998, 140, 233–258. [Google Scholar] [CrossRef] [Green Version]
- Druault, P.; Lardeau, S.; Bonnet, J.P.; Coiffet, F.; Delville, J.; Lamballais, E.; Largeau, J.F.; Perret, L. Generation of three-dimensional turbulent inlet conditions for large-eddy simulation. AIAA J. 2004, 42, 447–456. [Google Scholar] [CrossRef]
- Johansson, P.S.; Andersson, H.I. Generation of inflow data for inhomogeneous turbulence. Theor. Comput. Fluid Dyn. 2004, 18, 371–389. [Google Scholar] [CrossRef]
- Perret, L.; Delville, J.; Manceau, R.; Bonnet, J.-P. Generation of turbulent inflow conditions for large eddy simulation from stereoscopic PIV measurements. Int. J. Heat Fluid Flow 2006, 27, 576–584. [Google Scholar] [CrossRef]
- Hanna, S.R.; Tehranian, S.; Carissimo, B.; Macdonald, R.W.; Lohner, R. Comparisons of model simulations with observations of mean flow and turbulence within simple obstacle arrays. Atmos. Environ. 2002, 36, 5067–5079. [Google Scholar] [CrossRef]
- Xie, Z.T.; Castro, I.P. LES and RANS for turbulent flow over arrays of wall-mounted obstacles. Flow Turbul. Combust. 2006, 76, 291–312. [Google Scholar] [CrossRef] [Green Version]
- Xie, Z.T.; Castro, I.P. Efficient generation of inflow conditions for large eddy simulation of street-scale flows. Flow Turbul. Combust. 2008, 81, 449–470. [Google Scholar] [CrossRef] [Green Version]
- Mare, L.; Klein, M.; Jones, W.P.; Janicka, J. Synthetic turbulence inflow conditions for large-eddy simulation. Phys. Fluids 2006, 18, 025107. [Google Scholar] [CrossRef]
- Veloudis, I.; Yang, Z.; McGuirk, J.J.; Page, G.J.; Spencer, A. Novel implementation and assessment of a digital filter based approach for the generation of LES inlet conditions. Flow Turbul. Combust. 2007, 79, 1–24. [Google Scholar] [CrossRef]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef] [Green Version]
- Deck, S.; Renard, N.; Laraufie, R.; Sagaut, P. Zonal detached eddy simulation (ZDES) of a spatially developing flat plate turbulent boundary layer over the Reynolds number range 3150 < Reθ < 14,000. Phys. Fluids 2014, 26, 025116. [Google Scholar] [CrossRef]
- Gupta, M.M.; Kalita, J.C. A new paradigm for solving Navier-stokes equations, streamfunction-velocity formulation, J. Comput. Phys. 2005, 207, 25–68. [Google Scholar] [CrossRef]
- Barragy, E.; Carey, G.F. Stream function-vorticity driven cavity solution using p finite elements. Comput. Fluids 1997, 26, 453–468. [Google Scholar]
- Bennacer, R.; Reggio, M.; Pellerin, N.; Ma, X.Y. Differentiated heated lid driven cavity interacting with tube a Lattice Boltzmann Study. Therm. Sci. 2017, 21, 89–104. [Google Scholar]
- Kareem, A.K.; Gao, S. Mixed convection heat transfer of turbulent flow in a three-dimensional lid-driven cavity with a rotating cylinder. J. Heat Mass Transf. 2017, 112, 185–200. [Google Scholar] [CrossRef] [Green Version]
- Moin, P.; Kim, J. Numerical investigation of turbulent channel flow. J. Fluid Mech. 1982, 118, 341–377. [Google Scholar] [CrossRef] [Green Version]
- Le, H.; Moin, P. Direct Numerical Simulation of Turbulent Flow Over a Backward-Facing Step; Standford Univ. Report TF-58; Department of Mechanical Engineering, Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Kim, Y.; Castro, I.P.; Xie, Z.T. Divergence-free turbulence inflow conditions for large-eddy simulations with incompressible flow solvers. Comput. Fluids 2013, 84, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Solorzano-Lopez, J.; Zenit, R.; Ramirez-Argaez, M.A. Mathematical and physical simulation of the interaction between a gas jet and a liquid free surface. Appl. Math. Model. 2011, 35, 4991–5005. [Google Scholar] [CrossRef]
- Taylor, G.I. The spectrum of turbulence. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef] [Green Version]
- Iwamoto, K.; Suzuki, Y.; Kasagi, N. Database of Fully Developed Channel Flow. Department of Mechanical Engineering, The University of Tokyo, THTLAB Internal Report No. ILR-0201, DNS Database (CH12_PG.WL7). 2002. Available online: http://www.thtlab.jp (accessed on 15 May 2021).
- Deck, S.; Weiss, P.E.; Pamies, M.; Garnier, E. Zonal detached eddy simulation of a spatially developing flat plate turbulent boundary layer. Comput. Fluids 2011, 48, 1–15. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef] [Green Version]
- Hinze, J. Turbulence; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Grass, A.J. Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 1971, 50, 233–255. [Google Scholar] [CrossRef]
- Kasagi, N.; Hirata, M.; Nishino, K. Streamwise pseudo-vortical structures and associated vorticity in the near-wall region of a wall-bounded turbulent shear flow. Exp. Fluids 1986, 4, 309–318. [Google Scholar] [CrossRef]
- Smith, C.; Schwartz, S. Observation of streamwise rotation in the near-wall region of a turbulent boundary layer. Phys. Fluids 1983, 26, 641–652. [Google Scholar] [CrossRef]


| Name | |||
|---|---|---|---|
| Case 01 | |||
| Case 02 | 0, random | 0, random | 0, random |
| Case 03 | |||
| Case 04 | |||
| Case 05 | |||
| Case 06 | |||
| Case 07 | |||
| Case 08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-T.; Gutti, L.K.; Lim, H.-C. Numerical Study of the Influence of the Inlet Turbulence Length Scale on the Turbulent Boundary Layer. Appl. Sci. 2021, 11, 5177. https://doi.org/10.3390/app11115177
Lee Y-T, Gutti LK, Lim H-C. Numerical Study of the Influence of the Inlet Turbulence Length Scale on the Turbulent Boundary Layer. Applied Sciences. 2021; 11(11):5177. https://doi.org/10.3390/app11115177
Chicago/Turabian StyleLee, Young-Tae, Lokesh Kalyan Gutti, and Hee-Chang Lim. 2021. "Numerical Study of the Influence of the Inlet Turbulence Length Scale on the Turbulent Boundary Layer" Applied Sciences 11, no. 11: 5177. https://doi.org/10.3390/app11115177
APA StyleLee, Y.-T., Gutti, L. K., & Lim, H.-C. (2021). Numerical Study of the Influence of the Inlet Turbulence Length Scale on the Turbulent Boundary Layer. Applied Sciences, 11(11), 5177. https://doi.org/10.3390/app11115177







