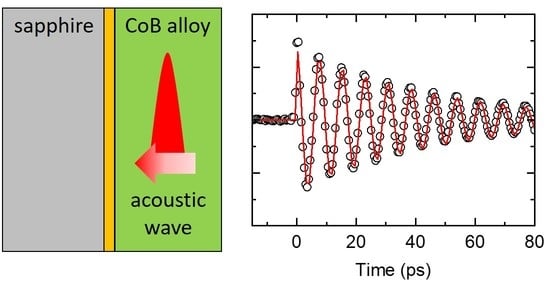
Using Amorphous CoB Alloy as Transducer to Detect Acoustic Propagation and Heat Transport at Interface
Abstract
:Featured Application
Abstract
1. Introduction
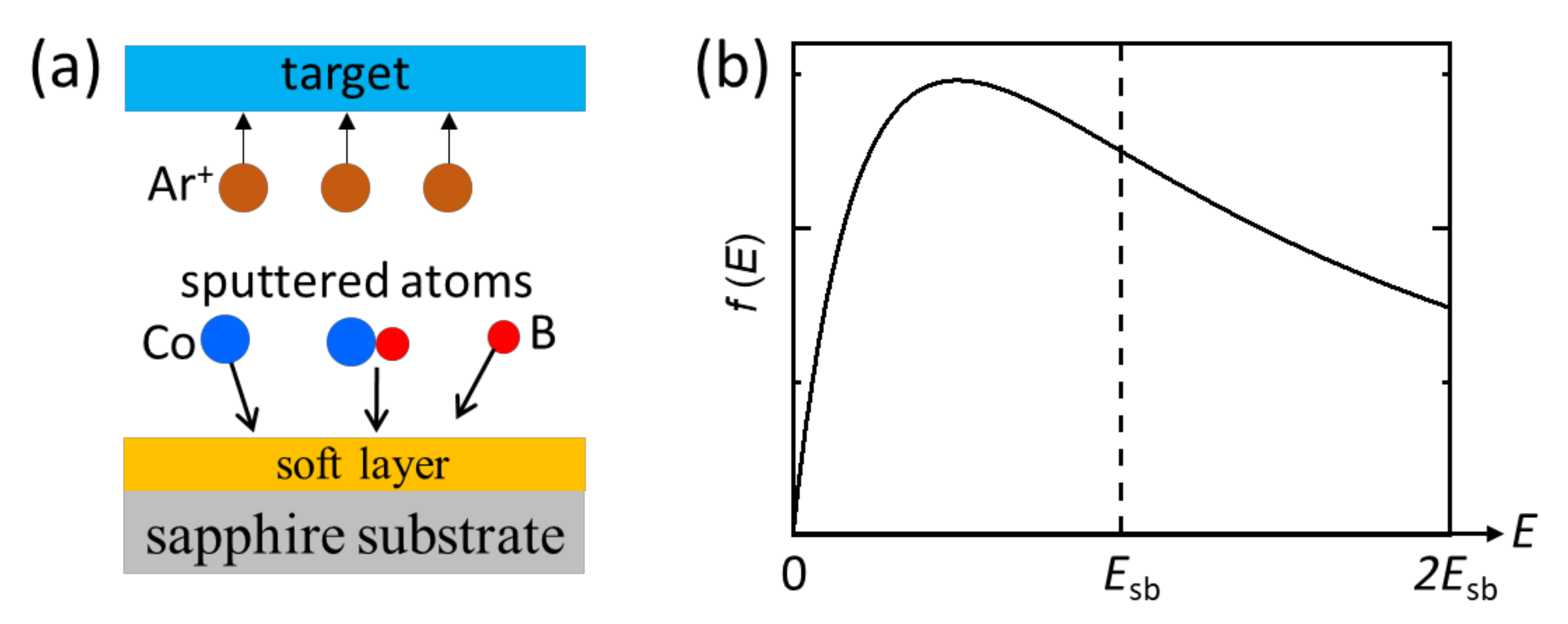
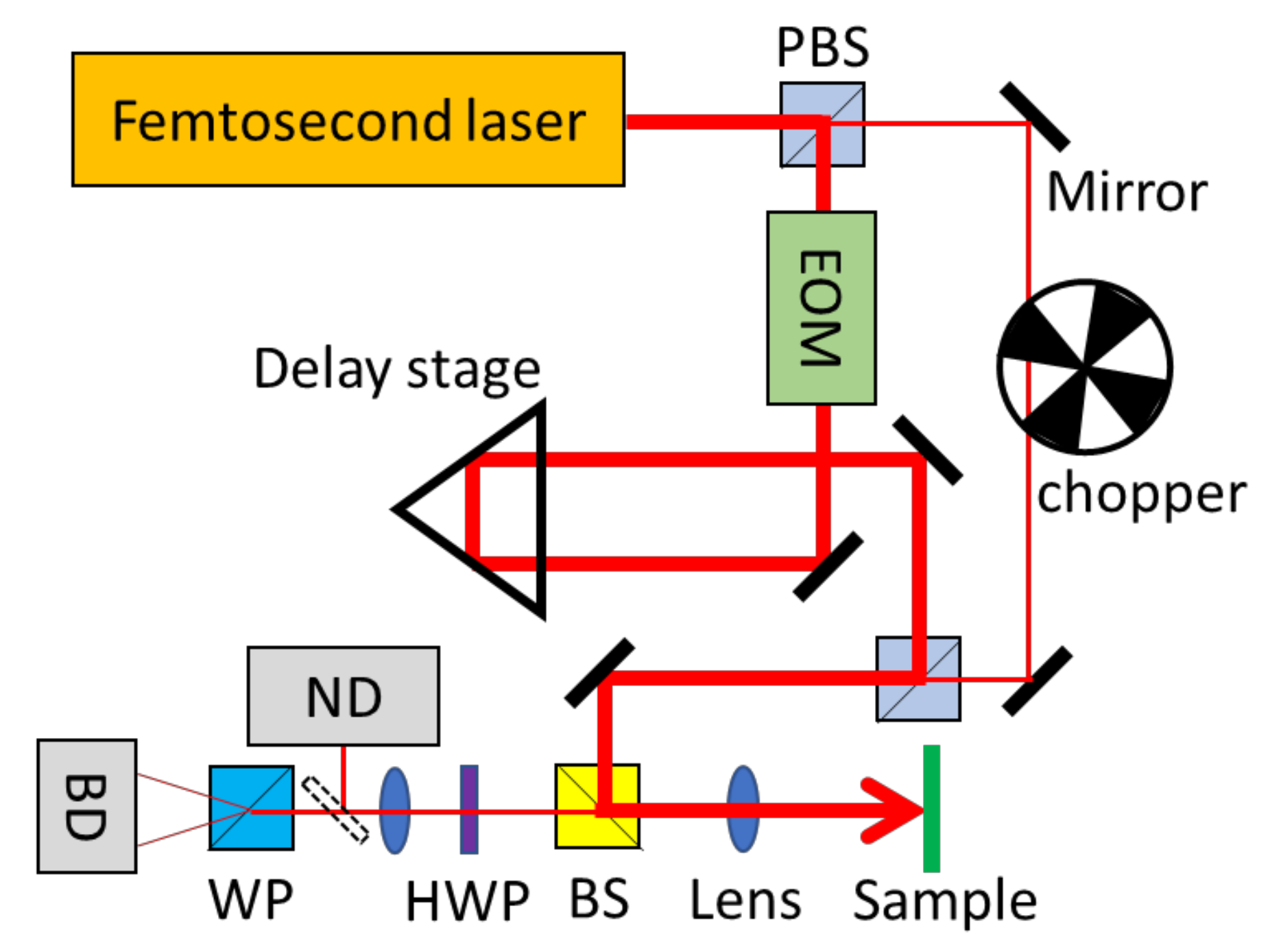
2. Materials and Methods
3. Results
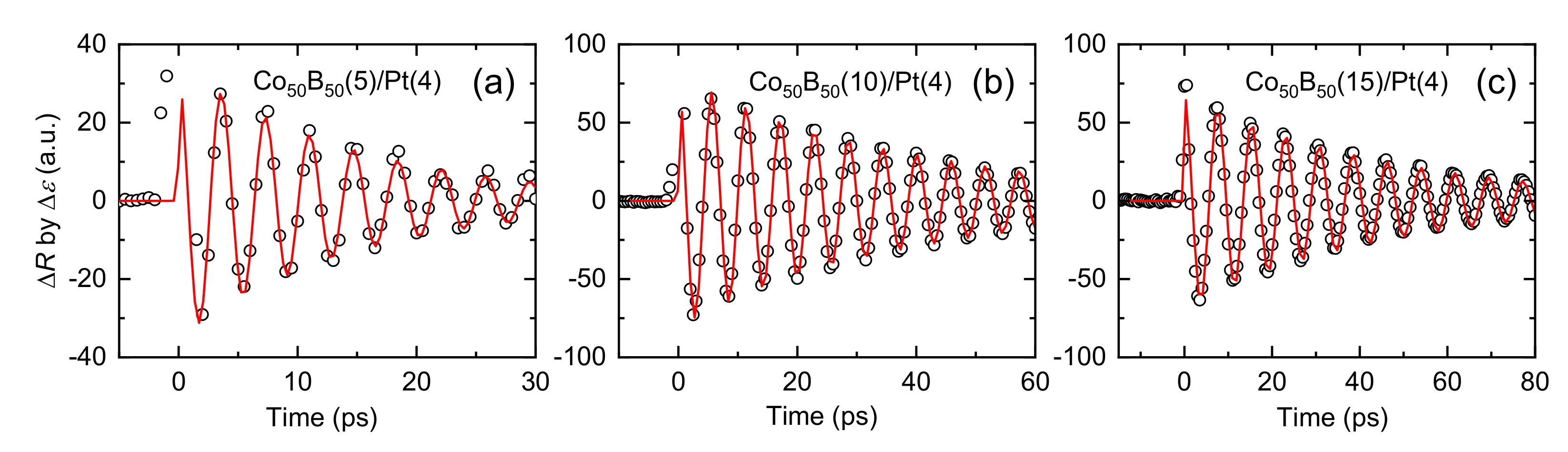
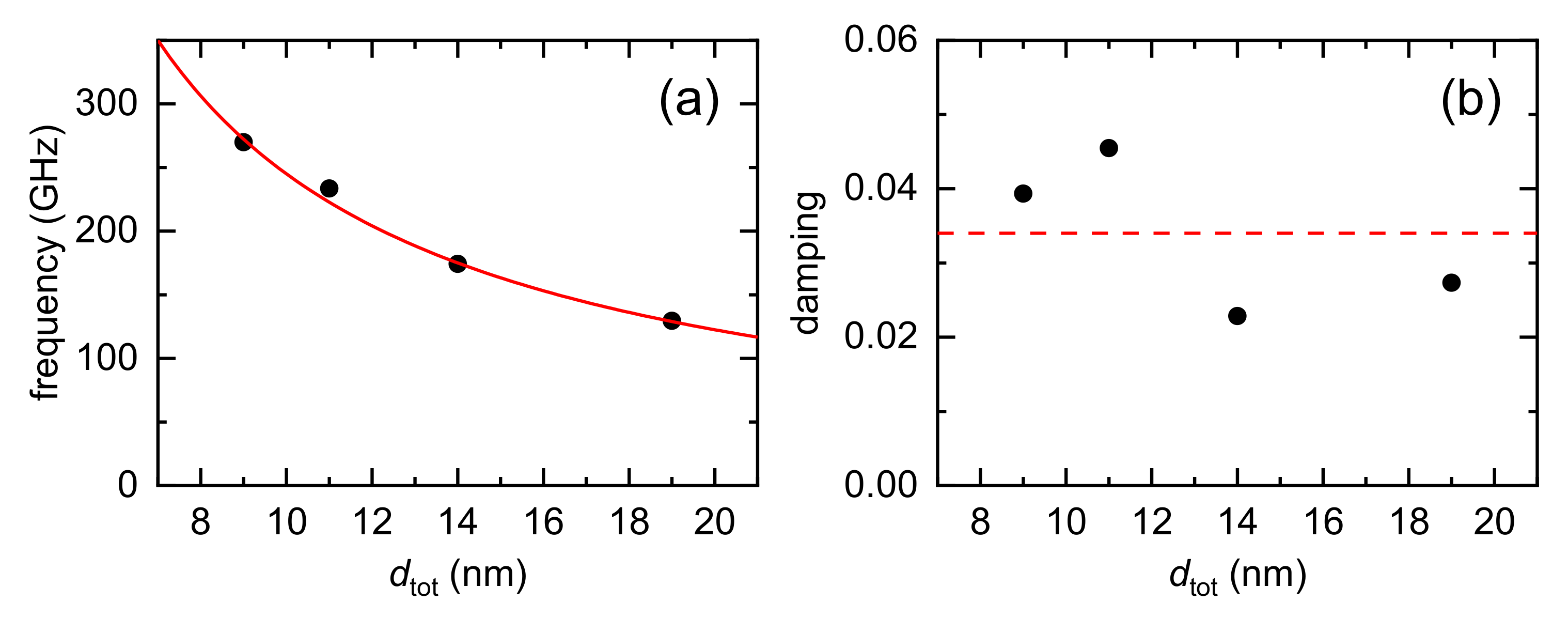
3.1. Acoustic Propagation at Interface
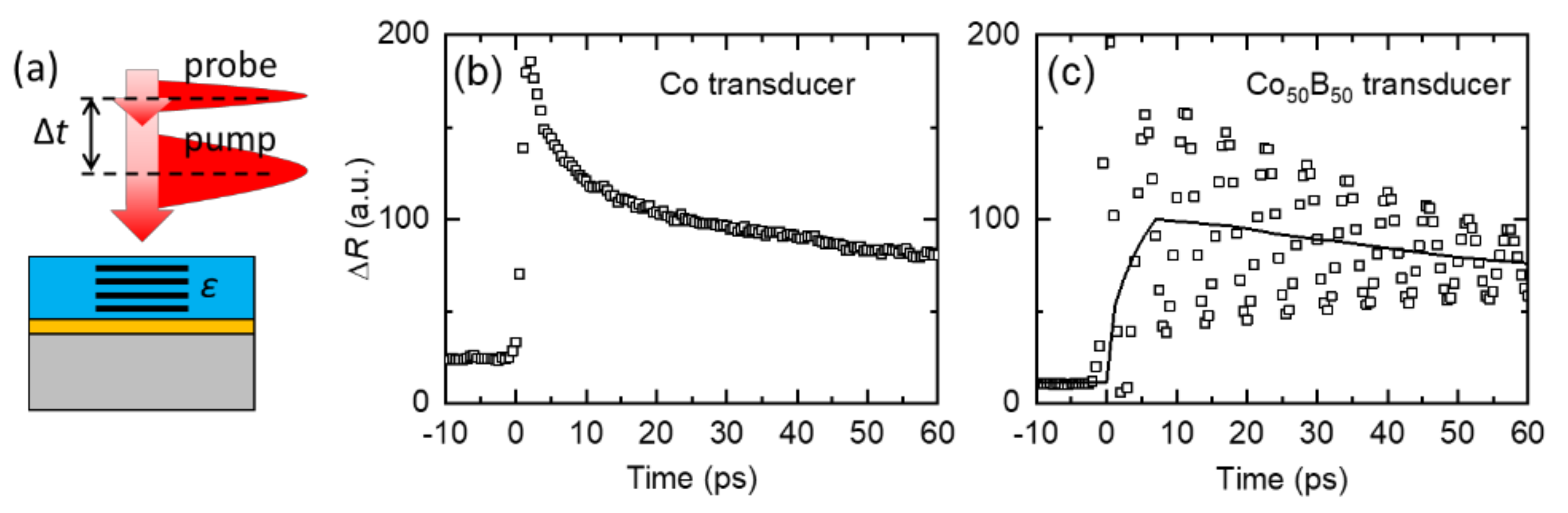
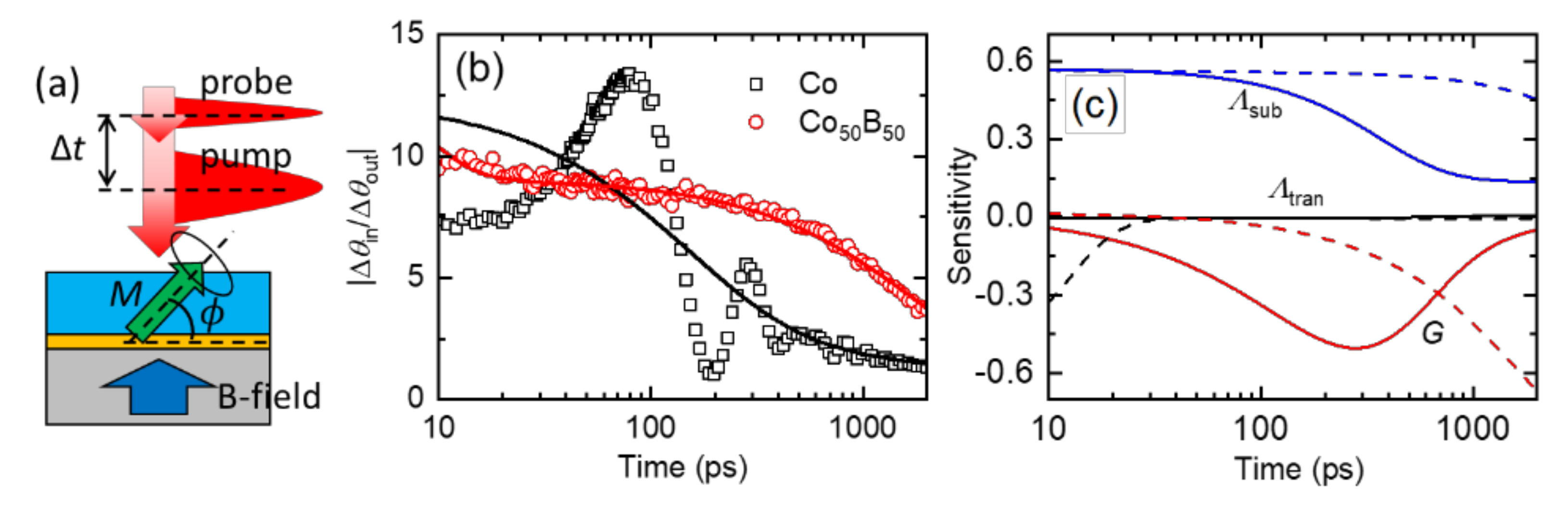
3.2. Heat Transport at Interface
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grahn, H.T.; Maris, H.J.; Tauc, J. Picosecond ultrasonics. IEEE J. Quantum Electron. 1989, 25, 2562–2569. [Google Scholar] [CrossRef]
- Lin, H.N.; Stoner, R.; Maris, H.; Tauc, J. Phonon attenuation and velocity measurements in transparent materials by picosecond acoustic interferometry. J. Appl. Phys. 1991, 69, 3816–3822. [Google Scholar] [CrossRef]
- Wright, O. Thickness and sound velocity measurement in thin transparent films with laser picosecond acoustics. J. Appl. Phys. 1992, 71, 1617–1629. [Google Scholar] [CrossRef]
- Lee, Y.C.; Bretz, K.C.; Wise, F.W.; Sachse, W. Picosecond acoustic measurements of longitudinal wave velocity of submicron polymer films. Appl. Phys. Lett. 1996, 69, 1692–1694. [Google Scholar] [CrossRef]
- Nye, R.A.; Kelliher, A.P.; Gaskins, J.T.; Hopkins, P.E.; Parsons, G.N. Understanding Molecular Layer Deposition Growth Mechanisms in Polyurea via Picosecond Acoustics Analysis. Chem. Mater. 2020, 32, 1553–1563. [Google Scholar] [CrossRef]
- Bonello, B.; Perrin, B.; Romatet, E.; Jeannet, J. Application of the picosecond ultrasonic technique to the study of elastic and time-resolved thermal properties of materials. Ultrasonics 1997, 35, 223–231. [Google Scholar] [CrossRef]
- Lee, T.; Ohmori, K.; Shin, C.-S.; Cahill, D.G.; Petrov, I.; Greene, J. Elastic constants of single-crystal TiNx (001)(0.67 ≤ x ≤ 1.0) determined as a function of x by picosecond ultrasonic measurements. Phys. Rev. B 2005, 71, 144106. [Google Scholar] [CrossRef]
- Mante, P.; Robillard, J.; Devos, A. Complete thin film mechanical characterization using picosecond ultrasonics and nanostructured transducers: Experimental demonstration on SiO2. Appl. Phys. Lett. 2008, 93, 071909. [Google Scholar] [CrossRef]
- Viel, A.; Peronne, E.; Sénépart, O.; Becerra, L.; Legay, C.; Semprez, F.; Trichet, L.; Coradin, T.; Hamraoui, A.; Belliard, L. Picosecond ultrasounds as elasticity probes in neuron-like cells models. Appl. Phys. Lett. 2019, 115, 213701. [Google Scholar] [CrossRef] [Green Version]
- Thompson, E.; Manzella, E.; Murray, E.; Pelletier, M.; Stuligross, J.; Daly, B.; Lee, S.; Redwing, R. Picosecond laser ultrasonic measurements of interlayer elastic properties of 2H-MoSe2 and 2H-WSe2. Mater. Today Chem. 2020, 18, 100369. [Google Scholar] [CrossRef]
- Morath, C.; Maris, H. Phonon attenuation in amorphous solids studied by picosecond ultrasonics. Phys. Rev. B 1996, 54, 203. [Google Scholar] [CrossRef]
- Hao, H.-Y.; Maris, H.J. Study of phonon dispersion in silicon and germanium at long wavelengths using picosecond ultrasonics. Phys. Rev. Lett. 2000, 84, 5556. [Google Scholar] [CrossRef]
- Pu, N.-W.; Bokor, J. Study of surface and bulk acoustic phonon excitations in superlattices using picosecond ultrasonics. Phys. Rev. Lett. 2003, 91, 076101. [Google Scholar] [CrossRef]
- Devos, A.; Foret, M.; Ayrinhac, S.; Emery, P.; Rufflé, B. Hypersound damping in vitreous silica measured by picosecond acoustics. Phys. Rev. B 2008, 77, 100201. [Google Scholar] [CrossRef] [Green Version]
- Daly, B.; Kang, K.; Wang, Y.; Cahill, D.G. Picosecond ultrasonic measurements of attenuation of longitudinal acoustic phonons in silicon. Phys. Rev. B 2009, 80, 174112. [Google Scholar] [CrossRef]
- Tas, G.; Loomis, J.; Maris, H.; Bailes Iii, A.; Seiberling, L. Picosecond ultrasonics study of the modification of interfacial bonding by ion implantation. Appl. Phys. Lett. 1998, 72, 2235–2237. [Google Scholar] [CrossRef]
- Rossignol, C.; Perrin, B.; Bonello, B.; Djemia, P.; Moch, P.; Hurdequint, H. Elastic properties of ultrathin permalloy/alumina multilayer films using picosecond ultrasonics and Brillouin light scattering. Phys. Rev. B 2004, 70, 094102. [Google Scholar] [CrossRef]
- Ezzahri, Y.; Grauby, S.; Dilhaire, S.; Rampnoux, J.-M.; Claeys, W. Cross-plan Si/Si Ge superlattice acoustic and thermal properties measurement by picosecond ultrasonics. J. Appl. Phys. 2007, 101, 013705. [Google Scholar] [CrossRef]
- Hohensee, G.T.; Hsieh, W.-P.; Losego, M.D.; Cahill, D.G. Interpreting picosecond acoustics in the case of low interface stiffness. Rev. Sci. Instrum. 2012, 83, 114902. [Google Scholar] [CrossRef]
- Swartz, E.; Pohl, R. Thermal resistance at interfaces. Appl. Phys. Lett. 1987, 51, 2200–2202. [Google Scholar] [CrossRef]
- Stoner, R.; Maris, H. Kapitza conductance and heat flow between solids at temperatures from 50 to 300 K. Phys. Rev. B 1993, 48, 16373. [Google Scholar] [CrossRef]
- Prasher, R.S.; Phelan, P.E. A scattering-mediated acoustic mismatch model for the prediction of thermal boundary resistance. J. Heat Transfer 2001, 123, 105–112. [Google Scholar] [CrossRef]
- Costescu, R.M.; Wall, M.A.; Cahill, D.G. Thermal conductance of epitaxial interfaces. Phys. Rev. B 2003, 67, 054302. [Google Scholar] [CrossRef]
- Hsieh, W.-P.; Lyons, A.S.; Pop, E.; Keblinski, P.; Cahill, D.G. Pressure tuning of the thermal conductance of weak interfaces. Phys. Rev. B 2011, 84, 184107. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Keblinski, P.; Schelling, P.K. Kapitza conductance of silicon–amorphous polyethylene interfaces by molecular dynamics simulations. Phys. Rev. B 2009, 79, 104305. [Google Scholar] [CrossRef]
- Estrada, D.; Li, Z.; Choi, G.-M.; Dunham, S.N.; Serov, A.; Lee, J.; Meng, Y.; Lian, F.; Wang, N.C.; Perez, A. Thermal transport in layer-by-layer assembled polycrystalline graphene films. NPJ 2D Mater. Appl. 2019, 3, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Hasegawa, R. Present status of amorphous soft magnetic alloys. J. Magn. Magn. Mater. 2000, 215, 240–245. [Google Scholar] [CrossRef]
- Johnson, W. Bulk amorphous metal—An emerging engineering material. JOM 2002, 54, 40–43. [Google Scholar] [CrossRef]
- Choi, G.-M.; Min, B.-C.; Shin, K.-H. FePdB layer for perpendicular magnetic tunnel junctions. Appl. Phys. Lett. 2010, 97, 202503. [Google Scholar] [CrossRef]
- Thompson, M.W., II. The energy spectrum of ejected atoms during the high energy sputtering of gold. Philos. Mag. 1968, 18, 377–414. [Google Scholar] [CrossRef]
- Cahill, D.G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 2004, 75, 5119–5122. [Google Scholar] [CrossRef]
- Kang, K.; Choi, G.-M. Thermal coupling parameters between electron, phonon, and magnon of Nickel. J. Magn. Magn. Mater. 2020, 514, 167156. [Google Scholar] [CrossRef]
- Pham Ngoc, L.L.; Kang, K.; Choi, G.-M. The measurement of anisotropic thermal transport using time-resolved magneto-optical Kerr effect. AIP Adv. 2021, 11, 025024. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; Wiley: Hoboken, United States, 1999. [Google Scholar]
- Wiley. Properties and Behavior of Polymers, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ryzy, M.; Grabec, T.; Österreicher, J.A.; Hettich, M.; Veres, I.A. Measurement of coherent surface acoustic wave attenuation in polycrystalline aluminum. AIP Adv. 2018, 8, 125019. [Google Scholar] [CrossRef] [Green Version]
- Povey, M.; Meredith, D.; Dobbs, E. Electromagnetic generation and attenuation of ultrasound in ferromagnetic metals. I. J. Phys. F Metal Phys. 1980, 10, 2041. [Google Scholar] [CrossRef]
- Shen, X.; Lu, Z.; Timalsina, Y.P.; Lu, T.-M.; Washington, M.; Yamaguchi, M. Coherent phonon transport measurement and controlled acoustic excitations using tunable acoustic phonon source in GHz-sub THz Range with variable bandwidth. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Mizutani, U.; Hasegawa, M.; Fukamichi, K.; Hattori, Y.; Yamada, Y.; Tanaka, H.; Takayama, S. Magnetic, electronic, and electron-transport properties of amorphous (Co0.85B0.15)100−xXx (X = B, Al, Si, and V) alloys. Phys. Rev. B 1993, 47, 2678. [Google Scholar] [CrossRef]
- Gundrum, B.C.; Cahill, D.G.; Averback, R.S. Thermal conductance of metal-metal interfaces. Phys. Rev. B 2005, 72, 245426. [Google Scholar] [CrossRef]
- Thermophysical Properties Research Center, Purdue University. Thermophysical Properties of High Temperature Solid Materials; Touloukian, Y.S., Ed.; Macmillan: New York, NY, USA, 1967. [Google Scholar]
- Matsuura, M.; Mizutani, U. Low-temperature specific heat study of amorphous Co1−xBx alloys. J. Phys. F Metal Phys. 1983, 13, 1539. [Google Scholar] [CrossRef]
- Terada, Y.; Ohkubo, K.; Mohri, T.; Suzuki, T. Thermal conductivity of cobalt-base alloys. Metall. Mater. Trans. 2003, 34, 2026. [Google Scholar] [CrossRef]
- Parchovianský, M.; Galusek, D.; Švančárek, P.; Sedláček, J.; Šajgalík, P. Thermal behavior, electrical conductivity and microstructure of hot pressed Al2O3/SiC nanocomposites. Ceram. Int. 2014, 40, 14421–14429. [Google Scholar] [CrossRef]
| Layer | d (nm) | C (106 J m−3 K−1) | Λ (W m−1 K−1) | G (MW m−2 K−1) |
|---|---|---|---|---|
| Co transducer | 12 1 | 3.8 4 | 100 6 | 300 ± 50 8 |
| CoB transducer | 14 2 | 4.1 5 | 20 6 | 35 ± 5 8 |
| Substrate | 500,000 3 | 3.1 4 | 30 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, L.; Choi, G.-M. Using Amorphous CoB Alloy as Transducer to Detect Acoustic Propagation and Heat Transport at Interface. Appl. Sci. 2021, 11, 5155. https://doi.org/10.3390/app11115155
Jian L, Choi G-M. Using Amorphous CoB Alloy as Transducer to Detect Acoustic Propagation and Heat Transport at Interface. Applied Sciences. 2021; 11(11):5155. https://doi.org/10.3390/app11115155
Chicago/Turabian StyleJian, Liu, and Gyung-Min Choi. 2021. "Using Amorphous CoB Alloy as Transducer to Detect Acoustic Propagation and Heat Transport at Interface" Applied Sciences 11, no. 11: 5155. https://doi.org/10.3390/app11115155
APA StyleJian, L., & Choi, G.-M. (2021). Using Amorphous CoB Alloy as Transducer to Detect Acoustic Propagation and Heat Transport at Interface. Applied Sciences, 11(11), 5155. https://doi.org/10.3390/app11115155