A Novel Exact Analytical Solution Based on Kloss Equation towards Accurate Speed-Time Characteristics Modeling of Induction Machines during No-Load Direct Startups
Abstract
:1. Introduction
2. Existing Methods and the Novel Expressions Proposed for Speed-Time Curve Representation during No-Load Direct Startup of IMs
2.1. Aree’s Method
2.2. Calasan’s Method
2.3. Proposed Expressions for Speed-Time Characteristics Representation, with Bearing Losses
2.3.1. The First Expression
2.3.2. The Second Expression
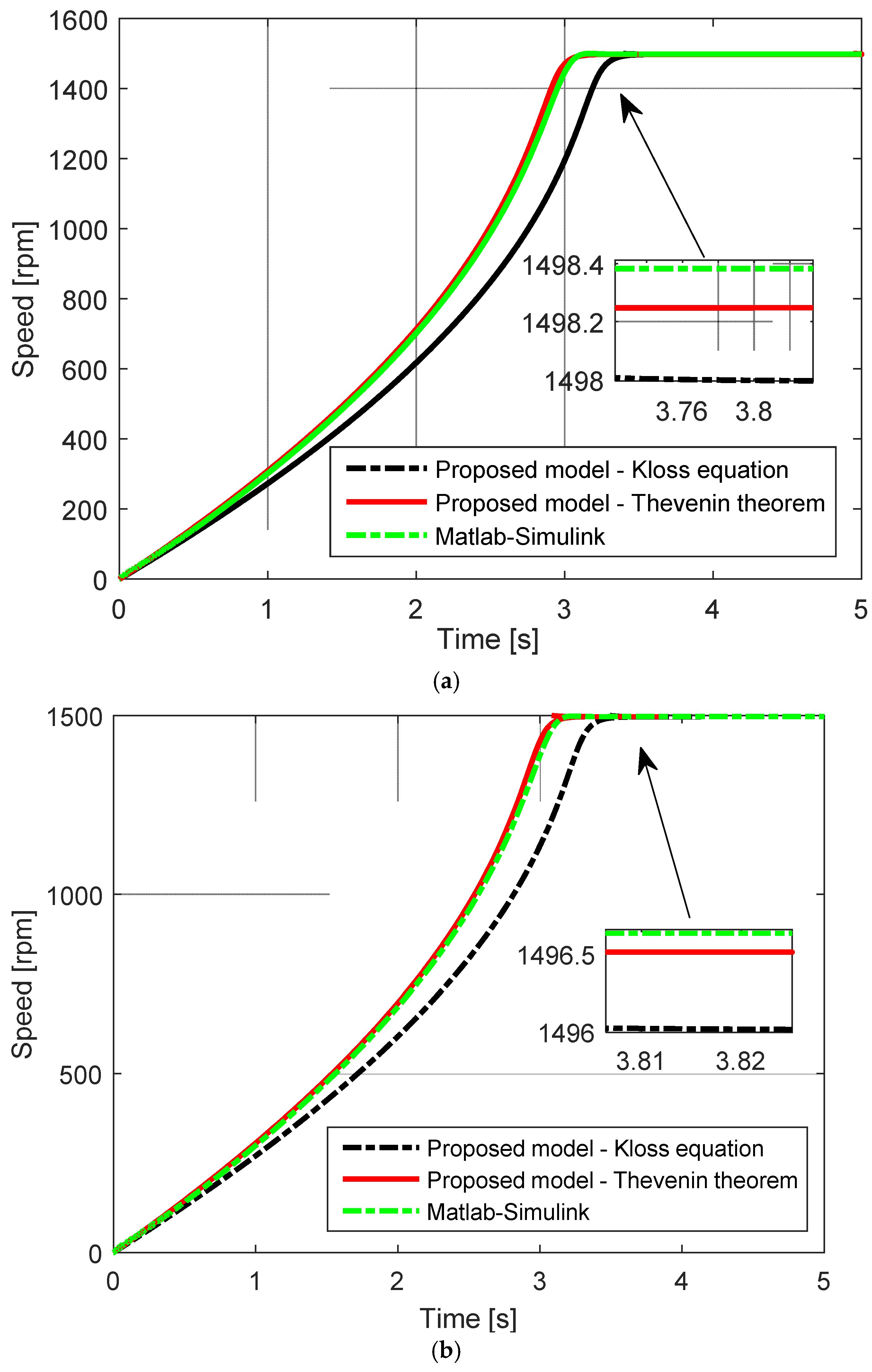
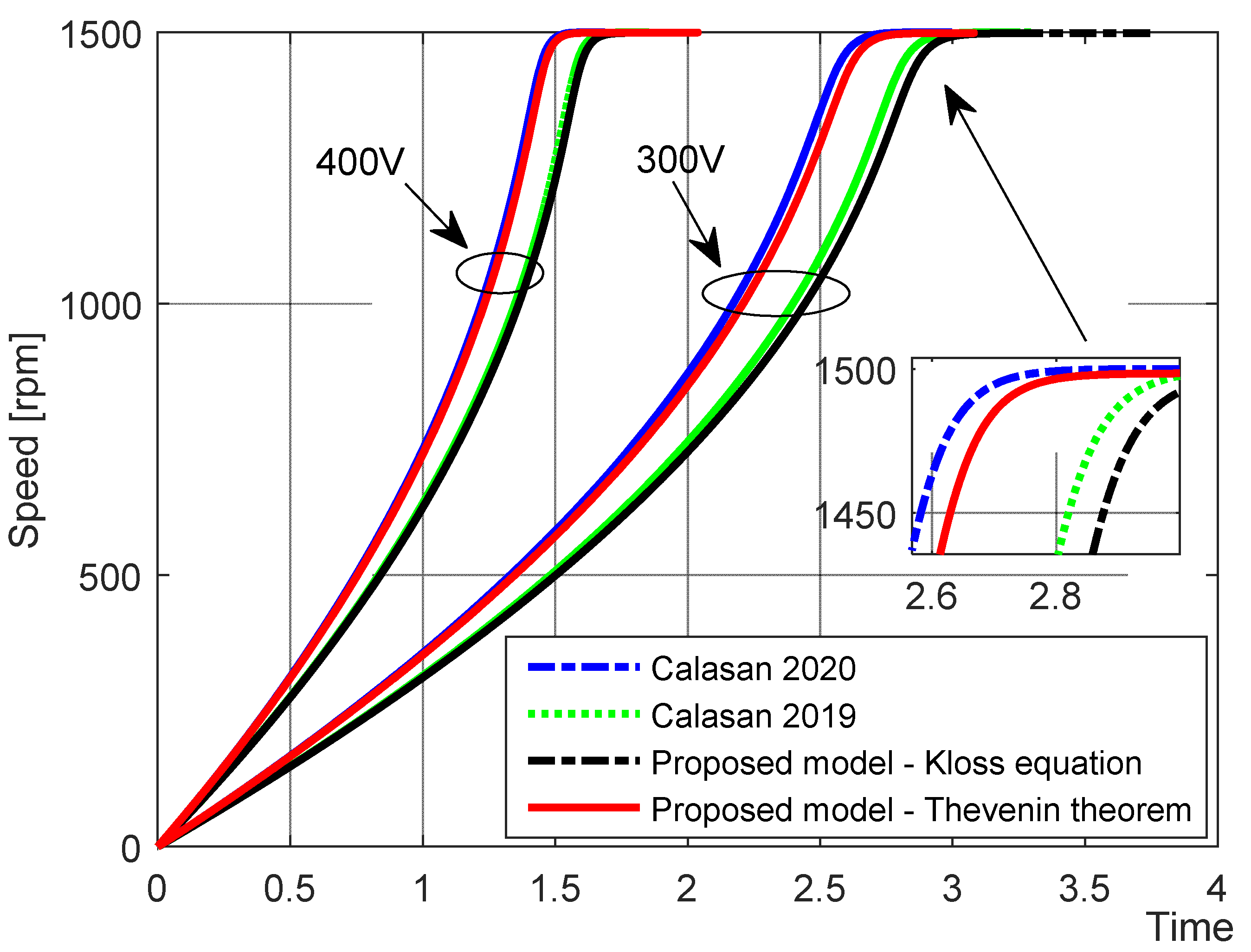
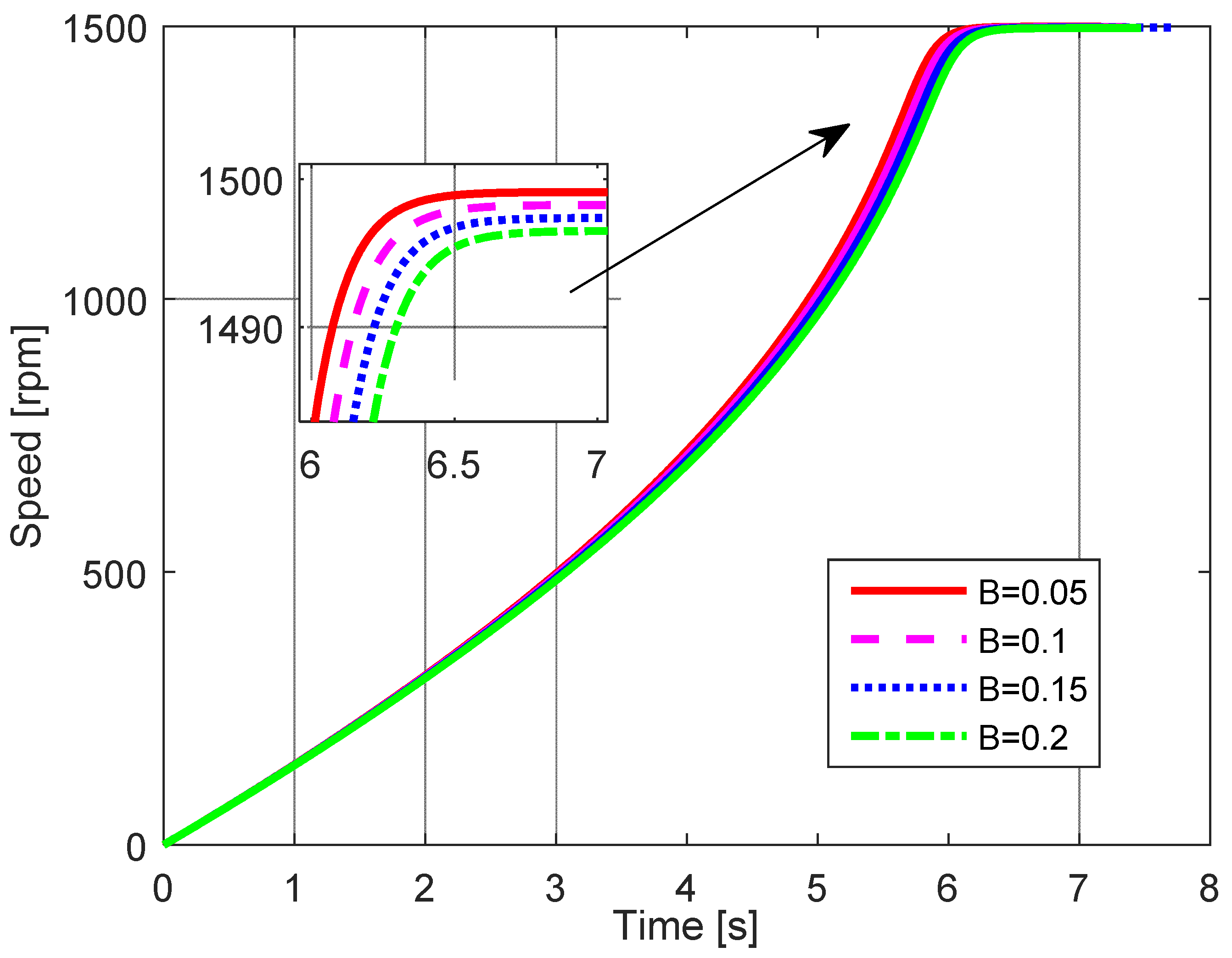
3. Simulation Results and Analyses
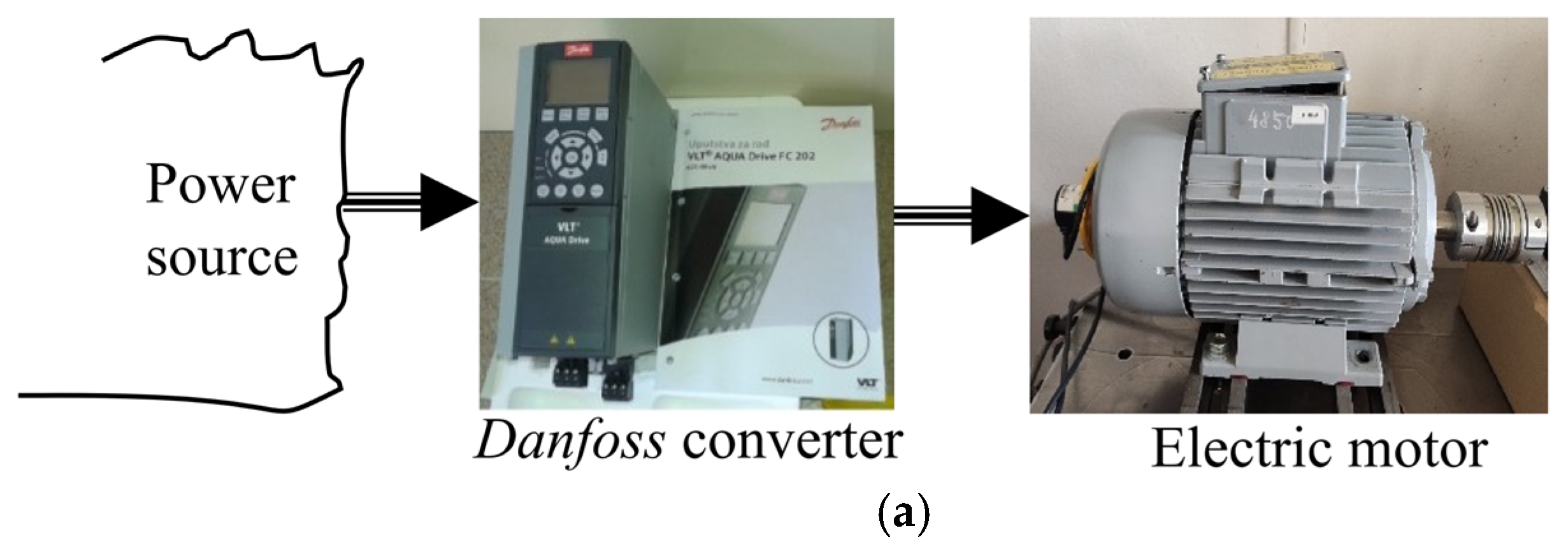
4. Experimental Results
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CVSRT | Critical voltage-sag removal time |
| DOL | Direct-on-line |
| DSP | Digital signal processor |
| FEMs | Finite element methods |
| IMs | Induction machines |
| PC | Personal computer |
| CVSRT | Critical voltage-sag removal time |
| DOL | Direct-on-line |
| DSP | Digital signal processor |
| FEMs | Finite element methods |
| IMs | Induction machines |
| PC | Personal computer |
Nomenclature
| B | Bearing loss |
| dt | Time increment |
| J | Moment of inertia (kgm2) |
| M | IM’s torque |
| Mbr | Maximum machine torque |
| Mem | Electromagnetic torque |
| Mfriction | Torque due to friction |
| n | Speed of rotation |
| nlo | Lower speed value |
| nrj, and kj | Coefficients that depend on load and machine data |
| ns | Synchronous speed |
| RT and XT | Thevenin equivalent resistance and reactance of the IM’s equivalent circuit |
| R1 | Stator resistance |
| R2 | Rotor resistance referred to the stator side |
| s | Slip of the machine |
| sbr | Corresponding slip at the maximum machine torque |
| t | Time to represent the IM’s speed-time curve during direct startup |
| UT | Thevenin equivalent voltage |
| U | Supply line-to-line voltage |
| X1 | Stator leakage reactance |
| X2 | Rotor leakage reactance referred to the stator side |
| Xm | Magnetizing reactance |
| ξ | Aree’s correction factor |
Appendix A
Appendix B
| Parameters | Values |
|---|---|
| Pn (kW) | 37.3 |
| Un (V) | 400 |
| f (Hz) | 50 |
| p | 2 |
| R1 (Ω) | 0.028 |
| R2 (Ω) | 0.081 |
| X1 (Ω) | 0.0169 |
| X2 (Ω) | 0.081 |
| Xm (Ω) | 1.5156 |
| Jn (kgm2) * | 4.9 |
| R2 (Ω) | 0.081 |
| Parameters | IM#1 | IM#2 |
|---|---|---|
| Rated power (kW) | 0.370 | 1.100 |
| Rated voltage (V) | 230/400 | 220/380 |
| Rated current (A) | 1.7/1 | 6.0/3.5 |
| Power factor | 0.83 | 0.7 |
| Rated speed (rpm) | 2790 | 920 |
| Maximal torque (Nm) | 4.5/1.5 | 32.5/10.5 |
| Breaking slip | 0.4 | 0.45 |
| Rated torque (Nm) | 1.26 | 11.42 |
References
- Bredthauer, J.; Struck, N. Starting of Large Medium Voltage Motors: Design, Protection, and Safety Aspects. IEEE Trans. Ind. Appl. 1995, 31, 1167–1176. [Google Scholar] [CrossRef]
- Pillay, K.; Nour, M.; Yang, K.H.; Harun, D.N.D.; Haw, L.K. Assessment and comparison of conventional motor starters and modern power electronic drives for induction motor starting characteristics. In Proceedings of the 2009 IEEE Symposium on Industrial Electronics and Applications, Kuala Lumpur, Malaysia, 4–6 October 2009; Volume 2, pp. 584–589. [Google Scholar]
- Hamouda, R.M.; Alolah, A.I.; Badr, M.A.; Abdel-halim, M.A. A comparative study on the starting methods of three phase wound-rotor induction motors—Part I. IEEE Trans. Energy Convers. 1999, 14, 918–922. [Google Scholar] [CrossRef]
- Badr, M.A.; Abdel-halim, M.A.; Alolah, A.I. A nonconventional method for fast starting of three phase wound-rotor induction motors. IEEE Trans. Energy Convers. 1996, 11, 701–707. [Google Scholar] [CrossRef]
- Banerjee, A.; Banerjee, A.; Rana, D.P.S.; Shubhanga, K.N. A study of starting methods for an induction motor using an arbitrary waveform generator. In Proceedings of the 2015 3rd International Conference on Advances in Electrical Engineering, Dhaka, Bangladesh, 17–19 December 2015; pp. 34–37. [Google Scholar]
- Goh, H.H.; Looi, M.S.; Kok, B.C. Comparison between Direct-On-Line, Star-Delta and Auto-transformer Induction Motor Starting Method in terms of Power Quality. Lect. Notes Eng. Comput. Sci. 2009, 2175, 1558–1563. [Google Scholar]
- Ellis, R.G.; Seggewiss, J.G.; Paes, R.H.; Kay, J.A. Methods for the control of large medium-voltage motors: Application considerations and guidelines. IEEE Trans. Ind. Appl. 2000, 36, 1688–1696. [Google Scholar] [CrossRef]
- Ćalasan, M.P. Analytical solution for no-load induction machine speed calculation during direct start-up. Int. Trans. Electr. Energy Syst. 2019, 29, e2777. [Google Scholar] [CrossRef]
- Aree, P. Precise analytical formula for starting time calculation of medium- and high-voltage induction motors under conventional starter methods. Electr. Eng. 2018, 100, 1195–1203. [Google Scholar] [CrossRef]
- Pereira, L.A.; Perin, M.; Pereira, L.F.A. A New Method to Estimate Induction Machine Parameters from the No-Load Startup Transient. J. Control Autom. Electr. Syst. 2019, 30, 41–53. [Google Scholar] [CrossRef]
- Benzaquen, J.; Rengifo, J.; Albánez, E.; Aller, J.M. Parameter Estimation for Deep-Bar Induction Machines Using Instantaneous Stator Measurements From a Direct Startup. IEEE Trans. Energy Convers. 2017, 32, 516–524. [Google Scholar] [CrossRef]
- Kojooyan-Jafari, H.; Monjo, L.; Corcoles, F.; Pedra, J. Using the Instantaneous Power of a Free Acceleration Test for Squirrel-Cage Motor Parameters Estimation. IEEE Trans. Energy Convers. 2015, 30, 974–982. [Google Scholar] [CrossRef] [Green Version]
- Aree, P. Starting time calculation of large induction motors using their manufacturer technical data. In Proceedings of the 19th International Conference on Electrical Machines and Systems, Chiba, Japan, 13–16 November 2016; pp. 1–5. [Google Scholar]
- Babau, R.; Boldea, I.; Miller, T.J.E.; Muntean, N. Complete parameter identification of large induction machines from no-load acceleration–deceleration tests. IEEE Trans. Ind. Electron. 2007, 54, 1962–1972. [Google Scholar] [CrossRef]
- Yadav, A.P.; Madani, R.; Amiri, N.; Jatskevich, J.; Davoudi, A. Induction Machine Parameterization from Limited Transient Data using Convex Optimization. IEEE Trans. Ind. Electron. 2021, 1. [Google Scholar] [CrossRef]
- Ćalasan, M.; Micev, M.; Ali, Z.M.; Zobaa, A.F.; Aleem, S.H.E.A. Parameter estimation of induction machine single-cage and double-cage models using a hybrid simulated annealing-evaporation rate water cycle algorithm. Mathematics 2020, 8, 1024. [Google Scholar] [CrossRef]
- Zobaa, A.F.; Aleem, S.H.E.A.; Abdelaziz, A.Y. Classical and Recent Aspects of Power System Optimization; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128124413. [Google Scholar]
- Aree, P. Effects of small and large induction motors on voltage sag profile. In Proceedings of the 2012 9th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Phetchaburi, Thailand, 16–18 May 2012; pp. 1–4. [Google Scholar]
- Saeed, A.M.; Abdel Aleem, S.H.E.; Ibrahim, A.M.; Balci, M.E.; El-Zahab, E.E.A. Power conditioning using dynamic voltage restorers under different voltage sag types. J. Adv. Res. 2016, 7, 95–103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ćalasan, M.P. An invertible dependence of the speed and time of the induction machine during no-load direct start-up. Automatika 2020, 61, 141–149. [Google Scholar] [CrossRef] [Green Version]
- ABB Motors. ABB Motor Guide: Basic Technical Information about Low Voltage Standard Motors; ABB: Zürich, Switzerland, 2014; ISBN 952-91-0728-5. [Google Scholar]
- ABB Technical Application Papers. Three-Phase Asynchronous Motors: Generalities and ABB proposals for the Coordination of Protective Devices; ABB: Zürich, Switzerland, 2009. [Google Scholar]
- Aree, P. Transient Torque Peak Reduction During DOL Starting of Three-Phase Induction Motors Using Zero-Crossing Switching Approach. IEEE Trans. Energy Convers. 2020, 1. [Google Scholar] [CrossRef]
- Koljčević, N.; Fuštić, Ž.; Ćalasan, M. Analytical solution for determination of induction machine acceleration based on Kloss equation. Serb. J. Electr. Eng. SJEE. 2020, 17, 247–256. [Google Scholar] [CrossRef]
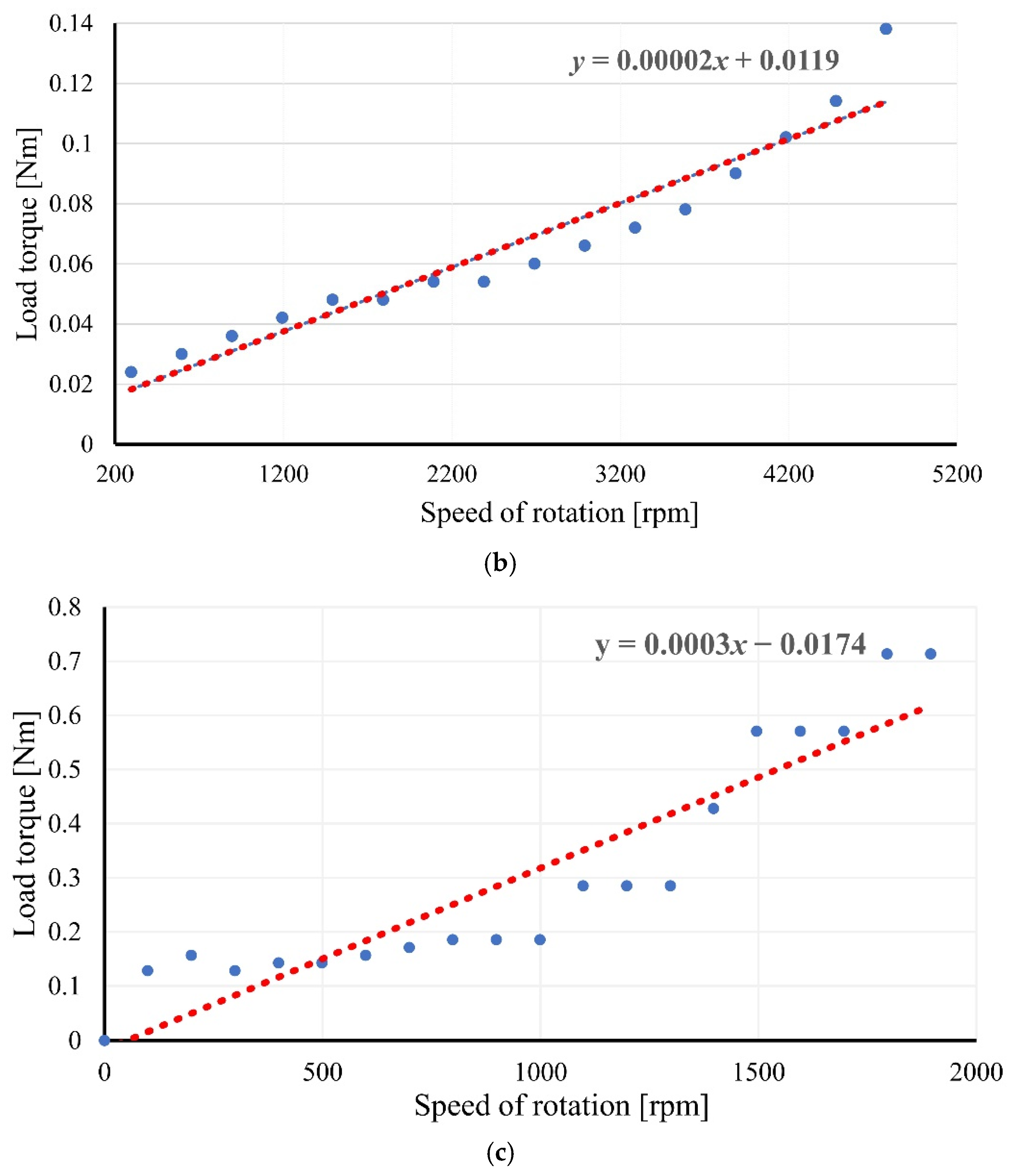
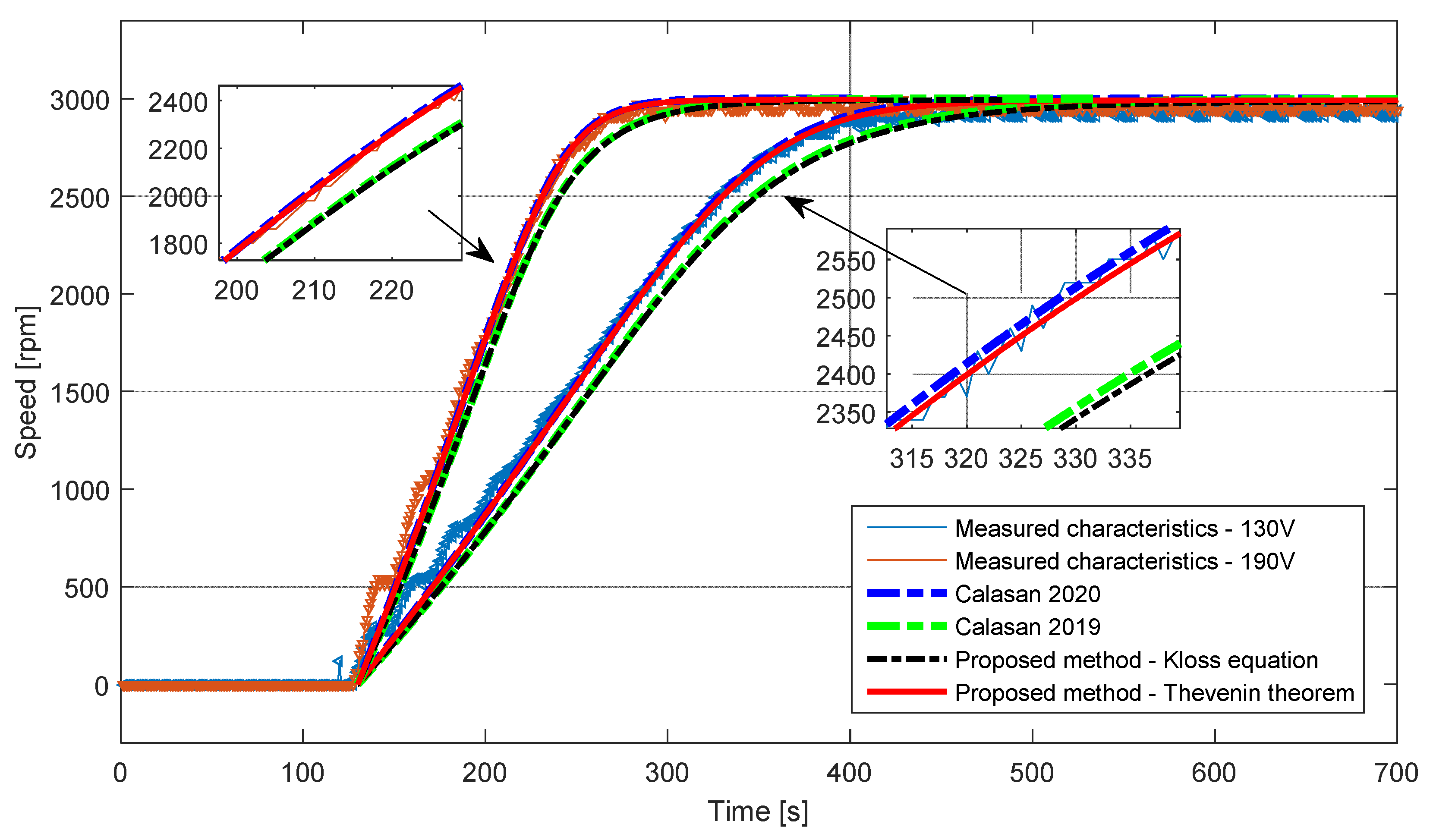
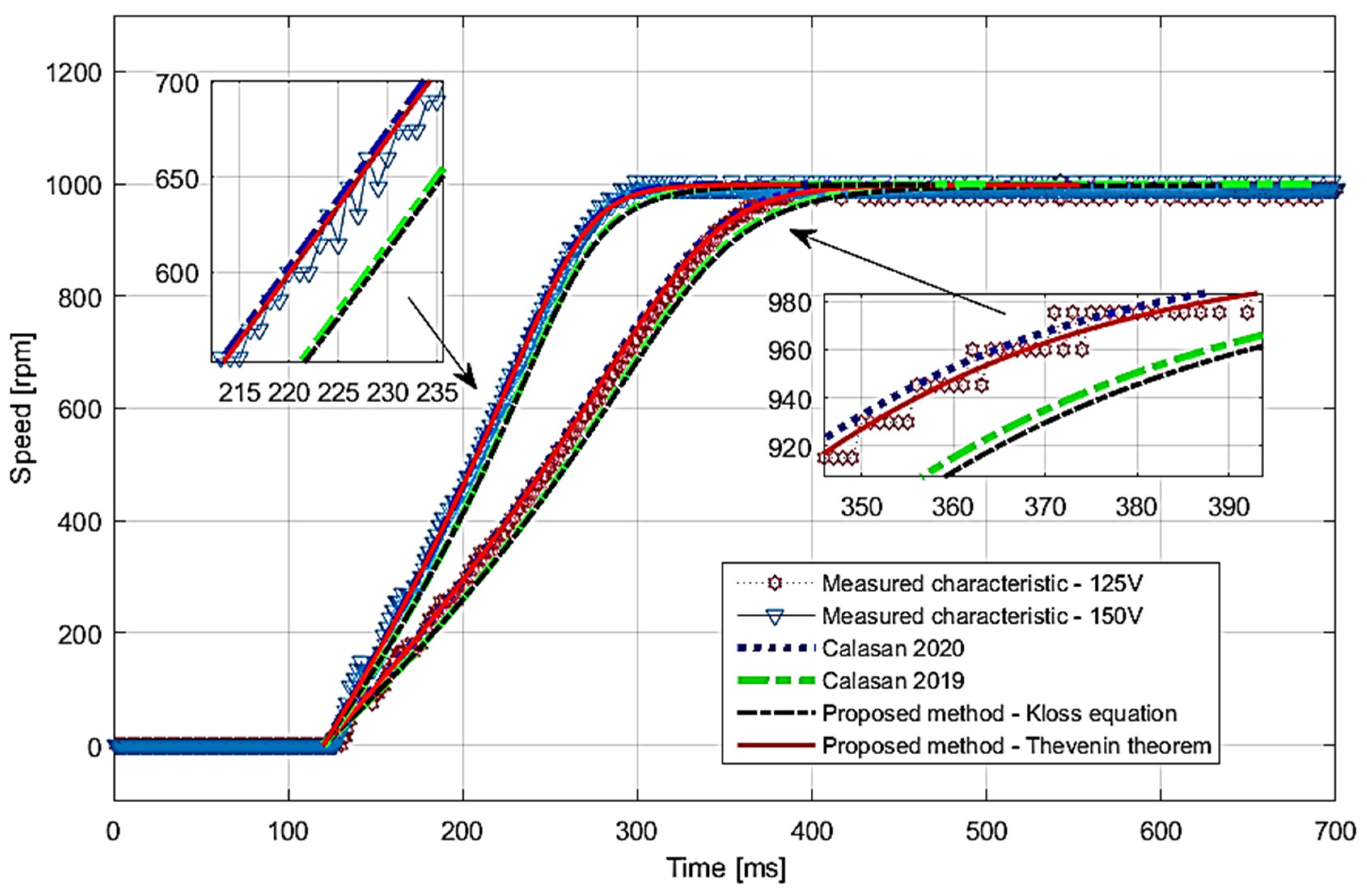
| Parameters | IM#1 | IM#2 |
|---|---|---|
| R1 (Ω) | 23.6000 | 7.3365 |
| R2 (Ω) | 17.4600 | 4.5736 |
| X1 (Ω) | 11.8378 | 5.7642 |
| X2 (Ω) | 11.8378 | 5.7642 |
| Xm (Ω) | 361.1000 | 87.2755 |
| J (kgm2) | 0.00035 | 0.0054 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ćalasan, M.; Alqarni, M.; Rosić, M.; Koljčević, N.; Alamri, B.; Abdel Aleem, S.H.E. A Novel Exact Analytical Solution Based on Kloss Equation towards Accurate Speed-Time Characteristics Modeling of Induction Machines during No-Load Direct Startups. Appl. Sci. 2021, 11, 5102. https://doi.org/10.3390/app11115102
Ćalasan M, Alqarni M, Rosić M, Koljčević N, Alamri B, Abdel Aleem SHE. A Novel Exact Analytical Solution Based on Kloss Equation towards Accurate Speed-Time Characteristics Modeling of Induction Machines during No-Load Direct Startups. Applied Sciences. 2021; 11(11):5102. https://doi.org/10.3390/app11115102
Chicago/Turabian StyleĆalasan, Martin, Mohammed Alqarni, Marko Rosić, Nikola Koljčević, Basem Alamri, and Shady H. E. Abdel Aleem. 2021. "A Novel Exact Analytical Solution Based on Kloss Equation towards Accurate Speed-Time Characteristics Modeling of Induction Machines during No-Load Direct Startups" Applied Sciences 11, no. 11: 5102. https://doi.org/10.3390/app11115102
APA StyleĆalasan, M., Alqarni, M., Rosić, M., Koljčević, N., Alamri, B., & Abdel Aleem, S. H. E. (2021). A Novel Exact Analytical Solution Based on Kloss Equation towards Accurate Speed-Time Characteristics Modeling of Induction Machines during No-Load Direct Startups. Applied Sciences, 11(11), 5102. https://doi.org/10.3390/app11115102








