Low-Latency Bit-Accurate Architecture for Configurable Precision Floating-Point Division
Abstract
:1. Introduction
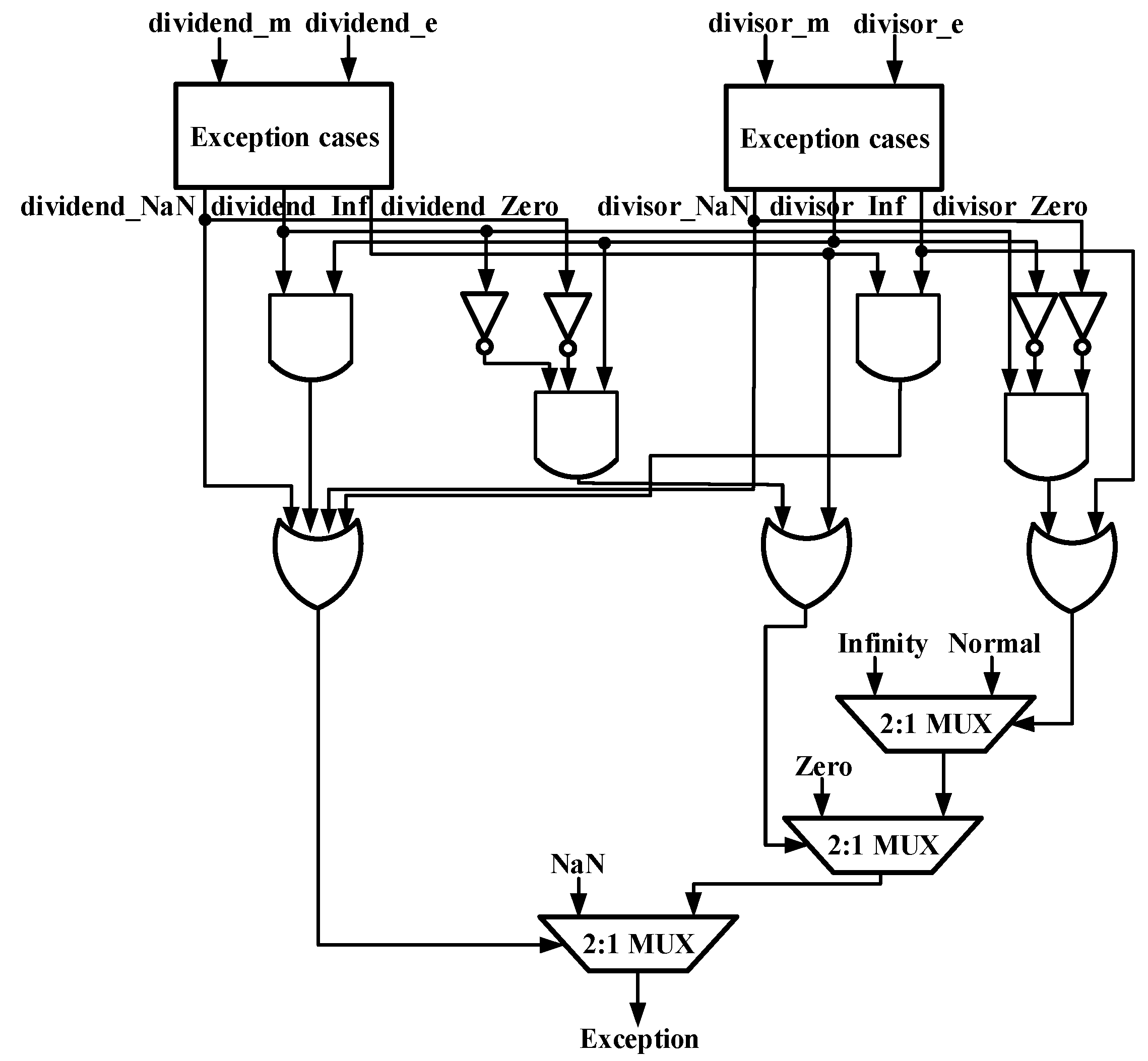
- Leading Zero Detection module to transfer subnormal inputs; Exception Judgement module to check exception conditions;
- Finite State Machine module to reduce the number of multipliers and to perform basic fast division steps;
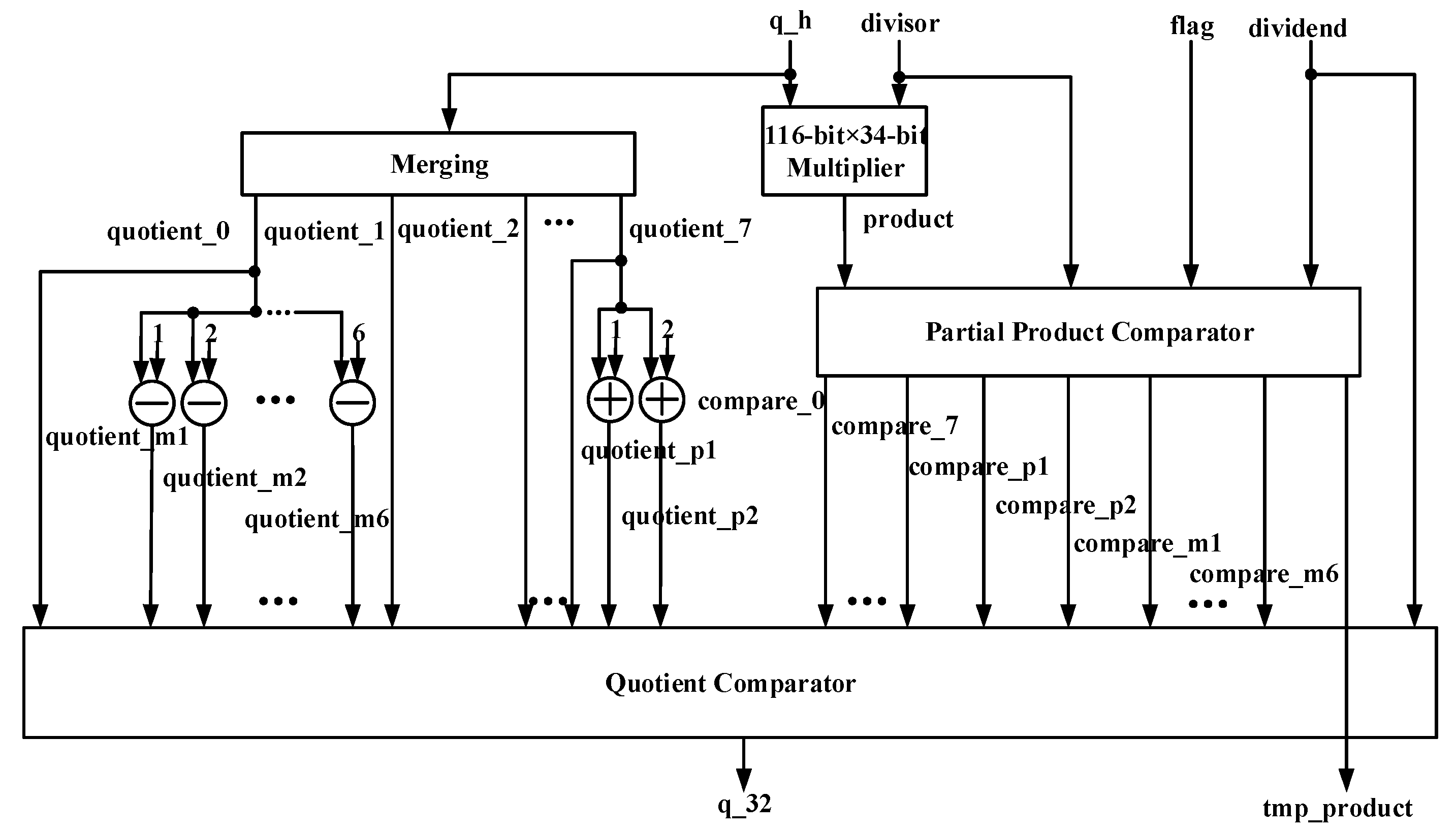
- Quotient Selection Unit module to finish the critical part of our proposed Predict–Correct algorithm and to gain the most approximative 32-bit quotient per cycle;
- Rounding Unit module to ensure the accuracy of unit at last place of quotient.
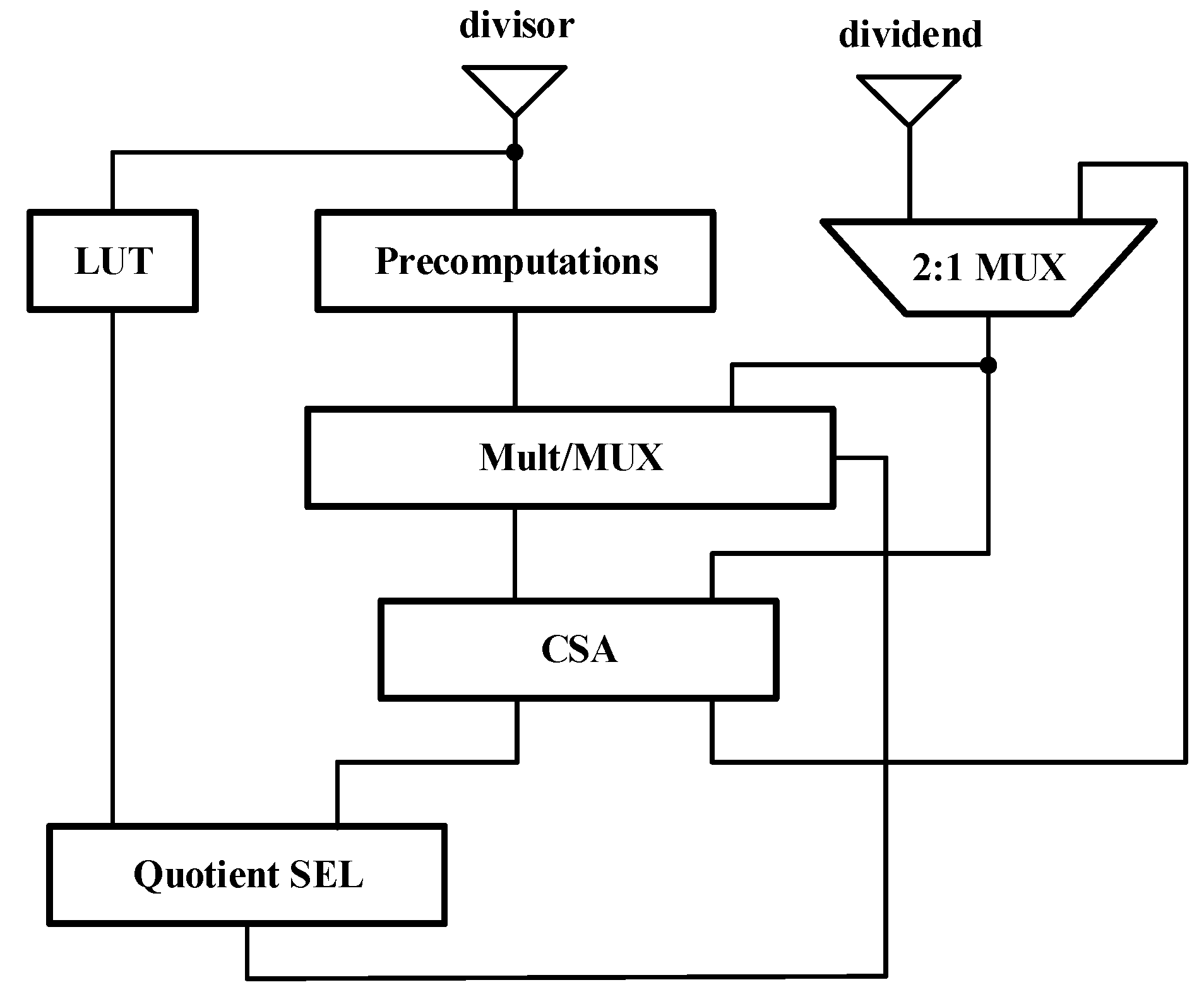
2. Background
3. Predict–Correct Algorithm for Division
3.1. Predict–Correct Algorithm with Accurate Quotient Approximation
| Algorithm 1 Predict–Correct Algorithm. |
| 1: Set Q and j to 0 initially. 2: With index of the leading m bits of Y, look b1 bits wide approximation of 1/Yh up in the table G1. Similarly, look b2 bits wide approximation of 1/Yh2 up in the table G2, …, look bt bits wide approximation of 1/Yht up in the table Gt. Table sizes are bi = (m × t − t) + ⌈log2t⌉ − (m × I − m − i), i = 1, 2, …, t, where t is the number of the used leading terms of (1). The relationship of parameter p and m is p = m × t − t + 2. 3: Compute an approximation B to 1/Y using the leading t terms of (1): B = 1/Yh − ∆Y/Yh2 + (∆Y)2/Yh3 − … + (−1)t−1 (∆Y)t−1/Yht. Truncate B to the most significant m × t − t + 4 bits, which reduces the sizing of multipliers. 4: Compute intermediate value P = Xh × B and round P to m × t − t − 1 bits to obtain P′. 5: List 2n kinds of (m × t − t + n − 1)-bit quotients that combinate the (m × t − t − 1)-bit intermediate value P′ with subsequent 2n kinds of n-bit predictive values ranging from 00…0 to 11…1. 6: Pick up the most approximative (m × t − t + n − 1)-bit quotient Qa from the 2n kinds of (m × t − t + n − 1)-bit quotients by multiplication and comparison. 7: Calculate j′ = j + m × t−t + n − 1. Update j with j′. 8: New dividend is X′ = X − Qa × Y. New quotient is Q′ = Q + Qa × 1/2(q−j). 9: Left-shift X′ by m × t − t + n − 1 bits. 10: Update Q with Q′. Update X with X′. 11: Repeat Step 4 through 10 until j ≥ q. 12: Final quotient is Q = Q(q−1)…Q0Q−1…Q−e = Qh + Ql where Qh = Q(q−1) …Q0, Ql = Q−1…Q−e and e is the number of redundant bits of the last cycle in Step 11. |
| Algorithm 2 Example of Fixed-point division using Predict–Correct Algorithm. |
| X = (1 0010 0011 1110 0110 1100 0111 0101 1011)2, Y = (1 1101 0101 1011 0010 1101 1110 0101 0010)2. Set q = 33, p = 20, m = 7, t = 3, n = 3. Then b1 = 21, b2 = 15, b3 = 9. Xh = (1 0010 0011 1110 0110 1100 0000 0000 0000)2, Yh = (1 1101 0111 1111 1111 1111 1111 1111 1111)2, ∆Y = (−0 0000 0010 0100 1101 0010 0001 1010 1101)2. B = 1/Yh − ∆Y/Yh2 + (∆Y)2/Yh3 and B is to be truncated to 22 bits. |
| 1: Q = 0, j = 0. 2: 1/Yh = (0 1000 1011 1000 0011 0011)2, 1/Yh2 = (0 0100 1100 0000 100)2, 1/Yh3 = (0 0010 1001)2. 3: B = (0 1000 1011 1000 0111 0001 1)2. 4: P = (0 1001 1111 0001 1000 0101 0100 0100 1100 1110 0010)2, and then P′ = (0 1001 1111 0001 1000)2. 5: 8 kinds of 20-bit possible quotients are: (0 1001 1111 0001 1000 000)2 (0 1001 1111 0001 1000 001)2 (0 1001 1111 0001 1000 010)2 (0 1001 1111 0001 1000 011)2 (0 1001 1111 0001 1000 100)2 (0 1001 1111 0001 1000 101)2 (0 1001 1111 0001 1000 110)2 (0 1001 1111 0001 1000 111)2 6: Qa = (0 1001 1111 0001 1000 010)2. 7: j′ = 20 and Update j with j′. 8: X′ = (0000 0000 0000 0000 0000 1100 0100 0101 0010 0000 1010 1110 1110 0)2, Q′ = (0 1001 1111 0001 1000 010)2. 9: Left-shift X′ by 20 bits. 10: Update Q and X with Q′ and X′ respectively. 11: Since j < q, repeat Step 4 through 10. 4′: P = (1101 0110 0000 0000 0011 1111 0100 1011 0110 0000)2 and then P′ = (1101 0110 0000 0000 0)2. 5′: 8 kinds of 20-bit possible quotients are: (1101 0110 0000 0000 0 000)2 (1101 0110 0000 0000 0 001)2 (1101 0110 0000 0000 0 010)2 (1101 0110 0000 0000 0 011)2 (1101 0110 0000 0000 0 100)2 (1101 0110 0000 0000 0 101)2 (1101 0110 0000 0000 0 110)2 (1101 0110 0000 0000 0 111)2 6′: Qa = (1101 0110 0000 0000 0 100)2. 7′: j′ = 40 and Update j with j′. 8′: X′ = (0000 0000 0000 0000 0000 0110 1010 0101 1010 1111 0001 1010 1110 0)2, Q′ = (0 1001 1111 0001 1000 0101 1010 1100 0000 0000 100)2. 9′: Left-shift X′ by 20 bits. 10′: Update Q and X with Q′ and X′ respectively. 11′: Since j > q, stop the iteration. 13: Final quotient is Q = Qh + Ql where Qh =(0 1001 1111 0001 1000 0101 1010 1100 0000)2, Ql = (0000 100)2. |
3.2. Guaranteed Bits per Cycle Using Predict–Correct Algorithm
3.3. Choice of Parameters m, t, and n in Predict–Correct Algorithm
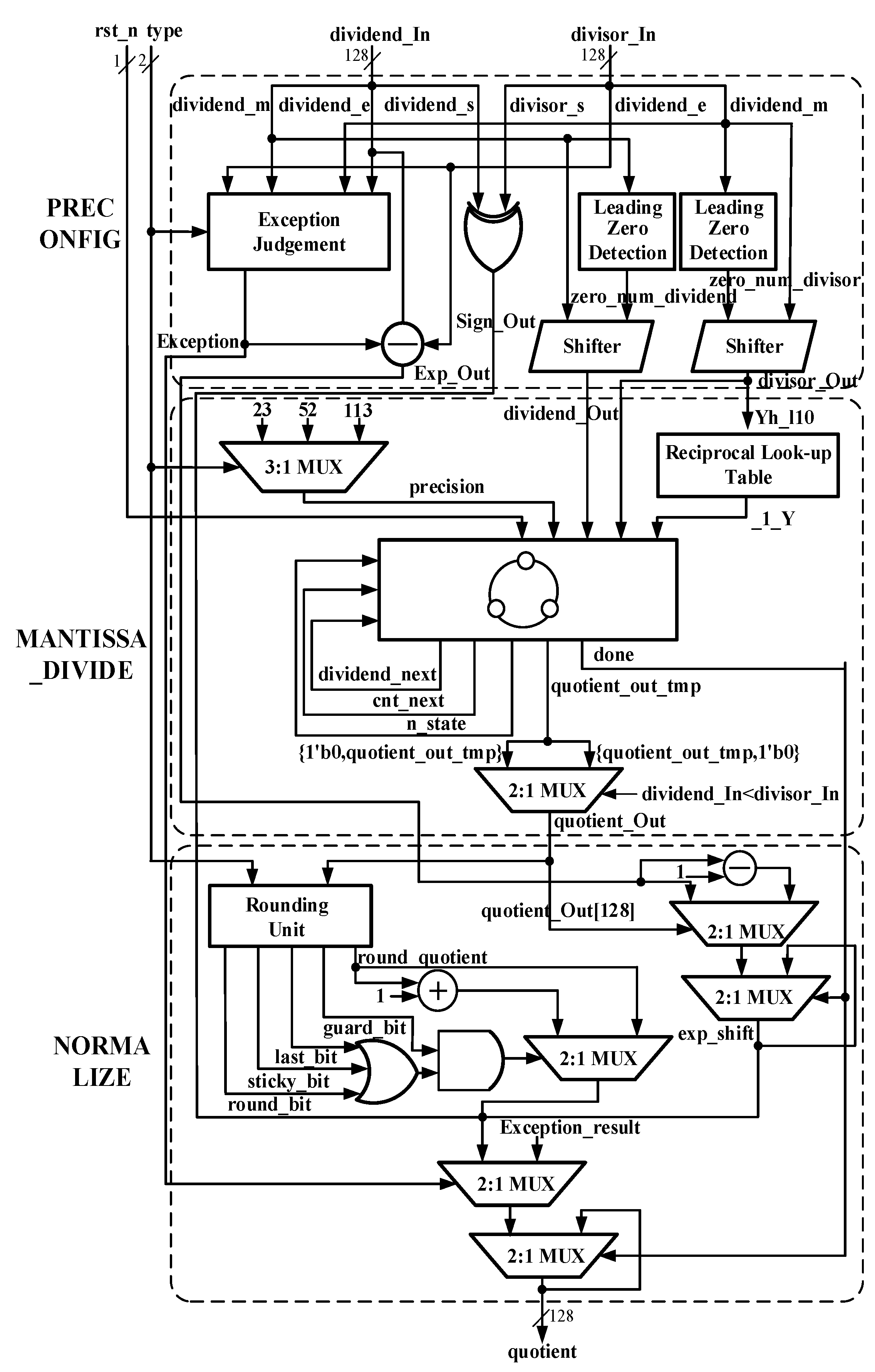
4. General Architecture and Main Parts
4.1. Part 1 PRECONFIG
4.2. Part 2 MANTISSA_DIVIDE
4.3. Part 3 NORMALIZE
5. Results and Comparisons
5.1. Functional Verification
5.2. Related Work and Comparisons
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Oberman, S.F.; Flynn, M.J. Design issues in division and other floating-point operations. IEEE Trans. Comput. 1997, 46, 154–161. [Google Scholar] [CrossRef]
- Obermann, S.F.; Flynn, M.J. Division algorithms and implementations. IEEE Trans. Comput. 1997, 46, 833–854. [Google Scholar] [CrossRef] [Green Version]
- Patankar, U.S.; Koel, A. Review of Basic Classes of Dividers Based on Division Algorithm. IEEE Access 2021, 9, 23035–23069. [Google Scholar] [CrossRef]
- Dixit, S.; Nadeem, M. FPGA accomplishment of a 16-bit divider. Imp. J. Interdiscip. Res. 2017, 3, 140–143. [Google Scholar]
- Boullis, N.; Tisserand, A. On digit-recurrence division algorithms for self-timed circuits. In Advanced Signal Processing Algorithms, Architectures, and Implementations XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2001. [Google Scholar]
- Sutter, G.; Biol, G.; Deschamps, J.-P. Comparative study of SRT dividers in FPGA. In Field Programmable Logic and Application (Lecture Notes in Computer Science); Becker, J., Platzner, M., Vernalde, S., Eds.; Springer: Berlin, Germany, 2004; pp. 209–220. [Google Scholar]
- Kaur, S.; Singh, M.; Agarwal, R. VHDL implementation of nonrestoring division algorithm using high-speed adder/subtractor. Int. J. Adv. Res. Electr., Electron. Instrum. Eng. 2013, 2, 3317–3324. [Google Scholar]
- Bruguera, J.D. Low Latency Floating-Point Division and Square Root Unit. IEEE Trans. Comput. 2020, 69, 274–287. [Google Scholar] [CrossRef]
- Vestias, M.P.; Neto, H.C. Revisiting the Newton-Raphson iterative method for decimal division. In Proceedings of the 2011 21st International Conference on Field Programmable Logic and Applications, Chania, Greece, 5–7 September 2011; pp. 138–143. [Google Scholar]
- Williams, T.E.; Horowitz, M.A. A zero-overhead self-timed 160- ns 54-b CMOS divider. IEEE J. Solid-State Circuits 1991, 26, 1651–1661. [Google Scholar] [CrossRef] [Green Version]
- Saha, P.; Kumar, D.; Bhattacharyya, P.; Dandapat, A. Vedic division methodology for high-speed very large scale integration applications. J. Eng. 2014, 2014, 51–59. [Google Scholar] [CrossRef]
- Fang, X.; Leeser, M. Vendor agnostic, high performance, double precision floating point division for FPGAs. In Proceedings of the 2013 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 10–12 September 2013; pp. 1–5. [Google Scholar]
- Liu, J.; Chang, M.; Cheng, C.-K. An iterative division algorithm for FPGAs. In Proceedings of the 2006 ACM/SIGDA 14th international symposium on Field programmable gate arrays, Monterey, CA, USA, 22–24 February 2006; pp. 83–89. [Google Scholar]
- Kwon, T.J.; Sondeen, J.; Draper, J. Floating-point division and square root using a Taylor-series expansion algorithm. In Proceedings of the 2007 50th Midwest Symposium on Circuits and Systems, Montreal, QC, Canada, 5–8 August 2007; pp. 305–308. [Google Scholar]
- Kumar, A.; Sasamal, T.N. Design of divider using Taylor series in QCA. Energy Procedia 2017, 117, 818–825. [Google Scholar] [CrossRef]
- Bannon, P.; Keller, J. Internal architecture of Alpha 21164 microprocessor. In Proceedings of the Digest of Papers. COMPCON’95. Technologies for the Information Superhighway, San Francisco, CA, USA, 5–8 March 1995; IEEE: Piscataway, NJ, USA; pp. 79–87. [Google Scholar] [CrossRef]
- Edmondson, J.H.; Rubinfeld, P.I.; Bannon, P.J.; Benschneider, B.J.; Bernstein, D.; Castelino, R.W.; Cooper, E.M.; Dever, D.E.; Donchin, D.R.; Fischer, T.C.; et al. Internal organization of the Alpha 21164, a 300-MHz 64-bit quad-issue CMOS RISC microprocessor. Digit. Tech. J. 1995, 7, 119–135. [Google Scholar]
- Wong, D.; Flynn, M. Fast division using accurate quotient approximations to reduce the number of iterations. IEEE Trans. Comput. 1992, 41, 981–995. [Google Scholar] [CrossRef]
- Lang, T.; Nannarelli, A. A radix-10 digit-recurrence division unit: Algorithm and architecture. IEEE Trans. Comput. 2007, 56, 727–739. [Google Scholar] [CrossRef]
- Vemula, R.; Chari, K.M. A review on various divider circuit designs in VLSI. In Proceedings of the 2018 Conference on Signal Processing and Communication Engineering Systems (SPACES), Vijayawada, India, 4–5 January 2018; pp. 206–209. [Google Scholar]
- Sarma, D.D.; Matula, D.W. Faithful bipartite ROM reciprocal tables. In Proceedings of the 12th Symposium on Computer Arithmetic, Bath, UK, 19–21 July 1995; pp. 12–25. [Google Scholar]
- Montuschi, P.; Lang, T. Boosting very-high radix division with prescaling and selection by rounding. In Proceedings of the 14th IEEE Symposium on Computer Arithmetic, Adelaide, SA, Australia, 14–16 April 1999; pp. 52–59. [Google Scholar]
- Lang, T.; Montuschi, P. Very high radix square root with prescaling and rounding and a combined division/square root unit. IEEE Trans. Comput. 1999, 48, 827–841. [Google Scholar] [CrossRef]
- Dormiani, P.; Ercegovac, M.D.; Muller, J. Low precision table based complex reciprocal approximation. In Proceedings of the 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009; pp. 1803–1807. [Google Scholar]
- Kasim, M.F.; Adiono, T.; Zakiy, M.F.; Fahreza, M. FPGA implementation of fixed-point divider using pre-computed values. Procedia Technol. 2013, 11, 206–211. [Google Scholar] [CrossRef] [Green Version]
- Oberman, S.F.; Flynn, M.J. Minimizing the complexity of SRT tables. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 1998, 6, 141–149. [Google Scholar] [CrossRef]
- Anane, M.; Bessalah, H.; Issad, M.; Anane, N.; Salhi, H. Higher Radix and Redundancy Factor for Floating Point SRT Division. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2008, 16, 774–779. [Google Scholar] [CrossRef]
- Akkas, A. Dual-Mode Quadruple Precision Floating-Point Adder. In Proceedings of the 9th EUROMICRO Conference on Digital System Design (DSD’06), Cavtat, Croatia, 30 August–1 September 2006; pp. 211–220. [Google Scholar]
- Ozbilen, M.M.; Gok, M. Multi-Precision Floating-Point Adder. Ph.D. Thesis, Microelectronics and Electronics, Istanbul, Turkey, 2008; pp. 117–120. [Google Scholar]
- Jaiswal, M.K.; Cheung, R.C.C.; Balakrishnan, M.; Paul, K. Unified Architecture for Double/Two-Parallel Single Precision Floating Point Adder. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 521–525. [Google Scholar] [CrossRef] [Green Version]
- Jaiswal, M.K.; Varma, B.S.C.; So, H.K.H. Architecture for Dual-Mode Quadruple Precision Floating Point Adder. In Proceedings of the 2015 IEEE Computer Society Annual Symposium on VLSI, Montpellier, France, 8–10 July 2015; pp. 249–254. [Google Scholar]
- Jaiswal, M.K.; Varma, B.S.C.; So, H.K.; Balakrishnan, M.; Paul, K.; Cheung, R.C.C. Configurable Architectures for Multi-Mode Floating Point Adders. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2079–2090. [Google Scholar] [CrossRef] [Green Version]
- Baluni, A.; Merchant, F.; Nandy, S.K.; Balakrishnan, S. A Fully Pipelined Modular Multiple Precision Floating Point Multiplier with Vector Support. In Proceedings of the 2011 International Symposium on Electronic System Design, Kochi, India, 19–21 December 2011; pp. 45–50. [Google Scholar]
- Manolopoulos, K.; Reisis, D.; Chouliaras, V.A. An efficient multiple precision floating-point multiplier. In Proceedings of the 2011 18th IEEE International Conference on Electronics, Circuits, and Systems, Beirut, Lebanon, 11–14 December 2011; pp. 153–156. [Google Scholar]
- Jaiswal, M.K.; So, H.K. Dual-mode double precision / two-parallel single precision floating point multiplier architecture. In Proceedings of the 2015 IFIP/IEEE International Conference on Very Large Scale Integration (VLSI-SoC), Daejeon, Korea, 5–7 October 2015; pp. 213–218. [Google Scholar]
- Akka¸s, A.; Schulte, M.J. Dual-mode floating-point multiplier architectures with parallel operations. J. Syst. Archit. 2006, 52, 549–562. [Google Scholar] [CrossRef]
- Bruguera, J.D. Radix-64 Floating-Point Divider. In Proceedings of the 2018 IEEE 25th Symposium on Computer Arithmetic (ARITH), Amherst, MA, USA, 25–27 June 2018; pp. 84–91. [Google Scholar]
- Saporito, A.; Recktenwald, M.; Jacobi, C.; Koch, G.; Berger, D.P.D.; Sonnelitter, R.J.; Walters, C.R.; Lee, J.S.; Lichtenau, C.; Mayer, U.; et al. Design of the IBM z15 microprocessor. IBM J. Res. Dev. 2020, 64, 7:1–7:18. [Google Scholar] [CrossRef]
- Burgess, N.; Williams, T. Choices of operand truncation in the SRT division algorithm. IEEE Trans. Comput. 1995, 44, 933–938. [Google Scholar] [CrossRef]
- Schwarz, E.M.; Flynn, M.J. Using a Floating-Point Multiplier’s Internals for High-Radix Division and Square Root; Tech. Rep. CSL-TR-93-554; Computer Systems Laboratory, Stanford University: Stanford, CA, USA, 1993. [Google Scholar]
- Pineiro, J.; Ercegovac, M.D.; Bruguera, J.D. High-radix iterative algorithm for powering computation. In Proceedings of the 2003 16th IEEE Symposium on Computer Arithmetic, Santiago de Compostela, Spain, 15–18 June 2003; pp. 204–211. [Google Scholar]
- Cortadella, J.; Lang, T. High-radix division and square-root with speculation. IEEE Trans. Comput. 1994, 43, 919–931. [Google Scholar] [CrossRef]
- Baesler, M.; Voigt, S.; Teufel, T. FPGA Implementations of Radix-10 Digit Recurrence Fixed-Point and Floating-Point Dividers. In Proceedings of the 2011 International Conference on Reconfigurable Computing and FPGAs, Cancun, Mexico, 30 November–2 December 2011; pp. 13–19. [Google Scholar]
- Chen, L.; Han, J.; Liu, W.; Montuschi, P.; Lombardi, F. Design, Evaluation and Application of Approximate High-Radix Dividers. IEEE Trans. Multi-Scale Comput. Syst. 2018, 4, 299–312. [Google Scholar] [CrossRef]
- Ercegovac, M.D.; Lang, T.; Montuschi, P. Very-high radix division with prescaling and selection by rounding. IEEE Trans. Comput. 1994, 43, 909–918. [Google Scholar] [CrossRef]
- Ercegovac, M.D.; McIlhenny, R. Design and FPGA implementation of radix-10 algorithm for division with limited precision primitives. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 762–766. [Google Scholar]
- Ercegovac, M.D.; McIlhenny, R. Design and FPGA implementation of radix-10 algorithm for square root with limited precision primitives. In Proceedings of the 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009; pp. 935–939. [Google Scholar]
- Vazquez, A.; Antelo, E.; Montuschi, P. A radix-10 SRT divider based on alternative BCD codings. In Proceedings of the 2007 25th International Conference on Computer Design, Lake Tahoe, CA, USA, 7–10 October 2007; pp. 280–287. [Google Scholar]
- Nannarelli, A. Radix-16 Combined Division and Square Root Unit. In Proceedings of the 2011 IEEE 20th Symposium on Computer Arithmetic, Tuebingen, Germany, 25–27 July 2011; pp. 169–176. [Google Scholar]
- Harris, D.L.; Oberman, S.F.; Horowitz, M.A. SRT division architectures and implementations. In Proceedings of the 13th IEEE Sympsoium on Computer Arithmetic, Asilomar, CA, USA, 6–9 July 1997; pp. 18–25. [Google Scholar]
- Carter, T.M.; Robertson, J.E. Radix-16 signed-digit division. IEEE Trans. Comput. 1990, 39, 1424–1433. [Google Scholar] [CrossRef]
- Atkins, D.E. Higher-radix division using estimates of the divisor and partial remainders. IEEE Trans. Comput. 1968, C-17, 925–934. [Google Scholar] [CrossRef]
- Chen, L.; Lombardi, F.; Montuschi, P.; Han, J.; Liu, W. Design of approximate high-radix dividers by inexact binary signed-digit addition. In Proceedings of the on Great Lakes Symposium on VLSI, Banff, AB, Canada, 10–12 May 2017; pp. 293–298. [Google Scholar]
- Nikmehr, H.; Phillips, B.; Lim, C. Fast Decimal Floating-Point Division. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2006, 14, 951–961. [Google Scholar] [CrossRef] [Green Version]
- Tenca, A.F.; Ercegovac, M.D. On the design of high-radix online division for long precision. In Proceedings of the 14th IEEE Symposium on Computer Arithmetic, Adelaide, SA, Australia, 14–16 April 1999; pp. 44–51. [Google Scholar]
- Narendra, K.; Ahmed, S.; Kumar, S.; Asha, G.H. FPGA implementation of fixed point integer divider using iterative array structure. Int. J. Eng. Sci. Tech. Res. 2015, 3, 170–179. [Google Scholar]
- Jaiswal, M.K.; So, H.K. Architecture for quadruple precision floating point division with multi-precision support. In Proceedings of the 2016 IEEE 27th International Conference on Application-specific Systems, Architectures and Processors (ASAP), London, UK, 6–8 July 2016; pp. 239–240. [Google Scholar]
- Jaiswal, M.K.; So, H.K. Area-Efficient Architecture for Dual-Mode Double Precision Floating Point Division. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 386–398. [Google Scholar] [CrossRef]
- Coke, J.; Baliga, H.; Cooray, N.; Gamsaragan, E.; Smith, P.; Yoon, K.; Abel, J.; Valles, A. Improvements in the Intels Cor2 Penryn processor family architecture and microarchitecture. Intel Technol. J. 2008, 12, 179–192. [Google Scholar]
- Gerwig, G.; Wetter, H.; Schwarz, E.M.; Haess, J. High performance floating-point unit with 116 bit wide divider. In Proceedings of the 2003 16th IEEE Symposium on Computer Arithmetic, Santiago de Compostela, Spain, 15–18 June 2003; pp. 87–94. [Google Scholar]
- Lichtenau, C.; Carlough, S.; Mueller, S.M. Quad precision floating point on the IBM z13TM. In Proceedings of the 2016 IEEE 23nd Symposium on Computer Arithmetic, Silicon Valley, CA, USA, 10–13 July 2016; pp. 87–94. [Google Scholar]
- Naini, A.; Dhablania, A. 1-GHz HAL SPARC64® dual floating-point unit with RAS features. In Proceedings of the 15th IEEE Symposium on Computer Arithmetic, Vail, CO, USA, 11–13 June 2001; pp. 173–183. [Google Scholar]
- Oberman, S.F. Floating point division and square root algorithms and implementation in the AMD-K7TM microprocessor. In Proceedings of the 14th IEEE Symposium on Computer Arithmetic, Adelaide, SA, Australia, 14–16 April 1999; pp. 106–115. [Google Scholar]
- Rupley, J.; King, J.; Quinnell, E.; Galloway, F.; Patton, K.; Seidel, P.M.; Dinh, J.; Bui, H.; Bhowmik, A. The floating-point unit of the Jaguar x86 Core. In Proceedings of the 2013 IEEE 21st Symposium on Computer Arithmetic, Austin, TX, USA, 7–10 April 2013; pp. 7–16. [Google Scholar]






| Parameter n | Additional Digits of Quotient | 2n Kinds of Possible Quotients |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 2 | 4 |
| 3 | 3 | 8 |
| 4 | 4 | 16 |
| 5 | 5 | 32 |
| Parameter m | Parameter t | Data Width of LUT Entries | Guaranteed Bits per Cycle | Clock Cycles | Achieved Bits per Cycle |
|---|---|---|---|---|---|
| 10 | 2 | 512 | 20 | 6 + 1 = 7 | 120 |
| 10 | 3 | 512 | 29 | 4 + 2 = 6 | 116 |
| 10 | 4 | 512 | 38 | 3 + 3 = 6 | 114 |
| 11 | 2 | 1024 | 22 | 6 + 1 = 7 | 132 |
| 11 | 3 | 1024 | 32 | 4 + 2 = 6 | 128 |
| 11 | 4 | 1024 | 42 | 3 + 3 = 6 | 126 |
| 12 | 2 | 2048 | 24 | 5 + 1 = 6 | 120 |
| 12 | 3 | 2048 | 35 | 4 + 2 = 6 | 140 |
| 12 | 4 | 2048 | 46 | 3 + 3 = 6 | 138 |
| Input Dividend | Input Divisor | Exception Signal Exception |
|---|---|---|
| NaN | NaN | NaN |
| NaN | Zero | NaN |
| NaN | Infinity | NaN |
| Zero | NaN | NaN |
| Zero | Zero | NaN |
| Zero | Infinity | Zero |
| Infinity | NaN | NaN |
| Infinity | Zero | NaN |
| Infinity | Infinity | NaN |
| SP | DP | QP | |
|---|---|---|---|
| Latency(cycle) | 3 | 4 | 6 |
| Period(ns) | 3.3 | 3.3 | 3.3 |
| Total time(ns) | 9.9 | 13.2 | 19.8 |
| Efficient average time (ns/bit) 1 | 0.43 | 0.25 | 0.17 |
| Area(μm2) | 542,650 | 545,905 | 550,567 |
| Power(mW) | 55.58 | 56.13 | 58.53 |
| [58] (with 1-Stage Multiplier) | [58] (with 2-Stage Multiplier) | This Paper | |
|---|---|---|---|
| Subnormal | √ | √ | √ |
| Tech. | 90 nm | 90 nm | 90 nm |
| Latency (cycle) | 11 (61.1%) | 18 (100%) | 4 (22.2%) |
| Period (ns) | 1.72 (175.5%) | 0.98 (100%) | 3.3 (336.7%) |
| Power (mW) | 30.9 (48.1%) | 64.21 (100%) | 58.53 (91.1%) |
| Total time (ns) | 18.92 (107.3%) | 17.64 (100%) | 13.2 (74.82%) |
| Total energy (fJ) | 584.65 (51.6%) | 1132.74 (100%) | 772.6 (68.2%) |
| Efficient average energy (fJ/bit) 1 | 11.24 (51.6%) | 21.78 (100%) | 12.07 (55.4%) |
| Algorithm | Tech. | Clock Speed (Hz) | SP | DP | |||
|---|---|---|---|---|---|---|---|
| Latency (Cycle) | Total Time (ns) | Latency (Cycle) | Total Time (ns) | ||||
| AMD K7 | multiplicative | − | 500 M | 16 | 32 | 20 | 40 |
| AMD Jaguar | multiplicative | 28 nm | 2 G | 14 | 7 | 19 | 9.5 |
| IBM zSeries | radix-4 | 130 nm | 1 G | 23 | 23 | 37 | 37 |
| IBM z13 | radix-8/4 | 22 nm | 5 G | 18 | 3.6 | 28 | 5.6 |
| HAL Sparc | multiplicative | 150 nm | 1 G | 16 | 16 | 19 | 19 |
| Intel Penryn | radix-16 | 45 nm | 2.33 G | 12 | 5.14 | 20 | 8.57 |
| This paper | Predict–Correct | 90 nm | 300 M | 3 | 9.9 | 4 | 13.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, J.; Fu, W.; Liu, M.; Wang, M. Low-Latency Bit-Accurate Architecture for Configurable Precision Floating-Point Division. Appl. Sci. 2021, 11, 4988. https://doi.org/10.3390/app11114988
Xia J, Fu W, Liu M, Wang M. Low-Latency Bit-Accurate Architecture for Configurable Precision Floating-Point Division. Applied Sciences. 2021; 11(11):4988. https://doi.org/10.3390/app11114988
Chicago/Turabian StyleXia, Jincheng, Wenjia Fu, Ming Liu, and Mingjiang Wang. 2021. "Low-Latency Bit-Accurate Architecture for Configurable Precision Floating-Point Division" Applied Sciences 11, no. 11: 4988. https://doi.org/10.3390/app11114988
APA StyleXia, J., Fu, W., Liu, M., & Wang, M. (2021). Low-Latency Bit-Accurate Architecture for Configurable Precision Floating-Point Division. Applied Sciences, 11(11), 4988. https://doi.org/10.3390/app11114988






