Chemotaxis Model for Drug Delivery Using Turing’s Instability and Non-Linear Diffusion
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Volume-Filling Chemotaxis Model
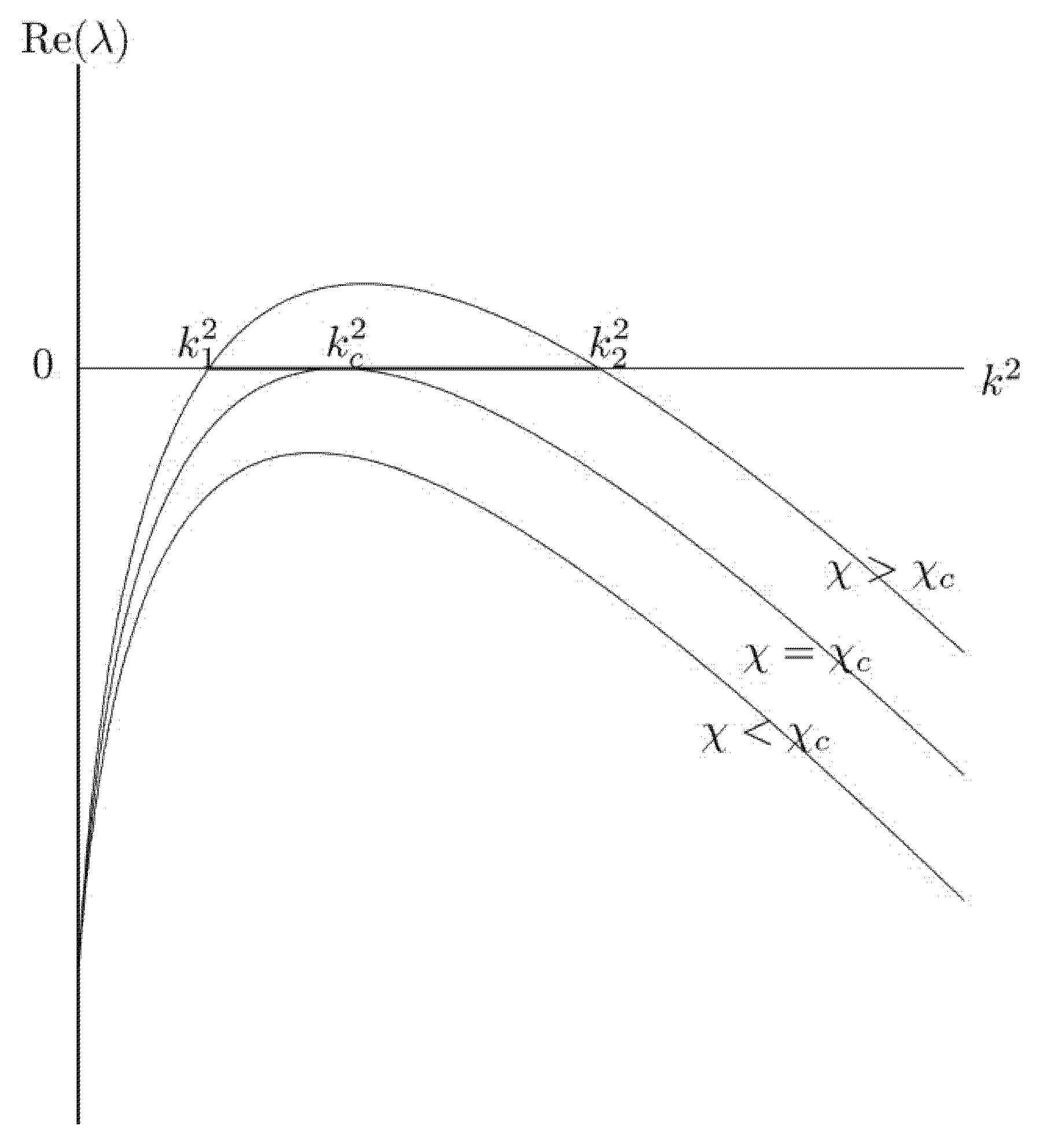
2.2. Pattern Formation
- Asymptotic expansion for the functions , and around
- Taking into account Equation (5);
- Equating first-order terms with respect to ;
- Neglecting higher-order terms, and dropping the tilde for the convenience.
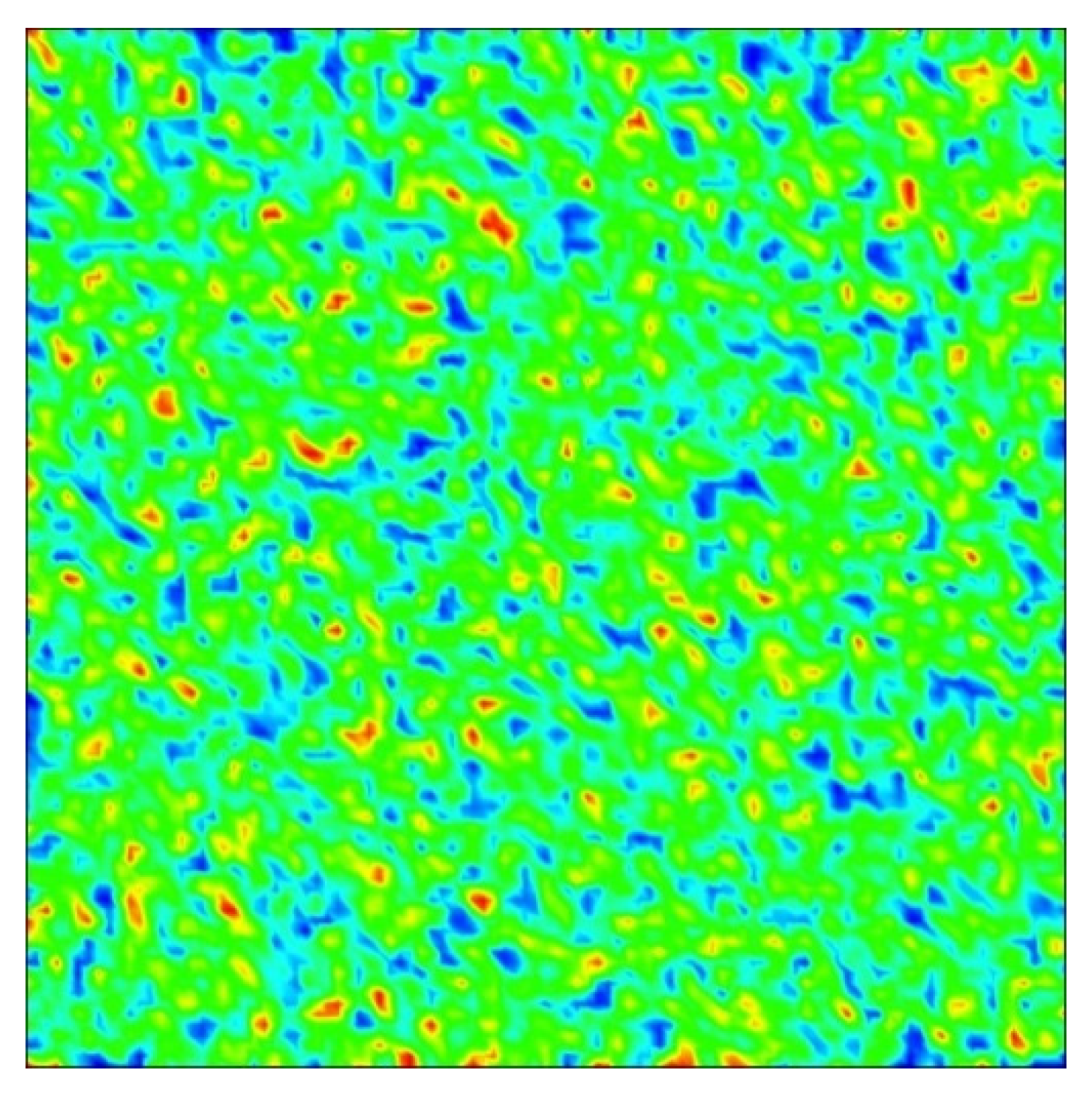
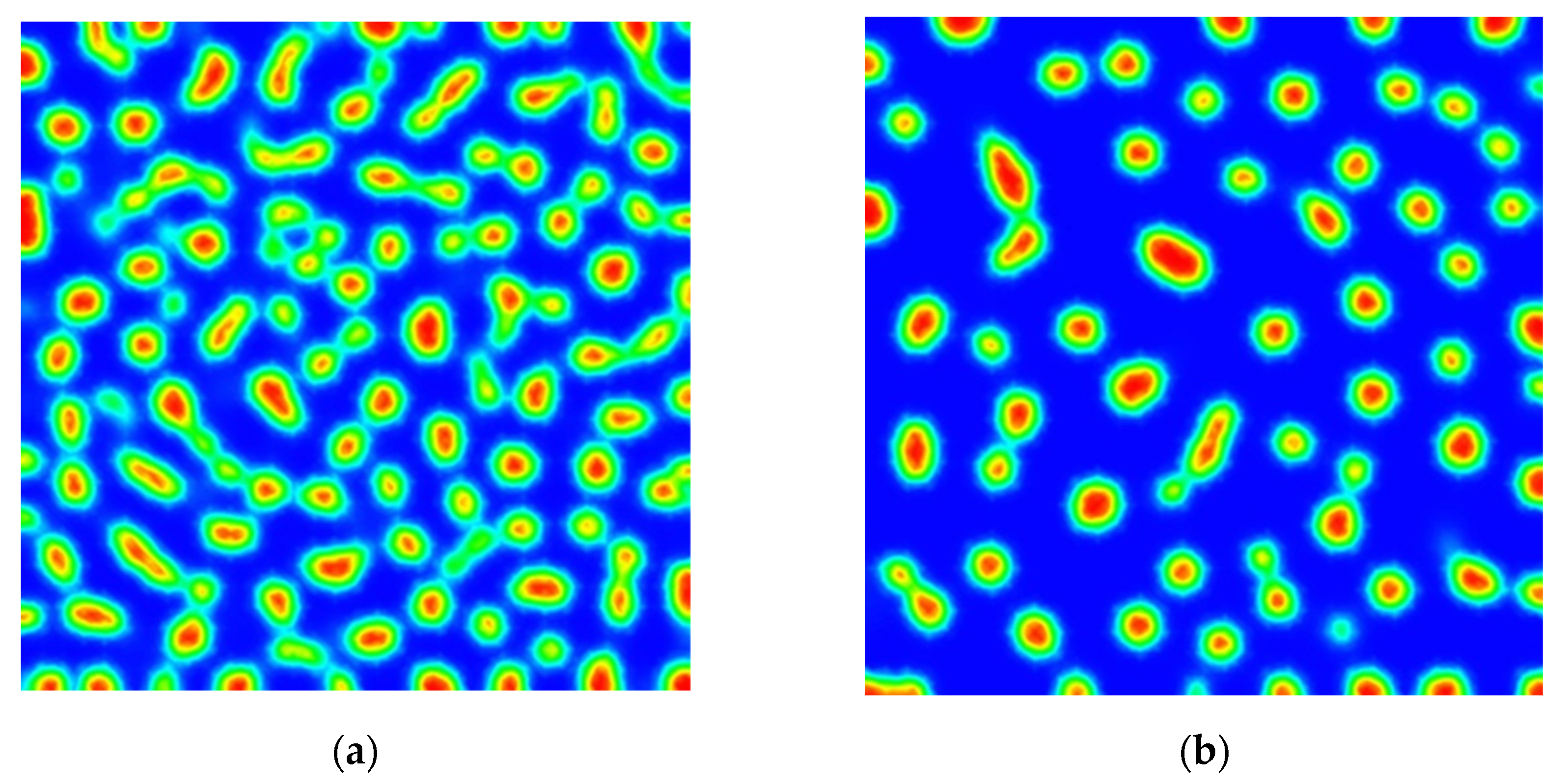
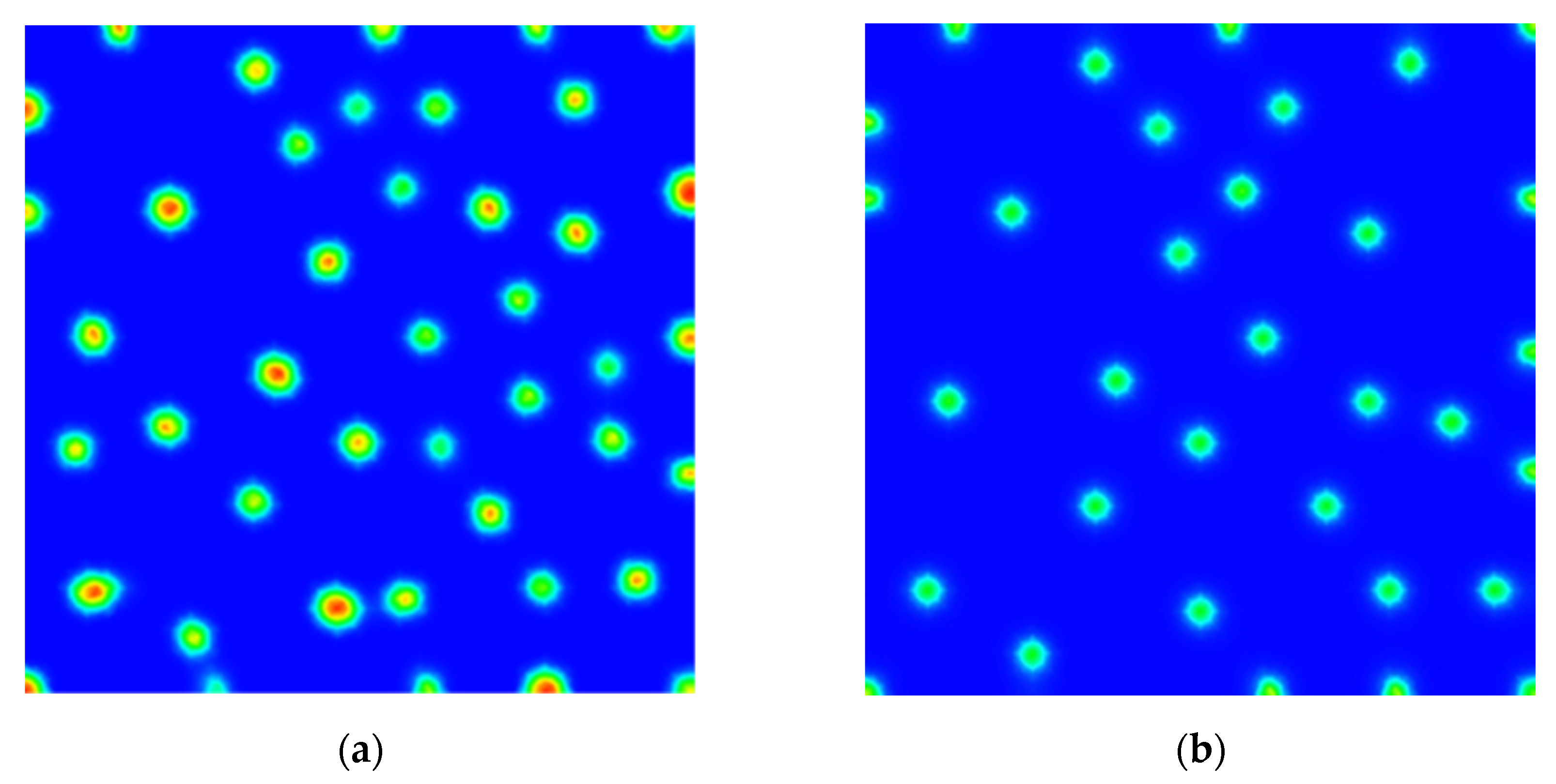
3. Results
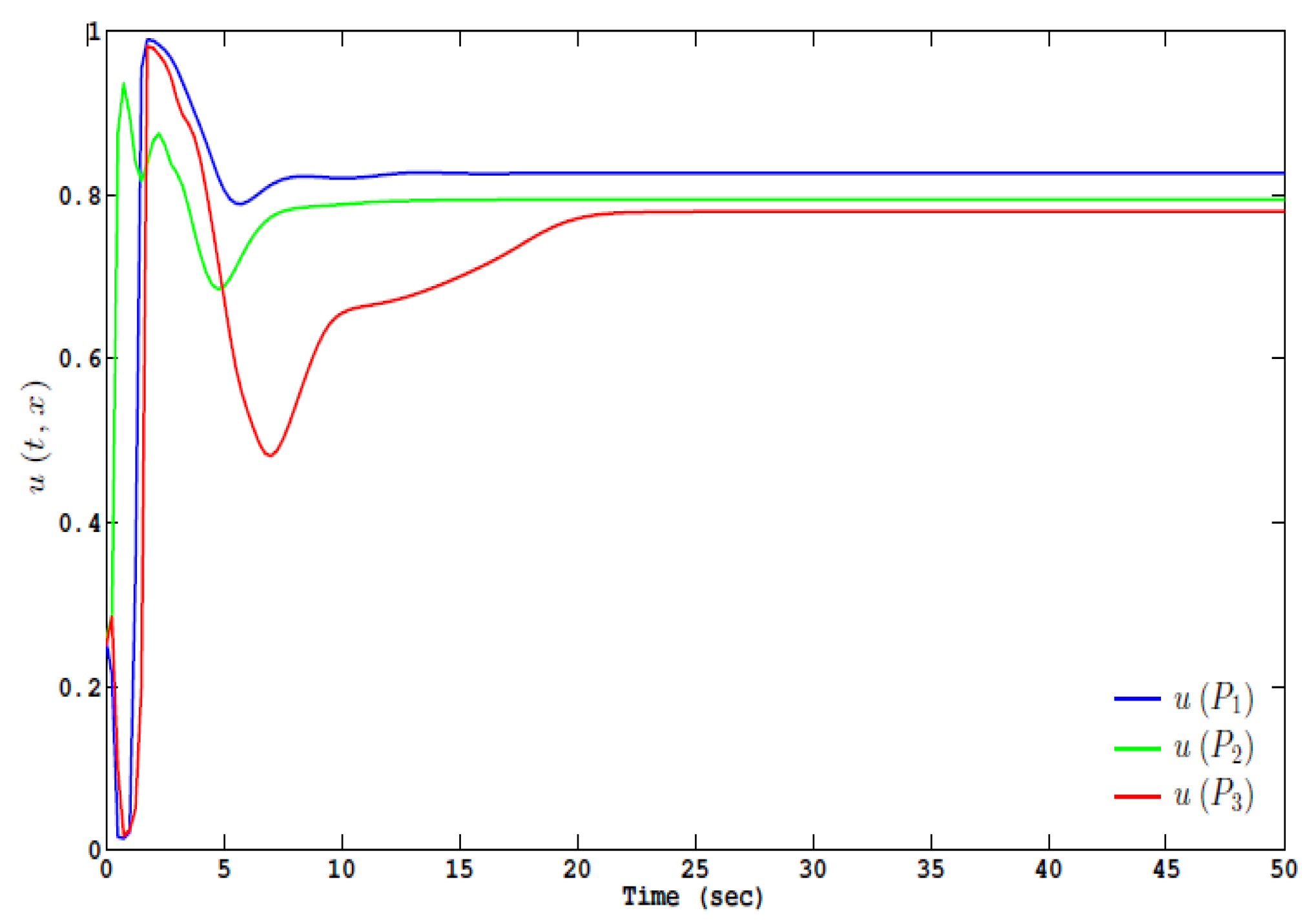
Numerical Scheme and Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Espinosa, E.; Zamora, P.; Feliu, J.; González Barón, M. Classification of anticancer drugs—A new system based on therapeutic targets. Cancer Treat. Rev. 2003, 29, 515–523. [Google Scholar] [CrossRef]
- Djamgoz, M.B.A.; Fraser, S.P.; Brackenbury, W.J. In vivo evidence for voltage-gated sodium channel expression in carcinomas and potentiation of metastasis. Cancers 2019, 11, 1675. [Google Scholar] [CrossRef] [PubMed]
- Jandaghi, N.; Jahani, S.; Foroughi, M.M.; Kazemipour, M.; Ansari, M. Cerium-doped flower-shaped ZnO nano-crystallites as a sensing component for simultaneous electrochemical determination of epirubicin and methotrexate. Microchim. Acta 2020, 187. [Google Scholar] [CrossRef]
- Nastasa, V.; Samaras, K.; Andrei, I.; Pascu, M.; Karapantsios, T. Study of the formation of micro and nano-droplets containing immiscible solutions. Colloids Surf. A Physicochem. Eng. Asp. 2011, 382, 246–250. [Google Scholar] [CrossRef]
- Saad, A.S.; Al Faraj, A. 3D visualization of iron oxide nanoparticles in MRI of inflammatory model. J. Vis. 2014, 18, 1–8. [Google Scholar] [CrossRef]
- Coluccio, M.L.; D’Attimo, M.A.; Cristiani, C.M.; Candeloro, P.; Parrotta, E.; Dattola, E.; Guzzi, F.; Cuda, G.; Lamanna, E.; Carbone, E.; et al. A passive microfluidic device for chemotaxis studies. Micromachines 2019, 10, 551. [Google Scholar] [CrossRef]
- Painter, K.; Maini, P.; Othmer, H. Stripe formation in juvenile pomacanthus explained by a generalized turing mechanism with chemotaxis. Proc. Natl. Acad. Sci. USA 1999, 96, 5549–5554. [Google Scholar] [CrossRef] [PubMed]
- Painter, K.J.; Hillen, T. Volume-filling and quorum-sensing in models for chemosensitive movement. Can. Appl. Math. Q. 2002, 10, 501–543. [Google Scholar]
- Owen, M.R.; Byrne, H.M.; Lewis, C.E. Mathematical modelling of the use of macrophages as vehicles for drug delivery to hypoxic tumour sites. J. Theor. Biol. 2004, 226, 377–391. [Google Scholar] [CrossRef]
- Zhabotinsky, A.M. Periodical oxidation of malonic acid in solution (a study of the belousov reaction kinetics). Biofizika 1964, 9, 306–311. [Google Scholar]
- Turing, A.M. The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar]
- Murray, J.D. Mathematical Biology: I. An Introduction; Springer: New York, NY, USA, 2002; Volume 17. [Google Scholar]
- Patlak, C.S. Random walk with persistence and external bias. Bull. Math. Biol. 1953, 15, 311–338. [Google Scholar] [CrossRef]
- Keller, E.F.; Segel, L.A. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar] [CrossRef]
- Keller, E.F.; Segel, L.A. Model for chemotaxis. J. Theor. Biol. 1971, 30, 225–234. [Google Scholar] [CrossRef]
- Horstmann, D. From 1970 until present: The Keller-Segel model in chemotaxis and its consequences. ii. Jahresber. Dtsch. Math. Ver. 2004, 106, 51–70. [Google Scholar]
- Horstmann, D. From 1970 until present: The Keller-Segel model in chemotaxis and its consequences. i. Jahresber. Dtsch. Math. Ver. 2003, 105, 103–165. [Google Scholar]
- Bendahmane, M.; Karlsen, K.H.; Urbano, J.M. On a two-sidedly degenerate chemotaxis model with volume-filling effect. Math. Model. Methods Appl. Sci. 2007, 17, 783–804. [Google Scholar] [CrossRef]
- Andreianov, B.; Bendahmane, M.; Saad, M. Finite volume methods for degenerate chemotaxis model. J. Comput. Appl. Math. 2011, 235, 4015–4031. [Google Scholar] [CrossRef]
- Schaaf, P.; Talbot, J. Surface exclusion effects in adsorption processes. J. Chem. Phys. 1989, 91, 4401–4409. [Google Scholar] [CrossRef]
- Potapov, A.; Hillen, T. Metastability in chemotaxis models. J. Dyn. Differ. Equat. 2005, 17, 293–330. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Hillen, T. Classical solutions and pattern formation for a volume filling chemotaxis model. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17. [Google Scholar] [CrossRef]
- Amann, H. Nonhomogeneous linear and quasilinear elliptic and parabolic boundary value problems. Funct. Spaces Differ. Oper. Nonlinear Anal. 1993, 133, 9–126. [Google Scholar]
- Murray, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2003; Volume 18. [Google Scholar]
- Eymard, R.; Gallouet, T.; Herbin, R. Finite volume methods. Handb. Numer. Anal. 2000, 7, 713–1018. [Google Scholar]
- Murray, J.; Myerscough, M. Pigmentation pattern formation on snakes. J. Theor. Biol. 1991, 149, 339–360. [Google Scholar] [CrossRef]
- Yang, X.; Dormann, D.; Münsterberg, A.E.; Weijer, C.J. Cell movement patterns during gastrulation in the chick are controlled by positive and negative chemotaxis mediated by fgf4 and fgf8. Dev. Cell 2002, 3, 425–437. [Google Scholar] [CrossRef]
- Bendahmane, M.; Saad, M. Mathematical analysis and pattern formation for a partial immune system modeling the spread of an epidemic disease. Acta Appl. Math. 2010, 115, 17–42. [Google Scholar] [CrossRef]
- Chaplain, M.A.; Ganesh, M.; Graham, I.G. Spatio-temporal pattern formation on spherical surfaces: Numerical simulation and application to solid tumour growth. J. Math. Biol. 2001, 42, 387–423. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.; Chaplain, M.A. Mathematical models for tumour angiogenesis: Numerical simulations and nonlinear wave solutions. Bull. Math. Biol. 1995, 57, 461–486. [Google Scholar] [CrossRef]
- Sahari, A.; Traore, M.A.; Scharf, B.E.; Behkam, B. Directed transport of bacteria-based drug delivery vehicles: Bacterial chemotaxis dominates particle shape. Biomed. Microdevices 2014, 16, 717–725. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almijalli, M.; Ibrahim, M.; Saad, A.; Saad, M. Chemotaxis Model for Drug Delivery Using Turing’s Instability and Non-Linear Diffusion. Appl. Sci. 2021, 11, 4979. https://doi.org/10.3390/app11114979
Almijalli M, Ibrahim M, Saad A, Saad M. Chemotaxis Model for Drug Delivery Using Turing’s Instability and Non-Linear Diffusion. Applied Sciences. 2021; 11(11):4979. https://doi.org/10.3390/app11114979
Chicago/Turabian StyleAlmijalli, Mohammed, Moustafa Ibrahim, Ali Saad, and Mazen Saad. 2021. "Chemotaxis Model for Drug Delivery Using Turing’s Instability and Non-Linear Diffusion" Applied Sciences 11, no. 11: 4979. https://doi.org/10.3390/app11114979
APA StyleAlmijalli, M., Ibrahim, M., Saad, A., & Saad, M. (2021). Chemotaxis Model for Drug Delivery Using Turing’s Instability and Non-Linear Diffusion. Applied Sciences, 11(11), 4979. https://doi.org/10.3390/app11114979





