Computational Evaluation of Shock Wave Interaction with a Cylindrical Water Column
Abstract
:1. Introduction
2. Computational Model
2.1. Case Study
2.2. CFD Analysis
2.2.1. VOF Method
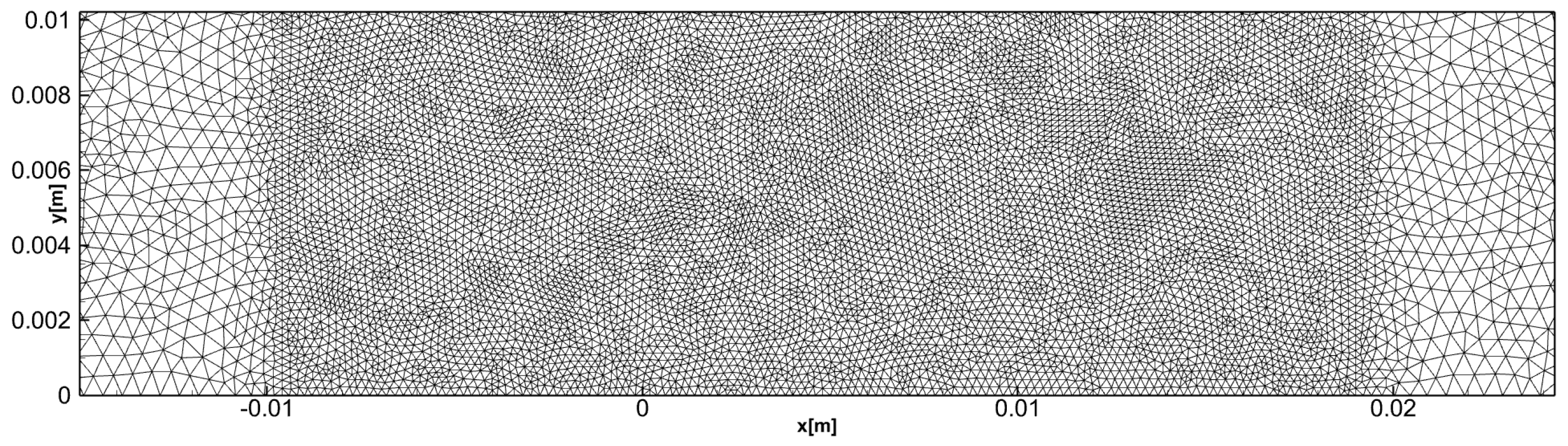
2.2.2. CFD Solution
3. Results
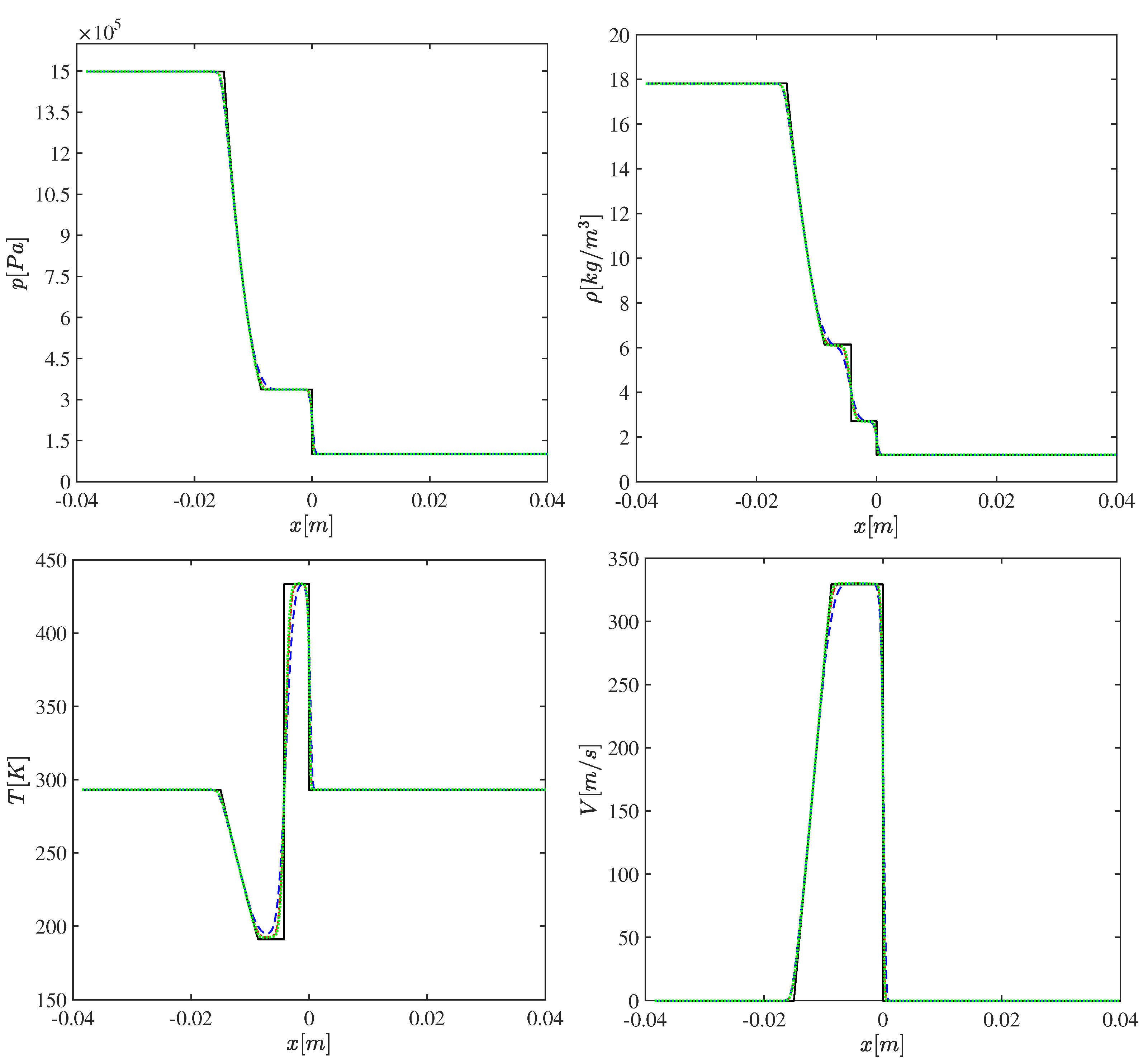
3.1. Shock Tube Flow
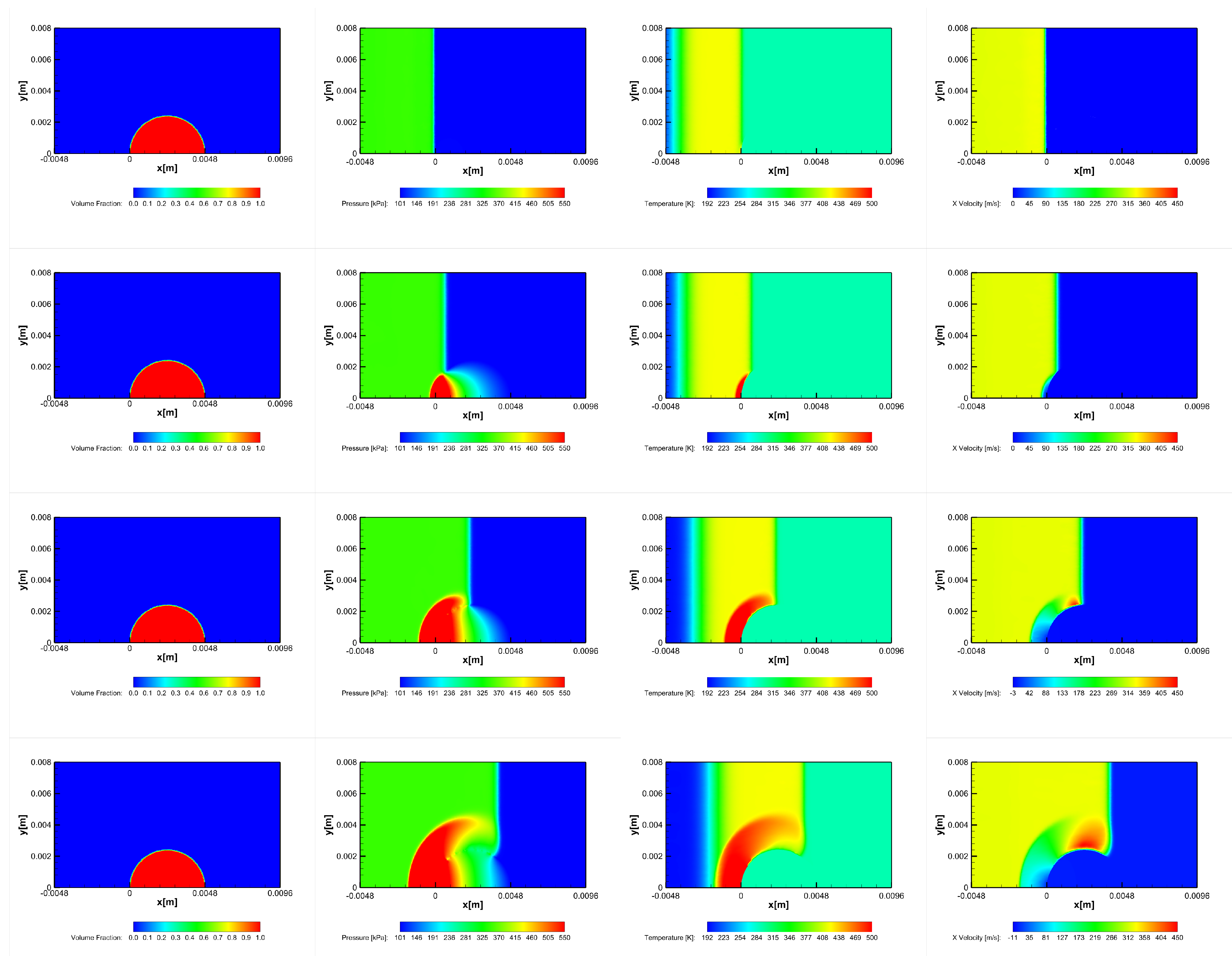
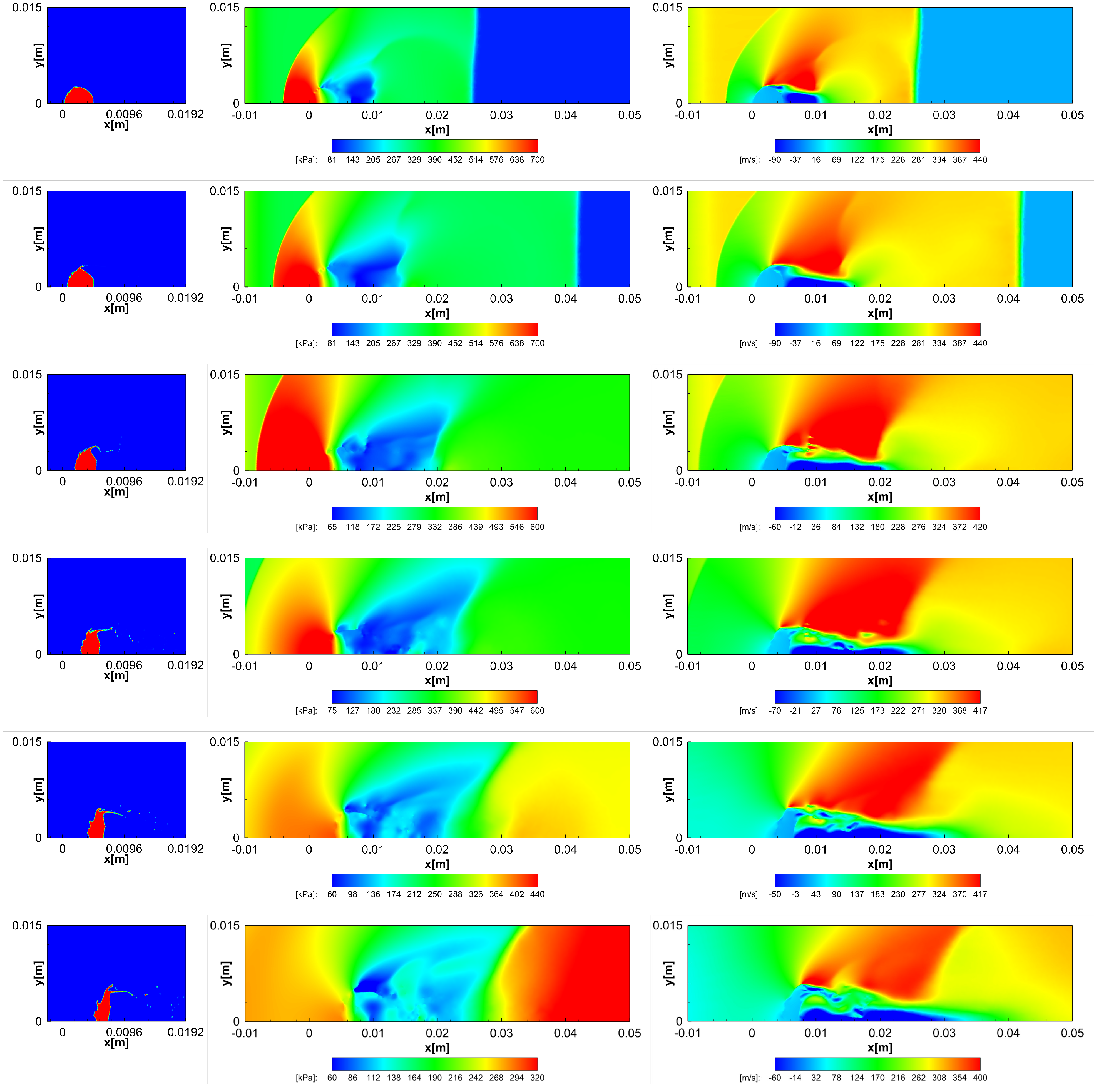
3.2. Shock–Column Interaction
3.2.1. Qualitative Analysis
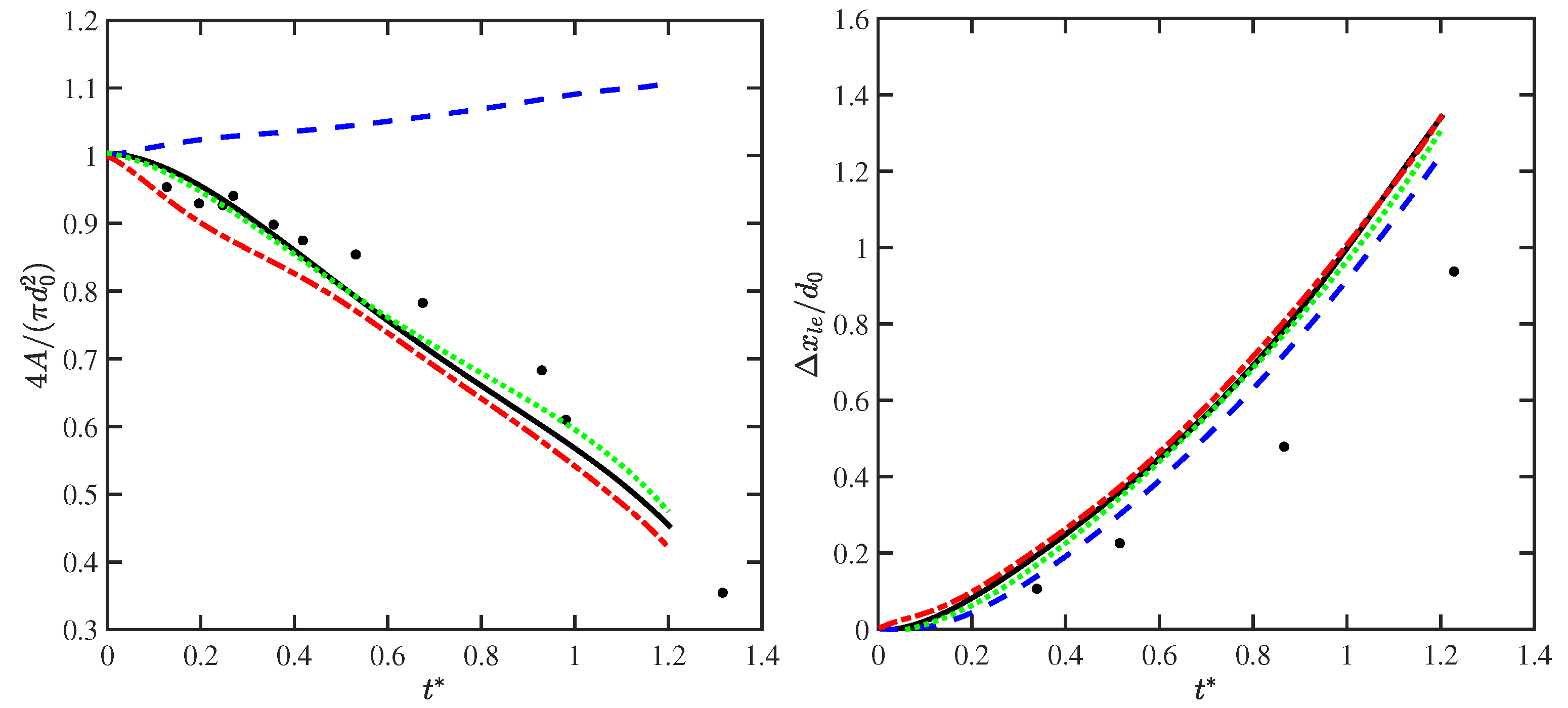
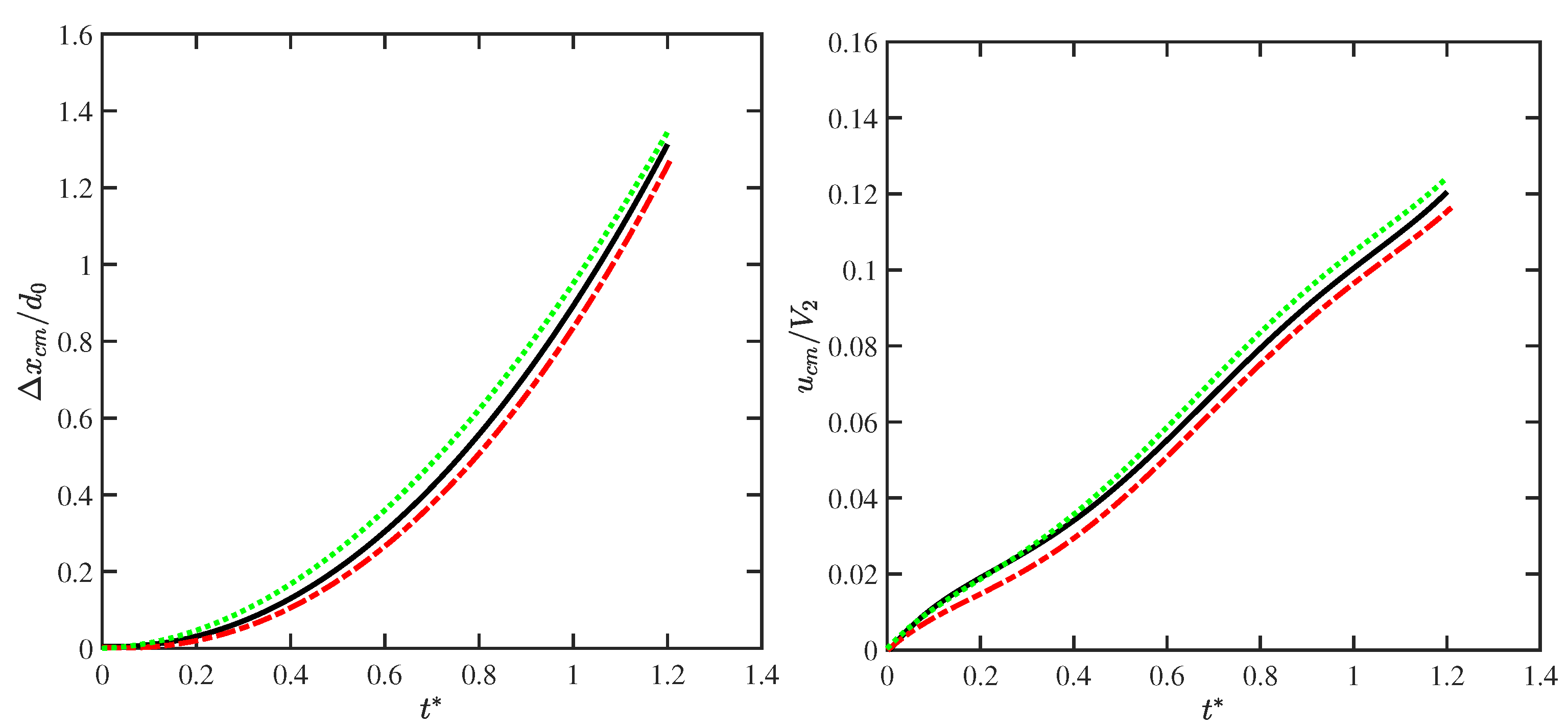
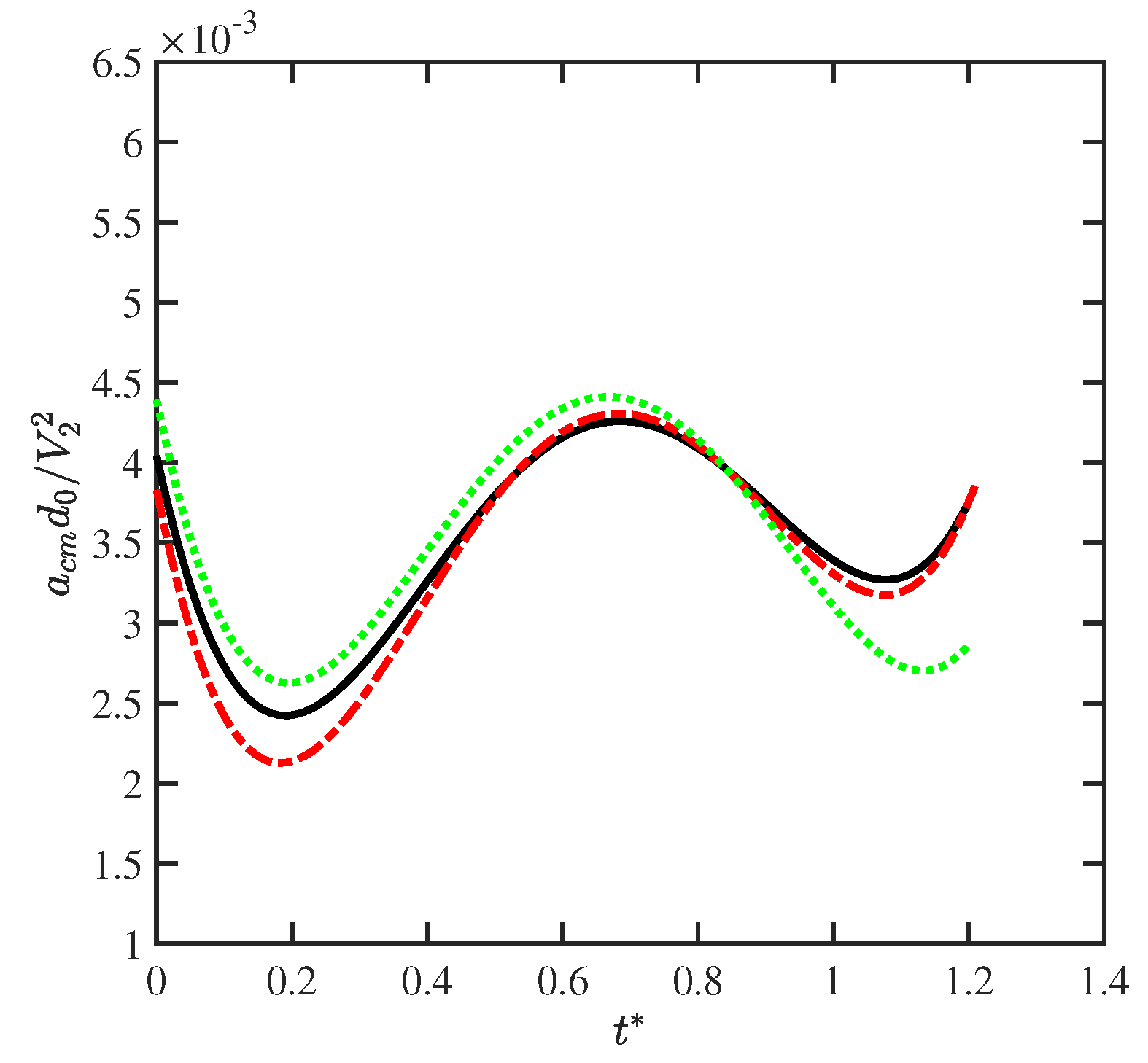
3.2.2. Quantitative Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RTP | Rayleigh–Taylor piercing |
| SIE | shear-induced entrainment |
| CFD | computational fluid dynamics |
| DNS | direct numerical simulation |
| LES | large eddy simulation |
| RANS | Reynolds-averaged Navier–Stokes |
| FV | finite volume |
| VOF | volume of fluid |
| CSF | continuum surface force |
| SST | shear stress transport |
| CM | center-of-mass |
References
- Villermaux, E. Fragmentation. Annu. Rev. Fluid Mech. 2007, 39, 419–446. [Google Scholar] [CrossRef]
- Liu, N.; Wang, Z.; Mingbo, S.; Wang, H.; Wang, B. Numerical simulation of liquid droplet breakup in supersonic flows. Acta Astronaut. 2018, 145, 116–130. [Google Scholar] [CrossRef]
- Wang, Z.; Hopfes, T.; Giglmaier, M.; Adams, N.A. Effect of Mach number on droplet aerobreakup in shear stripping regime. Exp. Fluids 2020, 61, 193. [Google Scholar] [CrossRef] [PubMed]
- Poplavski, S.; Minakov, A.; Shebeleva, A.; Boiko, V. On the interaction of water droplet with a shock wave: Experiment and numerical simulation. Int. J. Multiph. Flow 2020, 127, 103273. [Google Scholar] [CrossRef]
- Guildenbecher, D.R.; López-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 46, 371–402. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Li, J.G. On the physics of aerobreakup. Phys. Fluids 2008, 20, 052103. [Google Scholar] [CrossRef]
- Theofanous, T.G. Aerobreakup of Newtonian and viscoelastic liquids. Annu. Rev. Fluid Mech. 2011, 43, 661–690. [Google Scholar] [CrossRef]
- Chen, H.; Liang, S.M. Flow visualization of shock/water column interactions. Shock Waves 2008, 17, 309–321. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, B. Numerical study of a planar shock interacting with a cylindrical water column embedded with an air cavity. J. Fluid Mech. 2017, 825, 825–852. [Google Scholar] [CrossRef]
- Kaiser, J.W.J.; Winter, J.M.; Adami, S.; Adams, N.A. Investigation of interface deformation dynamics during high-Weber number cylindrical droplet breakup. Int. J. Multiph. Flow 2020, 132, 103409. [Google Scholar] [CrossRef]
- Igra, D.; Takayama, K. A Study of Shock Wave Loading on a Cylindrical Water Column; Institute of Fluid Science, Tohoku University: Miyagi, Japan, 2001; Volume 13, pp. 19–36. [Google Scholar]
- Sembian, S.; Liverts, M.; Tillmark, N.; Apazidis, N. Plane shock wave interaction with a cylindrical water column. Phys. Fluids 2016, 28, 056102. [Google Scholar] [CrossRef]
- Igra, D.; Ogawa, T.; Takayama, K. A parametric study of water column deformation resulting from shock wave loading. At. Sprays 2002, 12, 577–591. [Google Scholar] [CrossRef]
- Allaire, G.; Clerc, S.; Kokh, S. A five-equation model for the simulation of interfaces between compressible fluids. J. Comput. Phys. 2002, 181, 577–616. [Google Scholar] [CrossRef] [Green Version]
- Hosseinzadeh-Nik, Z.; Aslani, M.; Owkes, M.; Regele, J.D. Numerical simulation of a shock wave impacting a droplet using the adaptive wavelet-collocation method. In Proceedings of the ILASS-Americas 28th Annual Conference on Liquid Atomization and Spray Systems, Dearborn, MI, USA, 15–18 May 2016. [Google Scholar]
- Anderson, M.; Vorobieff, P.; Truman, C.R.; Corbin, C.; Kuehner, G.; Wayne, P.; Conroy, J.; White, R.; Kumar, S. An experimental and numerical study of shock interaction with a gas column seeded with droplets. Shock Waves 2015, 25, 107–125. [Google Scholar] [CrossRef]
- Rapagnani, D.; Buompane, R.; Di Leva, A.; Gialanella, L.; Busso, M.; De Cesare, M.; De Stefano, G.; Duarte, J.G.; Gasques, L.R.; Morales Gallegos, L.; et al. A supersonic jet target for the cross-section measurement of the 12C(α, γ)16O reaction with the recoil mass separator ERNA. Nucl. Instrum. Methods Phys. Res. B 2017, 407, 217–221. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Cantwell, B.J. Fundamentals of Compressible Flow; Department of Aeronautics and Astronautics, Stanford University: Stanford, CA, USA, 2018. [Google Scholar]
- Meng, J.C.; Colonius, T. Numerical simulations of the early stages of high-speed droplet breakup. Shock Waves 2015, 25, 399–414. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Turbulence Modelling for CFD, 3rd ed.; DCW Industries, Inc.: La Canada, CA, USA, 2006. [Google Scholar]
- Reina, G.P.; De Stefano, G. Computational evaluation of wind loads on sun-tracking ground-mounted photovoltaic panel arrays. J. Wind Eng. Ind. Aerodyn. 2017, 170, 283–293. [Google Scholar] [CrossRef]
- De Stefano, G.; Natale, N.; Reina, G.P.; Piccolo, A. Computational evaluation of aerodynamic loading on retractable landing-gears. Aerospace 2020, 7, 68. [Google Scholar] [CrossRef]
- Natale, N.; Salomone, T.; De Stefano, G.; Piccolo, A. Computational evaluation of control surfaces aerodynamics for a mid-range commercial aircraft. Aerospace 2020, 7, 139. [Google Scholar] [CrossRef]
- De Stefano, G.; Denaro, F.M.; Riccardi, G. High-order filtering for control volume flow simulation. Int. J. Numer. Methods Fluids 2001, 37, 797–835. [Google Scholar] [CrossRef]
- Shyue, K.M. A fluid-mixture type algorithm for barotropic two-fluid flow problems. J. Comput. Phys. 1998, 200, 718–748. [Google Scholar] [CrossRef]
- Sod, G.A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Nicholls, J.A.; Ranger, A.A. Aerodynamic shattering of liquid drops. AIAA J. 1969, 7, 285–290. [Google Scholar] [CrossRef]
- Engel, O.G. Fragmentation of waterdrops in the zone behind an air shock. J. Res. Natl. Bur. Stand. 1958, 60, 245–280. [Google Scholar] [CrossRef]
- Regele, J.D.; Vasilyev, O.V. An adaptive wavelet-collocation method for shock computations. Int. J. Comput. Fluid Dyn. 2009, 23, 503–518. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. Hierarchical adaptive eddy-capturing approach for modeling and simulation of turbulent flows. Fluids 2021, 6, 83. [Google Scholar] [CrossRef]
- De Stefano, G.; Vasilyev, O.V. Wavelet-based adaptive large-eddy simulation with explicit filtering. J. Comput. Phys. 2013, 238, 240–254. [Google Scholar] [CrossRef]
- De Stefano, G.; Brown-Dymkoski, E.; Vasilyev, O.V. Wavelet-based adaptive large-eddy simulation of supersonic channel flow. J. Fluid Mech. 2020, 901, A13. [Google Scholar] [CrossRef]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Hussaini, M.Y. Wavelet-based adaptive unsteady Reynolds-averaged Navier–Stokes computations of wall-bounded internal and external compressible turbulent flows. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- De Stefano, G.; Vasilyev, O.V.; Brown-Dymkoski, E. Wavelet-based adaptive unsteady Reynolds-averaged turbulence modeling of external flows. J. Fluid Mech. 2018, 837, 765–787. [Google Scholar] [CrossRef]
- Ge, X.; Vasilyev, O.V.; De Stefano, G.; Hussaini, M.Y. Wavelet-based adaptive unsteady Reynolds-Averaged Navier-Stokes simulations of wall-bounded compressible turbulent flows. AIAA J. 2020, 58, 1529–1549. [Google Scholar] [CrossRef]
- Shen, B.; Ye, Q.; Tiedje, O.; Domnick, J. Simulation of the primary breakup of non-Newtonian liquids at a high-speed rotary bell atomizer for spray painting processes using a VOF-Lagrangian hybrid model. In Proceedings of the 29th European Conference on Liquid Atomization and Spray Systems, Paris, France, 2–4 September 2019. [Google Scholar]
- Nejadmalayeri, A.; Vezolainen, A.; De Stefano, G.; Vasilyev, O.V. Fully adaptive turbulence simulations based on Lagrangian spatio-temporally varying wavelet thresholding. J. Fluid Mech. 2014, 749, 794–817. [Google Scholar] [CrossRef] [Green Version]


| Parameter | Symbol | Value |
|---|---|---|
| Driven section pressure | 101.3 kPa | |
| Driven section density | 1.204 kg/m | |
| Shock compression ratio | 3.32 | |
| Driver section pressure | 1.50 MPa | |
| Driver section density | 17.8 kg/m | |
| Temperature | 293.15 K |
| Parameter | Symbol | Value |
|---|---|---|
| Initial column diameter | 4.80 × 10 m | |
| Water density | 1000 kg/m | |
| Water viscosity | 1.003 × 10 Pa/s | |
| Surface tension | 7.286 × 10 N/m | |
| Air temperature | 433.86 K | |
| Air density | 2.706 kg/m | |
| Air viscosity | 1.80 × 10 Pa/s | |
| Air velocity | 329.3 m/s |
| Number | Symbol | Value |
|---|---|---|
| Mach | ||
| Reynolds | ||
| Ohnesorge | ||
| Weber |
| Solution | # of FV Cells | (m/s) | (m/s) | |
|---|---|---|---|---|
| CFD I | ||||
| CFD II | ||||
| CFD III | ||||
| Analytical | − | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossano, V.; De Stefano, G. Computational Evaluation of Shock Wave Interaction with a Cylindrical Water Column. Appl. Sci. 2021, 11, 4934. https://doi.org/10.3390/app11114934
Rossano V, De Stefano G. Computational Evaluation of Shock Wave Interaction with a Cylindrical Water Column. Applied Sciences. 2021; 11(11):4934. https://doi.org/10.3390/app11114934
Chicago/Turabian StyleRossano, Viola, and Giuliano De Stefano. 2021. "Computational Evaluation of Shock Wave Interaction with a Cylindrical Water Column" Applied Sciences 11, no. 11: 4934. https://doi.org/10.3390/app11114934
APA StyleRossano, V., & De Stefano, G. (2021). Computational Evaluation of Shock Wave Interaction with a Cylindrical Water Column. Applied Sciences, 11(11), 4934. https://doi.org/10.3390/app11114934







