Handling Enhancement of Autonomous Emergency Steering for Reduced Road Friction Using Steering and Differential Braking

Abstract

Steering has more potential than braking to prevent rear-end collisions at higher relative velocities. A path tracking controller based on multi-input multi-output (MIMO) model predictive control (MPC) is proposed to enhance the handling performance of autonomous emergency steering in this paper. A six-state MIMO bicycle model including actuator dynamics of steering and differential braking is used for model prediction. Two control inputs are front wheel steering angle and direct yaw moment. Two model outputs are lateral displacement and heading angle. According to the work load ratios at four wheels, control allocation is used to determine the optimal braking force distribution to prevent tire force saturation. The performance of a single-input single-output (SISO) MPC that uses only steering angle control to track the lateral displacement of the desired path is employed to benchmark the performance of the proposed algorithm. Simulation results show that both SISO MPC and MIMO MPC can track the path on nominal road surface with high road friction coefficient of 0.9. For a road surface with medium road friction coefficient of 0.7, the SISO MPC is unable to track the path and loses directional stability. However, the MIMO MPC can still track the path and demonstrate robust path tracking and handling enhancement against model uncertainty due to reduced road friction.

1. Introduction

According to Traffic Safety Facts [1], rear-end collisions account for 18% of the fatal collisions between motor vehicles. Singh et al. [2] pointed out that driver error is the primary cause for most accidents. The main factor is the recognition error caused by driver inattention, internal and external distractions, and inadequate surveillance. Advanced driver assistance systems (ADAS) can assist the driver to prevent possible collisions with the obstacle in front of the vehicle via braking or steering. Bosch [3] reported that the autonomous emergency braking (AEB) system would reduce 30% of rear-end collisions. Alfred et al. [4] showed that the necessary minimum distance to avoid a collision by steering is smaller than that by braking for maneuvers with large relative velocities. Especially for a suddenly appearing obstacle, AEB is not able to avoid a collision due to insufficient braking distance. The European New Car Assessment Programme introduced safety ratings for AEB in 2014, and has announced that [5] emergency steering assist (ESA) and autonomous emergency steering system (AES) tests will start in 2020 and 2022, respectively. The goal of the tests is to deliver a further significant reduction in crashes and casualties.

1.1. Related Work

Both ESA and AES can make a sudden lane change or evasive maneuver via steering actions to avoid a collision. The main difference between ESA and AES is the trigger mechanism. When the ESA [6,7,8,9] detects the risk of collision and the steering torque from the driver, the system provides additional overlay torques to adjust the steering angle to track the evasive path without collision or directional instability. However, Shimizu et al. [10] showed that 37.9% of drivers did not take any avoidance maneuvers when encountering the approaching danger. Therefore, collision avoidance cannot be guaranteed for inattentive maneuvers with late steering actions from the driver. Unlike ESA, the AES [11,12,13,14,15] can steer automatically when the detected risk of collision is over the designed threshold.

Three types of planning approaches, search-based, optimization-based, and parameter-based, are commonly used for generating a desired path to avoid the collision. Search-based methods [16,17,18] are designed to generate an action set of multiple drivable trajectories, allowing an adjacent behavior planner to pick the most appropriate action for the global state in the scene. Optimization-based methods [19,20,21] plan the path from a mapping run and offline compute an optimal trajectory around the track using the trajectory optimization module to maximize the progress rate, and minimize slip angle cost and input rate. However, the first and second types of planning approaches are not easy to implement on production control units due to high computation loads. Parameter-based methods [7] including circular, sine/cosine, s-shape, polynomial, and trapezoidal-acceleration-profile (TAP) trajectories are designed by specifying the desired lateral displacement for a lane change maneuver that can also be employed for collision avoidance. Among the parameter-based methods, only TAP can consider transition time and ride comfort at the same time [22].

Two types of path tracking controllers, model-free and model-based, are commonly used for tracking an evasive path. If the dynamic model of the plant to be controlled is not needed for the controller design, it is classified as the model-free approach. The conventional model-free controller calculates the steering angle command based on the lateral displacement error and the heading error at the previewed point [23,24,25]. Machine learning can also be classified as the model-free approach. A neural network model can be trained to generate the steering action using the dataset of human drivers [26] or deep reinforcement learning [27]. However, the major challenge is the difficulty in proving the safety issue of these methods [28]. As for model-based approaches, the single-input single-output (SISO) model predictive control (MPC) is often used to obtain the vehicle steering angle based on a four-state bicycle model, which is used to predict the future lateral displacement of a vehicle [29,30,31].

Differential braking via electric hydraulic braking (EHB) can be used to generate the desired direct yaw moment (DYM) to improve path tracking performance. Falcone et al. [32] proposed a multi-input multi-output (MIMO) MPC controller that uses four-wheel longitudinal slip ratios and front wheel steering angle as the control input to minimize errors in heading angle, yaw rate and lateral displacement. Their simulation results showed that path error can be reduced by 50%. However, intensive computations are required for online linearization and optimization due to the complexities of the prediction model with nonlinear tire dynamics. Hajiloo et al. [33] proposed a MIMO MPC controller to determine the optimal front lateral force and the yaw moment to improve the yaw rate responsiveness for collision avoidance without decreasing the stability. Lin et al. [34] proposed a MIMO MPC controller for AES using front wheel steering angle and direct yaw-moment control (DYC) to enhance the performance of path tracking. The pseudo inverse control allocation (CA) is used to allocate the four-wheel brake forces for generating the desired DYM. Their simulation results showed that the path tracking performance of the MIMO MPC is better than that of the conventional SISO MPC. However, the actuator dynamics of steering and differential braking are not discussed in their proposed approach. The control performance might be diminished or control lost if the actuator dynamics are not fast enough to be negligible.

Electric power steering (EPS) can be used to generate the desired front wheel steering angle. However, the actuator dynamics might cause the actual steering angle to lag slightly behind the steering angle command. Chen et al. [35] proposed a MPC controller by considering EPS actuator dynamics as a first-order model to enhance the tracking performance and ride comfort. Kim et al. [36] proposed a MPC controller by considering the EPS as a second-order model. Simulation results showed that tracking performance is improved by incorporating steering actuator dynamics in the prediction model. Thornton et al. [37] proposed a MPC controller with steering input to evaluate the average and maximum yaw rates of different actuator dynamics. Their experiment results showed that the lumped first-order dynamics can meet design objectives with low computational complexity.

1.2. Main Contributions

The proposed path-tracking controller for AES is an extension of the previous work [34] in which the actuator dynamics were neglected in the vehicle model.

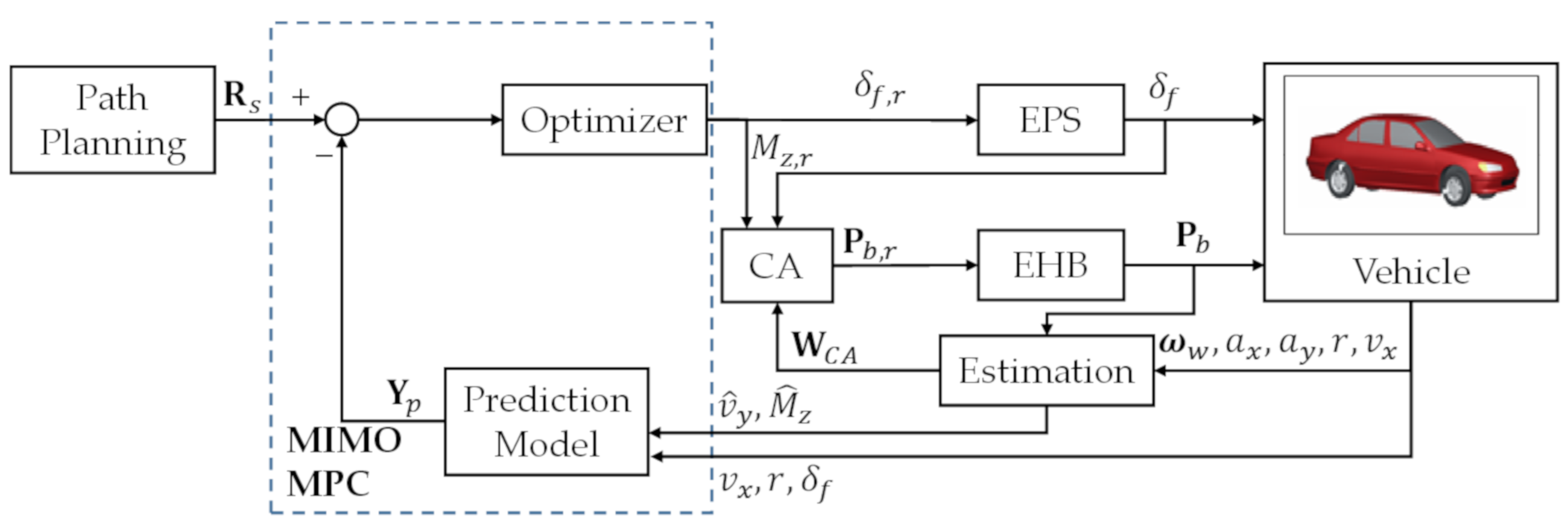
• The dynamic responses of the vehicle model in the previous work might deviate from those of the actual vehicle model with actuator dynamics for severe maneuvers. The EPS and EHB dynamics are integrated with the four-state bicycle model to enhance the accuracy of the prediction model.
• A diagonal matrix with components of tire workload ratios is used to replace the identity weighting matrix of CA to prevent saturating tire forces while generating the desired DYM.
• Different road friction coefficients are used for sensitivity analysis to evaluate the robustness and handling enhancement of the proposed algorithm at different vehicle velocities via simulation studies.

1.3. Organization

The remainder of this paper is organized as follows: system modeling for controller design is briefly introduced in Section 2, followed by the proposed algorithm in Section 3. Simulation results are presented in Section 4. Finally, conclusions are made in Section 5.

2. Modeling

2.1. Actuator Dynamics

First-order actuator dynamics of EPS and EHB as shown below are included in the plant model for MPC.

$${\dot{\delta }}_f=-\frac{1}{{\tau }_{EPS}}{\delta }_f+\frac{1}{{\tau }_{EPS}}{\delta }_{f,r}$$

(1)

$${\dot{M}}_z=-\frac{1}{{\tau }_{EHB}}{M}_z+\frac{1}{{\tau }_{EHB}}{M}_{z,r}$$

(2)

where ${\delta }_{f,r}$ and $M_{z,r}$ are the control commands of the front wheel steering angle and DYM, respectively;${\delta }_f$ and $M_z$ are the responses of front wheel steering angle and DYM, respectively; ${\tau }_{EPS}$ and ${\tau }_{EHB}$ are the time constants of EPS and EHB, respectively. ${\tau }_{EPS}$ is set to be 0.125 s [37] and ${\tau }_{EHB}$ is set to be 0.1 s [38] in this paper.

2.2. Bicycle Model

The six-state bicycle model is obtained by integrating the actuator dynamics with the four-state bicycle model that is linearized using small angle approximation and constant longitudinal velocity [39]. The state-space representation can be expressed as follows.

$$\begin{array}{l}\dot{x}=A_{m}x+B_{m}u\hfill \\ y=C_{m}x\hfill \end{array}$$

(3)

where $x={\left[\begin{array}{cccccc}y& v_y& \psi & r& {\delta }_f& M_z\end{array}\right]}^T$ is the state vector, $u={\left[\begin{array}{cc}{\delta }_{f,r}& M_{z,r}\end{array}\right]}^T$ is the input vector, and $y={\left[\begin{array}{cc}y& \psi \end{array}\right]}^T$ is the output vector; $v_y$ and $r$ are the lateral velocity and yaw rate of the vehicle, respectively; $y$ and $\psi$ are the lateral displacement and heading angle of the vehicle, respectively; $A_m$, $B_m$ and $C_m$ are system matrix, input matrix and output matrix as shown below.

$$A_m=\left[\begin{array}{cccccc}0& 1& v_x& 0& 0& 0\\ 0& \frac{-\left(C_{\alpha f}+C_{\alpha r}\right)}{m{v}_x}& 0& \frac{l_r{C}_{\alpha r}-l_f{C}_{\alpha f}}{m{v}_x}-v_x& \frac{C_{\alpha f}}{m}& 0\\ 0& 0& 0& 1& 0& 0\\ 0& \frac{l_r{C}_{\alpha r}-l_f{C}_{\alpha f}}{I_z{v}_x}& 0& \frac{-\left(l_f{}^2{C}_{\alpha f}+l_r{}^2{C}_{\alpha r}\right)}{I_z{v}_x}& \frac{l_f{C}_{\alpha f}}{I_z}& \frac{1}{I_z}\\ 0& 0& 0& 0& -\frac{1}{{\tau }_{EPS}}& 0\\ 0& 0& 0& 0& 0& -\frac{1}{{\tau }_{EHB}}\end{array}\right]$$

(4)

$$B_m={\left[\begin{array}{cccccc}0& 0& 0& 0& \frac{1}{{\tau }_{EPS}}& 0\\ 0& 0& 0& 0& 0& \frac{1}{{\tau }_{EHB}}\end{array}\right]}^T$$

(5)

$$C_m=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\end{array}\right]$$

(6)

where $m$ is the vehicle mass; $v_x$ is the vehicle longitudinal velocity; $C_{\alpha f}$ and $C_{\alpha r}$ are the cornering stiffness of the front and rear axles, respectively; $l_f$ and $l_r$ are the distances from the C.G. to the front and rear axles, respectively; $I_z$ is the yaw-plane rotational inertia of vehicle. The ranks of controllability matrix $\mathcal{C}$ and observability matrix $\mathcal{O}$ of the six-state bicycle model can be calculated as follows.

$$rank\left(\mathcal{C}\right)=rank\left(\left[\begin{array}{ccccc}{A}_m& A_m{B}_m& A_m^2{B}_m& \dots & A_m^5{B}_m\end{array}\right]\right)$$

(7)

$$rank\left(\mathcal{O}\right)=rank\left({\left[\begin{array}{ccccc}{C}_m& C_m{A}_m& C_m{A}_m^2& \dots & C_m{A}_m^5\end{array}\right]}^T\right)$$

(8)

Since both $\mathcal{C}$ and $\mathcal{O}$ are full rank of 6, the proposed model is fully controllable and observable.

2.3. Model Discretization

A D-Class Sedan in CarSim is selected as the host vehicle to obtain the parameter values of $m$, $a$, $b$, and $I_z$. Nominal values of $C_{\alpha f}$ and $C_{\alpha r}$ are identified on a road surface with the nominal friction coefficient of 0.9 by minimizing the path errors between the trajectory responses of CarSim and the bicycle model. The vehicle parameters used in CarSim are shown in

Table 1. Vehicle parameters.

Name	Value
Vehicle mass (m)	1530 kg
Yaw-plane rotational inertia of vehicle (Iz)	2315 kg–m2
Distances from the C.G. to the front axles (lf)	1.1 m
Wheel base (L)	2.78 m
Cornering stiffness of the front axles (Cαf)	150.3 kN/rad
Cornering stiffness of the rear axles (Cαr)	104.9 kN/rad

.

For the discrete controller design, the discretized plant model can be expressed as follows.

$$\begin{array}{l}{x}_{k+1}={\Phi }_m{x}_k+{\Gamma }_m{u}_k\hfill \\ y_k=H_m{x}_k\hfill \end{array}$$

(9)

where k denotes for the kth sample. The sample time $T_s$ is selected to be 0.04 s in this paper; $u_k$ is the discretized input vector; ${\Phi }_m$, ${\Gamma }_m$ and $H_m$ can be expressed as follows.

$${\Phi }_m=\left[\begin{array}{cccccc}1& T_s& v_x{T}_s& 0& 0& 0\\ 0& \frac{-\left(C_{\alpha f}+C_{\alpha r}\right)T_s}{m{v}_x}+1& 0& \frac{l_r{C}_{\alpha r}-l_f{C}_{\alpha f}}{m{v}_x}{T}_s-v_x{T}_s& \frac{C_{\alpha f}{T}_s}{m}& 0\\ 0& 0& 1& T_s& 0& 0\\ 0& \frac{l_r{C}_{\alpha r}-l_f{C}_{\alpha f}}{I_z{v}_x}{T}_s& 0& \frac{-{l_f}^2{C}_{\alpha f}+{l_f}^2{C}_{\alpha r}{T}_s}{I_z{v}_x}+1& \frac{l_f{C}_{\alpha f}{T}_s}{I_z}& \frac{T_s}{I_z}\\ 0& 0& 0& 0& -\frac{T_s}{{\tau }_{EPS}}+1& 0\\ 0& 0& 0& 0& 0& -\frac{T_s}{{\tau }_{EHB}}+1\end{array}\right]$$

(10)

$${\Gamma }_m={\left[\begin{array}{cccccc}0& 0& 0& 0& \frac{T_s}{{\tau }_{EPS}}& 0\\ 0& 0& 0& 0& 0& \frac{T_s}{{\tau }_{EHB}}\end{array}\right]}^T$$

(11)

$$H_m=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\end{array}\right]$$

(12)

3. Controller Design

The block diagram of the proposed algorithm is shown in Figure 1. The path planning module generates the reference path $R_s$ using the trapezoidal acceleration profile [7]. The six-state bicycle model is used to predict the future path. The PGC calculation module calculates the PGC index from $R_s$. The optimizer module is used to compute the best set of future control commands. The first two elements of the set are used as the desired control commands of front wheel steering angle and DYM. The CA module distributes brake pressure at the four wheels to generate the desired DYM. After the AES is triggered, the driver is disengaged from the vehicle until the driver’s intent to override the system is detected.

3.1. Model Predictive Controller

The predicted state vectors in the prediction horizon N_p with the future control commands in the control horizon N_c can be expressed as follows.

$$\begin{gathered} x_{k,i+1}={\Phi }_m{x}_{k,i}+{\Gamma }_m{u}_{k,i} \\ {x}_{k,i+2}={\Phi }_m^2{x}_{k,i}+{\Phi }_m{\Gamma }_m{u}_{k,i}+{\Gamma }_m{u}_{k,i+1} \\ ⋮ \\ {x}_{k,i+N_p}={\Phi }_m^{N_p}{x}_{k,i}+{\Phi }_m^{N_p-1}{\Gamma }_m{u}_{k,i}+\cdots +{\Phi }_m^{N_p-N_c}{\Gamma }_m{u}_{k,i+N_c-1} \end{gathered}$$

(13)

where the initial condition of the state vector $x_{k,i}$ can be expressed as follows.

$$x_{k,i}={\left[\begin{array}{cccccc}0& {\widehat{v}}_y& 0& r& {\delta }_f& {\widehat{M}}_z\end{array}\right]}^T$$

(14)

where the initial lateral displacement and heading angle are zero in the body coordinates of the vehicle;$r$ and ${\delta }_f$ can be measured using yaw rate and steering angle sensors, respectively; ${\widehat{v}}_y$ is the estimated lateral velocity that can be estimated using localization-based [40] or inertial-measurement-unit-based [41] approaches; ${\widehat{M}}_z$ can be estimated using estimated logitudinal tire forces as follows.

$${\widehat{M}}_z=B_{CA}{\widehat{F}}_x$$

(15)

where ${\widehat{F}}_x$ is the estimated longitudinal tire force that can be estimated using a closed-loop disturbance estimator [42];$B_{CA}$ is the effective matrix as shown below.

$$B_{CA}=\left[-\frac{d}{2}cos{\delta }_f+l_{f}sin{\delta }_f -\frac{d}{2} \frac{d}{2}cos{\delta }_f+l_{f}sin{\delta }_f \frac{d}{2}\right]$$

(16)

where d is the track width of the vehicle.

The predicted output vectors in the prediction horizon N_p can be expressed as follows.

$$\begin{gathered} y_{p,k,i+1}=H_m{\Phi }_m{x}_{k,i}+H_m{\Gamma }_m{u}_{k,i} \\ {y}_{p,k,i+2}=H_m{\Phi }_m^2{x}_{k,i}+H_m{\Phi }_m{\Gamma }_m{u}_{k,i}+H_m{\Gamma }_m{u}_{k,i+1} \\ ⋮ \\ {y}_{p,k,i+N_p}=H_m{\Phi }_m^{N_p}{x}_{k,i}+H_m{\Phi }_m^{N_p-1}{\Gamma }_m{u}_{k,i}+\cdots +H_m{\Phi }_m^{N_p-N_c}{\Gamma }_m{u}_{k,i+N_c-1} \end{gathered}$$

(17)

From Equations (11) and (15), the augmented prediction model can be formulated as follows.

$$Y_p=F{x}_{k,i}+G{U}_p$$

(18)

where $U_p$ is the input vector; $Y_p$ is the output vector; $F$ and $G$ are the system and input matrices, respectively. They are defined as follows.

$$U_p={\left[\begin{array}{cccc}{u}_{k,i}^T& u_{k,i+1}^T& \cdots & u_{k,i+N_c-1}^T\end{array}\right]}^T$$

(19)

$$Y_p={\left[\begin{array}{cccc}{y}_{p,k,i+1}^T& y_{p,k,i+2}^T& \cdots & y_{p,k,i+N_p}^T\end{array}\right]}^T$$

(20)

$$F={\left[\begin{array}{cccc}{H}_m{\Phi }_m& H_m{\Phi }_m^2& \cdots & H_m{\Phi }_m^{N_p}\end{array}\right]}^T$$

(21)

$$G=\left[\begin{array}{cccc}{H}_m{\Gamma }_m& 0& \cdots & 0\\ H_m{\Phi }_m{\Gamma }_m& H_m{\Gamma }_m& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ H_m{\Phi }_m^{N_p-1}{\Gamma }_m& H_m{\Phi }_m^{N_p-2}{\Gamma }_m& \cdots & H_m{\Phi }_m^{N_p-N_c}{\Gamma }_m\end{array}\right]$$

(22)

The optimizer calculates the optimal $U_p$ to minimize the cost function $J_p$ as shown below.

$$J_p={\left(R_s-Y_p\right)}^{T}Q\left(R_s-Y_p\right)+U_p^T\overline{R}{U}_p$$

(23)

where $R_s$ is the reference input in the prediction horizon; $Q$ and $\overline{R}$ are weighting matrices. They are defined as follows.

$$R_s={\left[\begin{array}{cccc}{r}_{r,k,i+1}^T& r_{r,k,i+2}^T& \dots & r_{r,k,i+N_p}^T\end{array}\right]}^T$$

(24)

$$r_{r,k,i+1}={\left[\begin{array}{cc}{y}_{r,k,i+1}& {\psi }_{r,k,i+1}\end{array}\right]}^T$$

(25)

$$Q={\left[\begin{array}{ccc}\begin{array}{cc}{Q}_1& 0\\ 0& Q_2\end{array}& \cdots & \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \cdots & \begin{array}{cc}{Q}_1& 0\\ 0& Q_2\end{array}\end{array}\right]}_{2N_p\times 2N_P}$$

(26)

$$\overline{R}={\left[\begin{array}{ccc}\begin{array}{cc}{R}_1& 0\\ 0& R_2\end{array}& \cdots & \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \cdots & \begin{array}{cc}{R}_1& 0\\ 0& R_2\end{array}\end{array}\right]}_{2N_c\times 2N_c}$$

(27)

where $y_r$ is the desired lateral displacement; ${\psi }_r$ is the desired heading angle; $Q_1$ is the weighting of lateral displacement error; $Q_2$ is the weighting of heading angle error; $R_1$ is the weighting of the steering angle; $R_2$ is the weighting of the DYM. These weightings are designed using Bryson’s rule [43] as shown below.

$$Q_1=\frac{1}{y_{e,max}^2}; Q_2=\frac{1}{{\psi }_{e,max}^2}$$

(28)

$$R_1=\frac{1}{{\delta }_{f,max}^2}; R_2=\frac{1}{M_{z,max}^2}$$

(29)

where $y_{e,max}$ is the maximum allowable lateral displacement error; ${\psi }_{e,max}$ is the maximum allowable heading angle error; ${\delta }_{f,max}$ is the maximum allowable steering angle; $M_{z,max}$ is the maximum allowable DYM. The optimal $U_p$ can be obtained as follows.

$$U_p={\left(G^{T}QG+R\right)}^{-1}{G}^{T}Q\left(R_s-F{x}_{k,i}\right)$$

(30)

The current optimal control input $u_{k,i}$ is equal to the vector that consists of the first and second components of $U_p$ as follows.

$$u_{k,i}={\left[\begin{array}{cc}{U}_p\left(1\right)& U_p\left(2\right)\end{array}\right]}^T$$

(31)

3.2. Evasive Path Generation

The desired evasive path is shown in Figure 2. A Trapezoidal Acceleration Profile (TAP) is used to design the desired global lateral displacement of the evasive path [7]. The lateral acceleration can be obtained by specifying the maximum allowable $a_{y,max}$, the maximum allowable jerk $J_{y,max}$, and the evasive lateral displacement $y_{eva}$. $t_1$ and $t_2$ of the TAP can be expressed as follows [7].

$$t_1=\frac{a_{y,max}}{J_{y,max}}, t_2=\frac{-t_1^2+\sqrt{t_1^4+4t_1\frac{y_{eva}}{J_y}}}{2t_1}$$

(32)

where $a_{y,max}=\widehat{\mu }g$; $g$ is the gravity; $\widehat{\mu }$ is the estimated road friction coefficient that is assumed to be obtained from other approaches [44,45,46]. The desired global lateral position $Y_d$ of the evasive path can then be obtained as follows by integrating the global lateral acceleration ${\ddot{Y}}_d$ twice [7].

$$Y_d\left(t\right)=\left\{\begin{array}{cc}\frac{1}{6}{J}_{y,max}{t}^3& for 0\le t\le t_1\\ Y_{d,1}+v_{y,1}\left(t-t_1\right)+\frac{1}{2}{a}_{y,max}{\left(t-t_1\right)}^2& for t_1<t\le t_2\\ Y_{d,2}+v_{y,2}\left(t-t_2\right)+\frac{1}{2}{a}_{y,max}{\left(t-t_2\right)}^2-\frac{1}{6}{J}_{y,max}{\left(t-t_2\right)}^3& for t_2<t\le t_3\\ Y_{d,3}+v_{y,3}\left(t-t_3\right)-\frac{1}{2}{a}_{y,max}{\left(t-t_3\right)}^2& for t_3<t\le t_4\\ Y_{d,4}+v_{y,4}\left(t-t_4\right)-\frac{1}{6}{J}_{y,max}{\left(t-t_4\right)}^3& for t_4<t\le t_5\\ y_{eva}& for t>t_5\end{array}\right.$$

(33)

where $v_{y,i}=v_y\left(t_i\right),Y_{d,i}=Y_d\left(t_i\right), i\in \left[0,5\right]$. By assuming the vehicle longitudinal velocity $v_x$ is constant along the evasive path, the desired global longitudinal velocity ${\dot{X}}_d$ of the evasive path can then be obtained as follows.

$${\dot{X}}_d\left(t\right)=\sqrt{v_x^2-{\dot{Y}}_d\left(t\right)}$$

(34)

where $v_{x,0}$ is the initial longitudinal velocity of vehicle; ${\dot{Y}}_d$ is the global lateral velocity that can be obtained by integrating ${\ddot{Y}}_d$ in Equation (31). We can then obtain the desired global $X_d$ by integrating ${\dot{X}}_d$.

The station number of the evasive path $S_d$ that is the distance along the designed evasive path can be defined as follows.

$$S_{d,j+1}=S_{d,j}+\sqrt{{\left(X_{d,j}-X_{d,j-1}\right)}^2+{\left(Y_{d,j}-Y_{d,j-1}\right)}^2}$$

(35)

where $j$ denotes the $j$th sample point of the evasive path. The initial values of $X_d$, $Y_d$, ${\dot{Y}}_d$, and $S_d$ are set to be zero. The desired evasive path can then be expressed as functions of the station number as follows.

$$X_d=f_{SX}\left(S_d\right),Y_d=f_{SY}\left(S_d\right)$$

(36)

The station number in the prediction horizon can be defined as follows with a constant $v_x$.

$$S_{p,k+i+1}=S_{p,k+i}+v_{x}i{T}_s,i\in \left[0, 1,\cdots , N_p-1\right]$$

(37)

where the initial station number $S_{p,k}$ is the current station number $S_c$. The desired evasive path in the preview horizon can then be expressed as follows.

$$X_{p,k}=f_{SX}\left(S_{p,k}\right),Y_{p,k}=f_{SY}\left(S_{p,k}\right)$$

(38)

The desired evasive path in the body coordinates of the vehicle can be calculated using coordinate transformation as shown below.

$$\left[\begin{array}{c}{x}_{r,k}\\ y_{r,k}\end{array}\right]=\left[\begin{array}{cc}cos\left({\Psi }_c\right)& sin\left({\Psi }_c\right)\\ -sin\left({\Psi }_c\right)& cos\left({\Psi }_c\right)\end{array}\right]\left[\begin{array}{c}{X}_{p,k}-X_c\\ Y_{p,k}-Y_c\end{array}\right]$$

(39)

where ${\Psi }_c$ is the current global heading angle of vehicle; $X_c$ and $Y_c$ are the current global position of the vehicle, respectively; $x_r$ and $y_r$ are the local coordinates of the evasive path. $X_c$, $Y_c$, ${\Psi }_c$ and $S_c$ are assumed to be available from the localization system. The desired lateral displacement of the evasive path can be expressed as $y_r=f_r\left(x_r\right)$ in the body coordinates of the vehicle. The heading angle reference, which is the first derivative of the desired path, can then be approximated as follows.

$${\psi }_{r,k+i}=f_r^{\prime }\left(x_{r,k+i}\right)=\frac{f_r\left(x_{r,k+i+1}\right)-f_r\left(x_{r,k+i}\right)}{x_{r,k+i+1}-x_{r,k+i}}$$

(40)

3.3. Control Allocation

Weighted pseudo inverse with constraints [47] is used to obtain the distributed brake forces at four wheels. The DYM command $M_{z,r}$ can be expressed as follows.

$$M_{z,r}=B_{CA}{F}_x$$

(41)

where $F_x$ is the tire force vector that consists of four tire forces.

$$F_x={\left[\begin{array}{cccc}{F}_{x,fl}& F_{x,rl}& F_{x,fr}& F_{x,rr}\end{array}\right]}^T$$

(42)

where the subscripts fl, rl, fr, and rr denote quantities at front-left, rear-left, front-right, and rear-right tires, respectively.

The pseudo inverse solution is a two-norm solution to the CA problem that can be formulated as follows.

$$\underset{F_x}{min}{J}_{CA}=\underset{F_x}{min}\frac{1}{2}{\left(F_x+C_{CA}\right)}^T{W}_{CA}\left(F_x+C_{CA}\right)$$

(43)

subject to:

$$M_{z,r}=B_{CA}{F}_x$$

(44)

$$F_{x,min}\le F_x\le 0$$

(45)

where $C_{CA}$ is the offset vector used to represent off-nominal condition with one or more tire forces; $F_{x,min}$ is the vector used to represent the minimum allowable tire forces. The maximum allowable tire forces are set to be 0 such that only braking forces are used. The optimal distribution can then be obtained as follows.

$$F_x=-C_{CA}+B_{CA}^{\#}\left(M_{z,r}+B_{CA}{C}_{CA}\right)$$

(46)

$$B_{CA}^{\#}=W_{CA}^{-1}{B}_{CA}^T{\left(B_{CA}{W}_{CA}^{-1}{B}_{CA}^T\right)}^{-1}$$

(47)

where $B_{CA}^{\#}$ is the pseudo inverse of $B_{CA}$. The $C_{CA}$ is zero in the normal condition, so (44) can be simplified as follows.

$$F_x=B_{CA}^{\#}{M}_{z,r}$$

(48)

where the diagonal weighting matrix $W_{CA}$ is designed with elements equal to the estimated tire workload ratios as follows [42] to prevent saturating tire forces. The larger the ratio is, the closer to saturation the corresponding tire force is. Thus, tire forces that are needed for generating the desired DYM are distributed to tires with lower tire work load ratios.

$$W_{CA}=\left[\begin{array}{cccc}{\widehat{\rho }}_{fl}& 0& 0& 0\\ 0& {\widehat{\rho }}_{rl}& 0& 0\\ 0& 0& {\widehat{\rho }}_{fr}& 0\\ 0& 0& 0& {\widehat{\rho }}_{rr}\end{array}\right]$$

(49)

where $\widehat{\rho }$ is the estimated tire workload ratio of each tire that can be obtained as follows [42].

$$\widehat{\rho }=\sqrt{\frac{{\widehat{F}}_x^2+{\widehat{F}}_y^2}{{\widehat{F}}_z^2}}$$

(50)

where ${\widehat{F}}_x$, ${\widehat{F}}_y$ and ${\widehat{F}}_z$ are the estimated tire forces at longitudinal, lateral and normal directions, respectively. If the ith element of $F_x$ exceeds the boundary values, the corresponding ith element in $C_{CA}$ is set to be the opposite number of the boundary value and the corresponding ith element in $B_{CA}$ is set to be zero. The adjusted vectors $B_{CA,a}$ and $C_{CA,a}$ can be obtained using the Algorithm 1 as shown below.

Algorithm 1 Saturation Prevention

$B_{CA,a}=B_{CA}$; $C_{CA,a}=C_{CA};$

$\mathrm{if} F_x\left(i\right)>0$

$B_{CA,a}\left(i\right)=0$

$\mathrm{else}\mathrm{if} F_x\left(i\right)<F_{x,min}\left(i\right)$

$B_{CA,a}\left(i\right)=0$

$C_{CA,a}\left(i\right)=-F_{x,min}\left(i\right)$

$\mathrm{end}$

After obtaining the adjusted vectors, we can replace $B_{CA}$ and $C_{CA}$ with $B_{CA,a}$ and $C_{CA,a}$, respectively, and obtain the adjusted tire force vector using Equations (44) and (45).

The four-wheel brake pressure command $P_{b,r}$ can be expressed as follows.

$$P_{b,r}=F_{x}diag\left(\left[\begin{array}{cccc}\frac{r_w}{G_{b,f}}& \frac{r_w}{G_{b,r}}& \frac{r_w}{G_{b,f}}& \frac{r_w}{G_{b,r}}\end{array} \right]\right)$$

(51)

where $G_{b,f}$ and $G_{b,r}$ are the brake gains of front and rear wheels, respectively; $r_w$ is the wheel radius; diag is a function that creates a square diagonal matrix with the input elements on the main diagonal. The EHB module is used to generate four-wheel brake pressure $P_b$.

4. Simulation Results

The proposed algorithm was evaluated using CarSim in MATLAB/Simulink. Figure 3 shows the test scenario used in this paper. There was one moving vehicle and one stationary vehicle in front of the host vehicle. After the front moving vehicle changed lanes at the last moment [48], the stationary vehicle was detected as a suddenly appearing obstacle by the CarSim Sensor module of the host vehicle at 5 m ahead the last point to steer (LPS) [4], which was defined as the last location to avoid a collision by steering. The longitudinal vehicle velocity was set at 80 km/h which is the highest longitudinal velocity for testing ESA. Since the stationary vehicle suddenly appeared in front of the host vehicle, the last point to brake (LPB), which was defined as the last location to avoid the collision by braking, was already behind the host vehicle. A single lane-change path generated using TAP was used as the evasive path to avoid the collision. When the host vehicle arrived at the LPS, the AES was trigged automatically.

The maximum angular rate of the front wheel steering angle was limited to 42$°/\mathrm{s}$ due to the EPS according to the requirement of the fishhook test [49]. The front wheel steering angle was limited between $-35°$ and $35°$ due to the pinion-rack configuration. Simulation results of the proposed MIMO MPC were compared with those of the SISO MPC [35]. For the first test scenario, the nominal road friction coefficient was 0.9 which was used to obtain the nominal cornering stiffness of the prediction model in MPC. The second test scenario was used to test the robustness of the proposed algorithm with a medium road friction coefficient of 0.7 which is 22% less than the nominal value; i.e., the actual cornering stiffness should be smaller than the nominal values used in the prediction model.

4.1. Comparison of Prediction Models

An open-loop test was used to compare the responses of three bicycle models. The structures of these models are listed in

Table 2. Structures of three bicycle models.

Model	State	Input	Output
Four-states	$y, v_y,\psi , r$	${\delta }_f, M_z$	$y, \psi$
Five-states	$y, v_y,\psi , r, {\delta }_f$	${\delta }_{f,r}$	$y$
Six-states	$y, v_y,\psi , r, {\delta }_f, M_z$	${\delta }_{f,r}, M_{z,r}$	$y, \psi$

. The four-state bicycle model [34] has two inputs and two outputs that are the same as those of the proposed six-state bicycle model in (3). However, the actuator dynamics of EPS and EHB were not considered for the four-state bicycle. The five-state bicycle model that includes the EPS actuator dynamics has one steering angle control input and the lateral displacement output. The DYM input was not considered in the five-state bicycle model. Dynamic responses of these models are shown in Figure 4. The step steering angle input was applied at the beginning of simulation, and the DYM step input was applied at 1 s. CarSim denotes the dynamic responses of CarSim with two inputs of steering angle and DYM. Before 1 s, the main difference between the four-state model and other models was the transient response due the lack of actuator dynamics. The steady-state responses of three bicycle models were almost the same. The responses of the five-state and the six-state bicycle models were similar to those of CarSim. After the DYM was applied at 1 s, only the responses of the six-state bicycle model were close to those of CarSim. Since the six-state model with actuator dynamics can achieve both transient and steady-state responses closest to those of CarSim, it was used as the prediction model in the proposed algorithm.

4.2. Nominal Road Friction Coefficient of 0.9

The simulation results with accurately estimated road-friction coefficient of 0.9, which is used to obtain the maximum allowable lateral acceleration for designing the desired evasive path, are shown in Figure 5, Figure 6 and Figure 7. The AES is assumed to be triggered at 3 s. SISO MPC and MIMO MPC can track the desired evasive path and complete the lane change maneuver.

Path tracking responses are shown in Figure 5. SISO MPC and MIMO MPC have similar responses of global lateral displacement. However, their global heading angle responses are less similar to each other. As can be seen from the vehicle dynamic responses in Figure 6, the values of $y_e$ of MIMO MPC are more negative than those of SISO MPC between 3.1 and 3.7 s. Thus, the lane change response of MIMO MPC is faster than that of SISO MPC at the beginning of lane change due to the additional DYM input. Meanwhile, the heading angle errors of MIMO MPC are smaller than those of SISO MPC during the lane change maneuver.

Figure 7 shows control commands and actuator responses. At the beginning of AES, MIMO MPC and SISO MPC have the same steering angle responses due to the angular rate limitation and the actuator dynamics of EPS. However, MIMO MPC has an additional DYM input, which can accelerate the response of $r$ and reduce the maximum steering angle to be smaller than that of SISO MPC. Since the heading angle is the integration of yaw rate, faster response of $r$ can lead to smaller ${\psi }_e$. The comparison of the $\beta -r$ phase plane plots is shown in Figure 8. MIMO MPC has better convergences due to a smaller circling area around the origin. This means that MIMO MPC can reduce $\beta$ in order to enhance handling performance and directional stability. Although DYM is generated using braking forces, the vehicle longitudinal velocity of MIMO MPC is only reduced slightly compared to that of SISO MPC.

4.3. Nominal Road Friction Coefficient of 0.7

The simulation results with a medium road friction coefficient of 0.7, which is 22% less than the nominal value, are shown in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. Assuming the AES is not aware of the overestimation of the road friction coefficient, the nominal value of 0.9 is still used to design the evasive path and the nominal cornering stiffnesses are still used in the prediction model.

Path tracking responses are shown in Figure 9. The AES is assumed to be triggered at 3 s. SISO MPC cannot complete the lane change maneuver and loses the directional stability. Conversely, MIMO MPC can track the desired evasive path and complete the lane change maneuver successfully. Similar to the analysis of Figure 8 in Section 4.1, we found that MIMO MPC has a lane change response faster than that of SISO MPC at the beginning of lane change, as shown in Figure 10. Meanwhile, the peak heading angle error of MIMO MPC is smaller than that of SISO MPC at about 4 s due to minimizing $y_e$ and ${\psi }_e$ simutaneously via both steering and DYM. From the yaw rate response, we can observe that the vehicle with SISO MPC starts to spin continuously after 4 s.

As can be seen from Figure 11, SISO MPC requires steering angles much larger than those of MIMO MPC after 4 s. Although SISO MPC tries to correct the steering angle as fast as possible, the steering angle response is not fast enough due to the angular rate limitation and actuator dynamics. Figure 12 shows that the side-slip angle of SISO MPC increases rapidly with large yaw rate after passing $\beta =0$. It also confirms the directional instability of SISO MPC. On the other hand, the $\beta -r$ phase plane plot of MIMO MPC converges to the origin after completing the lane change maneuver.

Figure 13 and Figure 14 show the responses of tire slip angle and lateral tire forces at four wheels. The dashed lines indicate the thresholds of the tire slip angles to saturate lateral tire forces. The front lateral tire forces of SISO MPC are found to be saturated at 4.1 s. Even though the steering angle of SISO MPC in Figure 11 is still increasing after 4 s, the corresponding lateral tire forces are not increased due to saturation as shown in Figure 14. Since the lateral tire force is no longer increased with the increment of the tire slip angle, the prediction model used in MPC is not accurate anymore. Thus, SISO MPC cannot effectively control the vehicle to track the desired evasive path and prevent directional instability. Although the rear tire slip angles of MIMO MPC are saturated around 4.5 s, the front tire slip angles are not saturated. Thus, the front tires can still provide more lateral tire forces via increasing the steering angle input if necessary. Meanwhile, MIMO MPC has additional DYM which can improve the responses of $r$ and prevent saturating the reference command of the steering angle. Figure 15 shows the responses of tire workload ratios. The CA distributes the longitudinal tire forces as shown in Figure 16 to the wheels with lower tire workload ratios in order to generate the required DYM without saturating the tire forces; thus, demonstrating better, more robust control performance and handling enhancement against model uncertainty due to reduced road friction coefficient.

4.4. Sensitivity Analysis

The estimated road friction coefficient be used not only for evasive path generation, but also for obtaining the equivalent front and rear cornering stiffnesses of the bicycle model used in MPC via a look-up table. However, the estimation might not be accurate due to the lack of enough excitation. Different road friction coefficients deviated from the estimated nominal value of 0.9 are used for sensitivity analysis to evaluate the robustness of the proposed algorithm. The minimum distance $D_L$ [50] between the host vehicle and the stationary vehicle to be avoided as shown in Figure 17 can be defined as follows.

$$D_L=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}-\frac{W_h}{2}-\frac{W_s}{2}$$

(52)

where $P_h\left(x_1,y_1\right)$ is the front center point of host vehicle; $P_s\left(x_2,y_2\right)$ is the front center point of stationary vehicle; $W_h$ is the width of host vehicle; $W_s$ is the width of stationary vehicle. $D_L$ at different road friction coefficients are shown in

Table 3. The minimal distance between host vehicle and stationary vehicle at 80 km/h.

$\mathbf{Road} \mathbf{Friction} \mathbf{Coefficient}, \mathit{\mu }$
	0.9	$0.85$	$0.8$	$0.75$	$0.7$
SISO	0.51 m	0.53 m	0.52 m	0.47 m	0.36 m
MIMO	0.48 m	0.49 m	0.51 m	0.51 m	0.45 m

. The collision can be avoided for all simulated scenarios.

The vehicle sideslip angle can be used to evaluate the yaw stability of the vehicle. The root-mean-square (rms) and maximum (max) values of sideslip angle responses at different road friction coefficients are shown in

Table 4. Sideslip angle at different road friction coefficients at 80 km/h.

$\mathbf{Road} \mathbf{Friction} \mathbf{Coefficient}, \mathit{\mu }$
		0.9	$0.85$	$0.8$	$0.75$	$0.7$
SISO	rms	1.1°	1.5°	3.2°	62.3°	77.2°
	max	4.4°	6°	14.2°	180°	180°
MIMO	rms	1°	1.2°	1.6°	2.2°	3.1°
	max	4.3°	4.7°	5.9°	9°	13°

. Those values are obtained using the responses from the beginning of control at 3–10 s. The more the road friction coefficient deviates from the nominal value of 0.9, the larger the rms and max values of sideslip angles are. MIMO can stabilize the vehicle in the new target lane for all scenarios. However, SISO exhibits large lateral responses as shown in Figure 10 and cannot stabilize the vehicle in the new target lane for $\mu \le 0.75$. The rms and max values of sideslip angle suddenly increase for $\mu \le 0.75$ which are indications of yaw instabilities. Thus, MIMO demonstrates better robustness of yaw stability and handling performance for reduced road friction coefficients.

In order to evaluate the robustness of the proposed algorithm at different velocities, the longitudinal velocity of host vehicle is increased to 120 km/h in Figure 18. The suddenly appearing obstacle is assumed to be detected at 7.5 m ahead of the LPS.$D_L$ at different road friction coefficients is shown in

Table 5. The minimal distance between host vehicle and stationary vehicle at 120 km/h.

$\mathbf{Road} \mathbf{Friction} \mathbf{Coefficient}, \mathit{\mu }$
	0.9	0.85	$0.8$	$0.75$	$0.7$	$0.65$	$0.6$
SISO	0.44 m	0.45 m	0.47 m	0.47 m	0.45 m	0.39 m	0.27 m
MIMO	0.40 m	0.42 m	0.43 m	0.43 m	0.42 m	0.36 m	0.24 m

. Similar to the results in Table 3, the collision can be avoided for all simulated scenarios. The rms and max values of sideslip angle responses at different road friction coefficients are shown in

Table 6. Sideslip angle at different road friction coefficients at 120 km/h.

$\mathbf{Road} \mathbf{Friction} \mathbf{Coefficient}, \mathit{\mu }$
		0.9	0.85	$0.8$	$0.75$	$0.7$	$0.65$	$0.6$
SISO	rms	1.7°	2.2°	3.1°	4.3°	6.2°	66.7°	73.2°
	max	5.1°	6.9°	9.9°	13.8°	19.1°	180°	180°
MIMO	rms	1.5°	1.7°	2.2°	3.1°	4.2°	5.6°	6.7°
	max	4.7°	5.4°	6.8°	9.8°	13.4°	17°	19.8°

. Similar to the results in Table 4, the more the road friction coefficient deviates from the nominal value of 0.9, the larger the rms and max values of sideslip angles are. MIMO can stabilize the vehicle in the new target lane for all scenarios. However, the rms and max values of sideslip angle suddenly increase for $\mu \le 0.65$ which are indications of yaw instabilities. Thus, MIMO demonstrates better robustness of yaw stability and handling performance for reduced road friction coefficients even at a much higher longitudinal vehicle velocity of 120 km/h.

5. Conclusions

MIMO MPC was employed to design the path tracking controller for autonomous emergency steering using steering and differential braking. The prediction model was based on a six-state road following bicycle model including the actuator dynamics of EPS and EHB. For nominal road friction, the path tracking responses of SISO MPC (using steering only) and MIMO MPC (using both steering and differential braking) are very similar, but the directivity of MIMO MPC can be improved by DYM. The usage of steering angle can be reduced, and the handling performance of MIMO MPC is better than SISO MPC. For medium road friction, SISO MPC is unable to track the path and loses directional stability. However, MIMO MPC can still reduce the maximum required steering angle and accelerate the response of $r$ via DYM. In order to prevent tire force saturation, the CA can distribute the longitudinal tire forces to wheels with lower tire work load ratios for generating the desired DYM. Thus, MIMO MPC can achieve robust path tracking and handling enhancement against model uncertainty due to road friction reduced by 22% and 33% at 80 and 120 km/h, respectively. In this paper, the handling performance was mainly discussed for avoiding the collision with a stationary vehicle via lateral dynamics control. For a slow moving vehicle in front of the host vehicle, collision avoidance via AES should be further investigated to demonstrate the effectiveness the proposed algorithm. Since the lateral tire forces at front steering wheels are affected by load transfer that can be created via acceleration or braking, coordinated longitudinal and lateral dynamics control might further enhance the handling performance for collision avoidance.