An Experimental Study of a Nailed Soil Slope: Effects of Surcharge Loading and Nails Characteristics

Abstract

The earth nailing system is a ground improvement technique used to stabilize earth slopes. The behavior of the earth nailing system is dependent on soil and nailing characteristics, such as the spacing between nails, the orientation, length, and method of installation of nails, soil properties, slope height and angle, and surcharge loading, among others. In the present study, a three-dimensional physical model was built to simulate a soil nailed slope with a model scale of 1:10 with various soil nail characteristics. The simulated models consist of Perspex strips as facing and steel bars as a reinforcing system to stabilize the soil slope. Sand beds in the model were formed, using a sand raining system. The performance of nailed soil slope models under three important nails characteristics, i.e., length, spacing and orientation, with varying surcharge loading were studied. It was observed that there is a reduction in the lateral movement of slope and footing settlements with an increase in length. It was found that the slope face horizontal pressure is non-linear with different nail characteristics. The increase in length and inclination of the soil nails decreased the vertical, horizontal stress and footing settlement, while the increase in spacing of the nails increased the vertical and horizontal stress behind the soil mass.

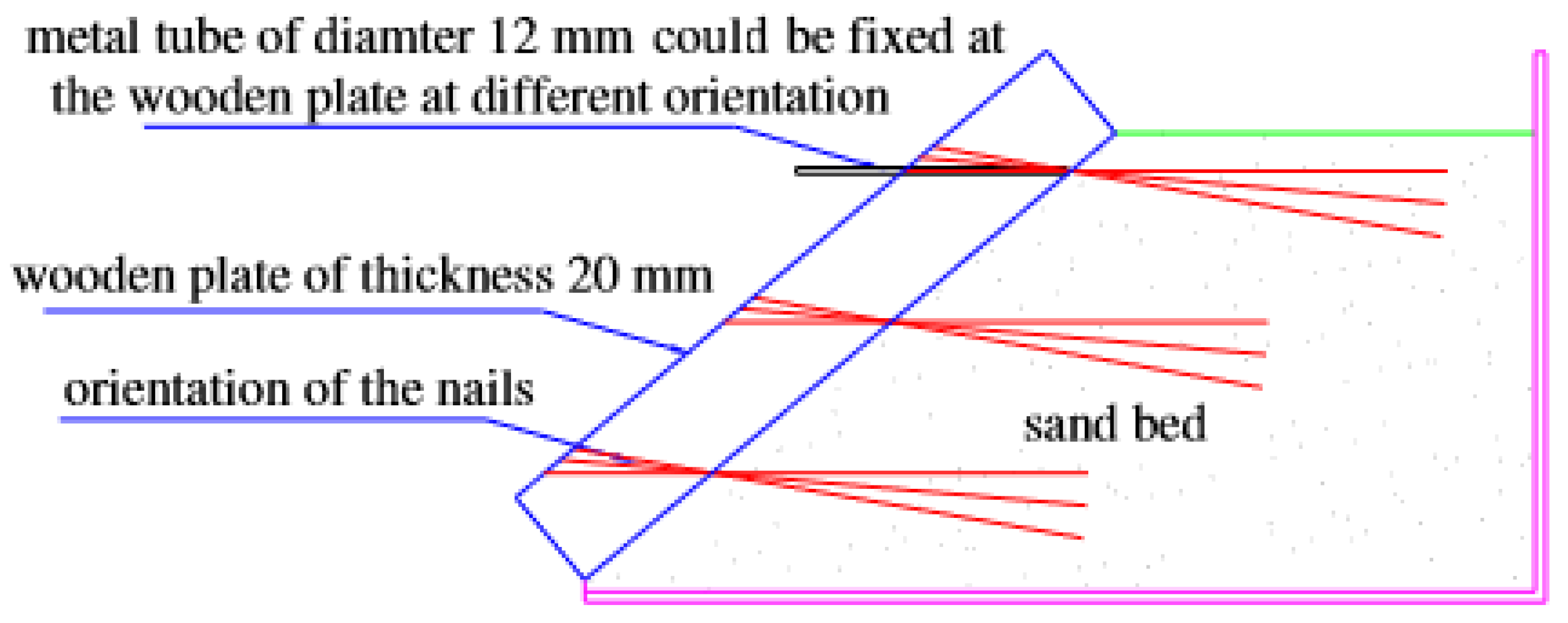
1. Introduction

The soil nailing system is a technique for stabilizing earth slopes and it is constructed in successive phases, as first illustrated by Stocker et al. [1], from top to bottom as excavation proceeds. A soil-nailed slope consists of three main elements, namely, the soil, steel reinforcements bars (nails), and the facing. The elements’ composite interactions determine the deformations and stability behavior of a soil nailing system. The shear and tensile strengths of the reinforcing element will increase the overall shear strength and self-supportability of the in situ soil. The function of the facing in a soil nailing system is to ensure the local stability of the ground between the nails and to limit its decompression; the facing should be flexible enough to withstand ground displacement during excavation [2]. Sharma et al. [3] have thoroughly reviewed the advancements in the soil nailing technique, different installation processes, failure modes of soil-nailed structures, design philosophies, effects of various construction parameters on the design method, and the analytical, numerical, field and lab testing procedures in the nails’ pull-out capacity. Lazarte et al. [4] submitted state-of-the-art practice documents (NCHRP Project 24–21) related to the analysis, LRF design, and construction of soil-nailed walls for highway applications. The accuracy of the pull-out capacity of the nails will result in the economical and safe design of the soil-nailed structure [5]. Yelti [6] analyzed and designed soil nailed walls in expansive soils and the recommended guidelines to improve the design procedures for soil-nailed walls, considering the lateral pressures generated by soil expansion. A simplified method to determine the movement at the crest of a soil nailed wall is developed by Bridges et al. [7] who concluded that soil effective cohesion has the greatest effect on crest displacement of the wall. Centrifuge and numerical tests were conducted by Viswanadham and Rotte [8] to study the significance of slope facing on the stability and deformation behavior of soil-nailed slopes subjected to seepage. They found that soil-nailed slopes without facing experience face failure due to bearing failure at the slope surface and the nail head surface as well as due to the build-up of excess pore water pressure at the toe region. The influence of the bending stiffness of the facing material—installed on a nailed slope surface of dense sand—on deformation and bearing capacity characteristics were studied by Kotake and Sato [9] by conducting tests on rigid and flexible models of footings. Several nailed soil-retaining structures were instrumented to establish a database for the evaluation of structure performance and development of reliable design methods. The material point method-based numerical model was developed by Ceccato et al. [10] to study the application of plate anchors for landslide stabilization. The numerical model was validated with the results of some small-scale laboratory tests. Sahoo et al. [11] caried out the shaking table tests to study the seismic behavior of nailed soil slopes. They found that the model nailed slope with a nail inclination of 15° provided a better reinforcement action than the horizontal and 30° inclined nails when stabilizing soil slopes. The failure modes of the slope stabilized by a frame beam with prestressed anchors were studied by Zhang et al. [12] on a large-scale shaking table. They observed that the seismic damage of the slope stabilized by the frame beam with prestressed anchors mainly occurs at the top of the sliding mass and on the free surface of the slope. A simplified limit equilibrium method is presented by Deng et al. [13] to analyze the stability of slopes reinforced with anchor cables, considering the nonlinear Mohr–Coulomb strength criterion for shear failure of the slip surface. The seismic design of the soil nailing was carried out by Villalobos et al. [14] with varying geometrical and mechanical parameters for the nail and soil of a slope. They observed that the global factor of safety increased with soil cohesion and friction as well as the nail length, diameter and inclination; nail inclinations higher than 15° reduced the factor of safety.

Yuan et al. [15] proposed a new approach for the stability analysis of soil-nailed walls and concluded that the shear strength of soil has a significant effect on the factor of safety and the reliability index of soil-nailed walls. Durgunoğlu et al. [16] presented the performance of very deep, temporary soil-nailed walls constructed in a very seismically active region. The displacement data for various projects were evaluated in terms of various design parameters of the soil-nailed walls and the excavation depth. Babu and Singh [17] studied the performance of a soil-nailed wall supporting a vertical slope under both static and seismic conditions by observing and computing the maximum lateral displacements, development of nail forces and failure modes of soil-nailed walls. Numerical analyses of the stabilizing mechanisms of loose fill slopes were carried out by Cheuk et al. [18] to study the influence of hybrid nail orientations on the behavior of the ground nailing system and concluded that the hybrid nail arrangement would limit slope movement and enhance the robustness of the system. Taule [19] applied Bishop’s Simplified Method to evaluate and rank the sensitivity of the soil properties, namely cohesion, unit weight and internal friction angle, with respect to the global factor of safety, using the Monte Carlo simulation in a soil nailing design. He showed that the internal friction angle is the most sensitive parameter, while cohesion and unit weight are less sensitive with respect to the global safety factor.

Jayawickrama et al. [20] developed non-destructive test methods for evaluation and checking the integrity of installed soil nails. Villalobos et al. [21] present the re-assessment stability analysis of soil nailing design and construction in heavily weathered granite (residual soil), using a limit equilibrium sliding block method (bi-linear failure surface). They found that even after a maximum acceleration of 0.63 g of a stronger earthquake, the nailed wall did not show any damage, probably due to the use of undrained shear strength parameters. Alhabshi [22] studied the hybrid, mechanically stabilized earth and soil nail wall system and proposed the optimum length of nails required to stabilize the structure and reduce the wall deformation. A slope stability analysis of a combined system of soil nails and stabilization piles on loess soil is presented by Wu et al. [23]. Benayoun et al. [24] proposed the optimization of soil nailing parameters for soil-nailed structure design, using the genetic algorithm method. A composite silt–soil nailed symmetrical foundation pit was numerically investigated by Han et al. [25] for stability and deformation characteristics. They found the critical values of inclination and spacing of the soil nails, and the diameter and embedded depth of the mixing pile for stability of the foundation pit.

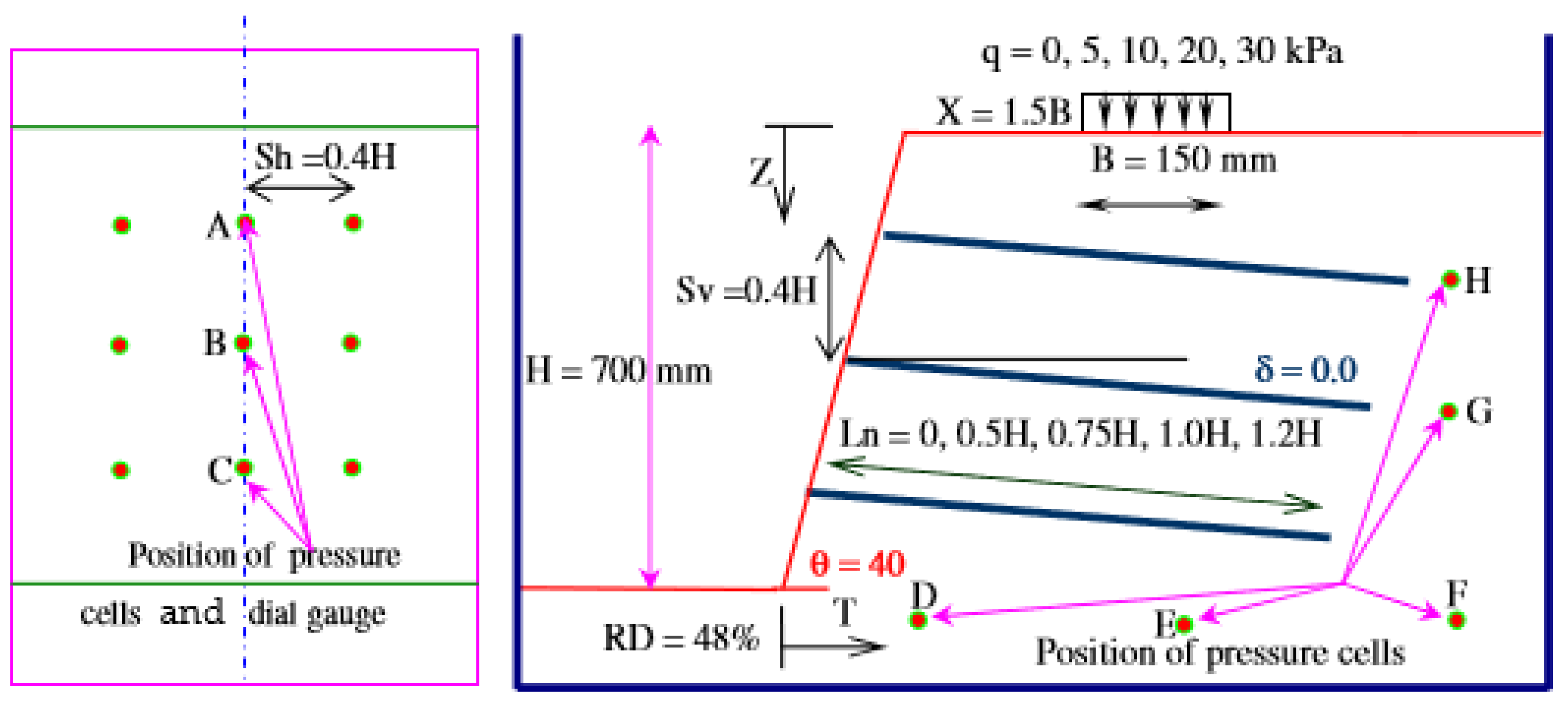
Despite the numerous research studies on soil nailing system behavior, laboratory modeling studies of various soil nailing system parameters are not sufficient and further parametric study under varying surcharge loading is clearly needed. The present paper studies the performance of soil-nailed slope physical models with varying nail parameters and surcharge loading. Three important nail parameters, namely, the length of the nail, the nails spacing and the angle, were selected for the study; the effect of the length, spacing and orientation of nails on the force mobilized in the nail, lateral displacement of the slope, settlement of the footing and the earth pressure at the slope face, under and behind the soil mass at various surcharging loading were observed. Four nail lengths, 0.5 H, 0.75 H, 1 H and 1.2 H in multiples of slope height (H), three nail orientations, i.e., 00, 50, and 100, and two horizontal and vertical spacings, i.e., 0.2 H and 0.4 H, were considered in the study. The surcharge pressure varied from 5.0, 10.0, 20.0, to 30.0 kPa. The results of the models without the nails were also obtained. The results for the lateral displacement and footing settlement are presented in terms of percentage of slope height.

2. Experimental Methodology

The present research study was carried out by designing and developing a three-dimensional experimental model of a dry sand slope with a steel nailing system. The experimental model—its dimensions, state of stress and strain, enclosing walls—were designed so that its performance would simulate the prototype behavior.

2.1. Testing Tank Dimensions

The dimensions of the testing tank and its material were chosen to fulfil the following criteria.

• The scale factor of 10 for simulation and dimensional analysis and to handle the material easily.
• The plane strain condition and minimum friction effect between the backfill soil and the sides of the testing tank.
• The pressure isobars of the strip footing extend laterally to almost two times the footing width, from the center line of the footing, and extend deeply to five times the footing width.
• The extent of the potential failure surface of slope stability analysis, using the slices method with no influence of tank boundaries on the tested elements: sand, nails, facing wall and the footing.
• The coefficient of the material friction is controlled by using the Perspex plates.
• A large ratio of width to height of the tank to minimize the effect of side wall shear stresses and consequently, reduce the active earth pressure.

Considering the above criteria for the material and dimensions of the tank, an open frontal Perspex box measuring 1760 × 850 × 1000 mm was chosen as the experimental model. The loading system used in this research work is specially designed to prevent any disturbance to the experimental model and is shown in Figure 1. The loading system consisted of the loading frame, loading frame base and hydraulic loading system. The box contained the nailed slope of 2250 kg of dry sand and steel bar nails. The sand used in the slope model experiments was air-dried, clean, siliceous yellow sand. The physical and mechanical properties of the sand used are given in

Table 1. Soil model properties.

Property	Value
% of clay	0.00
% of silt	1.33
% of fine sand	39.17
% of medium sand	58.63
% of coarse sand	0.87
% of fine gravel	0.00
Effective diameter (D10) mm	0.126
Coefficient of uniformity (Cu)	1.99
Coefficient of gradation (Cu)	1.00
Specific gravity (Gs)	2.62
Minimum unit weight (γmin) (kN/m3)	15.30
Maximum unit weight (γmax) (kN/m3)	17.80
Minimum void ratio (emin)	0.472
Maximum void ratio (emax)	0.712
Relative Density (Dr) (%)	48
Angel of internal friction (ϕ°)	34
Unit weight (γb) (kN/m3)	16.41
Void ratio (e)	0.597

. The sand bed in the model was formed, using an automatic sand raining system to control the soil density.

The thickness of the Perspex plate as a wall facing in the model was 5 mm to simulate the shotcrete facing with a thickness of 140 mm. A steel rigid plate of dimensions 840 × 150 × 22 mm thick was used as a footing to give distributed load on the soil. The properties of the facing and footing are given in

Table 2. Facing and footing plate properties.

Plate Element	Material	Width (mm)	Thickness (mm)	Young’s Modulus	Bending Stiffness (kN.mm2)	Axial Stiffness (kN)
Footing	Steel	150	22.0	21.2 × 107	188,186.6	4665.78
Facing	Perspex plate	140	5.0	4200	0.04375	0.021

. The diameter of the model nails was 5 mm to simulate the actual nail of diameter of 50 mm. The properties of the adopted nails were as follows.

Young’s modulus (E) = 21.2 × 107 kPa; flexural rigidity (EI) = 6.51 × 10⁻³ kPa/m.

Normal stiffness (EA) = 4165.9 kN/m; maximum tensile strength = 8.8 × 10⁵ kPa.

Strains at ultimate stress = 7625; maximum tensile force = 17.36 kN.

2.2. Testing Procedure

The testing of the experimental model was carried out in the following steps to match the true construction sequence as closely as possible to that in the field. This is due to the excavation of the soil, the construction of the slope soil nailing system and the subsequent placement of the surcharge load.

• The tank is cleaned, which has movable rear doors fixed with an opening to pass the tube containing the nails. The rest of the doors, in the rear and front sides, are in a closed position.
• The sand spreader forms the first layer of the sand and it is leveled, or compacted and leveled, as desired, to get the required predetermined density as was previously explained. This layer is a base sand layer, and its thickness was 150 mm.
• The lower middle nails with tubes are fixed in their positions.
• The hopper of the sand spreader forms the second layer and is leveled, or compacted and leveled, again, to reach the required density.
• In each layer, the horizontal and vertical pressure cells are installed in its predetermined positions.
• The above three steps are repeated until the tank is filled up.
• When the tank is filled with sand, the model is ready to begin the test.

To simulate the actual behavior of the prototype model, the test was divided in two stages. The first stage was the excavation stage to make sand slope and the second was the loading stage. This was done as follows and is depicted in Figure 2.

• The first layer of the sand, 140 mm thick, is excavated.
• The first paneled face is placed, which includes pressure cells flush with the middle of the panel, and this panel is held with two polyethylene strips (sticky tape) at the sides of the box to prevent sand spilling from the gap between the edges of the slope face unit and the box sides.
• The first row of the strain gauge fitted nails is installed in its position, tight to the nail face with nuts by pushing the nail into the sand.
• Dial gauges are installed to record the displacements of the facing due to excavation the second layer.
• In the case of inclined nails, the nails are hammered at the required inclined angle by means of a wooden plate with 20 mm thickness a 12 mm metal tube aligned at the predetermined holes as shown in Figure 3.
• Another four layers of the sand, 140 mm thick, are excavated and the facing panels are installed as before. At the third and fifth layers, a row of nails and pressure cells are installed.
• In each stage, displacement of the face, tensile force in the nails, and pressure (horizontal and vertical) are recorded.
• As the excavation is completed to the final depth of 700 mm, the rigid footing is placed at the required location from the nailed slope crest at the top surface and leveled by a water bulb level and then loaded to the required pressure.
• LVDTs are installed to measure the settlement of the footing. The electrical strain gauge reading is recorded simultaneously with the LVDTs and pressure cells in each loading case. Horizontal stresses on the wall face, pressure distribution under the reinforced mass, and the horizontal pressure behind the reinforced mass are measured by means of 5 soil pressure transducers, namely, 1, 2, 3, 4, 5, and 6 miniature strain gauge cells and local pressure cell transducers, namely, 2 L, 3 L, 4 L, 5 L, 7 L, 8 L which were designed, manufactured, and calibrated by the authors.

3. Results and Discussion

In the present study, the experimental models with a soil slope of 700 were prepared with four nails lengths, 0.5 H, 0.75 H, H and 1.2 H, in multiples of slope height (H), three nail orientations, i.e., 0°, 5°, 10°, and two horizontal and vertical spacings, i.e., 0.2 H and 0.4 H. The horizontal nails were used with equal horizontal and vertical spacing, i.e., 0.4 H, for the parametric study besides the inclined nail slope behavior. The results of the models without the nails were also obtained. The displacement of the slope, force in the nail, settlement of the footing and the earth pressure in the backfill soil due to the nailing parameters (nail length, inclination and spacing) were measured and the obtained results are discussed below. The lateral displacement of the nailed slope facing were recorded with 3 dial gauges at three measurements points, A, B and C, at distances of Z = 70, 350, and 630 mm from the top surface. These distances are expressed as 0.1 H, 0.5 H, and 0.9 H. Pressure cells were mounted flush with the back of the slope face in special arrangement to measure the horizontal pressure as shown in Figure 4 at points A, B, and C. The readings were measured after each increment of footing pressure from 5.0, 10.0, 20.0, to 30.0 kPa.

3.1. Length of Nails

3.1.1. Lateral Movement of the Soil Nailing Slope

The lateral movement of the slope face with and without the nailing system during the loading stages is shown in Figure 5. The figure depicts that, in general, the lateral movement of the slope in the middle third is higher than the top and bottom third and it has the lowest value at the toe of the slope. The maximum lateral displacement of the slope is in the top upper portion when the length is more than the slope height or at least equal to the slope height, but it shifts to the middle of the slope when the nail length is reduced to the slope height. The maximum displacement with different nail lengths is observed at the middle third of the slope, except with the nail length of 1.20 H wherein the maximum horizontal movement is at the upper third of the slope.

Figure 6 shows the relation between the nail length and horizontal movement at different nail lengths at the center of the slope (at point B). In general, the presence of nails decreases the lateral movement. The installation of nails mobilizes friction stresses around the sand and the surface of the nail. These friction stresses prevent lateral movement. By increasing the length of the nail, the total value of the shear stresses between the sand and nail increases. The lateral movement decreases rapidly when the nail length increases from 0.3 H to 0.75 H; however, further increases in the nail length, for example, up to 1.2 H, will not help in decreasing the lateral movement of the slope. This may be attributed to the fact that an increase in the nail length is effective up to a certain limit, i.e., when the nail length lies in a stable zone (inside the surface of failure).

3.1.2. Footing Settlement

The foundation settlements were measured at three points on the footing and then the average value was presented. The footing settlements were measured by means of three LVDTs. The footing settlements were measured at each surcharge load increment. Figure 7 presents the footing settlement in terms of the fraction of the slope height (S/H), i.e., vertical settlement/slope height, for different nail lengths at different footing pressures. It is clear from the figure that the footing settlement decreases from 12% to 51% with the increase in the nail length from half of the slope height to a nail length of more than the slope height, with respect to the footing settlement on the slope without nailing. The decrease in footing settlement is not large under a lower footing pressure range, but a large decrease in the footing settlement is observed with a higher footing pressure. This may be due to the fact that the lateral displacement of the facing slope decreases with the increase in nail length, and this will also result in a lower footing settlement. It can be inferred that the soil nailing system can sustain more surcharge load without failure.

3.1.3. Force in the Nail

The axial strains in the nails were measured by means of electrical resistance strain gauges. Each nail was instrumented with strain gauges on its upper and lower faces along its whole length. The distribution of the nail tensile force at different levels of the slope with the nail lengths is shown in Figure 8. From these figures, it is seen that in all cases, the distribution is non-uniform and the forces are tensile. The minimum tensile force occurs at the end of the nails, whereas the maximum tensile force is at the middle third of the nail. The tensile force increases with the increase in the surcharge loading and increasing length. It is also clear that the lower nails have lesser tensile force, as compared with the upper nails, and the middle nails have the maximum tensile force at all loading stages. This may be because the maximum horizontal displacement is at mid height of the slopes, which result in maximum mobilization of the nail tensile force at this level.

Figure 9 presents the presence of the maximum tensile force in nails of various lengths at different levels. Figure 9 shows that there is a linear increase in the maximum tensile forces with an increase in the nail length for the middle nails. However, for the upper and lower nails, maximum tensile forces first decrease with the increase in nail length, i.e., up to a nail length of three fourths of the slope height, and then the nails’ maximum tensile forces increase by further increasing the nail length. This may be due to disturbance of the soil under the footing and around the nail during the loading stages in the upper and lower part, but in the middle portion of slope, the soil moves only under steady expansion.

3.1.4. Horizontal Stresses on the Slope Face

Figure 10 presents the distribution of the horizontal stresses on the slope face with different nail lengths. The figure shows that the minimum horizontal stresses at the slope face occur at the bottom and upper levels, whereas the maximum horizontal stresses are at the mid height of the slope; the footing pressure increases the horizontal stresses at the slope face.

Figure 11 represents the influence of the nail length on the horizontal stresses at the slope face at the middle of the slope without surcharge loading and at a footing pressure of 30.0 kPa. It is clear from the figure that the percentage increases in horizontal stresses at the slope face range from 19.2% to 30.3% with the inclusion of nails and with the increase in nail length. This may be due to small, lateral displacements of the slope face with longer nails, producing larger horizontal stresses at the slope face.

3.1.5. Vertical Stress under Nailed Soil Mass

Figure 12 presents the distribution of the vertical stresses under the nailed soil mass with different nail lengths under different surcharge loading at three selected points, D, E, and F (point D is near the toe), at a level of 150 mm from the bottom of the tank at various distance ratios (T/H), i.e., distance from slope toe/slope height. From these figures, it is seen that the magnitude of the vertical stresses under the nailed soil mass is at a greater distance from the slope face; increase in the surcharge load leads to an increase in the vertical stresses under the nailed soil mass, especially at a far point from the slope face because it lies almost directly under the footing width. This may be attributed to the presence of nails in the soil mass, making the slope behave as a coherent mass. The figures also show that the observed distribution of vertical stresses under the nailed soil mass with different nail lengths is similar, and the effect is small on vertical stresses under the nailed soil mass with different nail lengths.

3.1.6. Horizontal and Vertical Stress behind the Nailed Soil Mass

Figure 13 and Figure 14 present the distribution of the horizontal and vertical stresses behind the soil mass with different nail lengths and with different footing loadings. From the figures, it is seen that the maximum horizontal and vertical stresses behind the soil mass occur at the lower measured point, whereas the minimum is at the upper measured point. There is no significant effect of the nail length on the horizontal and vertical stresses behind the nailed soil mass. Due to the application of the footing pressure, the soil starts to move, tensile stresses in the soil are transferred to the nails, and the nails hold the soil mass in position. The soil mass behind the nails behaves as a gravitational wall, and horizontal pressure develops in the soil mass, increasing at the lower part almost similarly to the hydrostatic pressure.

3.2. Inclinations of Nails

3.2.1. Lateral Movement of the Soil Nailing Slope

Figure 15 represents the effects of the nail inclinations on the horizontal movement of the slope face with and without footing pressure. The lateral displacements ratio (D/H) at the mid height of the slope is taken for different nail inclinations. It is evident from the figures that the increase in the inclination of the nails results in a decrease in the horizontal movement of the slope face. The percentage decrease in lateral movement with the increase in surcharge loading and nail inclination ranges from 7.1% to 25.0%.

3.2.2. Footing Settlement

The footing settlements at different nail inclinations are presented in Figure 16 at different footing pressures. From the figure, it is observed that the footing settlement decreases as the nail inclination increases, and the percentage increases with increases in the footing pressure. The percentage decrease, with the nail inclination of 00 to 100, in the footing settlement in terms of the slope height at lower footing pressures is around 20%, while at higher footing pressures, it is around 40%. The reason may be due to the fact that the inclined tensile force may be resolved in two components, resisting the horizontal settlement and vertical settlement, but horizontal nails resist horizontal settlement only.

3.2.3. Nail Maximum Tensile Force

Figure 17 shows the influence of the nail inclination on the maximum tensile force in the nails at different levels of soil slope. It is seen from the figure that with the increase in the nail’s inclination, the maximum tensile force in the nails is increased. In other words, reduction in the nail inclination results in a decrease in the maximum tensile force. A decrease in the nail maximum tensile force increases with the increase in the footing pressure and nail inclination. A maximum of 35% reduction in the maximum tensile force is observed with a 10° nail angle decrease.

3.2.4. Slope Face Horizontal Stress

Figure 18 shows the influence of the nail inclination on the slope face horizontal stress at mid height of the slope. It is clear from the figure that as the inclination of the nails increases, the horizontal stresses at the slope face decreases. The surcharge loadings up to 20 kN/m² with the inclined nail slope has no effect on the slope face horizontal stress. With further increase in surcharge loadings, the slope face horizontal stress decreases with an increase in the nail inclination.

3.2.5. Vertical Stress under Soil Mass

Figure 19, which presents the observed vertical stresses under the soil mass with different nail angles, clearly shows that the nail inclination has a small effect on vertical stresses under the soil mass and that there is a slight increase in the vertical stresses under the soil mass at a higher angle of inclination of the nails. With the increase to the maximum considered surcharge loading, the increase in the vertical stress is just 10%.

3.2.6. Horizontal and Vertical Stress behind Soil Mass

Figure 20 and Figure 21 show the influence of nail inclination on the horizontal and vertical stresses behind the soil mass at the middle of the soil slope. The figures depict that the vertical stress behind the soil mass decreases with the increase in the nail angle. With the increase in surcharge loading, the decrease in the vertical stress due to a larger nail angle further increases. The horizontal stress behind the soil mass at a lower footing pressure is constant under different nail inclinations but at a higher footing pressure, the horizontal stress considerably decreases with the increase in the nail inclination.

3.3. Spacing of Nails

3.3.1. Lateral Movement of the Nailed Soil Slope

Figure 22 shows the relation between the nails’ spacing and the horizontal movement of the slope at the middle of the slope. The figure clearly shows that a decrease in the nail spacing results in a decrease in the horizontal movement of the slope face. The percentage decrease in the lateral movement of the slope face decreases with the increase in the footing pressure. This may be due to the increase in the overall stiffness of the nailed soil mass with smaller spacing between the nails.

3.3.2. Footing Settlement

The footing settlements for different nails-spacing at various footing pressures are given in Figure 23. From the figure, it can be seen that the footing settlement decreases with the decrease in nail spacing. The decrease in footing settlements, in terms of the percentage ratio of the slope height, is increased with the increase in footing pressure and decrease in nail spacing. The decrease in footing settlements with decreases in the nail spacing varies from 31.8% to 60.0% at various footing pressures.

3.3.3. Nail Maximum Tensile Force

The effect of nail spacing on the maximum tensile force in the nails at different levels is presented in Figure 24 with various footing pressures. The figure depicts that increases in the nail spacing increases the maximum tensile force in the nails. The same effect of the spacing of the nails is visible at different footing pressures. The lower nails have lesser tensile force as compared to the upper nails, while the middle nails have the maximum tensile force. This may be because the maximum horizontal displacements are at mid height of the slope.

3.3.4. Slope Face Horizontal Stress

The influence of nail spacing on the horizontal stress at the slope face at the middle point of the slope is depicted in Figure 25 at various footing pressures. From the figure, it is evident that with the increase in the spacing between the nails, the face horizontal stress increases. The horizontal stress increases with the increase in footing pressure and nail spacing. The increase in the slope face horizontal stresses range from 9.1% to 18.5% at various footing pressures.

3.3.5. Vertical Stress under Soil Mass

Figure 26 shows the effect of nail spacing on the vertical stress under the nailed soil mass at mid-point, i.e., point E. From this figure, it is seen that the effect of nail spacing on vertical stresses under the soil mass is small. The increase in nail spacing leads to slight differences in vertical stress under the soil at different values of surcharge loading.

3.3.6. Horizontal and Vertical Stress behind Soil Mass

The effect of nail spacing on the horizontal and vertical stresses behind the soil mass at various surcharge loading values at the middle point are given in Figure 27 and Figure 28. It is clear from the figures that the vertical stress behind the soil mass increases with an increase in the nail spacing. With the increase in surcharge loading and nail spacing, there is a further increase in the vertical stress behind the soil mass. The horizontal stress behind the soil mass at a higher footing pressure is constant at different nail spacings, but at a lower footing pressure, there is a considerable increase in horizontal stresses at higher nail spacings.

4. Numerical Modeling: Validation

The finite element numerical model of earth slopes is analyzed to judge the accuracy and validity of the experimental slope model results. The two-dimensional model of the nailed-soil slope is developed, using the finite element method-based PLAXIS software because of the plane strain condition of soil slope. Four types of elements are used to model the sand, steel, and Perspex glass material. A nonlinear elastic (hyperbolic) model is used to simulate the sand material. The soil parameters used in the material model are given in

Table 3. Soil parameters of sand used in material model.

Density (kN/m3)	Mohr–Coulomb Model				Plastic Straining Due to Deviator Loading (E50) ref (kPa)	Plastic Straining Due to Primary Comp. (Eoed) ref (kPa)	Elastic Unloading/Reloading		Stress Dependent Stiffness (m)
	φ	C (kPa)	ψ	υ			(Eur) ref (kPa)	υur
16.41	34	0.2	4	0.31	1959	1959	5877	0.2	0.5

. The discretized model of the soil slope with boundary conditions is shown in Figure 29.

To verify the accuracy of the laboratory results, a numerical model of the nailed soil slope of height (H) of 700 mm is developed with the length of the horizontal nails as H and the vertical spacing of the nails as 0.4 H. The lateral or horizontal slope displacements are computed at the top, middle and bottom nail locations, i.e., at distances of Z = 70, 350, and 630 mm from the top surface. These distances are expressed as 0.1 H, 0.5 H, and 0.9 H. The results are taken at footing pressures of 0.0, 10.0, and 30.0 kPa. The plots of the computational and experimental results at different surcharge pressures, i.e., at the excavation stage and loading stage, are depicted in Figure 30.

It is clear from the figures of horizontal slope displacements (D/H, %) that the maximum horizontal slope displacement occurs at a surcharge loading of 30.0 kN/m² in both the laboratory and numerical models. The maximum horizontal displacement occurs at the lower point of the slope in the numerical model, whereas it occurs at the middle point in the laboratory model during the excavation stage. In the loading stages, the maximum displacement is at the mid-point in both models. Moreover, the percentage of difference at maximum displacement ranges between 14.68% at surcharge loading of 30.0 kN/m² and 29.01% at 10.0 kN/m². It is inferred from the results that the trend of the behavior of the slope is almost the same in the experimental model and the numerical model.

The settlement of the footing in the experimental model is also compared with numerical results of footing settlement at surcharge pressure of 0, 5, 10, 20, 30 kPa and Figure 31 shows the comparison of the footing settlement obtained in the experimental and finite element models. It can be seen from the figure that the maximum footing settlement occurs at a surcharge load exerting a foundation pressure of 30.0 kN/m² in both models. The percentage of difference in settlement between the laboratory and numerical model ranges from 13.37% to 40.59%.

5. Conclusions

The earth nailing system is an earth slope stabilization technique accomplished by installing in situ closely spaced nails in the ground. In the present study, an experimental investigation of earth nailing system models of non-cohesive soil, having different nailing parameters, such as nail spacing and orientations and length of nails, was carried out. The distribution of the mobilized tensile force in the nail and the slope face horizontal pressure is nonlinear with different nailing parameters. The nail tensile force approaches zero at the ends and increases toward the middle third of the nail. The maximum lateral displacement and slope face horizontal pressures of the slope occur in the middle third, and minimum lateral displacement and slope face horizontal pressures, the lower third of the slope with different surcharge loading and nailing parameters. The minimum and maximum vertical and horizontal pressures behind the soil mass occur in the upper third and lower third of the slope, respectively, with different nailing parameters.

There is a reduction in the lateral movement of the slope and footing settlements with an increase in the length and inclination of the nails and with a decrease in the nail spacing. The mobilized tensile forces in the nails are increased due to the increase in the nail length and spacing, while tensile forces reduce with the increase in the inclination of the nails.

The vertical stresses under the soil mass are not much affected by changing the nail parameters, i.e., length, inclination, and spacing. The horizontal stresses at the slope face decrease with the increase in the nail inclination, while they are increased with the increase in nail length and spacing.

The vertical and horizontal stresses behind the soil mass increase with the increase in the spacing of the nails, while the vertical and horizontal stresses decrease with the increase in nail inclination. The increase in the length of the nails causes a decrease in the vertical and horizontal stresses behind the soil mass, up to the length of the nail of about the slope height, while further increases in the nail length increase the vertical and horizontal stresses behind the soil mass.