A Local Search-Based Generalized Normal Distribution Algorithm for Permutation Flow Shop Scheduling

Abstract

This paper studies the generalized normal distribution algorithm (GNDO) performance for tackling the permutation flow shop scheduling problem (PFSSP). Because PFSSP is a discrete problem and GNDO generates continuous values, the largest ranked value rule is used to convert those continuous values into discrete ones to make GNDO applicable for solving this discrete problem. Additionally, the discrete GNDO is effectively integrated with a local search strategy to improve the quality of the best-so-far solution in an abbreviated version of HGNDO. More than that, a new improvement using the swap mutation operator applied on the best-so-far solution to avoid being stuck into local optima by accelerating the convergence speed is effectively applied to HGNDO to propose a new version, namely a hybrid-improved GNDO (HIGNDO). Last but not least, the local search strategy is improved using the scramble mutation operator to utilize each trial as ideally as possible for reaching better outcomes. This improved local search strategy is integrated with IGNDO to produce a new strong algorithm abbreviated as IHGNDO. Those proposed algorithms are extensively compared with a number of well-established optimization algorithms using various statistical analyses to estimate the optimal makespan for 41 well-known instances in a reasonable time. The findings show the benefits and speedup of both IHGNDO and HIGNDO over all the compared algorithms, in addition to HGNDO.

1. Introduction

The permutation flow shop scheduling problem (PFSSP) is a critical problem that needs to be solved accurately and effectively to minimize the makespan criteria. The solution to this problem involves finding the near-optimal permutation of n jobs to be processed in a set of m machines sequentially that will minimize the makespan required, even completing the last job in the last machine [1]. This problem has significant utilization in several fields, especially in industries such as computing designs, procurement, and information processing. According to its significant effectiveness and its nature, which is normally classified as nondeterministic polynomial time (NP)-hard [1,2,3,4,5,6], several techniques of exact, heuristic, and meta-heuristic properties have been extensively employed for solving this problem. Some of them will be surveyed in the rest of this section.

Exact methods such as linear programming [7] and branch and bound [8] could fulfill the optimal value for the small-scale problem, but for medium-scale and large-scale problems, their performance degrades significantly, in addition to increasing exponentially the computational cost. Therefore, the heuristics algorithms have been designed to overcome this expensive computational cost and high dimensionality. Involving the heuristic algorithms, the Nawaz-Enscore-Ham (NEH) algorithm employed by Nawaz et al. [9] for solving PFSSP could be the most effective heuristic algorithm, and their results are comparable with the meta-heuristic algorithms [10,11,12,13], which are being used for solving several optimization problems in a reasonable time. Broadly speaking, the image segmentation problem is an indispensable process in image processing fields, so several image segmentation methods have been suggested such as clustering, fractal-wavelet techniques [14,15,16,17,18,19,20], region growing, and thresolding; Among those techniques, the threshold-based segmentation technique is the most effective due to the metaheuristic algorithms which could segment the images based on this technique with high accuracy [21].

The particle swarm optimization (PSO)-based memetic algorithm (MA) [22], namely PSOMA, has been proposed for tackling the PFSSP as an attempt to find the near-optimal job permutation that minimizes the maximum completion time. In detail, to adapt the PSOMA for solving the PFSSP, the authors used a ranked order rule to convert the continuous values produced by the standard algorithms into discrete ones. In addition, to improve the quality and diversity of the initialized solutions, the NEH algorithm has been used. Furthermore, to balance between the exploration and exploitation operators, a local search operator has been used to be applied on some solutions selected using the roulette wheel mechanism with a specific probability. Ultimately, to avoid being stuck into local minima, PSOMA used the simulated annealing with multiple neighborhood search strategies. It is worth mentioning that the local search has been used with the PSO for tackling several optimization problems, and this confirms that the local search has a significant influence on the performance after integration; some of those works are comprehensive learning PSO with a local search for multimodal functions [23], PSO with local search [24], and many others [2,25,26,27,28,29].

The cuckoo search-based memetic algorithm (HCS) [30] has been adapted using the largest ranked values rule for tackling the PFSSP. Besides, HCS used the NEH algorithm to initialize the population to fulfill better quality and diversity. Furthermore, this algorithm used a fast local search to accelerate the convergence speed in an attempt to improve its exploitation algorithm. This algorithm was compared with a number of optimization algorithms: hybrid genetic algorithm (HGA), particle swarm optimization with variable neighborhood search, and the differential-evolution-based hybrid algorithm (HDE) on four benchmark instances to see its efficacy.

The hybrid discrete artificial bee colony algorithm (HDABC) [31] has been adapted for tackling the PFSSP. In HDABC, the initialization step was achieved based on the Greedy Randomized Adaptive Search Procedure (GRASP) with the NEH algorithm to include better quality and diversity. After that, the discrete operators such as insert, swap, GRASP, and path relinking are used to generate new solutions. Ultimately, a local search strategy has been applied to improve the quality of the best-so-far solution as an attempt to improve the searchability of HDABC. HDABC has been extensively compared with a number of the algorithms: ant colony system (ACS), PSO embedded with a variable neighborhood search (VNS) (PSOVNS), PSOMA, and HDABC.

Xie, Z., et al. [32] developed a hybrid teaching learning-based optimization (HTLBO) for tackling the PFSSP. Due to the continuous nature of the teaching-learning-based optimization, the largest ranked value rule is used to make it applicable to the PFSSP. In addition, HTLBO used simulated annealing as a local search to improve the quality of the obtained solutions. The differential evolution-based memetic algorithm (ODDE) [33] has been adapted using the largest ranked value rule for tackling the PFSSP. ODDE in the initialization step used the NEH algorithm to initialize the solutions with a certain quality and diversity. In ODDE, an approach based on the diversity of the population was used to tune the crossover rate, in addition to accelerating the convergence speed of the algorithm using the opposition-based learning. Finally, ODDE used a local search strategy to avoid being stuck into local minima by improving the best-so-far solution.

The whale optimization algorithm integrated with a local search-ability on the best solution and mutation operators have been suggested by Abdel-Basset, M., et al. [34] to propose a new variant, namely HWA, for tackling PFSSP. Broadly speaking, HWA used the NEH algorithm in the initialization step to create 10% of the populations with a certain diversity and quality as an attempt to avoid being stuck into local minima for reaching better outcomes. Afterward, to make WOA applicable to the PFSSP, the LRV rule was used to make the solutions generated by it relevant to this problem. Furthermore, it was integrated with two operators to improve the diversity for avoiding being stuck into the local minima problem: swap mutation and insert-reversed block. Finally, to accelerate the convergence speed toward the optimal solution and avoid being stuck in the local minimum, it was integrated with a fast local search strategy on the best-so-far solution.

In [35], Mishra developed a discrete Jaya optimization algorithm for tackling the PFSSP. Because the standard Jaya algorithm has been adapted for tackling the continuous optimization problem that is contradicted to the PFSSP, which is normally classified as a discrete one, the largest order value rule was used to convert those continuous values into discrete ones relevant to the PFSSP. This discrete Jaya algorithm was verified on a set of well-known benchmarks and compared extensively under various statistical analyses with hybrid genetic algorithm (HGA, 2003), hybrid differential evolution (HDE, 2008), hybrid particle swarm optimization (HSPO, 2008), teaching-learning based optimization (TLBO, 2014), and hybrid backtracking search algorithm (HBSA, 2015) that are not up to date, and its performance with the recent optimization algorithms published over the last three years are unknown.

The whale optimization algorithm (WOA) [36] improved using the chaos map and then integrated with the NEH algorithm has been proposed for tackling the PFSSP. In detail, the NEH algorithm and the largest ranked values rule are used in the initialization step of the chaos WOA (CWA) to initialize the solutions in better quality. After that, CWA used the chaotic maps to avoid being stuck into local minima and accelerate convergence speed by assisting two other operators: cross operator and reversal-insertion to improve its exploration capability. Ultimately, CWA used the local search strategy to improve the quality of the best-so-far solution to improve the exploitation capability of CWA. This algorithm was observed using various benchmarks and compared with various optimization algorithms to check its superiority.

Further, a new discrete multiobjective approach based on the fireworks algorithm (DMOFWA) has been recently proposed for solving the multi-objective flow shop scheduling problem with sequence-dependent setup times (MOFSP-SDST); this approach was abbreviately called DMOFWA [37]. Inside this approach, two various machine learning techniques have been integrated: The first one called opposition-based learning was used to improve the exploration operator of the standard algorithm to avert entrapment into local minima, and the second one is the clustering analysis and was used to cluster fireworks individuals.

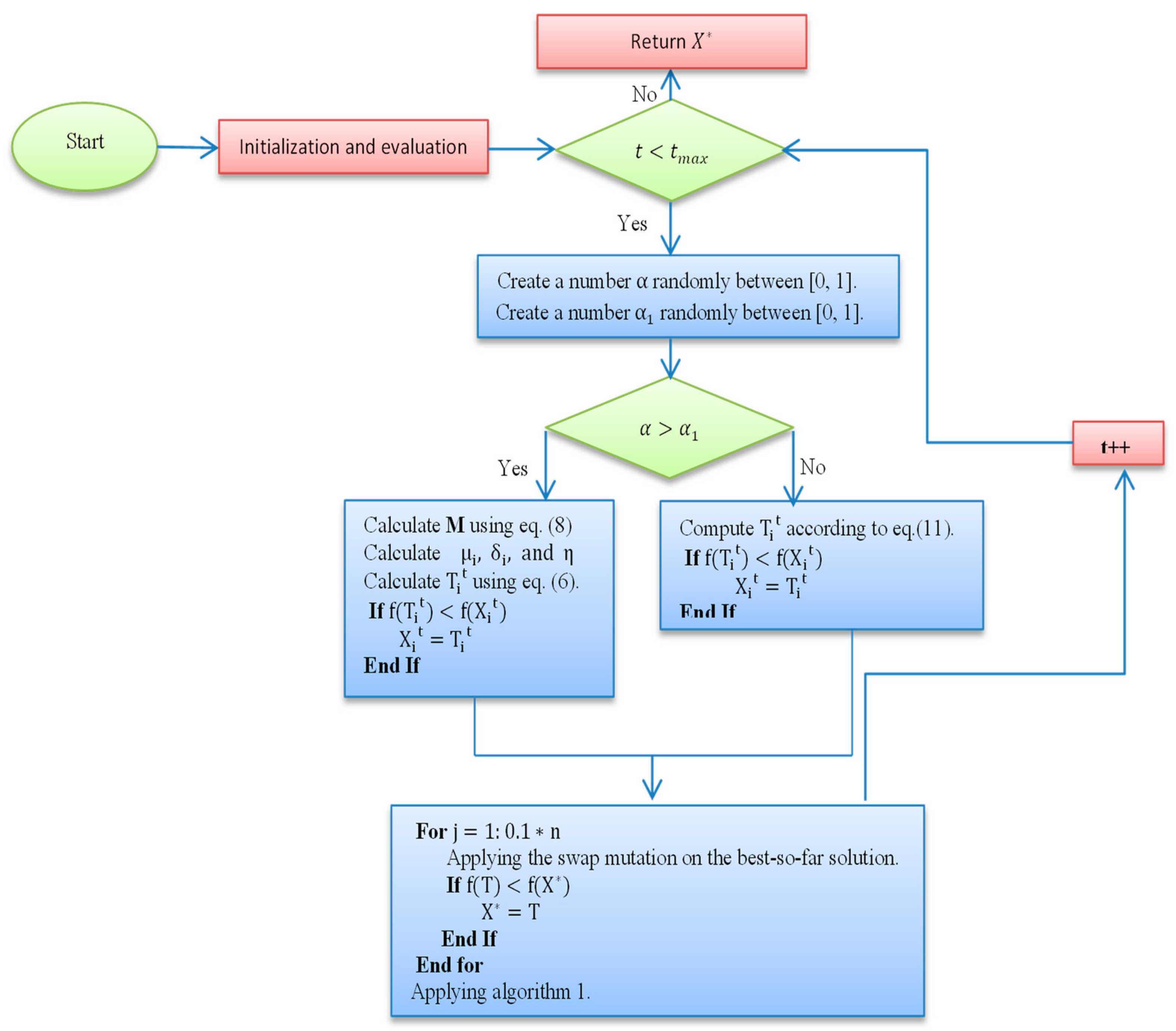
To overcome expensive computational costs and local minima problems that might suffer from most of the above-described algorithms, we developed a novel discrete optimization algorithm to tackle the PFSSP in a reasonable time compared to some existing techniques. Recently, a new optimization algorithm, namely generalized optimization algorithm (GNDO), based on the normal distribution theory, has been developed by Zhang [38] for tackling the parameter extraction problem of the single diode and double diode photovoltaic models. Due to its high ability to estimate the parameter values that minimize the error rate between the measured I-V curve and the estimated I-V curve, in this paper, we try to observe its performance for tackling the PFSSP. In order to make GNDO applicable to the PFSSP classified as a discrete problem contradicted by the continuous problems tackled using the standard GNDO, the largest ranked value (LRV) rule is used to convert those continuous values into job permutations adequate to solve the PFSSP. Furthermore, this discrete GNDO using the LRV rule is integrated with a local search strategy to avoid being stuck into local minima for reaching better outcomes; this version is named a hybrid GNDO (GNDO). In another attempt to improve the quality of HGNDO, it was integrated with the swap mutation operator applied on the best-so-far solution as another attempt to promote the exploitation capability for reaching better outcomes; this version was abbreviated as HIGNDO. Finally, to improve the quality of the solutions, the local search strategy is improved using the scramble mutation operator and then integrated with HIGNDO to produce a new version named IHGNDO. The proposed algorithms, HGNDO, HIGNDO, and IHGNDO, are verified using 41 well-known instances widely used in the literature and compared with a number of the recent well-established algorithms to verify their efficacy using various performance metrics. The experimental results affirm the superiority of IHGNDO and HIGNDO over the other algorithms in terms of standard deviation, computational cost, and makespan. Generally, our contributions in this work include the following:

• Develop GNDO using the LRV rule for PFSSP.
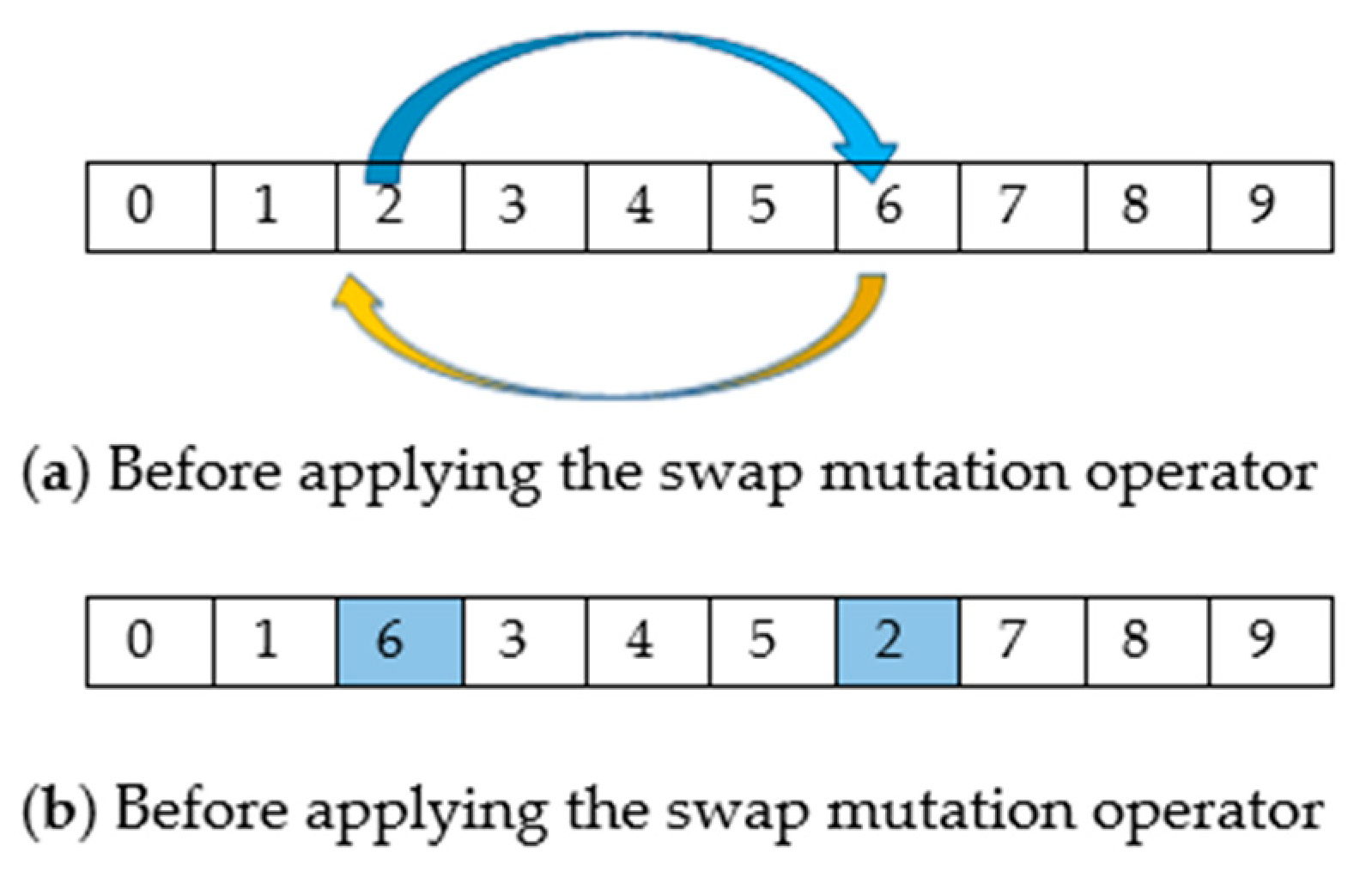
• Improve GNDO using the swap mutation operator to avoid being stuck into local minima.
• Enhance the local search strategy using the scramble mutation operator for accelerating the convergence speed toward the near-optimal solution.
• Integrate the improved local search strategy and the standard one with the improved GNDO and GNDO for tackling the PFSSP.
• The experimental findings show that IHGNDO and HIGNDO are better in terms of standard deviation and computational cost and final accuracy.

This work is organized as follows: Section 2 explains the PFSSP; Section 3 describes the standard generalized normal distribution optimization algorithm; Section 4 explains the proposed algorithm; Section 5 includes the results and discussion; and Section 6 illustrates our conclusions and future work.

2. Description of the Permutation Flow Shop Scheduling Problem

Assuming that n jobs are running sequentially over m machines in the permutation flow that will minimize the makespan, this problem is known as the permutation flow shop scheduling problem (PFSSP). The makespan is measured using time units such as seconds, milliseconds, etc. Therefore, to solve this problem, the best permutation $c^{*}$ that will minimize the makespan of execution of the last job on the last machine must be accurately extracted. In general, the following points summarize the PFSSP: (1) on each machine, each job $j_b|b=1,2,3,\dots \dots \dots ,n$ could run just once, where $n$ is the number of jobs; (2) just a job could be executed on a machine $i_z|z=1,2,3,\dots \dots ., m$ at a time with processing time PT, where $m$ is the number of machines; (3) each job $j_b$ will have a completion time c on a machine $v_z,$ and this time is symbolized as c($j_b$,$i_{\mathrm{z}}$); (4) each job has a processing time comprised of the set-up time of the machine and the running time; and (5) each job takes a time of 0 when starting. Mathematically, PFSSP could be modeled as follows:

$$c\left(j_1, i_1\right)=P{T}_{j_1, i_1}$$

(1)

$$c\left(j_b, i_1\right)=c\left(j_{b-1}, i_1\right)+P{T}_{j_b, i_1}, b=2,3, 4, \dots \dots , n$$

(2)

$$c\left(j_1, i_z\right)=c\left(j_b, i_{z-1}\right)+P{T}_{j_1, i_z}, z=2,3, 4, \dots \dots , m$$

(3)

$$c\left(j_b, i_z\right)=\max \left(c\left(j_{b-1}, i_z\right), c\left(j_b, i_{z-1}\right)\right)+P{T}_{j_b, i_z}, b=2,3, 4, \dots \dots , n, z=2,3,4,\dots \dots .., m$$

(4)

In our work, the objective function used by the suggested algorithm to evaluate each solution is described as follows:

$$f\left({\overrightarrow{j}}_i\right)=c\left(j_b, i_z\right)$$

(5)

where ${\overrightarrow{j}}_i$ is the jobs permutation of the ith solution. This objective function will be used to evaluate each permutation extracted by the algorithms, and the one with less makespan is considered the best.

3. Standard Algorithm: Generalized Normal Distribution Optimization

Zhang [38] developed a new optimization algorithm based on the normal distribution theory to tackle the parameter estimation problem of Photovoltaic models: single diode model and double diode model; this algorithm is called generalized normal distribution optimization (GNDO). The mathematical model of GNDO is extensively described in the rest of this section.

3.1. Exploitation Operator

This operator is utilized to search extensively around the best-so-far solution $X^{*}$ to check if there are better solutions as an attempt to accelerate the convergence speed. In GNDO, this operator is designed based on searching around the mean ${\mu }_i$ of $X^{*}$, the current $i\mathrm{th}$ solution $X_i{}^t$, and the mean $M$ of all solutions at generation $t$ calculated according to Equation (8); ${\mu }_i$ is computed using Equation (7). After that, GNDO exploits the solutions around this mean using a step size computed according to Equation (9) to generate a new trial solution $T_i{}^t$ using Equation (6) having the following characteristics: accelerating the convergence speed in addition to improving the quality of the solutions. $T_i{}^t$ is carried over to the next generation if its objective value is better than the objective of $X_i{}^t$.

$$T_i{}^t={\mu }_i+{\delta }_i\times \eta , \forall i=1: N$$

(6)

$${\mu }_i=(X_i{}^t+X^{*}+M)/3.0$$

(7)

$$M=\frac{{{\displaystyle \sum }}_{i=1}^N{X}_i{}^t}{N}$$

(8)

$${\delta }_i=\sqrt{\frac{1}{3}\left[{(X_i{}^t-\mu )}^2+{\left(X^{*}-\mu \right)}^2+{\left(M-\mu \right)}^2)\right]}$$

(9)

$$\eta =\{\begin{array}{c}\sqrt{-log\left({\gimel }_1\right)}\times cos\left(2\pi {\gimel }_2\right), r_1\le r_2\\ \sqrt{-log\left({\gimel }_1\right)}\times cos\left(2\pi {\gimel }_2+\pi \right), r_1>r_2\end{array}$$

(10)

$r_1,r_2$, ${\gimel }_1$, and ${\gimel }_2$ are four numbers generated randomly at the interval between 0 and 1.

3.2. Exploration Operator

However, ${\mu }_i$ may be local minima, and subsequently searching around it is futile to improve the quality of the solutions. Therefore, the exploration operator is used to explore the search space as much as possible to avoid being stuck into local minima. In mathematical terms, this operator is formulated as follows:

$$T_i{}^t=X_i{}^t+\beta \times \left(\left|{\gimel }_3\right|\times v_1\right)+\left(1-\beta \right)\times \left(\left|{\gimel }_4\right|\times v_2\right)$$

(11)

${\gimel }_3$ and ${\gimel }_4$ are two randomly generated numerical values based on the standard normal distribution; $\beta$ is a random number created between 0 and 1. $v_1$ and $v_2$ are generated as follows:

$$v_1=\{\begin{array}{c}{X}_i{}^t-X_{a1}{}^t, if f\left(X_i{}^t\right)\le f\left(X_{p1}{}^t\right)\\ X_{a1}{}^t-X_i{}^t, otherwise\end{array}$$

(12)

$$v_2=\{\begin{array}{c}{X}_{a2}{}^t-X_{a3}{}^t, if f\left(X_{p2}{}^t\right)\le f\left(X_{p3}{}^t\right)\\ X_{a3}{}^t-X_{a2}{}^t, otherwise\end{array}$$

(13)

$a1, a2, \mathrm{and} a3$ are three indices selected randomly from the population, such that $a1\ne a2\ne a3\ne i$. The exploration and exploitation operators are randomly swapped in the optimization process.

4. The Proposed Work

In this section, the steps of initialization, swap mutation and scramble mutation operators, and improved local search that comprise the proposed algorithms will be discussed in detail within this section.

4.1. Initialization

In the beginning, N solutions with n dimensions for each one are generated and initialized with distinct integers generated randomly between 0 and n. After that, those solutions will be evaluated, and the one with less makespan will be carried over to the next generation as the best-so-far solution. The ending to this phase considers starting the optimization process used to optimize the initial solutions to generate new better ones. However, unfortunately, the updated solutions generated by GNDO are continuous, not discrete, as required for the PFSSP, so the largest ranked value (LRV) is used to convert the continuous values generated by GNDO into a job permutation. The LRV sets the largest value in the updated solution as the first order of a job permutation and the second-largest value as the second one.

Table 1. Representation of the updated solution $T_i{}^t$.

Position, Job	0	1	2	3	4	5	6
Position, $T_i{}^t$	0.1	0.5	0.8	0.2	0.6	0.7	0.9
Job, $T{T}_i{}^t$	6	4	1	5	3	2	0

presents a simple example to illustrate the LRV rule for generating the job permutation from an updated solution $T_i{}^t$.

4.2. Swap Mutation Operator

This mutation operator is extensively used for solving the permutation problem by swapping the values of two positions selected randomly from the solution. In the proposed algorithm, this operation is applied on the best-so-far solution 0.1 times to search for other solutions with a smaller makespan than the current best-so-far. Figure 1 gives an example about the swap mutation operator, where Figure 1a shows the order of the positions before using this mutation operator, while Figure 1b shows the order after swapping the value in the third position with the values in the seventh position.

4.3. Scramble Mutation Operator

In this operator, two positions are randomly picked, and the jobs between those two positions are shuffled and inserted again, as depicted in the following table (

Table 2. Scramble mutation operator.

0

1

2

3

4

5

6

7

8

9

0

1

2

3

4

5

6

7

8

9

).

4.4. Improved Local Search Strategy (ILSS)

Additionally, in this work, a local search strategy is used to explore the solutions around the best-so-far solution for finding better solutions. This strategy will try according to a specific probability LSP each job in the best-so-far solution in all positions within this best solution to find a permutation with better makespan than the current best-so-far one. This strategy is used with the best-so-far solution without the others because the best-so-far solution might be so close to the optimal solution and need only simple changes to fulfill this optimal solution. This local search is integrated with the improved GNDO using the swap mutation operator to generate a version for tackling PFSSP, abbreviated as HIGNDO. In addition, in some cases, small changes may consume a large number of iterations without any benefit, so, in this research, a new addition to this LSS is made to make more changes to the best-so-far solution in the hope of finding a better solution. This addition is based on using the scramble mutation operator additionally with the LSS to explore more permutations. This improved local search strategy is abbreviated as ILSS, and its steps are listed in Algorithm 1. In Algorithm 2, the steps of improved GNDO (IGNDO) using the swap mutation operator hybridized with the LSS without the scramble mutation operator are extensively described to produce a version for tackling PFSSP known as HIGNDO. A new version using ILSS with IGNDO is developed to verify the efficacy of our improvement to the LSS for reaching better outcomes. This version is abbreviated as IHGNDO and is depicted in Figure 2.

Algorithm 1 Improved LSS (ILSS).

Input: $X^{*}$ For I = 1: n   $X=X^{*}$   For j = 1: n     $r:$ create a random number between 0 and 1.     If(r < LSP)       $X_j=X_i^{*}$       Applying scramble mutation operator on $X$       Calculate the fitness of $X$.       Update $X^{*}$ if $X$ is better.     End if   End for End for Return $X^{*}$

Algorithm 2 HIGNDO.

Input: N, $t_{max}$ $t=0$ Initialization phase. While $t<t_{max}$   For $i=1:N$      Create a number $\alpha$ randomly between [0, 1].      Create a number ${\alpha }_1$ randomly between [0, 1].     If $\alpha >{\alpha }_1$       Calculate M using Equation (8)       Calculate ${\mu }_i, {\delta }_i, and \eta$       Calculate $T_i{}^t$ using Equation (6).      If $f(T_i{}^t)<f\left(X_i{}^t\right)$         $X_i{}^t=T_i{}^t$      End If     Else       Compute $T_i{}^t$ according to Equation (11).      If $f(T_i{}^t)<f\left(X_i{}^t\right)$         $X_i{}^t=T_i{}^t$      End If     End If     For $j=1:0.1*n$       $T$: Applying the swap mutation on the best-so-far solution.      If $f\left(T\right)<f\left(X^{*}\right)$          $X^{*}=T$       End If      End for      Applying algorithm 1 without Line 7.    End For    $t++$; End while Output: return $X^{*}$

5. Results and Comparisons

In our experiments, the proposed algorithms are extensively validated on three benchmarks commonly used in the literature: (1) the first dataset is called the Carlier dataset, having eight instances with a number of jobs ranging between 7 and 14, and a number of machines at the interval between 4 and 9 [39]; (2) the second is the Reeves dataset with 21 instances, where the number of machines and the number of jobs ranges between 20 and 75, and 5 and 20, respectively [40]; and (3) finally, the third one is known as the Heller and involves two instances with a number of jobs ranging between 20 and 100, and a number of machines of 10, respectively [41]. Those datasets are taken from [42] with some characteristics about the number of jobs and machines, and the best-known makespan $z^{*}$ in

Table 3. Description of Carlier, Heller, Reeves instances.

Name	n	m	${\mathit{Z}}^{*}$	Name	n	m	${\mathit{Z}}^{*}$	Name	N	m	${\mathit{Z}}^{*}$	Name	n	m	${\mathit{Z}}^{*}$
Hel1	20	10	516	Car07	7	7	6590	Rec13	20	15	1930	Rec29	23	15	2287
Hel2	100	10	136	Car08	8	8	8366	Rec15	20	15	1950	Rec31	50	10	3045
Car01	11	5	7038	Rec01	20	5	1247	Rec17	20	15	1902	Rec33	50	10	3114
Car02	13	4	7166	Rec03	20	5	1109	Rec19	30	10	2017	Rec35	50	10	3277
Car03	12	5	7312	Rec05	20	5	1242	Rec21	30	10	2011	Rec37	75	20	4951
Car04	14	4	8003	Rec07	20	10	1566	Rec23	30	10	2011	Rec39	75	20	5087
Car05	10	6	7720	Rec09	20	10	1537	Rec25	30	15	2513	Rec41	75	20	4960
Car06	8	9	8505	Rec011	20	10	1431	Rec27	30	15	2373

. Furthermore, the proposed algorithms are extensively compared with a number of the well-established optimization algorithms: sine cosine algorithm (SCA) [43], slap swarm algorithm (SSA) [44], whale optimization algorithm (WOA) [34], genetic algorithm (GA), equilibrium optimization algorithm (EOA) [45], marine predators optimization algorithm (MPA) [42], and a hybrid tunicate swarm algorithm (HTSA) [46] integrated with the local search strategy to ensure a fair comparison and verify their efficacy in terms of six performance metrics: average relative error (ARE), worst relative error (WRE), best relative error (BRE), an average of makespan (Avg), standard deviation (SD), and computational cost (Time in milliseconds (ms)). BRE indicates how far the best-obtained solution $Z_B$ is close to the best-known solution and is formulated using the following formula:

$$BRE=\frac{\left|Z^{*}-Z_B\right|}{Z^{*}}$$

(14)

Meanwhile, WRE calculated using the next equation is a metric used to assess the remoteness between the worst-obtained makespan $Z_w$ and the best known.

$$WRE=\frac{\left|Z^{*}-Z_w\right|}{Z^{*}}$$

(15)

Regarding ARE, it is used to show the relative error with respect to the average makespan values within 30 independent runs and the best-known one. Mathematically, ARE is modeled as follows.

$$ARE=\frac{\left|Z^{*}-Z_{Avg}\right|}{Z^{*}}$$

(16)

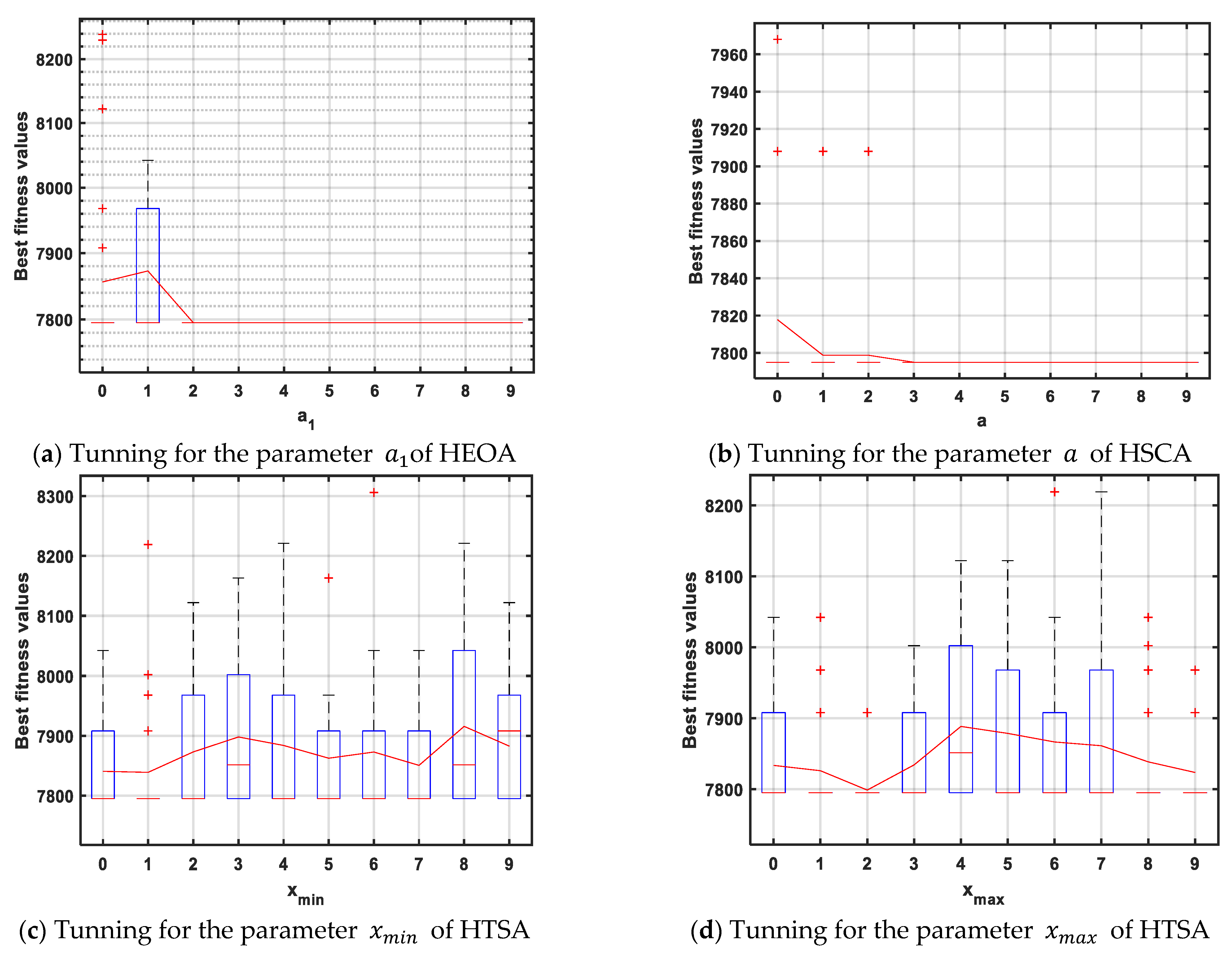
The algorithms used in our experiments after integrating local search are named a hybrid SCA (HSCA) [43], a hybrid SSA (HSSA) [44], a hybrid WOA (HWOA) [34], a hybrid GA (HGA), a hybrid EOA (HEOA) [45], a hybrid MPA (HMPA) [42], and a hybrid TSA (HTSA) [46]. Regarding the parameters of those algorithms, they were assigned after extensive experiments. The EOA has two parameters: $a_1$ (exploration factor) and $a_2$ (exploitation factor), which are needed to be accurately estimated, and after several experiments for extracting their optimal values, we note that all observed values for $a_2$ were significantly converged; therefore, it is set to 1 as used in the standard algorithm; $a_1$, which is responsible for the exploration operator, is assigned a value of 2 estimated after several experiments, pictured in Figure 3a. The SSA is self-adaptive algorithm since it does not have parameters to be assigned before beginning the optimization process; on the other hand, the HSCA has one parameter called a responsible for deterimining where the algorithm will search for the near-optimal solution, and the value to this parameter was set to 3, as shown in Figure 3b. The HMPA has one parameter P called the scaling factor, and it is set in our experiment as cited in the standard algorithm because we found that these parameters have no effect on the performance of the algorithm while solving this problem. Finally, the HTSA has two effective parameters, namely $x_{max}$ and $x_{min}$, representing the initial and subordinate speeds for social interaction and are assigned to 1 and 2, as described in Figure 3c,d which depict the outcomes of their tuning using various values. The HGA used a value of 0.02 and 0.8 for both the mutation and crossover probabilities, as recommended in [40]. All algorithms were executed under those parameters 30 independent times within the same environment with a maximum of iteration and population size: 200 and 50, respectively.

5.1. Comparison under Carlier

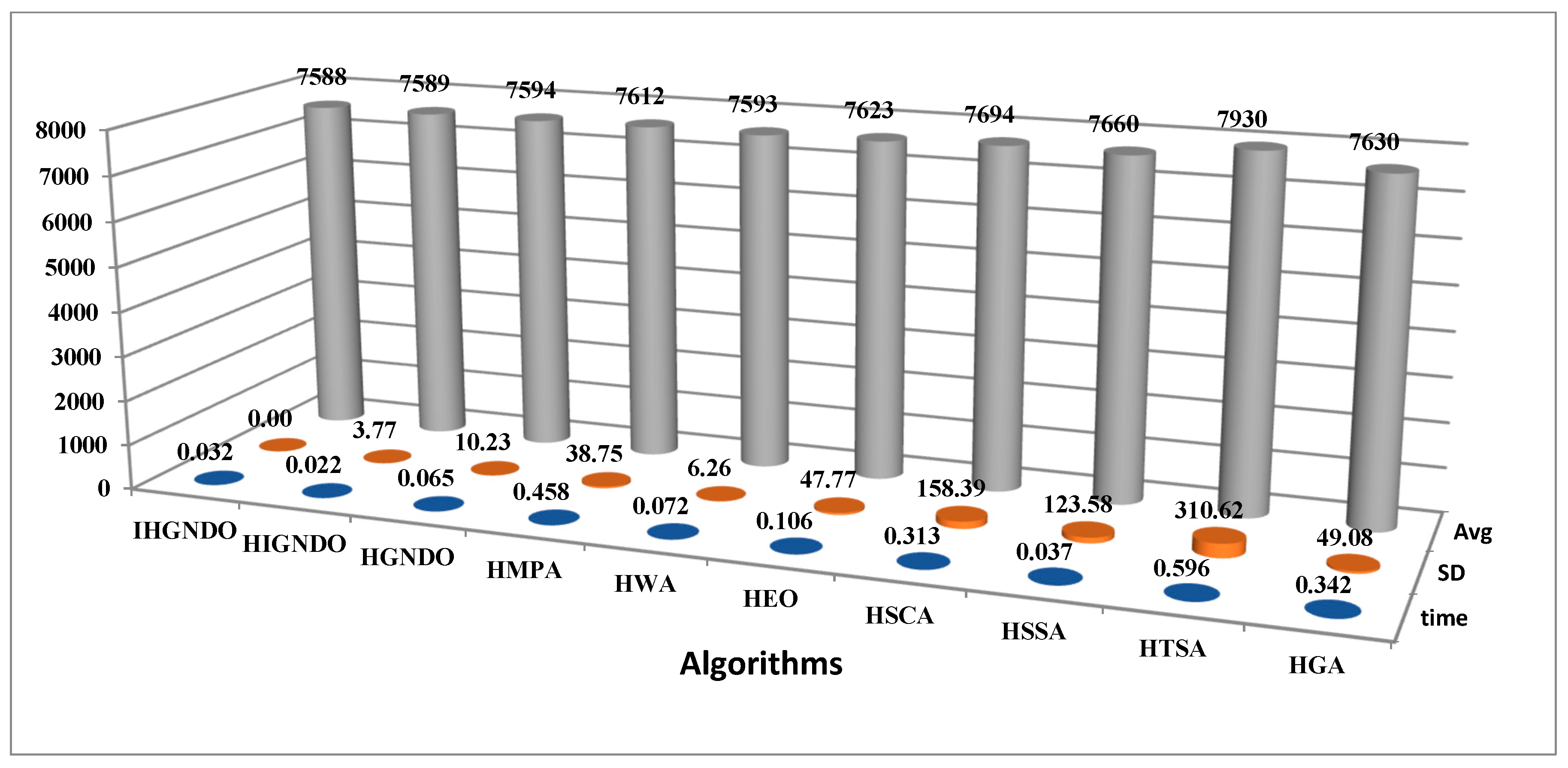
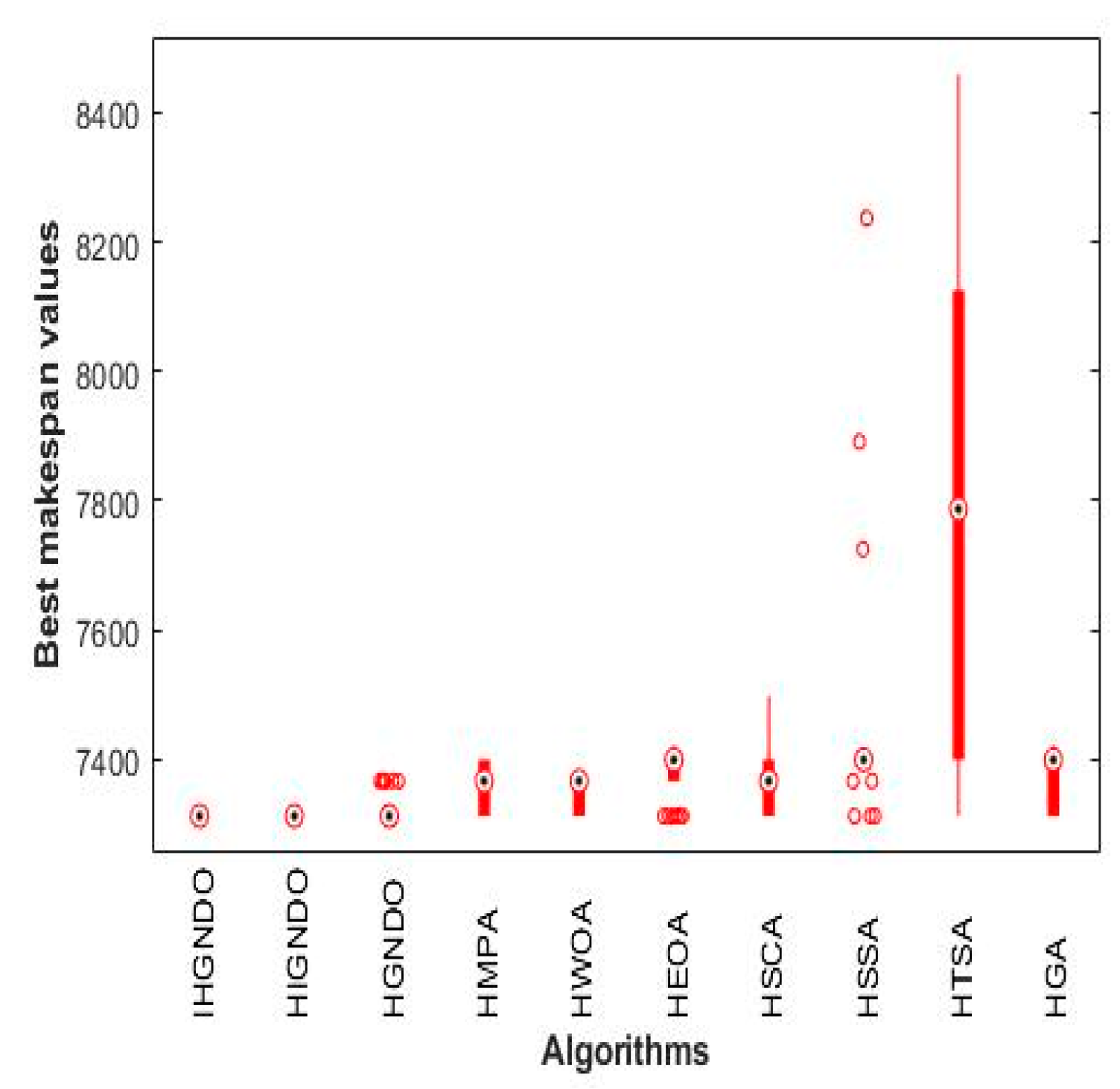
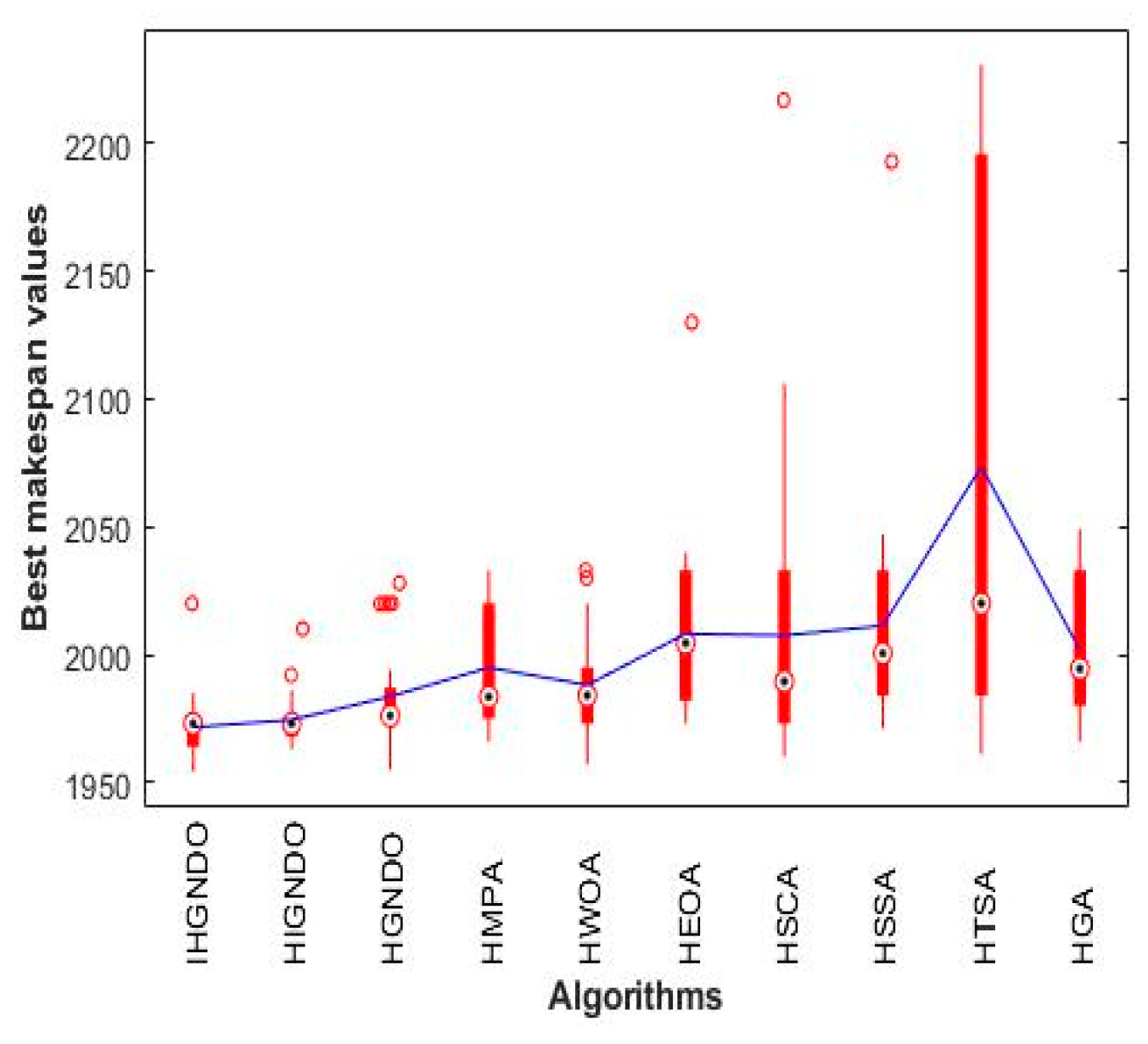
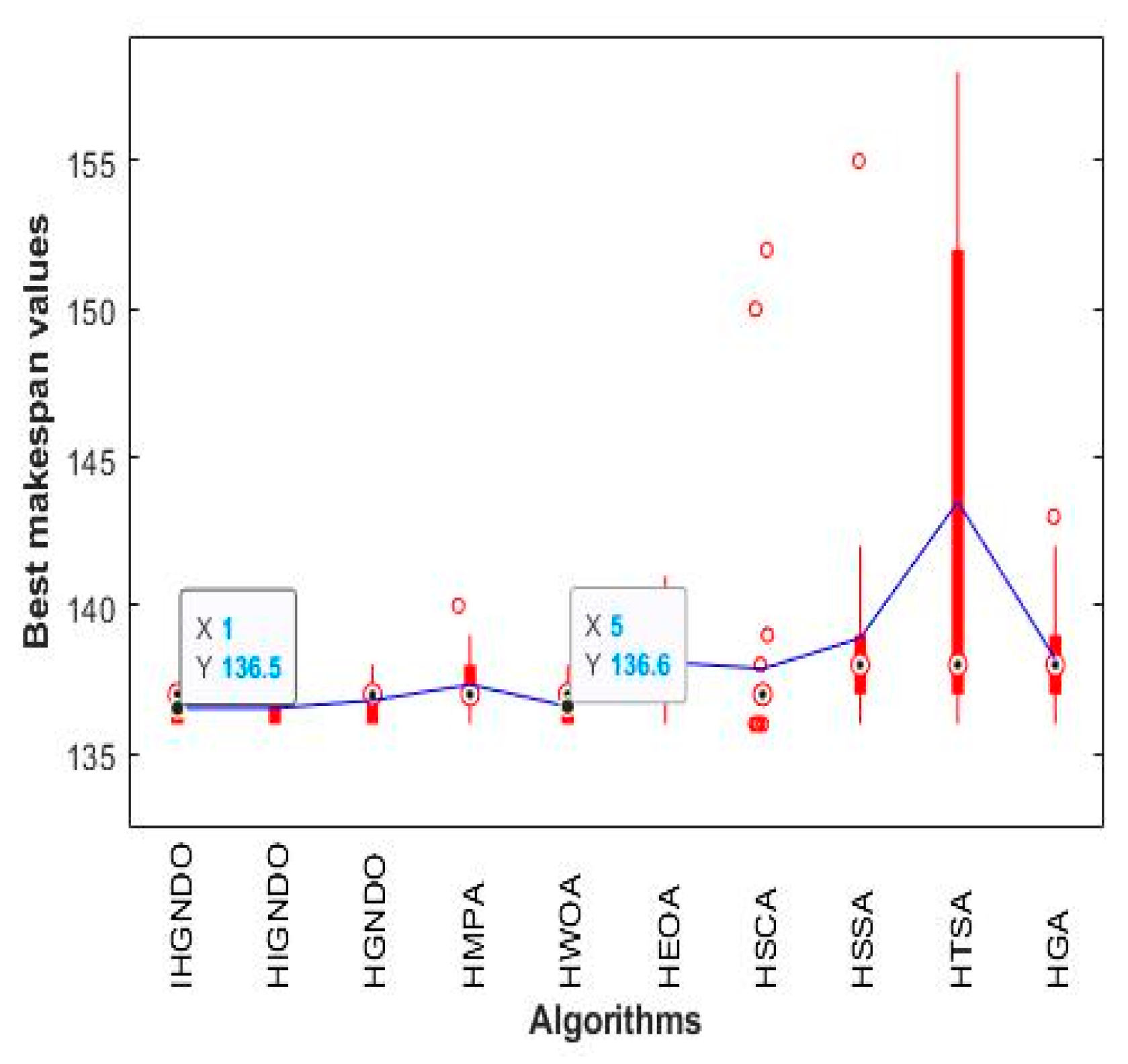
This section validates the performance of the algorithms on the Carlier instances to show the readers the efficacy of each one. Each algorithm is run 30 independent times on each instance out of eight instances of the Carlier dataset, and then the various performance metrics are calculated and presented in

Table 4. Comparison of carlier instances.

Instances	Algorithm	${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD		${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD
Car01	IHGNDO	7038	0.0000	0.0000	0.0000	7038.0000	0.0077	0.0000	Car04	7720	0.0000	0.0000	0.0000	7720.0000	0.0558	0.0000
	HIGNDO		0.0000	0.0000	0.0000	7038.0000	0.0078	0.0000			0.0000	0.0131	0.0014	7731.1667	0.0636	30.1575
	HGNDO		0.0000	0.0000	0.0000	7038.0000	0.0079	0.0000			0.0000	0.0131	0.0028	7741.9000	0.1949	36.3129
	HMPA		0.0000	0.0000	0.0000	7038.0000	0.0192	0.0000			0.0000	0.0039	0.0011	7728.4000	1.0569	10.1114
	HWOA		0.0000	0.0000	0.0000	7038.0000	0.0052	0.0000			0.0000	0.0039	0.0015	7731.4333	0.1961	11.6152
	HEO		0.0000	0.0195	0.0011	7045.9000	0.0091	29.9426			0.0000	0.0135	0.0048	7756.7000	0.2393	37.5501
	HSCA		0.0000	0.0456	0.0043	7068.2667	0.0830	76.6159			0.0000	0.0486	0.0076	7778.6667	0.4299	104.3537
	HSSA		0.0000	0.0617	0.0048	7072.1000	0.0079	107.6947			0.0000	0.0486	0.0078	7780.0000	0.0668	72.7736
	HTSA		0.0000	0.0997	0.0395	7315.6667	0.3338	286.3707			0.0000	0.1124	0.0334	7977.8333	0.6940	255.2532
	HGA		0.0000	0.0169	0.0018	7050.6000	0.0105	29.1692			0.0000	0.0153	0.0099	7796.1000	0.6052	40.0161
Car02	IHGNDO	7166	0.0000	0.0000	0.0000	7166.0000	0.0200	0.0000	Car05	8505	0.0000	0.0000	0.0000	8505.0000	0.0134	0.0000
	HIGNDO		0.0000	0.0000	0.0000	7166.0000	0.0151	0.0000			0.0000	0.0000	0.0000	8505.0000	0.0192	0.0000
	HGNDO		0.0000	0.0000	0.0000	7166.0000	0.0152	0.0000			0.0000	0.0076	0.0008	8511.5000	0.0713	19.5000
	HMPA		0.0000	0.0293	0.0010	7173.0000	0.3175	37.6962			0.0000	0.0540	0.0070	8564.4333	0.5601	101.8279
	HWOA		0.0000	0.0000	0.0000	7166.0000	0.0224	0.0000			0.0000	0.0076	0.0003	8507.1667	0.0552	11.6679
	HEO		0.0000	0.0293	0.0078	7222.0000	0.0980	92.8655			0.0000	0.0396	0.0076	8569.7000	0.1632	78.3812
	HSCA		0.0000	0.1136	0.0347	7414.6000	0.2283	344.7938			0.0000	0.0770	0.0223	8694.8667	0.5217	190.9799
	HSSA		0.0000	0.1231	0.0183	7297.4333	0.0313	262.8529			0.0000	0.0366	0.0109	8597.9667	0.0492	95.4919
	HTSA		0.0000	0.1749	0.0788	7730.5333	0.4812	420.7919			0.0000	0.1250	0.0461	8897.4000	0.8095	345.5301
	HGA		0.0000	0.0293	0.0063	7211.1000	0.1966	84.1088			0.0000	0.0582	0.0084	8576.1667	0.4249	115.9747
Car03	IHGNDO	7312	0.0000	0.0000	0.0000	7312.0000	0.0953	0.0000	Car06	6590	0.0000	0.0000	0.0000	6590.0000	0.0067	0.0000
	HIGNDO		0.0000	0.0000	0.0000	7312.0000	0.0455	0.0000			0.0000	0.0000	0.0000	6590.0000	0.0051	0.0000
	HGNDO		0.0000	0.0074	0.0027	7331.8000	0.2018	26.0223			0.0000	0.0000	0.0000	6590.0000	0.0067	0.0000
	HMPA		0.0000	0.0254	0.0073	7365.2000	1.3745	42.6375			0.0000	0.0478	0.0089	6648.5333	0.1175	81.3858
	HWOA		0.0000	0.0074	0.0042	7342.6000	0.2496	26.7589			0.0000	0.0000	0.0000	6590.0000	0.0206	0.0000
	HEO		0.0000	0.0150	0.0090	7378.0667	0.2009	37.8919			0.0000	0.0347	0.0067	6634.3333	0.0380	63.7377
	HSCA		0.0000	0.1002	0.0146	7418.7333	0.4578	174.9874			0.0000	0.0347	0.0125	6672.4667	0.4517	77.5735
	HSSA		0.0000	0.1265	0.0180	7443.3000	0.0630	184.0828			0.0000	0.0247	0.0062	6631.1667	0.0329	53.6452
	HTSA		0.0000	0.1570	0.0631	7773.0667	0.6972	401.4574			0.0000	0.0900	0.0313	6796.0333	0.7878	180.7279
	HGA		0.0000	0.0150	0.0084	7373.6667	0.6146	38.4598			0.0000	0.0437	0.0098	6654.2667	0.6137	67.0020
Car04	IHGNDO	8003	0.0000	0.0000	0.0000	8003.0000	0.0139	0.0000	Car07	8366	0.0000	0.0000	0.0000	8366.0000	0.0111	0.0000
	HIGNDO		0.0000	0.0000	0.0000	8003.0000	0.0082	0.0000			0.0000	0.0000	0.0000	8366.0000	0.0063	0.0000
	HGNDO		0.0000	0.0000	0.0000	8003.0000	0.0146	0.0000			0.0000	0.0000	0.0000	8366.0000	0.0070	0.0000
	HMPA		0.0000	0.0014	0.0000	8003.3667	0.1111	1.9746			0.0000	0.0225	0.0009	8373.7000	0.1041	34.3581
	HWOA		0.0000	0.0000	0.0000	8003.0000	0.0205	0.0000			0.0000	0.0000	0.0000	8366.0000	0.0085	0.0000
	HEO		0.0000	0.0112	0.0004	8006.0000	0.0479	16.1555			0.0000	0.0135	0.0008	8372.8000	0.0484	25.6013
	HSCA		0.0000	0.0659	0.0068	8057.3667	0.1228	151.0125			0.0000	0.0634	0.0092	8443.0333	0.2099	146.8188
	HSSA		0.0000	0.0947	0.0115	8095.0000	0.0291	212.0660			0.0000	0.0000	0.0000	8366.0000	0.0167	0.0000
	HTSA		0.0000	0.1369	0.0485	8390.7667	0.4935	366.4514			0.0000	0.0865	0.0233	8560.8333	0.4741	228.3998
	HGA		0.0000	0.0000	0.0000	8003.0000	0.1037	0.0000			0.0000	0.0069	0.0008	8372.9667	0.1663	17.8783

, which shows the superiority of IHGNDO, HIGNDO, and HGNDO on most test cases. Broadly speaking, IHGNDO could reach the best-known value for all instances and fulfill a value of 0 for ARE, WRE, BRE, and SD, in addition to its outperformance in the time metric for two instances. Meanwhile, HIGNDO could fulfill the best-known values of seven instances within all independent runs while failing incoming true the best-known value for Car04 instance in all runs. In addition, HIGNDO could be the best for the time metric in five instances. Generally, IHGNDO could occupy the first rank for the makespan metric and the second rank after HIGNDO in terms of the CPU time. 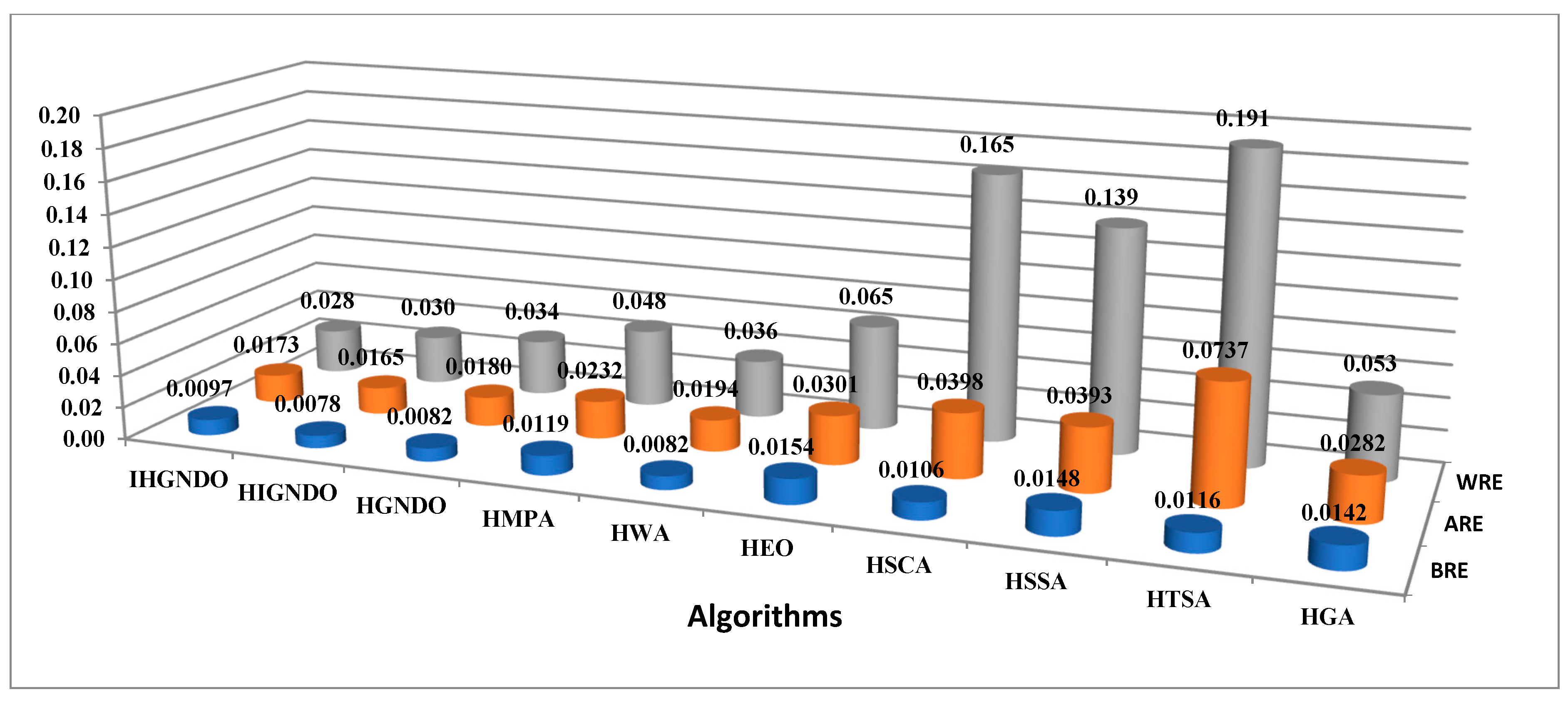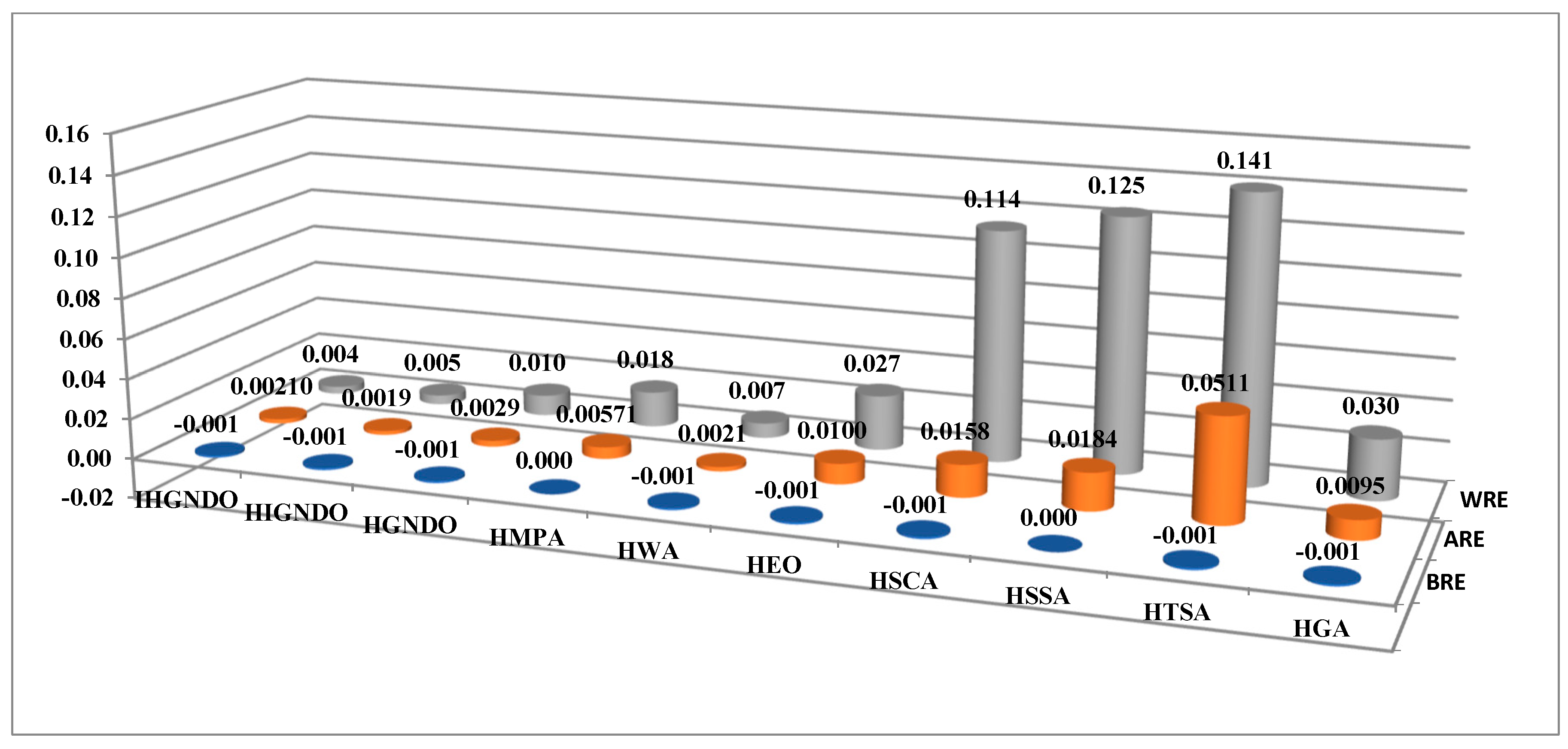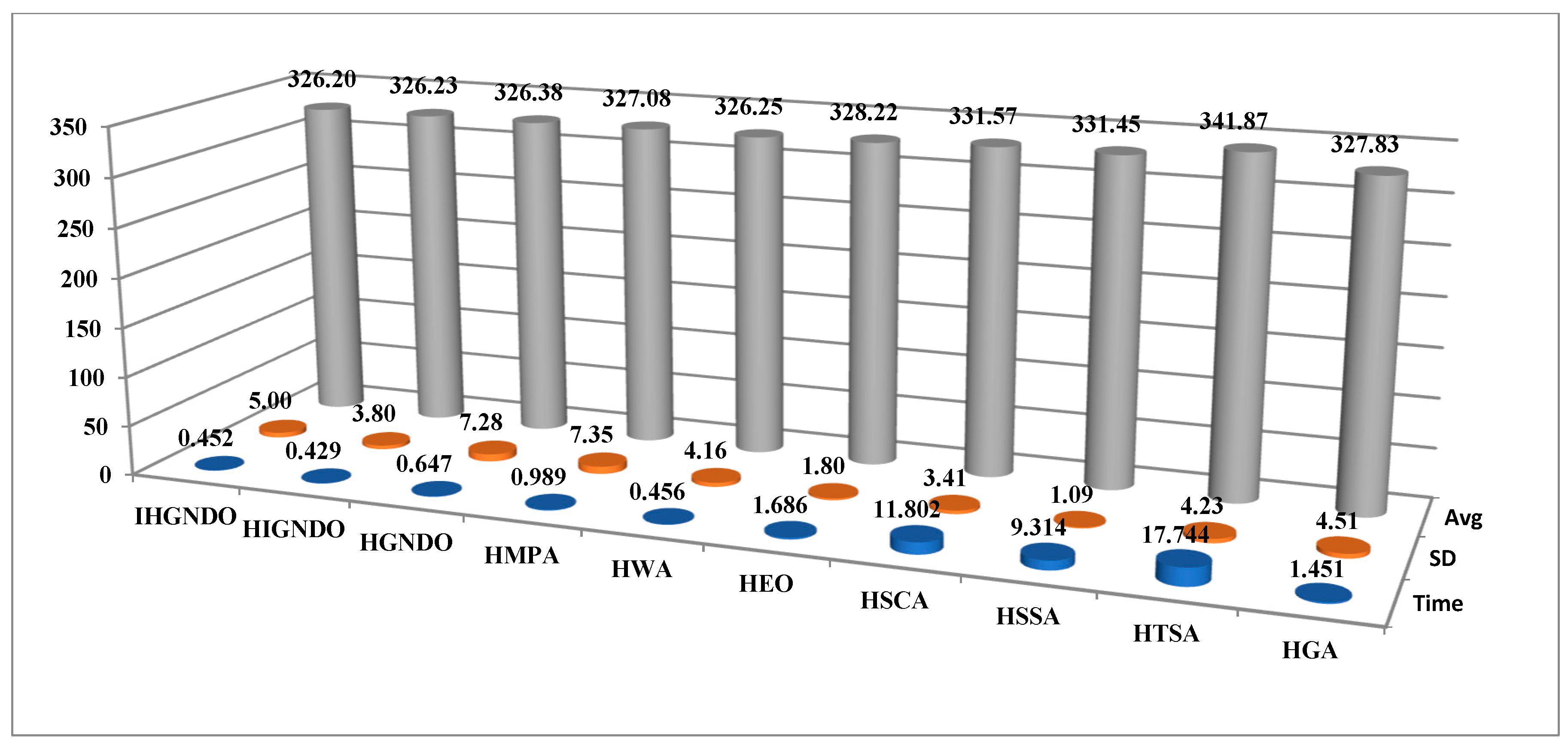Additionally, Figure 4 presents the average of ARE, WRE, and BRE on all instances, which shows that IHGNDO could occupy the first rank for WRE and ARE, while it is competitive with the others in terms of WRE. Regarding SD, an average of makespan, and time metrics depicted in Figure 5, HIGNDO comes in the first rank before IHGNDO for the time metric; IHGNDO could be the best for time and Avg metrics. Ultimately, Figure 6, Figure 7 and Figure 8 compare the makespan values obtained by the different algorithms based on the boxplot. Those figures show the superiority of IHGNDO in terms of the average makespan. From the above analysis, IHGNDO could achieve positive outcomes reasonably, which makes it a strong alternative to the existing algorithms developed for tackling the PFSSP.

5.2. Comparison under Reeves

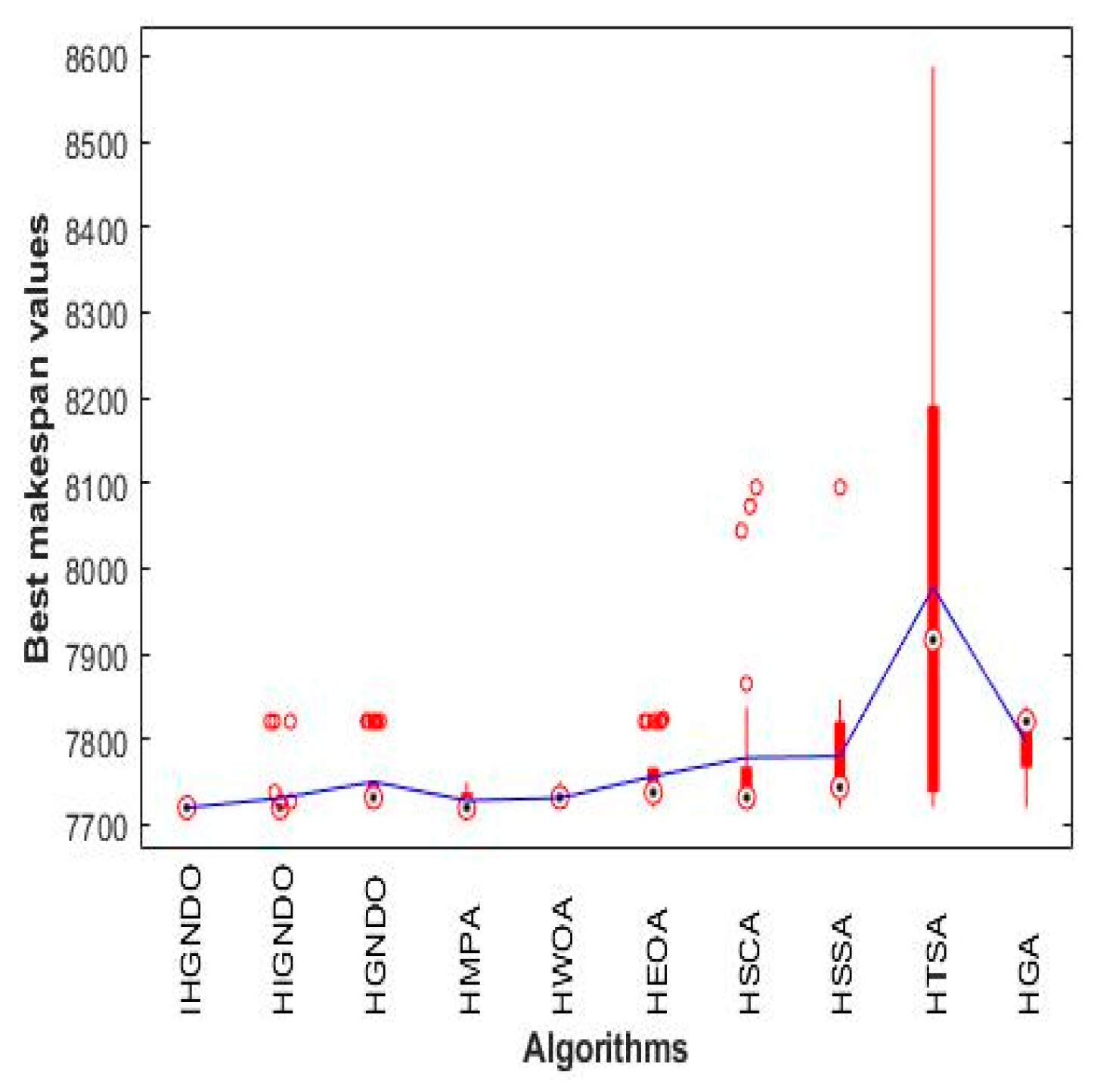
In this subsection, the proposed algorithms will be verified on the Reeve instances to verify their efficacy and compared to some state-of-the-art algorithms to show their superiority. After running and calculation, various metrics values are introduced in

Table 5. Comparison on the Reeve instances⸺(reC01–reC23).

Inst	Algorithm	${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD	Inst	${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD
reC01	IHGNDO	1247	0.0000	0.0016	0.0016	1248.9333	0.6132	0.3590	reC13	1930	0.0031	0.0249	0.0116	1952.3333	0.8099	12.3216
	HIGNDO		0.0000	0.0032	0.0015	1248.8667	0.6007	0.7180			0.0026	0.0212	0.0122	1953.5000	0.8224	10.1415
	HGNDO		0.0000	0.0144	0.0026	1250.2667	0.9136	3.3559			0.0052	0.0430	0.0196	1967.8000	0.9858	17.7696
	HMPA		0.0016	0.0265	0.0065	1255.1000	2.4415	8.9976			0.0093	0.0425	0.0191	1966.7667	2.6874	14.5709
	HWOA		0.0016	0.0465	0.0047	1252.8333	1.1080	10.3765			0.0026	0.0415	0.0166	1962.0000	1.4368	17.8419
	HEO		0.0016	0.0634	0.0133	1263.6333	0.3845	19.3503			0.0067	0.0974	0.0307	1989.1667	0.3930	31.0656
	HSCA		0.0000	0.1291	0.0112	1260.9667	0.8572	35.4847			0.0016	0.1528	0.0450	2016.8000	0.9266	93.9260
	HSSA		0.0016	0.1588	0.0401	1296.9667	0.1210	63.0611			0.0083	0.0383	0.0232	1974.7667	0.1342	15.1738
	HTSA		0.0016	0.1764	0.0640	1326.8000	1.0840	89.2007			0.0026	0.1741	0.0594	2044.6333	1.1585	125.2979
	HGA		0.0016	0.0634	0.0117	1261.5333	0.9869	19.5699			0.0088	0.0440	0.0231	1974.5667	1.2510	18.9520
reC03	IHGNDO	1109	0.0000	0.0018	0.0011	1110.2000	0.4757	0.9798	reC15	1950	0.0056	0.0200	0.0118	1973.0667	0.8296	6.4028
	HIGNDO		0.0000	0.0027	0.0013	1110.4667	0.5128	1.0873			0.0067	0.0308	0.0125	1974.4667	0.8251	9.7151
	HGNDO		0.0000	0.0036	0.0013	1110.4000	0.7720	1.1431			0.0026	0.0400	0.0172	1983.6000	0.9996	18.6683
	HMPA		0.0000	0.0216	0.0035	1112.8333	2.4883	5.8085			0.0082	0.0426	0.0230	1994.9333	2.6970	23.7079
	HWOA		0.0000	0.0090	0.0013	1110.4333	0.7880	1.9093			0.0036	0.0426	0.0195	1988.1000	1.4496	21.4357
	HEO		0.0000	0.0911	0.0124	1122.7000	0.3519	19.8899			0.0118	0.0923	0.0298	2008.1667	0.3997	32.4860
	HSCA		0.0000	0.1623	0.0361	1149.0667	0.8191	57.8653			0.0051	0.1369	0.0295	2007.5000	0.9629	49.8108
	HSSA		0.0018	0.1587	0.0314	1143.8000	0.1230	55.4403			0.0108	0.1246	0.0314	2011.3000	0.1352	40.7015
	HTSA		0.0000	0.1659	0.0768	1194.2000	1.0001	67.7655			0.0056	0.1441	0.0634	2073.6667	1.1775	103.7662
	HGA		0.0000	0.0379	0.0091	1119.1000	0.8489	11.2141			0.0082	0.0508	0.0266	2001.8000	1.2887	25.2645
reC05	IHGNDO	1242	0.0024	0.0024	0.0024	1245.0000	0.6343	1.9746	reC17	1902	0.0000	0.0484	0.0225	1944.7000	0.8176	17.6921
	HIGNDO		0.0024	0.0113	0.0027	1245.3667	0.6424	1.9746			0.0000	0.0389	0.0245	1948.5333	0.8119	15.7623
	HGNDO		0.0024	0.0113	0.0044	1247.5000	0.8638	3.8536			0.0079	0.0705	0.0319	1962.7000	1.0376	25.6621
	HMPA		0.0024	0.0217	0.0060	1249.4000	2.2647	6.5605			0.0105	0.0715	0.0337	1966.0667	2.9044	26.5806
	HWOA		0.0024	0.0113	0.0063	1249.8333	0.9428	4.3134			0.0000	0.0436	0.0302	1959.4333	1.3958	16.1734
	HEO		0.0024	0.0217	0.0102	1254.7000	0.3134	8.7527			0.0131	0.0615	0.0364	1971.2000	0.3743	20.4163
	HSCA		0.0024	0.0902	0.0178	1264.1333	0.7352	33.1831			0.0047	0.1456	0.0397	1977.4333	0.8843	57.9555
	HSSA		0.0024	0.1272	0.0241	1271.9000	0.1013	45.6350			0.0110	0.0589	0.0341	1966.9000	0.1288	22.1696
	HTSA		0.0024	0.1449	0.0401	1291.8000	0.9273	54.0724			0.0131	0.1887	0.0838	2061.4667	1.0997	108.3872
	HGA		0.0024	0.0250	0.0061	1249.6000	0.8465	7.5745			0.0179	0.0657	0.0369	1972.1333	1.1925	22.5961
reC07	IHGNDO	1566	0.0000	0.0115	0.0070	1576.9333	0.6078	8.4929	reC19	2017	0.0436	0.0645	0.0514	2120.7000	1.6120	9.2273
	HIGNDO		0.0000	0.0115	0.0039	1572.0667	0.5225	8.4456			0.0407	0.0649	0.0515	2120.8000	1.5874	10.9891
	HGNDO		0.0000	0.0115	0.0053	1574.3667	0.6376	8.7349			0.0446	0.0709	0.0516	2121.0667	1.9258	11.9022
	HMPA		0.0000	0.0383	0.0112	1583.4667	2.3519	10.6356			0.0471	0.1715	0.0613	2140.7000	3.5589	43.3083
	HWOA		0.0000	0.0115	0.0053	1574.2333	0.9048	8.4565			0.0436	0.0704	0.0538	2125.4333	2.4811	14.5113
	HEO		0.0013	0.0383	0.0160	1591.1000	0.3607	15.4561			0.0471	0.0788	0.0655	2149.0333	0.5302	14.6708
	HSCA		0.0000	0.1277	0.0272	1608.5333	0.8516	60.5286			0.0456	0.2152	0.0820	2182.3000	1.2905	112.9936
	HSSA		0.0000	0.0383	0.0153	1590.0000	0.1187	13.4313			0.0545	0.2181	0.0767	2171.7000	0.2010	77.7321
	HTSA		0.0000	0.1750	0.0684	1673.1000	1.1179	97.7628			0.0491	0.2583	0.1413	2302.0667	1.5909	159.0463
	HGA		0.0000	0.0230	0.0110	1583.3000	1.1020	7.7981			0.0530	0.0912	0.0680	2154.2333	1.5769	19.2036
reC09	IHGNDO	1537	0.0000	0.0241	0.0068	1547.4000	0.5749	11.7774	reC21	2011	0.0174	0.0224	0.0189	2049.0000	1.6123	2.2361
	HIGNDO		0.0000	0.0325	0.0065	1547.0667	0.5424	13.5153			0.0174	0.0194	0.0187	2048.5333	1.5865	1.9276
	HGNDO		0.0000	0.0390	0.0085	1550.1000	0.7766	14.3256			0.0174	0.0214	0.0185	2048.1333	2.0050	2.2470
	HMPA		0.0000	0.0410	0.0201	1567.9000	2.4736	16.1211			0.0174	0.0254	0.0192	2049.7000	3.7467	2.7221
	HWOA		0.0000	0.0416	0.0176	1564.0000	1.1298	16.4033			0.0104	0.0194	0.0186	2048.3333	2.5842	3.5056
	HEO		0.0085	0.0885	0.0251	1575.5667	0.3463	21.1624			0.0174	0.0363	0.0238	2058.7667	0.5330	10.2524
	HSCA		0.0065	0.1516	0.0387	1596.4333	0.8261	66.8265			0.0174	0.1914	0.0344	2080.1667	1.2679	92.3263
	HSSA		0.0072	0.1314	0.0308	1584.2667	0.1162	40.1355			0.0194	0.1875	0.0395	2090.3667	0.2040	91.4033
	HTSA		0.0000	0.1913	0.0501	1614.0333	1.0061	89.8719			0.0174	0.1994	0.0864	2184.6667	1.5538	156.4899
	HGA		0.0007	0.0416	0.0222	1571.1667	1.0296	15.5844			0.0174	0.0537	0.0266	2064.5333	1.5350	17.1692
reC11	IHGNDO	1431	0.0000	0.0210	0.0070	1441.0000	0.6339	8.4735	reC23	2011	0.0050	0.0234	0.0120	2035.0333	1.6254	12.0706
	HIGNDO		0.0000	0.0356	0.0091	1444.0667	0.5742	13.0024			0.0045	0.0338	0.0131	2037.2667	1.5891	14.7827
	HGNDO		0.0000	0.0314	0.0153	1452.8333	0.8737	11.5126			0.0050	0.0264	0.0141	2039.4333	1.8821	14.7912
	HMPA		0.0000	0.0894	0.0175	1456.1000	2.1720	23.8039			0.0060	0.0363	0.0220	2055.2333	3.4993	14.7098
	HWOA		0.0000	0.0594	0.0176	1456.2333	1.1155	18.7664			0.0035	0.0318	0.0165	2044.1333	2.4370	16.3477
	HEO		0.0049	0.0587	0.0240	1465.3000	0.3542	21.4043			0.0154	0.0467	0.0298	2070.9667	0.5241	16.7381
	HSCA		0.0000	0.1600	0.0378	1485.0667	0.7505	72.6443			0.0050	0.1611	0.0278	2066.8667	1.2726	70.7327
	HSSA		0.0000	0.1593	0.0273	1470.0333	0.1148	49.8233			0.0104	0.1785	0.0418	2095.1333	0.1994	77.4277
	HTSA		0.0000	0.1824	0.0733	1535.9333	0.9973	108.4789			0.0080	0.2004	0.0755	2162.8667	1.5456	149.6422
	HGA		0.0000	0.0496	0.0249	1466.6000	0.9958	18.7183			0.0050	0.0383	0.0266	2064.5667	1.5332	16.6046

and

Table 6. Comparison on the Reeve instances⸺(reC25-reC41).

Inst	Algorithm	${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD	Inst	${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD
reC25	IHGNDO	2513	0.0092	0.0342	0.0220	2568.2667	1.8688	16.9232	reC35	3277	0.0000	0.0000	0.0000	3277.0000	1.1526	0.0000
	HIGNDO		0.0131	0.0390	0.0259	2577.9667	1.8352	17.1065			0.0000	0.0000	0.0000	3277.0000	0.9999	0.0000
	HGNDO		0.0123	0.0390	0.0240	2573.2667	2.0970	19.5276			0.0000	0.0000	0.0000	3277.0000	0.6110	0.0000
	HMPA		0.0139	0.0493	0.0319	2593.2000	3.8974	22.4179			0.0000	0.0034	0.0005	3278.7667	3.6242	3.7299
	HWOA		0.0064	0.0458	0.0270	2580.8667	3.0302	21.6791			0.0000	0.0000	0.0000	3277.0000	1.2182	0.0000
	HEO		0.0163	0.0505	0.0373	2606.6333	0.5912	21.3690			0.0000	0.0275	0.0026	3285.6333	0.9912	16.8750
	HSCA		0.0107	0.1675	0.0493	2637.0000	1.4448	118.6139			0.0000	0.1202	0.0047	3292.5333	1.6490	70.4134
	HSSA		0.0111	0.0517	0.0362	2604.0667	0.2289	23.8005			0.0000	0.1428	0.0148	3325.4000	0.4445	125.6247
	HTSA		0.0147	0.1823	0.0729	2696.1000	1.7504	155.5443			0.0000	0.1385	0.0607	3476.0333	2.6465	199.8649
	HGA		0.0171	0.0505	0.0348	2600.3333	1.8883	19.7017			0.0000	0.0284	0.0029	3286.6667	2.6794	16.4100
reC27	IHGNDO	2373	0.0088	0.0388	0.0220	2425.1667	1.8698	17.2937	reC37	4951	0.0297	0.0562	0.0448	5172.7667	17.3840	31.6698
	HIGNDO		0.0097	0.0367	0.0191	2418.3333	1.8362	18.8279			0.0250	0.0578	0.0410	5154.2333	17.8260	34.6763
	HGNDO		0.0105	0.0641	0.0222	2425.6000	2.1352	28.8335			0.0218	0.0523	0.0384	5141.0000	20.0077	41.1671
	HMPA		0.0093	0.0426	0.0226	2426.5333	3.9037	17.9327			0.0382	0.0673	0.0495	5196.1333	13.1585	34.4710
	HWOA		0.0088	0.0396	0.0197	2419.6667	3.0528	19.2238			0.0315	0.0529	0.0426	5161.7333	27.3170	31.0987
	HEO		0.0147	0.0615	0.0303	2444.8667	0.5939	25.0941			0.0458	0.0766	0.0562	5229.4333	2.4868	35.6779
	HSCA		0.0097	0.1774	0.0279	2439.1333	1.4628	67.6307			0.0307	0.2135	0.0681	5287.9667	6.5152	262.3587
	HSSA		0.0139	0.1909	0.0364	2459.4667	0.2311	71.7378			0.0400	0.0755	0.0563	5229.8000	1.4355	42.7398
	HTSA		0.0122	0.2174	0.0778	2557.7333	1.7549	192.4243			0.0372	0.2127	0.0757	5325.9000	7.3935	288.5887
	HGA		0.0122	0.0590	0.0300	2444.2333	1.8881	24.9475			0.0404	0.0689	0.0562	5229.4667	7.4647	38.0059
reC29	IHGNDO	2287	0.0087	0.0468	0.0237	2341.1667	1.8542	22.1105	reC39	5087	0.0179	0.0352	0.0255	5216.5333	17.2536	20.5065
	HIGNDO		0.0031	0.0704	0.0259	2346.3333	1.8314	33.3320			0.0090	0.0271	0.0188	5182.6667	18.4729	22.1891
	HGNDO		0.0057	0.0503	0.0241	2342.1333	2.1269	25.1869			0.0094	0.0297	0.0208	5192.7333	20.9996	26.3438
	HMPA		0.0144	0.0647	0.0319	2359.8667	3.8849	27.4733			0.0173	0.0472	0.0293	5235.8667	13.1493	39.1550
	HWOA		0.0092	0.0582	0.0260	2346.5667	3.0756	28.2756			0.0132	0.0299	0.0202	5189.8667	27.4727	17.3661
	HEO		0.0240	0.1552	0.0470	2394.4667	0.6039	54.5422			0.0283	0.0554	0.0406	5293.4000	2.5226	38.4106
	HSCA		0.0153	0.2239	0.0772	2463.5000	1.4498	174.4799			0.0155	0.1928	0.0554	5368.9667	6.6178	299.1470
	HSSA		0.0210	0.2147	0.0600	2424.1667	0.2285	125.7885			0.0348	0.2048	0.0575	5379.3667	1.4566	230.4488
	HTSA		0.0149	0.2317	0.0726	2453.1000	1.7457	185.6707			0.0161	0.2058	0.0817	5502.6333	7.2613	387.9788
	HGA		0.0162	0.0700	0.0359	2369.1000	1.8481	28.7557			0.0261	0.0499	0.0368	5274.1000	7.0018	28.4843
reC31	IHGNDO	3045	0.0085	0.0276	0.0207	3108.0000	4.8699	18.6744	reC41	4960	0.0302	0.0569	0.0422	5169.2000	17.2578	31.5546
	HIGNDO		0.0039	0.0276	0.0131	3084.9667	4.7237	19.3278			0.0252	0.0466	0.0368	5142.5667	18.9444	30.6884
	HGNDO		0.0033	0.0276	0.0145	3089.2000	5.7295	24.3604			0.0204	0.0546	0.0359	5137.9333	20.3596	38.5650
	HMPA		0.0151	0.0309	0.0245	3119.5000	6.4491	12.0796			0.0310	0.0575	0.0425	5170.6667	13.1488	34.8715
	HWOA		0.0026	0.0348	0.0177	3098.9333	7.4365	26.6632			0.0236	0.0514	0.0373	5144.8667	27.8736	29.6533
	HEO		0.0197	0.0525	0.0334	3146.8000	1.0823	20.8477			0.0369	0.0722	0.0527	5221.5333	2.4905	36.3187
	HSCA		0.0154	0.1846	0.0547	3211.6000	2.6588	187.0270			0.0349	0.2119	0.0516	5216.0667	6.6015	151.4369
	HSSA		0.0187	0.2125	0.0695	3256.5333	0.5026	203.7153			0.0399	0.0704	0.0549	5232.0667	1.4595	36.8953
	HTSA		0.0138	0.1941	0.0663	3247.0000	3.1755	214.0903			0.0331	0.2407	0.0648	5281.2000	7.3321	276.2412
	HGA		0.0223	0.0693	0.0342	3149.2000	3.0078	27.9552			0.0411	0.0774	0.0547	5231.3333	7.0161	35.3802
reC33	IHGNDO	3114	0.0058	0.0109	0.0084	3140.1333	4.8495	2.1868
	HIGNDO		0.0000	0.0202	0.0085	3140.5000	4.7668	8.2735
	HGNDO		0.0013	0.0202	0.0078	3138.3333	5.6585	11.2497
	HMPA		0.0083	0.0202	0.0109	3147.9667	6.3048	13.6808
	HWOA		0.0083	0.0083	0.0083	3140.0000	7.0735	0.0000
	HEO		0.0071	0.0369	0.0160	3163.9000	1.0421	20.2227
	HSCA		0.0013	0.1532	0.0190	3173.2000	2.6069	98.5341
	HSSA		0.0039	0.1689	0.0250	3191.8667	0.4736	118.6611
	HTSA		0.0022	0.1811	0.0923	3401.2667	3.0636	240.2365
	HGA		0.0080	0.0466	0.0148	3160.0000	2.8183	24.0680

to observe the performance of the algorithms. Observing those tables shows the superiority of the proposed algorithms: IHGNDO, HIGNDO, and HGNDO for most performance metrics in most test cases. To confirm that, Figure 9 and Figure 10 are presented to show the average of each performance metric on all instances in the Reeves benchmark; those figures elaborate the superiority of HIGNDO over the others in terms of BRE, ARE, and Avg makespan, while IHGNDO could outperform in terms of SD and come in the six ranks for the time metric. Since the proposed algorithms could outperform the others in terms of final accuracy in a reasonable time, they are a strong alternative to the existing algorithms adapted for tackling the same problem. 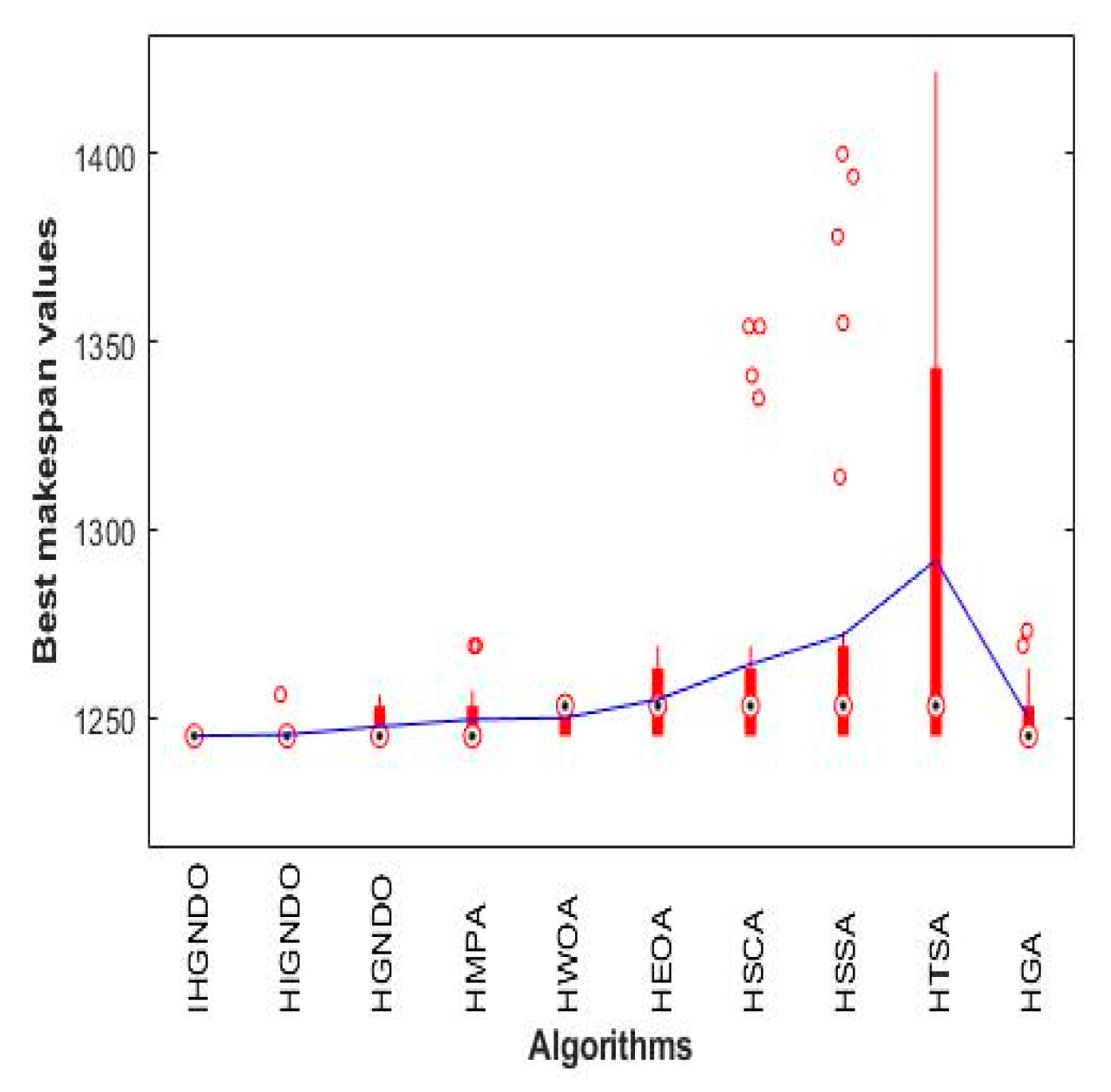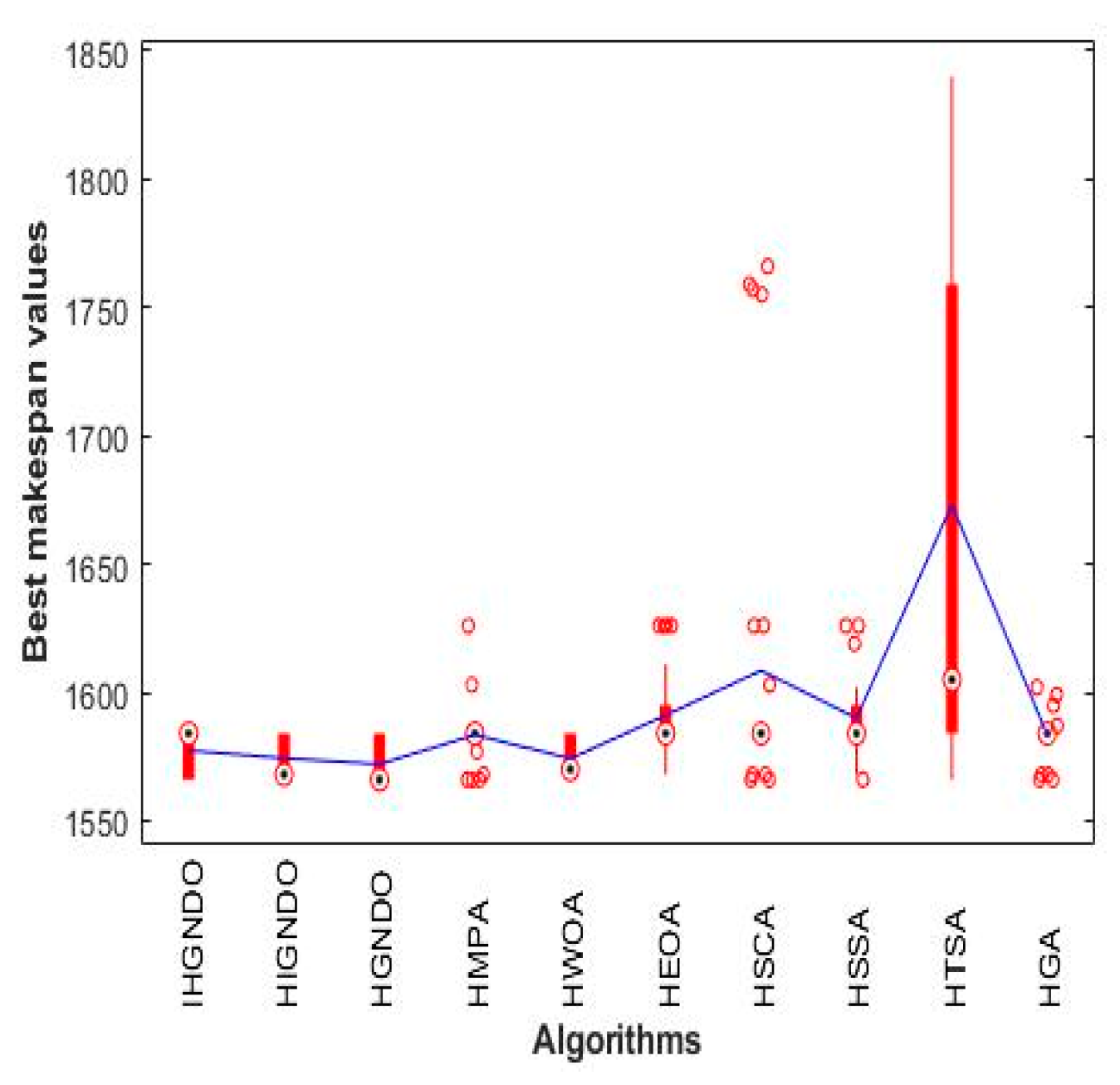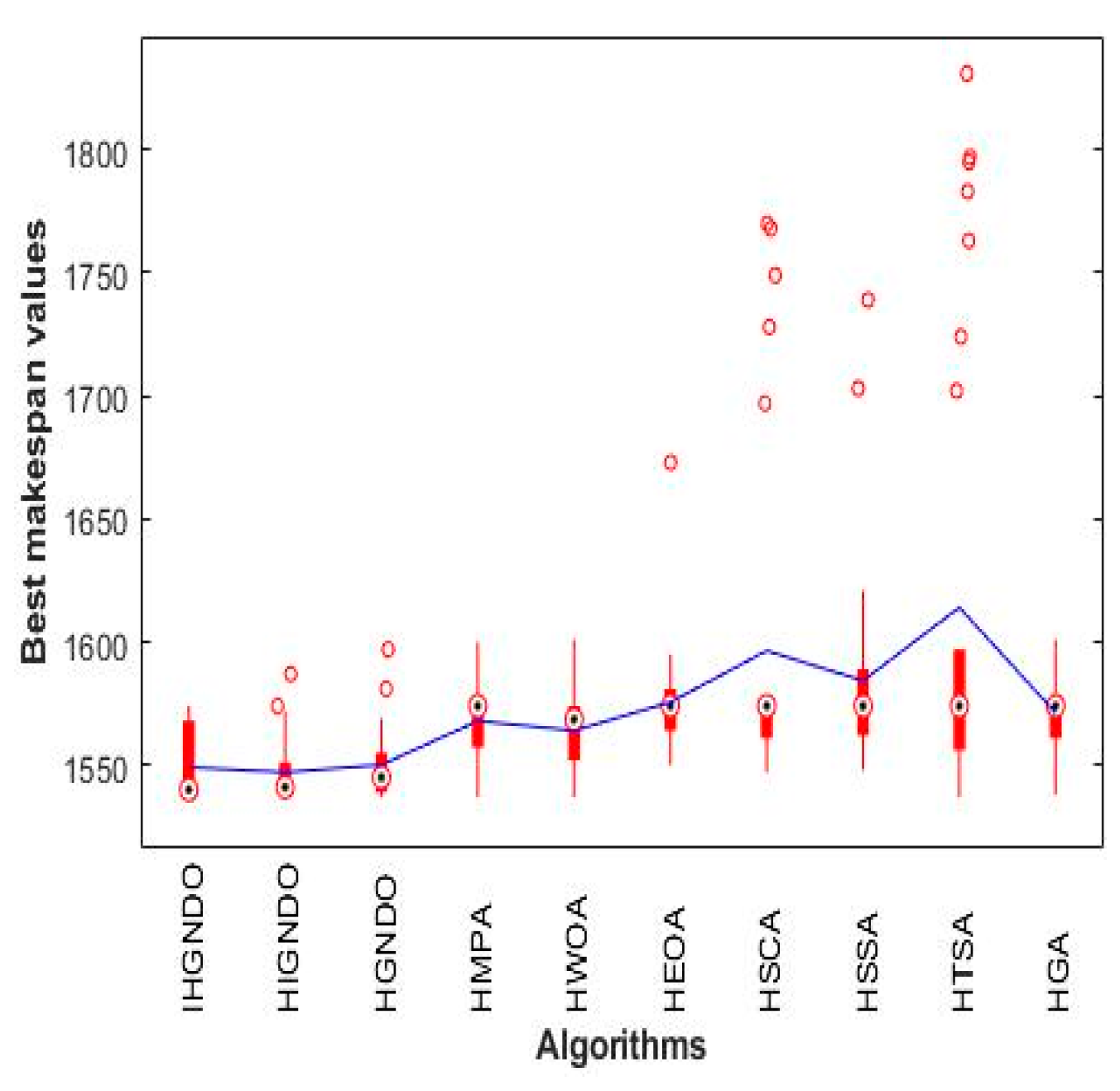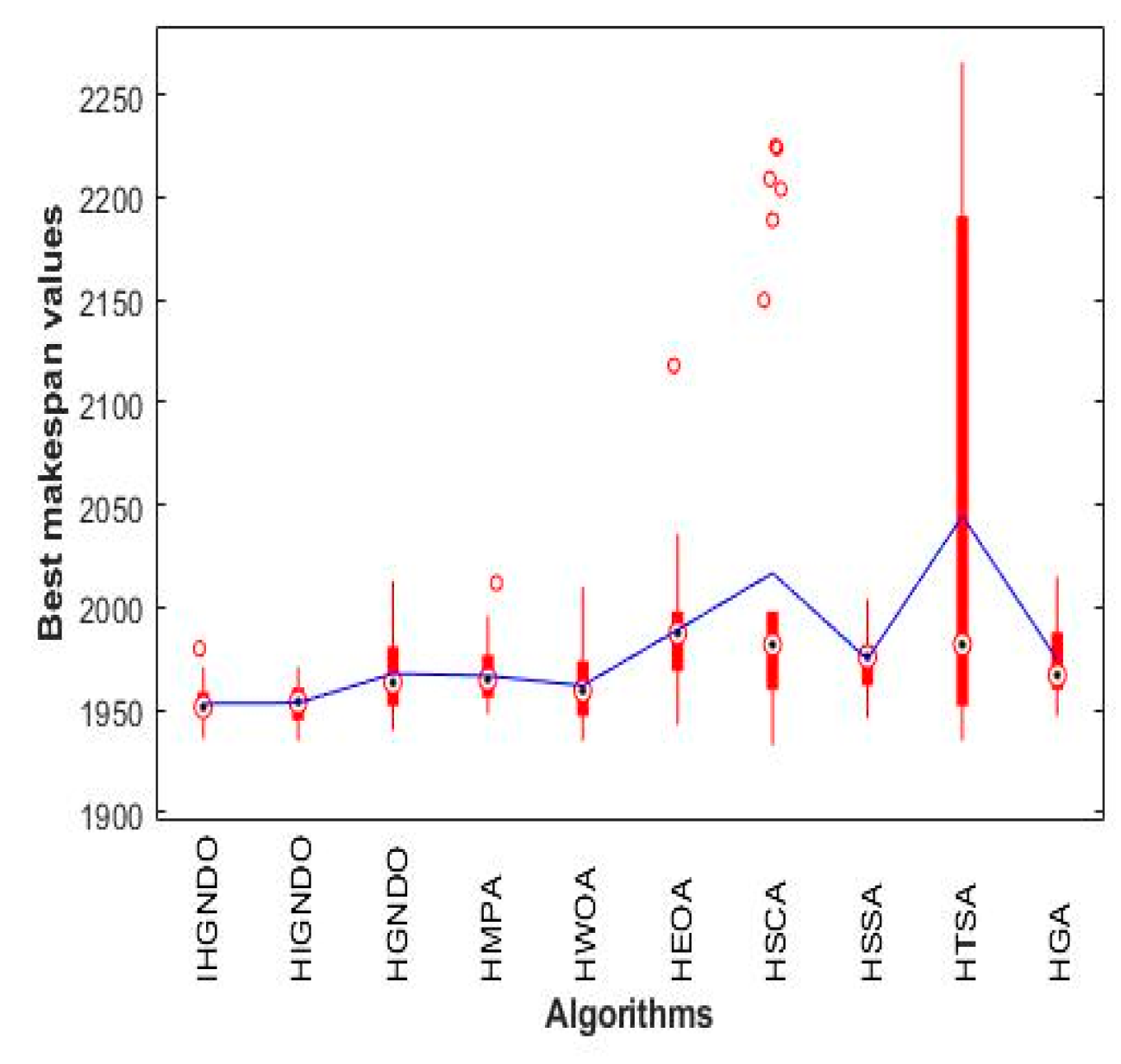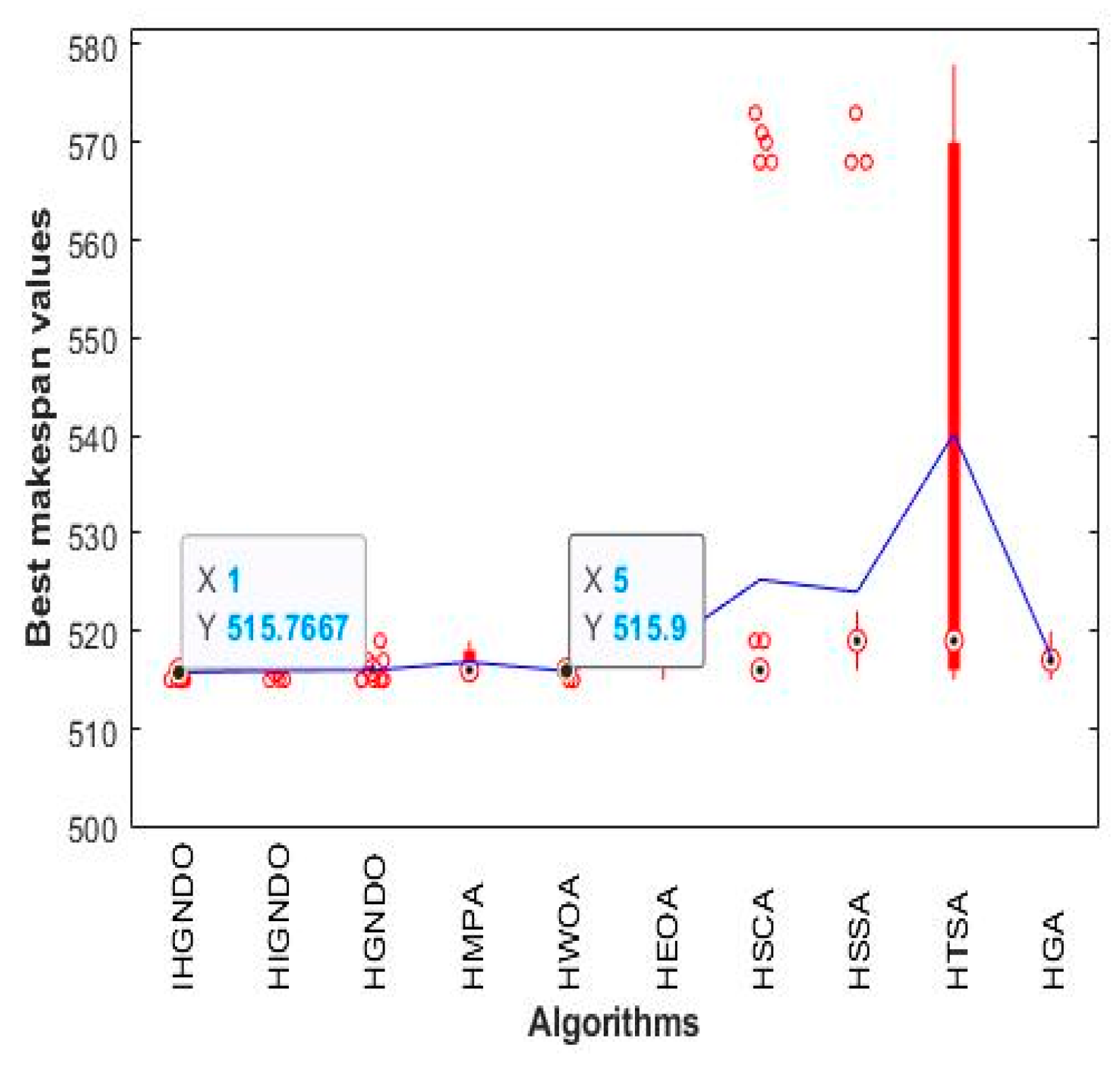In addition, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 show the boxplot of the makespan values obtained by various algorithms on the instances from reC01 to reC17, which confirm the superiority of IHGNDO and HIGNDO in comparison to the others.

5.3. Comparison under Heller

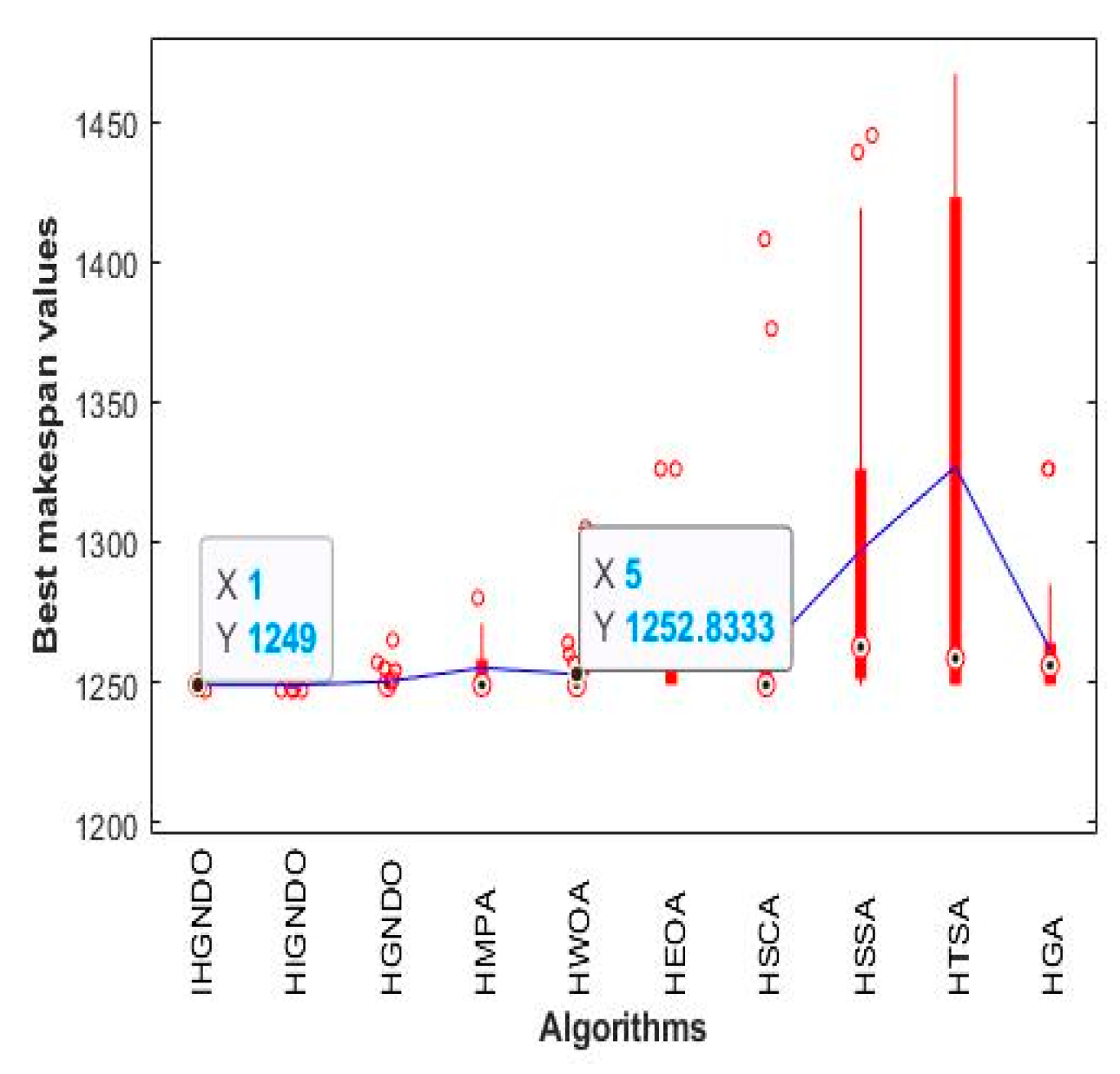
Here, the proposed algorithms will be compared to the other algorithms under the Heller instances. In

Table 7. Comparison on the Heller instances.

Inst	Algorithm	${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD	Inst	${\mathit{Z}}^{*}$	BRE	WRE	ARE	${\mathit{Z}}_{\mathit{A}\mathit{v}\mathit{g}}$	Time(MS)	SD
Hel1	IHGNDO	516	−0.0019	0.0000	−0.0005	515.7667	6.3275	0.4230	He12	136	0.0000	0.0074	0.0040	136.5333	0.6642	0.4819
	HIGNDO		−0.0019	0.0019	−0.0001	515.9333	7.0816	0.3590			0.0000	0.0074	0.0040	136.5333	0.5195	0.4819
	HGNDO		−0.0019	0.0058	−0.0001	515.9667	13.8456	0.7520			0.0000	0.0147	0.0059	136.8000	0.7227	0.5416
	HMPA		0.0000	0.0058	0.0016	516.8333	12.3427	1.0355			0.0000	0.0294	0.0098	137.3333	2.3587	0.9428
	HWOA		−0.0019	0.0000	−0.0002	515.9000	7.5461	0.3000			0.0000	0.0147	0.0044	136.6000	0.7650	0.6110
	HEO		−0.0019	0.0174	0.0045	518.3333	3.2206	2.0221			0.0000	0.0368	0.0154	138.1000	0.3749	1.3503
	HSCA		−0.0019	0.1105	0.0180	525.2667	6.0083	20.0382			0.0000	0.1176	0.0137	137.8667	0.8138	3.5659
	HSSA		0.0000	0.1105	0.0155	524.0000	2.0489	15.3188			0.0000	0.1397	0.0213	138.9000	0.1299	3.3101
	HTSA		−0.0019	0.1202	0.0470	540.2333	7.4086	27.0502			0.0000	0.1618	0.0551	143.5000	1.0492	8.4370
	HGA		−0.0019	0.0078	0.0028	517.4667	7.9189	1.4314			0.0000	0.0515	0.0162	138.2000	1.0993	1.4697

, various performance metrics values are exposed that show the superiority of IHGNDO in terms of ARE and $Z_{Avg}$ for the Hel1 instance and competitiveness with HIGNDO on Hel2 in terms of WRE, ARE, Time, SD, and $Z_{Avg}$. Furthermore, for doing that, Figure 20 and Figure 21 are exposed to show the average of WRE, ARE, SD, Time, Avg makespan, and BRE; those figures showed that IHGNDO is the best in terms of ARE, WRE, and Avg makespan; HIGNDO could be superior for Time and SD metrics; and all algorithms are competitive for BRE metric. Figure 22 and Figure 23 depict the boxplot of makespan values produced in 30 independent runs on Hel1 and Hel2 using various optimization algorithms. From those figures, it is concluded that IHGNDO is the best.

6. Conclusions and Future Work

As a new attempt to produce a new algorithm that could tackle the permutation flow shop scheduling problem (PFSSP), in this paper, we investigate the performance of a novel optimization algorithm, namely generalized normal distribution (GNDO), for solving this problem. Due to the continuous nature of GNDO and the discreteness of PFSSP, the largest ranked value (LRV) rule is used to make GNDO applicable for solving this problem. In a new attempt to improve the performance of the discrete GNDO, a new version of GNDO, namely a hybrid GNDO (HGNDO), is developed based on applying a local search strategy to improve the quality of the optimal global solution. In addition, the GNDO has an improvement by also applying the swap mutation operator on the best-so-far solution to find better solutions, and this improvement is integrated with HGNDO to produce a new version, namely HIGNDO. Finally, the scramble mutation operator is integrated with the local search strategy to utilize each attempt done by this local search for improving the best-so-far solution as much as possible; this local search is used with the improved GNDO using the swap mutation operator to produce a strong version abbreviated as IHGNDO for tackling the PFSSP. To validate the performance of the algorithms accurately, 41 common instances used widely in the literature are employed. Additionally, to check the proposed superiority, they are extensively compared with some well-established recently-published optimization algorithms using various performance metrics. The findings show that HIGNDO and IHGNDO could be superior in terms of standard deviation, CPU time, and makespan. Those findings also show that IHGNDO is better than HIGNDO for most performance metrics, and this confirms the effectiveness of our improvement to the local search strategy. Our future work involves applying those proposed algorithms for tackling other types of the flow shop scheduling problem.