Niching Grey Wolf Optimizer for Multimodal Optimization Problems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Grey Wolf Optimizer
- Tracking, chasing, proceeding towards the target;
- Chasing, encompassing, distressing the target;
- Attacking the target.
2.2. Niching Technique
2.3. Modified Velocity Update Equation
2.4. Local Search
| Algorithm 1 Local Search |
|
1: Update the present Pbest by NGWO 2: for i = 1 to NP (number of wolves) 3: Search Pbest_nearesti (the nearest Pbest member to Pbesti) 4: if fit(Pbest_nearesti) < = fit(Pbesti) 5: Temp = Pbesti + 1.5 * rand * (Pbest_nearesti–Pbesti) 6: else 7: Temp = Pbesti + 1.5 * rand * (Pbesti–Pbest_nearesti) 8: end if 9: Check for bounds violation, and assess Temp. 10: if fit(Temp) < fit(Pbesti) 11: Pbesti = Temp 12: end if 13: end for |
3. Result and Discussion
3.1. Experimental Setup
3.2. Classical Benchmark Functions
3.2.1. Exploitation Analysis
3.2.2. Exploration Analysis and Local Optima Avoidance
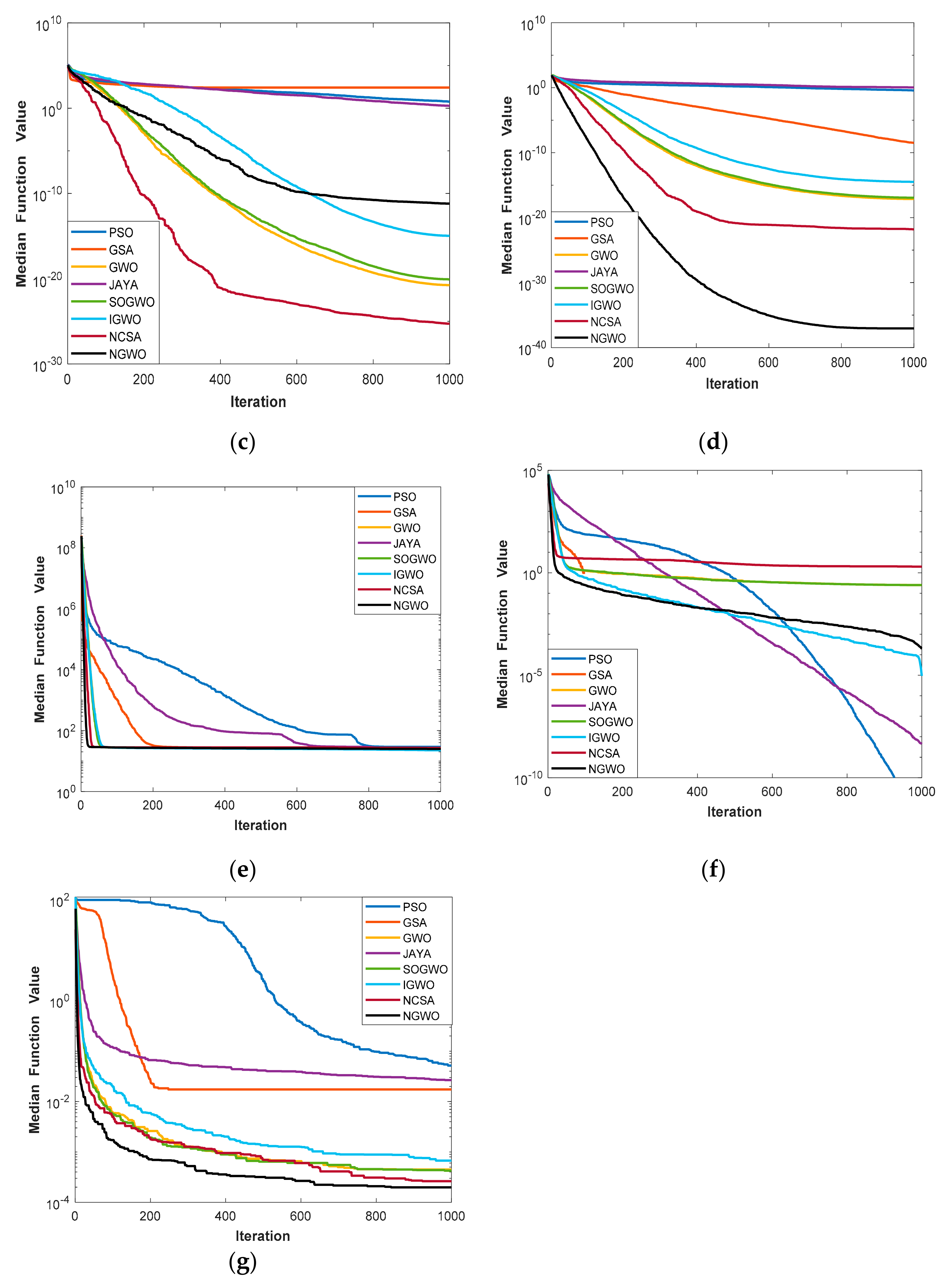
3.2.3. Convergence Analysis
3.2.4. Ranking of the Algorithms
3.3. Engineering Application of NGWO
3.3.1. Welded Beam Design
3.3.2. Tension–Compression Coil Spring Design
3.3.3. Three Bars Truss Design
3.4. Results of the Engineering Application
3.4.1. Optimization Result of Welded Beam Design
3.4.2. Result of Tension–Compression Coil Spring Design
3.4.3. Three Bars Truss Design Result
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Tang, Y.; Li, J.; Hua, C.; Guan, X. Dynamic multi-swarm particle swarm optimizer with cooperative learning strategy. Appl. Soft Comput. 2015, 29, 169–183. [Google Scholar] [CrossRef]
- Qu, B.; Liang, J.; Suganthan, P. Niching particle swarm optimization with local search for multi-modal optimization. Inf. Sci. 2012, 197, 131–143. [Google Scholar] [CrossRef]
- Al Amin, M.; Abdul-Rani, A.M.; Ahmed, R.; Rao, T.V.V.L.N. Multiple-objective optimization of hydroxyapatite-added EDM technique for processing of 316L-steel. Mater. Manuf. Process. 2021, 36, 1–12. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, MHS’95, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient adaptive scheme for global optimization over continuous spaces. J. Glob. Optim. 1995, 23, 1–15. [Google Scholar]
- Dorigo, M.; Gambardella, L. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Zhou, Y. A novel global convergence algorithm: Bee collecting pollen algorithm. In Advanced Intelligent Computing Theories and Applications. With Aspects of Artificial Intelligence. ICIC 2008. Lecture Notes in Computer Science; Huang, D.S., Wunsch, D.C., Levine, D.S., Jo, K.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5227. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization: A new metaheuristic with applications in applied electromagnetics. Prog. Electromagn. Res. 2007, 77, 425–491. [Google Scholar] [CrossRef] [Green Version]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Tabari, A.; Ahmad, A. A new optimization method: Electro-Search algorithm. Comput. Chem. Eng. 2017, 103, 1–11. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Rao, R.; Savsani, V.; Vakharia, D. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Alatas, B. ACROA: Artificial Chemical Reaction Optimization Algorithm for global optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithm, stochastic test functions and design optimization. Int. J. Bio Inspired Comput. 2010, 2, 78. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big Bang-Big Crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Tu, Q.; Chen, X.; Liu, X. Hierarchy strengthened Grey Wolf Optimizer for numerical optimization and feature selection. IEEE Access 2019, 7, 78012–78028. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Rais, H.M.; Abdulkadir, S.J.; Mirjalili, S. Feature selection based on Grey Wolf Optimizer for oil & gas reservoir classification. In Proceedings of the 2020 International Conference on Computational Intelligence (ICCI), Seri Iskandar, Perak, Malaysia, 8–9 October 2020; pp. 211–216. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C.; Hassenian, A.E. Feature subset selection approach by gray-wolf optimization. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2015; Volume 334. [Google Scholar] [CrossRef]
- Song, J.; Wang, J.; Lu, H. A novel combined model based on advanced optimization algorithm for short-term wind speed forecasting. Appl. Energy 2018, 215, 643–658. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Single and multi-objective optimal power flow using Grey Wolf Optimizer and differential evolution algorithms. Electr. Power Compon. Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. J. 2015, 32, 286–292. [Google Scholar] [CrossRef] [Green Version]
- Katarya, R.; Verma, O.P. Recommender system with Grey Wolf Optimizer and FCM. Neural Comput. Appl. 2018, 30, 1679–1687. [Google Scholar] [CrossRef]
- Kamboj, V.K. A novel hybrid PSO–GWO approach for unit commitment problem. Neural Comput. Appl. 2016, 27, 1643–1655. [Google Scholar] [CrossRef]
- Panwar, L.K.; Reedy, S.; Verma, A.; Panigrahi, B.K.; Kumar, R. Binary Grey Wolf Optimizer for large scale unit commitment problem. Swarm Evol. Comput. 2018, 38, 251–266. [Google Scholar] [CrossRef]
- Biswas, K.; Vasant, P.M.; Vintaned, J.A.G.; Watada, J. Cellular automata-based multi-objective hybrid Grey Wolf Optimization and particle swarm optimization algorithm for wellbore trajectory optimization. J. Nat. Gas Sci. Eng. 2021, 85, 103695. [Google Scholar] [CrossRef]
- Korayem, L.; Khorsid, M.; Kassem, S.S. Using Grey Wolf algorithm to solve the capacitated vehicle routing problem. Conf. Ser. Mater. Sci. Eng. 2015, 2015, 83. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Xiao, S.; Li, X.; Gao, L. An effective multi-objective discrete grey Wolf optimizer for a real-world scheduling problem in welding production. Adv. Eng. Softw. 2016, 99, 161–176. [Google Scholar] [CrossRef] [Green Version]
- Komaki, G.; Kayvanfar, V. Grey Wolf Optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time. J. Comput. Sci. 2015, 8, 109–120. [Google Scholar] [CrossRef]
- Asadzadeh, L. A local search genetic algorithm for the job shop scheduling problem with intelligent agents. Comput. Ind. Eng. 2015, 85, 376–383. [Google Scholar] [CrossRef]
- Jayabarathi, T.; Raghunathan, T.; Adarsh, B.; Suganthan, P.N. Economic dispatch using hybrid grey wolf optimizer. Energy 2016, 111, 630–641. [Google Scholar] [CrossRef]
- Pradhan, M.; Roy, P.K.; Pal, T. Grey Wolf optimization applied to economic load dispatch problems. Int. J. Electr. Power Energy Syst. 2016, 83, 325–334. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Load frequency control of large scale power system using quasi-oppositional Grey Wolf Optimization algorithm. Eng. Sci. Technol. Int. J. 2016, 19, 1693–1713. [Google Scholar] [CrossRef] [Green Version]
- Singh, N.; Singh, S. A novel hybrid GWO-SCA approach for optimization problems. Eng. Sci. Technol. Int. J. 2017, 20, 1586–1601. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C. Application of Grey Wolf Optimization for solving combinatorial problems: Job Shop and Flexible Job Shop scheduling cases. IEEE Access 2018, 6, 26231–26240. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Tang, M. An exploration-enhanced Grey Wolf Optimizer to solve high-dimensional numerical optimization. Eng. Appl. Artif. Intell. 2018, 68, 63–80. [Google Scholar] [CrossRef]
- Dhargupta, S.; Ghosh, M.; Mirjalili, S.; Sarkar, R. Selective opposition based Grey Wolf Optimization. Expert Syst. Appl. 2020, 151, 113389. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved Grey Wolf Optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Yin, X.; Germay, N. A Fast genetic algorithm with sharing scheme using cluster analysis methods in multimodal function optimization. In Artificial Neural Nets and Genetic Algorithms; Springer: Cham, Switzerland, 1993. [Google Scholar]
- Mahfound, S.W. Crowding and preselection revisited. In Parallel Problem Solving from Nature; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Petrowski, A. Clearing procedure as a niching method for genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nayoya, Japan, 20–22 May 1996. [Google Scholar] [CrossRef]
- Li, X. Niching without niching parameters: Particle swarm optimization using a ring topology. IEEE Trans. Evol. Comput. 2010, 14, 150–169. [Google Scholar] [CrossRef]
- Li, X. A multimodal particle swarm optimizer based on fitness Euclidean-distance ratio. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation—GECCO ’07, London, UK, 7–11 July 2007; pp. 78–85. [Google Scholar] [CrossRef] [Green Version]
- Li, X. Adaptively choosing neighbourhood bests using species in a particle swarm optimizer for multimodal function optimization. In Proceedings of the Genetic and Evolutionary Computation Conference 2004, Seattle, WA, USA, 26–30 June 2004; pp. 105–116. [Google Scholar] [CrossRef]
- Islam, J.; Rahaman, A.; Vasant, P.; Negash, B.; Hoqe, A.; Alhitmi, H.K.; Watada, J. A modified niching crow search approach to well placement optimization. Energies 2021, 14, 857. [Google Scholar] [CrossRef]
- Peram, T.; Veeramachaneni, K.; Mohan, C.K. Fitness-distance-ratio based particle swarm optimization. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS’03, Indianapolis, IN, USA, 24–26 April 2003. [Google Scholar] [CrossRef]
- Bergh, F.V.D.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Ray, T.; Saini, P. Engineering design optimization using a swarm with an intelligent information sharing among individuals. Eng. Optim. 2001, 33, 735–748. [Google Scholar] [CrossRef]
- Deb, K. Optimal design of a welded beam via genetic algorithms. AIAA J. 1991, 29, 2013–2015. [Google Scholar] [CrossRef]
- Ray, T.; Liew, K. Society and civilization: An optimization algorithm based on the simulation of social behavior. IEEE Trans. Evol. Comput. 2003, 7, 386–396. [Google Scholar] [CrossRef]
- Hedar, A.-R.; Fukushima, M. Derivative-free filter simulated annealing method for constrained continuous global optimization. J. Glob. Optim. 2006, 35, 521–549. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhou, Y. Accelerating adaptive trade-off model using shrinking space technique for constrained evolutionary optimization. Int. J. Numer. Methods Eng. 2009, 77, 1501–1534. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhou, Y.; Fan, Z. Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint-handling technique. Struct. Multidiscip. Optim. 2008, 37, 395–413. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Montes, E.M. Constraint-handling in genetic algorithms through the use of dominance-based tournament selection. Adv. Eng. Inform. 2002, 16, 193–203. [Google Scholar] [CrossRef]
- He, Q.; Wang, L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng. Appl. Artif. Intell. 2007, 20, 89–99. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Ozsoydan, F.B. Adaptive firefly algorithm with chaos for mechanical design optimization problems. Appl. Soft Comput. J. 2015, 36, 152–164. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, D. An astrophysics-inspired Grey Wolf algorithm for numerical optimization and its application to engineering design problems. Adv. Eng. Softw. 2017, 112, 231–254. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, W.; Wang, X. Differential evolution with dynamic stochastic selection for constrained optimization. Inf. Sci. 2008, 178, 3043–3074. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]










| Functions | Dimension | Range | Global Optima |
|---|---|---|---|
| F1 | 30 | [−100, 100] | 0 |
| F2 | 30 | [−10, 10] | 0 |
| F3 | 30 | [−100, 100] | 0 |
| F4 | 30 | [−100, 100] | 0 |
| F5 | 30 | [−30, 30] | 0 |
| F6 | 30 | [−100, 100] | 0 |
| F7 | 30 | [−1.28, 1.28] | 0 |
| F8 | 30 | [−500, 500] | −418 × D |
| F9 | 30 | [−5.12, 5.12] | 0 |
| F10 | 30 | [−32, 32] | 0 |
| F11 | 30 | [−600, 600] | 0 |
| F12 | 30 | [−50, 50] | 0 |
| F13 | 30 | [−50, 50] | 0 |
| F14 | 2 | [−65, 65] | 1 |
| F15 | 4 | [−5, 5] | 0.0003 |
| F16 | 2 | [−5, 5] | −1.0316 |
| F17 | 2 | [−5, 5] | 0.398 |
| F18 | 2 | [−2, 2] | 3 |
| F19 | 3 | [0, 1] | −3.86 |
| F20 | 6 | [0, 10] | −3.32 |
| F21 | 4 | [0, 10] | −10.1532 |
| F22 | 4 | [0, 10] | −10.4028 |
| F23 | 4 | [0, 10] | −10.5363 |
| Algorithm | Parameters and Their Numerical Values |
|---|---|
| PSO | c1 = 2, c1 = 2 |
| GSA | c1 = 2, c2 = 2, G0 = 1 |
| GWO | a = 2 to 0 |
| JAYA | N/A |
| SOGWO | a = 2 to 0 |
| IGWO | a = 2 to 0 |
| NCSA | Awareness probability = 0.30, flight length = 0.20 |
| NGWO | a = 2 to 0, NC = 0.5 |
| Functions | Index | PSO (1998) | GSA (2011) | GWO (2014) | JAYA (2016) | SOGWO (2020) | IGWO (2021) | NCSA (2020) | NGWO (This Work) |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 1.30 × 10−11 | 2.00 × 10−17 | 1.36 × 10−70 | 1.20 × 10−8 | 6.05 × 10−77 | 2.98 × 10−71 | 3.48 × 10−91 | 3.69 × 10−96 |
| SD | 8.80 × 10−11 | 5.50 × 10−18 | 2.57 × 10−70 | 3.40 × 10−8 | 1.49 × 10−76 | 5.60 × 10−71 | 1.05 × 10−90 | 8.25 × 10−96 | |
| Min | 1.10 × 10−15 | 1.10 × 10−17 | 9.07 × 10−73 | 1.71 × 10−10 | 3.81 × 10−79 | 1.52 × 10−73 | N/A | 1.38 × 10−107 | |
| F2 | Mean | 2.90 × 10−6 | 2.40 × 10−8 | 5.64 × 10−41 | 2.66 × 10−4 | 1.18 × 10−44 | 1.30 × 10−42 | 6.64 × 10−61 | 1.09 × 10−73 |
| SD | 1.30 × 10−5 | 4.40 × 10−9 | 6.43 × 10−41 | 1.70 × 10−4 | 1.34 × 10−44 | 1.26 × 10−42 | 1.71 × 10−60 | 5.96 × 10−73 | |
| Min | 4.40 × 10−9 | 1.40 × 10−8 | 3.59 × 10−42 | 1.45 × 10−6 | 3.50 × 10−44 | 1.36 × 10−43 | N/A | 1.46 × 10−88 | |
| F3 | Mean | 1.20 × 102 | 2.30 × 102 | 1.09 × 10−19 | 4.13 × 100 | 5.40 × 10−22 | 3.29 × 10−14 | 1.60 × 10−27 | 1.29 × 10−9 |
| SD | 7.50 × 101 | 1.00 × 102 | 3.11 × 10−19 | 8.26 × 100 | 2.60 × 10−21 | 9.26 × 10−14 | 5.97 × 10−27 | 2.67 × 10−9 | |
| Min | 1.90 × 101 | 7.50 × 101 | 2.56 × 10−25 | 2.19 × 10−1 | 1.17 × 10−28 | 1.69 × 10−18 | N/A | 1.70 × 10−18 | |
| F4 | Mean | 4.20 × 10−1 | 6.40 × 10−2 | 1.94 × 10−17 | 1.52 × 100 | 1.18 × 10−19 | 1.01 × 10−14 | 1.67 × 10−25 | 4.53 × 10−32 |
| SD | 1.90 × 10−1 | 2.50 × 10−1 | 3.68 × 10−17 | 1.04 × 100 | 1.51 × 10−19 | 1.64 × 10−14 | 7.64 × 10−25 | 1.01 × 10−31 | |
| Min | 1.40 × 10−1 | 2.10 × 10−9 | 1.28 × 10−18 | 2.92 × 10−1 | 7.08 × 10−21 | 1.72 × 10−16 | N/A | 8.49 × 10−40 | |
| F5 | Mean | 2.70 × 101 | 2.80 × 101 | 2.63 × 101 | 3.73 × 101 | 2.65 × 101 | 2.74 × 101 | 2.68 × 101 | 2.48 × 101 |
| SD | 8.40 × 100 | 1.00 × 101 | 6.69 × 10−1 | 2.54 × 101 | 7.62 × 10−1 | 3.05 × 10−1 | 4.18 × 10−1 | 1.86 × 10−1 | |
| Min | 2.50 × 101 | 2.60 × 101 | 2.51 × 101 | 8.44 × 100 | 2.50 × 101 | 2.47 × 101 | N/A | 2.45 × 101 | |
| F6 | Mean | 1.30 × 10−12 | 0.00 × 100 | 4.12 × 10−1 | 1.21 × 10−8 | 2.83 × 10−1 | 1.00 × 10−5 | 3.16 × 10−1 | 2.66 × 10−4 |
| SD | 7.10 × 10−12 | 0.00 × 100 | 2.45 × 10−1 | 2.28 × 10−8 | 2.47 × 10−1 | 3.07 × 10−6 | 2.39 × 10−1 | 1.24 × 10−4 | |
| Min | 8.30 × 10−16 | 0.00 × 100 | 1.09 × 10−5 | 1.24 × 10−10 | 6.19 × 10−6 | 4.87 × 10−6 | N/A | 1.61 × 10−4 | |
| F7 | Mean | 7.00 × 10−3 | 2.80 × 10−2 | 5.68 × 10−4 | 2.87 × 10−2 | 4.93 × 10−4 | 7.60 × 10−4 | 8.06 × 10−4 | 3.41 × 10−4 |
| SD | 2.50 × 10−3 | 1.70 × 10−2 | 3.54 × 10−4 | 1.09 × 10−2 | 2.71 × 10−4 | 2.94 × 10−4 | 4.80 × 10−4 | 2.26 × 10−4 | |
| Min | 1.70 × 10−3 | 8.40 × 10−3 | 1.49 × 10−4 | 1.27 × 10−2 | 8.57 × 10−5 | 3.33 × 10−4 | N/A | 8.38 × 10−5 |
| Functions | Index | PSO (1998) | GSA (2011) | GWO (2014) | JAYA (2016) | SOGWO (2020) | IGWO (2021) | NCSA (2020) | NGWO (This Work) |
|---|---|---|---|---|---|---|---|---|---|
| F8 | Mean | −9.00 × 103 | −2.70 × 103 | −6.07 × 103 | −7.66 × 103 | −6.57 × 103 | −9.53 × 103 | −7.25 × 103 | −1.25 × 104 |
| SD | 5.20 × 102 | 4.70 × 102 | 5.37 × 102 | 1.01 × 103 | 8.03 × 102 | 1.40 × 103 | 9.86 × 102 | 9.77 × 101 | |
| Min | −1.00 × 104 | −4.20 × 103 | −7.09 × 103 | −9.66 × 103 | −8.18 × 103 | −1.13 × 104 | N/A | −1.26 × 104 | |
| F9 | Mean | 4.10 × 101 | 1.70 × 101 | 5.20 × 100 | 2.68 × 101 | 0.00 × 100 | 1.42 × 101 | 0.00 × 100 | 0.00 × 100 |
| SD | 1.50 × 101 | 4.30 × 100 | 1.89 × 100 | 9.89 × 100 | 0.00 × 100 | 5.80 × 100 | 0.00 × 100 | 0.00 × 100 | |
| Min | 1.80 × 101 | 9.00 × 100 | 0.00 × 100 | 1.49 × 101 | 0.00 × 100 | 2.99 × 100 | N/A | 0.00 × 100 | |
| F10 | Mean | 9.10 × 10−8 | 3.40 × 10−9 | 1.31 × 10−14 | 2.63 × 100 | 8.88 × 10−16 | 9.41 × 10−15 | 4.44 × 10−8 | 4.44 × 10−15 |
| SD | 2.00 × 10−7 | 4.10 × 10−10 | 2.73 × 10−15 | 9.95 × 10−1 | 0.00 × 100 | 2.74 × 10−15 | 0.00 × 100 | 0.00 × 100 | |
| Min | 4.60 × 10−9 | 2.20 × 10−9 | 7.99 × 10−15 | 9.31 × 10−1 | 8.88 × 10−16 | 7.99 × 10−15 | N/A | 4.44 × 10−15 | |
| F11 | Mean | 1.20 × 10−2 | 4.30 × 100 | 5.23 × 10−4 | 1.99 × 10−2 | 0.00 × 100 | 9.55 × 10−3 | 0.00 × 100 | 0.00 × 100 |
| SD | 1.20 × 10−2 | 1.60 × 100 | 2.61 × 10−3 | 2.97 × 10−2 | 0.00 × 100 | 3.60 × 10−3 | 0.00 × 100 | 0.00 × 100 | |
| Min | 5.10 × 10−15 | 2.00 × 100 | 0.00 × 100 | 8.43 × 10−10 | 0.00 × 100 | 0.00 × 100 | N/A | 0.00 × 100 | |
| F12 | Mean | 1.50 × 10−13 | 2.50 × 10−2 | 2.66 × 10−2 | 1.58 × 10−1 | 5.61 × 10−2 | 7.50 × 10−7 | 1.66 × 10−2 | 2.10 × 10−5 |
| SD | 3.60 × 10−13 | 6.10 × 10−2 | 1.55 × 10−2 | 2.26 × 10−1 | 1.42 × 10−2 | 1.81 × 10−7 | 8.75 × 10−3 | 3.62 × 10−6 | |
| Min | 1.60 × 10−13 | 6.20 × 10−2 | 6.57 × 10−2 | 4.84 × 10−11 | 2.62 × 10−2 | 4.45 × 10−7 | N/A | 1.69 × 10−5 | |
| F13 | Mean | 2.00 × 10−31 | 2.10 × 10−18 | 3.25 × 10−1 | 1.97 × 100 | 3.53 × 10−1 | 1.42 × 10−5 | 4.08 × 10−1 | 1.12 × 10−2 |
| SD | 4.30 × 10−31 | 5.00 × 10−19 | 1.56 × 10−1 | 3.71 × 100 | 1.28 × 10−1 | 4.31 × 10−6 | 2.27 × 10−1 | 1.07 × 10−2 | |
| Min | 9.90 × 10−31 | 1.22 × 10−18 | 1.58 × 10−5 | 6.58 × 10−9 | 1.42 × 10−5 | 7.42 × 10−6 | N/A | 3.42 × 10−4 | |
| F14 | Mean | 1.00 × 100 | 3.80 × 100 | 3.11 × 100 | 9.98 × 10−1 | 3.43 × 100 | 9.98 × 10−1 | 1.13 × 100 | 9.98 × 10−1 |
| SD | 3.20 × 10−17 | 2.60 × 100 | 3.73 × 100 | 0.00 × 100 | 3.72 × 100 | 5.83 × 10−17 | 5.03 × 10−1 | 1.11 × 10−16 | |
| Min | 1.00 × 100 | 1.00 × 100 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | N/A | 9.98 × 10−1 | |
| F15 | Mean | 1.20 × 10−3 | 4.10 × 10−3 | 4.36 × 10−3 | 4.30 × 10−4 | 2.38 × 10−3 | 3.07 × 10−4 | 3.75 × 10−4 | 3.08 × 10−4 |
| SD | 4.00 × 10−3 | 3.20 × 10−3 | 8.17 × 10−3 | 3.17 × 10−4 | 6.03 × 10−3 | 6.57 × 10−10 | 7.73 × 10−5 | 4.22 × 10−8 | |
| Min | 3.10 × 10−3 | 1.40 × 10−3 | 3.07 × 10−4 | 3.07 × 10−4 | 3.07 × 10−4 | 3.07 × 10−4 | N/A | 3.07 × 10−4 | |
| F16 | Mean | −1.00 × 100 | −1.00 × 100 | −1.02 × 100 | −1.03 × 100 | −1.03 × 100 | −1.03 × 100 | −1.03 × 100 | −1.03 × 100 |
| SD | 2.30 × 10−16 | 4.00 × 10−16 | 4.80 × 10−9 | 6.78 × 10−6 | 3.75 × 10−9 | 6.78 × 10−6 | 2.39 × 10−6 | 0.00 × 100 | |
| Min | −1.00 × 100 | −1.00 × 100 | −1.03 × 100 | −1.03 × 100 | −1.03 × 100 | −1.03 × 100 | N/A | −1.03 × 100 | |
| F17 | Mean | 4.00 × 10−1 | 4.00 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.97 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| SD | 3.40 × 10−16 | 3.40 × 10−16 | 3.36 × 10−7 | 0.00 × 100 | 4.86 × 10−7 | 0.00 × 100 | 1.09 × 10−5 | 0.00 × 100 | |
| Min | 4.00 × 10−1 | 4.00 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | N/A | 3.98 × 10−1 | |
| F18 | Mean | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 |
| SD | 3.10 × 10−15 | 2.20 × 10−15 | 4.88 × 10−6 | 1.51 × 10−15 | 4.63 × 10−6 | 1.24 × 10−14 | 9.98 × 10−6 | 1.49 × 10−15 | |
| Min | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | N/A | 3.00 × 100 | |
| F19 | Mean | −3.90 × 100 | −3.60 × 100 | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 |
| SD | 3.10 × 10−15 | 3.00 × 10−1 | 1.05 × 10−3 | 2.71 × 10−15 | 2.71 × 10−3 | 2.71 × 10−15 | 2.67 × 10−4 | 1.51 × 10−15 | |
| Min | −3.90 × 100 | −3.90 × 100 | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 | N/A | −3.86 × 100 | |
| F20 | Mean | −3.30 × 100 | −1.90 × 100 | −3.25 × 100 | −3.29 × 100 | −3.27 × 100 | −3.32 × 100 | −3.29 × 100 | −3.32 × 100 |
| SD | 5.50 × 10−2 | 5.40 × 10−1 | 7.04 × 10−2 | 5.11 × 10−2 | 7.37 × 10−2 | 3.63 × 10−2 | 4.45 × 10−2 | 3.83 × 10−7 | |
| Min | −3.30 × 100 | −3.30 × 100 | −3.32 × 100 | −3.32 × 100 | −3.32 × 100 | −3.32 × 100 | N/A | −3.32 × 100 | |
| F21 | Mean | −7.20 × 100 | −5.10 × 100 | −9.95 × 100 | −1.02 × 101 | −9.66 × 100 | −1.02 × 101 | −7.73 × 100 | −1.02 × 101 |
| SD | 3.30 × 100 | 7.40 × 10−3 | 1.01 × 100 | 7.23 × 10−15 | 1.51 × 100 | 3.12 × 10−8 | 2.19 × 100 | 1.55 × 10−3 | |
| Min | −1.00 × 101 | −5.10 × 100 | −1.02 × 101 | −1.02 × 101 | −1.02 × 101 | −1.02 × 101 | N/A | −1.02 × 101 | |
| F22 | Mean | −9.10 × 100 | −7.50 × 100 | −1.02 × 101 | −1.04 × 101 | −1.04 × 101 | −1.04 × 101 | −8.82 × 100 | −1.04 × 101 |
| SD | 2.80 × 100 | 2.70 × 100 | 1.05 × 100 | 9.33 × 10−16 | 2.66 × 10−4 | 3.12 × 10−8 | 1.90 × 100 | 4.40 × 10−2 | |
| Min | −1.00 × 101 | −1.00 × 101 | −1.04 × 101 | −1.04 × 101 | −1.04 × 101 | −1.04 × 101 | N/A | −1.04 × 101 | |
| F23 | Mean | −9.40 × 100 | −1.00 × 101 | −1.03 × 101 | −1.05 × 101 | −1.05 × 101 | −1.04 × 101 | −9.16 × 100 | −1.05 × 101 |
| SD | 2.80 × 100 | 7.80 × 10−1 | 1.08 × 100 | 1.81 × 10−15 | 5.41 × 10−1 | 7.40 × 10−8 | 1.86 × 100 | 6.64 × 10−10 | |
| Min | −1.10 × 101 | −1.10 × 101 | −1.05 × 101 | −1.05 × 101 | −1.05 × 101 | −1.04 × 101 | N/A | −1.05 × 101 |
| Functions | PSO (1998) | GSA (2011) | GWO (2014) | JAYA (2016) | SOGWO (2020) | IGWO (2021) | NCSA (2020) | NGWO (This Work) | p-Value |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 7.000 | 5.967 | 4.433 | 8.000 | 4.067 | 3.400 | 1.833 | 1.267 | 4.902 × 10−39 |
| F2 | 7.060 | 6.000 | 4.667 | 6.877 | 4.267 | 2.967 | 2.000 | 1.000 | 8.466 × 10−41 |
| F3 | 6.830 | 8.000 | 2.067 | 6.100 | 2.567 | 4.033 | 1.400 | 4.933 | 8.027 × 10−40 |
| F4 | 7.000 | 6.033 | 3.133 | 7.967 | 3.500 | 4.967 | 2.400 | 1.000 | 4.720 × 10−40 |
| F5 | 5.400 | 4.700 | 5.533 | 4.367 | 5.733 | 2.400 | 4.767 | 1.133 | 1.633 × 10−17 |
| F6 | 2.000 | 1.000 | 6.167 | 3.000 | 6.300 | 4.133 | 8.000 | 5.400 | 1.259 × 10−39 |
| F7 | 7.900 | 6.300 | 3.400 | 6.800 | 3.367 | 4.300 | 2.400 | 1.533 | 2.906 × 10−35 |
| F8 | 5.133 | 8.000 | 6.333 | 4.267 | 5.600 | 2.667 | 3.000 | 1.000 | 1.584 × 10−34 |
| F9 | 7.767 | 5.733 | 2.633 | 6.933 | 2.500 | 5.567 | 2.433 | 2.433 | 2.922 × 10−39 |
| F10 | 7.000 | 6.000 | 4.217 | 8.000 | 4.417 | 3.267 | 1.650 | 1.450 | 1.618 × 10−40 |
| F11 | 6.000 | 8.000 | 3.133 | 6.333 | 3.383 | 3.617 | 2.733 | 2.700 | 3.735 × 10−33 |
| F12 | 1.767 | 2.333 | 5.667 | 5.567 | 5.867 | 3.033 | 7.567 | 3.433 | 3.310 × 10−27 |
| F13 | 2.367 | 1.300 | 5.900 | 4.867 | 6.267 | 3.033 | 7.767 | 3.533 | 4.302 × 10−32 |
| F14 | 4.617 | 6.733 | 6.067 | 2.817 | 5.133 | 2.817 | 5.000 | 2.817 | 3.877 × 10−20 |
| F15 | 6.500 | 7.700 | 4.817 | 2.333 | 4.983 | 2.817 | 5.213 | 1.517 | 1.506 × 10−31 |
| F16 | 3.767 | 3.767 | 6.783 | 3.767 | 6.617 | 3.767 | 3.767 | 3.767 | 7.581 × 10−28 |
| F17 | 3.517 | 3.517 | 7.567 | 3.517 | 7.333 | 3.517 | 3.517 | 3.517 | 4.257 × 10−40 |
| F18 | 3.500 | 3.500 | 7.533 | 3.500 | 7.467 | 3.500 | 3.500 | 3.500 | 7.003 × 10−40 |
| F19 | 3.500 | 3.500 | 7.533 | 3.500 | 7.467 | 3.500 | 3.500 | 3.500 | 7.003 × 10−41 |
| F20 | 4.750 | 2.550 | 6.700 | 3.583 | 6.900 | 3.433 | 3.400 | 2.683 | 7.641 × 10−23 |
| F21 | 4.133 | 5.233 | 5.967 | 2.500 | 6.067 | 2.767 | 5.250 | 4.083 | 3.014 × 10−15 |
| F22 | 3.483 | 2.983 | 6.867 | 2.983 | 6.967 | 3.050 | 4.750 | 4.917 | 3.309 × 10−25 |
| F23 | 4.650 | 1.500 | 6.633 | 1.500 | 6.867 | 4.033 | 5.500 | 5.317 | 2.890 × 10−31 |
| Algorithms | y1 | y2 | y3 | y4 | f (Best) | f (Mean) | f (Worst) | SD | NFEs |
|---|---|---|---|---|---|---|---|---|---|
| NGWO | 0.34094 | 3.5810 | 9.0321 | 0.2063 | 2.036 | 2.046 | 2.0632 | 1.02 × 102 | 20,100 |
| GA [54] | 0.2489 | 6.173 | 8.1789 | 0.2533 | 2.4331 | N/A | N/A | N/A | N/A |
| SC [55] | 0.2444 | 6.238 | 8.2886 | 0.2446 | 2.3854 | 3.2551 | 6.3997 | 9.60 × 10−1 | 33,095 |
| FSA [56] | 0.2443 | 6.2158 | 8.2939 | 0.2443 | 2.3811 | 2.4042 | 2.489 | N/A | 56,243 |
| AATM [57] | 0.2441 | 6.2209 | 8.2982 | 0.2444 | 2.3823 | 2.387 | 2.3916 | 2.20 × 10−3 | 30,000 |
| HEAA [58] | 0.2444 | 6.2175 | 8.2915 | 0.2444 | 2.381 | 2.381 | 2.381 | 1.30 × 10−5 | 30,000 |
| EEGWO [41] | 0.2444 | 6.217 | 8.2928 | 0.2444 | 2.3813 | 2.3817 | 2.3824 | 4.18 × 10−4 | 50,000 |
| Algorithms | y1 | y2 | y3 | f (Best) | f (Mean) | f (Worst) | SD | NFEs |
|---|---|---|---|---|---|---|---|---|
| NGWO | 10.32826 | 0.35486 | 0.05026 | 0.011053 | 0.011755 | 0.012454 | 5.21 × 10−4 | 20,100 |
| GA [59] | 10.89052 | 0.36396 | 0.05198 | 0.01268 | 0.01274 | 0.01297 | 5.90 × 10−5 | 80,000 |
| FSA [56] | 11.21390 | 0.35800 | 0.05174 | 0.01266 | 0.01266 | 0.01266 | 2.20 × 10−8 | 49,531 |
| CPSO [60] | 11.24454 | 0.35764 | 0.05172 | 0.01267 | 0.01273 | 0.01292 | 5.20 × 10−5 | 200,000 |
| HPSO [60] | 11.26503 | 0.35712 | 0.05170 | 0.01266 | 0.01270 | 0.01271 | 1.58 × 10−5 | 81,000 |
| GSA [13] | 14.22867 | 0.05 | 0.31731 | 0.01287 | 0.01343 | 0.01421 | 1.34 × 10−2 | 30,000 |
| GWO [18] | 12.04249 | 0.34454 | 0.05117 | 0.01267 | 0.01269 | 0.01272 | 2.10 × 10−5 | 30,000 |
| AFA [61] | 11.31956 | 0.35619 | 0.05166 | 0.01266 | 0.01266 | 0.01280 | 1.27 × 10−2 | 50,000 |
| TEO [62] | 11.16839 | 0.35879 | 0.05177 | 0.01266 | 0.01268 | 0.01271 | 4.41 × 10−2 | 300,000 |
| MGWO [63] | 11.80809 | 0.34819 | 0.05133 | 0.01266 | 0.01267 | 0.01270 | 1.10 × 10−5 | 30,000 |
| EEGWO [41] | 11.3113 | 0.35634 | 0.05167 | 0.01266 | 0.01268 | 0.01272 | 2.22 × 10−5 | 50,000 |
| Algorithms | y1 | y2 | f (Best) | f (Mean) | f (Worst) | SD | NFEs |
|---|---|---|---|---|---|---|---|
| NGWO | 0.789186 | 0.406806 | 263.8959 | 263.8964 | 263.8971 | 5.58 × 10−4 | 20,100 |
| PSO [6] | 0.781224 | 0.432548 | 264.2183 | 265.9553 | 267.459 | 1.38 × 100 | 30,000 |
| SC [55] | 0.788621 | 0.408401 | 263.8958 | 263.9033 | 263.9697 | 1.30 × 10−2 | 17,610 |
| DEDS [64] | 0.788651 | 0.408316 | 263.8958 | 263.8958 | 263.8958 | 9.70 × 10−7 | 15,000 |
| GSA [13] | 0.777662 | 0.448853 | 264.8299 | 271.0348 | 279.7925 | 4.12 × 100 | 30,000 |
| HEAA [58] | 0.78868 | 0.408234 | 263.8958 | 263.8959 | 263.8961 | 4.90 × 10−5 | 15,000 |
| AATM [57] | 0.788682 | 0.408229 | 263.8958 | 263.8966 | 263.9004 | 1.10 × 10−3 | 17,000 |
| WCA [65] | 0.788651 | 0.408316 | 263.8958 | 263.8959 | 263.8962 | 8.71 × 10−5 | 5250 |
| MBA [66] | 0.788565 | 0.40856 | 263.8959 | 263.898 | 263.916 | 3.93 × 10−3 | 13,280 |
| GWO [18] | 0.788409 | 0.409003 | 263.8959 | 263.8966 | 263.898 | 4.37 × 10−4 | 30,000 |
| MVO [67] | 0.788993 | 0.407351 | 263.8959 | 263.8961 | 263.8971 | 2.49 × 10−4 | 30,000 |
| SCA [68] | 0.789068 | 0.407162 | 263.8984 | 263.9356 | 263.9951 | 2.88 × 10−2 | 30,000 |
| MGWO [63] | 0.788561 | 0.408572 | 263.8959 | 263.8963 | 263.8976 | 4.29 × 10−4 | 30,000 |
| EEGWO [41] | 0.78841 | 0.40899 | 263.896 | 263.8963 | 263.8966 | 2.19 × 10−4 | 50,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, R.; Nazir, A.; Mahadzir, S.; Shorfuzzaman, M.; Islam, J. Niching Grey Wolf Optimizer for Multimodal Optimization Problems. Appl. Sci. 2021, 11, 4795. https://doi.org/10.3390/app11114795
Ahmed R, Nazir A, Mahadzir S, Shorfuzzaman M, Islam J. Niching Grey Wolf Optimizer for Multimodal Optimization Problems. Applied Sciences. 2021; 11(11):4795. https://doi.org/10.3390/app11114795
Chicago/Turabian StyleAhmed, Rasel, Amril Nazir, Shuhaimi Mahadzir, Mohammad Shorfuzzaman, and Jahedul Islam. 2021. "Niching Grey Wolf Optimizer for Multimodal Optimization Problems" Applied Sciences 11, no. 11: 4795. https://doi.org/10.3390/app11114795
APA StyleAhmed, R., Nazir, A., Mahadzir, S., Shorfuzzaman, M., & Islam, J. (2021). Niching Grey Wolf Optimizer for Multimodal Optimization Problems. Applied Sciences, 11(11), 4795. https://doi.org/10.3390/app11114795





