1. Introduction
In recent years, the deployment of lower DoF mechanisms has grabbed the attention of industries and academia due to its interesting properties such as lower cost, kinematic simplicity, fast dynamic response and higher accuracy. For several applications, such as pointing devices, surgical robots, parallel kinematic machines (PKMs), parallel manipulators (PMs) with less than six DoFs can be preferable [
1,
2,
3,
4,
5]. Because such tasks can be well performed with manipulators having less than 6-DoFs. For example, surgical devices require 4 DoFs at most including one external yaw motion of the tool [
6].
Lower mobility PMs as a pointing device:Replacing conventional antenna and telescope positioning methods with PMs dates back to 1980 when first suggested by Fichter and McDowell and later continued by Jones at the Canterbury University [
7]. Pointing devices often operate in a complex environment that could heavily affect their accuracy, such as telescopes on satellite continuously changes its pose in relation to the telescope mounted on the ground. However, these devices require higher accuracy and precision to guarantee strong signals in tracking and communication. To ensure the pointing precision under complex operational environment, engineers employed 6-DoFs PM instead of the conventional mounting methods [
8,
9,
10]. Yu et al. introduced a new 6-PSS (prismatic-spherical-spherical) telescope’s secondary mirror alignment mechanism [
8]. Sun et al. proposed another 6-DoFs hybrid manipulator for pointing and positioning purposes in aerospace applications [
11]. However, manipulation of the secondary mirror of the telescope requires 3-DoFs at most [
12]. The remaining degrees of freedom of the manipulator are to avoid singularities. But singularity can be handled by PMs with less than 6-DoFs [
12,
13]. To avoid the use of such complicated manipulators for lower DoFs tasks, researchers shifted their attention to fewer DoFs mechanisms. Carretero et al. designed a 3-PRS (prismatic-revolute-spherical) manipulator to perform tip/tilt pointing (2 rotational freedoms) and focusing (1 translational freedom) for the secondary mirrors of a Cassegrain telescope [
12]. In 2008, a 3-PRS PM was proposed for orienting television satellite antenna [
14]. Likewise, the high-performance antenna pointing device (3POD) in a micro-gravity environment was proposed by CENS [
13].
Lower mobility PMs as high precision PKMs: PKMs use their actuators working side-by-side to enhance rigidity, fast dynamic response, and accuracy. Due to these advantages, the interest has increased both in academia and industry to use lower mobility PMs as a machining device. The first PKM was introduced at the international machine tool show (IMTS) in 1994. Along that track, there have been intensive research and innovations to meet the conceptual potentials of PKMs [
15,
16,
17,
18]. In 2016, the most successful sprint Z3 [
19] of the Ecospeed series from Starrag Group had received significant orders in the double-digit million from customers. This success indicates the Ecospeed series with sprint Z3-head has become a choice to achieve 5-axis precision machining in spacecraft and automobile industries. Inspired by Z3-head, Tianjin university developed a PKM with identical motion but with RPS(Revolute-Prismatic-Spherical) joint arrangements in a limb [
18]. Both manipulators are extensively studied and are the most used examples to demonstrate different theoretical and experimental approaches.
Lower mobility PMs as surgical devices: One of the medical industry’s growing trends is to use robotic-assisted surgery to take advantage of parallel manipulators’ high accuracy and accessibility. Robots in the medical sector can help surgeons handle routine tasks, complement their skills with manipulators’ accuracy and repeatability, and several researchers focused on exploring PMs’ capabilities in medical applications. Guaranteeing manipulators’ successful usage in the medical field requires few critical requirements to be fulfilled, such as simple operation, efficient control, limited workspace, safe behaving near the singular configurations, etc. Considering the PMs promising features to achieve the medical sector’s requirements, several researchers are developing surgical lower-mobility PMs [
20,
21].
1.1. The Effect of Parasitic Motion on the Application of Lower Mobility Parallel Manipulators
The applications of robotic manipulators described above require lower DoFs with higher accuracy. Thus, researchers showed keen interest in the use of PMs with lower DoFs instead of the serial ones. Even though parallel manipulators are comparatively accurate enough, a hidden property of lower mobility PMs named parasitic motion can considerably affect accuracy [
12]. Parasitic motion is a small dependent movement that occur in the restricted DoFs due to the nature of constraint [
12]. For the applications that require higher precision, such as machining, pointing devices, and robotic surgery, parasitic motion causes accuracy problems and control complexity [
22]. Because parasitic motion is an unwanted auto-generated movement only to satisfy the structural constraint, and the internal controller cannot correct it.
Therefore, researchers aim to describe parasitic motion, introduce methods to remove the parasitic terms, and invent manipulators without parasitic movement considering various applications sensitive to this natural behavior [
12,
21,
22]. Through the extensive research carried out to define and analyze parasitic motion, Carretero et al. were the first to address it appropriately at the position-level [
12]. Their study has also introduced the optimal configuration of a 3-PRS manipulator that minimizes this undesired motion. Later in 2011, Li. et al. [
22] also investigated 3-PRS manipulator without and with small amplitude parasitic motion using different limb arrangements. In 2010, Li and Hervé synthesized 1T2R manipulators without parasitic motion [
18]. Qu et al. also introduced a method to remove the parasitic motion of 3-UPU by adding a redundant active leg [
23]. A simplified method to describe the rotational parasitic motion was introduced by Liu et al. in 2008 [
24]. However, the proposed approach is also at the position-level.
In this study, the optimum geometric parameters are obtained purely at the velocity level. Deriving the parasitic motion equation at the velocity level avoids unnecessary explicit position relation coverage. It also suits the commonly used velocity-level control scheme. Previously, the procedure had to start from the position-level relations. However, that is ineffective for someone who does not necessarily need the position information. Note that the parallel manipulator’s control scheme is commonly based on the velocity information since the theory for the velocity analysis is well-established for such mechanisms. Also, embedding the constraint information in the position equation is not uniformly applicable for all manipulators since it is obtained differently for each mechanism. The analytic constraint equation used to formulate parasitic velocity is obtained via screw theory using instantaneous restriction and motion spaces [
25,
26]. Consequently, the manipulators that optimize the parasitic velocities are obtained.
Moreover, the paper introduces an enhanced performance manipulator without parasitic motion after the performance evaluation of optimized manipulators.
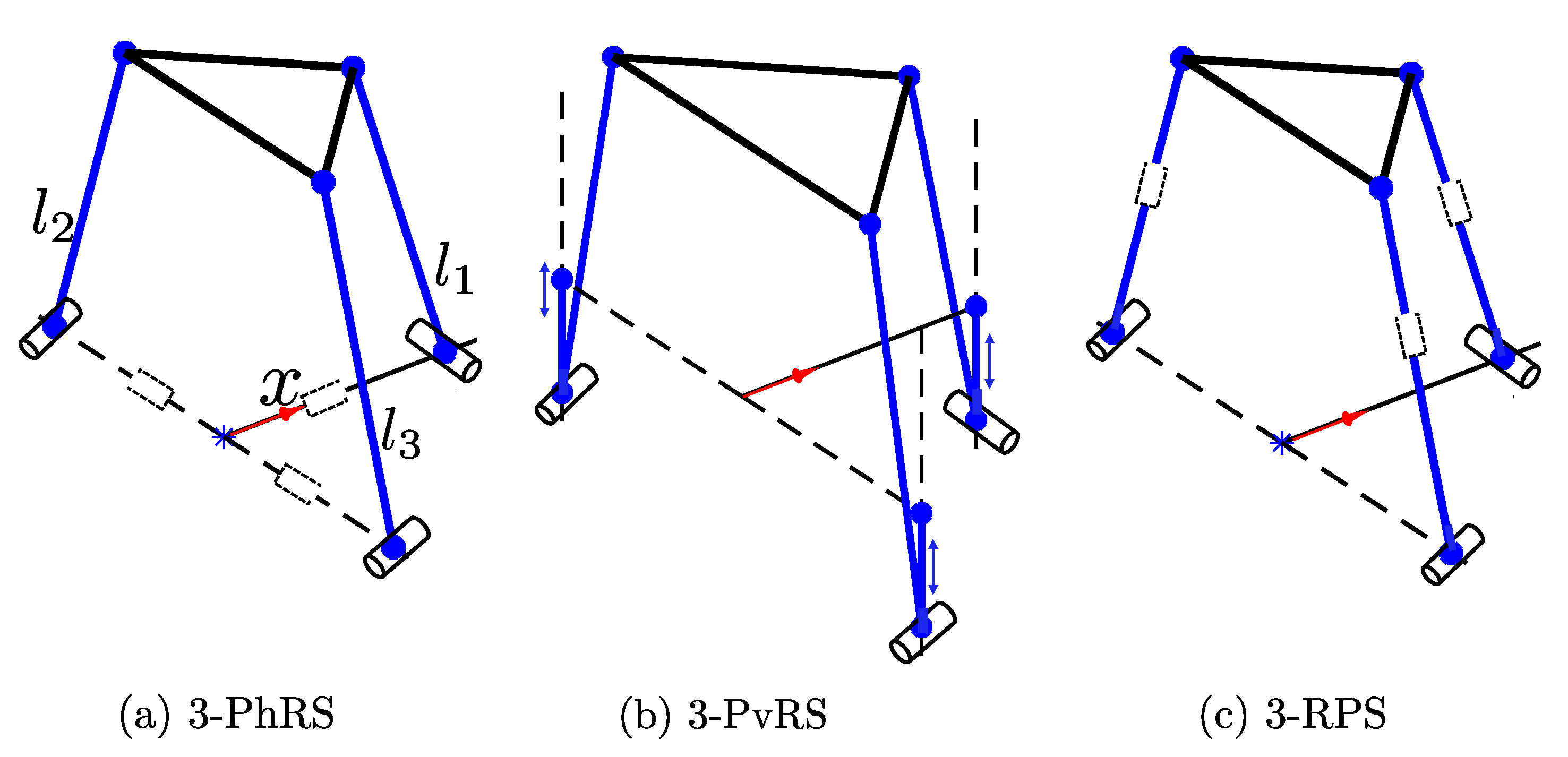
1.2. Description of Example Manipulators
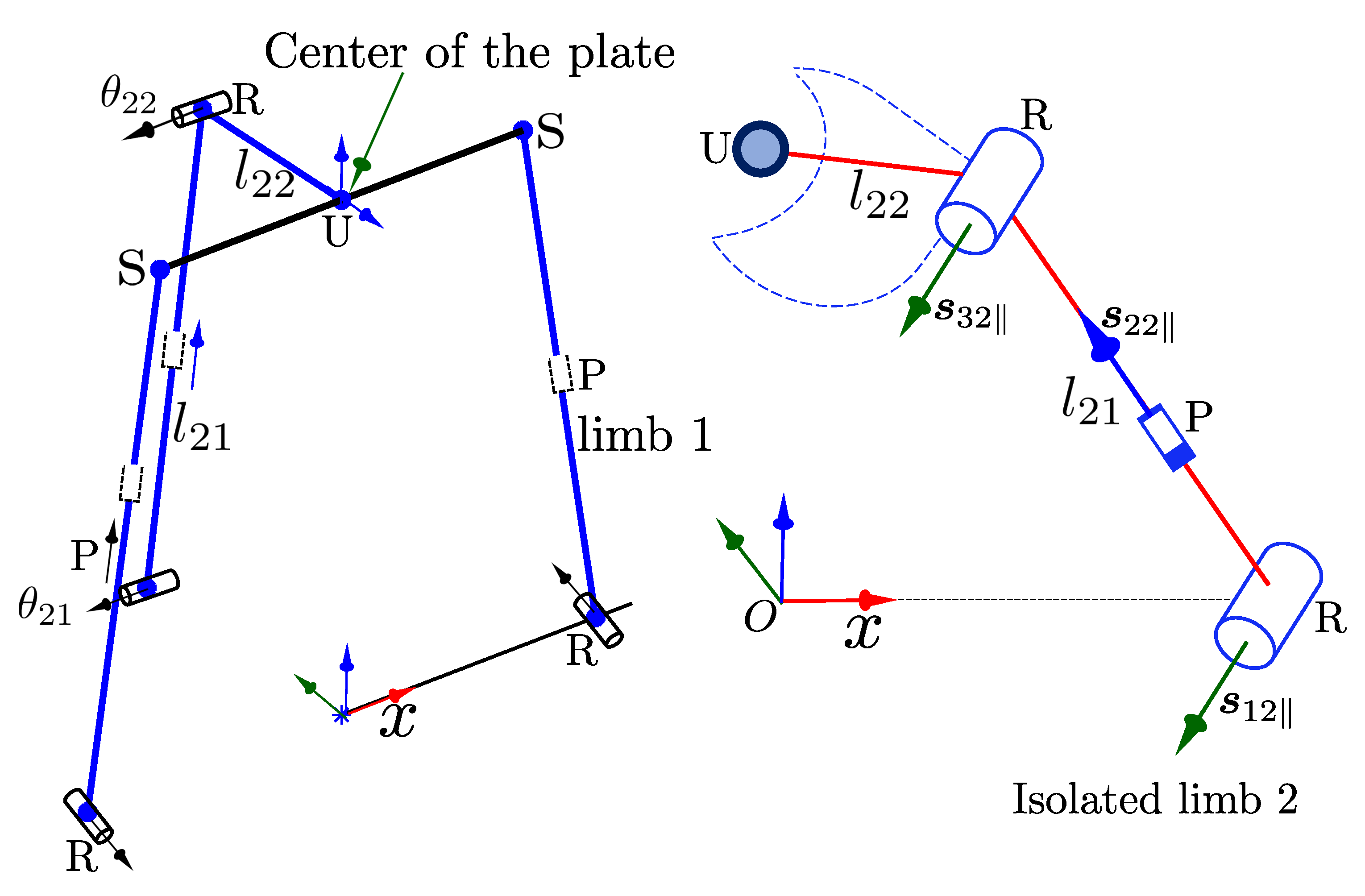
For the example manipulators used in this paper (
Figure 1,
Figure 2 and
Figure 3), the fixed and moving platforms are described by the frames
and
, respectively. The orientation of the moving plate with respect to the base plate is represented by:
whereas the position of the moving plate with respect to the base is described by a vector
. Considering the moving plates as a rigid plane, the position of spherical joints is described by the vector
, which is directed from
to
and written as follows:
Variable
in Equation (
2) implies the radius of the moving platform’s circumscribed circle and
represents a translation vector in the x- direction by the specified magnitude, in this case
. The angle
defines the location of three spherical joints measured from the positive x-axis parallel to the moving platform and is given as:
whereas the revolute joints located on the fixed platform can be measured by the angle
from the positive x-axis and parallel to the fixed platform as in Equation (
4).
The vector from
to
can be denoted by
. So, it can be described by the following relation:
Note that
and
of
Figure 1 and
Figure 2 are initially the same and can be equally represented in Equation (
5). In solving the inverse kinematics,
is the varying length associated to the prismatic joint. Accordingly, for the manipulators shown in
Figure 1 and
Figure 2, the kinematic transformation from
to
can be represented by the following relation:
where
, which is a Euclidean space group. Note that the radius of the fixed platform is not constant for the 3-PhRS manipulator because of the actuator layout. Thus, vector
in Equation (
5) is also not constant for this manipulator.
Similarly, the transformation from
to
for the manipulator shown in
Figure 3 can be given by:
Using Equations (6) and (7), the position relation can be derived. However, the detail is left for the readers since it is not complicated, and not the purpose of this paper.
2. Constraint Analysis at the Velocity Level
The kinematics of parallel manipulators, in general, and lower mobility manipulators, in particular are usually described with a well-established procedure at the velocity level known as screw-based rate kinematics. Consequently, the control scheme of most of these manipulators is designed based on the rate kinematics algorithms. This section’s main objective is to create a foundation for analyzing the moving platform’s motion by examining the legs’ structural constraints. Therefore, two approaches to studying the PMs will be employed, i.e., (a) several serial limbs restrict the moving plate’s motion, and (b) analyzing the PMs by considering the moving plate as a rigid body that restricts the legs. Although these two approaches of analyzing the motion and constraints of the PMs are connected, this paper will discuss the two in separate sections. To analyze each serial limb’s kinematic feature that connects the fixed and the moving plates, the entire PM is breakdown into subsystems by isolating the limbs and then integrating back to describe the PM’s motion.
A general manipulator has instantaneous motion
. But when subjected to certain constraints, some regions can or cannot be reached by the manipulator, and consequently, the kinematic analysis needs to consider those regions. Hence, two sub-spaces need to be considered for a complete description of the robot manipulators. These regions, in general, consist of the sub-space that the manipulator is free to move in, and the sub-space that the manipulator is restricted from entering. These two regions are described with two complementary sub-spaces named Instantaneous Motion Space (IMS) and Instantaneous Restriction Space (IRS) [
27]. As discussed earlier, since PM has resulted from multiple serial limb combinations, the entire manipulator’s kinematic behavior can be determined by separately analyzing the limbs IMS and IRS.
Instantaneous Motion Space (IMS): It is the tangent space of SE(3) spanned by the linearly independent motion vectors at the moving-plate (IMS ). From the leg point of view, this space is spanned by the intersection of twists in all legs, and it can be physically interpreted as the motion of the moving platform in the region where all legs commonly operate.
Instantaneous restriction Space (IRS): It is an orthogonal complementary subspace of the instantaneous motion space in , which belongs to the unreachable region due to the structural constraints and formed by the union of all restriction screws induced from each leg.
PMs’ constraints are a union of those legs restriction, and thus the entire motion is described by the legs IMS and IRS. In a serial manipulator, IMS (
) is obtained from the forward rate kinematics whereas, IRS (
) is obtained by taking the orthogonal complement (
. Hence, the IMS fully describes the serial manipulator’s motion, and the corresponding IRS is {
IMS} which represents the space that the manipulator cannot reach. Thus, the generic extended forward-rate kinematics (FRK) of an isolated limb can be written with the
extended Jacobian matrix
as follows:
where
and
denote the velocity of the end-effector and extended joint velocities, respectively.
The dimension of is a Jacobian matrix and that of is a constraint matrix, where f is the total DoF. Note that the extended joint velocity, is composed of usual joint velocity and zero for constraints .
Generally, the inverse rate kinematics of Equation (
8) can be obtained by inverting
in Equation (
8):
where
is the inverse of
, and
is a
extended Jacobian comprising the two complementary orthogonal sub-spaces called IMS and IRS given as follows;
Since our objective is to utilize the constraint relation, we will be restricted to focus on obtaining and .
Analytic Constraint Equation
Utilizing a reciprocity relation is a well-known approach to get the structural constraint information, and there are geometric, numeric, and analytic techniques to obtain the reciprocal screw’s basis elements. Geometric and numeric approaches suffer from two contradicting limitations, as discussed in the previous sections. On the one hand, the geometric method is well related to the physical meaning, but it cannot be consistently applied to complicated systems. On the other hand, the numerical method cannot be easily interpreted, but it can solve any type of screw system. This study uses an analytic approach introduced by Kim and Chung [
25,
26,
27], since it can give a consistent derivation process with physical and geometrical meanings.
Each manipulator limb is isolated and is considered a serial mechanism to obtain the manipulator’s structural information. Then, limb motion generators, that span the limb IMS, are used to get the limb restriction screw.
For the manipulators shown in
Figure 1,
Figure 2 and
Figure 3, the limb IMS is spanned by
screws, where
and
are zero and infinite screws, respectively. Hence, the Jacobian matrix of the
ith leg is:
Then, the limb restriction screw is obtained from the following constraint equation.
where
and
are the sub-matrices spanned by the direction and moment vectors, respectively. The symbol, “∧”, is an operator for reciprocal relation. Then, the direction and moment vectors of restriction screws are obtained by solving Equation (
14):
where
is the relative moment arm between the fifth and
ith joints.
Scalars in Equation (
15) can be dropped, and the vector part is further simplified by vector triple product and limb geometric conditions. Such that, the direction vector is parallel to
.
Then, the moment vector is obtained using the derived direction vector and Equation (
15). The result gives a zero moment vector, and it can be verified by checking the linear independence of the first three zero pitch screws in Equation (
14). Finally, the limb restriction can be written as:
For the limb, point
is regarded as the reference point of motion, however, for the manipulator, the reference point of motion must be moved to the center of the moving platform by the following transformation matrix:
The limb constraint is then obtained from the restriction screw by the the transformation of correlation [
28].
After transformation, the three limbs constraints are combined to get the manipulator constraint as:
With Equation (
18), any constraint-compatible task velocity used to solve the inverse rate kinematics should satisfy the following constraint:
3. Analytic Coupling Relation
Usually, the parasitic motion equation is derived analytically at the position-level [
12] and takes the time derivative when the information is required for higher-level problems. However, the procedureexplained in this paper does not require any position information to describe the parasitic motion. The parasitic motion can also be incorporated at the velocity-level without deriving any coupling relation as suggested in [
29] by projecting arbitrary motion onto the null space of the constraint matrix. In this section, the coupling relation between parasitic and independent terms is formulated analytically. After detecting and identifying the parasitic terms it can be written as a function of the independent terms. This is called the coupling relationship of the task space variables. For the example manipulators used in this paper, the variables
,
, and
were identified as the independent variables, whereas
,
, and
were the parasitic terms [
12,
18,
22], and the following general relation can describe it.
To rearrange the manipulator’s task motion variables in the format shown in Equation (
20), the general constraint given in Equation (
19) is used. Then, we can obtain the velocity-level analytic coupling relation between the parasitic and independent velocity terms by substituting the manipulator’s structural constraint information in Equation (
19). Obtaining the coupling relation between dependent and independent variables enables us to understand the parasitic motion in-depth. It also can be used to understand the geometric parameters that cause the parasitic motion for eventual optimization of the structure. The method of obtaining the coupling relation from the relation in Equation (
19) is advantageous over the position-level approach when the manipulator is designed at the velocity-level. Moreover, obtaining
is a well-established procedure at the velocity-level compared to the geometric-based point-plane constraint approach. This section briefly shows the detailed derivation of parasitic terms as a function of the independent motion by manipulating the velocity constraint element-wise. From the Equation (
19), we have the
ith limb constraint’s relation with the task velocity and can be rewritten as:
where
Then, by distributing the elements of
we can get:
Unpacking
and
in Equation (
23) to further expanding the equation yields:
Then, by rearranging the parasitic terms on one side and the independent terms on the other side as shown below:
Finally, rewriting Equation (
25) in matrix form gives:
Writing
and
for
makes them a
and
mapping matrices, respectively. From the relation in Equation (
27), we can obtain the parasitic motion of the moving plate as a function of the main motions, i.e.,
where,
In Equation (
28), we can freely define
and
and obtain
. The z-axis linear velocity is zero if the manipulator is not moving along the z-axis. Equation (
28), we can see that the z-axis linear motion is not related to the parasitic motion.
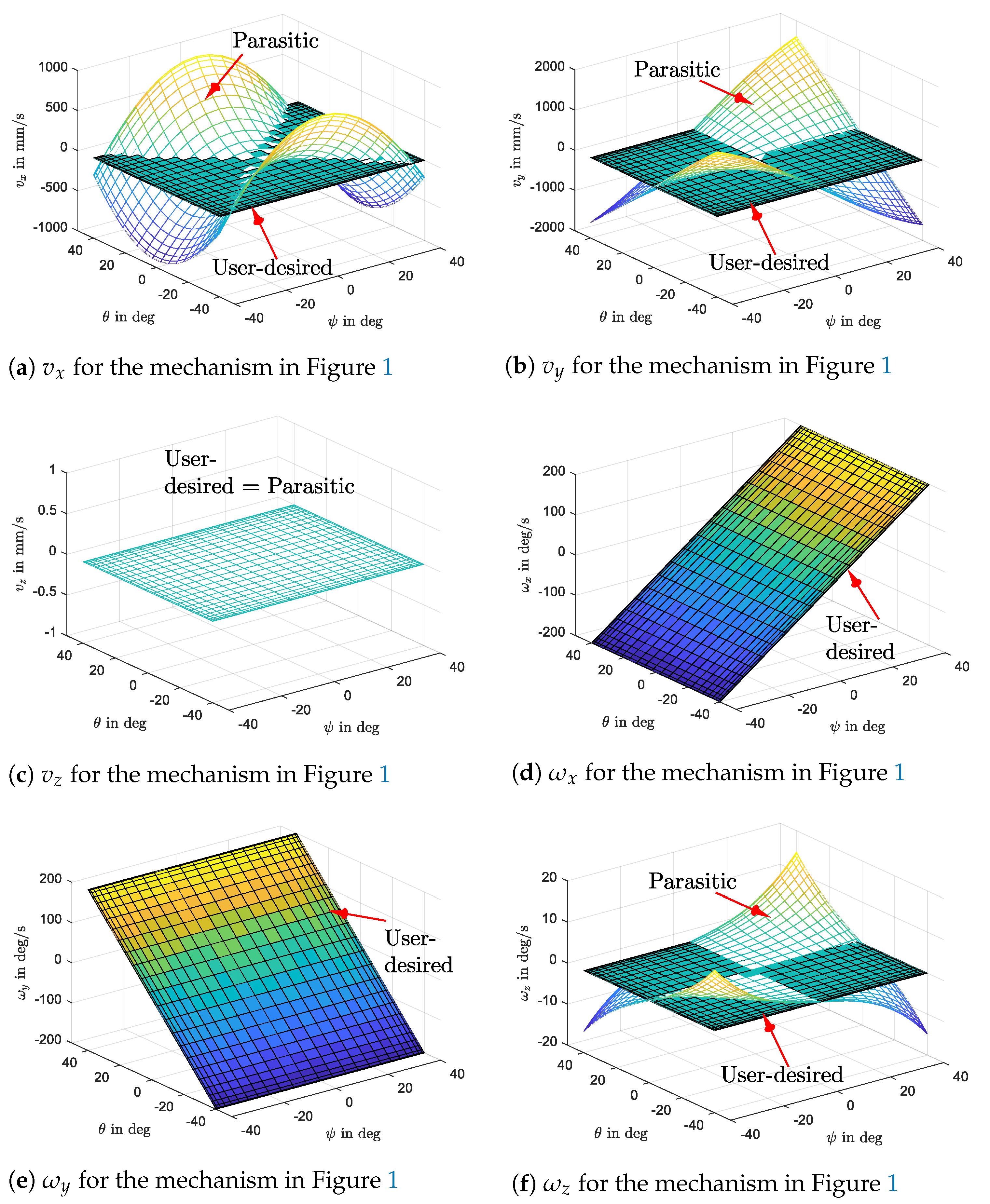
Numerical simulation: A numerical simulation is presented to visualize the parasitic motion-induced for satisfying the structural constraint. Because the simulation result for all manipulators has shown the same property, a 3-RPS manipulator is chosen as a representative example. So, other manipulators also have similar outcomes regardless of the amplitude of the parasitic motion. The user-defined (desired) motion is the angular velocity in rad/sec shown in Equation (
29). The motion along the z-axis is set to zero. The geometric parameter shown in
Table 1 is used to obtain the solution shown in
Figure 4. From
Figure 4, we can see that our desired motion is different from what the manipulator can execute. If the parasitic motion obtained in
Figure 4 is not incorporated in the task motion, the manipulator cannot function well or will be broken in the worst case. However, the parasitic motion is undesired from users’ perspective. The result in
Figure 4c demonstrates that the linear motion along the z-axis has no relation with the parasitic motion as in Equation (
28). The user input variables
and
are shown in
Figure 4d,e. As can be seen from the result, these terms are not entirely affected by the parasitic motion since they are freely chosen. In general, the task velocity in
Figure 4 is constraint compatible motion that can be used to solve the joint rate.
Note that
s and
c in Equation (
29) stands for sine and cosine, respectively.
From the simulation, we can see the motions that are undesired for the user but necessary for the manipulator to operate safely. Optimization should be performed to match the user’s requirements and manipulator’s specifications.
4. Optimization of Parasitic Motion
The parasitic motion has been recognized as one of the major drawbacks of the lower mobility PMs. Consecutively, several researchers have tried to eliminate it from the workspace. However, most attempts are entirely geometry dependent and applied at the position-level while most parallel manipulators control scheme is designed at the velocity-level. In this paper, the parasitic terms in the constraint-compatible velocity are optimized using the velocity-level relation derived in
Section 3. From Equation (
28), we can see that parasitic motions are dependent on two generic parameters, i.e.,
and
. The angles
and
are simultaneously altered during the optimization procedure; the algorithm simultaneously changes the distal and proximal joint of the limbs, to determine the optimal configuration. Thus, all of them are in the vector
. i.e,
. By denoting
, the inverse of
can be rewritten in the form shown in
Appendix A. Then, Equation (
28) can be described in analytic form as:
where
The expression for variable
is given in Equation (
4). The detail elements of the vector
given in Equation (
2) can be expanded as:
where
is the angle to locate the spherical joints from the x-axis of frame
as in Equation (
3).
Our objective in this section is to remove the parasitic motion from the workspace. Through careful observation of the parasitic motion equation, only and are the relevant geometric parameters that can be meaningfully altered to get the configuration of the manipulator without parasitic motion. The radius of the moving platform does linearly relate to the parasitic motion, and from the equation, it is observed that the optimal solution is trivial, which is . Thus, only angle and will be considered as feasible design parameters and are denoted by vector . By obtaining optimum for limbs 2 and 3 from the x-axis, the minimum parasitic motion can be achieved for all choices of . Thus, the choice of can be left to the designers.
Subsequently, it is required to transform Equation (
30) in the form that is suitable to the selected optimization algorithm. The algorithms can be single-objective such as Quasi-Newton or multi-objective such as pattern-search or Pareto-front. In this paper, the quasi-newton algorithm is used for the direction-specific optimization and the pattern search to simultaneously optimize all parasitic motions. We prefer the Quasi-Newton methods for a direction-specific optimization because it is simple and convenient when the Hessian is quite difficult to compute analytically due to system nonlinearity. For the vectorized evaluation, the pattern-search is chosen because it is a non-gradient rapid convergence algorithm for multi-objective nonlinear system. Moreover, thus solvers are valiance in Matlab optimization toolbox. For the direction-specific optimization, the x- and y-axis linear motions can be rewritten as:
and,
To minimize the parasitic motion in a specific direction with the Equations (32) and (33) over the intended rotational workspace, the linear motion along the z-axis has no role. Moreover, it is difficult to use linear programming due to the nonlinearity of
and
. Thus, the average
along the specified direction and entire rotational workspace is obtained by summing over all the columns to create a row of sums and then summing across the row to get the array’s total sum as in Equations (34) and (35).
Then, the Quasi-Newton algorithm is applied consecutively for Equations (34) and (35) as shown in Equation (
36).
Quasi-Newton method: The quasi-Newton methods build up a curvature information at each iteration to formulate a quadratic model problem of the form:
where
is a positive definite symmetric matrix and
is a constant vector. The condition for the optimality of Equation (
36) is:
Then, the optimal solution is obtained by inverting Equation (
37):
Although several methods exists for updating the Hessian matrix (
) in Equation (
36), Broyden–Fletcher–Goldfarb–Shanno (BFGS) is known to be effective [
30]. The BFG method updates the Hessian matrix using the following relation:
where,
The inverse of
is updated through the Davidon–Fletcher–Powell (DFP) method at each iteration [
30].
At each iteration, a line search is performed in the direction:
The optimization result tells varying
over the intended workspace, for the optimal parasitic motion, is the same result for all example manipulators used in this paper. This is demonstrated in the simulation and is shown in
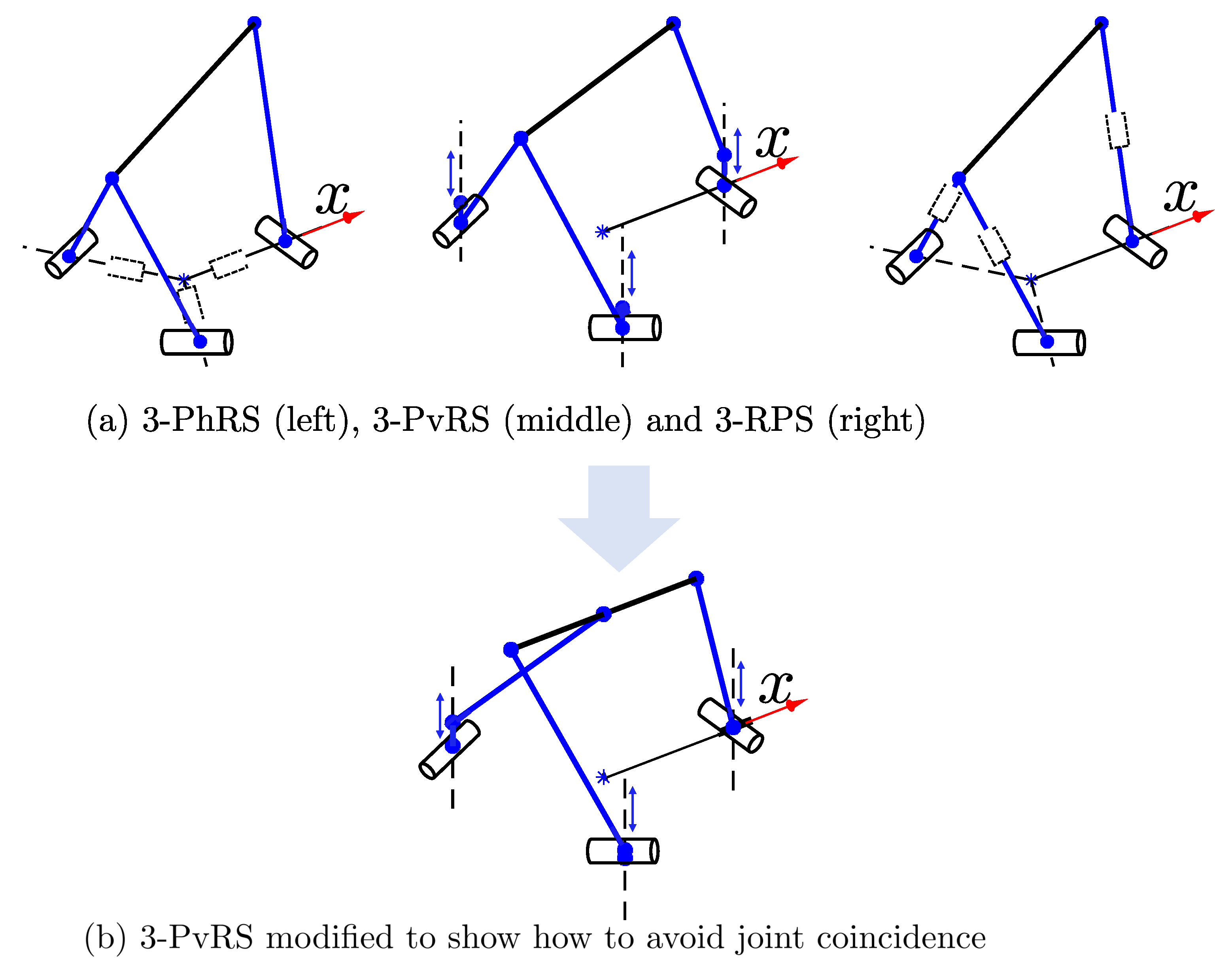
Figure 5a–c.
Figure 5a shows the configuration of zero x-axis parasitic motion for the PhRS manipulator.
Figure 5b,c shows the configuration (limb arrangement) that eliminates the x-axis parasitic motion for the PvRS and RPS manipulators, respectively. Note that the limb number convention is consistently applied for all figures and counted counterclockwise starting from the +ve x-axis throughout the paper.
The results shown in
Figure 5 is the leg (limb) arrangement of the manipulator for zero parasitic motion along the x-axis, and these parameters are
,
,
. Substituting the angular values and all the corresponding elements in Equation (
32) proves the result is true. Based on the result obtained, the following optimality condition can be drawn:
Conditions for : To eliminate the parasitic motion along the x-axis, the center of the second and third limb’s spherical joints must be collinear, and both should be orthogonal to the first limb.
Similarly, the appropriate limb arrangement or configuration for the zero parasitic motion along the y-axis is obtained by optimizing Equation (
35). Accordingly, the zero parasitic motion along this particular axis is obtained at
,
and
for all three manipulators. Likewise, the following optimality condition can be drawn for
.
Conditions for : To eliminate the parasitic motion along the y-axis, the center of the first and the third limb’s spherical joints must be collinear. i.e., , and .
Pattern-search algorithm: Considering the Quasi-Newton algorithm is suitable only for a single-digit output objective function, the non-gradient vector optimization (multi-objective algorithm) called pattern-search is used to simultaneously optimize and . The pattern-search method is a family of derivative free nonlinear numerical optimization. To reach to the optimal point, it looks a long certain specified direction, and evaluate the cost function at a given step length each of these directions. These points form a frame around the current iteration. Depending on whether any point within the pattern has a lower cost function value than the current point, the frame shrinks or expands in the next iteration. The search stops after the minimum pattern size is reached. The key condition to choose a search direction is that at least one direction in this set should give a descent direction for the cost function whenever the current point is not a stationary point.
From the sequential optimization of
and
, we have noticed that the parasitic motion along the x- and y-axes are antagonistic functions. Therefore, the pattern-search algorithm achieved a simultaneous optimization of parasitic motions along the x- and y-axes by coinciding the center of the second limb’s spherical joint with the center of the third limb’s spherical joint, as shown in
Figure 6a. Although the resulting configuration seems meaningless, it accurately tells the condition for eliminating both
and
parasitic motions from the workspace.
As can be seen from
Figure 6a, the limb arrangement that eliminates both parasitic motions have two coincident spherical joints. This is because of the constant length radius of the moving platform. In general, the result tells, all spherical joints need to be collinear in order for the manipulator to perform without parasitic motion. Thus, the following condition can be drawn.
Condition for
: To eliminate the parasitic motion in all directions, the three joints on the moving platform must be collinear. Moreover, the direction of the two revolute joints axes at the base should be parallel, while the remaining is perpendicular for both. Other example manipulators also have a similar result to that shown in
Figure 6a. Thus, the example can be representative. When the two spherical joints meet at one point, as shown in
Figure 6a, the design becomes complex. To avoid this problem, the radius of a limb perpendicular to the other two limbs can be adjusted to zero without loss of generality, as shown in
Figure 6b. Setting
for this particular limb does not violate the condition for
. The numerical example is provided to show these manipulators have removed the parasitic motion in the required direction.
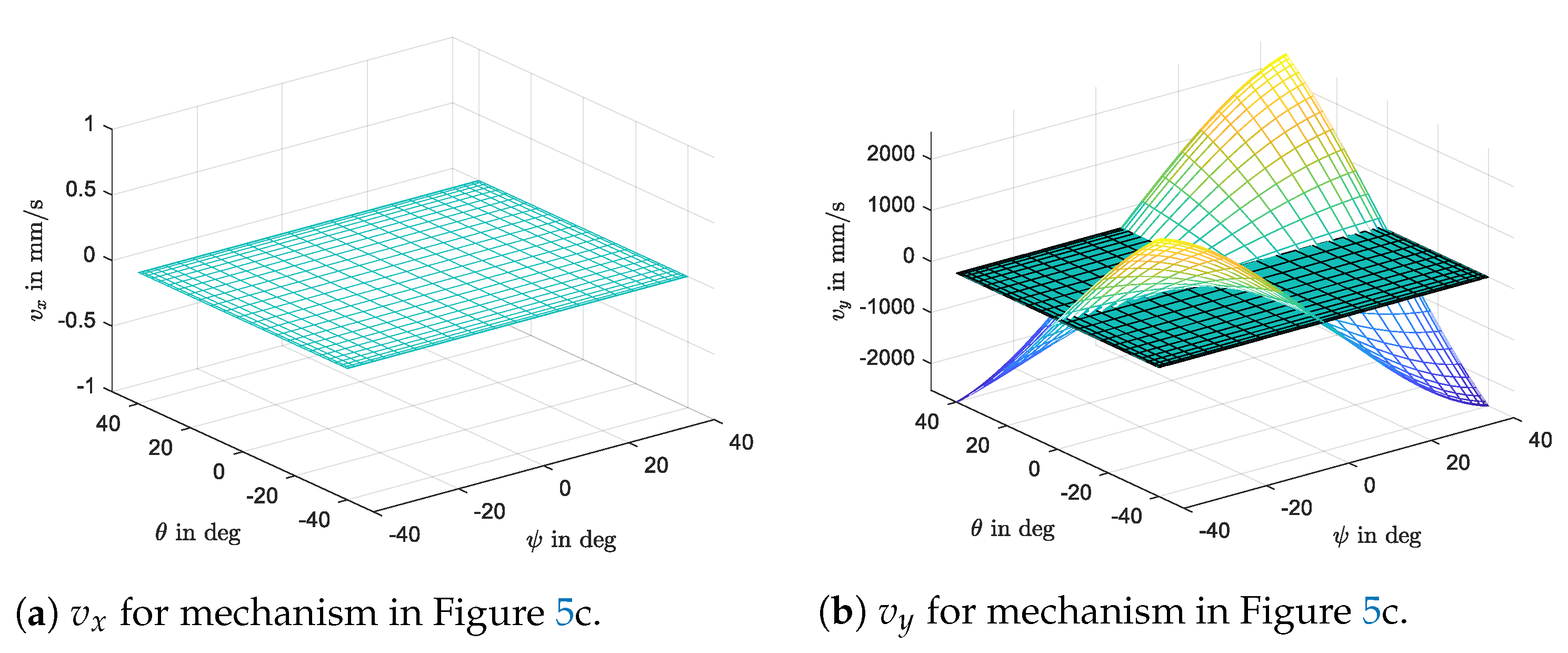
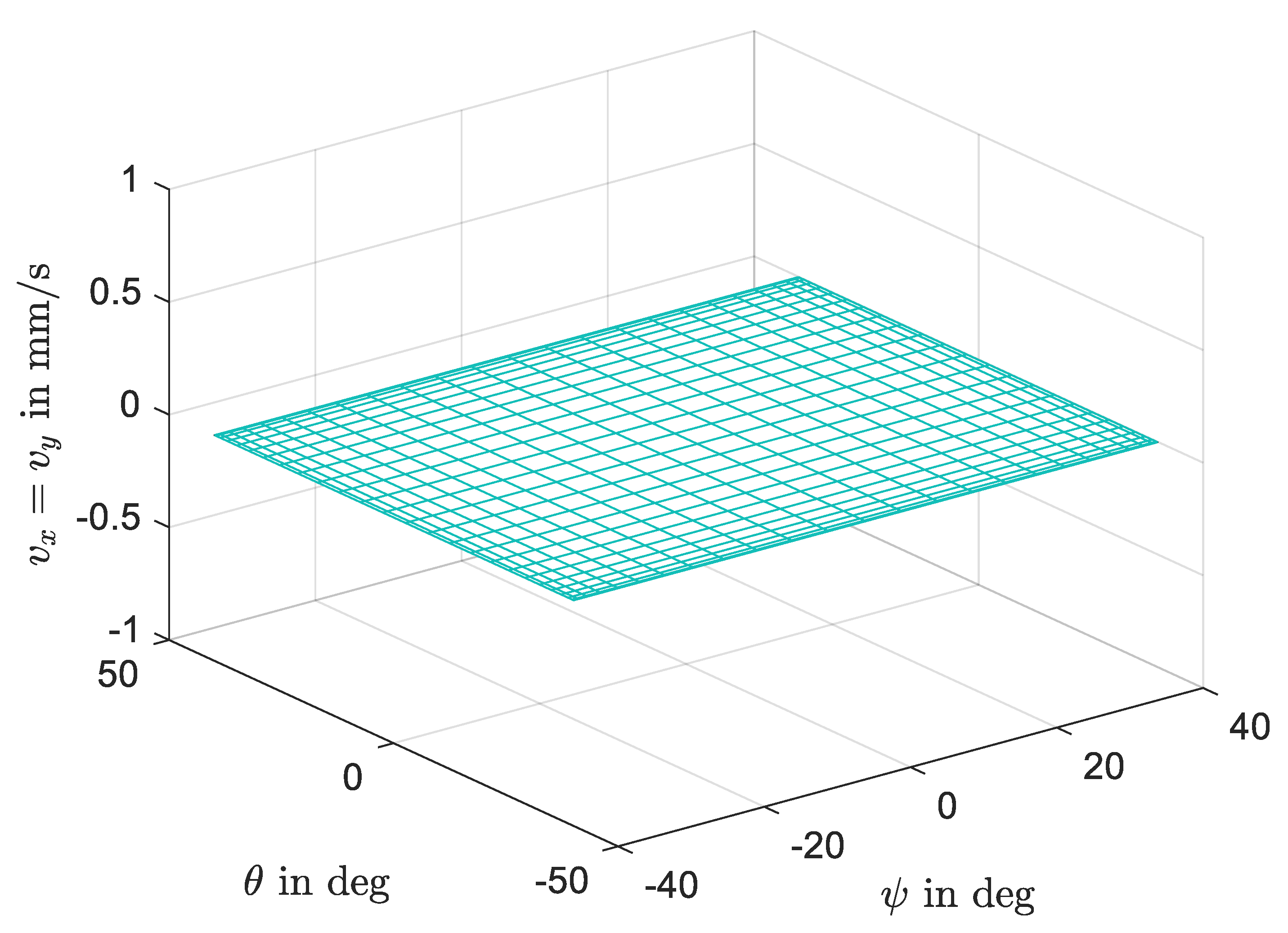
Figure 7 and
Figure 8 are the task velocity for the optimal parasitic motion presented by taking the 3-RPS manipulator as a representative example.
Figure 7 is the linear parasitic motion for the RPS manipulator shown in
Figure 5. The simulation result shows that the x-axis parasitic motion is zero in the entire rotational workspace. Similarly, the y-axis parasitic motion is eliminated when the condition for
is satisfied. Finally, the simulation for
Figure 6b implies no parasitic motions in all directions. The result is shown in
Figure 8. Thus, the manipulator is capable of performing pure rotation about the center of the moving plate. The resulting motion is purely spherical but with a non-spherical spatial manipulator. It is known that the rotational motion about a fixed point has usually been achieved by a spherical manipulator. Achieving a pure independent rotational motion with non-spherical spatial manipulator can improve the problems that are existed in the spherical manipulators.
During the optimization of the parasitic motion, two types of optimal structures are obtained, i.e., direction-specific optimal manipulator and manipulators with zero parasitic motion in all directions. Depending on the desired application, the direction-specific optimal manipulator can be chosen. For example, suppose the task strictly requires zero parasitic motion along the x-axis but loosens-up sensitivity for the y-parasitic motion. In that case, the result shown in
Figure 5 can be used. Likewise, when the x-axis parasitic motion is not critical, the manipulator with the zero parasitic motion along the y-axis can be used.