Abstract
An abundance of objective image quality metrics have been introduced in the literature. One important essential aspect that perceived image quality is dependent on is the viewing distance from the observer to the image. We introduce in this study a novel image quality metric able to estimate the quality of a given image without reference for different viewing distances between the image and the observer. We first select relevant patches from the image using saliency information. For each patch, a feature vector is extracted from a convolutional neural network model and concatenated at the viewing distance, for which the quality is predicted. The resulting vector is fed to fully connected layers to predict subjective scores for the considered viewing distance. The proposed method was evaluated using the Colourlab Image Database: Image Quality and Viewing Distance-changed Image Database. Both databases provide subjective scores at two different viewing distances. In the Colourlab Image Database: Image Quality we obtain a Pearson correlation of 0.87 at both 50 cm and 100 cm viewing distances, while in the Viewing Distance-changed Image Database we obtained a Pearson correlation of 0.93 and 0.94 at viewing distance of four and six times the image height. The results show the efficiency of our method and its generalization ability.
1. Introduction
Image quality assessment is central in acquisition, processing, analysis and reproduction of images. The interest and need for image quality assessment has increased in the last decades, resulting in increasing research on this topic. Subjective assessment is even considered to be the ”gold standard”, but objective assessment is becoming increasingly popular. A plethora of objective assessment methods, commonly known as Image Quality Metrics (IQMs), have been suggested in the literature over the last decades [1,2,3,4,5,6]. These metrics have also been considerably evaluated [7,8,9,10,11,12]. Despite the large number of existing IQMs and their extensive evaluation, there are still several limitations and unsolved challenges [8,13,14,15,16].
IQMs can, depending on the availability of the reference image, be divided into full-reference, reduced-reference, or no-reference [17]. Full-reference IQMs need the complete reference, while reduced-reference IQMs need partial information of the images, and no-reference IQMs do not need access to the reference image. Conventional IQMs only utilize information on the intensity of the distortion, such as mean-squared-error and peak-signal-to-noise-ratio (PSNR). In spite of this, these IQMs have been used with success in different applications, but they have only been moderately correlated with perceived quality for natural images [11]. IQMs based on structural similarity have become very popular in the last decade [18], and they showed to correlate better with subjective scores than PSNR [11]. There were also proposed many other IQMs based on different approaches, such as the spatial CIELAB [19], total variation of difference [20], PSNR-HVS-M [21], Difference of Gaussians [22], machine learning [23], spatial hue angle metric [24]. They have also incorporated different aspects related to the human visual system, such as contrast sensitivity [19], visual masking [25,26], gaze information [27,28]. These IQMs have been applied to a a wide range of applications, including color printing [29,30,31], displays [32], compression [33,34], cameras [35], image enhancement [36], gamut mapping [37,38], medical imaging [39,40], and biometrics [41,42,43].
Recently the use of deep learning has attracted the attention of many researchers in image quality [44,45,46,47,48,49,50,51]. The distance from the image to the observers is an important aspect when observers evaluate quality [20,52,53]. This well-known fact was, however, overlooked in many of the existing IQMs, and very few of the IQMs based on deep learning incorporate viewing distance. In addition, the existing datasets for evaluation of the performance of IQMs were only carried out at a single viewing distance or the distance was not controlled (i.e., fixed). The Colourlab Image Database: Image Quality (CID:IQ) [52] is one of a handful publicly available datasets where observers evaluated quality of images at two different viewing distances, namely 50 cm and 100 cm.
The main contributions of this work are:
- The integration of the viewing distance on a modified version of the pre-trained VGG16 model.
- The integration of the saliency information to extract patches according to their importance.
- The comparison of our modified model with several configurations.
- Evaluation of the proposed method against other state-of-the-art methods on two datasets.
We utilize a Convolutional Neural Network (CNN) to predict perceived image quality at different viewing distances. To the best of our knowledge, this is the first work where viewing distance is included in a CNN-based IQM. First, we will introduce related background, then we present the proposed method. Furthermore, we present our experimental results, and then the conclusion is given.
2. Background
There is a large number of IQMs in the literature [1,2,3,4,5], and many different approaches have been taken. In recent years, more and more IQMs based on deep learning have been proposed, and the use of deep learning has been postulated to result in better performing IQMs [15].
Chetouani et al. [54] handled image quality as a classifying problem through linear discriminant analysis. The authors first extract characterizing features from both the original and degraded images. Then, the type of degradation in the image is found by using a minimum distance criterion. The most appropriate IQM for a given distortion is finally applied. Evaluation was carried out on the TID2008 dataset [10] and the LIVE Image Quality Assessment Dataset [55]. The results showed that the suggested method is improving the correlation coefficients, but that the improvement is distortion dependent.
In [56], Chetouani extended the previous work by Chetouani et al. [54] through a CNN model for identifying the degradation and prediction of quality. The degraded image goes through two parallel processes, where the distortion type is identified using a CNN model in one process and for the other the most salient patches are found. The quality estimation is also done through a CNN model with two convolutional layers, two pooling steps, one fully connected layer and one output layer. Evaluation was carried out on the TID2008 dataset [10], Categorical Subjective Image Quality [57], and the LIVE Image Quality Assessment Dataset [55], using the following distortion types: white noise, JPEG, JPEG2000, blur and fast fading. The results indicated that the proposed method gave higher correlation coefficients compared to other no-reference IQMs, and comparable results of the best full-reference IQMs.
Chetouani [58] used the pre-trained VGG16 model in a no-reference IQM. A patch selection step based on saliency information using a scanpath predictor was incorporated in the IQM. Patches of the fixation points from the scanpath predictor was used as input to the CNN model. The IQM was evaluated on the CU-Nantes dataset [59]. The results showed that the proposed CNN model had the highest quality performance.
Hou et al. [50] suggested a no-reference IQM based on a discriminative deep learning model that was trained to classify natural scene statistics features in five quality levels (excellent, good, fair, poor, and bad). The final predicted quality score was obtained from a quality pooling step. The proposed IQM was evaluated on the LIVE Image Quality Assessment Dataset [55], TID2008 [10], Categorical Subjective Image Quality [57], IVC [60], and MICT [61].
Kang et al. [45] introduced a no-reference metric that predicted image quality of patches in images using CNNs. They contrast normalize the grayscale image, before selecting non-overlapping patches, where each patch is inputted to the network. The network consisted of five layers, where the first convolutional layers filtered the input with 50 kernels. 50 feature maps are created, which are pooled into one max and one min. Further, two fully connected layers of 800 nodes are used. The final layer is a linear regression, giving the final quality score. The no-reference IQM was evaluated on the LIVE Image Quality Assessment Dataset [55] and the TID2008 dataset [10]. The proposed IQM showed an overall correlation higher than other no-reference metrics in the evaluation.
Li et al. [46] extracted simple features from images by using a Shearlet transform, and then further treated image quality as a classification problem using deep neural networks. The first step of extracting features were based on that the statistics of the Shearlet coefficients changed as an image were distorted. The features are extracted from each of the color channels (RGB) and normalized, these features are then evolved in stacked auto-encoders before the final features are inputted to a Softmax classifier. The authors used the LIVE Image Quality Assessment Dataset [55], TID2008 [10] and the LIVE multiply distorted dataset [62]. Their results showed comparable results to other no-reference IQMs, but not as high correlation coefficients compared to the best full-reference metrics.
Lv et al. [48] apply a multi-scale Difference of Gaussian to generate features, which were processed in a deep neural network in their proposed IQM. It used a combination of a stacked auto-encoder with three hidden layers and a support vector machine regression. The IQM was evaluated on the TID2008 dataset [10] and the LIVE Image Quality Assessment Dataset [55]. The proposed no-reference IQM showed higher correlation coefficients compared to other state-of-the-art no-reference IQMs, and comparable correlation coefficients to state-of-the-art full-reference IQMs.
Bianco et al. [44] introduced a no-reference IQM using CNNs for generic distortions, where quality scores (categories such as bad, poor, fair, good and excellent) are predicted for sub-regions within the image and support vector regression is applied on the CNN features. Their architecture is based on the Caffe network [63], but pre-trained on three image classification tasks. The authors experimented with selecting between 5 and 50 sub-regions randomly from the images. Evaluation was performed using the LIVE In the Wild dataset [64], and they showed higher correlation coefficients than state-of-the-art IQMs. They also evaluated their method on the LIVE Image Quality Assessment Dataset [55], Categorical Subjective Image Quality [57], TID2008 [10], TID2013 [65]. Their correlation coefficients were similar or higher compared to other metrics.
Li et al. [66] merged CNNs and Prewitt magnitude on a segmented image to estimate the quality of images. The CNN model is based on seven layers, using normalized pixel image patches as input. The authors computed weights for the image patches, which is based on a graph-based segmentation of the original image, where the weight is the sum after applying the Prewitt operator on the image. The IQM was evaluated on the TID2008 dataset [10] and the LIVE Image Quality Assessment Dataset [55]. The results show that the introduced IQM has higher correlation coefficients compared to no-reference IQMs, and similar to the best full-reference IQMs.
Kim et al. [47] utilized local quality maps as intermediate targets for CNNs. In the proposed IQM, the CNN is trained with respect to each non-overlapping patch in the image, also giving equal weights for every pixel in the image. This results in a local quality score. Further, the pooling stage is incorporated for training. All parameters of the model are optimized simultaneously. The CNN architecture consisted of two convolutional layers and five fully connected layers. The proposed IQM was evaluated on the TID2008 dataset [10] and the LIVE Image Quality Assessment Dataset [55], and the results showed that it is comparable to the best performing IQMs.
Gao et al. [49] introduced a full-reference IQM to measure the local similarities between the features from the distorted and reference images using deep neural networks. The reference image and the degraded image are fed separately to the VGGnet [67]. Further, the output of each layer is computed being the feature map. Then, local similarities between the feature map of the reference and the feature map of the degraded image are found. At last, the local similarities are pooled as a final quality score. They evaluated their method on the LIVE Image Quality Assessment Dataset [55], Categorical Subjective Image Quality [57], the LIVE multiply distorted dataset [62], and TID2013 [65]. The performance of the full-reference IQM was similar to that of the best state of the art IQMs.
Fan et al. [68] introduced a no-reference IQM. The first step was to identify the distortion of the input image, which was done using a shallow CNN with one convolution layer. Further, for every distortion type they designed a CNN, which is used to calculate a quality score for each patch in the image. At last, a fusion algorithm was used to generate one single quality score for the entire image. Evaluation was carried out on the LIVE Image Quality Assessment Dataset [55] and Categorical Subjective Image Quality [57] dataset. Performance of the introduced no-reference IQM was comparable to state of the art IQMs, but the correlation coefficients were slightly lower than the best full-reference IQMs.
Ravela et al. [69] proposed a no-reference IQM, in which they classify the distortions present in the degraded image. For each distortion class they compute a quality score. These are further combined through a weighted average-pooling algorithm to obtain a single regressor output. The IQM was evaluated on LIVE Image Quality Assessment Dataset [55], Categorical Subjective Image Quality [57] and the TID2008 dataset [10]. The evaluation showed comparable results to other state of the art IQMs. This approach can be is similar to that of [54,56].
Varga [70] introduced no-reference IQM using multi-level inception features from a pretrained CNN. The method uses the entire to extract image resolution independent features. The IQM was evaluated on the LIVE in the wild dataset [64], and obtained higher correlation values compared to many state of the art methods.
Ma et al. [71] proposed a no-reference IQM mimicking the mimicking the human visual system, more precisely by using an active inference module of a generative adversarial network to predict the main content of the image. Then by using a multi-stream convolutional neural network (CNN) they assess the quality related to scene information, distortion type and content degradation. The proposed IQM was evaluated on LIVE Image Quality Assessment Dataset [55], Categorical Subjective Image Quality [57], TID2013 [65], LIVE In the Wild dataset [64] and LIVE multiply distorted dataset [62]. The method showed comparable or higher correlation values compared to other state of the art IQMs.
Amirshahi et al. [51] introduced a full-reference IQM using self-similarity and a CNN model. It used CNN features across multiple levels to calculate the similarity between the reference image and the degraded image. The IQM was based on the Alexnet [72] architecture. The method extracts feature maps at five convolutional layers, and these are compared using a histogram-based quality metric. A quality value at each layer is computed, and further pooled using a geometrical mean to get a final quality value. The proposed IQM was evaluated on the LIVE Image Quality Assessment Dataset [55], Categorical Subjective Image Quality [57], the Colourlab Image Quality Dataset [52], and TID2013 [65]. The results showed that the proposed IQM gave similar performance to the best state-of-the-art IQMs. The same IQM was also evaluated on a dataset for image contrast enhancement evaluation [73], where it also performed quite well [36].
The approach by Amirshahi et al. [51] was improved in [74] where the feature maps were compared using traditional IQMs such as SSIM [18], PSNR and mean squared error. The proposed IQM was evaluated on the LIVE Image Quality Assessment Dataset [55], Categorical Subjective Image Quality [57], the Colourlab Image Quality Dataset [52], and TID2013 [65]. They showed an improvement in performance of the IQMs (on average an increase of 23%) using a CNN based approach.
In this study, we advance the current research compared to the existing CNN-based IQMs by predicting image quality without a reference for different viewing distances. To achieve this, relevant patches were selected based on saliency information and the viewing distance was included to features extracted from a modified pre-trained CNN model.
3. Proposed Method
The pipeline of the proposed no-reference IQM is summarized in Figure 1. For a given degraded image, we first select the most relevant patches based on their saliency weights. For each patch, we extract a feature vector from a CNN model and concatenate it at the viewing distance for which the quality is predicted. The resulting vector is then fed to fully connected layers to predict the subjective quality for the considered viewing distance. Each of these steps is described in this section.
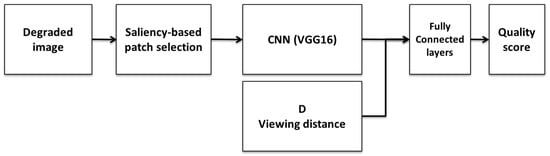
Figure 1.
Flowchart of the proposed IQM.
3.1. Saliency-Based Patch Selection
Visual attention is one of the selective mechanisms of our human visual system that involves an attractiveness towards some regions of the image. These attractive regions highly influence our subjective judgement and therefore impact the subjective quality of an image. In this study, we exploited this perceptual mechanism to select the most relevant patches that have high perceptual impact. To do so, we employed the scanpath predictor described in [75], which aims to mimic the behavior of our human visual system when it faces a real image. It predicts fixation points of the scanpath via a given saliency map. Figure 2 shows an image (Figure 2a), its corresponding saliency map (Figure 2b), its highlighted image (Figure 2c), and the predicted scanpath (Figure 2d). The predicted fixation points of the scanpath are represented by the blue points.

Figure 2.
Example of a predicted scanpath of a given image: (a) Distorted image, (b) its saliency map from the GBVS method [78], (c) its highlight image and (d) the predicted scanpath.
For each predicted fixation point, a small patch was extracted. In [45,76], they examined the impact of the patch size and found that a size of constitutes a decent trade-off between the performance and the time computation. The same size, , was used in our approach. As found by Vigier et al. [77] observers at visual angles up to 60 reach the same salient region, indicating that saliency is the same at different distances. The saliency map was computed using the Graph-Based Visual Saliency (GBVS) method [78]. GBVS has shown to be very good for fixation location and scanpath predictor [79], and is therefore used. The number of fixation points and its impact on the performance will be discussed in Section 4.1. For more details about the saliency-based patch section, readers are referred to [80].
3.2. Cnn Model
A wide range of CNN models with various architectures have been proposed in the literature. Some researchers proposed their own models [45] trained from scratch, while others employed pre-trained models like AlexNet [72] and ResNet [81]. In our technique, we used the model introduced by the Oxford Visual Geometry Group (VGG), as this model is widely utilized and provided decent results in many applications [67,82,83,84,85,86]. More precisely, we fine-tuned the pre-trained VGG16 model without data augmentation, since these treatments change the structure of the data and thus modify the perceived quality [87]. VGG16 is composed of 13 convolutional layers and 3 fully connected layers with an input of size (color image) and an output of size 1000 (i.e., 1000 classes). In order to adapt this model to our context, we first replaced the input image layer of VGG16 by another image layer of size . The 3 initial fully connected layers were also replaced by 2 other fully connected layers of size 128 and 1, where the last fully connected layer is a regression layer to predict “continuous values”. In order to predict the quality of a given image for different viewing distances, a feature vector was extracted from the last convolutional layer of our model and concatenated to the viewing distance D, normalized between 0 and 1 with 0 corresponds to 0*H and 1 to 6*H. In order to not give more importance to the viewing distance, the feature vector to which the viewing distance is concatenated was also normalized between 0 and 1. The resulting vector is then fed as input to the first fully connected layer as described in Figure 3. All these modifications allow us to adjust the model to our task, but it also leads to reduce the number of learnable parameters, since we have now around 14 M of learnable parameters compared to the initial 138 M.
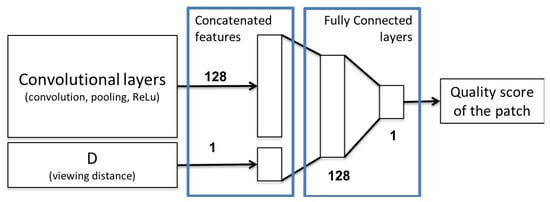
Figure 3.
Fully connected layers of the considered model. D is the viewing distance.
To train our model, the learning rate and the momentum were set to 0.01 and 0.9. We utilized stochastic gradient descent as the optimization function, and the mean square error as the loss function. The number of epochs and the batch size were set to 25 and 32, respectively. After each epoch, the training data were shuffled, and then we stored the model. The model providing the best performance was finally retained. All the experiments were carried-out with the configuration listed in Table 1.

Table 1.
Computer configuration used in our experiments.
3.3. Datasets
Two different datasets that provide subjective quality scores for two different viewing distances were used to evaluate our method.
- CID:IQ (Colourlab Image Database: Image Quality) [52]: This dataset is one of the few publicly available datasets with subjective scores collected at different viewing distances. CID:IQ has 690 distorted images made from 23 original images with high-quality. Subjective scores were collected at two viewing distances (50 cm and 100 cm, which correspond respectively to 2.5 and 5 times the image height) for each distorted image. Distorted images were generated with six types of degradation at different five levels: JPEG2000 (JP2K), JPEG, Gaussian Blur (GB), Poisson noise (PN), gamut mapping (DeltaE) and SGCK gamut mapping (SGCK). An original image and five distorted images are presented in Figure 4.
 Figure 4. Samples of the CID:IQ dataset.
Figure 4. Samples of the CID:IQ dataset. - VDID2014 (Viewing Distance-changed Image Database) [53]: This dataset has 160 distorted images made from 8 high-quality images. For each distorted image, subjective scores were collected at two different distances (4 and 6 times the image height). Distorted images were made using four types of degradation at five different levels: JPEG2000 (JP2K), JPEG, Gaussian Blur (GB) and White Noise (WN). An example of distorted images is shown in Figure 5.
 Figure 5. Samples of the VDID2014 dataset.
Figure 5. Samples of the VDID2014 dataset.
3.4. Evaluation Criteria
Pearson (PCC) and Spearman (SROCC) correlation coefficients were employed to evaluate the quality prediction of the introduced IQM. The coefficients were calculated between the subjective scores and the predicted image quality values for each viewing distance. A correlation coefficient of 1 indicates a perfect prediction and a correlation coefficient of 0 indicates no correlation.
The predicted scores were mapped to the subjective scores through the following non-linear logistic function:
where and Q are the predicted and the mapped scores. – are the fitting parameters.
4. Experimental Results
In this section, we first study the impact on the performance of the number of extracted patches. Our method is then evaluated on each dataset individually. After comparing the results to the state-of-the-art, we test the generalization capacity of our method through a cross dataset evaluation.
4.1. Impact of the Number of Fixation Points
As mentioned above, the number of patches extracted per image is fixed by the number of fixation points. Its impact on the performance was here analyzed by varying the number of fixation points from 10 to 200. For each value of the number of fixation points, PCC and SROCC values were calculated. Figure 6 shows the correlation coefficients obtained on the CID:IQ dataset by splitting the database according to the reference images. The test set was composed of one-fold (20% of the reference image and its degraded versions), while the training-validation set included the remaining images. The latter was split randomly without overlapping (80% for training and then 20% for validation). This protocol ensures non-overlap or redundancy (in terms of image content) between sets. This procedure was repeated five times and the correlations were calculated by concatenating the scores.
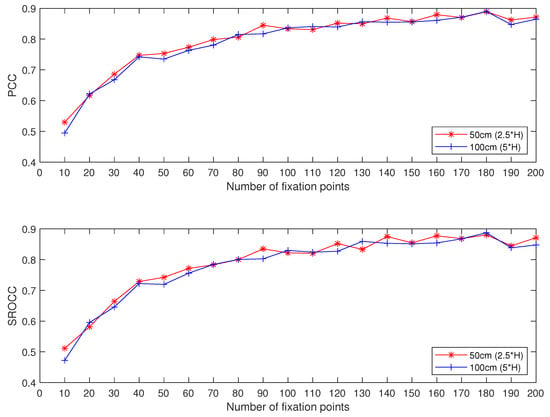
Figure 6.
Correlation values when changing the number of fixation points.
As expected, the lower the number of fixation points, the lower the correlation. Indeed, the number of fixation points fixes the amount of data of the training set, which directly impacts the capacity of our model to learn the data. Correlations of the two viewing distances were close and increased with the number of fixation points. The best performance was raised for number of fixation points = 180 (i.e., 180 patches extracted per image). In the following, the quality of each image is thus predicted through 180 patches, where the quality is the average of the quality for each of the 180 patches.
The attention of an observer can be influenced by the viewing distance or the distortions [88], and as the incorporated scanpath predictor does not account for this, it may have an influence and should be investigated in future work.
In order to better show the relevance of our pipeline, we compared the proposed saliency-based patch selection with the classical approach (i.e., no selection) and a random selection. These tests were carried out using the modified version of VGG16 and the baseline model, which corresponds to the modified version of VGG16 without integrating the viewing distance (i.e., one input and one output). The latter was trained using subjective scores of one viewing distance (i.e., 2.5*H) and tested on two distances (i.e., 2.5*H and 5*H). This procedure was applied to not associate several outputs to a single input. Table 2 shows the correlations obtained on CID:IQ dataset. As can be seen, a random selection of patches provided poorer results, while the proposed saliency-based patch selection improved the performance. Compared to the random selection, the use of all patches (i.e., no selection) improved the performance, but the global correlation still lower than that achieved with the proposed saliency-based patch selection. In addition, the integration of the viewing distance as input (i.e., proposed model) to the baseline model highly improved the performance whatever the selection type, especially when the proposed saliency-based selection step was applied.

Table 2.
Impact of the patch selection step. Pearson (PCC) and Spearman (SROCC) values obtained with and without the saliency-based patch selection as well as with a random patch selection for each viewing distance of the CID:IQ database. Highest values are in bold.
Figure 7 shows the loss values obtained in the training and validation sets across the number of epochs for one random splitting of the CID:IQ dataset. The loss values of both sets decreased until stabilizing, indicating no-overfitting.
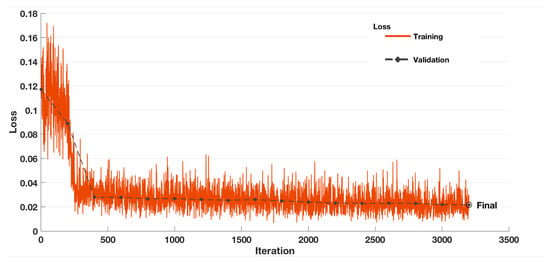
Figure 7.
Loss in training and validation sets across the number of epochs for one splitting of the CID:IQ dataset.
Figure 8 shows the patch scores predicted for a given image and the corresponding subjective scores for two viewing distances. As can be seen, there is a gap between the predicted patch scores for the distance 50 cm (blue curve) and those predicted for the distance 100 cm (green curve). This gap reflects well the gap between the corresponding subjective scores (black and red dotted lines). Therefore, the integration of the viewing distance as input to our model allowed to well shift the predicted score according to the viewing distance considered.
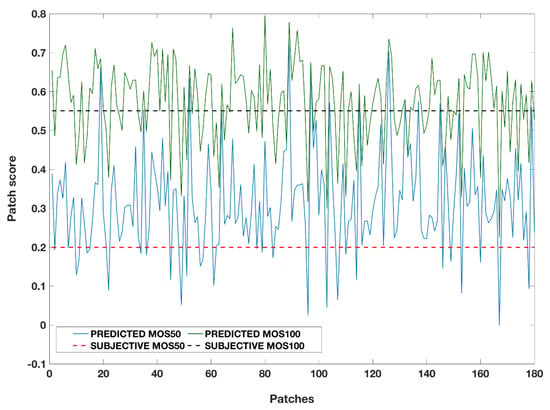
Figure 8.
Predicted scores of a given distorted image for two different viewing distances and their corresponding subjective scores.
4.2. Individual Evaluation
In this section, we present the results of our method for both datasets (CID:IQ and VDID2014). For each of them, we computed the correlations according to the viewing distances as well as the correlations per degradation type.
4.2.1. CID:IQ
We evaluated our method on CID:IQ dataset by applying the protocol described in Section 4.1 (i.e., 5 fold cross validation). Table 3 shows the correlations for each viewing distance. The results were compared to our previous work (CNN-VD) [58], where only one CNN model with two outputs was used. As can be seen, high performances were obtained for the two viewing distances with close correlation values. Compared to CNN-VD, the correlations increased with an improvement in terms of PCC of 1.4% for the two distances.

Table 3.
Pearson (PCC) and Spearman (SROCC) correlation coefficients between the predicted quality scores and the subjective ones for each viewing distance of the CID:IQ database. Highest values are in bold.
In Table 4, the correlation coefficients for each distortion, at five levels, are shown and compared to those of MSSIM and CNN QUALITY. In general, the performances were high for all distortions and viewing distances. The highest values were obtained for SGCK at 50 cm and at 100 cm, while the lowest ones were obtained for JPEG at 50 cm and JP2K for 100 cm. We also noticed that for SGCK, JPEG, GB, and DeltaE the proposed method has slightly higher coefficients for the 100 cm viewing distance compared to 50 cm, while it was the opposite for JP2K and PN. Compared to the MSSIM and CNN Quality metrics the proposed metric has good performance, giving a higher correlation value for JPEG, PN, SGCK and DeltaE for 50 cm and JPEG, SGCK and DeltaE for 100 cm. It is also noticeable that the proposed method is more stable compared to MSSIM.

Table 4.
Pearson (PCC) correlation coefficients between the predicted quality scores and the subjective ones for each distortion of the CID:IQ database.
4.2.2. Vdid2014
To evaluate our method on VDID2014, the dataset was split into 4-fold (i.e., 25% of the reference image and its degraded versions for the test set and the rest for the training-validation set). As can be seen in Table 5, the performances were higher than those obtained on CID:IQ and the best results were obtained for the distance 4*H. Compared to CNN-VD, the improvements in terms of PCC are 5.43% for the distance 4*H and 2.84% for 6*H.

Table 5.
Pearson (PCC) and Spearman (SROCC) correlation coefficients between the predicted quality scores and the subjective ones for 4*H and 6*H viewing distances of the VDID2014 database. Highest correlation coefficients are in bold.
Table 6 presents the result of each degradation type, where each degradation has five levels. The correlations were generally high for all distortions. Contrary to the results of CID:IQ, all the correlations of our method were higher for the distance 6*H. The highest values were obtained for JPEG and JP2K for both 4*H and 6*H. Compared to the MSSIM and CNN Quality metrics, the proposed method has good performance, giving a higher correlation value for JP2K, JPEG and GB for 4*H and for JP2K, JPEG and WN for 6*H. MSSIM obtained the best results for WN for 4*H, while CNN Quality achieved the best results for GB for 6*H.

Table 6.
Pearson (PCC) correlation coefficients between the predicted quality scores and the subjective ones for each distortion of the VDID2014 database.
4.2.3. Computation Time
We also compared the computation time of the proposed pipeline to that with no-selection. It is worth noting that we compared here only the computation time related to the quality prediction without integrating the saliency-based patch selection. As shown in Table 7, the quality of an given image is predicted using 180 patches whatever the dimension of the image, while 625 and 310 patches are used for images of CID:IQ and VDID14 datasets, respectively. The results show that the proposed method based on saliency is faster compared to using all patches.

Table 7.
Mean number of patches extracted per image on both datasets and their computation time.
4.2.4. Comparison with the State-Of-The-Art
The results of our method were compared to the state-of-the-art IQMs (PSNR, PSNR-HVS-M [89], PSNR-HA [89], C-PSNR-HVS-M [89], C-PSNR-HA [89], SSIM [18], CSSIM [90], CSSIM4 [90], WASH [91], VIF/VIFP [92], IFC [93], UQI [94], WSNR [95], SNR, NQM [96], MSSIM [97], FSIM [98], GMSD [99], CNN Quality [51]). In addition, we compared against no-reference IQMs (BRISQUE [100], DIVINE [101], AQI [102], ARISMC [103], BQMS [104], CPBD [105]). For fair comparison, the BRISQUE and DIVINE IQMs were retrained on both databases. Three distance-based metrics were also considered. The well-known metric Visual Difference Predictor (VDP) [106], that exploits the contrast sensitivity function that integrates the viewing distance, was evaluated against the proposed method. In [53], the authors improved the well-known metrics PSNR and SSIM by integrating an optimal scale selection model in discrete wavelet transform domain. This model aims to consider viewing distance and image resolution before using existing metrics. The latter are respectively labelled here as PSNR2 and SSIM2.
Table 8 shows the results for both databases, the same results for Pearson correlation is shown in Figure 9, Figure 10, Figure 11 and Figure 12. 95% confidence intervals were calculated using Fishers Z-transform. Globally, the correlations achieved on VDID2014 dataset were higher than those of CID:IQ. The metrics better predict the quality for 50 cm on CID:IQ, while higher correlations were obtained for 6*H on VDID2014.

Table 8.
Pearson (PCC) and Spearman (SROCC) correlation coefficients between the predicted quality scores and the subjective ones for each viewing distance of CID:IQ and VDID2014. Highest values per category are shown in bold and the highest one has a grey background.
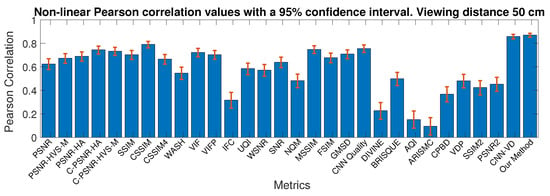
Figure 9.
Performance of the IQMs on the CID:IQ dataset for 50 cm viewing distance. The figure shows Pearson correlation with a 95% confidence interval.
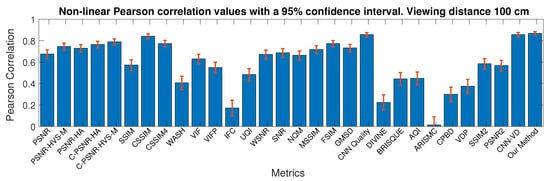
Figure 10.
Performance of the IQMs on the CID:IQ dataset for a 100-cm viewing distance. The figure shows Pearson correlation with a 95% confidence interval.
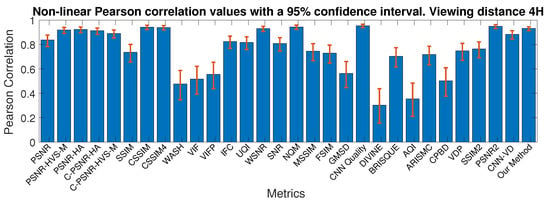
Figure 11.
Performance of the IQMs on the VDID dataset for 4H viewing distance. The figure shows Pearson correlation with a 95% confidence interval.
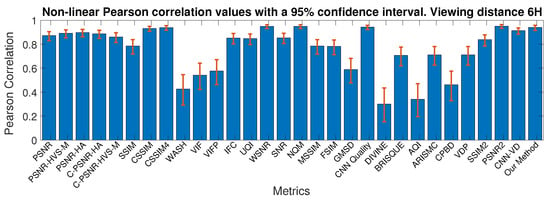
Figure 12.
Performance of the IQMs on the VDID dataset for 6H viewing distance. The figure shows Pearson correlation with a 95% confidence interval.
For FR approaches, the best performance on CID:IQ was obtained by CSSIM for 2.5*H and MSSIM for 5*H. CSSIM is a metric based on predictability of blocks simulating the visual system, and has also been shown to perform better than SSIM [90]. The main difference between SSIM and MSSIM is the multi scale analysis that allowed an improvement of 6% on CID:IQ. On VDID2014, CNN Quality achieved the best results for the two viewing distances. No-reference IQMs failed to predict quality for both databases, even after being retrained. Our distance-based method performed better than all the compared ones by more than 1.4% on CID:IQ. On VDID2014, our method obtained competitive results, since PSNR2 and SSIM2 performed better than our method for 6*H. However, our method is blind and thus does not need any information from the reference image. Furthermore, our method performed better than most of the FR metrics.
To show the global performance of the suggested method, we calculated the correlation whatever the viewing distance and the degradation type. Table 9 and Table 10 present the results on CID:IQ and VDID2014 datasets, respectively. Our method performed better than all the compared ones by more than 2.7% on CID:IQ. On VDID2014, the results show that the suggested IQM achieved the second best PCC value. However, our method remains highly competitive since most of the compared methods obtained a PCC smaller than 0.9 and best results (i.e., SSIM2 and PSNR2) were achieved by two FR metrics.

Table 9.
PCC and SROCC values whatever the viewing distance computed on CID:IQ.

Table 10.
PCC and SROCC values whatever the viewing distance computed on VDID2014.
4.3. Cross Dataset Evaluation
We evaluated the generalization ability of our method by training our model on CID:IQ and testing it on VDID2014 without overlap between both. It is worth noting that cross dataset evaluation in our context is more difficult than those traditionally carried out in image quality assessment. Indeed, in addition to the difference in terms of content between both datasets, the two viewing distances considered by each of the databases are different. In other words, we evaluated here the efficiency of our method to predict the quality of unknown image for unknown viewing distances.
Table 11 shows the correlations obtained for both viewing distances as well as the global performance. Compared to the individual evaluation, the performance decreased but still high. The same PCC value was obtained for the two distances. In addition to the viewing distances and the content (2.5*H and 5*H on CID:IQ against 4*H and 6*H on VDID2014), this decrease is certainly due to the fact that certain degradation types were not considered during the training step (White Noise on VDID2014 and Poisson Noise on CID:IQ).

Table 11.
Cross dataset evaluation using CID:IQ as training set and VDID2014 as test set.
5. Conclusions
We have proposed a novel CNN-based blind image quality method that predicts subjective scores for different viewing distances was introduced. The method first selects relevant patches from the image based on a scanpath predictor, further these patches are used to extract features from a CNN based on VGG16. Feature vector concatenated with the viewing distance is fed to a fully connected layer to predict the perceived quality. Our method was evaluated on two different databases. Results obtained by our method were compared to the state-of-the-art and showed its consistency with the subjective judgments. A cross-dataset experiment was also carried out and showed the generalization ability of our method to predict the quality of unknown images for unknown viewing distances.
In future work, the combination of several deep learning-based features should be studied. In addition, the use of other techniques for incorporating attention, foveation [107] and multi scale analysis can be seen as potential future work. The integration of more viewing distances will also be investigated.
Author Contributions
Both authors have contributed equally. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pedersen, M.; Hardeberg, J.Y. Full-reference image quality metrics: Classification and evaluation. Found. Trends® Comput. Graph. Vis. 2012, 7, 1–80. [Google Scholar]
- Lin, W.; Kuo, C.C.J. Perceptual visual quality metrics: A survey. J. Vis. Commun. Image Represent. 2011, 22, 297–312. [Google Scholar] [CrossRef]
- Engelke, U.; Zepernick, H.J. Perceptual-based quality metrics for image and video services: A survey. In Proceedings of the 2007 Next Generation Internet Networks, Trondheim, Norway, 21–23 May 2007; pp. 190–197. [Google Scholar]
- Thung, K.H.; Raveendran, P. A survey of image quality measures. In Proceedings of the 2009 International Conference for Technical Postgraduates (TECHPOS), Kuala Lumpur, Malaysia, 14–15 December 2009; pp. 1–4. [Google Scholar]
- Eskicioglu, A.M.; Fisher, P.S. Image quality measures and their performance. IEEE Trans. Commun. 1995, 43, 2959–2965. [Google Scholar] [CrossRef]
- Ahumada, A.J. Computational image quality metrics: A review. SID Dig. 1993, 24, 305–308. [Google Scholar]
- Pedersen, M. Evaluation of 60 full-reference image quality metrics on the CID:IQ. In Proceedings of the IEEE International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015; pp. 1588–1592. [Google Scholar]
- Chetouani, A. Full Reference Image Quality Assessment: Limitation. In Proceedings of the 2014 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 833–837. [Google Scholar]
- Avcibas, I.; Sankur, B.; Sayood, K. Statistical evaluation of image quality measures. J. Electron. Imaging 2002, 11, 206–224. [Google Scholar]
- Ponomarenko, N.; Lukin, V.; Zelensky, A.; Egiazarian, K.; Carli, M.; Battisti, F. TID2008-a database for evaluation of full-reference visual quality assessment metrics. Adv. Mod. Radioelectron. 2009, 10, 30–45. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. A comprehensive evaluation of full reference image quality assessment algorithms. In Proceedings of the IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 1477–1480. [Google Scholar] [CrossRef]
- Lahoulou, A.; Bouridane, A.; Viennet, E.; Haddadi, M. Full-reference image quality metrics performance evaluation over image quality databases. Arab. J. Sci. Eng. 2013, 38, 2327–2356. [Google Scholar] [CrossRef]
- Wang, Z. Objective Image Quality Assessment: Facing The Real-World Challenges. Electron. Imaging 2016, 2016, 1–6. [Google Scholar] [CrossRef][Green Version]
- Chandler, D.M. Seven challenges in image quality assessment: Past, present, and future research. ISRN Signal Process. 2013, 2013. [Google Scholar] [CrossRef]
- Amirshahi, S.A.; Pedersen, M. Future Directions in Image Quality. In Color and Imaging Conference; Society for Imaging Science and Technology: Paris, France, 2019; Volume 2019, pp. 399–403. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Lu, L. Why is image quality assessment so difficult? In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; Volume 4, p. IV-3313. [Google Scholar]
- Wang, Z.; Bovik, A.C. Modern image quality assessment. Synth. Lect. Image Video Multimed. Process. 2006, 2, 1–156. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, X.; Wandell, B. A spatial extension of CIELAB for digital color-image reproduction. J. Soc. Inf. Disp. 1997, 5, 61–63. [Google Scholar] [CrossRef]
- Pedersen, M. An image difference metric based on simulation of image detail visibility and total variation. In Color and Imaging Conference. Society for Imaging Science and Technology; Society for Imaging Science and Technology: Boston, MA, USA, 2014; Volume 2014, pp. 37–42. [Google Scholar]
- Ponomarenko, N.; Silvestri, F.; Egiazarian, K.; Carli, M.; Astola, J.; Lukin, V. On between-coefficient contrast masking of DCT basis functions. In Proceedings of the Third International Workshop on Video Processing and Quality Metrics; Scottsdale, AZ, USA, 2007; Volume 4. [Google Scholar]
- Ajagamelle, S.A.; Pedersen, M.; Simone, G. Analysis of the difference of gaussians model in image difference metrics. In Conference on Colour in Graphics, Imaging, and Vision; Society for Imaging Science and Technology: Joensuu, Finland, 2010; Volume 2010, pp. 489–496. [Google Scholar]
- Charrier, C.; Lézoray, O.; Lebrun, G. Machine learning to design full-reference image quality assessment algorithm. Signal Process. Image Commun. 2012, 27, 209–219. [Google Scholar] [CrossRef]
- Pedersen, M.; Hardeberg, J.Y. A new spatial filtering based image difference metric based on hue angle weighting. J. Imaging Sci. Technol. 2012, 56, 50501-1. [Google Scholar] [CrossRef]
- Fei, X.; Xiao, L.; Sun, Y.; Wei, Z. Perceptual image quality assessment based on structural similarity and visual masking. Signal Process. Image Commun. 2012, 27, 772–783. [Google Scholar] [CrossRef]
- Pedersen, M.; Farup, I. Simulation of image detail visibility using contrast sensitivity functions and wavelets. In Color and Imaging Conference; Society for Imaging Science and Technology: Los Angeles, CA, USA, 2012; Volume 2012, pp. 70–75. [Google Scholar]
- Bai, J.; Nakaguchi, T.; Tsumura, N.; Miyake, Y. Evaluation of Image Corrected by Retinex Method Based on S-CIELAB and Gazing Information. IEICE Trans. 2006, 89-A, 2955–2961. [Google Scholar] [CrossRef]
- Pedersen, M.; Hardeberg, J.Y.; Nussbaum, P. Using gaze information to improve image difference metrics. In Human Vision and Electronic Imaging XIII; International Society for Optics and Photonics: San Jose, CA, USA, 2008; Volume 6806, p. 680611. [Google Scholar]
- Pedersen, M.; Zheng, Y.; Hardeberg, J.Y. Evaluation of image quality metrics for color prints. In Scandinavian Conference on Image Analysis; Springer: Berlin/Heidelberg, Germany, 2011; pp. 317–326. [Google Scholar]
- Falkenstern, K.; Bonnier, N.; Brettel, H.; Pedersen, M.; Viénot, F. Using image quality metrics to evaluate an icc printer profile. In Color and Imaging Conference; Society for Imaging Science and Technology: San Antonio, TX, USA, 2010; Volume 2010, pp. 244–249. [Google Scholar]
- Gong, M.; Pedersen, M. Spatial pooling for measuring color printing quality attributes. J. Vis. Commun. Image Represent. 2012, 23, 685–696. [Google Scholar] [CrossRef]
- Zhao, P.; Cheng, Y.; Pedersen, M. Objective assessment of perceived sharpness of projection displays with a calibrated camera. In Proceedings of the 2015 Colour and Visual Computing Symposium (CVCS), Gjovik, Norway, 25–26 August 2015; pp. 1–6. [Google Scholar]
- Charrier, C.; Knoblauch, K.; Maloney, L.T.; Bovik, A.C. Calibrating MS-SSIM for compression distortions using MLDS. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 3317–3320. [Google Scholar]
- Brooks, A.C.; Pappas, T.N. Using structural similarity quality metrics to evaluate image compression techniques. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP’07, Honolulu, HI, USA, 15–20 April 2007; Volume 1, p. I-873. [Google Scholar]
- Seybold, T.; Keimel, C.; Knopp, M.; Stechele, W. Towards an evaluation of denoising algorithms with respect to realistic camera noise. In Proceedings of the 2013 IEEE International Symposium on Multimedia, Anaheim, CA, USA, 9–11 December 2013; pp. 203–210. [Google Scholar]
- Amirshahi, S.A.; Kadyrova, A.; Pedersen, M. How do image quality metrics perform on contrast enhanced images? In Proceedings of the 2019 8th European Workshop on Visual Information Processing (EUVIP), Roma, Italy, 28–31 October 2019; pp. 232–237. [Google Scholar]
- Cao, G.; Pedersen, M.; Barańczuk, Z. Saliency models as gamut-mapping artifact detectors. In Conference on Colour in Graphics, Imaging, and Vision; Society for Imaging Science and Technology: Joensuu, Finland, 2010; Volume 2010, pp. 437–443. [Google Scholar]
- Hardeberg, J.Y.; Bando, E.; Pedersen, M. Evaluating colour image difference metrics for gamut-mapped images. Coloration Technol. 2008, 124, 243–253. [Google Scholar] [CrossRef]
- Pedersen, M.; Cherepkova, O.; Mohammed, A. Image Quality Metrics for the Evaluation and Optimization of Capsule Video Endoscopy Enhancement Techniques. J. Imaging Sci. Technol. 2017, 61, 40402-1. [Google Scholar] [CrossRef]
- Völgyes, D.; Martinsen, A.; Stray-Pedersen, A.; Waaler, D.; Pedersen, M. A Weighted Histogram-Based Tone Mapping Algorithm for CT Images. Algorithms 2018, 11, 111. [Google Scholar] [CrossRef]
- Yao, Z.; Le Bars, J.; Charrier, C.; Rosenberger, C. Fingerprint Quality Assessment Combining Blind Image Quality, Texture and Minutiae Features. In Proceedings of the 1st International Conference on Information Systems Security and Privacy; ESEO: Angers, Loire Valley, France, 2015; pp. 336–343. [Google Scholar]
- Liu, X.; Pedersen, M.; Charrier, C.; Bours, P. Performance evaluation of no-reference image quality metrics for face biometric images. J. Electron. Imaging 2018, 27, 023001. [Google Scholar] [CrossRef]
- Jenadeleh, M.; Pedersen, M.; Saupe, D. Blind Quality Assessment of Iris Images Acquired in Visible Light for Biometric Recognition. Sensors 2020, 20, 1308. [Google Scholar] [CrossRef] [PubMed]
- Bianco, S.; Celona, L.; Napoletano, P.; Schettini, R. On the Use of Deep Learning for Blind Image Quality Assessment. Signal Image Video Process. 2018, 12, 355–362. [Google Scholar] [CrossRef]
- Kang, L.; Ye, P.; Li, Y.; Doermann, D. Convolutional Neural Networks for No-Reference Image Quality Assessment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1733–1740. [Google Scholar]
- Li, Y.; Po, L.M.; Xu, X.; Feng, L.; Yuan, F.; Cheung, C.H.; Cheung, K.W. No-reference image quality assessment with shearlet transform and deep neural networks. Neurocomputing 2015, 154, 94–109. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S. Fully deep blind image quality predictor. IEEE J. Sel. Top. Signal Process. 2017, 11, 206–220. [Google Scholar] [CrossRef]
- Lv, Y.; Jiang, G.; Yu, M.; Xu, H.; Shao, F.; Liu, S. Difference of Gaussian statistical features based blind image quality assessment: A deep learning approach. In Proceedings of the IEEE International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015; pp. 2344–2348. [Google Scholar]
- Gao, F.; Wang, Y.; Li, P.; Tan, M.; Yu, J.; Zhu, Y. DeepSim: Deep similarity for image quality assessment. Neurocomputing 2017, 257, 104–114. [Google Scholar] [CrossRef]
- Hou, W.; Gao, X.; Tao, D.; Li, X. Blind image quality assessment via deep learning. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1275–1286. [Google Scholar]
- Amirshahi, S.A.; Pedersen, M.; Yu, S.X. Image quality assessment by comparing CNN features between images. J. Imaging Sci. Technol. 2016, 60, 60410-1. [Google Scholar] [CrossRef]
- Liu, X.; Pedersen, M.; Hardeberg, J. CID:IQ-A New Image Quality Database. In Image and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 193–202. [Google Scholar]
- Gu, K.; Liu, M.; Zhai, G.; Yang, X.; Zhang, W. Quality assessment considering viewing distance and image resolution. IEEE Trans. Broadcasting 2015, 61, 520–531. [Google Scholar] [CrossRef]
- Chetouani, A.; Beghdadi, A.; Deriche, M.A. A hybrid system for distortion classification and image quality evaluation. Sig. Proc. Image Comm. 2012, 27, 948–960. [Google Scholar] [CrossRef]
- Sheikh, H. LIVE Image Quality Assessment Database Release 2. 2005. Available online: http://live.ece.utexas.edu/research/quality (accessed on 12 April 2021).
- Chetouani, A. Convolutional Neural Network and Saliency Selection for Blind Image Quality Assessment. In Proceedings of the IEEE International Conference on Image Processing, Athens, Greece, 7–10 October 2018; pp. 2835–2839. [Google Scholar]
- Larson, E.C.; Chandler, D.M. Most apparent distortion: Full-reference image quality assessment and the role of strategy. J. Electron. Imaging 2010, 19, 011006. [Google Scholar]
- Chetouani, A. Blind Utility and Quality Assessment Using a Convolutional Neural Network and a Patch Selection. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 459–463. [Google Scholar]
- Rouse, D.M.; Hemami, S.S.; Pépion, R.; Le Callet, P. Estimating the usefulness of distorted natural images using an image contour degradation measure. JOSA A 2011, 28, 157–188. [Google Scholar] [CrossRef]
- Ninassi, A.; Le Callet, P.; Autrusseau, F. Subjective Quality Assessment-IVC Database. 2006. Available online: http://www.irccyn.ec-nantes.fr/ivcdb (accessed on 24 March 2018).
- Horita, Y.; Shibata, K.; Kawayoke, Y.; Sazzad, Z.P. MICT Image Quality Evaluation Database. 2011. Available online: http://mict.eng.u-toyama.ac.jp/mictdb.html (accessed on 27 July 2015).
- Jayaraman, D.; Mittal, A.; Moorthy, A.K.; Bovik, A.C. Objective quality assessment of multiply distorted images. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 4–7 November 2012; pp. 1693–1697. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 675–678. [Google Scholar]
- Ghadiyaram, D.; Bovik, A.C. Massive online crowdsourced study of subjective and objective picture quality. IEEE Trans. Image Process. 2015, 25, 372–387. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, N.; Jin, L.; Ieremeiev, O.; Lukin, V.; Egiazarian, K.; Astola, J.; Vozel, B.; Chehdi, K.; Carli, M.; Battisti, F.; et al. Image database TID2013: Peculiarities, results and perspectives. Signal Process. Image Commun. 2015, 30, 57–77. [Google Scholar] [CrossRef]
- Li, J.; Zou, L.; Yan, J.; Deng, D.; Qu, T.; Xie, G. No-reference image quality assessment using Prewitt magnitude based on convolutional neural networks. Signal Image Video Process. 2016, 10, 609–616. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Fan, C.; Zhang, Y.; Feng, L.; Jiang, Q. No reference image quality assessment based on multi-expert convolutional neural networks. IEEE Access 2018, 6, 8934–8943. [Google Scholar] [CrossRef]
- Ravela, R.; Shirvaikar, M.; Grecos, C. No-reference image quality assessment based on deep convolutional neural networks. In Real-Time Image Processing and Deep Learning 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10996, p. 1099604. [Google Scholar]
- Varga, D. Multi-Pooled Inception Features for No-Reference Image Quality Assessment. Appl. Sci. 2020, 10, 2186. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.; Li, L.; Dong, W.; Xie, X.; Shi, G.; Lin, W. Blind Image Quality Assessment With Active Inference. IEEE Trans. Image Process. 2021, 30, 3650–3663. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Beghdadi, A.; Qureshi, M.A.; Sdiri, B.; Deriche, M.; Alaya-Cheikh, F. Ceed-A Database for Image Contrast Enhancement Evaluation. In Proceedings of the 2018 Colour and Visual Computing Symposium (CVCS), Gjovik, Norway, 19–20 September 2018; pp. 1–6. [Google Scholar]
- Amirshahi, S.; Pedersen, M.; Beghdadi, A. Reviving Traditional Image Quality Metrics Using CNNs. In Color and Imaging Conference; Society for Imaging Science and Technology: Paris, France, 2018; pp. 241–246. [Google Scholar]
- Le Meur, O.; Liu, Z. Saccadic model of eye movements for free-viewing condition. Vis. Res. 2015, 116, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Bosse, S.; Maniry, D.; Müller, K.; Wiegand, T.; Samek, W. Deep Neural Networks for No-Reference and Full-Reference Image Quality Assessment. IEEE Trans. Image Process. 2018, 27, 206–219. [Google Scholar] [CrossRef]
- Vigier, T.; Da Silva, M.P.; Le Callet, P. Impact of visual angle on attention deployment and robustness of visual saliency models in videos: From SD to UHD. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 689–693. [Google Scholar]
- Harel, J.; Koch, C.; Perona, P. Graph-based visual saliency. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2007; pp. 545–552. [Google Scholar]
- Borji, A.; Tavakoli, H.R.; Sihite, D.N.; Itti, L. Analysis of scores, datasets, and models in visual saliency prediction. In Proceedings of the IEEE International Conference on Computer Vision, 2013, Sydney, NSW, Australia, 1–8 December 2013; pp. 921–928. [Google Scholar]
- Chetouani, A. A Blind Image Quality Metric using a Selection of Relevant Patches based on Convolutional Neural Network. In Proceedings of the European Signal Processing Conference, Rome, Italy, 3–7 September 2018; pp. 1452–1456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Chetouani, A.; Treuillet, S.; Exbrayat, M.; Jesset, S. Classification of engraved pottery sherds mixing deep-learning features by compact bilinear pooling. Pattern Recognit. Lett. 2020, 131, 1–7. [Google Scholar] [CrossRef]
- Elloumi, W.; Chetouani, A.; Charrada, T.; Fourati, E. Anti-Spoofing in Face Recognition: Deep Learning and Image Quality Assessment-Based Approaches. In Deep Biometrics. Unsupervised and Semi-Supervised Learning; Jiang, R., Li, C.T., Crookes, D., Meng, W., Rosenberger, C., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Abouelaziz, I.; Chetouani, A.; El Hassouni, M.; Latecki, L.; Cherifi, H. No-reference mesh visual quality assessment via ensemble of convolutional neural networks and compact multi-linear pooling. Pattern Recognit. 2020, 100, 107174. [Google Scholar] [CrossRef]
- Chetouani, A.; Li, L. On the use of a scanpath predictor and convolutional neural network for blind image quality assessment. Signal Process. Image Commun. 2020, 89, 115963. [Google Scholar] [CrossRef]
- Chetouani, A. Image Quality Assessment Without Reference By Mixing Deep Learning-Based Features. In Proceedings of the IEEE International Conference on Multimedia and Expo, ICME 2020, London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Furmanski, C.S.; Engel, S.A. An oblique effect in human primary visual cortex. Nat. Neurosci. 2000, 3, 535–536. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Lee, S. Transition of Visual Attention Assessment in Stereoscopic Images with Evaluation of Subjective Visual Quality and Discomfort. IEEE Trans. Multimed. 2015, 17, 2198–2209. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Ieremeiev, O.; Lukin, V.; Egiazarian, K.; Carli, M. Modified image visual quality metrics for contrast change and mean shift accounting. In Proceedings of the 2011 11th International Conference The Experience of Designing and Application of CAD Systems in Microelectronics (CADSM), Polyana, Ukraine, 23–25 February 2011; pp. 305–311. [Google Scholar]
- Ponomarenko, M.; Egiazarian, K.; Lukin, V.; Abramova, V. Structural similarity index with predictability of image blocks. In Proceedings of the 2018 IEEE 17th International Conference on Mathematical Methods in Electromagnetic Theory (MMET), Kyiv, UKraine, 2–5 July 2018; pp. 115–118. [Google Scholar]
- Reenu, M.; David, D.; Raj, S.A.; Nair, M.S. Wavelet based sharp features (WASH): An image quality assessment metric based on HVS. In Proceedings of the 2013 2nd International Conference on Advanced Computing, Networking and Security, Wavelet Based Sharp Features (WASH): An Image Quality Assessment Metric Based on HVS, Mangalore, India, 15–17 December 2013; pp. 79–83. [Google Scholar]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, H.R.; Bovik, A.C.; de Veciana, G. An information fidelity criterion for image quality assessment using natural scene statistics. IEEE Trans. Image Process. 2005, 14, 2117–2128. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Mitsa, T.; Varkur, K.L. Evaluation of contrast sensitivity functions for the formulation of quality measures incorporated in halftoning algorithms. In Proceedings of the 1993 IEEE International Conference on Acoustics, Speech, and Signal Processing, Minneapolis, MN, USA, 27–30 April 1993; Volume 5, pp. 301–304. [Google Scholar] [CrossRef]
- Damera-Venkata, N.; Kite, T.D.; Geisler, W.S.; Evans, B.L.; Bovik, A.C. Image quality assessment based on a degradation model. IEEE Trans. Image Process. 2000, 9, 636–650. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the The Thrity-Seventh Asilomar Conference on Signals, Systems Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient Magnitude Similarity Deviation: A Highly Efficient Perceptual Image Quality Index. IEEE Trans. Image Process. 2014, 23, 684–695. [Google Scholar] [CrossRef]
- Anish Mittal, A.K.M.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef] [PubMed]
- Moorthy, A.K.; Bovik, A.C. Blind image quality assessment: From natural scene statistics to perceptual quality. IEEE Trans. Image Process. 2011, 20, 3350–3364. [Google Scholar] [CrossRef]
- Gabarda, S.; Cristóbal, G. Blind image quality assessment through anisotropy. JOSA A 2007, 24, B42–B51. [Google Scholar] [CrossRef] [PubMed]
- Gu, K.; Zhai, G.; Lin, W.; Yang, X.; Zhang, W. No-reference image sharpness assessment in autoregressive parameter space. IEEE Trans. Image Process. 2015, 24, 3218–3231. [Google Scholar] [PubMed]
- Gu, K.; Zhai, G.; Lin, W.; Yang, X.; Zhang, W. Learning a blind quality evaluation engine of screen content images. Neurocomputing 2016, 196, 140–149. [Google Scholar] [CrossRef]
- Narvekar, N.D.; Karam, L.J. A no-reference perceptual image sharpness metric based on a cumulative probability of blur detection. In Proceedings of the 2009 International Workshop on Quality of Multimedia Experience, San Diego, CA, USA, 29–31 July 2009; pp. 87–91. [Google Scholar]
- Daly, S.J. Visible differences predictor: An algorithm for the assessment of image fidelity. In Proceedings of the SPIE 1666, Human Vision, Visual Processing, and Digital Display III; International Society for Optics and Photonics’: San Jose, CA, USA, 1992. [Google Scholar]
- Wang, Z.; Bovik, A.C. Embedded foveation image coding. IEEE Trans. Image Process. 2001, 10, 1397–1410. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).