Enhancement of Heterogeneous Microfluidic Immunosensors Using New Sensing Area Shape with Electrothermal Effect
Abstract
1. Introduction
2. Biosensor Geometry and Theory
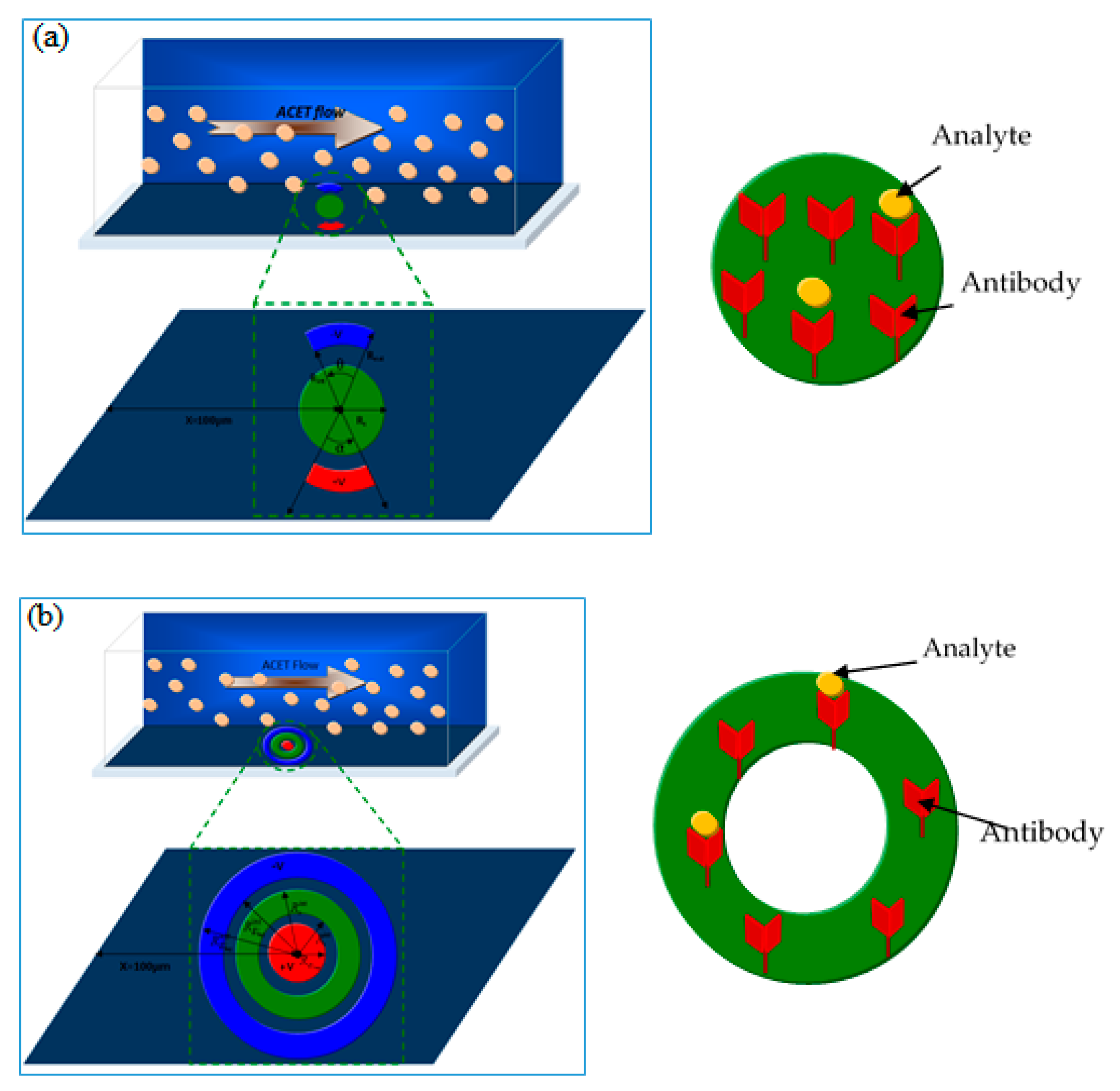
2.1. Biosensor Design
2.2. Governing Equations
3. Results and Discussion
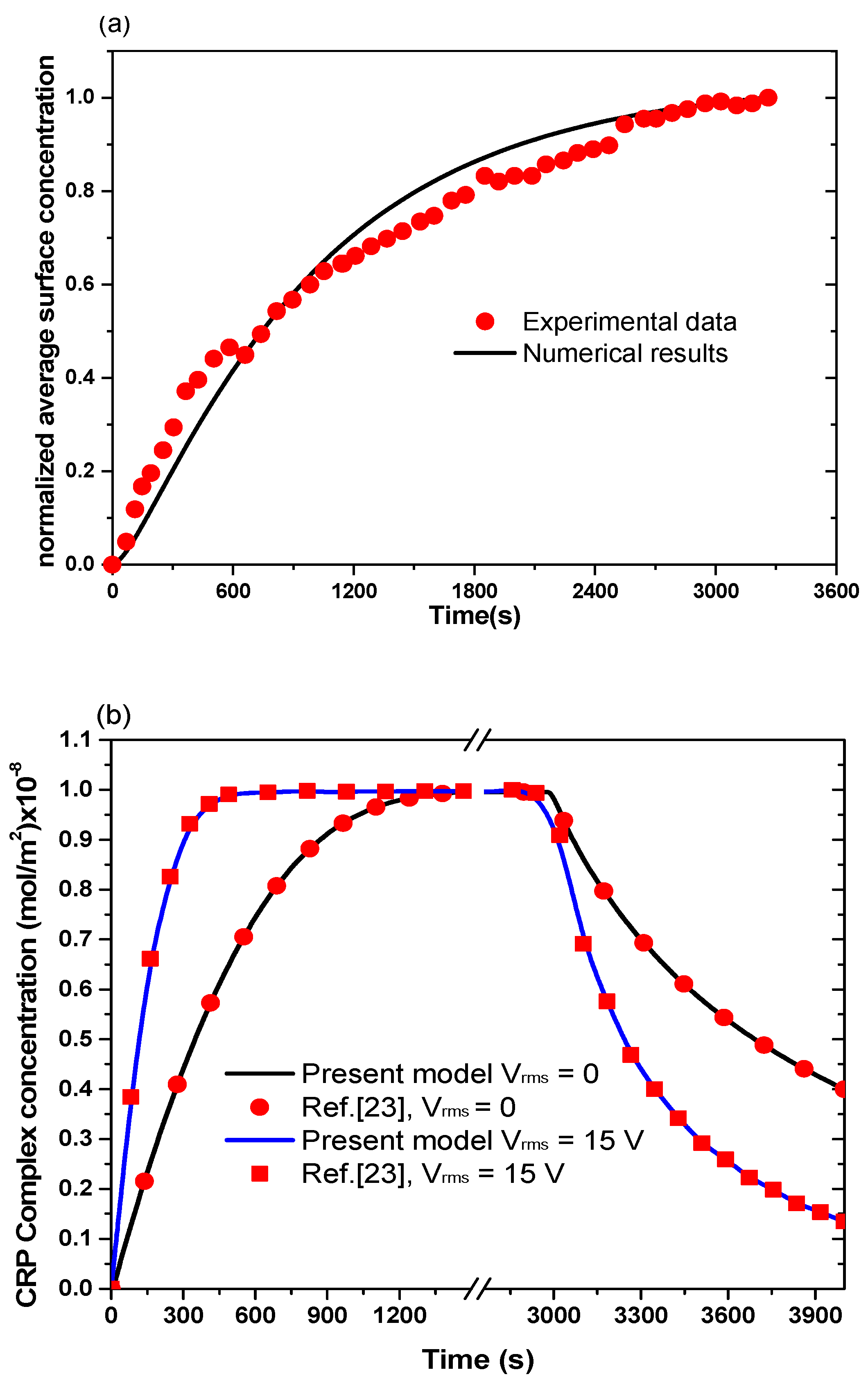
3.1. Model Validation
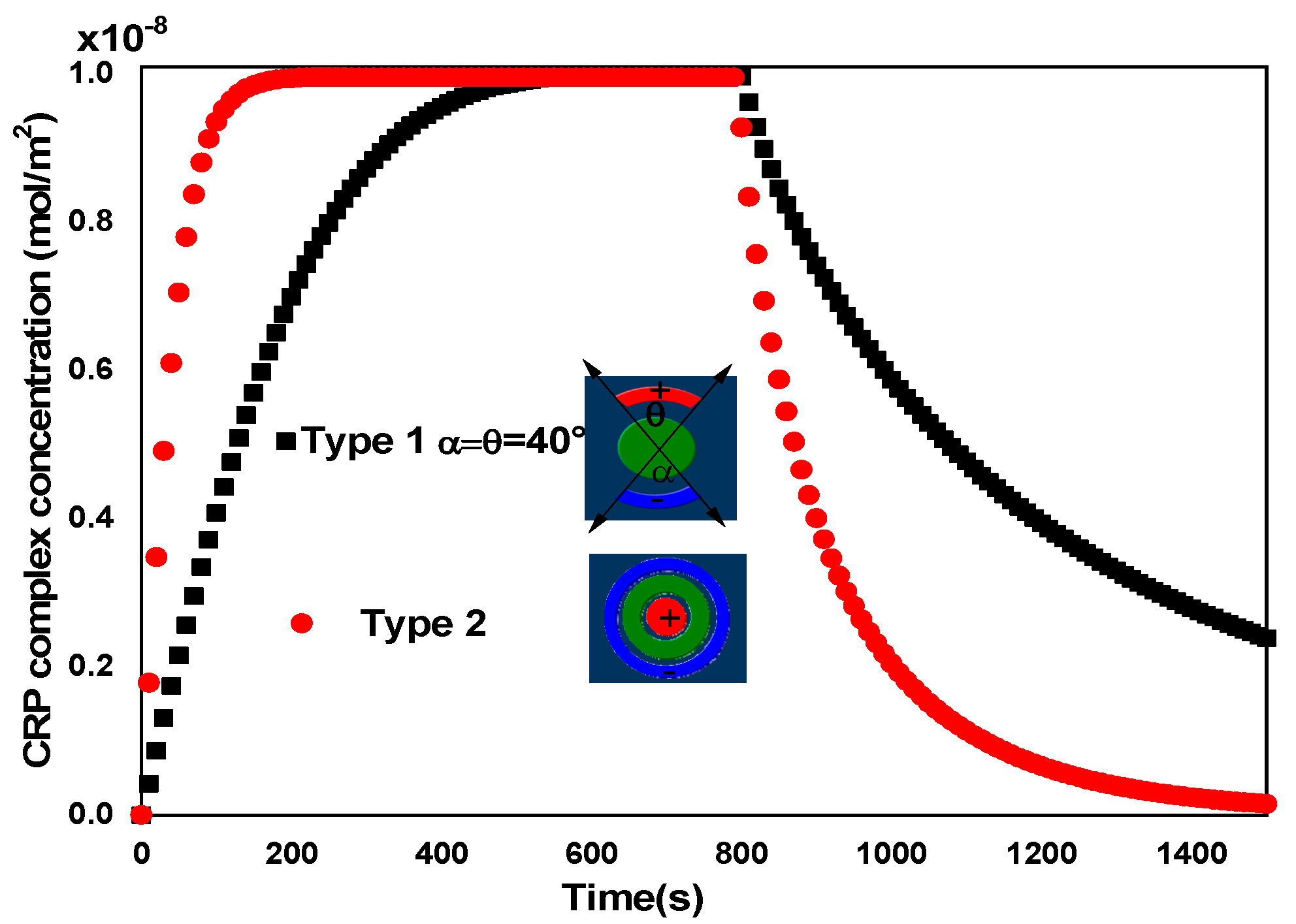
3.2. Effect of Surface Reaction Shape
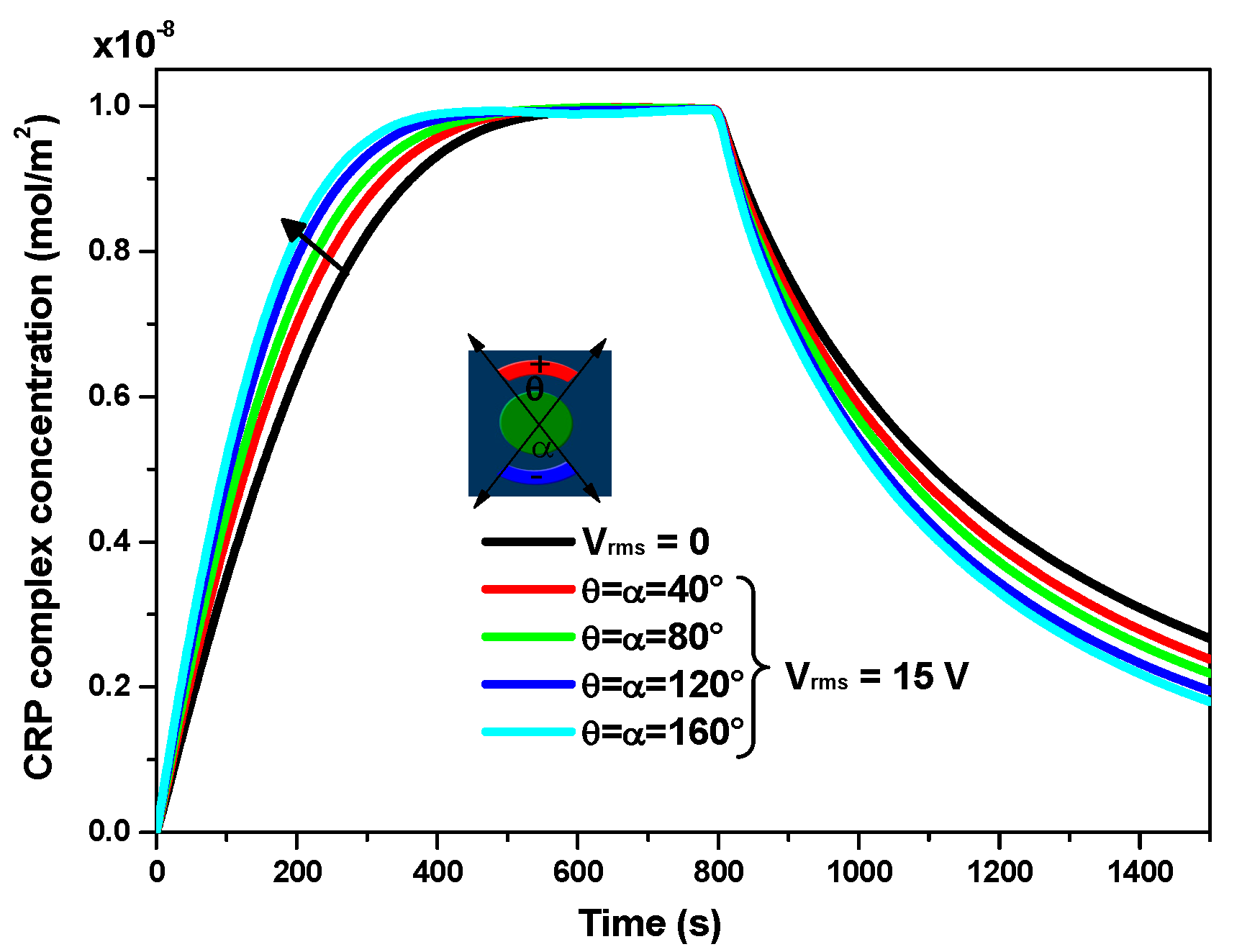
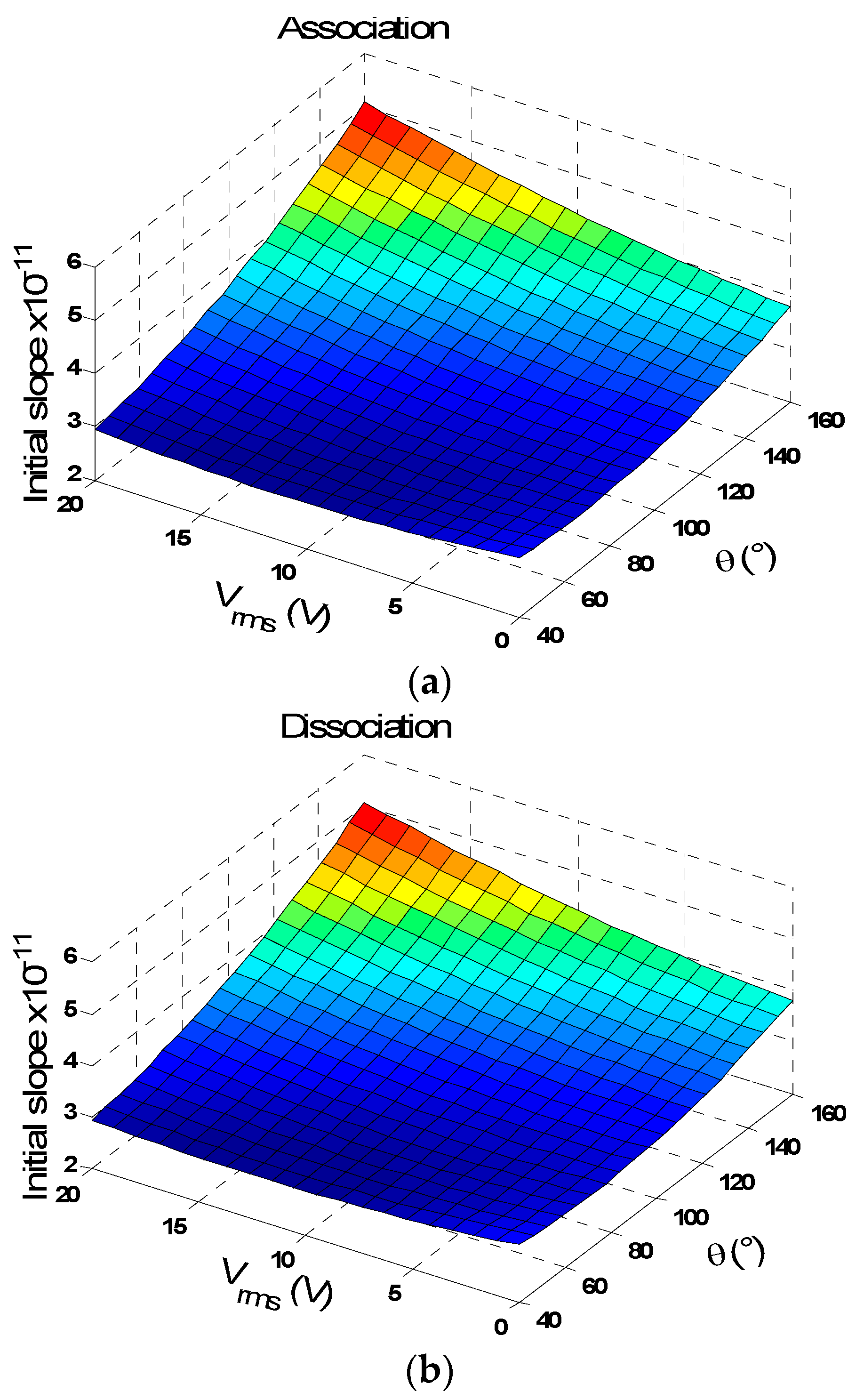
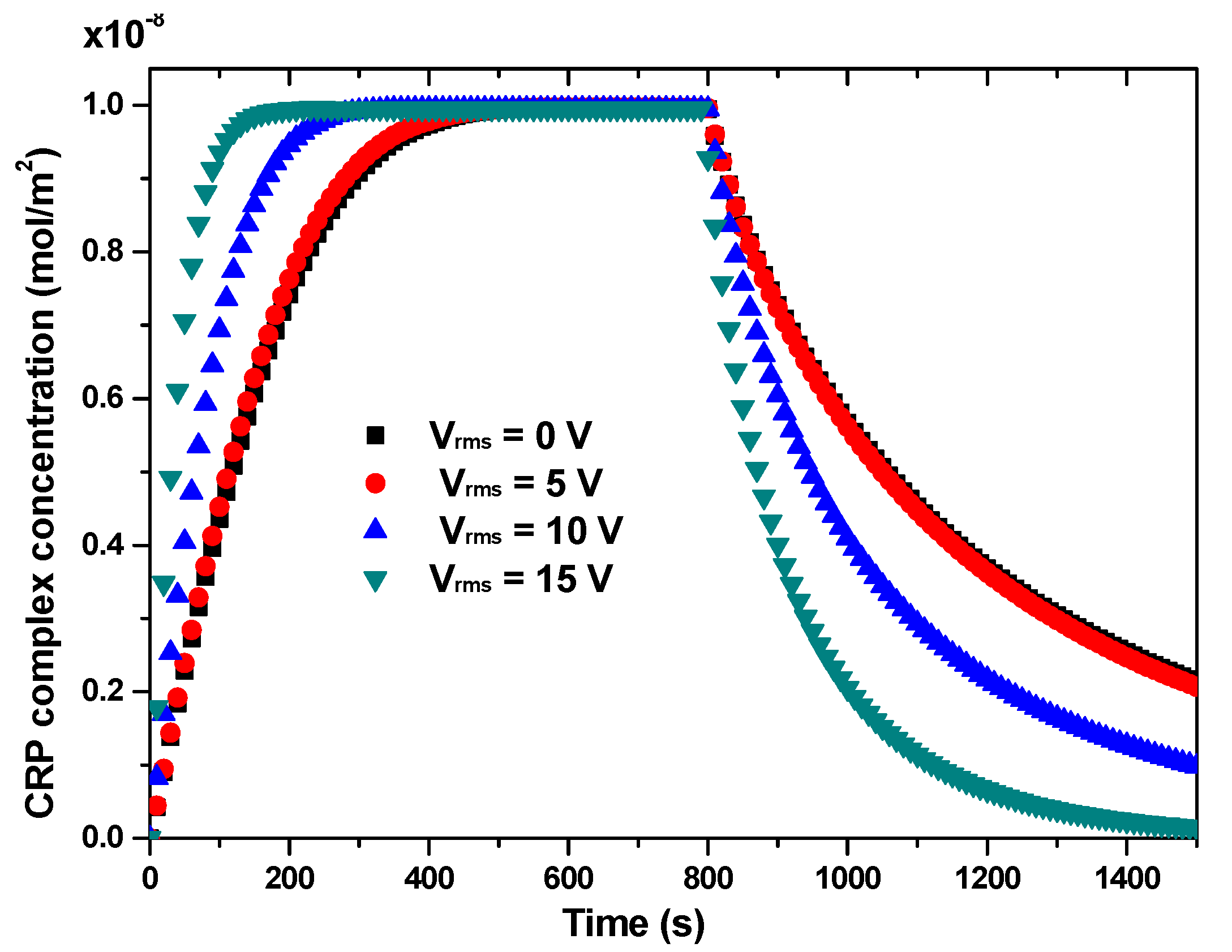
3.3. Effect of the Applied Voltage
3.4. Effect of Inlet Velocity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, S.-B.; Chen, M.-M.; Wang, Y.-K.; Sun, Z.-H.; Xie, M.; Huang, W. Current techniques and future advance of microfluidic devices for circulating tumor cells. TrAC Trends Anal. Chem. 2019, 117, 116–127. [Google Scholar] [CrossRef]
- Dabighi, A.; Toghraie, D. A new microfluidic device for separating circulating tumor cells based on their physical properties by using electrophoresis and dielectrophoresis forces within an electrical field. Comput. Methods Progr. Biomed. 2020, 185, 105147. [Google Scholar] [CrossRef]
- Luo, G.; Du, L.; Wang, Y.; Wang, K. Recent developments in microfluidic device-based preparation, functionalization, and manipulation of nano- and micro-materials. Particuology 2019, 45, 1–19. [Google Scholar] [CrossRef]
- Walczak, R.; Kawa, B.; Adamski, K. Inkjet 3D printed microfluidic device for growing seed root and stalk mechanical characterization. Sens. Actuators A Phys. 2019, 297, 111557. [Google Scholar] [CrossRef]
- Sheng, W.; Ogunwobi, O.O.; Chen, T.; Zhang, J.; George, T.J.; Liu, C.; Fan, Z.H. Capture, release and culture of circulating tumor cells from pancreatic cancer patients using an enhanced mixing chip. Lab Chip 2014, 14, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Ding, R.; Lisak, G. Sponge-based microfluidic sampling for potentiometric ion sensing. Anal. Chim. Acta 2019, 1091, 103–111. [Google Scholar] [CrossRef]
- Santangelo, M.F.; Shtepliuk, I.; Filippini, D.; Ivanov, I.; Yakimova, R.; Eriksson, J. Real-time sensing of lead with epitaxial graphene-integrated microfluidic devices. Sens. Actuators B Chem. 2019, 288, 425–431. [Google Scholar] [CrossRef]
- Zheng, Z.; Wu, L.; Li, L.; Zong, S.; Wang, Z.; Cui, Y. Simultaneous and highly sensitive detection of multiple breast cancer biomarkers in real samples using a SERS microfluidic chip. Talanta 2018, 188, 507–515. [Google Scholar] [CrossRef] [PubMed]
- Ng, A.H.C.; Uddayasankar, U.; Wheeler, A.R. Immunoassays in microfluidic systems. Anal. Bioanal. Chem. 2010, 397, 991–1007. [Google Scholar] [CrossRef]
- Lebedev, K.; Mafe, S.; Stroeve, P. Convection, diffusion and reaction in a surface-based biosensor: Modeling of cooperativity and binding site competition on the surface and in the hydrogel. J. Colloid Interface Sci. 2006, 296, 527–537. [Google Scholar] [CrossRef]
- Hibbert, D.B.; Gooding, J.J.; Erokhin, P. Kinetics of Irreversible Adsorption with Diffusion: Application to Biomolecule Immobilization. Langmuir 2002, 18, 1770–1776. [Google Scholar] [CrossRef]
- Huang, K.-R.; Chang, J.-S.; Der Chao, S.; Wu, K.-C.; Yang, C.-K.; Lai, C.-Y.; Chen, S.-H. Simulation on binding efficiency of immunoassay for a biosensor with applying electrothermal effect. J. Appl. Phys. 2008, 104, 064702. [Google Scholar] [CrossRef]
- Hofmann, O.T.; Voirin, G.; Niedermann, P.; Manz, A. Three-Dimensional Microfluidic Confinement for Efficient Sample Delivery to Biosensor Surfaces. Application to Immunoassays on Planar Optical Waveguides. Anal. Chem. 2002, 74, 5243–5250. [Google Scholar] [CrossRef]
- Feldman, H.C.; Sigurdson, M.; Meinhart, C.D. AC electrothermal enhancement of heterogeneous assays in microfluidics. Lab Chip 2007, 7, 1553–1559. [Google Scholar] [CrossRef] [PubMed]
- Hart, R.; Lec, R.; Noh, H.M. Enhancement of heterogeneous immunoassays using AC electroosmosis. Sens. Actuators B Chem. 2010, 147, 366–375. [Google Scholar] [CrossRef]
- Liu, X.; Yang, K.; Wadhwa, A.; Eda, S.; Li, S.; Wu, J. Development of an AC electrokinetics-based immunoassay system for on-site serodiagnosis of infectious diseases. Sens. Actuators A Phys. 2011, 171, 406–413. [Google Scholar] [CrossRef]
- Mahmoodi, S.R.; Bayati, M.; Hosseinirad, S.; Foroumadi, A.; Gilani, K.; Rezayat, S.M. AC electrokinetic manipulation of selenium nanoparticles for potential nanosensor applications. Mater. Res. Bull. 2013, 48, 1262–1267. [Google Scholar] [CrossRef]
- Selmi, M.; Echouchene, F.; Belmabrouk, H.; Marwa, S.; Fraj, E.; Hafedh, B. Analysis of Microfluidic Biosensor Efficiency Using a Cylindrical Obstacle. Sens. Lett. 2016, 14, 26–31. [Google Scholar] [CrossRef]
- Selmi, M.; Echouchene, F.; Gazzah, M.H.; Belmabrouk, H. Flow Confinement Enhancement of Heterogeneous Immunoassays in Microfluidics. IEEE Sens. J. 2015, 15, 7321–7328. [Google Scholar] [CrossRef]
- Selmi, M.; Khemiri, R.; Echouchene, F.; Belmabrouk, H. Enhancement of the Analyte Mass Transport in a Microfluidic Biosensor by Deformation of Fluid Flow and Electrothermal Force. J. Manuf. Sci. Eng. 2016, 138, 081011. [Google Scholar] [CrossRef]
- Selmi, M.; Khemiri, R.; Echouchene, F.; Belmabrouk, H. Electrothermal effect on the immunoassay in a microchannel of a biosensor with asymmetrical interdigitated electrodes. Appl. Therm. Eng. 2016, 105, 77–84. [Google Scholar] [CrossRef]
- Echouchene, F.; Alshahrani, T.; Belmabrouk, H. Simulation of the Slip Velocity Effect in an AC Electrothermal Micropump. Micromachines 2020, 11, 825. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.-R.; Chang, J.-S. Three dimensional simulation on binding efficiency of immunoassay for a biosensor with applying electrothermal effect. Heat Mass Transf. 2013, 49, 1647–1658. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; González, A.; Castellanos, A.; Morgan, H. Electrothermally induced fluid flow on microelectrodes. J. Electrost. 2001, 53, 71–87. [Google Scholar] [CrossRef]
- Chou, C.; Hsu, H.-Y.; Wu, H.-T.; Tseng, K.-Y.; Chiou, A.; Yu, C.-J.; Lee, Z.-Y.; Chan, T.-S. Fiber optic biosensor for the detection of C-reactive protein and the study of protein binding kinetics. J. Biomed. Opt. 2007, 12, 024025. [Google Scholar] [CrossRef] [PubMed]




| Parameter | Value |
|---|---|
| External radius of electrode Rext (µm) | 25 |
| Internal radius of electrode Rint (µm) | 20 |
| Radius of reaction surface Rs (µm) | 15.96 |
| Bottom electrode angle α (°) | 40→160 |
| Top electrode angle θ (°) | 40→160 |
| Distance from the inlet X (µm) | 100 |
| Parameter | Value |
|---|---|
| Positive electrode radius (µm) | 10 |
| Internal radius of reaction surface (µm) | 15 |
| External radius of reaction surface (µm) | 22 |
| Internal radius of the negative electrode (µm) | 25 |
| External radius of the negative electrode (µm) | 30 |
| Electric Field | Temperature | Velocity | Analyte | |
|---|---|---|---|---|
| Inlet | Insulation | Parabolic profile | ||
| Outlet | Insulation | No viscous stress | ||
| Walls (except reaction surface and electrodes) | Insulation | Insulation | No-slip | Impermeable |
| Reaction surface | Insulation | Insulation | No-slip | |
| Electrodes | No-slip | Impermeable |
| Parameter | Value | Unit |
|---|---|---|
| Adsorption rate constant | m3/(mol·s) | |
| Desorption rate constant | s−1 | |
| Ligand concentration | mol/m2 | |
| Diffusion coefficient | m2/s | |
| Inlet concentration | 6.4 | μmol/m3 |
| Thermal conductivity | 0.6 | W/(K·m) |
| Fluid density | 1000 | kg/m3 |
| Dynamic viscosity | Pa·s | |
| Specific heat | 4.184 | kJ/(kg·K) |
| Electrical conductivity | S/m | |
| Relative permittivity | 80.2 | |
| Frequency | 100 | kHz |
| Initial Slope (Association) × 10−11 | Initial Slope (Dissociation) × 10−11 | Enhancement Factor (Association) | Enhancement Factor (Dissociation) | |
|---|---|---|---|---|
| 4.37 | 3.37 | 1.22 | 1.14 | |
| 4.85 | 3.66 | 1.36 | 1.24 | |
| 4.43 | 3.98 | 1.52 | 1.35 | |
| 5.90 | 4.25 | 1.65 | 1.44 |
| Applied Voltage (V) | 0 | 5 | 10 | 15 |
|---|---|---|---|---|
| Temperature rise (K) | 0 | 0.3 | 1.3 | 3.0 |
| Enhancement factor for association | - | 1.05 | 1.88 | 3.84 |
| Enhancement factor for dissociation | - | 1.01 | 1.58 | 2.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Echouchene, F.; Al-shahrani, T.; Belmabrouk, H. Enhancement of Heterogeneous Microfluidic Immunosensors Using New Sensing Area Shape with Electrothermal Effect. Appl. Sci. 2021, 11, 4566. https://doi.org/10.3390/app11104566
Echouchene F, Al-shahrani T, Belmabrouk H. Enhancement of Heterogeneous Microfluidic Immunosensors Using New Sensing Area Shape with Electrothermal Effect. Applied Sciences. 2021; 11(10):4566. https://doi.org/10.3390/app11104566
Chicago/Turabian StyleEchouchene, Fraj, Thamraa Al-shahrani, and Hafedh Belmabrouk. 2021. "Enhancement of Heterogeneous Microfluidic Immunosensors Using New Sensing Area Shape with Electrothermal Effect" Applied Sciences 11, no. 10: 4566. https://doi.org/10.3390/app11104566
APA StyleEchouchene, F., Al-shahrani, T., & Belmabrouk, H. (2021). Enhancement of Heterogeneous Microfluidic Immunosensors Using New Sensing Area Shape with Electrothermal Effect. Applied Sciences, 11(10), 4566. https://doi.org/10.3390/app11104566






