1. Introduction
In distribution networks, the large penetration of distributed energy resources (DERs), such as distributed generators (DGs), storage systems, electrical vehicles, and controllable loads, has a significant impact on voltage control. Then, the proper selection of the voltage control strategy and architecture, the adequate settings of local controllers and, in the near future, the coordination of the transmission system operators (TSOs) and distribution system operators (DSOs) are the many challenges that need to be faced for voltage control in smart grids [
1].
Presently, the voltage control strategies can be divided into four categories on the basis of communication: local, centralized, distributed, and decentralized [
2].
Optimizing the voltages of the distribution networks in a centralized way would seem the most natural approach to solve the problem of the voltage regulation as it projects the method used in the transmission system into the distribution ones. Centralized controls consist of collecting measurements from the field, solving a constrained optimization problem using a distribution management system (DMS) and sending the optimal set-points to the local voltage control devices. Conventional devices employed for voltage control in distribution networks are: on-load tap changer (OLTC) of the transformer in HV/MV substation, step voltage regulators (SVRs), and capacitor banks (CBs); innovative devices are inverter-interfaced DERs, which can respond much faster than the previous ones by varying their active and/or reactive generation and consumption. Although the centralized approach provides the optimal global solution to the problem, it is expected to encounter technical obstacles resultant from the distributed nature of the electrical system. In fact, the high number of nodes, the increasing integration of DERs, and their participation in the voltage regulation reflect on a large number of measurements to be acquired from the field, sent to, and processed by the DMS as well as on many signals to be dispatched to the control devices. It results in a high cost of investments for advanced measuring technologies, high-speed two-way communication infrastructures, and a powerful computing facility with high computation efficiency [
3]. Furthermore, a centralized control architecture is unable to quickly respond to adverse events becoming vulnerable in the face of cyber and physical attacks to the DMS [
4].
To mitigate the drawbacks of centralized strategies, a great potential is offered by decentralized controls. The basic idea is, firstly, to decompose the large distribution network into smaller voltage control zones (VCZs), in which the nodes are strongly coupled from an electrical point of view; and, then, to achieve the regulation of the voltage profiles of the entire distribution network through intra VCZ control and inter VCZ coordination. In particular, inside a VCZ, a centralized control optimizes the voltages of its cluster of nodes acting on only its local voltage control devices; among VCZs, a distributed control, consisting of a data exchanges among specified nodes of VCZs, is used to drive the VCZ solutions to the global optimization of the whole distribution system. By reducing the size of the problem to be solved in each VCZ, computing facilities will process a limited amount of data; furthermore, information exchange and communication infrastructure will cover limited network areas with the great advantage of lower investment costs and higher resilience to faults and cyber attacks. Despite of these undoubtable advantages, decentralised approaches provide a sub-optimal solution with respect to the centralized one.
To formulate and solve the voltage optimization problem (VOP) in a decentralized manner, first of all, the VOP must be formulated according to a centralized approach. Typically, it is a constraint optimization program that: (
i.) minimizes an objective function (e.g., the deviation of the nodal voltages from their reference values, the network losses, and/or the DG active power curtailments); (
ii.) is subject to equality constraints (i.e., power flow (PF) equations) and to inequality constraints (i.e., limits on bus voltage magnitudes, operation range of conventional, and innovative voltage control devices); and (
iii.) determines the optimal set-points of the local controllers (i.e., tap positions of OLTC/SVRs, optimal status of CBs, active, and or reactive powers of DER local controllers). The centralized VOP is a mixed-integer nonlinear programming. It is difficult to solve for two reasons: firstly, it is not convex due to the quadratic relationship between bus voltages and powers; then, it is of large dimension in dependence on the size of the network and the number of variables to be controlled [
5]. To make the VOP convex and reduce its complexity, linearization techniques [
6,
7,
8], semi-definite relaxation (SDR) [
5,
9], and second-order conic (SOC) [
10,
11] programming have been proposed. Once the non-convex centralized VOP is transformed into a convex one, to some extent, it is easier solving it also according to a decentralized approach. To this aim, the original centralized VOP is decomposed into a number of simple optimization sub-problems (equal to the number of VCZs obtained by the network partitioning); the consistency between centralized and decentralized optimization is assured by the local information exchanges among VCZs; this coordinating action can be implemented in various ways. In [
12], the voltage of the dynamic subcommunity that presents the worst violations of the nodal voltage boundaries is independently controlled by employing a particle swarm optimization method; then, to address the interaction between different sub-communities, an overall network power flow calculation is conducted: if all the network nodal voltages are in the allowable range, the regulation is stopped; otherwise, the process is repeated for all the subcommunities. Despite of the limited processing time at subcommunity level, such an approach requires a heavy centralized coordination. In [
13], a distributed sequential quadratic programming is used for optimizing DGs in each zone; coordination is based on a master–slave approach and requires an iterative boundary data exchange and power flow recalculation; the drawback is that no convergence conditions are provided. One of the most popular and effective method to perform a distributed optimization control between clusters is based on the alternating direction method of multipliers (ADMM) [
7,
8,
14,
15,
16,
17,
18,
19]. The solution is based upon a cluster-based optimization process, where a limited amount of information is exchanged between neighboring clusters; the main benefits of ADMM are the absence of centralized coordination or load flow recalculation, and robust convergence characteristics.
Recently, in [
20], a new method for the decentralized voltage optimization of balanced active distribution systems with radial topology has been proposed. Firstly, a centralized VOP, minimizing the distance of the voltages from their reference values, is formulated as a strictly-convex constrained quadratic program to determine the optimal set-points of the reactive power controllers of DGs. To this end, a new linearized model formulation of the DistFlow equations is exploited [
21]. Then, the centralized VOP is reformulated by partitioning the network into two VCZs with pilot nodes (PNs); the PN voltage variation best represents the variation of the voltages in the VCZ [
22]. However, the new objective function, accounting only for voltage magnitude at PNs, keeps the centralized VOP convex but not in a strict sense. Therefore, for overcoming the lack of strict convexity, a dual approach is considered; the dual VOP works on the augmented Lagrangian function (ALF), and it is iteratively solved by the method of multipliers (MM) [
14]; this latter is a two-level iterative method which solves at each step the VOP to obtain the values of the optimization variables that are used in the second level to update the Lagrange multipliers. Unfortunately, quadratic terms in the ALF make the VOP still not separable among the VCZs. Eventually, the VOP is solved in a fully decentralized form by using the auxiliary problem principle (APP) [
23,
24]. Generally speaking, the APP involves linearizing the non-separable terms in the ALF and adding convex terms which can be chosen to be separable [
25], so as to decompose the VOP into zone VOPs. In each iteration step, the zone VOPs are solved in parallel, each one by the solver assigned to the related VCZ; then, an information exchange allows for updating the Lagrange multipliers so as to re-formulate the zone VOPs for the next step. The iterative process continues until convergence is reached. In general, the APP technique has convergence conditions [
26] and a better convergence behavior than the ADMM in the case of non-convex problems [
27]. According to the authors’ best knowledge, this is the first time that APP has been applied to the decentralized voltage optimization of distribution networks by varying active and reactive powers of DERs.
This paper extends and improves the method outlined in [
20]. First of all, the proposed decentralized VOP is generalized to the case of a distribution systems partitioned into an appropriate number of VCZs. Moreover, since, in distribution networks, the nodal voltage magnitudes are often fairly sensitive to variations of active rather than reactive power injections; in this paper, the VOP determines not only the reactive power generation of DGs but also the active and reactive powers provided by electric storage systems. Finally, since DER controllers are much faster then conventional voltage control devices, the optimal setting of the slow time-scale actuators are evaluated a priori and assigned as parameters in the formulation of the VOP linearized around a particular initial operating point [
8].
The main features of the proposed decentralized VOP are summarized hereafter.
- –
In the centralized formulation of VOP, the linearized DistFlow equations, based on a Jacobian method proposed in [
21], assures an improvement of the accuracy of the results with respect to other linearization techniques. In fact, the adoption of a peculiar set of variables for the analytical derivatives does not require to neglect or to approximate as constants the nonlinear terms of the DistFlow equations as in [
7,
8,
16,
19]. Consequently, the adoption of such technique limits the approximation of the solution with respect to classical VOP using nonlinear PF equations.
- –
To decompose the centralized VOP into subproblems, the adopted partitioning method takes into account the dependence of the nodal voltages on both active and reactive powers injected in all the nodes of the grid [
22,
28]; in such a way, the network partitioning considers the R/X ratio which characterizes the distribution networks. The method is based on the definition of the electrical distance, which is evaluated by using once again the linear model in [
21] that provides in a closed form the sensitivity of the voltage magnitudes to the power variations; consequently, the partition is extracted from structural characteristics of the network independently from the number and position of the DERs in a specific configuration.
- –
The reformulation of the VOP that accounts only for PNs, allows for acquiring a reduced number of voltage measurements from the field (i.e., one for each VCZ) and does not require a system state-estimation; consequently, it can be easily implemented in practice. As a drawback, not all the network voltages are optimized, and, from the theoretical point of view, it is not guaranteed that a nodal voltage could exceed normal operating bounds. However, if the number of VCZs is large enough to adequately represent the network by the PNs and the number of DERs involved in the optimization is large enough to effectively control the voltages, this latter possibility is extremely reduced.
- –
The decentralized VOP obtained by applying APP allows for:
i. solving in each VCZ a constrained quadratic programming problem of small dimension which presents a global minimum; and
ii. to exchange among the VCZs only scalar values. Thanks to these two features, the distributed iterative algorithm guarantees convergence with a limited number of iterations. Finally, it is worth noticing that, differently from other APP applications [
27,
29], neither fictitious nodes nor overlapping variables among interconnected VCZs are introduced to obtain the fully-distributed VOP solution, due to the adoption of PNs in VCZs.
The paper is organized as follows:
Section 2 illustrates the centralized formulation of the proposed VOP. In
Section 3, the VOP is revisited to get its decentralized formulation, highlighting the main steps of the proposed approach that are network partitioning, MMs, and APP. Finally, in
Section 4, a case study is developed referring to a 123 node distribution test feeder with 15 DERs; detailed analysis of the results are presented in various operating conditions and a different number of VCZs, giving evidence of the effectiveness of the proposed decentralized VOP and comparing its performance with centralized VOP.
4. Case Study
To verify the feasibility and the effectiveness of the proposed VOP, numerical studies are carried out on the IEEE 123-bus system [
31], shown in
Figure 2. A 115/4.16 kV substation supplies a main feeder, branching off into several laterals and sublaterals, with unbalanced loads, voltage regulators, shunt capacitor banks, and switches. To apply the proposed approach, the test distribution system is changed into a three-phase balanced network. In particular, at each node, the unbalanced loads have been replaced by balanced loads with the same rated three-phase power, modeled as constant shunt impedances; for each line, the single-phase equivalent pi-model has been adopted, assuming, for its parameters, the average values of the three-phase model parameters. The total balanced rated load connected to the network is equal to about 3.49 MW and 1.17 MVAr. Furthermore, the action of the voltage regulators has been disabled, that is, constant ratios have been fixed, and the status of the switches has been assumed in the basic configuration.
In addition, 15 DERs are connected to the grid at nodes 3, 9, 17, 2, 160, 105, 63, 112, 18, 25, 40, 51, 38, 77, and 87, as shown in
Figure 2. In particular, seven DERs are DGs connected to the grid by inverters with a rectangular capability chart. DGs inject a fixed active power equal to 200 kW and a reactive power that vary in the range (−100, 100) kVAr, independently from the value of the active powers; in the absence of any optimization, DGs inject active power with a power factor equal to 1 that is with null reactive power. The remaining six DERs are DGs with battery energy storage systems: DGs generate a fixed active power equal to 200 kW; the state-of-charge of the storage allows for varying the active power injected by DER in the range (100, 300) kW. In addition, in this case, the inverter is equipped with a rectangular capability chart that varies the reactive power in the range (−150, 150) kVAr; in the absence of any optimization, the injected active power is equal to 200 kW and no reactive power is injected or absorbed. The admissible range of variation of the active and reactive powers injected/absorbed by DERs are summarized in
Table 1.
Three different operational cases are considered by varying the amplitude of the nodal voltage at the HV busbar (slack bus) and the total load connected to the grid:
Case 1: the voltage amplitude of the HV busbar is fixed at 1.025 p.u.; the loads are equal to 100% of their rated values;
Case 2: the voltage amplitude of the HV busbar is fixed at 1.03 p.u.; the loads are equal to 50% of their rated values;
Case 3: the voltage amplitude of the HV busbar is fixed at 1.02 p.u.; the loads are equal to 120% of their rated values.
The linearized DistFlow Equation (
2) has been obtained by applying the method in [
21] and assuming the same operating conditions as the ones in
Case 1, as far as loads and slack bus are concerned, but disconnecting all the DERs. The obtained matrix
is the only sensitivity matrix that has been used in all the VOP problems and in all the three considered cases.
To test the proposed voltage optimization methods, numerical analysis was performed in environment through the use of the package, by a CPU Intel Core i7-2670QM with 8 GB of RAM.
4.1. Impact of the Linearization on the Centralized VOP
To evaluate the approximations introduced by the linearization of the PF equations, in this subsection, the results obtained by executing the centralized VOP (
1) subject to the linearized PF equations (referred to as
LinearDistFlow VOP) are compared with the results obtained by a VOP subject to the PF equations (referred in the following to as the
Benchmark VOP).
In the reminder, the performance of the optimization methods is evaluated by a voltage performance index (VPI) that is calculated as the sum of the squared deviations of the squared voltages of all the nodes of the MV feeders and subfeeders with respect to the reference values, fixed at 1.0 p.u. in all the analyzed cases; it is worth noting that the VPI does not include neither the HV slack bus nor the MV substation busbar.
Table 2 compares the values of the VPI obtained by the
LinearDistFlow VOP and the
Benchmark VOP in the three considered cases. From the results reported in
Table 2, it is evident that the VPI values are in the same order of magnitude for the two VOP methodologies: it is obvious that, in all the three operating conditions, the
Benchmark VOP performs better than the
LinearDistFlow VOP. Particularly, in
Case 1, the VPI values are only 0.3
p.u. different one with the other, in
Case 2, the distance increases to 0.9
p.u., finally, in
Case 3, the performance of the
LinearDistFlow VOP is about 3
p.u. different from the one of the
Benchmark VOP, but the two values are still comparable.
To further confirm the accuracy of the
LinearDistFlow VOP, some statistical parameters related to the distribution of the voltage amplitudes into the grid have been evaluated for both
Benchmark VOP and
LinearDistFlow VOP.
Table 3 reports the mean value
V, the standard deviation
, the maximum value
, and the minimum value
of the voltage amplitude of all the network nodes, derived by applying
benchmark VOP and
LinearDistFlow VOP for the three considered cases. Similarly to the VPI, hereafter, the statical parameters are evaluated with reference to nodes of the MV feeders and subfeeders, excluding the HV slack bus and the MV substation busbar. From
Table 3, it is apparent that, for all the three operating conditions, the reported values for the two algorithms are very close.
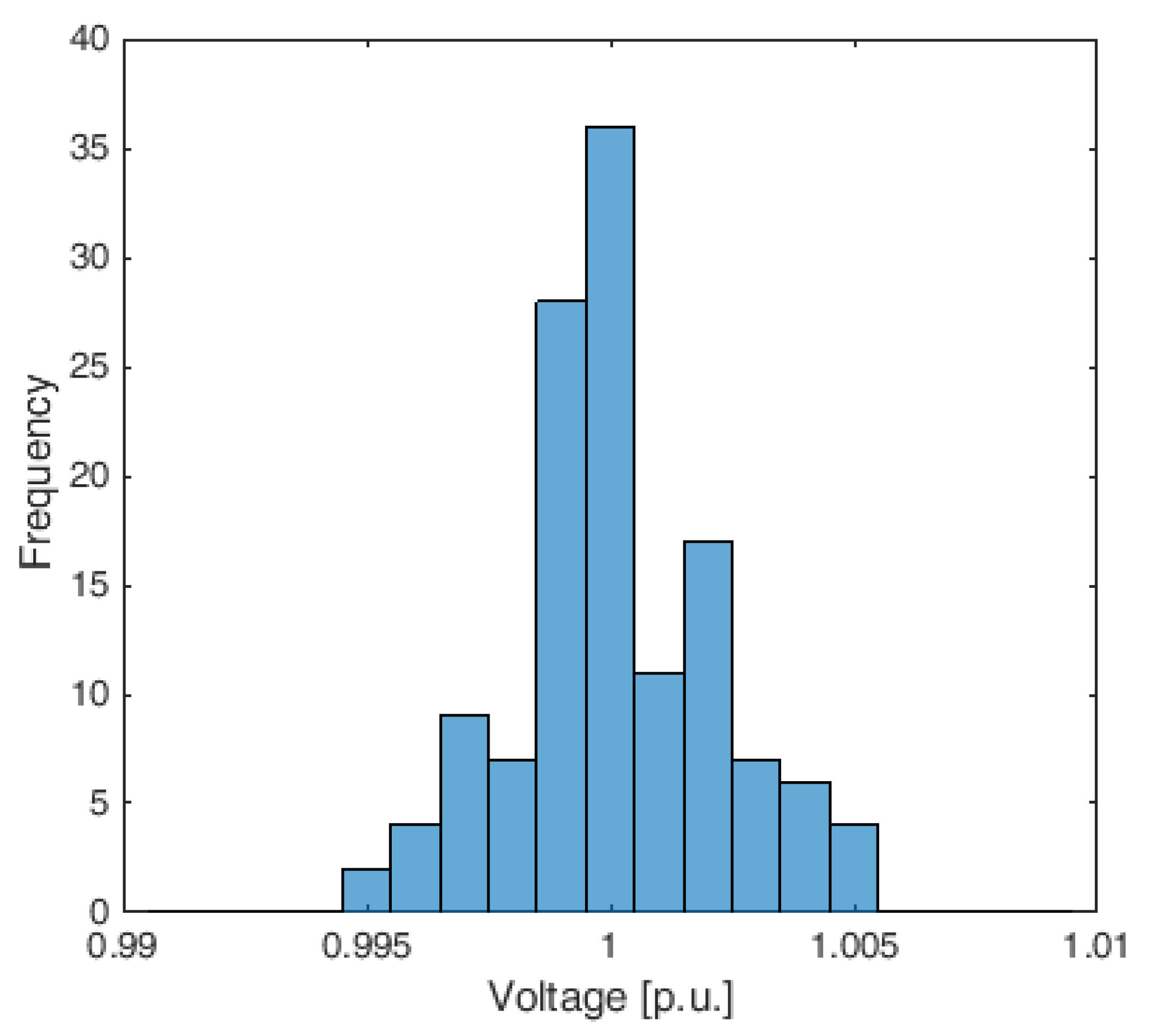
The histograms of the distributions of the network node voltages for the
Benchmark VOP and the
LinearDistFlow VOP are reported in
Figure 3 and
Figure 4, respectively, with reference to the only
Case 3, which is the worst case according to
Table 2. Both histograms show bell-shaped curves; the entire range of values, that goes from 0.99 to 1.01 p.u., is divided into 20 intervals. The peaks of both bell-shape histograms show more or less the same height, between 30 and 40, which represents the number of voltages falling into the most populated interval. For both
Figure 3 and
Figure 4, the largest number of voltages are concentrated in the range between 0.995 and 1 p.u., slightly closer to 1 p.u. for the
Benchmark VOP.
As a final consideration, it is important to underline that, in all the considered cases, the linearization of the PF equations uses the same matrix , which, as previously explained, has been obtained in the same operating conditions as Case 1, but in absence of any DER. It is evident that the larger the difference between the considered case and the operating conditions in which linearization is performed, the larger the approximation introduced by the LinearDistFlow VOP; this is the reason why the results in Case 1 are the best and the ones in Case 3 are the worst. Nevertheless, the reported results give evidence that the differences between the nodal voltages obtained by the LinearDistFlow VOP with respect to those obtained by the Benchmark VOP are small and, consequently, the LinearDistFlow VOP provides a good approximation of the benchmark optimization. Obviously, to reduce such approximations, it is advisable to evaluate various offline matrices for different operating conditions of the distribution system; in these applications, the worst condition for the proposed method has been assumed.
4.2. Impact of the Network Partitioning in the Centralized VOP
The zoning methodology in [
22] is applied to obtain a simplified representation of the distribution network suitable for voltage control. Two partitions of the grid are performed: the first one considers four VCZs and, the second one, seven VCZs, as shown in
Figure 5 and
Figure 6, respectively. They are performed taking into account for the sensitivities of the nodal voltages to the only reactive power, being in an MV network the reactive part of the line impedance bigger than its resistive counterpart.
Table 4 and
Table 5 report the PNs and the DER nodes in the four VCZs and the seven VCZs network partition, respectively.
Hereafter, the impact of the different partitioning on the results provided by the solution of the problem (
3) is analyzed.
Firstly, the comparison is carried out by using the VPI values provided by the optimization with four VCZs and seven VCZs; results are reported in
Table 6. In
Case 1, the partition in four VCZs provides a VPI value larger than the one obtained by partitioning the network in seven VCZs; in
Case 2, opposite results are obtained; in
Case 3, the partition in four VCZs provides a VPI value three times smaller than that obtained by the partition in seven VCZs. From the analysis of
Table 6, the partition in four VCZs gives results that are comparable with and in some cases even better than the partition in seven VCZs in terms of VPI. The above results are also confirmed by the statistical parameters that are reported in
Table 7.
Then, the comparison is carried out by using the VPI values provided by the
LinearDistFlow VOP in a network without partitioning and reported in
Table 2. Comparing
Table 6 with
Table 2, it appears that, in both
Case 1 and
Case 2, the VPI values are almost one order of magnitude larger than the VPI values calculated by solving the
LinearDistFlow VOP; on the contrary, in
Case 3, the VPI value for the partition in four VCZs is similar to the one obtained by solving the
LinearDistFlow VOP. These results give evidence that, since the objective function adopted for a network partitioned in four VCZs (or in seven VCZs) is a reduced representation of the voltages of the network, the effect of the optimization in terms of VPI is strongly dependent of the operating conditions and cannot be predicted a priori.
The above results are also confirmed by comparing the statistical parameters for four VCZs and seven VCZs reported in
Table 7 with the ones for the
LinearDistFlow VOP in
Table 3. The mean values confirm that, in
Case 1 and
Case 2, the obtained results for four VCZs and seven VCZs are worse than the ones provided by the
LinearDistFlow VOP, whereas, in
Case 3, while the partitioning in seven VCZs is still the worst, the partitioning in four VCZ gives a result comparable with the one provided by the
LinearDistFlow VOP. Similar considerations can be done for the maximum and minimum values. Concerning the standard deviations, it is interesting to highlight that they present the same small order of magnitude in all the considered cases for the VOP performed in a network clustered in VCZs and in the network without partitioning. Generally speaking,
LinearDistFlow VOP flattens all the nodal voltages to values that are very close to the reference values; the same behavior is shown by the VOP in four VCZs and seven VCZs, although around a value of the nodal voltage slightly lower than 1.0 p.u.
For the sake of completeness, as in the previous subsection, with reference only to
Case 3, the histograms of the distribution of the network node voltages for the partitioning in four VCZs and in seven VCZs are reported in
Figure 7 and
Figure 8, respectively.
Figure 7 shows a bell-shaped histogram with the peak centered in the same voltage interval as in
Figure 4.
Figure 8 does not show a markedly bell shape histogram but shows an almost uniformly distributed shape histogram with a slight peak in the middle of the voltage range [0.995, 1] p.u.
Drawing some conclusions, it can be stated that the linear optimizations based on the partition in four VCZs and in seven VCZs are quite equivalent in terms of VPI. Since the practical implementation would require a smaller number of measurements of the nodal voltages of the PNs in the partition in four VCZs with respect to the partition in seven VCZs and a reduced data exchange among VCZs, the partition in four VCZs is preferable. Furthermore, the results in terms of standard deviation show that the VOP polarizes the voltage profiles around the reference value, guaranteeing in practice that all the nodal voltages should not exceed the normal operating bounds.
4.3. Decentralized VOP
In this subsection, the performance of the decentralized VOP based on the APP algorithm, referred to in the following as
Decentralized APP, is tested by solving the problem (
14)–(16) for the partitioning in both four and seven VCZs.
Table 8 shows the final values of the objective function obtained by the APP algorithm for the two considered partitioning and in the three considered cases. For the sake of comparison,
Table 8 reports also the results obtained by the centralized solution of the original problem (
3), referred to as
Centralized VCZ-based VOP. From the results, it is apparent that the values of the objective function obtained by decentralized and centralized algorithms are comparable for both the network partitions and in all the cases. As expected, these results give evidence that the
Decentralized APP converges to solutions that are equal or slightly worse to the ones given by
Centralized VCZ-based VOP in terms of objective function. However, the optimal solutions may correspond to different set-points of active and reactive powers of DER controllers. Consequently, the resulting voltage profiles could be different, as evidenced by the values assumed by the VPI.
To this aim,
Table 9 shows the values of the VPI obtained by the
Decentralized APP for four VCZs and seven VCZs in the three considered cases. By comparing
Table 9 with
Table 6, it is apparent that the values of VPI for the
Decentralized APP are higher or lower than that for the
Centralized VCZ-based VOP.
For sake of completeness,
Table 10 shows the statistical parameters of the nodal voltages distribution obtained by the
Decentralized APP for both the partitions and in the three operating conditions. In addition, in this case, the values assumed by the standard deviations are almost equal to the ones obtained by the centralized approach and always very small. With reference only to
Case 3, the histograms of the nodal voltage distribution calculated by the
Decentralized APP for both the partitions are reported in
Figure 9 and
Figure 10, respectively.
In summary, comparing decentralized and centralized solutions, although the objective functions are very similar, the optimal set-points of the active and reactive power controllers of DERs are different because the problem (
3) is not strictly convex. In practice, there are infinite combinations of DERs active and reactive powers that give, as solutions, the same objective functions. However, different power injections cause different voltage profiles, as confirmed by the VPI and statistical parameters of the voltages distribution. Anyway, the amplitudes of the nodal voltages are always polarized around the reference values.
In addition to the considerations related to the final solution achieved by the decentralized algorithm, it is important to also investigate the convergence characteristics. In particular, the number of iterations that the
Decentralized APP needs to reach convergence is different for the two network partitions. Convergence is achieved when the coupling error is smaller than a tolerance value, which is fixed to 2.5
p.u. The coupling error is defined as the infinity norm of the vector composed of all the errors on the equalities in (
5), which are calculated by each VCZ to update the Lagrangian multipliers according to (
15) and (16). Obviously, the convergence rate also depends on the values of the parameters
,
c and
in the
decentralized APP algorithm. In this analysis, the set was equal to:
- -
4 VCZs partition: , and ;
- -
7 VCZs partition: , and .
Figure 11 and
Figure 12 show the evolutions of, respectively, the objective function and the coupling error, for the partitioning in four VCZs in the three cases. It is evident that in all the cases the number of iterations does not exceed the value of 400. The worst performance is in
Case 3, where the number of iterations to convergence is almost equal to 400.
Figure 13 and
Figure 14 show the evolutions of the same quantities for the partitioning in seven VCZs. In comparison with the partitioning in four VCZs, it is evident that, for a network partitioned in seven VCZs, the
Decentralized APP nearly doubles the number of iterations to reach convergence, as expected from the theory. It is important to notice that the evolution of objective function always presents a rapid decrease in the first iterations. Consequently, if the algorithm stops after few tens of iterations, the value of the objective function is already close to the optimal solution. In addition, the evolution of the coupling error is also strongly decreasing after the first iterations, reaching in few tens of iterations the order of magnitude of
, which is already acceptable being expressed in voltage p.u. These considerations are important from a practical perspective point of view because they allow for relaxing the communication requirements of the decentralized solution.
4.4. Voltage Profiles
In the previous sections, the analysis has focused on each step of the proposed method. In this final section, the performance of the
Decentralized APP solution is analyzed in absolute terms. To this aim, the voltage profiles of the feeders and subfeeders are reported and compared with the ones obtained by the
Benchmark VOP and the one obtained without any optimization, referred to as
no VOP that is obtained by solving the DistFlow problem with fixed active powers and null reactive powers injected by DERs.
Figure 15,
Figure 16 and
Figure 17 show the network voltage profiles respectively for
Case 1,
Case 2, and
Case 3, also including the HV busbar (slack node) and the MV substation busbar. It is evident how the profiles obtained by the
Decentralized APP are closer to the
Benchmark VOP ones than the ones obtained by
no VOP, in all the considered cases. These results show that, although the proposed algorithm does not guarantee the same profiles as the reference centralized VOP, it represents a significant improvement with respect to the absence of optimization. At the same time, it is worth mentioning that, compared with the reference centralized VOP, the proposed
Decentralized APP requires a very limited number of voltage measurements and a significant reduction of communication requirements.