Fusion Method and Application of Several Source Vibration Fault Signal Spatio-Temporal Multi-Correlation
Abstract
1. Introduction
- (1)
- A model of spatial correlation of multiple vibration sensors is proposed;
- (2)
- Propose a method of spatial and temporal multi-correlation fusion of vibration sensors;
- (3)
- The proposed method can handle different types of rotor faults and can effectively implement fault diagnosis.
2. Introduction to Basic Theory
2.1. Wavelet Noise Reduction
2.2. Linear Normalization
2.3. Hilbert–Huang Transform
- (1)
- The signal x(t) and its HHT energy spectrum and amplitude spectrum are the same, but the phase spectrum is different.
- (2)
- Signal x(t) and are orthogonal to each other, namely:
- (3)
- If you perform x(t) twice using HHT, you will get -x(t), namely .
3. Multi-Sensors Spatio-Temporal Multi-Correlation Fusion Analysis
3.1. Spatial Correlation Analysis
3.2. Time Deviation Correlation
3.3. Temporal Correlation Analysis
3.4. Signal Fusion Based on Spatio-Temporal Multiple Cross-Correlation and Correlation Function
4. Experimental Verification
4.1. Experimental Device and Fault Setting
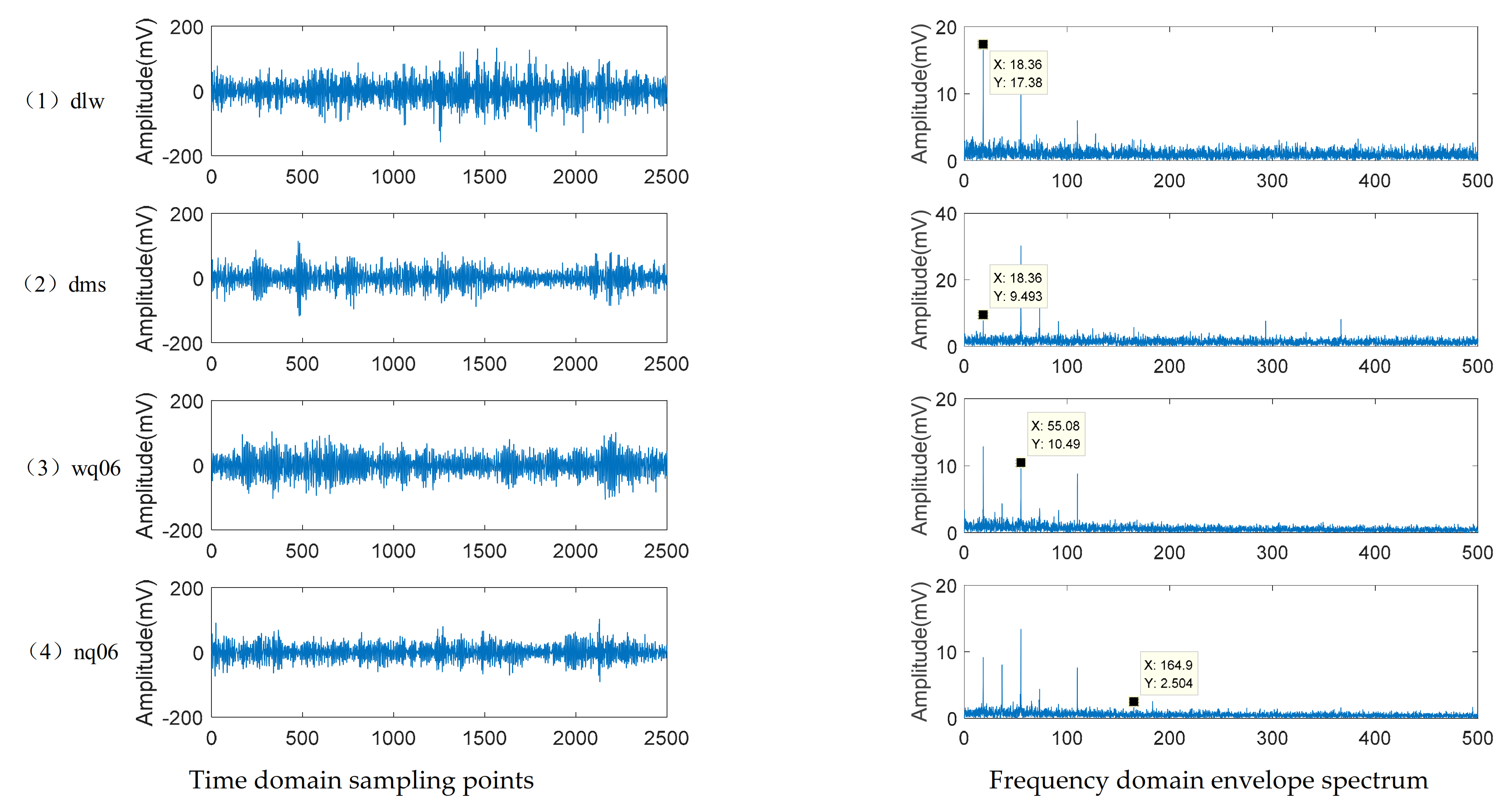
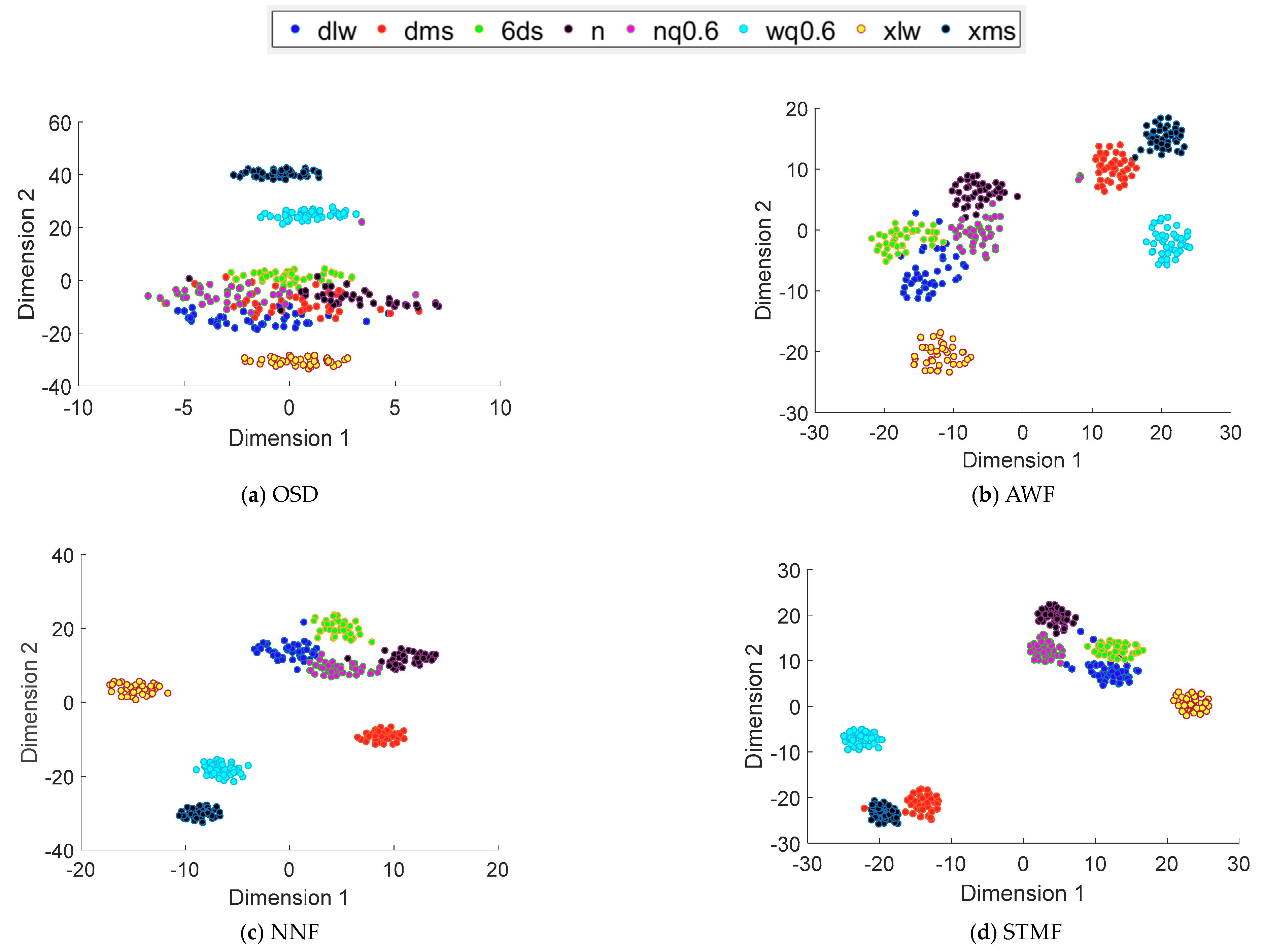
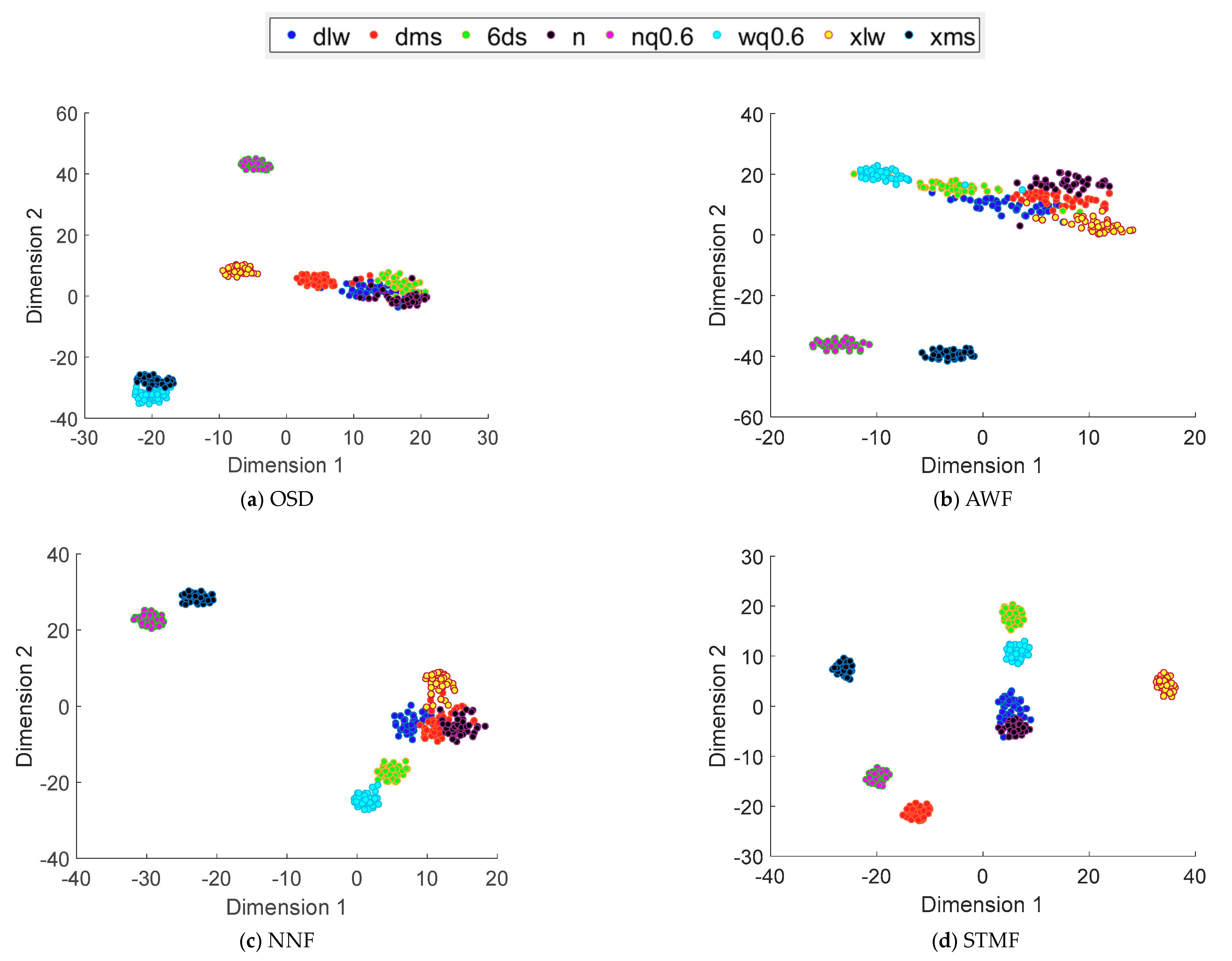
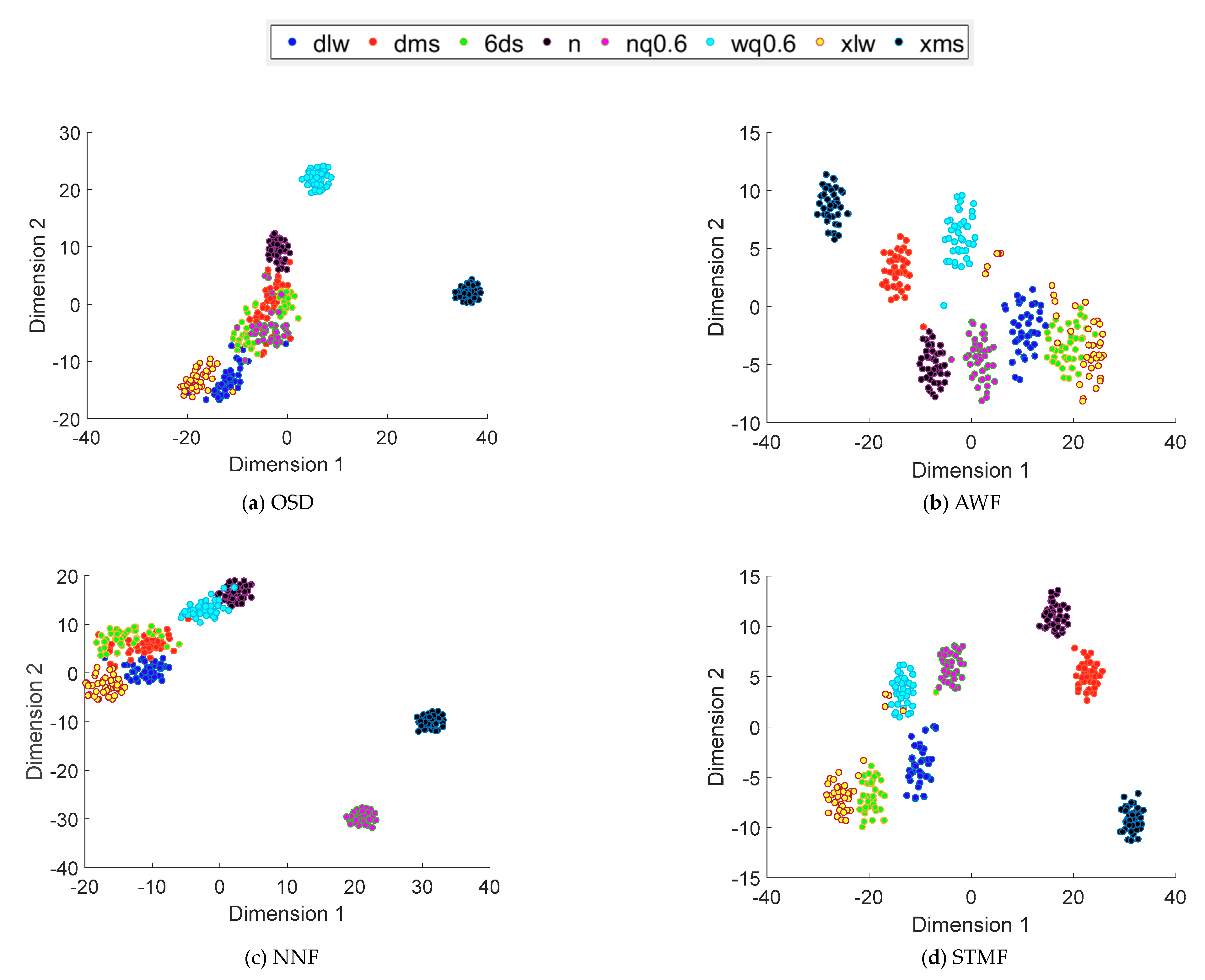
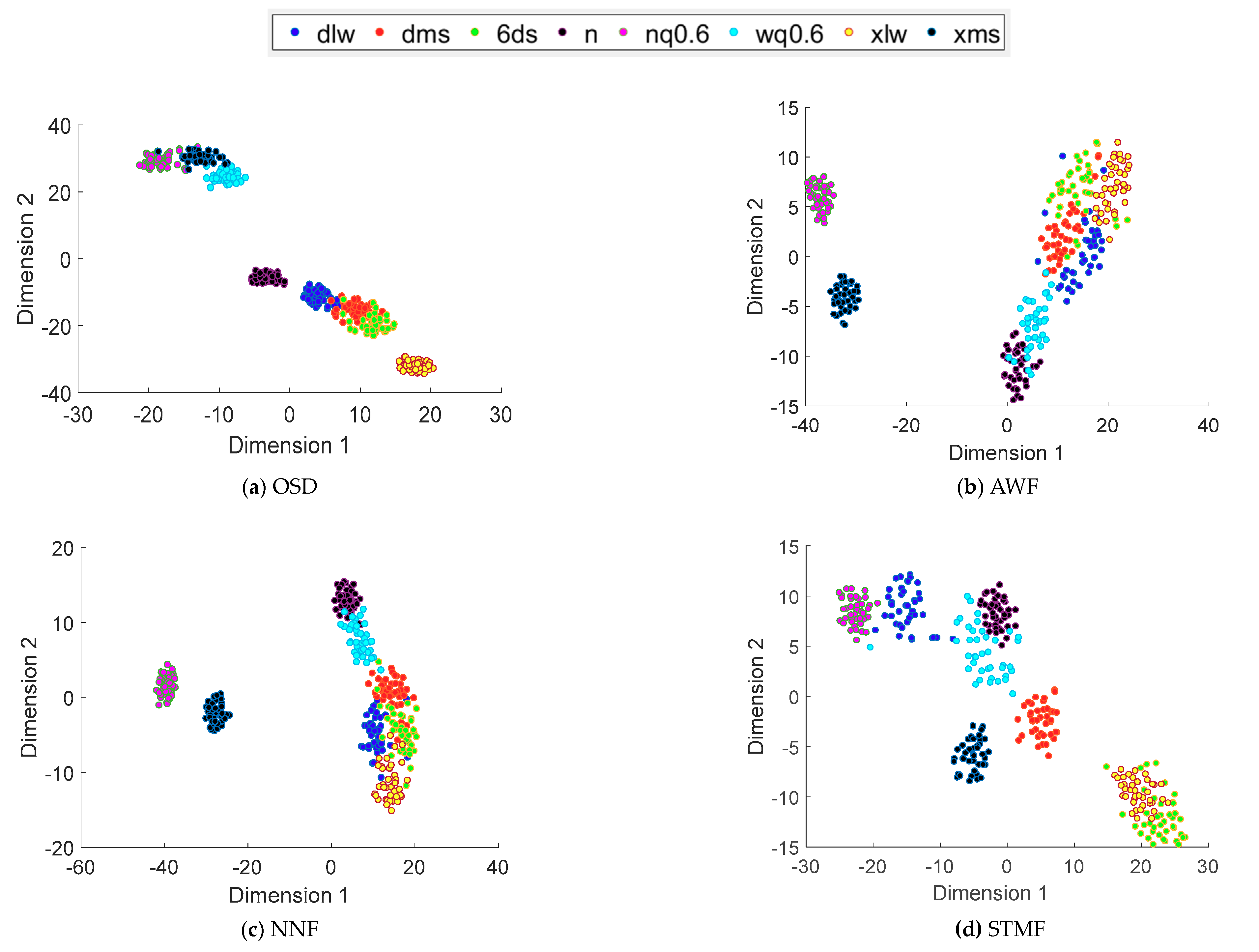
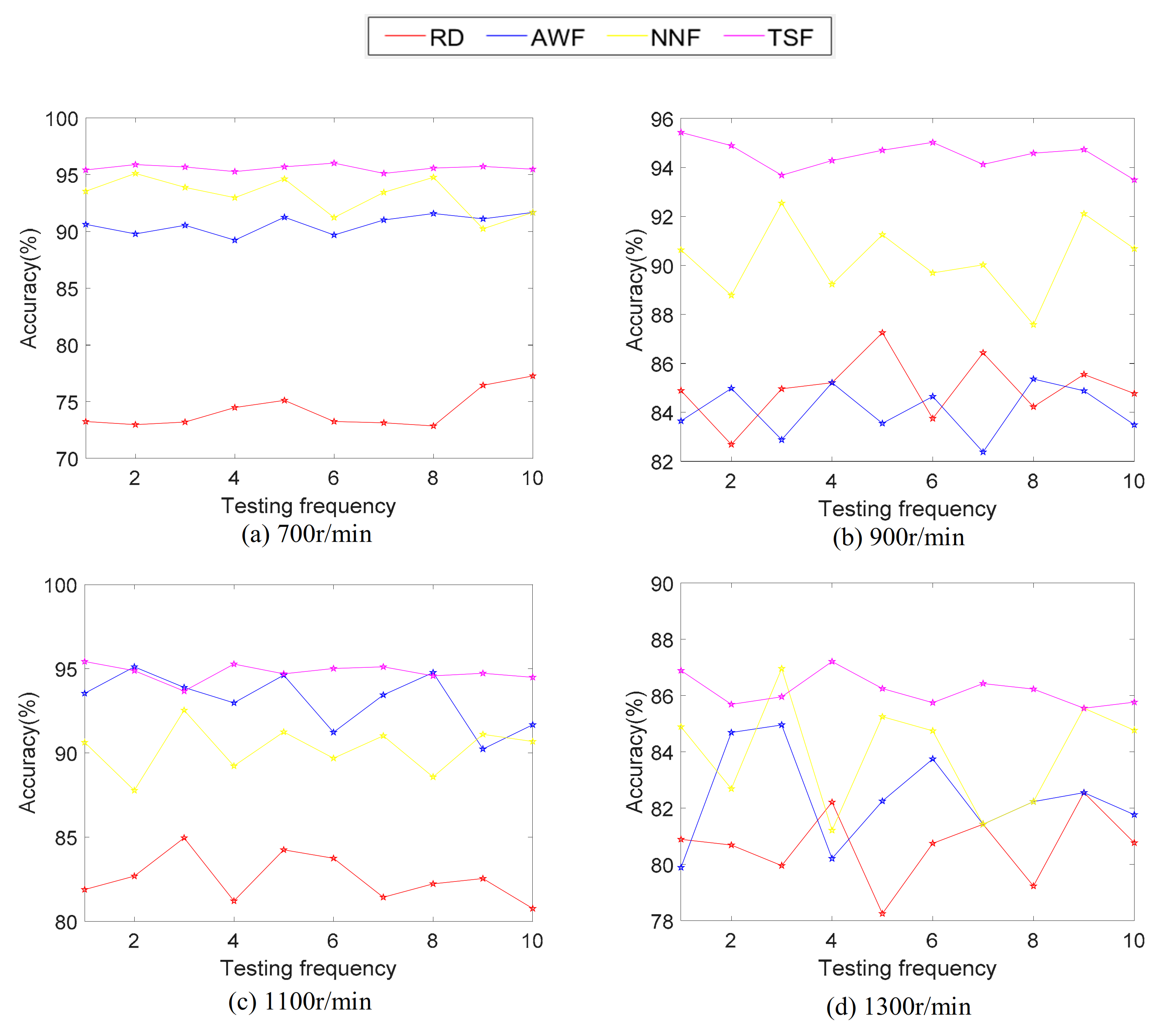
4.2. Analysis of Test Results
- (1)
- 700 rpm test conditions
- (2)
- 900 rpm test conditions
- (3)
- 1100 rpm test conditions
- (4)
- 1300 rpm test conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; Xi’an Jiao Tong University Press: Xi’an, Shaanxi, China, 2017. [Google Scholar]
- Wang, J.; Li, S.; Han, B.; An, Z.; Xin, Y.; Weiwei, Q.; Wu, Q. Construction of a batch-normalized auto encoder network and its application in mechanical intelligent fault diagnosis. Meas. Sci. Technol. 2019, 30, 14. [Google Scholar] [CrossRef]
- He, Y.-L.; Wang, K.; Zhong, H.; Meng, Y.; Wang, X.; Tang, G. Enhanced detection of generator characteristic vibration signal based on maximum correlation kurtosis deconvolution algorithm. J. N. China Electr. Power Univ. 2017, 44, 67–73, 89. [Google Scholar]
- Fan, Z.; Wang, L.; Zhao, Z.; Mao, Z. Research on Diesel Engine Fault Early Warning Method Based on Correlation Analysis of Cylinder Head Vibration Signal Envelope. J. Beijing Univ. Chem. Technol. 2018, 45, 76–81. [Google Scholar]
- Gao, H.B.; Ouyang, G.Y. Diesel engine misfire fault detection based on cylinder head vibration signal analysis. Automot. Engine 2005, 1, 32–34. [Google Scholar]
- Cheng, Y.; Chen, B.; Mei, G.; Wang, Z.; Zhang, W. A novel blind deconvolution method and its application to fault identification. J. Sound Vib. 2019, 460, 114900. [Google Scholar] [CrossRef]
- Janjarasjitt, S.; Ocak, H.; Loparo, K.A. Bearing condition diagnosis and prognosis using applied nonlinear dynamical analysis of machine vibration signal. J. Sound Vib. 2008, 317, 112–126. [Google Scholar] [CrossRef]
- Rahmatian, M.; Vahidi, B.; Ghanizadeh, A.J.; Gharehpetian, G.B.; Alehosseini, H.A. Insulation failure detection in transformer winding using cross-correlation technique with ANN and k-NN regression method during impulse test. Int. J. Electr. Power Energy Syst. 2013, 53, 209–218. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Cheng, Y.; Lu, C. Fault diagnosis of gearbox using empirical mode decomposition and multi-fractal detrended cross-correlation analysis. J. Sound Vib. 2016, 385, 350–371. [Google Scholar] [CrossRef]
- Zhan, L.; Ruo, C.; Bao, Z. Research on the data-level fusion algorithm of similar multi-sensor adaptive weight estimation. J. Lanzhou Univ. Technol. 2006, 32, 78–82. [Google Scholar]
- Chopr, P.; Yadav, S.K. Fault detection and classification by unsupervised feature extraction and dimensionality reduction. Complex Intell. Syst. 2015, 1, 25–33. [Google Scholar] [CrossRef]
- Maltseff, P.A.; Winter, S. Systems, Methods and Devices for Collecting Data from Wireless Sensor Nodes. U.S. Patent No. 7,978,639, 12 July 2011. [Google Scholar]
- Krishnamoorthy, G.; Ashok, P.; Tesar, D. Simultaneous sensor and process fault detection and isolation in multiple-input-multiple-output systems. IEEE Syst. J. 2017, 9, 335–349. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- He, Z.; Shao, H.; Cheng, J.; Yang, Y.; Xiang, J. Kernel flexible and displaceable convex hull based tensor machine for gearbox fault intelligent diagnosis with multi-source signals. Measurement 2020, 163, 107965. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Hu, Y.; Guo, H.; Lei, Y. The multi-correlation acoustic source identification study of a type combine harvester. J. Vib. Meas. Diagn. 2013, 33, 66–69. [Google Scholar]
- Pan, G.; Li, S.; Zhu, Y. A Time-Frequency Correlation Analysis Method of Time Series Decomposition Derived from Synchrosqueezed S Transform. Appl. Sci. 2019, 9, 777. [Google Scholar] [CrossRef]
- Xiao, F. A Novel Evidence Theory and Fuzzy Preference Approach-Based Multi-Sensor Data Fusion Technique for Fault Diagnosis. Sensors 2017, 17, 2504. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X. Deep coupling auto encoder for fault diagnosis with multimodal sensory data. IEEE Trans. Ind. Inform. 2018, 14, 1137–1145. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X.; Zhang, X.; Yan, R. A Deep Coupled Network for Health State Assessment of Cutting Tools Based on Fusion of Multisensory Signals. IEEE Trans. Ind. Inform. 2019, 15, 6415–6424. [Google Scholar] [CrossRef]
- Hao, S.; Ge, F.-X.; Li, Y.; Jiang, J. Multi sensor Bearing Fault Diagnosis Based on One-dimensional Convolutional Long Short-Term Memory Networks. Measurement 2020, 159, 107802. [Google Scholar] [CrossRef]
- Chen, H.; Hu, N.; Cheng, Z.; Zhang, L.; Zhang, Y. A deep convolutional neural network based fusion method of two-direction vibration signal data for health state identification of planetary gearboxes. Measurement 2019, 146, 268–278. [Google Scholar] [CrossRef]
- Jiang, Z.; Jia, Q.-S.; Guan, X. Optimization of sensor location for improving wind power prediction accuracy. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017. [Google Scholar]
- Mednikov, V. Method and Sensor Arrangement for Determining the Position and/or Change of Position of a Measured Object Relative to a Sensor. U.S. Patent No. 8,476,896, 2 July 2013. [Google Scholar]
- Chen, W.; Li, J.; Wang, Q.; Han, K. Fault feature extraction and diagnosis of rolling bearings based on wavelet thresholding denoising with CEEMDAN energy entropy and PSO-LSSVM. Measurement 2021, 172, 108901. [Google Scholar] [CrossRef]
- Purashotham, V.; Narayanan, S.; Prasad, S.A.N. Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition. NDT E Int. 2005, 38, 654–664. [Google Scholar] [CrossRef]
- Shao, R.; Hu, W.; Wang, Y.; Qi, X. The fault feature extraction and classification of gear using principal component analysis and kernel principal component analysis based on the wavelet packet transform. Measurement 2014, 54, 118–132. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform. Mech. Syst. Signal Process. 2010, 24, 119–137. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Liu, Z.; Wang, J. Weak feature enhancement in machinery fault diagnosis using empirical wavelet transform and an improved adaptive bistable stochastic resonance. ISA Trans. 2019, 84, 283–295. [Google Scholar] [CrossRef] [PubMed]
- Ya, G.; Ping, Y. Analysis of the properties of linear dimensionless methods. Stat. Res. 2008, 2, 93–100. [Google Scholar]
- Macêdo, D.; Zanchettin, C.; Oliveira, A.L.I.; Ludermir, T. Enhancing batch normalized convolutional networks using displaced rectifier linear units: A systematic comparative study. Expert Syst. Appl. 2019, 124, 271–281. [Google Scholar] [CrossRef]
- Ondra, V.; Severb, I.A.; Schwingshackl, C.W. Identification of complex non-linear modes of mechanical systems using the Hilbert-Huang transform from free decay responses. J. Sound Vib. 2021, 495, 115912. [Google Scholar] [CrossRef]
- Mahata, S.; Shakya, P.; Babu, N.R. A robust condition monitoring methodology for grinding wheel wear identification using Hilbert Huang transform. Precis. Eng. 2021, 70, 77–91. [Google Scholar] [CrossRef]
- Li, S.; Cheng, Y.; Wang, H.; Gao, S. Time offset calibration distributed multi-sensor multi-target tracking algorithm. J. Northwestern Poly Tech. Univ. 2020, 38, 797–805. [Google Scholar] [CrossRef]
- Timothy, G.C.; Francesca, M. Spatial correlation robust inference with errors in location or distance. J. Econom. 2006, 140, 76–96. [Google Scholar]
- Zhou, C.; Xi, C.; Pang, J.; Lin, Y. Ambient noise data selection based on the asymmetry of cross-correlation functions for near surface applications. J. Appl. Geophys. 2018, 159, 803–813. [Google Scholar] [CrossRef]
- Ma, Z.; Gu, C.; Wang, J.; Zeng, M.; Chao, G.; Jian, W. Research on fault diagnosis method of rolling bearing based on cross-correlation function. J. Appl. Basic Sci. Eng. 2017, 25, 646–655. [Google Scholar]
- Wang, Y.; Yang, H.; Yuan, X.; Shardt, Y.A.W.; Yang, C.; Gui, W. Deep learning for fault-relevant feature extraction and fault classification with stacked supervised auto-encoder. J. Process Control 2020, 92, 79–89. [Google Scholar] [CrossRef]


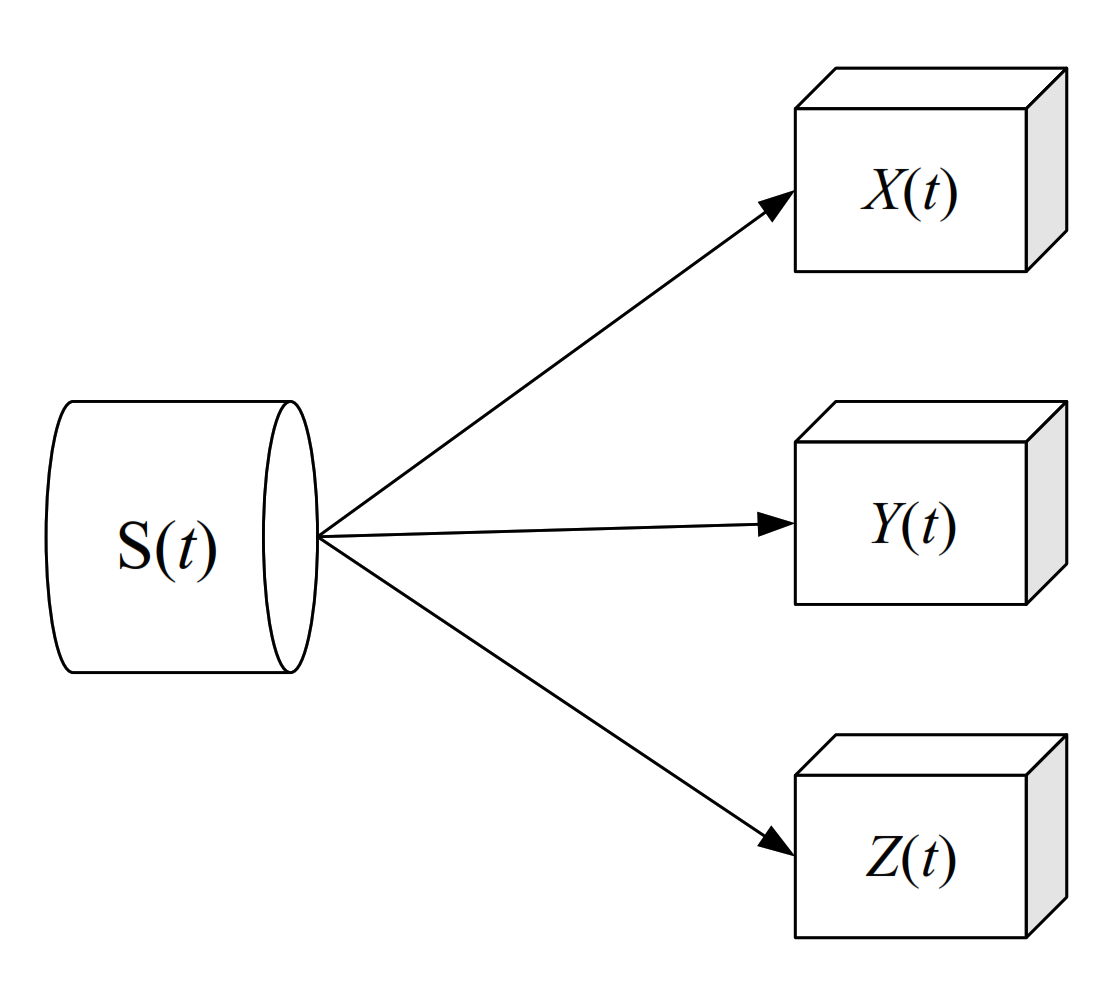

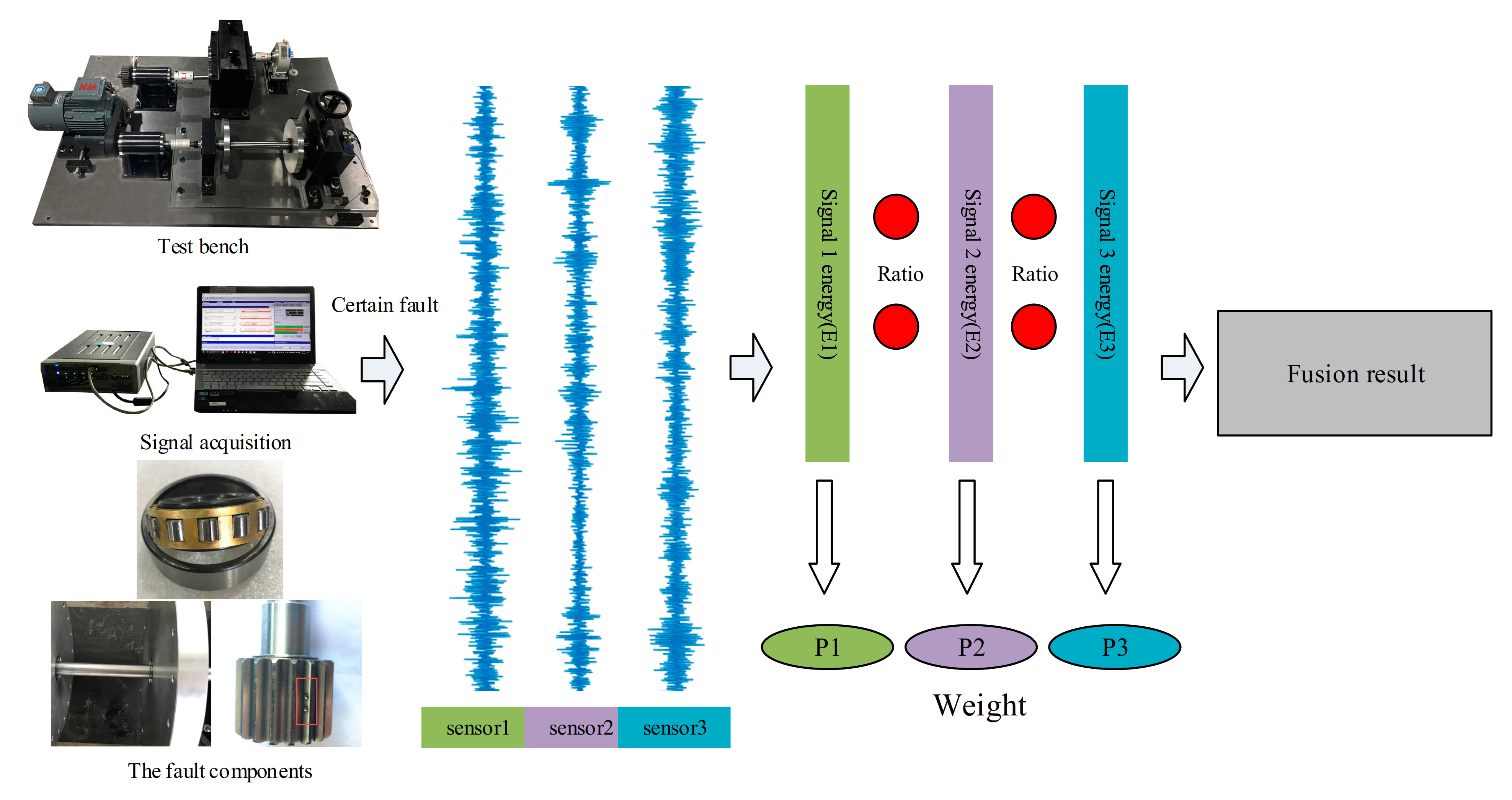



| Sensor 1 | Sensor 2 | Sensor 3 | |
|---|---|---|---|
| X distance | 0 | a2 | a3 |
| Y distance | b1 | 0 | b3 |
| Z distance | c1 | c2 | c3 |
| Gear | Number of Teeth | Modulus (mm) | Engagement Angle (deg.) | Material |
|---|---|---|---|---|
| Sun gear | 55 | 2 | 20 | S45C |
| Planetary gear | 75 | 2 | 20 | S45C |
| Parameters | Inner Ring Diameter | Outer Ring Diameter | Rolling Body Diameter | Pitch Diameter | Number of Rolling Elements |
|---|---|---|---|---|---|
| Value | 30 mm | 62 mm | 9.6 mm | 46 mm | 9 |
| Working Condition | Fusion Method | Total Sample | Training Samples | Testing Sample | Accuracy |
|---|---|---|---|---|---|
| 700 rpm | OSD | 200 | 40 | 160 | 74.20% ± 2.52% |
| AWF | 90.65% ± 0.71% | ||||
| NNF | 93.15% ± 2.65% | ||||
| STMF | 95.59% ± 0.07% | ||||
| 900 rpm | OSD | 200 | 40 | 160 | 84.97% ± 1.67% |
| AWF | 84.10% ± 1.09% | ||||
| NNF | 90.25% ± 2.30% | ||||
| STMF | 94.48% ± 0.36% | ||||
| 1100 rpm | OSD | 200 | 40 | 160 | 82.57% ± 1.88% |
| AWF | 93.15% ± 2.65% | ||||
| NNF | 90.25% ± 2.02% | ||||
| STMF | 94.79% ± 0.24% | ||||
| 1300 rpm | OSD | 200 | 40 | 160 | 80.67% ± 1.66% |
| AWF | 82.37% ± 2.90% | ||||
| NNF | 83.97% ± 3.77% | ||||
| STMF | 86.17% ± 0.30% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Lu, J.; Li, S.; Ding, R.; Xu, K.; Li, X. Fusion Method and Application of Several Source Vibration Fault Signal Spatio-Temporal Multi-Correlation. Appl. Sci. 2021, 11, 4318. https://doi.org/10.3390/app11104318
Cheng L, Lu J, Li S, Ding R, Xu K, Li X. Fusion Method and Application of Several Source Vibration Fault Signal Spatio-Temporal Multi-Correlation. Applied Sciences. 2021; 11(10):4318. https://doi.org/10.3390/app11104318
Chicago/Turabian StyleCheng, Longhuan, Jiantao Lu, Shunming Li, Rui Ding, Kun Xu, and Xianglian Li. 2021. "Fusion Method and Application of Several Source Vibration Fault Signal Spatio-Temporal Multi-Correlation" Applied Sciences 11, no. 10: 4318. https://doi.org/10.3390/app11104318
APA StyleCheng, L., Lu, J., Li, S., Ding, R., Xu, K., & Li, X. (2021). Fusion Method and Application of Several Source Vibration Fault Signal Spatio-Temporal Multi-Correlation. Applied Sciences, 11(10), 4318. https://doi.org/10.3390/app11104318








