Abstract
Here, we present a critical review of recent developments in Casimir physics motivated by discoveries of novel materials. Specifically, topologically nontrivial properties of the graphene family, Chern and topological insulators, and Weyl semimetals have diverse manifestations in the distance dependence, presence of fundamental constants, magnitude, and sign of the Casimir interaction. Limited studies of the role of nonlinear optical properties in the interaction are also reviewed. We show that, since many new materials have greatly enhanced the nonlinear optical response, new efficient pathways for investigation of the characteristic regimes of the Casimir force need to be explored, which are expected to lead to new discoveries. Recent progress in the dynamical Casimir effect is also reviewed and we argue that nonlinear media can open up new directions in this field as well.
1. Introduction
The ubiquitous Casimir force originates from the exchange of electromagnetic fluctuations between objects, and it is determined by the material’s magnetic and dielectric properties and boundary conditions for the fields. The complicated interplay between such properties and geometry has been shown to yield many different scaling laws and wide variations in magnitude, sign, and characteristic dependences upon fundamental constants (such as, e.g., Plank’s constant or the speed of light) [1,2]. The basic understanding of the Casimir force is important for probing novel physics involving materials at a small relative distance and for better design of micro and nanoscale devices [3]. The closely related van der Waals interaction (corresponding to the Casimir force in the non-retarded regime, where the speed of light can be considered infinite) has also recently received much interest due to its importance for materials science, especially in layered systems [4]. Consequently, advances in first principles simulations have resulted in computational tools for making qualitative and quantitative predictions in materials in which long-ranged collective electronic effects are important [5].
In the past several years, the discovery of many materials with nontrivial topological properties has given a new direction for the field of Casimir physics [6,7,8]. Materials with Dirac-like energy dispersions in 2D and 3D dimensions have a wide variety of optical response properties, which in turn can significantly affect electromagnetic interactions. In this Perspective article, we give an overview of key results regarding the Casimir force involving materials from the graphene family, Weyl semimetals, topological, and Chern insulators. This research has moved forward not only our fundamental understanding of properties of topologically nontrivial materials, but also of electromagnetism in such media.
Recent theoretical and experimental works have shown that many Weyl semimetals and layered transition metal dichalcogenides can also experience enhanced nonlinear optical properties [9,10]. These, in turn, can result in photogalvanic effects, photocurrents, and nonlinear Hall effect, which is especially encouraging for novel optical effects in the visible and infrared regimes [11,12]. The potential of new and improved optical applications has stimulated much work in calculating the nonlinear optical response in different systems. Nonlinear properties can also affect the Casimir interaction, however, this direction has not been considered much by the scientific community as current research on dispersive forces has been primarily within linear response theories. Here, we show that the limited studies in the nonlinear optical response regime demonstrate even further diversity of dependences in the Casimir interactions. We argue that discoveries of strongly nonlinear materials bring forward the necessity to investigate light-matter fluctuation induced interaction beyond the linear response regime. Such materials can serve as excellent platforms bringing together nonlinear optics and its connection to Casimir phenomena for probing novel properties of Dirac-like systems.
Other Casimir-related phenomena can also benefit from discoveries of new materials with nontrivial properties. One such phenomenon is the Dynamical Casimir Effect (DCE), which shows how real photons can be generated from the “empty” vacuum [13,14]. While most methods of describing DCE rely on treating different boundary conditions, understanding the microscopic and materials-related nature of this effect can also be beneficial. In this Perspective, we give a short overview of recent achievements in this field and demonstrate that experimental observation of the DCE relies on nonlinear optics, and we argue that nonlinear media can give new directions of exploration.
2. Nontrivial Topology in Materials
Topological Insulators: The discovery of 3D Topological Insulators (TIs) has been inspired by the search for topological invariants in condensed matter systems, and in particular by the prediction of the quantum spin Hall effect [6]. Experiments have shown that TI phases exist in BixSb1-x, layered Hg(Cd)Te structures, half-Heuslers, and others [15]. TIs differ from ordinary materials as their bulk is typically gapped or insulating, while the surface states are gapless and they are a consequence of the unique band structure of the material. In fact, because of the insensitivity of the topology to perturbations, the surface states are considered to be rather stable.
A distinguishing feature for the electromagnetism of TIs is the presence of coupling between electric and magnetic fields in the electromagnetic action . Specifically, in addition to the usual component, the total action contains a topologically nontrivial term that is proportional to the fine structure constant and the axion field . In the case of a system whose bulk is insulating under a perturbation that breaks the time reversal symmetry on the surface, the axion field becomes quantized. The integer depends on the type of perturbation, which usually is a magnetic layer on the surface of the TI [16]. Furthermore, the direction of polarization of the layer can result in having a positive or negative sign. Trivial materials are characterized by , while TIs exhibit topological magnetoelectric susceptibility that can be positive or negative, inducing mixing between the electric and magnetic fields at the surface. The presence of modifies the constitutive equations for the electric and magnetic fields in TIs accordingly, thus that in frequency space
As a result, the electromagnetic boundary conditions now yield off-diagonal components of Fresnel coefficients, i.e., the two polarizations are coupled. This situation challenges the calculation of the Casimir interaction, especially in determining analytical expressions in various limiting cases.
It has been realized that the term plays an important role in achieving repulsion in the Casimir interaction between semi-infinite TIs [17,18,19] at certain distance ranges. In fact, at large separations (corresponding to the high-temperature limit), the force per unit area between two isotropic TIs with the same bulk dielectric function , taken as a Drude–Lorentz model, has been found to have the form
where are the magnetoelectric topological susceptibilities for the surfaces of the materials. The function is complicated [18], and its numerical evaluation shows that repulsion is possible when and have opposite signs. Figure 1 shows the regimes of attraction and repulsion in terms of and , in the limit of high temperature. More generally, the (unstable) equilibrium distance separating the attractive and repulsive regions was found to have the characteristic behavior and in the case of zero temperature .
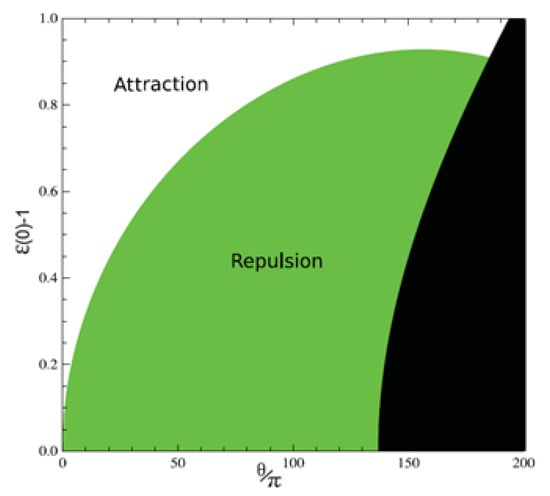
Figure 1.
Attraction and repulsion at and . The forbidden region is given in black. (Figure is taken from reference [18]).
The Casimir interaction between TI slabs of finite thickness has also been studied [20]. It has been shown that the repulsive regime depends on the slab thickness, and for slabs thinner than the inter-slab separation, the interaction is attractive. Additionally, the anisotropy of the TIs has been found to be important [18,19,20]. The strength and sign of the interaction can be modified using the anisotropy through the off-diagonal elements being suppressed or enhanced with respect to the diagonal terms in the Fresnel reflection matrix. Reference [21] has also found that the van der Waals force oscillates with respect to the angle between the optical axes of two anisotropic TIs, which can lead to van der Waals torque. Interestingly, the torque is weakened when and have opposite signs. The strength of the Casimir repulsion can also be enhanced in TI multilayered composites [22]. The Casimir–Polder energy between an atom and a TI was found to be generally attractive, although some repulsive regimes were also uncovered due to the interplay between the -term and the atomic states [23].
It is important to note that the Casimir/van der Waals interaction is closely affected by the optical response of the actual TI materials. The above results have been obtained using generic models for the bulk and surface dielectric response, characterized by adjustable parameters. However, the frequency dependence of the optical properties of TI materials will definitely affect the interaction [1]. For example, the nontrivial topological contribution resulting in a constant conductivity is observed in the low-frequency regime, meV, while transitions between the surface and bulk states are responsible for the higher frequency range. Additionally, temperature, electron density, and other factors can affect the optical properties of TIs [24,25,26]. Thus, even though the nontrivial topology is expected to be present in large distance separations, a more complete model for the optical conductivity may be necessary to examine the survival of repulsion and the role of distance and other factors in the interaction for material-specific TIs.
Chern Insulators: Chern insulators (CIs) are another type of topological materials for which the Casimir/vdW interaction has been studied. CIs are 2D band insulators with a quantized Hall conductivity whose origin comes from the broken time-reversal symmetry [27]. Such materials give rise to the quantum anomalous Hall effect since there is no net magnetic field (external and internal magnetic fields are zero). Several types of lattices have been shown to be CIs, including hexagonal [27], kagome [28], triangular [29], and several others [30]. The signature feature for Chern insulators is the Chern number , which sums up the signs of the non-zero mass gaps of the Dirac cones and it essentially determines the Hall conductivity at zero frequency .
One of the first works to consider the Casimir interaction in CIs is reference [31], where it has been shown that at large distances, the zero-temperature quantum mechanical limit of the energy is determined by the zero frequency optical properties and that the anomalous quantum Hall effect plays an important role. In fact, the interaction energy per area in the lowest order of is found as
where are the Chern numbers of the two CIs. Later studies [32,33,34] have shown that in the case of planar Chern–Simons materials, forward and backward electromagnetic field scattering must be considered explicitly, which modifies the Casimir energy to
where the two CIs are with vanishing longitudinal conductivity and is the polylogarithmic function. Equations (4) and (5) have very similar large distance tails for comparable optical response properties characterized by small Chern numbers (as noted in reference [32]).
It is interesting to note that the scaling law is the same as for typical metal, however, the interaction magnitude is quite small due to the proportionality to . These results further indicate that when the Chern numbers are small, the interactions between different pairs of CIs essentially differ only by the product of their Chern numbers (or Hall conductivities equivalently). Given that can be positive or negative, in that case, Casimir repulsion or attraction can be obtained. In general, however, the sign of the interaction is determined by the real part of the polylogarithmic function in Equation (5).
References [32,33,34] have further examined this problem showing that the behavior shown in Equations (4) and (5) may be overtaken by making the longitudinal conductivity of the interacting materials more prominent or by considering shorter separations, for which the interaction is similar to the one for two regular dielectrics. In the case of dielectric substrates covered with Chern–Simons layers, however, a repulsive Casimir regime is observed at shorter separations, while at larger distances, the interaction resembles one of ordinary dielectrics [35,36]. The Casimir–Polder energy between an atom and a Chern–Simons surface may be repulsive or attractive depending on the sign of the Chern number [37].
The recent discoveries of graphene-related materials, such as silicene, germanene, and stanene [38,39,40], have offered a platform to further study Casimir phenomena in 2D materials with tunable topological properties. The finite buckling between the two sublattices and strong spin-orbit interaction in silicene, germanene, and stanene allow accessing several phases specific for CIs using external electric fields and laser irradiation [41]. Reference [42] reports a rich phase diagram of the Casimir energy between such 2D materials arranged in a Fabry–Perot cavity under externally applied fields (Figure 2a). It is interesting to note that the interaction is precisely of the form as in Equation (4) when the external electric and laser fields drive both materials in the anomalous quantum Hall effect regime. Indeed, in this case, the quantum mechanical energy is quantized and repulsive (denoted by the purple color in Figure 2b) when the product of Chern numbers is negative. Nevertheless, through external field modulations, one can access various interaction regimes characterized by widely different magnitudes and scaling laws (as depicted by the different colors in Figure 2b). Increasing temperature leads to smearing the boundaries between the different phases and for ( is the spin-orbit coupling strength) the interaction is described by the classical result .
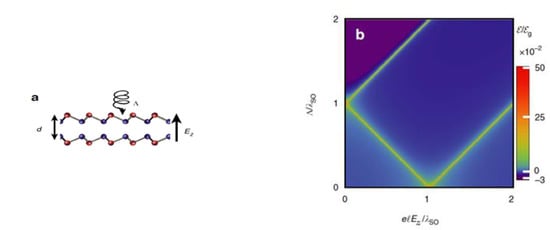
Figure 2.
(a) Fabry–Perot cavity of two graphene-like materials under an external electric field and laser light ; (b) Casimir force phase diagram of two identical dissipationless graphene-like materials with . (Figure taken from reference [42]).
Here, it is important to compare these results with the special case of graphene/graphene systems, which has been extensively studied in recent years [43,44,45]. The zero-temperature limit of the Casimir energy has been found to be
This shows that, after taking into account the fine structure constant relation, the energy does not depend on any fundamental constants except the electronic charge, and the distance dependence is the same as the one for perfect metals. The result in Equation (6) characterizes the large distance separation, and it has been obtained based on the constant optical graphene conductivity , specific to the low-frequency regime. Equation (6) applies in the limit of appropriate for graphene. Other studies have shown that at smaller separations, the spatial dispersion and higher frequency dispersion in the optical response can lead to deviations from this asymptotic limit [46,47,48,49]. The interplay between temperature, various models of graphene optical response, and other factors (such as doping, for example) have been studied in the Casimir and Casimir–Polder interactions involving single-layered and multilayered graphene systems [50,51,52,53]. Interesting proposals of fluctuation-induced forces from real charges competing with the Casimir force, Faraday screening effects in vdW interactions, and quantum friction involving graphene systems have also been put forward [54,55,56].
Weyl Semimetals: Very recently, researchers started investigating Casimir interactions in other 3D topological materials, such as Dirac and Weyl semimetals, in order to probe novel axion electrodynamics features. There are many materials characterized as Dirac semimetals with degenerate cones of linear dispersion in 3D, which makes these materials similar to 2D graphene [7]. When either inversion or time-reversal symmetries are broken, the cones are not degenerate anymore, and the Dirac semimetal becomes a Weyl semimetal [8]. The nodes of the nondegenerate cones are sources of magnetic monopoles in reciprocal space and Weyl semimetals have topologically nontrivial surface states termed as Fermi arcs. Additionally, Weyl semimetals with broken time-reversal symmetry can exhibit an anomalous Hall effect, which was found to be important for the unique Casimir interaction in 2D Chern insulators.
Weyl semimetals can also host an axion electromagnetic field, whose origin does not depend on the details of the electronic structure, thus it is topological in nature, but it is not quantized. The resultant mixing between the electric and magnetic field changes the constitutive electrodynamic equations and the boundary conditions, which are necessary for calculating the Casimir interaction in Weyl semimetals. It turns out that the optical response of Weyl semimetals, even for the simplest effective models, is anisotropic with many characteristic dependences [57], which coupled with the complicated Fresnel reflection matrices leads to difficulties in obtaining analytical expressions for the Casimir interaction [58,59]. Nevertheless, it was found that at short separations, the 3D anomalous Hall effect leads to the following Casimir interaction energy between Weyl semimetals,
where are the Dirac cone separations of the interacting materials. Since the product can be positive or negative as the cone separation can be in positive or negative momentum space domains, the Casimir interaction can be attractive or repulsive [58,59]. Note that the -parameters, which essentially determine the axion term in the electrodynamics, are continuous. Thus, the interaction energy is not quantized, which contrasts to the case of Chern or 3D topological insulators, where repulsive quantized force is possible. Even though this is an interesting result, it appears that the Casimir energy is dominated by the bulk diagonal components of the optical response leading to metallic-like behavior. In effect, the topological signatures are secondary in the Casimir energy, which is essentially similar to the one for 3D Dirac semimetals [58].
To enhance the repulsive nature and tunability of the Casimir force between Weyl semimetals, it was suggested that the gap in-between is filled with chiral media [60]. Photons with different chiralities propagate with different velocities leading to time-reversal symmetry breaking [61], which can lead to conditions of a repulsive force. In fact, for such materials, the interplay between distance, separation between the Weyl cones, and velocities of photons propagating in opposite directions give a tunable oscillatory-like Casimir force behavior, as shown in Figure 3.
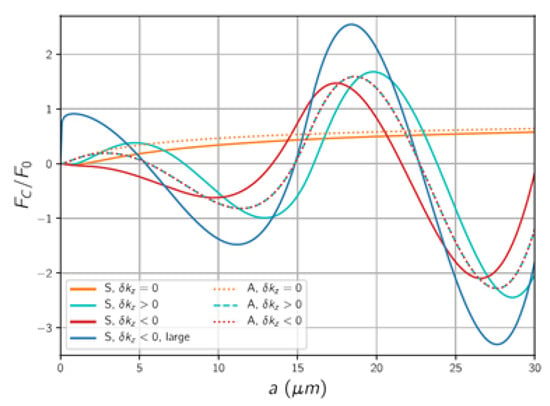
Figure 3.
Casimir force between Weyl semimetals filled with chiral medium normalized to the one for perfect metals as a function of separation. Here ( —Verdet constant, —applied magnetic field); corresponds to a vacuum filled gap, while the nonvanishing . In addition, . The curves marked with correspond to , while the rest correspond to . The line marked as “large” correspond to (Figure is taken from reference [60]).
The topologically nontrivial materials have been a fruitful ground for probing properties of Dirac-like systems in Casimir phenomena. Such investigations have been exclusively within the linear response regime. However, recent studies have shown that Weyl semimetals, for example, can experience 10 or even 100 times enhancement in their second order nonlinear optical polarizabilities when compared with standard systems [9,10,11,12]. Since optical response properties are key components in dispersive interactions, it appears that Casimir phenomena need to be considered beyond the linear response regime as discussed in what follows.
3. Nonlinear Optical Response
The pioneering experiments by Franken et al., demonstrating second harmonic generation, have opened up the field of nonlinear optics [62]. This area of investigation deals with light-matter interactions involving media whose dielectric and magnetic response properties are nonlinear functions of the electric and magnetic fields. The discoveries of new materials, in bulk, and at the nanoscale, have created novel opportunities for fundamental studies and applications of nonlinear optics. Recent works have shown that Weyl semimetals and transition metal dichalcogenide layers, for example, can experience much enhanced nonlinear optical response, which in turn can give rise to photogalvanic effects, photocurrents, and nonlinear Hall effect [11,12,63,64]. On the other hand, although electromagnetic fluctuations in nonlinear classical systems and quantum field theories have been studied in the past, the concept of fluctuational electrodynamics in the context of Casimir interactions has been explored only in limited situations. These include some general questions of noise [65,66], forces for small particles with nonlinear polarizability [67,68,69], or some limited scenarios of nonlinear parallel plates [70,71,72,73]. There have also been studies of thermal radiation in classical nonlinear Langevin models [74,75].
The approach of references [70,71] for fluctuational electrodynamics including nonlinear optics starts from the nonlinear Helmholtz equation for the vector electric field , including stochastic sources ,
The optical response of the involved materials enters via the displacement field , which is a nonlinear function of the electric field, and it is determined by the material properties. While the linear response is expressed in terms of the permittivity , nonlinear terms are expressed by higher-order susceptibilities, and, with Einstein summation convention, the component of the displacement field is,
We restrict the following discussion to symmetric materials, for which the polarization field is an odd function of the electric field, thus that in the series expansion of Equation (9), the dots represent fifth-order terms and so on. The nonlinear (third-order) term in Equation (9), expressed via the third-order susceptibility , couples different frequency modes, and, in general, different directions of the electric field.
Equations (8) and (9) pose the mathematical difficulty of being nonlinear, which can be addressed in a perturbative manner: The results reviewed here are valid in leading order of . Another task is the treatment of the stochastic sources in Equation (8). Following references [70,71], one starts by computing the linear response of Equation (8). The presence of in combination with the noise render it nontrivial. Assuming the noise has zero mean, one arrives at the following form for the effective dielectric function , describing the physical linear response of Equation (8),
where provides the Bose distribution of frequencies and are the components of the retarded dyadic Green’s tensor of the corresponding linear system. Note that the dependence on the position is included explicitly in the above equation. The effective permittivity in Equation (10) results from fluctuations in the linear system, quantified by as well as the imaginary part of the Green’s function , which excite nonlinear responses. The noise in Equation (8) thus enters via the imaginary part of . Notably, the effective dielectric function carries interesting properties, for example, being nonlocal in the following sense: For two bodies, is a function of their distance [71].
Because Equation (10) gives the physical linear response, the known formulations for Casimir forces, such as the Lifshitz formula, can be used with replacing the bare permittivity. By virtue of the fluctuation dissipation theorem, it is the physical linear response, which governs fluctuations. Figure 4 shows as an example the Casimir force for two parallel plates separated by a vacuum gap of width , at zero temperature. One of the plates is made of a nonlinear material (details given in the figure), while the other plate is a perfect reflector. The graph displays the force while taking the known power law of at a larger distance, shows a cross over to a law of at smaller distances. This displays the mentioned effect: At a small distance, the distance dependence of the permittivity is notable, thus that the force depends on distance in a two-fold manner: Via confinement of modes, and via the distance dependence of dielectric permittivity . The combination yields the observed power law. Figure 4 also displays that the power law of even persists when the bare permittivity approaches unity. This means that an object, which in isolation has no linear response, still feels a Casimir force when close to another object.
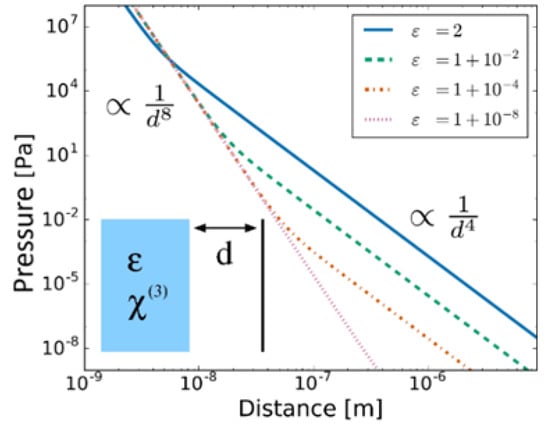
Figure 4.
Casimir pressure between a perfect mirror and a nonlinear material (see inset sketch), as a function of distance at K. For simplicity, the force is given for a real, frequency-independent linear permittivity as labeled, and a symmetric nonlinear response, , with a value measured for glass fused with silver nanoparticles [72]. Figure adapted from Reference [70].
This analysis shows that the effects of nonlinear optics drastically alter the Casimir effect at small distances, i.e., when the two surfaces strongly interact. Even more drastic effects of nonlinear optics are expected to occur under non-equilibrium conditions, e.g., for objects at different temperatures [71,73,74], or for dynamic scenarios discussed below. The inclusion of strong external fields is also a very promising route, and it is expected to allow for a large variety of effects concerning Casimir forces and nonlinear optics (see also the section on DCE below). Last, Casimir forces for mesoscopic bodies with strong even order nonlinear effects, e.g., with large [11], remain mostly unexplored.
4. Dynamical Casimir Effect
The Dynamical Casimir effect (DCE) is another fluctuation-induced phenomenon, which has been studied extensively in the past. Moore was the first to propose that quanta of the electromagnetic field from the vacuum can be generated from the vacuum in an ideal 1D cavity with moving boundaries [13]. Experimental demonstrations of this effect have been quite challenging since the number of generated quanta is tiny due to the small relative displacement of the wall with respect to the wavelength. In addition to using different cavity geometries to enhance this effect, the role of different materials has only recently started to be explored.
It was clear from the very beginning that an observation of the DCE in the pure form can be extremely difficult due to the small velocities (in comparison with the speed of light c) of real boundaries that could be achieved in a laboratory. Maia Neto and Machado [76] have calculated the rate of photon emission from an ideal mirror of area , oscillating with frequency
where is the number of photons generated during time , , and is the maximum velocity of the boundaries. For GHz, cm2, and cm we obtain photons/s, or one photon pair every two days. However, the effect can be significantly amplified inside cavities with oscillating boundaries, provided the frequency of oscillations is close to the doubled eigenfrequency of some field mode when the conditions of parametric resonance are satisfied. The main result, obtained within quite different schemes [77,78,79,80], is a simple formula for the number of quanta, created from the initial vacuum state during time ,
where is the maximal relative displacement of the boundary with respect to the wavelength and is a number coefficient, which depends on the cavity geometry. The problem is that cannot exceed the value of the order of for realistic boundaries. For this reason, the DCE in its pure form was not confirmed experimentally till now. In view of these difficulties, different ways to simulate the DCE were discussed for the past three decades by many authors, starting from reference [81]. Among the first proposals were ideas about possibilities of the DCE analogs in superconducting circuit devices [82,83,84], which were realized in experiments reported in [14,85,86]. The success of these experiments was related to the possibility of achieving the effective velocity of the boundary up to 25% of the light velocity in vacuum (although the analogy with the motion of real boundaries is not perfect). Many theoretical papers suggesting further improvements of the experimental schemes were published during the past decade: see more references in [87,88,89,90].
Another idea was to use effective semiconductor mirrors [81,91,92,93,94], which can be created by strong periodic laser pulses. Unfortunately, attempts to implement this idea in practice [95] met severe difficulties due to high losses in semiconductor materials [96]. However, a new idea to use the resonance between the field mode and cyclotron transitions inside a semiconductor heterostructure in a strong and rapidly varying magnetic field was suggested recently in reference [97].
The main mechanism of the DCE is the amplification of vacuum fluctuations due to fast variations of instantaneous eigenfrequencies of the field modes. These variations can happen either due to change of real dimensions of the cavity confining the field or due to changes of the effective (optical) length when dielectric properties of the medium inside the cavity depend on time. The main problem is how to realize fast variations of the dielectric permeability in real experiments. The idea of using laser beams passing through a material with nonlinear optical properties was put forward in references [81,91], while concrete experimental schemes were proposed two decades later [98,99,100,101]. The experiment based on the suggestion [99] was realized recently [102] for the infrared light. An evaluation of a possibility to obtain parametric amplification of the microwave vacuum field, using a reentrant cavity enclosing a nonlinear crystal with a strong third-order nonlinearity, whose refractive index is modulated by near-infrared high-intensity laser pulses, was performed in reference [103]. Several new proposals were published recently in papers [104,105,106].
Analogs of the DCE in Bose–Einstein condensates and ultracold gases with time-dependent parameters were considered in references [107,108,109,110,111,112]. An obvious advantage of replacing EM waves with their sound analogs is the possibility of achieving high ratios of effective velocities to the sound speed, including the supersonic regimes. The use of plasmon resonances in metallic nanoparticles surrounded by an amplifying medium, excited by femtosecond lasers, was suggested in reference [113]. The DCE with polaritons was studied in references [114,115,116]. The DCE for phonons was considered in references [117,118,119]. Very exciting applications of the DCE to space flights were discussed in reference [120].
5. Conclusions
The field of Casimir and van der Waals physics has experienced new ideas and developments, which to a large degree, have been motivated by discoveries of many new materials. Systems with topologically nontrivial properties have served as fruitful platforms to bridge concepts between condensed matter and high energy physics and bring forward our understanding of Dirac-like phenomena in light-matter interactions, such as the Casimir and van der Waals forces. In this Perspective, we show that there are promising but limited studies of the role of nonlinear optical properties in the context of Casimir physics. We argue that many new materials have much enhanced nonlinear optical response, which should be explored by the scientific community as effective means to control this type of universal interaction. Nonlinear optical media are also of great importance for the dynamical Casimir effect, which potentially can be used to generate photons from a vacuum. New research in this direction also promises further to broaden the basic understanding of this interesting phenomenon.
Author Contributions
Conceptualization, L.M.W.; Writing, review & editing: L.M.W., M.K., and V.V.D. All authors have read and agreed to the published version of the manuscript.
Funding
L.M.W. acknowledges funding from the US Department of Energy under Grant No. DE-FG02-06ER46297.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Woods, L.M.; Dalvit, D.A.R.; Tkatchenko, A.; Rodriguez-Lopez, P.; Rodriguez, A.W.; Podgornik, R. Materials perspective on Casimir and van der Waals interactions. Rev. Mod. Phys. 2016, 88, 045003. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827. [Google Scholar] [CrossRef]
- Barcenas, J.; Reyes, L.; Esquivel-Sirvent, R. Scaling of micro- and nanodevices actuated by Casimir forces. Appl. Phys. Lett. 2005, 87, 263106. [Google Scholar] [CrossRef]
- Duong, D.L.; Yun, S.J.; Lee, Y.H. Van der Waals layered materials: Opportunities and challenges. ACS Nano 2017, 11, 11803. [Google Scholar] [CrossRef]
- Hermann, J.; DiStasio, R.A., Jr.; Tkatchenko, A. First-principles models for van der Waals interactions in molecules and materials: Concepts, theory, and applications. Chem. Rev. 2017, 117, 4714. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Wehling, T.O.; Black-Schaffer, A.M.; Balatsky, A.V. Dirac materials. Adv. Phys. 2014, 63, 1–76. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Wen, X.; Gong, Z.; Li, D. Nonlinear optics of two-dimensional transition metals dichalcogenides. InfoMat 2019, 1, 317. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, Y.; Koepernik, K.; Shi, W.; van der Brink, J.; Felser, C.; Sun, Y. Comprehensive scan for nonmagnetic Weyl semimetals with nonlinear optical response. NPJ Comp. Mater. 2020, 32, 1–7. [Google Scholar] [CrossRef]
- Wu, L.; Patankar, S.; Morimoto, T.; Nair, N.L.; Thewalt, E.; Little, A.; Analytis, J.G.; Moore, J.E.; Ornstein, J. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetal. Nat. Phys. 2017, 13, 350. [Google Scholar] [CrossRef]
- De Huan, F.; Grushin, A.G.; Morimoto, T.; Moore, J.E. Quantized circular photogalvanic effect in Weyl semimetals. Nat. Comm. 2017, 8, 15995. [Google Scholar]
- Moore, G.T. Quantum theory of the electromagnetic field in a variable-length one-dimensional cavity. J. Math. Phys. 1970, 11, 2679. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Moore, J.E. Three-dimensional topological insulators. Annu. Rev. Condens. Matter Phys. 2011, 2, 55. [Google Scholar] [CrossRef]
- Qi, X.-L.; Li, R.; Zang, J.; Zhang, S.-C. Inducing a magnetic monopole with topological surface states. Science 2009, 323, 1184. [Google Scholar] [CrossRef]
- Grushin, A.G.; Cortijo, A. Tunable casimir repulsion with three-dimensional topological insulators. Phys. Rev. Lett. 2011, 106, 020403. [Google Scholar] [CrossRef]
- Grushin, A.G.; Rodriguez-Lopez, P.; Cortijo, A. Effect of finite temperature and uniaxial anisotropy on the Casimir effect with three-dimensional topological insulators. Phys. Rev. B 2011, 84, 045119. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P. Casimir repulsion between topological insulators in the diluted regime. Phys. Rev. B 2011, 84, 165409. [Google Scholar] [CrossRef]
- Nie, W.; Zeng, R.; Lan, Y.; Zhu, S. Casimir force between topological insulator slabs. Phys. Rev. B 2013, 88, 085412. [Google Scholar] [CrossRef]
- Lu, B.-S. Van der Waals torque and force between anisotropic topological insulator slabs. Phys. Rev. B 2018, 97, 045427. [Google Scholar] [CrossRef]
- Zeng, R.; Chen, L.; Nie, W.J.; Ni, M.H.; Yang, Y.P.; Zhu, S.Y. Enhancing Casimir repulsion via topological insulator multilayers. Phys. Lett. A 2016, 380, 2861. [Google Scholar] [CrossRef]
- Martin-Ruiz, A.; Urrutia, L.F. Interaction of a hydrogenlike ion with a planar topological insulator. Phys. Rev. A 2018, 97, 022502. [Google Scholar] [CrossRef]
- Li, L.L.; Peeters, F.M. Optical conductivity of topological insulator thin films. J. Appl. Phys. 2015, 117, 175305. [Google Scholar] [CrossRef]
- Li, Z.; Carbotte, J.P. Magneto-optical conductivity in a topological insulator. Phys. Rev. B 2013, 88, 045414. [Google Scholar] [CrossRef]
- Rahim, K.; Ullah, A.; Tahir, M.; Sabeeh, K. Magneto-optical properties of topological insulator thin films with broken inversion symmetry. J. Phys. Condens. Matter 2017, 29, 425304. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M. Model for a quantum Hall effect without landau levels: Condensed matter realization of the “Parity Anomaly”. Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef]
- Tang, E.; Mei, J.-W.; Wen, X.-G. High-temperature fractional Quantum Hall States. Phys. Rev. Lett. 2011, 106, 236802. [Google Scholar] [CrossRef]
- Verberos, J.W.F.; Kourtis, S.; van der Brink, J.; Daghofer, M. Fractional quantum-hall liquid spontaneously generated by strongly correlated t2g electrons. Phys. Rev. Lett. 2012, 108, 125405. [Google Scholar]
- Rachel, S. Interacting topological insulators: A review. Rep. Prog. Phys. 2018, 81, 116501. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Grushin, A. Repulsive Casimir effect with Chern insulators. Phys. Rev. Lett. 2014, 112, 056804. [Google Scholar] [CrossRef] [PubMed]
- Fialkovsky, N.K.; Vassilevich, D. Quest for Casimir repulsion between Chern-Simons surfaces. Phys. Rev. B 2018, 97, 165432. [Google Scholar] [CrossRef]
- Vassilevich, D. On the (im) possibility of Casimir repulsion between Chern-Simons surfaces. Mod. Phys. Lett. A 2020, 35, 2040017. [Google Scholar] [CrossRef]
- Marachevsky, V.N. Casimir effect for Chern-Simons layers in the vacuum. Theor. Math. Phys. 2017, 190, 315. [Google Scholar] [CrossRef]
- Marachevsky, V.N. Casimir interaction of two dielectric half spaces with Chern-Simons boundary layers. Phys. Rev. B 2019, 99, 075420. [Google Scholar] [CrossRef]
- Marachevsky, V.N. Chern-Simons boundary layers in the Casimir effect. Mod. Phys. Lett. A 2020, 35, 2040015. [Google Scholar] [CrossRef]
- Marachevsky, V.N.; Pis’mak, Y.M. Casimir-Polder effect for a plane with Chern-Simons interaction. Phys. Rev. D 2010, 81, 065005. [Google Scholar] [CrossRef]
- Vogt, P.; de Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Arsenio, M.C.; Resta, A.; Ealet, B.; le Lay, G. Silicene: Compelling experimental evidence for graphene-like two-dimensional silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef]
- Da’vila, M.E.; Xian, L.; Cahangirov, S.; Rubio, A.; Lay, G.L. Germanene: A novel two-dimensional germanium allotrope akin to graphene and silicene. New J. Phys. 2014, 16, 095002. [Google Scholar] [CrossRef]
- Zhu, F.-F.; Chen, W.-J.; Gao, C.-L.; Guan, D.-D.; Liu, C.-H.; Qian, D.; Zhang, S.-C.; Jia, J.-F. Epitaxial growth of two-dimensional stanene. Nat. Mater. 2015, 14, 1020–1026. [Google Scholar] [CrossRef]
- Ezawa, M. Photoinduced topological phase transition and a single Dirac-cone state in silicene. Phys. Rev. Lett. 2013, 110, 026603. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Lopez, P.; Kort-Kamp, W.J.M.; Dalvit, D.A.R.; Woods, L.M. Casimir force phase transitions in the graphene family. Nat. Comm. 2017, 8, 14699. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Santos, G. Thermal van der Waals interaction between graphene layers. Phys. Rev. B 2009, 80, 245424. [Google Scholar] [CrossRef]
- Drosdoff, D.; Woods, L.M. Casimir forces and graphene sheets. Phys. Rev. B 2010, 82, 155459. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M. Thermal Casimir effect in the interaction of graphene with dielectric and metals. Phys. Rev. B 2012, 86, 165429. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Kort-Kamp, W.J.M.; Dalvit, D.A.R.; Woods, L.M. Nonlocal optical response in topological phase transitions in the graphene family. Phys. Rev. Mater. 2018, 2, 014003. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sernelius, B.E. Two approaches for describing the Casimir interaction in graphene: Density-density correlation function versus polarization tensor. Phys. Rev. B 2014, 89, 125407. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Theory of the Casimir interaction from graphene-coated substrates using the polarization tensor and comparison with experiment. Phys. Rev. B 2014, 89, 115419. [Google Scholar] [CrossRef]
- Fialkovsky, V.; Marachevsky, N.; Vassilevich, D.V. Finite-temperature Casimir effect for graphene. Phys. Rev. B 2011, 84, 035446. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Casmir effect for a stack of conductive planes. Phys. Rev. D 2015, 92, 045002. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Thermal Casimir and Casimir-Polder effects in N parallel 2D Dirac materials. 2D Mater. 2018, 5, 035032. [Google Scholar] [CrossRef]
- Henkel, C.; Klimchitskaya, G.L.; Mostepanenko, V.M. Influence of the chemical potential on the Casimir-Polder interaction between an atom and gapped graphene or graphene-coated substrate. Phys. Rev. A 2018, 97, 032504. [Google Scholar] [CrossRef]
- Cycne, T.; Kort-Kamp, W.J.M.; Oliver, D.; Pinheiro, F.A.; Rosa, F.S.S.; Farina, C. Tuning the Casimir-Polder interaction via magneto-optical effects in graphene. Phys. Rev. A 2014, 90, 052511. [Google Scholar]
- Drosdoff, D.; Bondarev, I.V.; Widom, A.; Podgornik, R.; Woods, L.M. Charge induced fluctuation forces in graphitic nanostructures. Phys. Rev. X 2016, 6, 011004. [Google Scholar] [CrossRef]
- Li, M.S.; Reimers, J.R.; Dobson, J.F.; Gould, T. Faraday cage screening reveals intrinsic aspects of the van der Waals attraction. Proc. Natl. Acad. Sci. USA 2018, 115, E10295. [Google Scholar] [CrossRef]
- Farias, M.B.; Kort-Kamp, W.J.M.; Dalvit, D.A.R. Quantum friction in two-dimensional topological materials. Phys. Rev. B 2018, 97, 161407. [Google Scholar] [CrossRef]
- Tabert, C.J.; Carbotte, J.P. Optical conductivity of Weyl semimetals and signatures of the gapped semimetal phase transition. Phys. Rev. B 2016, 93, 085442. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Popescu, A.; Fialkovsky, I.; Khusnutdinov, N.; Woods, L.M. Signatures of complex optical response in Casimir interactions of type I and II Weyl semimetals. Comm. Mater. 2020, 1, 14. [Google Scholar] [CrossRef]
- Wilson, J.H.; Allocca, A.A.; Galistki, V. Repulsive casimir force between Weyl semimetals. Phys. Rev. B 2015, 91, 235115. [Google Scholar] [CrossRef]
- Farias, M.B.; Zyuzin, A.Z.; Schmidt, T.L. Casimir force between Weyl semimetals in a chiral medium. Phys. Rev. B 2020, 101, 235446. [Google Scholar] [CrossRef]
- Jiang, Q.-D.; Wilczek, F. Chiral Casimir force: Repulsive, enhanced, tunable. Phys. Rev. B 2019, 99, 125403. [Google Scholar] [CrossRef]
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of optical harmonics. Phys. Rev. Lett. 1961, 7, 118. [Google Scholar] [CrossRef]
- You, J.-S.; Fang, S.; Xu, S.-Y.; Kaxiras, E.; Low, T. Berry curvature dipole current in the transition metal dichalcogenide family. Phys. Rev. B 2018, 98, 121109. [Google Scholar] [CrossRef]
- Rostami, H.; Polini, M. Nonlinear anomalous photocurrents in Weyl semiemtals. Phys. Rev. B 2018, 97, 195151. [Google Scholar] [CrossRef]
- Drummond, P.D. Electromagnetic quantization in dispersive inhomogeneous nonlinear dielectrics. Phys. Rev. A 1990, 42, 6845. [Google Scholar] [CrossRef]
- Scheel, S.; Welsch, D.G. Quantum theory of light and noise polarization in nonlinear optics. Phys. Rev. Lett. 2006, 96, 073601. [Google Scholar] [CrossRef]
- Kysylychyn, D.; Piatnytsia, V.; Lozovski, V. Electrodynamical interaction between a nanoparticle and the surface of a solid. Phys. Rev. E 2013, 88, 052403. [Google Scholar] [CrossRef]
- Makhnovets, K.; Kolezhuk, A. On short-range enhancement of Van-der-Waals forces. Materwiss. Werksttech. 2016, 47, 222. [Google Scholar] [CrossRef]
- Soo, H.; Dean, D.S.; Krüger, M. Particles with nonlinear electric response: Suppressing van der Waals forces by an external field. Phys. Rev. E 2017, 95, 012151. [Google Scholar] [CrossRef]
- Soo, H.; Krüger, M. Fluctuational electrodynamics for nonlinear media. Eur. Lett. 2016, 115, 41002. [Google Scholar] [CrossRef][Green Version]
- Soo, H.; Krüger, M. Fluctuational electrodynamics for nonlinear materials in and out of thermal equilibrium. Phys. Rev. B 2017, 97, 045412. [Google Scholar] [CrossRef]
- Karvonen, L.; Rönn, J.; Kujala, S.; Chen, Y.; Säynätjoki, A.; Tervonen, A.; Svirko, Y.; Honkanen, S. High non-resonant third-order optical nonlinearity of Ag-glass nanocomposite fabricated by two-step ion exchange. Opt. Mater. 2013, 36, 328. [Google Scholar] [CrossRef]
- Kheirandish, F.; Amooghorban, E.; Soltani, M. Finite-temperature Casimir effect in the presence of nonlinear dielectrics. Phys. Rev. A 2011, 83, 032507. [Google Scholar] [CrossRef]
- Khandekar, F.; Pick, A.; Johnson, S.G.; Rodriguez, A.W. Radiative heat thermal transfer in nonlinear Kerr media. Phys. Rev. B 2015, 91, 115406. [Google Scholar] [CrossRef]
- Khandekar, C.; Rodriguez, A.W. Near-field thermal upconversion and energy transfer through a Kerr medium. Opt. Express 2017, 25, 23164. [Google Scholar] [CrossRef]
- Neto, P.A.M.; Machado, L.A.S. Quantum radiation generated by a moving mirror in free space. Phys. Rev. A 1996, 54, 3420. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Klimov, A.B. Generation and detection of photons in a cavity with a resonantly oscillating boundary. Phys. Rev. A 1996, 53, 2664. [Google Scholar] [CrossRef]
- Lambrecht, A.; Jaekel, M.T.; Reynaud, S. Motion induced radiation from a vibrating cavity. Phys. Rev. Lett. 1996, 77, 615. [Google Scholar] [CrossRef]
- Crocce, M.; Dalvit, D.A.R.; Mazzitelli, F.D. Resonant photon creation in a three-dimensional oscillating cavity. Phys. Rev. A 2001, 64, 013808. [Google Scholar] [CrossRef]
- Uhlmann, M.; Plunien, G.; Schützhold, R.; Soff, G. Resonant cavity photon creation via the dynamical Casimir effect. Phys. Rev. Lett. 2004, 93, 193601. [Google Scholar] [CrossRef]
- Yablonovitch, E. Accelerating reference frame for electromagnetic waves in a rapidly growing plasma: Unruh-Davies-Fulling-De Witt radiation and the nonadiabatic Casimir effect. Phys. Rev. Lett. 1989, 62, 1742. [Google Scholar] [CrossRef]
- Srivastava, Y.; Widom, A. Quantum electrodynamic processes in electrical engineering circuits. Phys. Rep. 1987, 148, 1–65. [Google Scholar] [CrossRef]
- Segev, E.; Abdo, B.; Shtempluck, O.; Buks, E.; Yurke, B. Prospects of employing superconducting stripline resonators for studying the dynamical Casimir effect experimentally. Phys. Lett. A 2007, 370, 202. [Google Scholar] [CrossRef][Green Version]
- Fuji, T.; Matsuo, S.; Hatakenaka, N.; Kurihara, S.; Zeilinger, A. Quantum circuit analog of the dynamical Casimir effect. Phys. Rev. B 2011, 84, 174521. [Google Scholar] [CrossRef]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Nat. Acad. Sci. 2013, 110, 4234. [Google Scholar] [CrossRef]
- Johansson, J.R.; Johansson, G.; Wilson, C.M.; Delsing, P.; Nori, F. Nonclassical microwave radiation from the dynamical Casimir effect. Phys. Rev. A 2013, 87, 043804. [Google Scholar] [CrossRef]
- Nation, P.D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Colloquium: Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1. [Google Scholar] [CrossRef]
- Nation, P.D.; Suh, J.; Blencowe, M.P. Ultrastrong optomechanics incorporating the dynamical Casimir effect. Phys. Rev. A 2016, 93, 022510. [Google Scholar] [CrossRef]
- Wustmann, W.; Shumeiko, V. Parametric effects in circuit quantum electrodynamics. Low Temp. Phys. 2019, 45, 848. [Google Scholar] [CrossRef]
- Dodonov, V.V. Fifty years of the dynamical Casimir effect. Physics 2020, 2, 67. [Google Scholar] [CrossRef]
- Yablonovitch, E.; Heritage, J.P.; Aspnes, D.E.; Yafet, Y. Virtual photoconductivity. Phys. Rev. Lett. 1989, 63, 976. [Google Scholar] [CrossRef]
- Okushima, T.; Shimizu, A. Photon emission from a false vacuum of semiconductors. Jpn. J. Appl. Phys. 1995, 34, 4508. [Google Scholar] [CrossRef]
- Lozovik, Y.E.; Tsvetus, V.G.; Vinogradov, E.A. Parametric excitation of vacuum by use of femtosecond laser pulses. Phys. Scr. 1995, 52, 184. [Google Scholar] [CrossRef]
- Braggio, C.; Bressi, G.; Carugno, G.; del Noce, C.; Galeazzi, G.; Lombardi, A.; Palmieri, A.; Ruoso, G.; Zanello, D. A novel experimental approach for the detection of the dynamic Casimir effect. Eur. Lett. 2005, 70, 754. [Google Scholar] [CrossRef][Green Version]
- Agnesi, A.; Braggio, C.; Carugno, G.; della Valle, F.; Galeazzi, G.; Messineo, G.; Pirzio, F.; Reali, G.; Ruoso, G. A laser system for the parametric amplification of electromagnetic fields in a microwave cavity. Rev. Sci. Instr. 2011, 82, 115107. [Google Scholar] [CrossRef]
- Kim, W.-J.; Brownell, J.H.; Onofrio, R. Comment on ‘Novel experimental approach for the detection of the dynamical Casimir effect’ by C. Braggio et al. EPL Europhys. Lett. 2007, 78, 21002. [Google Scholar] [CrossRef]
- Hagenmüller, D. All-optical dynamical Casimir effect in a three-dimensional terahertz photonic band gap. Phys. Rev. B 2016, 93, 235309. [Google Scholar] [CrossRef]
- Dezael, F.X.; Lambrecht, A. Analogue Casimir radiation using an optical parametric oscillator. EPL Europhys. Lett. 2010, 89, 14001. [Google Scholar] [CrossRef][Green Version]
- Faccio, D.; Carusotto, I. Dynamical Casimir effect in optically modulated cavities. EPL Europhys. Lett. 2011, 96, 24006. [Google Scholar] [CrossRef][Green Version]
- Hizhnyakov, V.; Kaasik, H.; Tehver, I. Spontaneous nonparametric down-conversion of light. Appl. Phys. A 2014, 115, 563. [Google Scholar] [CrossRef]
- Hizhnyakov, V.; Loot, A.; Azizabadi, S.C. Enhanced dynamical Casimir effect for surface and guided waves. Appl. Phys. A 2016, 122, 333. [Google Scholar] [CrossRef]
- Vezzoli, S.; Mussot, A.; Westerberg, N.; Kudlinski, A.; Saleh, H.D.; Prain, A.; Biancalana, F.; Lantz, E.; Faccio, D. Optical analogue of the dynamical Casimir effect in a dispersion-oscillating fibre. Comm. Phys. 2019, 2, 84. [Google Scholar] [CrossRef]
- Braggio, C.; Carugno, G.; Borghesani, A.F.; Dodonov, V.V.; Pirzio, F.; Ruoso, G. Generation of microwave fields in cavities with laser-excited nonlinear media: Competition between the second- and third-order optical nonlinearities. J. Opt. 2018, 20, 095502. [Google Scholar] [CrossRef]
- Sanz, M.; Wieczorek, W.; Groblacher, S.; Solano, E. Electro-mechanical Casimir effect. Quantum 2018, 2, 91. [Google Scholar] [CrossRef]
- Wang, H.; Blencowe, M.P.; Wilson, C.M.; Rimberg, A.J. Mechanically generating entangled photons from the vacuum: A microwave circuit-acoustic resonator analog of the oscillatory Unruh effect. Phys. Rev. A 2019, 99, 053833. [Google Scholar] [CrossRef]
- Qin, W.; Macrì, V.; Miranowicz, A.; Savasta, S.; Nori, F. Emission of photon pairs by mechanical stimulation of the squeezed vacuum. Phys. Rev. A 2019, 100, 062501. [Google Scholar] [CrossRef]
- Carusotto, I.; Balbinot, R.; Fabbri, A.; Recati, A. Density correlations and analog dynamical Casimir emission of Bogoliubov phonons in modulated atomic Bose-Einstein condensates. Eur. Phys. J. D 2010, 56, 391. [Google Scholar] [CrossRef]
- Jaskula, J.-C.; Partridge, G.B.; Bonneau, M.; Lopes, R.; Ruaudel, J.; Boiron, D.; Westbrook, C.I. Acoustic analog to the dynamical Casimir effect in a Bose-Einstein condensate. Phys. Rev. Lett. 2012, 109, 220401. [Google Scholar] [CrossRef]
- Balbinot, R.; Fabbri, A. Amplifying the Hawking signal in BECs. Adv. High. Energy Phys. 2014, 2014, 713574. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Mendonca, J.T. Dynamical Casimir effect in ultra-cold matter with a time-dependent effective charge. Phys. Scr. 2014, T160, 014008. [Google Scholar] [CrossRef]
- Eckel, S.; Kumar, A.; Jacobson, T.; Spielman, I.B.; Campbell, G.K. A rapidly expanding Bose-Einstein condensate: An expanding universe in the lab. Phys. Rev. X 2018, 8, 021021. [Google Scholar] [CrossRef] [PubMed]
- Michael, M.H.; Schmiedmayer, J.; Demler, E. From the moving piston to the dynamical Casimir effect: Explorations with shaken condensates. Phys. Rev. A 2019, 99, 053615. [Google Scholar] [CrossRef]
- Lawandy, N.M. Scattering of vacuum states by dynamic plasmon singularities: Generating photons from vacuum. Opt. Lett. 2006, 31, 3650. [Google Scholar] [CrossRef]
- Ciuti, C.; Bastard, G.; Carusotto, I. Quantum vacuum properties of the intersubband cavity polariton field. Phys. Rev. B 2005, 72, 115303. [Google Scholar] [CrossRef]
- Koghee, S.; Wouters, M. Dynamical Casimir emission from polariton condensates. Phys. Rev. Lett. 2014, 112, 036406. [Google Scholar] [CrossRef] [PubMed]
- Hizhnyakov, V.; Loot, A.; Azizabadi, S.C. Dynamical Casimir effect for surface plasmon polaritons. Phys. Lett. A 2015, 379, 501. [Google Scholar] [CrossRef]
- Naylor, W. Vacuum-excited surface plasmon polaritons. Phys. Rev. A 2015, 91, 053804. [Google Scholar] [CrossRef]
- Wang, X.; Qin, W.; Miranowicz, A.; Savasta, S.; Nori, F. Unconventional cavity optomechanics: Nonlinear control of phonons in the acoustic quantum vacuum. Phys. Rev. A 2019, 100, 063827. [Google Scholar] [CrossRef]
- Wittemer, M.; Hakelberg, F.; Kiefer, P.; Schröder, J.-P.; Fey, C.; Schützhold, R.; Warring, U.; Schaetz, T. Phonon pair creation by inflating quantum fluctuations in an ion trap. Phys. Rev. Lett. 2019, 123, 180502. [Google Scholar] [CrossRef]
- Maclay, G.J.; Forward, R.L. A Gedanken spacecraft that operates using the quantum vacuum (dynamic Casimir effect). Found. Phys. 2004, 34, 477. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).