Abstract
Functional connectivity analysis aims at assessing the strength of functional coupling between the signal responses in distinct brain areas. Usually, functional magnetic resonance imaging (fMRI) time series connections are estimated through zero-lag correlation metrics that quantify the statistical similarity between pairs of regions or spectral measures that assess synchronization at a frequency band of interest. Here, we explored the application of a new metric to assess the functional synchronization in phase space between fMRI time series in a resting state. We applied a complete topological analysis to the resulting connectivity matrix to uncover both the macro-scale organization of the brain and detect the most important nodes. The synchronization metric is also compared with Pearson’s correlation coefficient and spectral coherence to highlight similarities and differences between the topologies of the three functional networks. We found that the individual topological organization of the resulting synchronization-based connectivity networks shows a finer modular organization than that identified with the other two metrics and a low overlap with the modular partitions of the other two networks suggesting that the derived topological information is not redundant and could be potentially integrated to provide a multi-scale description of functional connectivity.
1. Introduction
A wide range of biological phenomena are characterized by synchronization of systems whose complex cooperation and integration explain the emergence of vital functions [1]. Several synchronization metrics have been introduced to quantify the coupling behavior of interacting dynamic systems [2,3]. In particular, there has been a growing body of literature addressing the application of complex network analysis for the characterization of dynamical systems based on time series. These combined approaches have clarified fundamental issues about the organization of nonlinear dynamics in different fields. As an example, the complex and nonlinear nature of brain dynamics is widely discussed in the literature [4,5,6]. The human brain is modeled as a complex network composed of anatomical and functional sub-systems whose interactions allow the performance of both high- and low-level cognitive functions. Such interactions have been extensively modeled through the mathematical framework of the complex networks, which allows the treating of each subsystem as a node of a network and to identify specific topological properties of nodes and links in the network [7,8]. Topological data analysis have been largely applied to investigate the architecture of brain networks and connectivity differences between individuals at several levels of the data hierarchy [9,10,11]. These techniques can be applied both to functional data, which describe the dynamic brain activity through functional magnetic resonance imaging (fMRI) or electrophysiological acquisitions [12,13]. In particular, over the past decade, there has been an increasing interest in inferring connectivity properties from fMRI data [14,15]. Functional connectivity (FC) analysis aims at assessing the strength of functional coupling between the signal responses in distinct brain areas [16]. According to the complex network framework, the anatomical regions of interest are modeled as the nodes of the network, linked by edges resulting from the selected synchronization metric. Pairwise Blood oxygenation level dependent (BOLD) time series connections can be estimated through different metrics including cross-correlation, cross-coherence and causal modeling [17]. Each FC metric quantifies different forms of dependency between the BOLD signals: zero-lag correlation metrics quantify the statistical similarity between pairs of region, other metrics assess synchronization at frequency band of interest [18,19], others capture direct coupling between time series [20,21].
Recently, new metrics to assess the coupling behavior of BOLD time series have been introduced to capture both linear and nonlinear interactions in human brain. In particular, a generalized synchronization index (SYNC) has been proposed to assess the functional connectivity with fMRI data [22,23]. Such metric has been proven effective in detecting active sub-networks during a high-level cognitive process, describing age-related functional patterns [24] and identifying and quantifying pathological states [25].
The analyses of functional brain connectivity in the state of rest have revealed different modular configurations of the brain activity, which reflect specific functions and varied spatial topologies [26]. Moreover, the role of specific regions acting as network hubs for the efficient functioning of the human brain has been extensively documented [27,28]. Brain hubs facilitate the integration of functionally specialized neural systems by supporting long-range connections [29,30] and by routing a large amount of neural information [31]. The dysfunction of some brain hubs has been also related to pathological conditions and psychiatric disorders [32,33].
In this work, we performed a comparison of the synchronization connectivity pattern derived from the SYNC metric, statistical Pearson correlation and spectral coherence functional connectivity. In particular, we exploited the resting state fMRI data of a single subject to construct three functional connectivity networks and explore the topological organization of their macro-scale architectures by means of a modularity analysis. We investigated the topological properties of the most important nodes of the networks to detect stable hubs. Here, the SYNC hub nodes represent regions with a high level of synchronization over the entire time interval with different functional sub-systems. Such nodes differ from the hubs of correlation and coherence networks as statistical correlation is related to the average synchronization level over the observation period, while spectral coherence can identify the frequencies that drive the linear association between the two time courses. One of the principal objectives of this work is to verify whether an overlap of these nodes exists with respect to those identified in the Pearson and coherence networks in order to better elucidate the synchronization index method in functional connectivity analysis. We stress that the main focus of this exploratory analysis is a detailed comparison of the three network topologies concerning their modular organization and the roles of the regions acting as hubs in such modular configurations. Recent precision functional mapping has shown that individual brain organization is qualitatively different from group average estimates and that individuals can exhibit distinct brain network topologies [34,35]. For this reason, we have chosen a single subject-based analysis. Indeed, the individual analysis address a targeted comparison of the regions included in each module and the hub roles between the three functional networks obtained respectively with SYNC metric, Pearson statistical correlation and spectral coherence. We also tested the reliability of the results by analyzing ten scans of the same subjects.
The rest of this paper is structured as follows. In Section 2 a description of the data is provided. In Section 3.1 the analysis of synchronization of dynamic processes in the phase space is described with an illustrative example of the proposed metric. Section 3.2 is devoted to both topological and modularity analysis of fMRI connectivity matrices. In Section 4 the results of the analysis for the SYNC, the Pearson and coherence networks are presented with a discussion on the modular organization and the most important nodes of the three networks and a comparison between them. Finally, the conclusion of the work is presented in Section 5.
2. Materials
fMRI Data
We included ten resting-state baseline fMRI sessions of two subjects (first subject 0025427, sex: male, age: 23 years; second subject 0025432, sex: male, age: 21 years) from the Hangzhou Normal University (HNU) cohort of the Consortium for Reliability and Reproducibility (CoRR) [36]. During functional scanning, subjects of the sample were presented with a fixation cross and were instructed to keep their eyes open, relax and move as little as possible while observing the fixation cross. Subjects were also instructed not to engage in breath counting or meditation. More details about recruitment, inclusion criteria and assessment protocols are available on the project website (http://fcon_1000.projects.nitrc.org/indi/CoRR/html/hnu_1.html).
The data sessions were preprocessed using the configurable pipeline for the analysis of connectomes (CPAC). CPAC preprocessing includes slice time correction, motion correction, skull strip, global mean intensity normalization and nuisance signal regression with 24-motion parameters, signals from white matter (WM) and cerebrospinal fluid (CSF), and linear and quadratic low-frequency drifts. After band-pass filtering (– Hz), the brain volume of each session was divided in 116 non-overlapping anatomical regions of interest according to the AAL Atlas [37] and the average fMRI time series of each ROI was collected, obtaining 116 time series for each session.
3. Methods
Functional synchronization connectivity between all pairwise combinations of ROI time series was assessed by estimating their cross-recurrence plots (CRP) and then by calculating the SYNC index as detailed in Section 3.1 resulting in a weighted connectivity matrix for each fMRI session. We also computed the correlation between each couple of time series by means of the Pearson correlation coefficient and the coherence metric, resulting in a Pearson connectivity matrix and a coherence connectivity matrix. We performed a modularity analysis to determine the most representative community structure of each functional network across sections and compare them as explained in Section 3.2.1. Finally, we investigated the topological roles of the most important hubs in each connectivity networks to verify the overlap across the three networks as reported in Section 3.2.2. We repeated the same processing steps and analysis on another subject of the same dataset whose results are included in Supplementary Materials file
3.1. Synchronization in Phase Space
A system could be represented in the phase space, i.e., a topological representation of its behavior under different initial conditions. This method assumes that each signal represents a projection of a higher-dimensional dynamical system evolving in time, whose trajectories are embedded into a manifold, i.e., a region of its phase space. The phase space of a system could be reconstructed by means of the Takens’s Theorem [38]. For a generic single temporal observation of a system , the trajectory is expressed as:
where m is the embedding dimension and is the time delay. Both parameters must be properly selected to avoid redundancy in the phase space. The dimension m of the reconstructed phase space should be large enough to preserve the properties of the dynamical system: , where D is the correlation dimension of the original phase space. The correct time delay should be chosen by determining when the samples of the time series are independent enough to be useful as coordinates of the time delayed vectors. For the estimation of the embedded parameters m and several techniques have been proposed. As an example, the first local minimum of average mutual information algorithm [39] can be used to select the proper time delay. The minimum embedding dimension is usually estimated through the false nearest neighbors (FNN) algorithm [40].
After the reconstruction of the dynamic trajectories of the two systems in the phase space, it is possible to quantify their interacting behavior by projecting the phase space into the bidimensional cross-recurrence plots (CRPs) [41]:
where is the Heaviside function, is a threshold for closeness, N is the number of considered states for each system and the maximum norm function. A CRP represents an effective method to reduce the dimensionality of the phase space and compare the trajectories of the interacting systems as it is a matrix whose entries include information on the degree of closeness of each state of the first system with each state of the second system.
A CRP exhibits characteristic patterns that show local time relationships of the segments of the trajectories of the two interacting systems. As an example, diagonal lines occur when the evolution of the states is similar at different times and their lengths are related to the periods during which the two systems move in similar ways remaining close to each other [42]. The main diagonal of a CRP represents a line of synchronization (LOS), since it implies the identity of the states of the two systems in the same time intervals. The LOS structure can be analyzed to extract information about the synchronization of the two time series [43]. In particular, the presence of LOS suggests that the two time series are fully synchronized, while discontinuities appear when the two signals are not fully synchronized. We defined the synchronization time metric (SYNC) to quantify the mean period during which the two systems are synchronized in order to reflect the dynamical synchronization behavior of the series throughout the observation period [22,25]. SYNC is proportional to the ratio of the sum of the lengths of the subsegments along the LOS to the total number of samples N:
The coupling behavior in phase space can be illustrated by referring to a pair of simple sine waves. We compare the SYNC approach to Pearson correlation coefficient computed as:
where and are the two time series and and denote their sample means.
We also compared the SYNC index to spectral coherence across the low-frequency band (– Hz):
where and are the power spectrums of the time series estimated using Welch’s method [44] and is their cross spectrum.
In Figure 1, the CRPs and the extracted LOS are represented for three different cases:
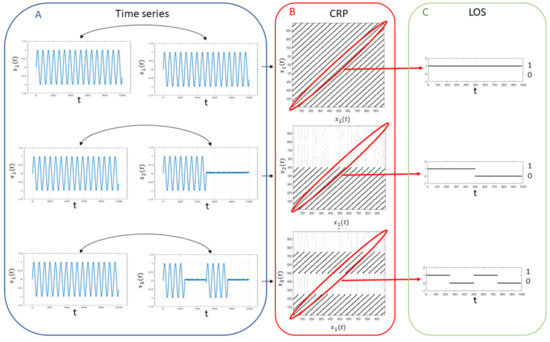
Figure 1.
Example of synchronization quantification: for two fully synchronized sine waves (top panel A), two sine waves synchronized for half of the observational period (middle panel A) and two sine waves synchronized in intermittent way (bottom panel A), the CRPs are computed by using the Takens’ theorem (panel B) and the LOS is extracted from each plot (panel C) in order to assess the SYNC index.
- a sine wave synchronized with itself throughout the observation period 0–T;
- a sine wave and a second sine wave fully synchronized during half of the observation period 0–;
- a sine wave and a second intermittently synchronized sine wave during a first observation interval 0– and a second observation interval –.
For the first case, , and , since the LOS is complete. For the second case , and , while for the third case , and . The Person correlation measures the overall statistical similarity between the two time series, the coherence metric measures their linear relationship in the frequency domain while the SYNC metric takes into account also the intermittency.
3.2. Analysis of fMRI Synchronization-Based Connectivity
3.2.1. Identification and Analysis of Functional Modules
Louvain algorithm [45] has been used to find communities of ROIs in the three functional networks obtaining three partitions for each fMRI session. This method aims at maximizing a modularity metric that evaluates the quality of a partition by comparing the density of connections within a community to that expected in a random network. This algorithm optimizes the modularity function defined as:
where is the edge weight between i and j, is the sum of the weights of the links attached to node i, is the community assigned to the node i, m is the sum of all of the links of the networks and if and if .
An overview of the analysis is shown in Figure 2. To select the best resolution value, the algorithm was applied for . We performed 1000 iterations of the Louvain algorithm for each value of . Finally, we selected the value corresponding to the maximum Q value averaged over the 1000 partitions. This procedure returns a robust resolution index value, but also a set of different partitions corresponding to the optimal value. To identify the most representative community partition, we applied a consensus algorithm. This approach removes the statistical fluctuations of the modularity algorithm and provides a stable output, as well as identifying only one partition for each network [46].
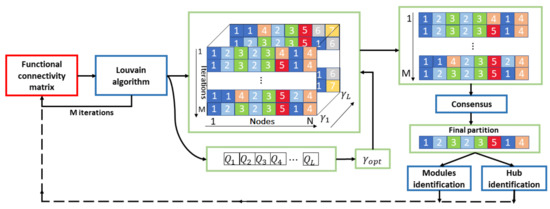
Figure 2.
Flowchart of the modularity analysis. The Louvain algorithm is applied for iterations to each functional connectivity matrix for different values of . is the resolution value corresponding to the maximum Q value averaged over the M partitions. This procedure returns a set of different partitions corresponding to the optimal value. Hence, a consensus algorithm is applied to identify the most representative final community partition that is used to identify both the functional modules and the hub nodes of the matrix.
We compared the community partitions resulting from the three networks within each session by using the normalized mutual information (NMI) [47]. For two networks with partitions, respectively, A and B, it is defined as:
where is the mutual information between the two partitions and and are the entropy of A and B. This metric ranges between zero (if and are completely independent) and one (if and are identical).
3.2.2. Identification of Hub Nodes
Two graph metrics have been used to characterize the topological organization of the synchronization-based functional network, Pearson correlation network and coherence network. More specifically, the participation coefficient and within-module degree z score were computed to assess the regional importance of the brain nodes. For a community partition,
- the participation coefficient is defined as:where is the sum of the weighted links attached to i, is the sum of weighted links from i to community s and is the total number of modules. Thus, the participation coefficient quantifies how the links of a node are distributed across modules. A node’s participation coefficient is maximum if it has an equal sum of edge weights to each module in the network. A node’s participation coefficient is 0 if all its links are within a single community.
- the within-module degree z score for each node is computed as:where is the number of links of node i to other nodes in its community , is the average of k over all of the nodes in and is the standard deviation of k in . Thus, the within-module degree z score measures how well-connected node i is to other nodes in the community relative to other nodes in the community.
These graph metrics are often used to capture the centrality of nodes in brain networks and to map regions that act as hubs [48]. Here, we used a cartographic system mapping each node in a plane through the ordered pair of values to identify the connective hubs, i.e., those nodes with higher connection strength and high centrality values [49,50,51]. This cartographic system allows identification through a statistical threshold level, different roles of the nodes in a network. Hub nodes are central nodes, so they are characterized by high z values. In addition, hubs can be divided into three different categories: provincial hubs, i.e., hub nodes with the vast majority of links within their module (lower values of ); connector hubs with many links to most of the other modules and kinless hubs with links homogeneously distributed among all modules (highest values). We used the 25th and 75th percentile of both metrics to divide the plane into nine regions to identify the hubs of the networks. To compare the topologies of the three functional networks across all the sections of the subject, we included into the final three sets only the hubs that appear with a specific role in at least six sessions of each functional connectivity network.
4. Results and Discussions
4.1. Network Structure
The three functional connectivity networks are shown in Figure 3 with the empirical probability distributions of the weights in semi-logarithmic scale. The three matrices are very different form each other: the SYNC network is sparser, with only a small number of entries with high synchronization values. This aspect is also emphasized by the probability distribution which shows a right long-tailed trend, with few outliers between and 1. This finding highlights a fist important difference between the connectivity matrices, i.e., most regions exhibit a very intermittent synchronization behavior, although on average the pairs of ROIs are moderately statistically correlated in time and frequency (median value of Pearson matrix ∼0.3 and median value of coherence matrix ∼0.25). The same results were found for all the sessions of the subjects as reported in Figures SI-1 and SI-2. Additionally, the Wilcoxon rank sum test was used to compare the distributions of each couple of metrics, i.e., SYNC-Pearson, SYNC-coherence, Pearson-coherence within each session. For each comparison we found confirming that the connectivity matrices are statistically different at 5% significance level.
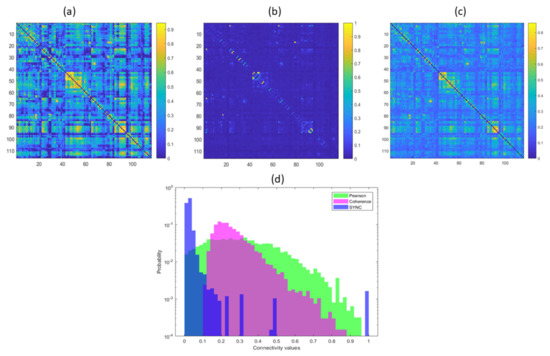
Figure 3.
Pearson correlation matrix (a), SYNC matrix (b) and coherence matrix (c) with the empirical probability distributions of the links of the three matrices in semi-logarithmic scale (d).
4.2. Modularity Analysis
To explore the topological functional organization of the brain regions, the Louvain algorithm was computed 1000 for each network. Figure 4 shows the error bars of modularity index Q over the 1000 iterations of the algorithm for the optimum resolution value . It is worth noting that the modularity index is related to the difference between the within-module interactions and the between-module interactions of a network, so it statistically quantifies the goodness of a network partition into modules [52]. Here, the SYNC network, exhibits a significantly higher value of Q with respect the Pearson and coherence networks for all sessions, pointing out a better hard partition into modules. This result confirms the findings of our previous work in which a modularity analysis was applied to networks defined with both the SYNC index and Pearson’s correlation coefficient of task-related fMRI data [22]. In particular, both a greater Q value and a higher number of functional communities activated during the working memory task were better identified in SYNC networks, while in Pearson’s correlation networks modularity patterns reflecting the working memory load were not detected during the task.
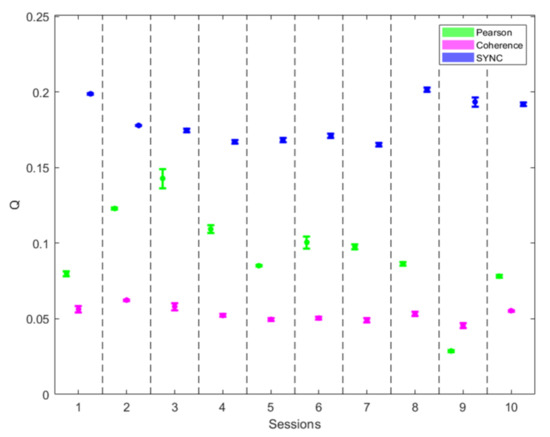
Figure 4.
Error bars (mean and std) of modularity index Q over the 1000 iterations of the algorithm for the optimum resolution value for the three functional networks for all the sessions.
The NMI values reported in Figure 5 highlight that the three partitions are quite different from each other for all the sessions. However, the NMI values between the Pearson and coherence networks are slightly higher, showing a higher degree of agreement between the partitions of these two networks.
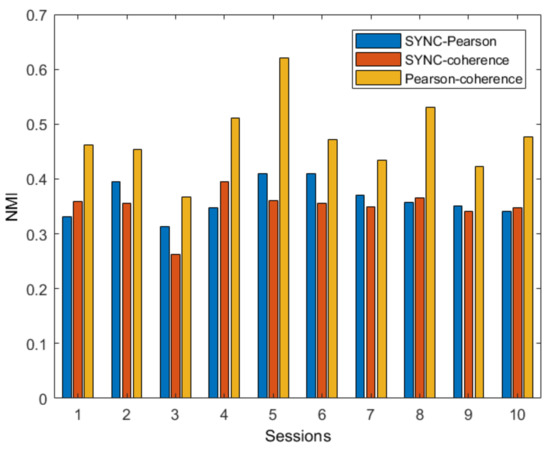
Figure 5.
NMI values resulting from the comparisons between each couple of network partitions for all fMRI sessions of the subject.
Figure 6 shows the most representative network partition across the fMRI session of the subject. Seven modules were detected in the SYNC matrix; the first module comprises areas almost becoming from the cingulate cortex, e.g., cincgulate gyrus, anterior and mid cingulate. Several specialized control areas of frontal regions such as medial orbital superior frontal gyrus are included in the second module. The third module resembles both peripheral and central visual networks as it includes all the occipital lobe, the calcarine fissure and surrounding cortex. The fourth module resulted the largest as it includes all the other regions from the frontoparietal network. The fifth module overlaps with most regions of the cerebellar network; the sixth module includes: superior frontal gyrus, middle temporal gyrus, inferior temporal gyrus and cerebellar crus areas. These modules are equally distributed across the default and control networks previously described in the resting-state literature [53,54]. The seventh is mainly composed by areas from the limbic system such as amygdala and para-hippocampal gyrus.
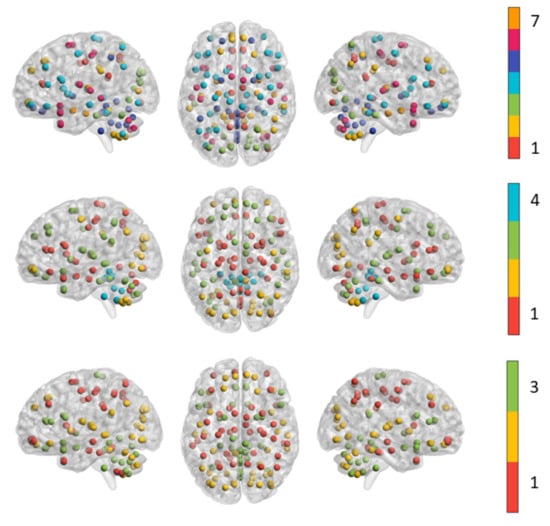
Figure 6.
The functional modules detected in SYNC networks (top panel), Pearson correlation network (middle panel) and coherence network (bottom panel). All the ROIs within the same module are indicated with spheres of the same color.
In contrast, the Pearson and coherence network are composed by only four and three modules, respectively. The first module includes some central structures such as caudate nucleus, putamen and thalamus, the inferior frontal and orbital gyrus and several regions from cerebellar networks. The second module resulted the most specialized as it covers all the occipital lobe and several regions from cerebellar network. Most of the regions from parietal, frontal and temporal lobe are equally distributed across the first and third module. In particular, the third module comprises the cerebellar crus 1 and 2, all the areas of the superior and middle frontal lobe and orbital gyrus. The fourth module resulted the smallest one including most of the regions from cerebellum and vermis.
The first module of the coherence network covers all the parietal lobe and middle frontal areas. The second module includes the areas of the occipital lobe, superior frontal, orbital and temporal regions and the cerebellar crus 1 and 2. Finally, the third module is mainly composed of the cerebellar network, inferior frontal gyrus and sub-cortical regions.
The three network configurations resemble different functional organization of the brain during the resting state. The SYNC network shows very specialized co-synchronized patterns, also including very small modules clearly related to salient control functions of the brain; on the other hand, both Pearson and coherence connectivity capture functional organization at macro-scale highlighting patterns of different degree of average statistical correlation between regions. These findings suggest that the modular organization of the three functional connectivity could be integrated to describe the hierarchical behavior of the multi-scale synchronization between the interacting regions during different cognitive states or conditions.
4.3. Hub Identification
A cartographic system with the statistical thresholds of 25th and 75th percentiles for both distributions of and z was used to identify the hub regions. As an example, in Figure 7 nine sectors of the resulting partitions are shown for the SYNC network related to the first session of the subject together with the distributions of the two topological metrics. The hub regions are confined in the upper part of the plane. In details, kinless hubs, associated with more modules, are localized in the upper right, peripheral hubs with most of the connections within their own module are localized in the upper left side, while the other connector hubs are identified as between these two extreme categories.
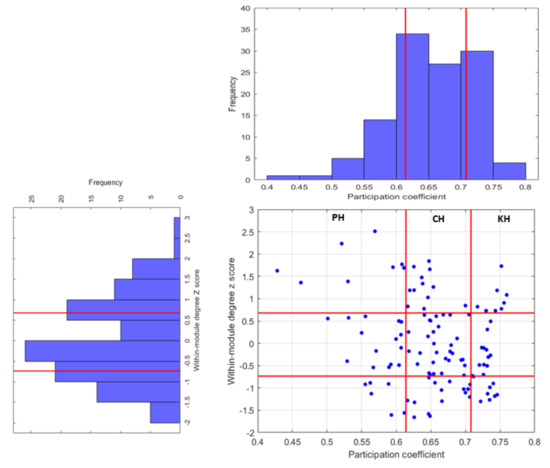
Figure 7.
Cartographic presentation of nodes classification in the SYNC network of the first session. The red lines indicate the 25th and 75th of the two distributions of and z selected as the statistical thresholds to perform the plane partitions.
In Table 1 is reported the complete list of all the regions identifies as hubs with their categories for the three functional networks. It is interesting to note that beyond the specific role designated to each hub in the three network configurations, in the Pearson’s network many connector hubs are located in the temporal lobe, which instead show just two hubs in the SYNC network, while most of the hubs of the coherence are located in the frontal lobe. Several nodes we detected as connector hubs were also identified as integrative nodes in frontal, inferior parietal areas, cingulate and some regions of both default-mode and executive control networks in the adult brain [55,56,57]. In addition, in both SYNC and Pearson networks, the cerebellar crus regions are detected as important hubs, confirming the complex associations among the cerebellar regions and the cerebral cortex captured during the resting state by means of functional connectivity MRI [58].

Table 1.
Abbreviation of hub regions with the macro regions in which they are located and their roles for the three functional connectivity networks.
Another interesting aspect concerns the presence of kinless hubs: such kind of nodes belong to any modules, hence they particularly facilitate the integration of information among the brain areas. These nodes are identified in the upper right side of the plane. However, in many works, advanced methodologies are proposed to identify functional connectivity hubs [59]. In this work, we explored an intuitive approach to depict central and influential nodes in functional connectivity networks. In general, hubs are identified by using consensus scores across several centrality metrics: the nodes with the highest scores on a set centrality measures are usually designated as hubs [60]. However, the level of influence of such nodes depends on the distribution of the metrics used to define hubness. As an example, if the distribution is long-tailed, the network contains a subset of outlier nodes that are considerably more central than others; therefore, they can be considered influential hubs [57]. Here, the range limits for the participation coefficient are defined by simple statistical thresholds, hence these ranges correspond to the extreme values assumed by the coefficient in both networks. Actually, in the literature, a strict definition of the kinless hub role corresponds to . According to many studies, these nodes are almost completely absent in the cortex of primates [60]. As shown in Figure 8, we found lower values of the upper limit of PC in both Pearson and coherence networks in all the sessions, while the SYNC networks exhibit values of corresponding to the formal definition, effectively detecting the presence of highly versatile hub nodes. These results are confirmed in the connectivity analysis of another subject reported in the Supplementary Materials file.
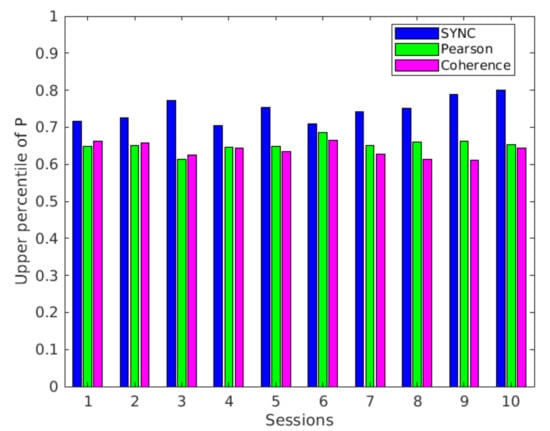
Figure 8.
Upper percentile (75th) of the distribution of participation coefficient P for the three networks and all the fMRI sections.
In summary the three networks showed significant differences among them. First, the modularity analysis showed higher values of modularity index Q in SYNC networks than the other two networks thus indicating a clearer division into communities. Second, the analysis of NMI values highlighted that the three networks showed modular partitions with a low overlap between them (below 50%). The different topological configurations in the three networks were confirmed by the analysis of the hubs, which outlined the presence of different central roles of functional areas. The results suggest that statistical correlation and coherence networks show more evenly distributed synchronization patterns of comparable size in the brain, while SYNC networks exhibit more granular partitions, highlighting more varied synchronization patterns.
5. Conclusions
In this work, we analyzed the topological organization of SYNC-based, Pearson correlation and spectral coherence networks of a single subject. We showed that even if the metrics are mutually linked, the SYNC metric emphasizes the intermittent behavior of the interacting systems showing a greater matrix sparsity. The resulting network topologies were examined to identify the macro-scale modular organization of the nodes and compared to each other. Our analysis revealed some interesting aspects of the structure of SYNC network during resting rest such as the presence of multi-domains highly synchronized brain regions. In addition, the hub nodes of the networks were detected showing only a partial overlap across the three networks. It is important to note that the three measures provide different descriptions of the interaction behaviors between BOLD signals. Indeed the results suggest that the topological information derived from each matrix is not redundant and could be integrated into a multi-view logic to retrieve different information on the interaction and integration of functional sub-systems by using a multilayer connectivity matrix. Future work will explore more in detail the structure of the SYNC connectivity and different features for several tasks and cognitive states in larger populations in order to further elucidate the association between the proposed metric and different synchronization mechanisms in the brain.
Supplementary Materials
The following are available online at https://www.mdpi.com/2076-3417/10/9/3275/s1, Figure SI-1: empirical probability distributions of the links of the three matrices in semi-logarithmic scale resulting from the ten fMRI sessions of the first subject, Figure SI-2: empirical probability distributions of the links of the three matrices in semi-logarithmic scale resulting from the ten fMRI sessions of the second subject, Figure SI-3: error bars (mean and std) of modularity index Q over the 1000 iterations of the Louvain algorithm for the optimum resolution value for the three functional networks for all the sessions of the second subject, Figure SI-4: NMI values resulting from the comparisons between each couple of network partitions for all fMRI sessions of the second subject, Figure SI-5: the functional modules detected in the three networks for the second subject, Figure SI-6: upper percentile of the distribution of participation coefficient P for the three networks and all the fMRI sections of the second subject. Table SI-1: Abbreviation of hub regions with the macro regions in which they are located and their roles for the three functional connectivity networks.
Author Contributions
Conceptualization, A.L. and S.T.; data curation, A.L.; investigation, A.L.; software, A.L.; writing—original draft preparation, A.L.; methodology, A.L., S.T. and R.B.; formal analysis A.L.; visualization, A.L.; resources, D.D.; supervision, R.B. and S.T.; validation, all authors; writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This paper has been partially supported by the Apulian regional INNONETWORK project SINACH (Sistemi Integrati di Navigazione per Chirurgia Mini Invasiva), project code BNLGWP7.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Synchronization approach to analysis of biological systems. Fluct. Noise Lett. 2004, 4, L53–L62. [Google Scholar] [CrossRef]
- Zou, Y.; Donner, R.V.; Marwan, N.; Donges, J.F.; Kurths, J. Complex network approaches to nonlinear time series analysis. Phys. Rep. 2019, 787, 1–97. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.; Zhou, C. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Faure, P.; Korn, H. Is there chaos in the brain? I. Concepts of nonlinear dynamics and methods of investigation. Comptes Rendus de l’Académie des Sciences-Series III-Sciences de la Vie 2001, 324, 773–793. [Google Scholar] [CrossRef]
- Stephan, K.E.; Kasper, L.; Harrison, L.M.; Daunizeau, J.; den Ouden, H.E.; Breakspear, M.; Friston, K.J. Nonlinear dynamic causal models for fMRI. Neuroimage 2008, 42, 649–662. [Google Scholar] [CrossRef]
- Rabinovich, M.I.; Muezzinoglu, M. Nonlinear dynamics of the brain: emotion and cognition. Phys. Uspekhi 2010, 53, 357. [Google Scholar] [CrossRef]
- Amoroso, N.; La Rocca, M.; Bruno, S.; Maggipinto, T.; Monaco, A.; Bellotti, R.; Tangaro, S. Multiplex networks for early diagnosis of Alzheimer’s disease. Front. Aging Neurosci. 2018, 10, 365. [Google Scholar] [CrossRef]
- Lella, E.; Amoroso, N.; Lombardi, A.; Maggipinto, T.; Tangaro, S.; Bellotti, R.; Initiative, A.D.N. Communicability disruption in Alzheimer’s disease connectivity networks. J. Complex Netw. 2019, 7, 83–100. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Jahanshad, N.; Lenglet, C.; McMahon, K.L.; De Zubicaray, G.I.; Martin, N.G.; Wright, M.J.; Thompson, P.M.; Sapiro, G. Hierarchical topological network analysis of anatomical human brain connectivity and differences related to sex and kinship. Neuroimage 2012, 59, 3784–3804. [Google Scholar] [CrossRef]
- Ellis, C.T.; Lesnick, M.; Henselman-Petrusek, G.; Keller, B.; Cohen, J.D. Feasibility of topological data analysis for event-related fMRI. Netw. Neurosci. 2019, 3, 695–706. [Google Scholar] [CrossRef]
- Bernstein, A.; Burnaev, E.; Sharaev, M.; Kondrateva, E.; Kachan, O. Topological data analysis in computer vision. In Proceedings of the Twelfth International Conference on Machine Vision (ICMV 2019), Amsterdam, The Netherlands, 16–18 November 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11433, p. 114332. [Google Scholar]
- Bullmore, E.; Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Stam, C. Characterization of anatomical and functional connectivity in the brain: a complex networks perspective. Int. J. Psychophysiol. 2010, 77, 186–194. [Google Scholar] [CrossRef] [PubMed]
- Callicott, J.H.; Mattay, V.S.; Bertolino, A.; Finn, K.; Coppola, R.; Frank, J.A.; Goldberg, T.E.; Weinberger, D.R. Physiological characteristics of capacity constraints in working memory as revealed by functional MRI. Cereb. Cortex 1999, 9, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Van Den Heuvel, M.P.; Pol, H.E.H. Exploring the brain network: a review on resting-state fMRI functional connectivity. Eur. Neuropsychopharmacol. 2010, 20, 519–534. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Functional and effective connectivity: A review. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef] [PubMed]
- Fiecas, M.; Ombao, H.; Van Lunen, D.; Baumgartner, R.; Coimbra, A.; Feng, D. Quantifying temporal correlations: A test–retest evaluation of functional connectivity in resting-state fMRI. NeuroImage 2013, 65, 231–241. [Google Scholar] [CrossRef]
- Freeman, W.J.; Holmes, M.D.; Burke, B.C.; Vanhatalo, S. Spatial spectra of scalp EEG and EMG from awake humans. Clin. Neurophysiol. 2003, 114, 1053–1068. [Google Scholar] [CrossRef]
- Mumtaz, W.; Ali, S.S.A.; Yasin, M.A.M.; Malik, A.S. A machine learning framework involving EEG-based functional connectivity to diagnose major depressive disorder (MDD). Med. Biol. Eng. Comput. 2018, 56, 233–246. [Google Scholar] [CrossRef]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. Neuroimage 2003, 19, 1273–1302. [Google Scholar] [CrossRef]
- Runge, J.; Heitzig, J.; Marwan, N.; Kurths, J. Quantifying causal coupling strength: A lag-specific measure for multivariate time series related to transfer entropy. Phys. Rev. E 2012, 86, 061121. [Google Scholar] [CrossRef]
- Lombardi, A.; Tangaro, S.; Bellotti, R.; Bertolino, A.; Blasi, G.; Pergola, G.; Taurisano, P.; Guaragnella, C. A novel synchronization-based approach for functional connectivity analysis. Complexity 2017, 2017, 7190758. [Google Scholar] [CrossRef]
- Lombardi, A.; Lella, E.; Diacono, D.; Amoroso, N.; Monaco, A.; Bellotti, R.; Tangaro, S. Cross Recurrence Quantitative Analysis of Functional Magnetic Resonance Imaging. In Image Processing; Lecture Notes in Computational Vision and Biomechanics 34; Springer: Berlin/Heidelberg, Germany, 2019; pp. 86–92. [Google Scholar]
- Lombardi, A.; Amoroso, N.; Diacono, D.; Lella, E.; Bellotti, R.; Tangaro, S. Age related topological analysis of synchronization-based functional connectivity. In Proceedings of the International Conference on Complex Networks and Their Applications, Cambridge, UK, 11–13 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 652–662. [Google Scholar]
- Lombardi, A.; Guaragnella, C.; Amoroso, N.; Monaco, A.; Fazio, L.; Taurisano, P.; Pergola, G.; Blasi, G.; Bertolino, A.; Bellotti, R.; et al. Modelling cognitive loads in schizophrenia by means of new functional dynamic indexes. NeuroImage 2019, 195, 150–164. [Google Scholar] [CrossRef]
- Smitha, K.; Akhil Raja, K.; Arun, K.; Rajesh, P.; Thomas, B.; Kapilamoorthy, T.; Kesavadas, C. Resting state fMRI: A review on methods in resting state connectivity analysis and resting state networks. Neuroradiol. J. 2017, 30, 305–317. [Google Scholar] [CrossRef] [PubMed]
- Van Den Heuvel, M.P.; Sporns, O. Rich-club organization of the human connectome. J. Neurosci. 2011, 31, 15775–15786. [Google Scholar] [CrossRef] [PubMed]
- Harriger, L.; Van Den Heuvel, M.P.; Sporns, O. Rich club organization of macaque cerebral cortex and its role in network communication. PLoS ONE 2012, 7, e46497. [Google Scholar] [CrossRef] [PubMed]
- van den Heuvel, M.P.; Kahn, R.S.; Goñi, J.; Sporns, O. High-cost, high-capacity backbone for global brain communication. Proc. Natl. Acad. Sci. USA 2012, 109, 11372–11377. [Google Scholar] [CrossRef]
- Fulcher, B.D.; Fornito, A. A transcriptional signature of hub connectivity in the mouse connectome. Proc. Natl. Acad. Sci. USA 2016, 113, 1435–1440. [Google Scholar] [CrossRef]
- Mišić, B.; Sporns, O.; McIntosh, A.R. Communication efficiency and congestion of signal traffic in large-scale brain networks. PLoS Comput. Biol. 2014, 10, e1003427. [Google Scholar] [CrossRef]
- Fornito, A.; Bullmore, E.T. Reconciling abnormalities of brain network structure and function in schizophrenia. Curr. Opin. Neurobiol. 2015, 30, 44–50. [Google Scholar] [CrossRef]
- Fornito, A.; Zalesky, A.; Breakspear, M. The connectomics of brain disorders. Nat. Rev. Neurosci. 2015, 16, 159–172. [Google Scholar] [CrossRef]
- Dubois, J.; Adolphs, R. Building a science of individual differences from fMRI. Trends Cogn. Sci. 2016, 20, 425–443. [Google Scholar] [CrossRef] [PubMed]
- Oliver, I.; Hlinka, J.; Kopal, J.; Davidsen, J. Quantifying the Variability in Resting-State Networks. Entropy 2019, 21, 882. [Google Scholar] [CrossRef]
- Zuo, X.N.; Anderson, J.S.; Bellec, P.; Birn, R.M.; Biswal, B.B.; Blautzik, J.; Breitner, J.C.; Buckner, R.L.; Calhoun, V.D.; Castellanos, F.X.; et al. An open science resource for establishing reliability and reproducibility in functional connectomics. Sci. Data 2014, 1, 140049. [Google Scholar] [CrossRef] [PubMed]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazoyer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002, 15, 273–289. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403. [Google Scholar] [CrossRef]
- Marwan, N.; Kurths, J. Nonlinear analysis of bivariate data with cross recurrence plots. Phys. Lett. A 2002, 302, 299–307. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Marwan, N.; Thiel, M.; Nowaczyk, N.R. Cross recurrence plot based synchronization of time series. arXiv 2002, arXiv:physics/0201062. [Google Scholar]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Alexander-Bloch, A.; Lambiotte, R.; Roberts, B.; Giedd, J.; Gogtay, N.; Bullmore, E. The discovery of population differences in network community structure: new methods and applications to brain functional networks in schizophrenia. Neuroimage 2012, 59, 3889–3900. [Google Scholar] [CrossRef] [PubMed]
- Kuncheva, L.I.; Hadjitodorov, S.T. Using diversity in cluster ensembles. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No. 04CH37583), The Hague, The Netherlands, 10–13 October 2004; Volume 2, pp. 1214–1219. [Google Scholar]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Guimera, R.; Amaral, L.A.N. Functional cartography of complex metabolic networks. Nature 2005, 433, 895–900. [Google Scholar] [CrossRef]
- Hilger, K.; Ekman, M.; Fiebach, C.J.; Basten, U. Intelligence is associated with the modular structure of intrinsic brain networks. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef]
- Bertolero, M.A.; Yeo, B.T.; Bassett, D.S.; D’Esposito, M. A mechanistic model of connector hubs, modularity and cognition. Nat. Hum. Behav. 2018, 2, 765–777. [Google Scholar] [CrossRef]
- Braun, U.; Schäfer, A.; Walter, H.; Erk, S.; Romanczuk-Seiferth, N.; Haddad, L.; Schweiger, J.I.; Grimm, O.; Heinz, A.; Tost, H.; et al. Dynamic reconfiguration of frontal brain networks during executive cognition in humans. Proc. Natl. Acad. Sci. USA 2015, 112, 11678–11683. [Google Scholar] [CrossRef]
- Buckner, R.L.; Andrews-Hanna, J.R.; Schacter, D.L. The brain’s default network: Anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 2008, 1124, 1–38. [Google Scholar] [CrossRef]
- Thomas Yeo, B.; Krienen, F.M.; Sepulcre, J.; Sabuncu, M.R.; Lashkari, D.; Hollinshead, M.; Roffman, J.L.; Smoller, J.W.; Zöllei, L.; Polimeni, J.R.; et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 2011, 106, 1125–1165. [Google Scholar] [CrossRef]
- van den Heuvel, M.P.; Sporns, O. Network hubs in the human brain. Trends Cogn. Sci. 2013, 17, 683–696. [Google Scholar] [CrossRef]
- van den Heuvel, M.I.; Turk, E.; Manning, J.H.; Hect, J.; Hernandez-Andrade, E.; Hassan, S.S.; Romero, R.; van den Heuvel, M.P.; Thomason, M.E. Hubs in the human fetal brain network. Dev. Cogn. Neurosci. 2018, 30, 108–115. [Google Scholar] [CrossRef] [PubMed]
- Oldham, S.; Fornito, A. The development of brain network hubs. Dev. Cogn. Neurosci. 2019, 36, 100607. [Google Scholar] [CrossRef] [PubMed]
- Buckner, R.L.; Krienen, F.M.; Castellanos, A.; Diaz, J.C.; Yeo, B.T. The organization of the human cerebellum estimated by intrinsic functional connectivity. J. Neurophysiol. 2011, 106, 2322–2345. [Google Scholar] [CrossRef] [PubMed]
- Power, J.D.; Schlaggar, B.L.; Lessov-Schlaggar, C.N.; Petersen, S.E. Evidence for hubs in human functional brain networks. Neuron 2013, 79, 798–813. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O.; Honey, C.J.; Kötter, R. Identification and classification of hubs in brain networks. PLoS ONE 2007, 2, e1049. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).