Application of Solution Strategies for Numerical Estimation of Thermodynamic Equilibrium Parameters for an Acetone–Butanol Mixture
Abstract
1. Introduction
2. Materials and Methods
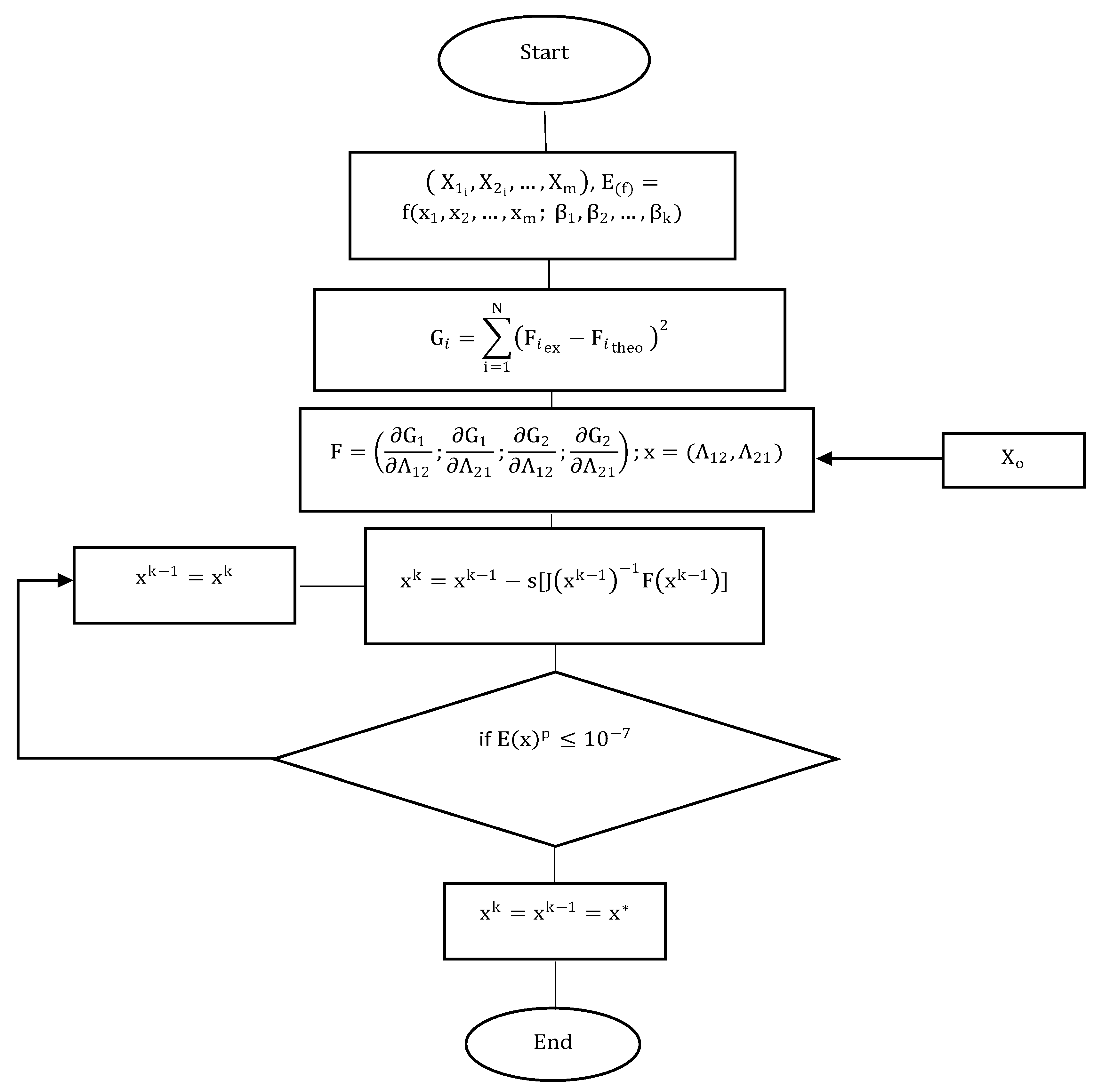
2.1. Newton’s Method
2.2. Broyden’s Method
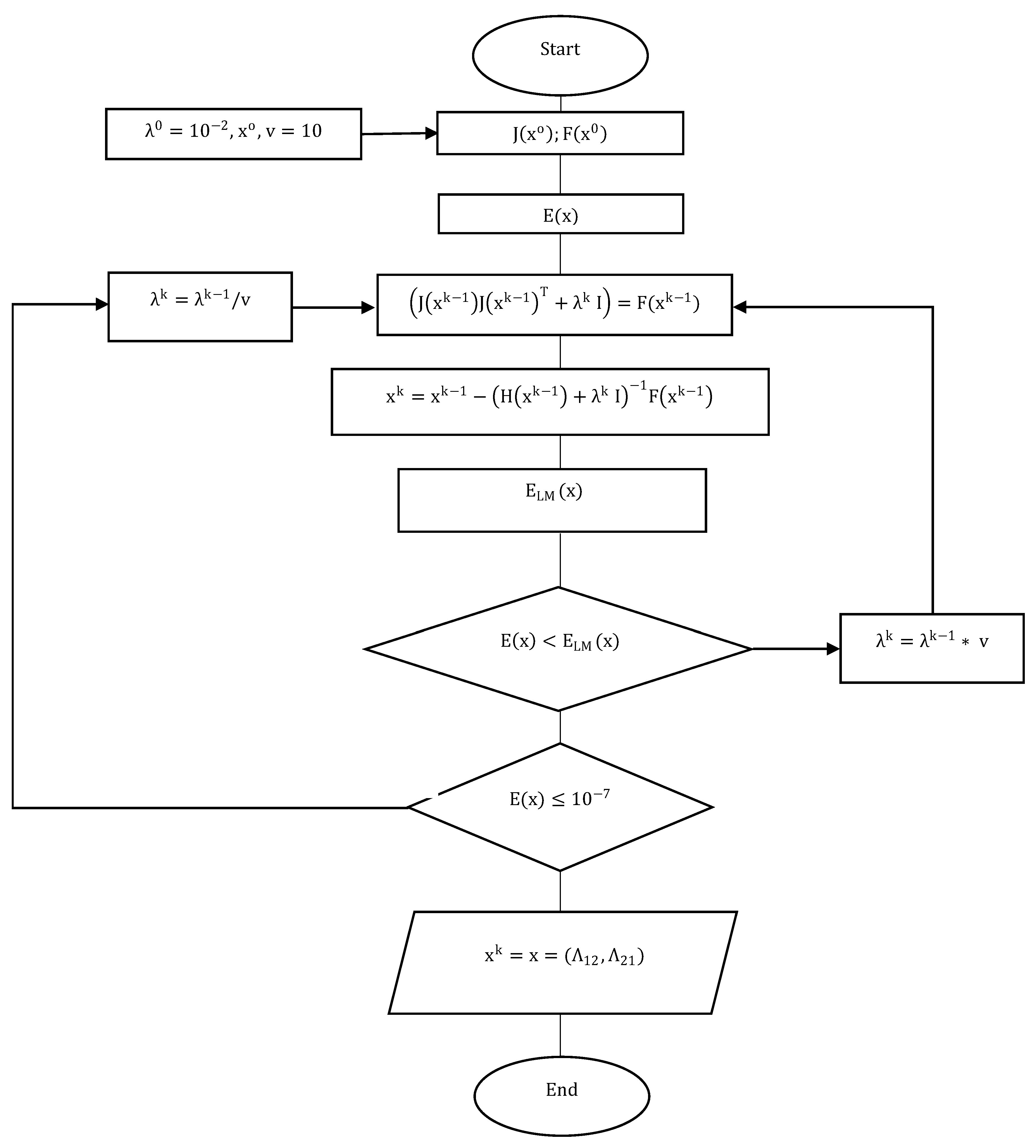
2.3. Levenberg–Marquardt Method
3. Results
3.1. Estimation of Thermodynamic Properties and Parameters
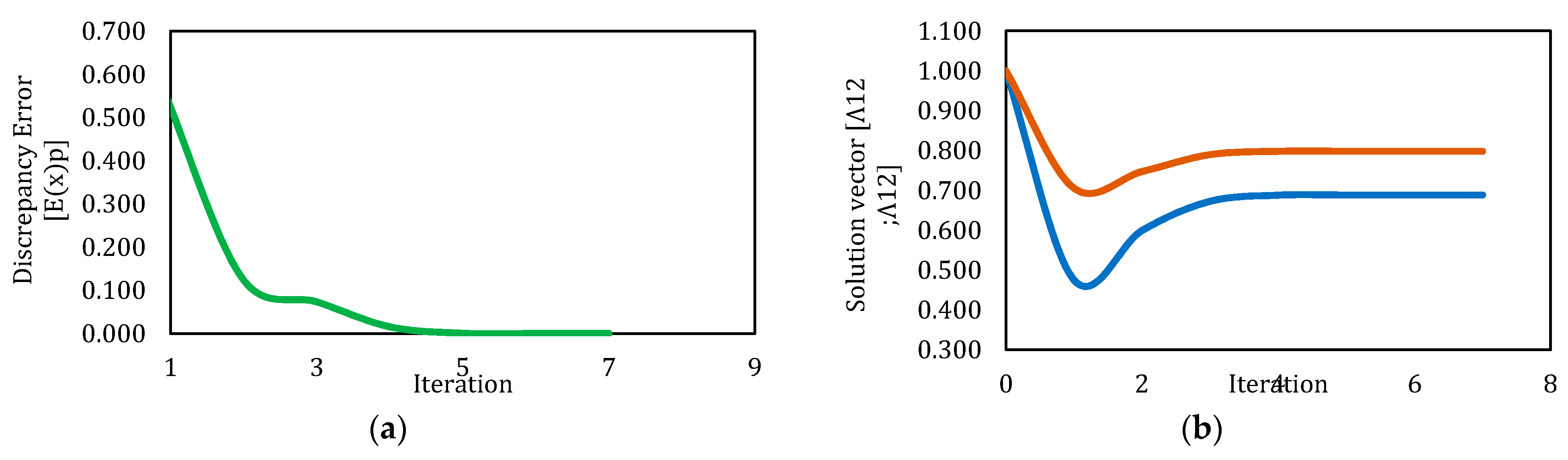
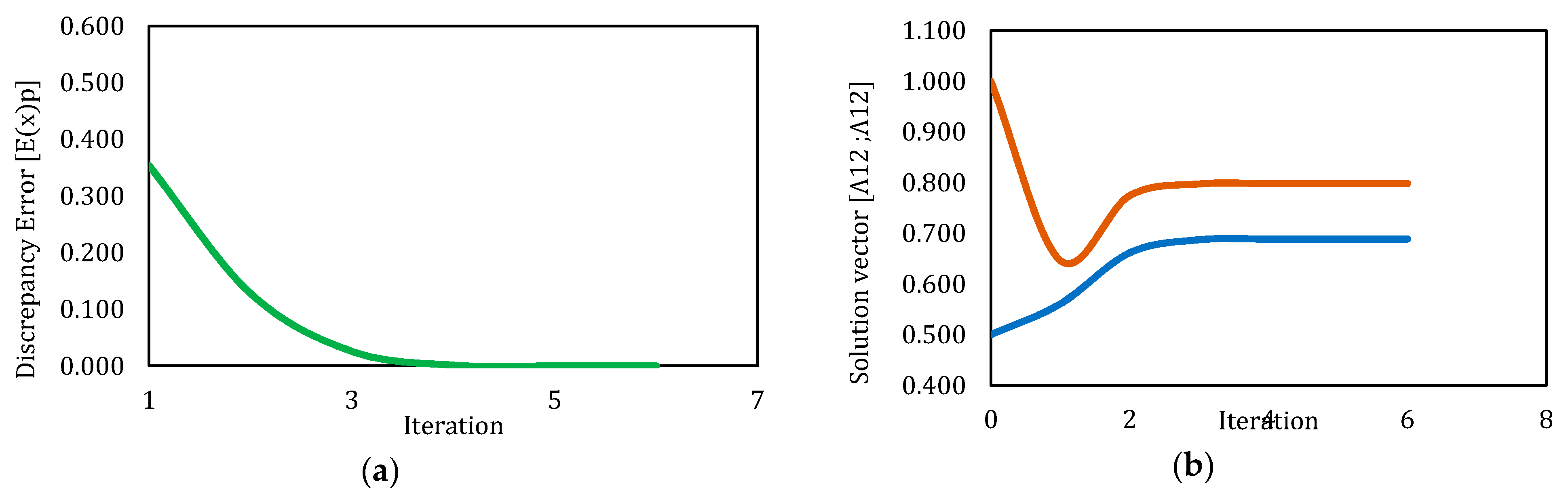
3.2. Solution by Newton’s Method
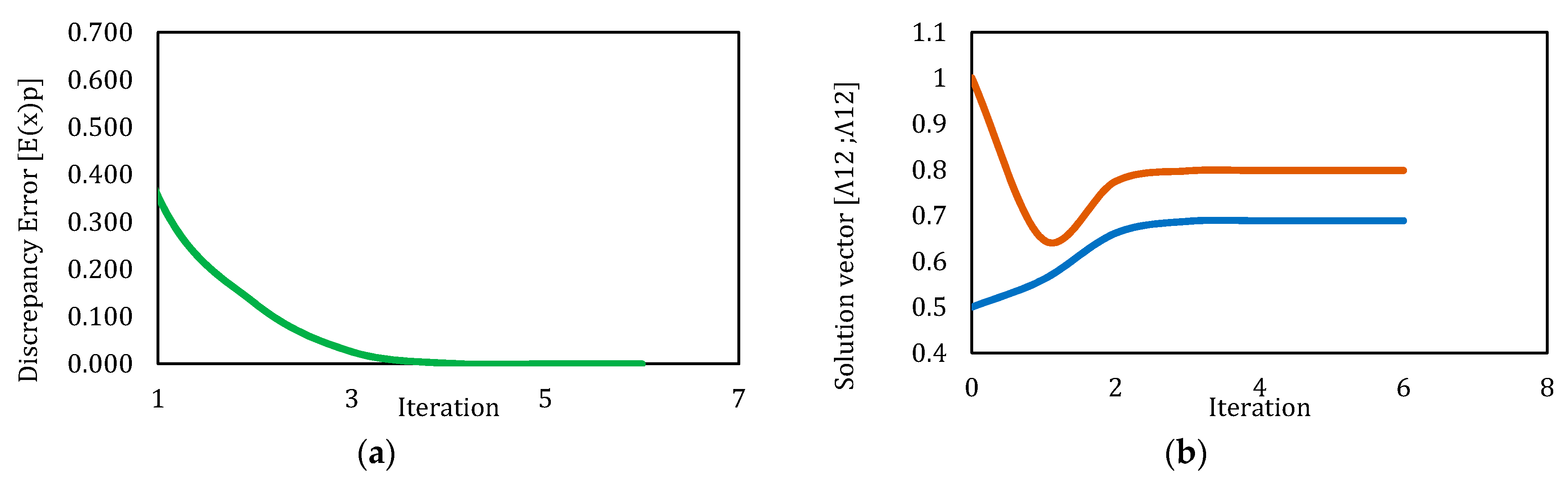
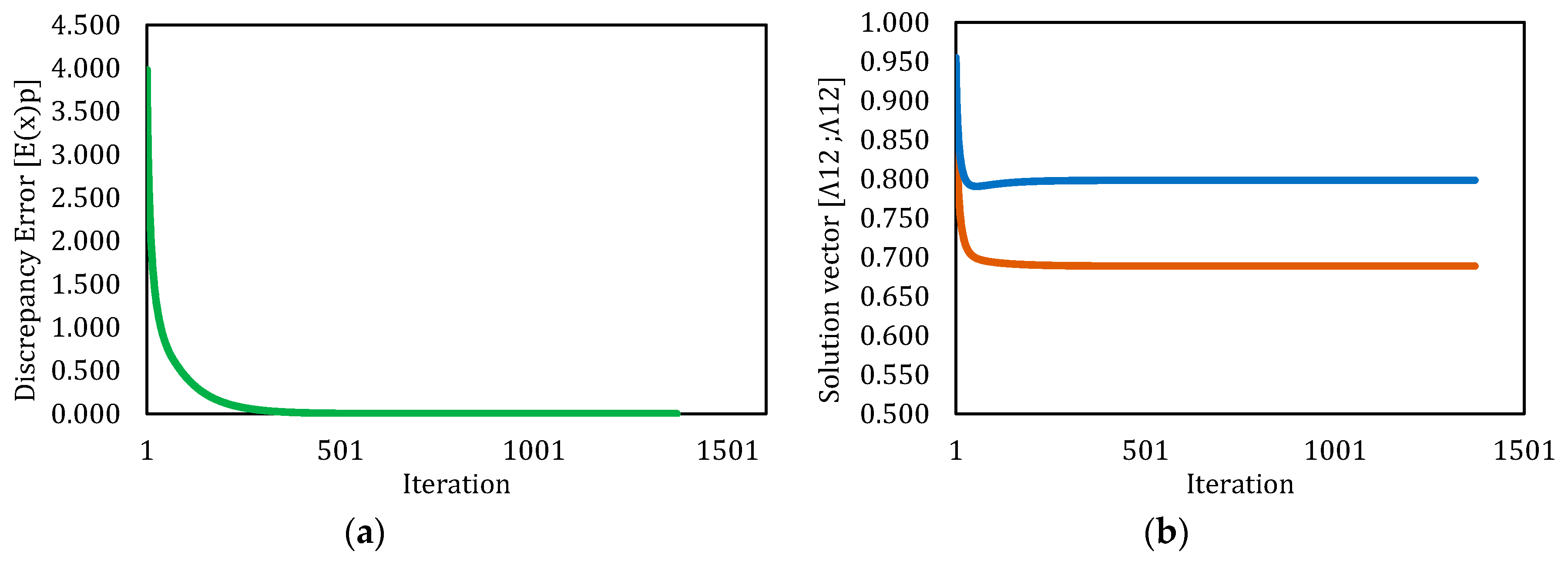
3.3. Solution by Broyden’s Method
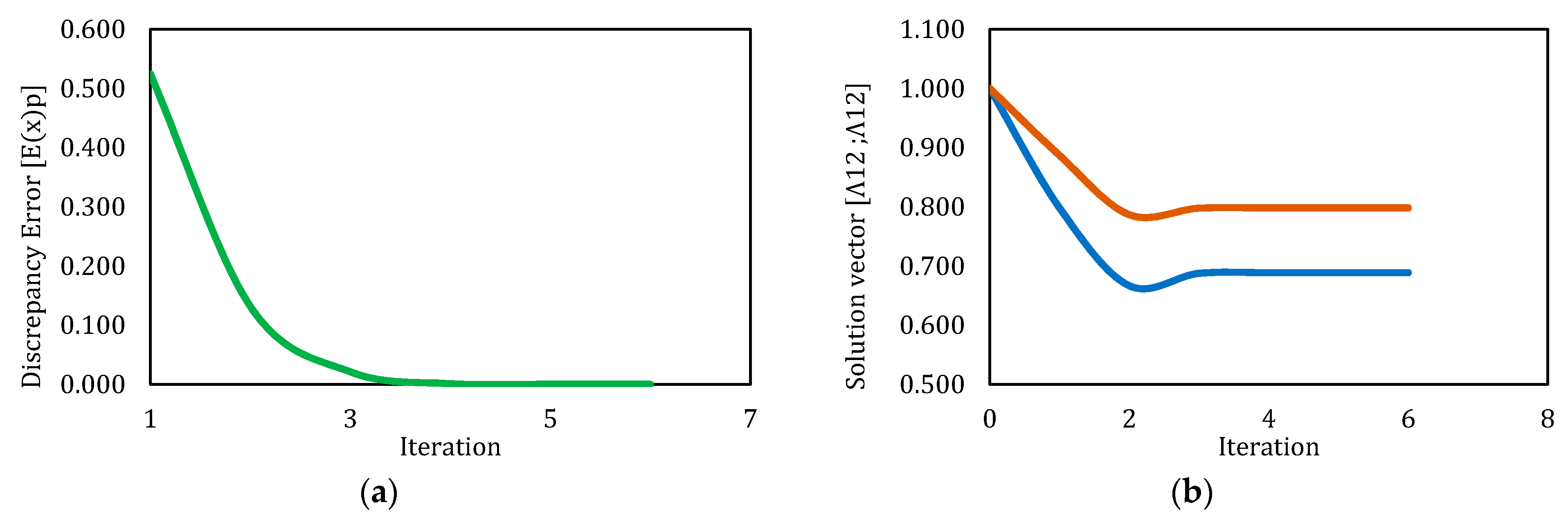
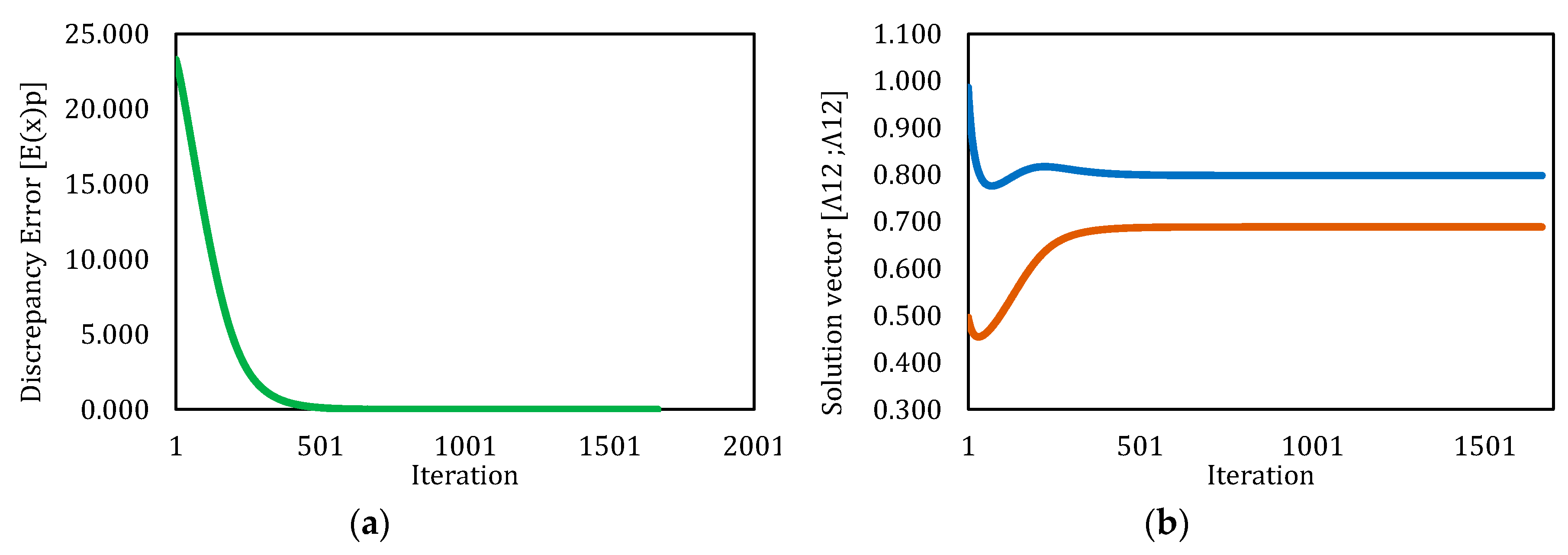
3.4. Solution by Levenberg–Marquardt Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ojeda, K.; Sanchez, E.; Kafarov, V. Sustainable ethanol production from lignocellulosic biomass—Application of exergy analysis. Energy 2011, 36, 2119–2128. [Google Scholar] [CrossRef]
- Zoder, M.; Balke, J.; Hofmann, M.; Tsatsaronis, G. Simulation and Exergy Analysis of Energy Conversion Processes Using a Free and Open-Source Framework—Python-Based Object-Oriented Programming for Gas- and Steam Turbine Cycles. Energies 2018, 11, 2609. [Google Scholar] [CrossRef]
- Elmeligy, A.; Mehrani, P.; Thibault, J. Artificial neural networks as metamodels for the multiobjective optimization of biobutanol production. Appl. Sci. 2018, 8, 961. [Google Scholar] [CrossRef]
- Carlson, E.C. Don ’ t Gamble With Physical Properties. Chem. Eng. Process. 1996, 92, 35–46. [Google Scholar]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introducción a la Termodinámica en Ingeniería Química; Mexico, D.F., Ed.; McGraw Hill: New York, NY, USA, 1997; 876p. [Google Scholar]
- Markočič, E.; Knez, Ž. Redlich-Kwong equation of state for modelling the solubility of methane in water over a wide range of pressures and temperatures. Fluid Phase Equilib. 2016, 408, 108–114. [Google Scholar] [CrossRef]
- Bader, A.; Keller, P.; Hasse, C. The influence of non-ideal vapor-liquid equilibrium on the evaporation of ethanol/iso-octane droplets. Int. J. Heat Mass Transf. 2013, 64, 547–558. [Google Scholar] [CrossRef]
- Galeotti, N.; Burger, J.; Hasse, H. Vapor-liquid equilibrium in the ternary systems acetic acid + water + (xylose or glucose). Fluid Phase Equilib. 2018, 473, 323–329. [Google Scholar] [CrossRef]
- Kobuchi, S.; Ishige, K.; Yonezawa, S.; Fukuchi, K.; Arai, Y. Correlation of vapor-liquid equilibria of polar mixtures by using wilson equation with parameters estimated from solubility parameters and molar volumes. J. Chem Eng. Japan. 2011, 44, 449–454. [Google Scholar] [CrossRef]
- Kamiński, W.; Górak, A.; Kubiczek, A. Modeling of liquid-liquid equilibrium in the quinary system of water, acetone, n-butanol, ethanol, and ionic liquid. Fluid Phase Equilib. 2014, 384, 114–121. [Google Scholar] [CrossRef]
- Abderafi, S.; Bounahmidi, T. Measurement and estimation of vapor-liquid equilibrium for industrial sugar juice using the Peng-Robinson equation of state. Fluid Phase Equilib. 1999, 162, 225–240. [Google Scholar] [CrossRef]
- Chandra, A.; Keblinski, P.; Sahni, O.; Oberai, A.A. A continuum framework for modeling liquid-vapor interfaces out of local thermal equilibrium. Int. J. Heat Mass Transf. 2019, 144, 118597. [Google Scholar] [CrossRef]
- Arteaga-Díaz, S.J.; Meramo-Hurtado, S.I.; León-Pulido, J.; Zuorro, A.; González-Delgado, A.D. Environmental Assessment of Large Scale Production of Magnetite (Fe3O4) Nanoparticles via Coprecipitation. Appl. Sci. 2019, 9, 1682. [Google Scholar] [CrossRef]
- Skogestad, S. Entropy and Equilibrium. In Chemical and Energy Process Engineering; Taylor and Francis: Milton Park, UK, 2009; pp. 179–196. [Google Scholar]
- Jabbari, M.; Soltanpour, Z.; Nabavi-Amri, S.A. Measurement and thermodynamic analysis of the acid-base equilibria of two bioactive flavanone glycosides in different temperatures and non-aqueous mixtures. J. Mol. Liq. 2017, 248, 7–12. [Google Scholar] [CrossRef]
- Montazeri, H.; Soleymani, F.; Shateyi, S.; Motsa, S.S. On a new method for computing the numerical solution of systems of nonlinear equations. J. Appl Math. 2012. [Google Scholar] [CrossRef]
- Dyke, V.; Liao, S. Introduction. In Homotopy Analysis Method in Nonlinear Differential Equations; Springer International Publishing: Cham, Switzerland, 2012; pp. 2–14. [Google Scholar]
- Mirzaee, M.M.; Zolfaghari, A.; Minuchehr, A.; Aghaie, M. A drift-flux analysis of the diversely heated channel using the Broyden method. Appl. Therm. Eng. 2019, 150, 464–481. [Google Scholar] [CrossRef]
- Shaw, S.; Mukhopadhyay, B. An improved Regula falsi method for finding simple roots of nonlinear equations. Appl. Math. Comput. 2015, 254, 370–374. [Google Scholar] [CrossRef]
- Kreyszig, E.; Kreyszig, H.; Norminton, E. Advanced Engineering Mathematics, 10th ed.; John Wiley & Sons: Danvers, MA, USA, 2011; 1094p. [Google Scholar]
- Smith, M.R.; Lin, Y.H. Analysis of the convergence properties for a non-linear implicit Equilibrium Flux Method using Quasi Newton–Raphson and BiCGStab techniques. Comput Math. Appl. 2016, 72, 2008–2019. [Google Scholar] [CrossRef]
- Aslam Noor, M.; Waseem, M. Some iterative methods for solving a system of nonlinear equations. Comput Math. Appl. 2009, 57, 101–106. [Google Scholar] [CrossRef]
- Mamat, M.; Ramli, A.; Abdullah, M.L. Broyden’s method for solving fuzzy nonlinear equations. In Advances in Fuzzy Systems; Hindawi: London, UK, 2010. [Google Scholar]
- Sharif Ahmadian, A. Numerical Methods and Procedures. In Numerical Models for Submerged Breakw|Aters; Elsevier Ltd.: Oxford, UK, 2016; pp. 93–108. [Google Scholar]
- Amador, S.; El-Kafafy, M.; Cunha, Á.; Brincker, R. A New Maximum Likelihood Estimator Formulated in Pole-Residue Modal Model. Appl. Sci. 2019, 9, 3120. [Google Scholar] [CrossRef]
- Mangili, P.V.; Prata, D.M. Improvement of the butyl acetate process through heat integration: A sustainability-based assessment. Chem. Eng. Process. Process. Intensif. 2019, 135, 93–107. [Google Scholar] [CrossRef]
- Dojčanský, J.; Bafrncová, S.; Surový, J. Application of the Wilson equation with binary parameters to the prediction of the isothermal vapour-liquid equilibrium data of ternary and quaternary systems in the assessment of the polar solvent in extractive distillation. Chem. Pap. 2001, 55, 71–74. [Google Scholar]
- Puig-Arnavat, M.; Bruno, J.C. Artificial Neural Networks for Thermochemical Conversion of Biomass. In Recent Adv Thermochem Convers Biomass; Elsevier: Amsterdam, The Netherlands, 2015; pp. 133–156. [Google Scholar]
- Jabri, M.; Jerbi, H. Comparative study between Levenberg Marquardt and genetic algorithm for parameter optimization of an electrical system. In IFAC Proceedings Volumes (IFAC-PapersOnline); IFAC: Geneva, Switzerland, 2009; pp. 77–82. [Google Scholar] [CrossRef]
- Antonio, J.; Lobo, C. Equilibrio líquido-vapor para el sistema cuaternario Agua-Acetona-Butanol-Etanol a Presiones Bajas Liquid-vapor equilibrium for the Water-Acetone-Butanol- Ethanol quaternary system at Low Pressures. Cienc en Desarro. 2019, 10, 103–116. [Google Scholar]
- Darkwah, K.; Knutson, B.L.; Seay, J.R. A Perspective on Challenges and Prospects for Applying Process Systems Engineering Tools to Fermentation-Based Biorefineries. ACS Sustain Chem Eng. 2018, 6, 2829–2844. [Google Scholar] [CrossRef]
- Dumitrescu, A.M.; Banu, I.; Bumbac, G. Process modeling and simulation for butanol removing from fermentation broth by extraction with biodiesel. Renew. Energy 2019, 131, 137–143. [Google Scholar] [CrossRef]


| Pressure (P/kPa) | x1 | y1 |
|---|---|---|
| 46.38 | 0.000 | 0.000 |
| 50.70 | 0.018 | 0.093 |
| 51.29 | 0.020 | 0.107 |
| 55.18 | 0.036 | 0.175 |
| 59.50 | 0.063 | 0.270 |
| 60.18 | 0.057 | 0.258 |
| 67.19 | 0.089 | 0.355 |
| 78.01 | 0.141 | 0.469 |
| 80.26 | 0.151 | 0.489 |
| 82.06 | 0.166 | 0.513 |
| 92.24 | 0.214 | 0.576 |
| 98.57 | 0.247 | 0.621 |
| 129.30 | 0.440 | 0.761 |
| 145.50 | 0.541 | 0.820 |
| 160.20 | 0.632 | 0.859 |
| 174.80 | 0.762 | 0.916 |
| 185.10 | 0.829 | 0.943 |
| 190.50 | 0.864 | 0.956 |
| 202.60 | 0.937 | 0.981 |
| 203.40 | 0.943 | 0.983 |
| 213.80 | 1.000 | 1.000 |
| Component | Tc (K) | Pc (kPa) | ω | Psat (kPa) | Bii |
|---|---|---|---|---|---|
| Acetone | 508.10 | 4700 | 0.307 | 212.06 1 | −0.873 |
| Butanol | 536.05 | 4179 | 0.594 | 46.26 1 | −1.247 |
| ɸ1 | ɸ2 | γ1 | γ2 |
|---|---|---|---|
| 1.052 | 1.000 | - | 1.052 |
| 1.050 | 0.998 | 1.287 | 1.060 |
| 1.050 | 0.998 | 1.348 | 1.058 |
| 1.049 | 0.996 | 1.316 | 1.068 |
| 1.047 | 0.994 | 1.249 | 1.047 |
| 1.047 | 0.994 | 1.334 | 1.069 |
| 1.045 | 0.991 | 1.310 | 1.072 |
| 1.041 | 0.987 | 1.264 | 1.083 |
| 1.041 | 0.986 | 1.265 | 1.084 |
| 1.040 | 0.985 | 1.234 | 1.075 |
| 1.037 | 0.981 | 1.204 | 1.113 |
| 1.035 | 0.979 | 1.200 | 1.107 |
| 1.026 | 0.966 | 1.073 | 1.220 |
| 1.021 | 0.960 | 1.053 | 1.256 |
| 1.016 | 0.954 | 1.035 | 1.345 |
| 1.012 | 0.949 | 0.994 | 1.346 |
| 1.009 | 0.945 | 0.993 | 1.342 |
| 1.007 | 0.943 | 0.993 | 1.338 |
| 1.003 | 0.938 | 0.995 | 1.322 |
| 1.003 | 0.938 | 0.995 | 1.312 |
| 1.000 | 0.934 | 1.000 | - |
| Simulation | Initial Λ12 | Initial Λ21 | Final Λ12 | Final Λ21 | No Iterations | CT (s) | Final Error | Converged |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.000 | 5.000 | NaN | NaN | 101 | 11.390 | NaN | No |
| 2 | 1.000 | 1.000 | 0.689 | 0.798 | 7 | 7.578 | 9.65 × 10−13 | Yes |
| 3 | 0.500 | 1.000 | 0.689 | 0.798 | 6 | 4.593 | 2.50 × 10−11 | Yes |
| Simulation | Initial Λ12 | Initial Λ21 | Final Λ12 | Final Λ21 | No Iterations | CT (s) | Final Error | Converged |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.000 | 5.000 | 0.689 | 0.798 | 21 | 5.591 | 1.31 × 10−13 | Yes |
| 2 | 1.000 | 1.000 | 0.689 | 0.798 | 6 | 4.950 | 1.22 × 10−11 | Yes |
| 3 | 0.500 | 1.000 | 0.689 | 0.798 | 6 | 4.263 | 2.50 × 10−11 | Yes |
| Simulation | Initial Λ12 | Initial Λ21 | Final Λ12 | Final Λ21 | No Iterations | CT (s) | Final Error | Converged |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.000 | 5.000 | NaN | NaN | 312 | 24.171 | NaN | No |
| 2 | 1.000 | 1.000 | 0.689 | 0.798 | 1370 | 94.312 | 9.92 × 10−8 | Yes |
| 3 | 0.500 | 1.000 | 0.689 | 0.798 | 1667 | 4.263 | 9.99 × 10−8 | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meramo-Hurtado, S.; Puello, P.; Rodriguez, J. Application of Solution Strategies for Numerical Estimation of Thermodynamic Equilibrium Parameters for an Acetone–Butanol Mixture. Appl. Sci. 2020, 10, 3136. https://doi.org/10.3390/app10093136
Meramo-Hurtado S, Puello P, Rodriguez J. Application of Solution Strategies for Numerical Estimation of Thermodynamic Equilibrium Parameters for an Acetone–Butanol Mixture. Applied Sciences. 2020; 10(9):3136. https://doi.org/10.3390/app10093136
Chicago/Turabian StyleMeramo-Hurtado, Samir, Plinio Puello, and Julio Rodriguez. 2020. "Application of Solution Strategies for Numerical Estimation of Thermodynamic Equilibrium Parameters for an Acetone–Butanol Mixture" Applied Sciences 10, no. 9: 3136. https://doi.org/10.3390/app10093136
APA StyleMeramo-Hurtado, S., Puello, P., & Rodriguez, J. (2020). Application of Solution Strategies for Numerical Estimation of Thermodynamic Equilibrium Parameters for an Acetone–Butanol Mixture. Applied Sciences, 10(9), 3136. https://doi.org/10.3390/app10093136






